Формулы перестановки сочетания размещения: Перестановки, размещения и сочетания. Формулы.

Формулы комбинаторики — Дискретная математика (Математика)

2.1. Формулы комбинаторики

2.1.1. Перестановки    

1) Перестановки без повторений.

Перестановки — это комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком расположения этих элементов. Возьмем n различных элементов a₁, a₂, a₃, … a_n; будем переставлять эти элементы всевозможными способами, оставляя без изменения число элементов и меняя только порядок их расположения. Обозначим общее число полученных таким образом перестановок P(n). P — первая буква французского слова permutation — перестановка.

Составив таблицу перестановок для n элементов и применив (n — 1) раз правило произведения, получим число всех возможных перестановок:

P(n) = n • (n -1) • (n — 2) • … • 3 • 2 • 1 = n!

Такие перестановки называются перестановками без повторений (один и тот же элемент не может повториться в комбинации, все элементы различны).

Задача: шесть человек могут в разном порядке сесть за круглый стол, сколько существует способов разместить эти шесть человек за столом?

Решение: т.к. все люди различны и  их комбинации различаются только порядком следования, то мы имеем перестановки без повторений. Определим их число:

Р(6) = 6! = 1 • 2 • 3 • 4 • 5 • 6 = 720.

2) Перестановки с повторениями

Рассматривая различные перестановки, мы предполагали, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.

Если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., n_k элементов к-го вида, то имеем перестановки с повторениями, их число:

, где n₁+…+n_k = n.

Задача: сколько различных «слов» можно составить из букв слова ДЕД, МАТЕМАТИКА.

Решение: имеем перестановки с повторениями.

А) ДЕД    n=3, k=2, n₁=2, n₂=1

P₃(2, 1) = 3!/(2! • 1!) = 6 / 2 = 3;

Б) МАТЕМАТИКА n=10, k=6, n₁=2, n₂=3, n₃=2, n₄=n₅=n₆=1

P₁₀(2,3,2,1,1,1)=10!/(2! • 3! • 2!)=2•4•5•6•7•9•10 = 134 400.

2.1.2. Размещения

1) Размещения без повторений.

Размещениями называют комбинации, составленные из n данных элементов по k элементов (k<=n, k>0), которые отличаются либо составом элементов, либо порядком расположения элементов. Обозначаются размещения A_n^k . А — первая буква французского слова arrangement, что в переводе означает «размещение», «приведение в порядок». Число всех возможных размещений находится по формуле:

.

Задача: расписание одного дня состоит из двух пар. Определить число вариантов расписания при выборе из пяти дисциплин, если не может быть одинаковых пар.

Решение: имеем размещения без повторений из пяти элементов по два, из число: .

2) Размещения с повторениями.

Пусть существуют n различных элементов. Выберем из них m штук, действуя по следующему принципу: возьмем любой элемент, но не будем устанавливать его в какой-либо ряд, а просто запишем под номером 1 его название, сам же элемент вернем к остальным элементам. Затем опять из всех n элементов выберем один, запишем его название под номером 2 и снова вернем элемент обратно. Будем выполнять эти операции, пока не получим m названий. Размещения с повторениями вычисляются по формуле:

.

Задача: сколько четырехзначных номеров можно составить из 10 цифр?

Решение: имеем размещения с повторениями из 10 элементов по 4, их число: .

2.1.3. Сочетания

1) Сочетания без повторений.

Сочетаниями называют комбинации, составленные из n различных элементов по k (k =< n) элементов, которые отличаются хотя бы одним элементом. Сочетания обозначаются: C_n^k C — первая буква французского слова combinasion — сочетание.

Составим из n элементов всевозможные сочетания по k элементов в каждом. Их будет C_n^k . Внутри каждого сочетания, состоящего из k элементов, образуем всевозможные комбинации, учитывающие порядок следования в них элементов. Таких комбинаций будет P_k, т.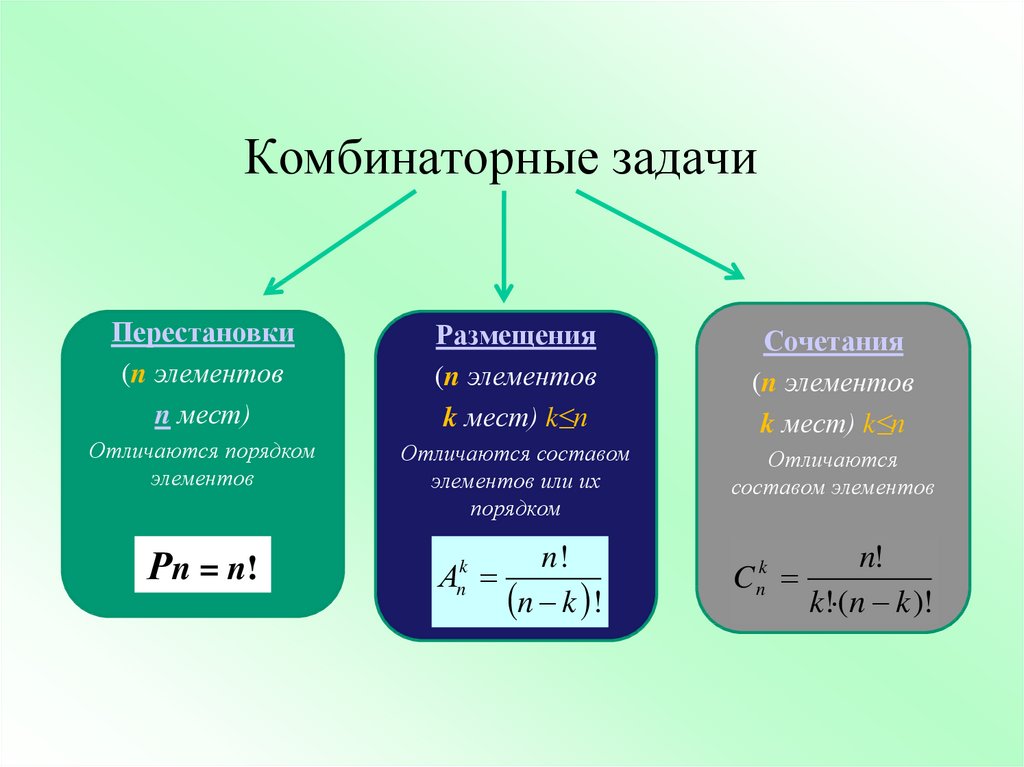 к. мы в нашем сочетании образовываем перестановки. Всего различных комбинаций из n элементов по k в каждой, отличающихся друг от друга либо составом (элементами), либо порядком их следования, будет C_n^k • P_k . Но такие комбинации называются размещениями. Таким образом, A_n^k = C_n^k • P_k, тогда:

.

Рекомендация для Вас — 4.2. Методы статистического анализа.

Задача: в шахматном турнире участвует 7 человек; сколько партий будет сыграно, если между любыми двумя участниками должна быть сыграна партия?

Решение: имеем сочетания без повторений из 7 элементов по 2; их число:  .

2) Сочетания с повторениями.

Если в сочетаниях некоторые элементы (или все) могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями. Их число определяется по формуле:                               .

Задача: сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных?

Решение: имеем сочетания с повторениями из четырех по 7 по, их число: .

Элементы комбинаторики, размещения, перестановки, сочетания. Упорядоченное множество. Случайные события, алгебра событий, формулы де Моргана

Математика \ Математика

Страницы работы

55 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

1.  Элементы комбинаторики, размещения, перестановки, сочетания.

Упорядоченное множество – это множество с заданным порядком элементов.

Правило произведения: Пусто А некоторое множество. Пусть элемент а1А можно выбрать n1 способами. После этого а2 можно выбрать n2 способами и тд. Тогда одновременный выбор а1, а2…аn можно сделать n1*n2…*nk способами/

Правило суммы: Пусто А некоторое множество. Пусть элемент а1А можно выбрать n1 способами. После этого а2 можно выбрать n2 способами и тд. Тогда выбор одного из элементов (а1 или а2 или аn) можно сделать n1+n2+…+nk способами.

Размещение из n по k: Размещением из n по k называется каждое упорядоченное подмножество из к элементов, выбранных из n элементов

Перестановка – упорядоченное множество

Сочетания – подмножестов из к элементов, выбранных во множестве из n переменных

1)            2)

2. Случайные события, алгебра событий, формулы де Моргана.

Событие – исход эксперимента

Эксперимент – создание определенного комплекса условий

Пространство событий – совокупность событий при данном эксперименте

Ø – пустое подмножество(невозможное событие)

Ω — все множество (достоверное событие)

Несовместные события – события А и В называются несовместными, если они не могут наступить вместе

Противоположные события – это совокупность событий, противоположных А. (дополнение)

Алгебра событий

А+В=АВ  wA+B ówA V wB

A·B=AB  wA·BówAwB

Свойства операций:

1)  А+В=В+А  2) А*В=В*А  3) А+ =Ω  4) А*Ω=А  5)АВ С А  6) *А= Ø  7) =А   8) А-В=А*  9)   10)

3.Классическая вероятность, теорема сложения вероятностей.

Вероятность события – это число, характеризующее возможность наступления данного события P(A)

Вероятность невозможнгого=0, а достоверного=1. Вероятность любого другого [0,1].

Классическая вероятность – это классическое пространство событий, состоящее из конечного числа элементарных событий и все они равновозможны. P(A)=na/n, где na-благоприятные исходы, n- все возможные исходы

Теорема сложения вероятностей

Если А и В два события, то вероятность их суммы P(A+B)=P(A)+P(B)-P(AB)

Для несовместных событий:

P(A+B)=P(A)+P(B)

Для 3-х: P(A)+P(B)+P(C)-P(AC)-P(AB)-P(BC)+P(ABC)

P()=1-P(A)

4.   Статистическое определение вероятности, геометрическая вероятность.

Пусть при проведении n испытаний, некоторое событие А появилось m раз.Многочисленные эксперименты такого рода показывают, что при больших n отношение m/n, называемое частостью события А, остается примерно постоянным. Статистическое определение вероятности заключается в том, что за вероятность события А принимается постоянная величина, вокруг которой колеблются значения частостей при неограниченном возрастании числа n.

Геометрическая вероятность

Обобщением классической схемы является пространство событий, элементарные исходы которого можно представить в виде точек, заполняющих некоторою область Ω в (трехмерном) пространстве в R³ . Если при этом  событию А благоприятствуют элементарные события, заполняющие некоторую подобласть D из Ω, то геометрической вероятностью события А  называется отношение объема области D к объему области Ω: P(A)=V(D)/V(Ω). Аналогично определяется геометрическая вероятность события, когда множество Ω представляет собой некоторую область на плоскости или отрезок на прямой линии. В этих случаях объемы областей заменяются , соответственно, площадями фигур или длинами отрезков.

5. Аксиоматическое определение вероятностей.

Ω={ω} —  набор элементарных событий

Рассмотрим набор подмножеств F={A/A c Ω}

Аксиома 1: Если А1, А2…Аn…  F => A1+A2+…+An+…  F

Аксиома 2:  Для любого АF =>   F

Любой набор подмножеств данного множества, обладающий свойствами 1 и 2 – σ-алгебра

Из этих аксиом следует, что произведение любого подмножества тоже принадлежит σ-алгебре.

Аксиомы вероятностей

Вероятность события АF(A c Ω) называется число  P(A), которое обладает следующими свойствами:

1)  P(Ω)=1 P(A)>=0

2)  Если семейство событий А1, А2…Аn… попарно несовместны, т. е. Ai*Aj=Ø, то вероятность суммы  P(A1+A2+…+An+…)=P(A1)+P(A2)+…+P(An)+…

Дискретное вероятностное пространство —  вероятностное пространство, в  котором пространство событий конечно или счетно, а σ-алгебра F  — множество всевозможных подмножеств дискретного множества Ω .

6.

Условные вероятности и теорема умножения.

На практике часто встречаются ситуации, когда наступление некоторого события значительно меняет возможности наступления других событий и их вероятности. Если произошло событие B, то новая вероятность события А называется условной вероятностью и обозначается P_B(A), говорят: «вероятность события А при условии B». При этом B оказывается достоверным событием и играет роль пространства элементарных событий Ω.

Условная вероятность P_B(A) определяется формулой (при P(B) >0):

P_B(A)= (1)

Из (1) следует формула:

P(A*B)= P_B(A) P(B), P(B)>0,  (2)

И симметричная формула:

P(A*B)= P_A(B)P(A), P(A)>0     (3)

Независимыми

называются такие события

Похожие материалы

Информация о работе

Скачать файл

Комбинации и перестановки – подготовка к экзамену Каплана

Давайте попрактикуемся в математике GRE. Проблемы с комбинациями и перестановками часто заставляют учащихся задуматься, с чего же начать. Знание уравнения для каждой операции полезно, но недостаточно — вы также должны быть в состоянии определить, какая формула необходима для ответа на поставленный вопрос.

Комбинации и перестановки на GRE

Эмпирическое правило состоит в том, что комбинации неупорядочены, а перестановки упорядочены, но что это значит? Нам нравится иллюстрировать разницу с помощью социального клуба.

• Представьте, что в социальном клубе 10 разных членов, и вас спросят: » Сколько групп из 3 членов вы можете выбрать из социального клуба, чтобы создать партийный комитет?
  ” Вам нужно было бы делать комбинации или перестановки, чтобы сформулировать ответ? Откуда вы знаете?
• В качестве альтернативы, представьте, что мы немного изменим вопрос и спросим: «  Офицерский состав состоит из президента, вице-президента и казначея. Сколько разных офицерских списков вы можете выбрать из членства в социальном клубе? ” Это тот же вопрос? Или это другое? Вам нужно использовать комбинации или перестановки?

Вопросы, на самом деле, совсем другие. Итак, как вы применяете каждый метод на GRE?

Решение задач с комбинациями

Первый вопрос (« Сколько групп из 3… ») указывает на то, что мы считаем группы из 3 человек, и нам не нужно беспокоиться о том, кого выбрать первым, вторым или третьим, т. е. порядок не имеет значения. По этой причине это проблема комбинаций.

Чтобы ответить на вопрос, мы будем использовать формулу комбинаций, где n  = общее количество элементов (10) и k  = количество выбранных элементов (3). Обратите внимание, что k может равняться n , но никогда не может быть больше n (мы можем выбрать все элементы в группе, но не можем выбрать больше элементов, чем общее количество). Вот формула комбинаций:

Обратите внимание, что восклицательный знак означает факториал; Факториал означает умножение числа на каждое целое число под ним до 1. Например, 4! = 4 * 3 * 2 * 1.
Подставив наши значения в уравнение, мы получим следующее (убедитесь, что вы уменьшили числа в расширенных вычислениях, чтобы упростить фактическое умножение, которое вам нужно сделать):

Таким образом, мы могли выбрать 120 различных групп из 3 партийных комитетов.

Решение задач перестановки

Второй вопрос спрашивает: « Сколькими различными способами вы можете выбрать список офицеров из 3 человек? ”Эта формулировка говорит нам, что мы должны отслеживать каждый выбор независимо, а не группами по 3 человека. Например, выбор Ника в качестве президента, затем Ким в качестве вице-президента, затем Приянки в качестве казначея – это не то же самое, что выбор Ким в качестве президента, затем Приянка в качестве вице-президента, затем Ник в качестве казначея, что не то же самое, что выбрать Ким в качестве президента, затем Ника в качестве вице-президента, затем Приянку в качестве казначея и так далее, то есть порядок имеет значение. По этой причине это проблема перестановок. Чтобы ответить на этот вопрос, воспользуемся следующей формулой перестановок:

Как видите, знаменатель — это точка различия между формулами комбинаций и перестановок. Для любых значений n и k количество комбинаций, которые мы можем составить, всегда будет меньше, чем количество перестановок, которые мы можем составить. Эта проблема не исключение. Подставив наши значения в уравнение, а затем максимально уменьшив, мы получим:

Таким образом, когда порядок имеет значение и мы отслеживаем каждый выбор по-разному, мы можем выбрать 3 офицеров 720 различными способами.

Разработчики тестов GRE создают сложные задачи, используя тонкий язык, чтобы указать, следует ли вам использовать формулу комбинации или перестановки для ответа на поставленный вопрос. Комбинированные вопросы укажут на то, что вам нужно сформировать группы или наборы; Вопросы перестановки будут содержать слова или фразы, указывающие порядок, например «первый, второй, третий» или «сколько разных способов». Некоторые действительно сложные задачи могут сочетать в себе и то, и другое.
Как гласит старая поговорка, «практика делает совершенным» — чем больше этих задач вы решите (и чем больше соответствующих объяснений вы прочитаете), тем лучше вы будете подготовлены к ответам на вопросы о комбинациях и перестановках в день экзамена GRE.

Перестановка/комбинация — GRE Math

Все математические ресурсы GRE

13 Диагностические тесты 452 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 Следующая →

GRE Math Help » Арифметика » Перестановка/комбинация

Правление торговой палаты состоит из семи членов, выбранных из двадцати кандидатов. Процесс выборов в совет состоит из двух этапов. Сначала избираются президент, секретарь и казначей. После этого четыре члена выбираются «на свободе» без какого-либо конкретного титула или округа. Сколько возможных досок можно было выбрать?

Possible Answers:

390,700,800

16,279,200

5,426,400

10,465,200

2,713,200

Correct answer:

16,279,200

Объяснение:

Мы должны рассмотреть два случая. Во-первых, группа, состоящая из президента, секретаря и казначея, представляет собой случай перестановки. Поскольку в такой группе порядок имеет значение, мы можем выбрать из наших первоначальных 20 кандидатов 20*19* 18 или 6840 возможных группировок.

После этого группа в целом представляет собой случай комбинаций, в которых порядок не имеет значения. Поскольку мы уже выбрали 3 на первые три слота, останется 17 человек. Формула выбора набора из 4 человек из 17 кандидатов представлена ​​формулой комбинации такого вида:

17! / ((17-4)! * 4!) = 17! / (13! * 4!) = (17 * 16 * 15 * 14) / (4 * 3 * 2) = 17 * 4 * 5 * 7 = 2380

Таким образом, мы имеем 6840 и 2380 возможных группировок. Каждый из них можно комбинировать друг с другом, что означает, что у нас есть 6840 * 2380, или 16 279.200 потенциальных досок.

Сообщить об ошибке

Сколько заказанных образцов из 5 карт можно взять из колоды из 52 карт без замены?

Possible Answers:

42,365,000

311,875,200

500,320,000

11,452,000

65,690,040

Correct answer:

311,875,200

Объяснение:

Ключевые моменты, которые мы должны помнить, это то, что порядок имеет значение и что мы делаем выборку без замены. Тогда это становится простой проблемой перестановки. У нас есть 52 карты, которые нужно выбрать по 5 за раз, поэтому ответ 52 * 51 * 50 * 49.* 48.

Сообщить об ошибке

Количественное сравнение

Из стандартной колоды в 52 карты выбираются 3 карты.

Количество A: Количество способов выбрать 3 карты с заменой

Количество B: Количество способов выбрать 3 карты без замены

Возможные ответы:

Связь не может быть определена из предоставленной информации.

Количество B больше.

Количество A больше.

Обе величины равны.

Правильный ответ:

Количество A больше.

Объяснение:

Количество A говорит  с заменой , поэтому у нас есть 52 способа выбрать первую карту, затем мы заменяем ее, так что у нас снова есть 52 способа выбрать вторую карту, и аналогично у нас есть 52 способа выбрать 3-ю карту.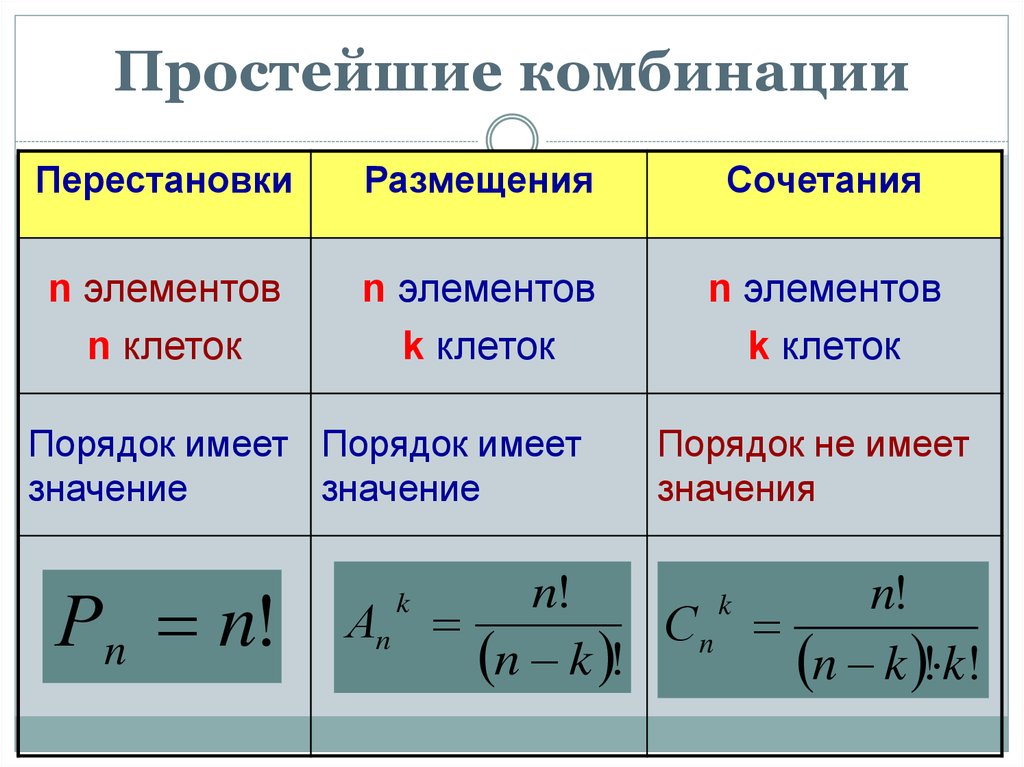 . Таким образом, у нас есть 52 * 52 * 52 способа выбора 3-х карт с заменой.

Количество B говорит без замены , поэтому у нас есть 52 способа выбрать первую карту, но затем мы не кладем эту карту обратно в колоду, поэтому у нас есть 51 способ выбрать вторую карту. Мы снова не кладем эту карту обратно, оставляя 50 способов выбрать третью карту. Таким образом, есть 52 * 51 * 50 способов выбрать 3 карты без замены.

Очевидно, количество A больше. В общем, всегда должно быть больше способов выбрать что-то с заменой , чем без замены , как мы показали выше. Если бы вы уже знали это, вы могли бы выбрать количество А без математики. Обратите внимание, что в любом случае вы придете к ответу здесь, нет НИКАКОЙ причины заканчивать вычисления полностью. Это сэкономит вам время при решении многих задач количественного сравнения. Например, мы знаем, что 52 * 52 * 52 больше, чем 52 * 51 * 50, но на самом деле не выяснили, чему равны эти два выражения.

Сообщить об ошибке

Сколькими способами можно посадить 6 розовых кустов разного цвета в ряд, в котором есть место только для 4 кустов?

Возможные ответы:

120

480

240

220

360

Правильный ответ:

360

Пояснение:

Есть 6 способов выбрать первый розовый куст, 5 способов выбрать второй, 4 способа выбрать третий и 3 способа выбрать четвертый. Всего есть 6 * 5 * 4 * 3 = 360 способов расположить кусты роз.

Сообщить об ошибке

Сколькими способами можно расположить в ряд пять разноцветных шаров?

Возможные ответы:

Правильный ответ:

Пояснение:

Нам нужно расставить 5 шаров по 5 позициям: _ _ _ _ _. Первую позицию может занять любой из 5 шаров. Затем остается 4 шара, чтобы заполнить вторую позицию, и так далее. Поэтому количество аранжировок равно 5! = 5 * 4 * 3 * 2 * 1 = 120.

Сообщить об ошибке

Дейзи хочет поставить четыре вазы в ряд за пределами своего сада. У нее есть восемь ваз на выбор. Сколько ваз она может сделать?

Возможные ответы:

Правильный ответ:

Объяснение:

В этой задаче, поскольку порядок ваз имеет значение (красный синий желтый отличается от синего красного желтого), мы имеем дело с перестановками.

При выборе из возможных вариантов общее количество возможных перестановок (порядок имеет значение):

Сообщить об ошибке

Какое минимальное количество рукопожатий может произойти между пятнадцатью людьми на собрании, если каждый человек пожимает друг другу руку только один раз?

Возможные ответы:

105

250

210

32 760

Правильный ответ:

105

Объяснение:

Это комбинированная задача вида «15 выбирают 2», потому что наборы рукопожатий не имеют значения по порядку. (То есть «A пожимает руку B» — это то же самое, что «B пожимает руку A».) Используя стандартную формулу, получаем: 15!/((15 – 2)! * 2!) = 15!/(13! * 2!) = (15 * 14)/2 = 15 * 7 = 105,

Сообщить об ошибке

20 человек имеют право быть избранными в городской совет, в который входят трое избираемых членов.

Количество A

Количество возможных комбинаций членов совета при условии отсутствия различий между должностными лицами.

Количество B

Количество возможных комбинаций членов совета, учитывая, что в совете есть президент, вице-президент и казначей.

Возможные ответы:

Количество B больше.

Количества равны.

Количество A больше.

Связь не может быть определена на основании предоставленной информации.

Правильный ответ:

Количество B больше.

Объяснение:

Это вопрос перестановок и комбинаций. Вы можете решить это, используя соответствующие формулы, но всегда случай, когда вы можете сделать больше перестановок, чем комбинаций для всех групп размером больше единицы, потому что порядок выбора имеет значение; поэтому, не занимаясь математикой, вы знаете, что ответом должно быть B.

Сообщить об ошибке

У Джо есть набор из 10 книг, которые он еще не читал. Если он возьмет 3 из них в отпуск, сколько возможных наборов книг он сможет взять?

Возможные ответы:

1145

240

Ни один из этих

720

120

Правильный ответ:

120

Объяснение:

Он может выбрать из 10, затем 9, затем 8 книг, но поскольку порядок не имеет значения, нам нужно разделить на 3 факториал

 (10 * 9 * 8) ÷ (3 * 2 * 1) = 720/6 = 120

Сообщить об ошибке

Сколько различных лицензионных паролей можно составить, если указанный пароль должен содержать ровно 6 символов, два из которых являются различными числами, одно из которых должно быть заглавной буквой, а остальные 3 могут быть любой цифрой или буквой (заглавной или строчной), чтобы в пароле не было повторений каких-либо символов?

Возможные ответы:

619652800

219

231

456426360

365580800

Правильный ответ:

456426360

Объяснение:

Начните с рассмотрения трех «жестких и быстрых условий» — цифр и одной буквы верхнего регистра.