Формулы прогрессий: Формулы прогрессий, формулы арифметической прогрессии и геометрической прогрессии

Содержание

Применение понятия «прогрессия» в жизни

Авторы
Руководители
Файлы работы
Наградные документы

Черенкова Ю.С. 1

1МБОУ СОШ № 16

Драйцель И.В. 1

1МБОУ СОШ № 16

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

В настоящее время актуальным вопросом становится проблема соотношения, изучаемого в школьном курсе математики, материала с жизнью. В 9 классе мы сталкиваемся с темой «Прогрессии», даем определение термину, также используем основные формулы прогрессии для решения задач. В заданиях ОГЭ используются задачи на применение основных формул прогрессий, но как эти понятия связаны с жизнью. В заданиях ЕГЭ по математике также есть задачи на применение арифметической и геометрической прогрессий, но уже с практическим содержанием.

Цель работы:

1. Выяснить, имеют ли прогрессии практическое применение в повседневной жизни.

Объект исследования:

1. Арифметическая и геометрическая прогрессии.

Предмет исследования:

1. Практическое применение прогрессий в жизни.

Результаты анкетирования

С целью выявления наиболее правильно ответа на наш основной вопрос «Знаете ли вы как применить свойства прогрессии в повседневной жизни?», мы провели анкетирование среди учащихся 10 – го класса и членов моей семьи.

(см. Приложение 1)

Результаты анкетирования оказались неоднозначными.

Всего было опрошено 35 человек, из них 31 % ответили на вопрос положительно, а 69 % не знают, как применять свойства прогрессии в жизни.

Также мы провели еще одно анкетирование и выяснили, что большая часть опрошенных (83 %) хотела бы узнать о необычном применении прогрессии в жизни. В связи с этим, мы считаем, что данная тема является интересной для изучения на сегодняшний день.

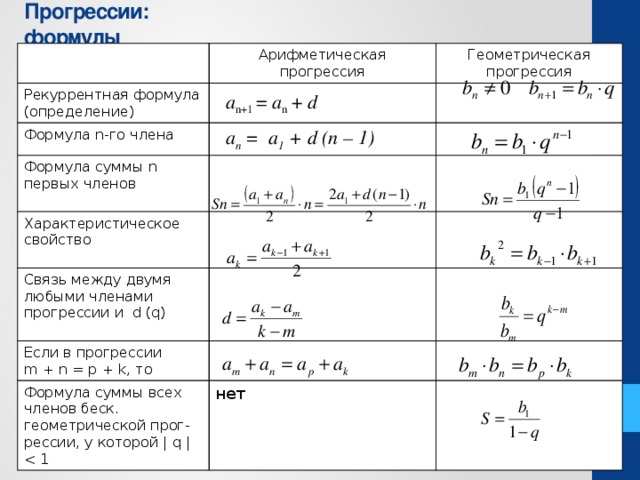
Определения и формулы

Арифметическая прогрессия

— это числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d.

Число d называется разностью прогрессии.

Любой член арифметической прогрессии вычисляется по формуле:

an = a1 + d (n – 1)

Сумма n первых членов арифметической прогрессии вычисляется по формуле:

Геометрическая прогрессия

— это числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q.

Число q называется знаменателем прогрессии.

Любой член геометрической прогрессии вычисляется по формуле:

bn = b1 * qn — 1

Сумма n первых членов геометрической прогрессии вычисляется по формуле:

Зная эти формулы можно решить большое количество интересных задач: литературного, исторического и практического содержания.

Историческая справка

Первые представления об арифметической и геометрической прогрессиях были еще у древних народов. Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.

На связь между прогрессиями первым обратил внимание великий ученый Архимед (287–212 гг. до н. э). Для нахождения площадей и объемов фигур он вывел формулу суммы квадратов натуральных чисел.

Термин “прогрессия” (от латинского progression, что означает движение вверх) был введен римским автором Боэцием (в VI веке) и понимался в более широком смысле, как бесконечная числовая последовательность.

Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке).

Формула суммы членов геометрической прогрессии дана в книге Евклида “Начала” (3 век до н.э.).

Древняя Греция

Сведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции. Уже в V в. до н. э. греки знали следующие прогрессии и их суммы:

Германия

Известна интересная история о знаменитом немецком математике К. Гауссе (1777 – 1855), который еще в детстве проявлял выдающиеся способности к математике. Учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за одну минуту, сообразив, что суммы 1+100, 2+99 и т.д равны, он умножил 101 на 50, т.е. на число таких сумм. Иначе говоря, он заметил закономерность, присущую арифметическим прогрессиям.

Задача – легенда:

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.

Изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – в 2 раза больше, т. е. два зерна, на третью – еще в 2 раза больше, т. е. 4 зерна и так далее до 64 – ой клетки.

Царь был удивлен, когда узнал, что такую, казалось бы, скромную просьбу невозможно выполнить.

Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.

Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая моря, и океаны, и горы, и пустыню, и Арктику с Антарктикой, и получить удовлетворительный урожай, то, пожалуй, лет за 5 он смог бы рассчитаться.

Применение прогрессий в жизни

1. Финансовая пирамида.

Разберёмся в механизмах этих организаций.

Финансовая пирамида – способ обеспечения дохода участникам структуры за счет постоянного привлечения денежных средств. Доход первым участникам пирамиды выплачивается за счет вкладов последующих участников.

В большинстве случаев истинный источник получения дохода скрывается, а декларируется вымышленный или малозначимый. Подобная подмена является мошенничеством.

Как правило, в финансовой пирамиде обещается высокая доходность, которую невозможно поддерживать длительное время, а погашение обязательств пирамиды перед всеми участниками является заведомо невыполнимым. Закономерным итогом такой ситуации является банкротство проекта и убытки последних инвесторов.

Человек собирается организовать финансовую пирамиду.

Представим, что число участников увеличивается в 5 раз с каждым кругом. В первом кругу участвуют 120 человек, во втором – 600, в третьем – 3 000, на четвертом – 15 000, на пятом – 75 000, на шестом – 375 000, на седьмом – 1 875 000, на восьмом – 9 375 000, на девятом – 46 875 000, на десятом – 234 375 000 человек.

Численность населения Воронежа составляет 1 039 801 человек (данные 2018 года). Следовательно, на седьмом кругу количество участников финансовой пирамиды превысит численность населения нашего города.

Численность населения России составляет 146 877 088 человек (данные 2018 года). Можно заметить, что на десятом кругу количество участников значительно превышает численность населения страны.

Так что участник, включившийся на седьмом или десятом круге, уже ничего не получит.

Такая закономерность чисел, также является геометрической прогрессией

2. «Сложные проценты»

В жизненной практике геометрическая прогрессия появляется в первую очередь в задаче об исчислении так называемых “сложных процентов”.

Каждому в жизни приходится решать задачи, связанные с денежными вкладами.

Применение понятия на практике

Воспользуемся конкретным примером. Размер материнского капитала составляет 453 000 р. Можно ли вложить такую сумму в банк под выгодный процент и к совершеннолетию ребенка приобрести ему квартиру?

Решение:

Самый выгодный вклад, отвечающий нашим условиям, является вклад «Сохраняй» в Сбербанке России под 5 % годовых.

Первоначально вложено 453 000 р. через год сумма возрастет на 5% составит 105% от 453 000 р.

453 000 * 1, 05 (сумма составит через год)

453 000; 453 000 * 1, 05; 453 000 * 1, 05

2; 453 000 * 1, 05³; 453 000 * 1, 05⁴

Последовательность имеет вид геометрической прогрессии, где

b₁ = 453 000; g = 1, 05

453 000 * 1, 05¹⁸ = 1, 0902 * 10⁶= 1090200 р.

Вывод:

Учитывая, что средняя стоимость однокомнатной квартиры в г. Воронеже составляет 1900000 р., на сумму 1090200 приобрести жилище не возможно, но подобное вложение денежных средств является достаточно выгодным.

Справка:

В XIII веке в Англии ростовщики давали деньги под 50% годовых. Это вызывало страшное недовольство. Издавались законы, ограничивающие процент. Король Генрих VII даже совсем отменил взимание процентов, что привело в упадок, как банковское дело, так и промышленность, лишившуюся возможности получения кредитов. В конце концов, взимание процентов было разрешено, но не должно было быть большим 10%.

3. Изменение массы радиоактивного вещества со временем — еще один пример геометрической прогрессии.

Известно, что за единицу времени такое вещество теряет определенную часть своей массы (она переходит в другое вещество и энергию). Для каждого радиоактивного вещества определяется величина T –период полураспада. Массы нераспавшегося вещества в моменты 0, T, 2T, 3T,… будут образовывать бесконечно убывающую геометрическую прогрессию.

4. Прирост древесины в лесном массиве происходит по законам геометрической прогрессии. При этом у каждой породы дерева свой коэффициент годового роста объема. Учет этих изменений позволяет планировать вырубку части лесных массивов и одновременную работу по восстановлению лесов.

5. Прогрессии в природе

Все организмы обладают интенсивностью размножения в геометрической прогрессии.

Бактерии.

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. (геометрическая прогрессия). Результат каждого удвоения называется поколением.

Справка:

Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.

Справка:

Интенсивность размножения бактерий использую в пищевой промышленности (для приготовления напитков, кисломолочных продуктов, при квашении, солении и др.), в фармацевтической промышленности (для создания лекарств, вакцин), в сельском хозяйстве (для приготовления силоса, корма для животных), в коммунальном хозяйстве и природоохранных мероприятиях (для очистки сточных вод, ликвидации нефтяных пятен).

6. Прогрессии — оправдание войн

Английский экономист епископ Мальтус использовал геометрическую и арифметическую прогрессии для оправдания войн: средства потребления (пища, одежда) растут по законам арифметической прогрессии, а люди размножаются по законам геометрической прогрессии. Мальтус считал, для того, чтобы избавиться от лишнего населения, необходимы войны.

8. Наследство

Человек получил наследство. Первый месяц он истратил 100$, а каждый следующий месяц он тратил на 50$ больше, чем в предыдущий. Каков размер наследства, если денег хватило на год такой безбедной жизни?

9. Прогрессии в музыке

В музыке прогрессией называется постепенное повторение мотива в один или два такта в восходящем или нисходящем порядке. При таком повторении мотива выбирается интервал, на который мотив должен постоянно перестанавливаться в восходящем или нисходящем направлении. Прогрессия бывает точная или неточная. В точной, мотив повторяется на другой ступени буквально, т. е. с сохранением не только названий всех своих интервалов, но и их точной величины. В неточной прогрессии допускаются отступления от точной величины интервалов мотива, и интервала, на которой мотив перестанавливается. Прогрессия в музыке называется секвенцией.

10. Прогрессии в литературе

Даже в литературе мы встречаемся с математическими понятиями. Вспомним строки из «Евгения Онегина».

…Не мог он ямба от хорея,

Как мы не бились отличить…

Ямб — это стихотворный размер с ударением на чётных слогах 2; 4; 6; 8… Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.

«Мой дЯдя сАмых чЕстных прАвил…»

Прогрессия: 2; 4; 6; 8…

Хорей — это стихотворный размер с ударением на нечётных слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7… С первым членом 1 и разностью прогрессии 2.

«Я пропАл, как звЕрь в загОне»

Прогрессия: 1; 3 ;5; 7. ..

Заключение.

Как вы могли заметить, исходя из вышеизложенного материала, что зная основные формулы геометрической и арифметической прогрессий, можно решить большое количество интересных задач литературного, исторического и практического содержания. Формулы и математические законы описывают явления в разных областях знаний, на первый взгляд далеких от математики.

На сегодняшний день, изучение происхождения и использования в жизни геометрической и арифметической прогрессий является актуальной и важной задачей для современных ученых.

Данное исследование позволило углубиться в изучение загадочного понятия «прогрессия», а также расширить кругозор знаний учащихся.

Список литературы

Дэвисон Р. К. Прогрессии / Р. К. Дэвисон. — М. Мир Урании 2016г. 328 стр.

Рассел Д. Геометрическая прогрессия / Д. Рассел. — Издательство: «VSD» (2012)

Рассел Д. Арифметическая прогрессия / Д. Рассел. — Издательство: VSD, 2012 г.

Интернет – ресурсы

Википедия — свободная энциклопедия. – Режим доступа: https://ru.wikipedia.org/

Вся элементарная математика. – Режим доступа: http://www.bymath.net- math34.ru

Математический портал. – Режим доступа: http://www.webmath.ru- astro-online.ru

Российский федеральный образовательный портал. – Режим доступа: http://www.edu.ru/

Приложение 1

Анкета для учащихся 10 — го класса.

№

п/п

Содержание вопроса

Ответ на поставленный

вопрос

Знаете ли Вы как применить свойства прогрессии в повседневной жизни?

Интересно ли Вам узнать об этом?

Просмотров работы: 4795

Исследовательская работа «Прогрессии вокруг нас» • Наука и образование ONLINE

Главная Работы на конкурс Предметное образование Физико-математические дисциплины Исследовательская работа «Прогрессии вокруг нас»

Автор: Джахуа Ангелина Игоревна

Место работы/учебы (аффилиация): МОУ СОШ № 2, ст-ца Григорополисская, Ставропольский край, 9 класс

Научный руководитель: Колбасова Лариса Александровна

В настоящее время актуальным вопросом становится проблема соотношения, изучаемого в школьном курсе математики, материала с жизнью. В 9 классе мы сталкиваемся с темой «Прогрессии», даем определение термину, также используем основные формулы прогрессии для решения задач. В заданиях ОГЭ используются задачи на применение основных формул прогрессий, но как эти понятия связаны с жизнью. Найдя ответы на вопросы: имеет ли это какое — либо практическое значение и как давно люди знают последовательности, как возникло это понятие, мы подтвердим или опровергнем утверждение о том, что математика – наука очень древняя и возникла она из практических нужд человека, что алгебра является частью общечеловеческой культуры.

Цель исследования: установить картину возникновения понятия прогрессии и выявить примеры их применения.

Объект исследования:

Арифметическая и геометрическая прогрессии.
Практическое применение прогрессий в жизни.

Задачи исследования:

Изучить наличие задач на прогрессии с практическим содержанием в различных учебных пособиях.
Выяснить:

когда и в связи с какими потребностями человека появилось понятие последовательности, в частности — прогрессии;
какие ученые внесли большой вклад в развитие теоретических и практических знаний по изучаемой проблеме.

Установить: имеют ли арифметическая и геометрическая прогрессии прикладное значение? Найти примеры применения прогрессий в нашей жизни.

Методы исследования:

Анализ школьных учебников математики, КИМ ОГЭ 2019-2021, математической, справочной литературы, литературы по истории математики, материала из Интернета.
Обобщение найденных фактов в учебниках по биологии и по экологии и в медицинских справочниках.

Загрузка…

Проект «Алгебра в экономике (бизнес планирование)»

В экономической науке широко используется методы анализа, синтеза, индукции, научного абстрагирования, а также математический инструментарий. Гипотеза: Математические законы и понятия, которыми мы владеем, используются ли в экономике. Цель работы: По…

Посмотреть работу

Проектная работа «Нестандартные способы умножения»

Тема очень актуальна, поскольку простое умножение — это долгое и скучное занятие, а вот с нестандартными способами это занятие становиться весёлым и быстрым. Цель: подробно рассмотреть несколько нестандартных способов умножения и выявить самый удобны…

Посмотреть работу

Исследовательская работа «Многоугольники на целочисленной решетке»

Мы часто предпочитаем рисовать и чертить на клетчатой бумаге. И даже не задумываемся о том, что она (а точнее – узлы клетчатой бумаги) являются одним из важнейших примеров точечной решетки на плоскости. Решетки на плоскости позволяют переводить на ге…

Посмотреть работу

4″>Исследовательский проект «Уравнения высших степеней»

Решение алгебраических уравнений высших степеней с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Интерес к ним велик, так как эти уравнения тесно связаны с поиском корней уравнений, не рассматриваемых школ…

Посмотреть работу

Проект «Решение систем линейных уравнений различными методами»

Доступна к просмотру полнотекстовая версия работы

В работе рассмотрены различные математические методы решения систем линейных уравнений, показаны алгоритмы и примеры решения линейных алгебраических уравнений различными методами. Дается краткая историческая справка о жизни ученых, занимавшихся данно…

Посмотреть работу

Мероприятие завершено

Теория музыки: Аккордовые прогрессии

Темы по теории музыки

Нажмите на эти ссылки, чтобы узнать больше об этих темах.

Обратный цикл
Основы аккордов
Удлинители аккордов
Названия аккордов
Аккордовые последовательности
Замена аккорда
Пятый круг
Энгармоники
Гамма гармонического минора
Импровизация
Интервалы
Мелодический минор
Режимы
Модуляция
Параллельная минорная гамма
Весы
Экзотическая чешуя
Гармонизированные весы
Шкала Градус
Вторичные доминантные аккорды
Транспонирование

Попробуйте интерактивную
Карта последовательности аккордов

Используйте эту интерактивную карту для создания последовательности аккордов для ваших собственных песен.
(Нажмите на изображение выше.)

Скачать бесплатно
Получите 15 диаграмм последовательности аккордов
, когда вы зарегистрируетесь, чтобы получать полезные видео, советы и лайфхаки по электронной почте.
Нажмите кнопку, чтобы узнать подробности.

Книги и инструменты На компьютере или по книге изучение музыки слишком важно, чтобы ждать. Выберите книги и инструменты, которые подходят именно вам.

«Когда ученик будет готов, появится учитель.» -Buddha

Количество способов сочетания аккордов для создания новых и интересных звуков почти бесконечно. Музыканты используют свою интуицию и опыт, чтобы расставлять аккорды таким образом, чтобы музыка двигалась вперед. Это понятие движения важно для понимания того, как сочинять и импровизировать музыкальное произведение. Последовательность аккордов — это то, что придает музыкальному произведению гармоническое движение.

Гармоническое движение
Обычно игра аккордов в музыкальном произведении создает ощущение движения и изменения. Некоторые комбинации аккордов звучат бодряще, другие — мрачно, а некоторые напоминают океанские волны. Хотя эти гармонии и то, как мы их интерпретируем, почти бесконечны, действует очень простой принцип.

Большинство музыкальных произведений имеют тенденцию сначала создавать ощущение стабильности, отходить от него, создавать напряжение, а затем возвращаться к ощущению стабильности. Хотя некоторые музыкальные произведения демонстрируют это более ярко, чем другие, по мере тренировки слуха вы будете все больше осознавать это.

Формулы прогрессии
То, как аккорды располагаются один за другим в музыкальном произведении, называется последовательностью аккордов. Аккорды в прогрессии имеют разные гармонические функции. Какие-то аккорды обеспечивают стабильность, какие-то — отклонение, а какие-то — динамическое напряжение.

Римские цифры используются для обозначения аккордов в последовательности. Цифры основаны на гамме диатонической гаммы. Например, в тональности до мажор последовательность I, IV, V7 (один, четыре, пять) указывает на аккорды Cmaj, Fmaj и Gdom7. В тональности F такими аккордами будут Fmaj, Bbmaj и Cdom7.

На приведенной ниже диаграмме показаны формулы наиболее распространенных последовательностей аккордов в мажорной и минорной тональностях.

Римские цифры в формуле последовательности аккордов означают трезвучие аккорда. Гармонически допустимо расширять эти аккорды дополнительными диатоническими тонами для создания других аккордов. Другими словами, вы можете добавлять ноты к этим аккордам, если они являются частью диатонической гаммы. Гармоническая функция аккорда не меняется.

Римские цифры обозначают положение каждого аккорда в диатонической гамме. На приведенной ниже диаграмме показано, как можно интерпретировать степень римской шкалы с помощью различных аккордов. Все приведенные ниже примеры можно интерпретировать из одной и той же формулы аккордов.

Формулы аккордов записываются римскими цифрами, чтобы представить общую форму прогрессии. Часто музыканты учат музыкальное произведение по формуле последовательности аккордов. Одна из причин этого заключается в том, что его легче запомнить, поскольку многие песни основаны на одной и той же формуле. Другая причина в том, что легче играть песню в разных тональностях, если знаешь формулу. Однако это предполагает, что вы знаете, какие аккорды составляют какие тональности.

Нередко разговор на репетиции выглядит так:

Певец: «Эй, у меня есть новая песня, которую я хочу написать. Это последовательность шесть-два-пять».

Пианист: «Какая тональность тебе нравится?»

Певец: «Я не знаю. Может быть, Bb.»

Вы можете увидеть, если вы пианист, вам нужно быть готовым играть одну и ту же прогрессию в нескольких тональностях.

Аккорды, обозначенные римскими цифрами, также имеют имена. Например, первый аккорд гаммы — это тоника. Пятый аккорд является доминантой. На приведенной ниже диаграмме показаны функциональные названия и ступень диатонической гаммы. Ниже приведены ноты от нескольких общих клавиш, которые соответствуют функции и степени.

Другим гаммам, структура которых отличается от диатонической шкалы, назначаются степени аккорда в соответствии с резкостью или плоскостью их нот. То есть диатоническая шкала создает «линейку», по которой измеряются другие шкалы. Вот почему результирующий аккорд, основанный на третьей ноте гаммы до натурального минора, будет bIIIm (Ebm), а не III, как в диатонической гамме.

В приведенной ниже таблице показано сравнение различных шкал. Поскольку ноты гаммы расположены по-разному, они создают разные аккорды.

Замена аккордов
Чтобы разнообразить движение, вы можете заменять аккорды, играть доминирующие аккорды вместо минорных и наоборот. Играйте уменьшенные аккорды вместо доминанты. Играйте аккорды с расширениями. Другими словами, изучите различные способы соединения аккордов для создания гармонического движения.

Пример: Одной из наиболее распространенных музыкальных последовательностей является I, IV, V (один, четыре, пять), и, скажем, мы хотим исследовать эту прогрессию в тональности до мажор.
Поскольку мы находимся в тональности до мажор, наш тонический аккорд будет мажорным аккордом с до в качестве его корня. Есть несколько аккордов, которые мы могли бы выбрать, но для этого примера давайте выберем Cmaj7.

Далее у нас есть IV (четвертый аккорд). Это также мажорный аккорд, но поскольку он происходит от четвертой ступени гаммы до мажор, его корень должен быть F. Обычно мы можем выбрать Fmaj7, но давайте отойдем от правил и поэкспериментируем. Давайте сделаем это аккордом Fm7b5 (F, Ab, B, Eb). В F7 есть Eb и Ab, которые не принадлежат тональности до мажор. Однако самое главное мы меняем мажорный аккорд на минорный. Это создает совершенно другой звук. Вот где мы нарушаем правила. Тем не менее, самое основное правило в теории музыки состоит в том, что если это звучит хорошо, это разрешено.

Аккорд V может действовать как более сильный доминантный аккорд, если мы добавим 7-ю ноту миксолидийского лада. В этом случае мы производим Gdom7 (G, B, D, F). Теперь у нас есть прогрессия I, IV7, V7. Мы можем оживить эту прогрессию еще больше.

V (пятый аккорд) — это аккорд, выражающий наибольшее напряжение в последовательности, и если мы хотим добавить больше напряжения, мы можем изменить аккорд. Это означает, что мы можем добавлять ноты, не принадлежащие тональности, что почти всегда создает диссонансную гармонию, создающую напряжение.

Итак, если мы повысим пятую и девятую ступень аккорда G7, мы получим G7#5#9 (G, B, Eb, Bb). Наша окончательная формула: Imaj7, IVm7b5, V7#5#9. Обратите внимание, как это звучит по сравнению с оригинальным I, IV, V.

Можно сделать больше замен. Это только начало. Экспериментируйте и исследуйте, чтобы создавать различные гармонические движения. Пусть ваше ухо решает, что правильно, а что нет.

Ознакомьтесь с этими интерактивными справочными инструментами по теории музыки. Нажмите на любое из действий ниже, чтобы перейти к теме интерактивной теории музыки.

Гармонизированная мажорная гамма
См. лады и аккорды мажорной гаммы.

Мажорные последовательности аккордов
Узнайте, как аккорды работают вместе, создавая музыку.

Карта мажорных аккордов
Исследуйте последовательности аккордов в мажорных тональностях.

Cirlce of Fifths
Смотрите простые аккорды в каждой тональности.

Дерево аккордов
См. ноты и интервалы, из которых состоят аккорды.

Интервальная тренировка слуха
Услышать и увидеть тональное расстояние между нотами.

Карта минорных аккордов
Исследуйте последовательности аккордов в минорной тональности.

Cirlce of Fifths for Jazz
См. аккорды джазовой гитары по кругу в каждой тональности.

Арифметическая прогрессия, Сумма, Формула, Примечания, Класс 10 Глава 5

Содержание

Что такое арифметическая прогрессия?

Арифметическая прогрессия — это последовательность чисел, полученная путем прибавления фиксированного числа к предыдущему члену, начиная с первого члена, так что разница между каждым последующим членом остается неизменной.

Каждое из чисел в списке называется термом, а фиксированное число называется общей разностью AP, которая может быть любым целым числом.

Например: 2,5,8,11…. общая разность равна 3.

Арифметическая прогрессия — общий термин AP

Общая форма AP:

a ,a+d ,a+2d ,a+3d ,….,a+(n−1)d

1)d как последний член.

Например:

Конечная ТД: 1,3,5,7,….,25

ТД, которая не имеет ни конечного числа членов, ни последнего члена, называется бесконечной ТД.

Например:

Бесконечная ЗД: 2,4,6,8…..∞

3 N-й член ЗД: an=a+(n−1)d, где a – первый член последовательности, а d — общая разность.

Второй член: a2=a+(2−1)d=a+d

Аналогично третий член a3=a+(3−1)d=a+2d

Четвертый член a4=a+(4−1)d=a+3d и так далее до последнего члена.

Арифметическая прогрессия – Примеры

Пример 1:

АП имеет первый член 3, общую разность 4. Найдите третий и пятый члены АП.

Ответ:

a=3, d=4

a3=3+(3−1)4

a3=11

Аналогично,

a5=3+(90−10) a5=19

4-й член ПД с конца: tn=L−(n−1)d, где L — последний член ПД.

Пример 2:

ЗД имеет общую разность 2 и последний член 24. Найдите четвертый член ЗД с конца.

Ответ:

d=2, L=24

t4=24−(4−1)2

t4=18

Сумма членов 0AP: 90n4 Сумма членов 0AP AP, если задан первый член и общая разность:

S=n2(2a+(n−1)d)

Сумма n членов AP, если заданы первый член и последний член l:

S=n2(a+l)

Пример 3:

Найдите сумму первых 10 членов АП 1,4,7,10…..34.

Ответ:

S=102(2×1+(10−1)3)

=5(2+27)

=5×29

=145

Класс 1004 5

Теперь присоединяйтесь к группе Adda247 по подготовке к экзамену на доске и сдайте экзамен на доске.

Арифметическая прогрессия Класс 10
Арифметическая прогрессия — это последовательность чисел, которые отличаются друг от друга общей разностью. Например, , последовательность 3, 6, 9, 12, ….. является ДП с общей разностью 3.

Общая разность:
называется общей разностью. Например, в последовательности 3, 6, 9, 12…. общая разность равна 3.

Классификация общей разности:
Положительный, когда АД увеличивается.
Ноль, когда АД постоянно.
Отрицательный, когда АД снижается.
Общая форма арифметической прогрессии
Предположим, что члены a1, a2, a3……an находятся в A.P. Если первый член равен «a», а его общая разность равна «d». Тогда термины также могут быть выражены следующим образом.
1 -й семестр A1 = A
2 -й семестр A2 = A + D
3 -й термин A3 = A + 2D
Поэтому мы также можем представлять арифметические прогрессии как:
.0191

a, a + d, a + 2d, ……

Это представление называется общей формой арифметической прогрессии.
Конечная и бесконечная А.П.

В конечной А. П. число членов конечно, и существует последний член А.П.
В бесконечной А.П. количество членов бесконечно, и последний член А.П. не существует.
Сумма арифметических прогрессий
Сумма n членов АП с первым членом «а» и общей разностью «d» определяется по формуле:

Sn=n2(2a+(n−1)d)

Среднее арифметическое
Среднее арифметическое — это просто среднее арифметическое двух чисел. Если у нас есть два числа n и m, мы можем добавить число L между ними, чтобы эти три числа образовали арифметическую последовательность, такую как n, L, m. В этом случае число L является средним арифметическим чисел n и m. На основании свойств арифметической прогрессии мы можем сказать:
L – n = m – L, то есть среднее арифметическое n и m.
L=n+m2

Узнайте больше об арифметической прогрессии
Формулы арифметической прогрессии
Здесь мы предоставили все арифметические формулы в таблице ниже для учащихся 10 класса.
Последовательность а, а+г, а+2д, ……, а + (п – 1)д, ….
Общая разница d = (a ₂ – a ₁ ), где a ₂ и a ₁ – это последующий и предшествующий термины соответственно.
Общий срок (n ^th срок) а _n = а + (n – 1)d
n ^th Срок с последнего срока a _n’ = l – (n – 1)d, где l – последний член
Сумма первых n слагаемых S _n = n/2[2a + (n – 1)d]
Сумма первых n членов, если заданы первый и последний члены S _n = n/2[первый член + последний член]
Свойства арифметических прогрессий Класс 10 Примечания
Если к каждому члену А. П. прибавить или вычесть одно и то же число, результирующие члены в последовательности также будут в А.П. с той же общей разницей. делится или умножается на одно и то же ненулевое число, результирующий ряд также находится в A.P.

Три числа x, y и z будут А.П., если 2y = x + z.\

Ряд является А.П., если n-й член представляет собой линейное выражение.

Если мы выберем термины из АП через равные промежутки времени, эти выбранные термины также составят АП

Если члены арифметической прогрессии увеличиваются или уменьшаются на одинаковую величину, результирующая последовательность также будет арифметической прогрессией.
Важные сведения об арифметических прогрессиях для 10 класса
Если каждый член AP увеличить, уменьшить, умножить или разделить на одну и ту же ненулевую константу, результирующая последовательность также будет в AP

В А. П. число термов, равноудаленных от начала до конца, будет постоянным.

Для решения большинства задач, связанных с А.П., термины удобно принять в виде:

3 Члена: (а – г), а, (а + г).

4 Члены: (а – 3г), (а – г), (а + г), (а + 3г).

Нашли эту статью полезной?
Свяжитесь с нами через чат или позвоните нашему старшему эксперту-консультанту по телефону +91-9625869989 t , чтобы узнать больше о различных потоках и доступных вариантах.
Мы были бы рады, если бы мы могли добавить некоторые из ваших идей. Если у вас есть определенная цель — получить самые высокие оценки, вы можете разрешить свои сомнения с помощью нашего приложения/викторин и помощи класса YouTube (https://youtube.com/c/Adda247Class9).и 10)
Связанный пост:
Реальные системы системы класс 10 Глава 1
Класс полиномов 10 Глава 2
Пара линейных уравнений в двух переменных класса 10 Глава 3

9
179999999999999999999999999999999999179 9051 Пара линейных уравнений. Progression- FAQs
Вопрос 1 Легко ли арифметическая прогрессия?
Ответ. Арифметическая прогрессия — наиболее часто используемая последовательность в математике с простыми для понимания формулами.

Вопрос 2 Что такое n в формуле AP?
Ответ. Сумма n членов АП представляет собой сумму (сложение) первых n членов арифметической прогрессии. Он равен n, деленному на 2, умноженному на сумму удвоенного первого члена — «a» и произведения разницы между вторым и первым термином — «d», также известной как общая разность, и (n-1), где n количество добавляемых терминов.

Вопрос 3 Какой член AP равен 81?
Ответ. Следовательно, 35-й член равен -81.

Вопрос 4 Какова формула GP?
Ответ. Формула для вычисления суммы первых n членов ГП имеет вид: Sn = a[(rn – 1)/(r – 1)], если r ≠ 1 и r > 1. Sn = a[(1 – rn)/(1 – r)], если r ≠ 1 и r < 1. Член n с конца ГП с последним членом l и знаменателем r = l/[r(n – 1)].

Вопрос 5 Если число терминов в ЗП не конечно, то ЗП называется бесконечным ЗП. Формула для нахождения суммы до бесконечности заданных
Ответ. ВП это: S ∞ знак равно ∑ п знак равно 1 ∞ а р п — 1 знак равно а 1 — р ; − 1 < r < 1.

Вопрос 6 Что такое формула TN?
Ответ. Формула для n-го члена имеет вид: Tn = a + (n − 1)d = dn + (a − d) (2) где a и d фиксированы, а n — переменная (целое число ≥ 1). Это соответствует y = mx + b, где m и b фиксированы, а x является переменным.

Вопрос 7 Что такое обыкновенное отношение?
Ответ. Обыкновенный коэффициент — это число, на которое вы умножаете или делите на каждом этапе последовательности. Его можно найти, разделив две последовательные пары терминов.

Вопрос 8 Что такое постоянный коэффициент?
Ответ. Если у вас есть точки с постоянным соотношением, это означает, что ваше отношение y:x или x:y одинаково для всех точек.
No related posts.