Основный тригонометрические формулы. Формулы синуса и косинуса от суммы и разности
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами?
Ответ
В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.

Последние отзывы
Валентина:
Вы спасли нашего сына от увольнения! Дело в том что недоучившись в институте, сын пошел в армию. А вернувшись, восстанавливаться не захотел. Работал без диплома. Но недавно начали увольнять всех, кто не имеет «корочки. Поэтому решили обратиться к вам и не пожалели! Теперь спокойно работает и ничего не боится! Спасибо!
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90
градусов.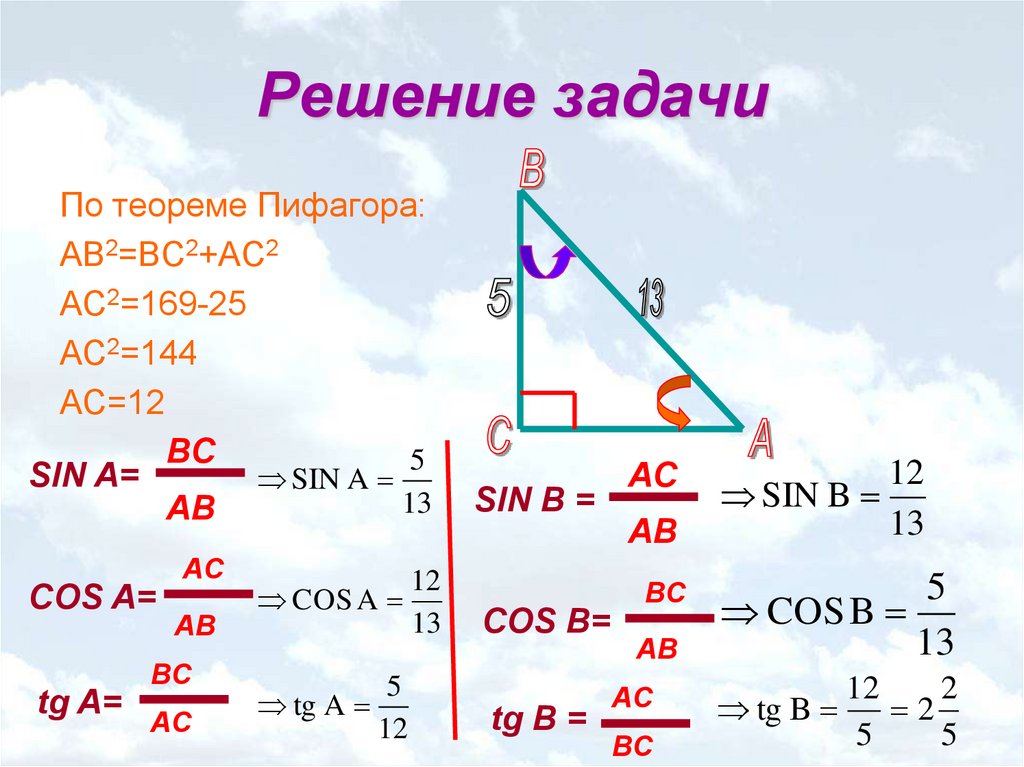
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .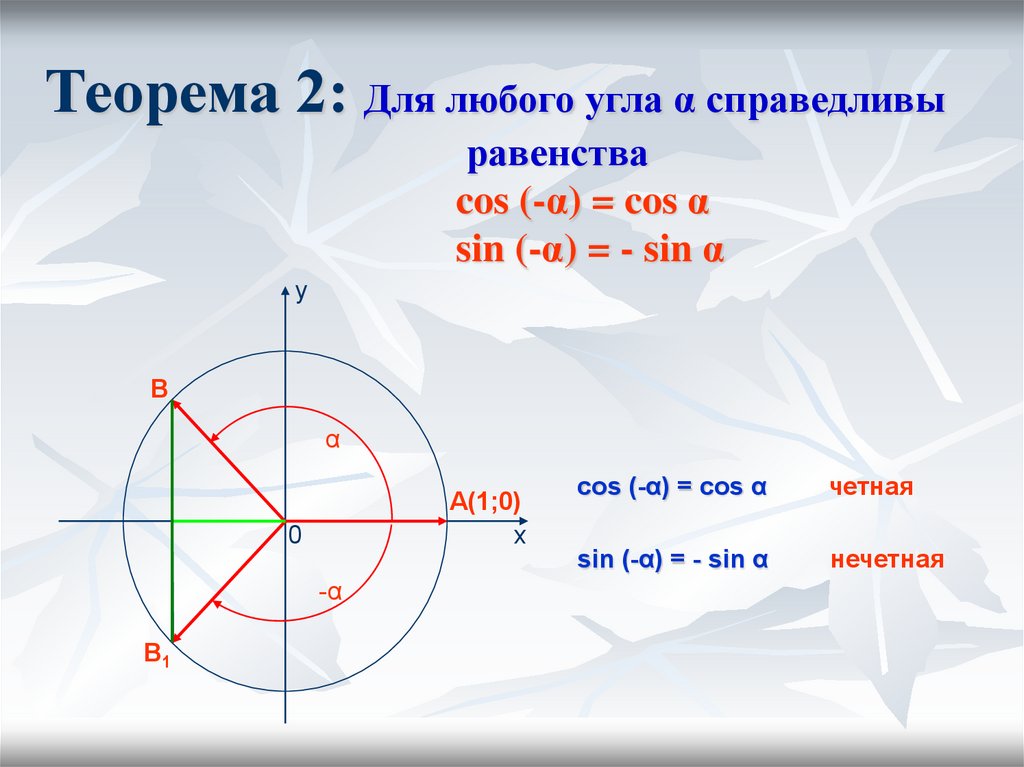
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Тригонометрия — один из разделов математики, в центре изучения которого находятся углы и взаимосвязи между ними. Основы науки закладываются в школьные годы, когда вводятся определения функций угла. В дальнейшем полученная база используется при освоении астрономии, приборостроения, архитектуры и других областей знаний. Как и любая точная наука, тригонометрия не обходится без формул. Практическое применение нашли выражения для определения двойного аргумента. Например, прибегая к соответствующему уравнению, легко можно узнать двойной угол синуса.
В дальнейшем полученная база используется при освоении астрономии, приборостроения, архитектуры и других областей знаний. Как и любая точная наука, тригонометрия не обходится без формул. Практическое применение нашли выражения для определения двойного аргумента. Например, прибегая к соответствующему уравнению, легко можно узнать двойной угол синуса.
Тригонометрическое выражение для расчёта
Выражение просто записывается и запоминается: синус двойного угла вычисляется как двукратное произведение синуса и косинуса одинарного аргумента.
Эта формула выводится на основе выражения синуса суммы углов (Q 1 + Q 2 ) :
sin(Q 1 + Q 2) = sin Q 1 * cos Q 1 + sin Q 2 * cos Q 2 .
Полагая, что заданные углы равны друг другу, формула записывается в привычной форме.
Использовать выражение можно при любых значениях аргумента функции. Вычислить двойной угол синуса по ней достаточно просто, убедиться в этом помогут примеры ниже.
Пример использования
Вот несколько иллюстраций применения полученной формулы. Пусть требуется рассчитать значение тригонометрической функции синуса угла равного 60 градусам. Соответствующий одинарный угол составит 30 градусов. Поскольку величины синуса и косинуса угла в 30 градусов известны, двойной угол синуса составит sin 60 = 2 * sin 30 * cos 30.
Формула используется не только для вычисления «вручную», найти значения по ней можно и с помощью математических пакетов или таблиц MS Excel.
Несмотря на простоту тригонометрического тождества, оно вызывает затруднения у выпускников школы. Именно на это рассчитывают разработчики заданий ЕГЭ, предлагая тесты на проверку основных формул. Вывод — формулу, чтобы подсчитать двойной угол синуса, нужно знать наизусть!
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α)
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу?
Ответ
Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами?
Ответ
В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Валентина:
Вы спасли нашего сына от увольнения! Дело в том что недоучившись в институте, сын пошел в армию. А вернувшись, восстанавливаться не захотел. Работал без диплома. Но недавно начали увольнять всех, кто не имеет «корочки. Поэтому решили обратиться к вам и не пожалели! Теперь спокойно работает и ничего не боится! Спасибо!
А вернувшись, восстанавливаться не захотел. Работал без диплома. Но недавно начали увольнять всех, кто не имеет «корочки. Поэтому решили обратиться к вам и не пожалели! Теперь спокойно работает и ничего не боится! Спасибо!
Страница не найдена — РОО «Ассоциация победителей олимпиад»
Ваши ФИО*
Ваш email*
Ваш номер телефона*
Какой предмет вы хотели бы преподавать?*
Расскажите кратко о своих олимпиадных достижениях*
Приложите резюме*
Объём файлов не должен превышать 20 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt
Please leave this field empty.
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
Ваша электронная почта*
Из какого вы региона?*
Расскажите, как мы могли бы сотрудничать*
Please leave this field empty.
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО*
Ваша электронная почта*
Ваш номер телефона*
Образовательное учреждение*
Расскажите кратко, какая у вас сложилась ситуация с олимпиадным движением в школе и какого результата вы ожидаете от сотрудничества с АПО*
Please leave this field empty.
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
Ваш email
Каким предметом вы интересуетесь
Выберите наиболее подходящий статус Статус не выбранУченикРодительПредставитель школыПедагог
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО ученика
Дата рождения ученика
Класс
Образовательное учреждение
Город образовательного учреждения
ФИО родителя
Телефон родителя
Email родителя
Выберите группу Группа не выбрана
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО ученика
Дата рождения ученика
Класс
Образовательное учреждение
Город образовательного учреждения
ФИО родителя
Телефон родителя
Email родителя
Выберите группу Группа не выбрана
Мотивационное письмо Объём файла не должен превышать 2 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО
Телефон
Образовательное учреждение
Город образовательного учреждения
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО
Телефон
Проект / отдел
Должность
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО ребенка
Название образовательного учреждения
Город образовательного учреждения
ФИО родителя
Телефон родителя
Email родителя
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
Войти
Родитель
Буду покупать курсы для своего ребёнка ЗарегистрироватьсяОбучающийся
Сам буду проходить курсы ЗарегистрироватьсяПредставитель школы
Буду заказывать услуги для своего образовательного учреждения и контролировать их исполнение ЗарегистрироватьсяСлушатель КПК
Буду проходить курсы повышения квалификации для учителей ЗарегистрироватьсяФормулы Sin Cos в тригонометрии с примерами
Тригонометрия, как следует из ее названия, изучает треугольники. Это важный раздел математики, изучающий взаимосвязь между длинами сторон и углами прямоугольного треугольника, а также помогающий определить недостающие длины сторон или углы треугольника.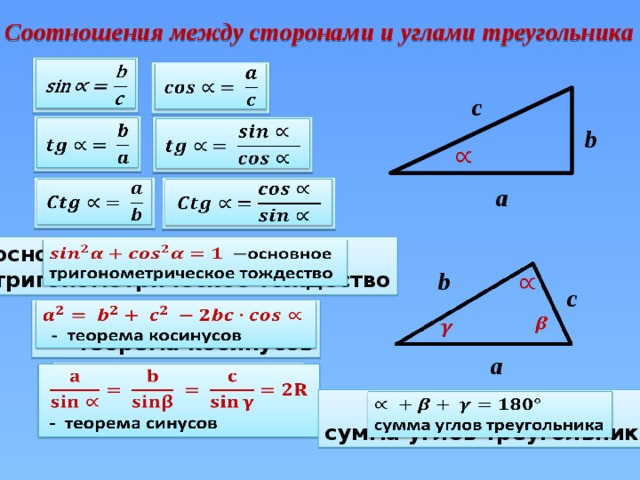 Существует шесть тригонометрических отношений или функций: синус, косинус, тангенс, косеканс, секанс и котангенс, где косеканс, секанс и котангенс являются обратными функциями трех других функций, то есть синуса, косинуса и тангенса соответственно. Тригонометрическое отношение определяется как отношение длин сторон прямоугольного треугольника. Тригонометрия используется в различных областях нашей повседневной жизни. Это помогает определить высоту холмов или зданий. Он также используется в таких областях, как криминология, строительство, физика, археология, разработка морских двигателей и т. д.
Существует шесть тригонометрических отношений или функций: синус, косинус, тангенс, косеканс, секанс и котангенс, где косеканс, секанс и котангенс являются обратными функциями трех других функций, то есть синуса, косинуса и тангенса соответственно. Тригонометрическое отношение определяется как отношение длин сторон прямоугольного треугольника. Тригонометрия используется в различных областях нашей повседневной жизни. Это помогает определить высоту холмов или зданий. Он также используется в таких областях, как криминология, строительство, физика, археология, разработка морских двигателей и т. д.
Формулы шести тригонометрических соотношений/функций
Рассмотрим прямоугольный треугольник XYZ, где ∠Y = 90°. Пусть угол при вершине Z равен θ. Сторона, примыкающая к «θ», называется смежной стороной, а сторона, противоположная «θ», называется противоположной стороной. Гипотенуза — это сторона, противоположная прямому углу или самая длинная сторона прямого угла.
9004 Формула
- sin θ = Противоположная сторона/Гипотенуза
- cos θ = Прилегающая сторона/Гипотенуза
- tan θ = Противоположная сторона/Прилегающая сторона
- cosec θ = 1/sin θ = гипотенуза/противоположная сторона
- sec θ = 1/ cos θ = гипотенуза/прилегающая сторона
- cot θ = 1/ tan θ = примыкающая сторона/противоположная сторона
Синус угла в прямоугольном треугольнике равен отношению длины противолежащего катета к длине гипотенузы к данному углу.
Функция синуса представлена как «sin».
sin θ = противолежащая сторона/гипотенуза
Формула косинуса
Косинусом угла в прямоугольном треугольнике называется отношение длины прилежащего катета к длине гипотенузы к данному углу. Функция косинуса представлена как «cos».
cos θ = смежная сторона/гипотенуза
Некоторые основные формулы синуса и косинуса четвертые квадранты.
Функция косинуса положительна в первом и четвертом квадрантах и отрицательна во втором и третьем квадрантах.
Степень 0003
от 0° до 90°
1-й квадрант
+ (положительный)
+ (положительный) 9от 90° до 180° 85
180° до 270°
3-й квадрант
– (отрицательный)
– (отрицательный)
270° до 360°
9-й квадрант 0085
– (отрицательный)
+ (положительный)
Идентичность отрицательного угла функций синуса и косинуса
- Синус отрицательного угла всегда равен отрицательному синусу угла.
sin (– θ) = – sin θ
- Косинус отрицательного угла всегда равен косинусу угла.
cos (– θ) = cos θ
Связь между функцией синуса и косинуса
sin θ = cos (90° – θ)
Функции, обратные функциям синуса и косинуса
cosec θ = 1/sin θ
- Функция секанса является обратной функцией функции косинуса.
сек θ = 1/cos θ
Тождество Пифагора
sin 2 θ + cos 2 θ = 1
Периодические тождества функций синуса и косинуса
30 2nπ) = sin θcos ( θ + 2nπ) = cos θ
Формулы двойного угла для синуса и косинуса 21 2 θ – sin 2 θ = 2 потому что 2 θ – 1 = 1 – 2 sin 2 θ
Тождества половин углов для функций синуса и косинуса
sin (θ/2) = ±√ 2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Тождества тройного угла для функций синуса и косинуса
sin 3 – 4 sin 3 θ
cos 3θ = 4cos 3 θ – 3 cos θ
Формулы суммы и разности
- Синусоидальная функция
sin (A + B) = sin A cos B + cos A sin B
sin B (A cos B) (9003 B) – cos A sin B
- Функция косинуса
cos (A + B) = cos A cos B – sin A sin B
900 cos + sin A sin B
Закон синусов или правило синусов
Закон синусов по правилу синусов — это тригонометрический закон, определяющий соотношение между длинами сторон и углами треугольника.
a/sin A = b/sin B = c/sin C
Где a, b и c — длины трех сторон треугольника ABC, а A, B и C — углы.
Закон косинусов
Закон косинусов используется для определения отсутствующих или неизвестных углов или длин сторон треугольника.
а 2 = б 2 + с 2 – 2bc cos А
1 2 9032 б 2 = 2 2 222 + a 2 – 2ca cos B
c 2 = a 2 + b 2 – 2ab cos C
Где a, b и c — длины трех сторон треугольника ABC, а A, B и C — углы .
Таблица значений функций синуса и косинуса
Угол (в градусах) | Угол (в радианах) | sin θ 9 0065 | |||||
|---|---|---|---|---|---|---|---|
0° | 0 | 0 | 1 | ||||
30° | π/6 | _3/2 | |||||
45° | π/4 | 1/√2 | 1/√2 | ||||
| 8 0 9090 8 0 082 π/3 | √3/2 | 1/2 | |||||
90° | π/2 | 1 | 30 90 0061 | 120° | 2π/3 | √3/ 2 | -1/2 |
150° | 5π/6 | 1/2 | 5 -√03 78 | ||||
180° | π | 0 | -1 |
Задачи на формулы синуса и косинуса
Задача 1: Если cos α = 24/25, то найти значение sin α.
Решение:
Дано,
cos α = 24/25
Из пифагорейских тождеств мы имеем;
cos 2 θ + sin 2 θ = 1
(24/25) 2 + sin 2 α = 1
– α = 1
2
2 sin
1 25) 2
sin 2 α = 1 – (576/625) = (625 – 576)/625
sin 2 α = (625 – 576)/625 = 49/626
9000†2 = α /625 = ±7/25Следовательно, sin α = ±7/25.
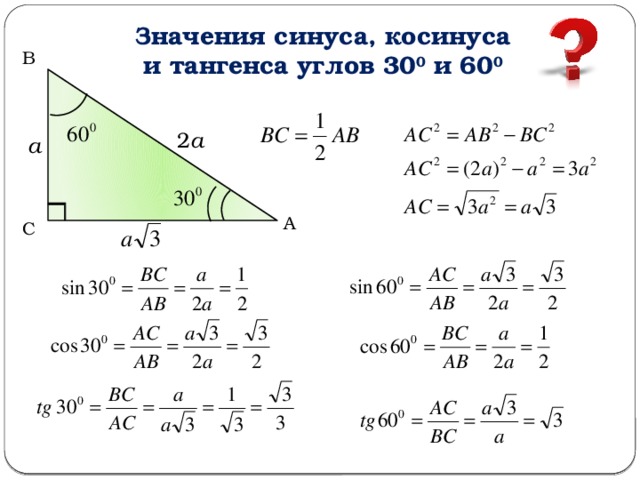
Задача 2. Докажите формулы sin 2A и cos 2A, если ∠A= 30°.
Решение:
Дано, ∠A= 30°
Мы знаем, что
1) sin 2A = 2 sin A cos A
sin 2 cos 2(30°)0 = °
sin 60° = 2 × (1/2) × (√3/2) {Поскольку sin 30° = 1/2, cos 30° = √3/2 и sin 60° = √3/2}
√3/2 = √3/2
Л.В.С. = ПРАВ.В.С.0003
cos 60° = 2(√3/2) 2 – 1 = 3/2 – 1 {Поскольку, cos 60° = 1/2 и cos 30° = √3/2}
1/2 = 1/2
L.
H.S = R.H.S
Отсюда доказано.
Задача 3: Найдите значение cos x, если tan x = 3/4.
Решение:
Учитывая, что tan x = 3/4
Мы знаем, что
tan x = противоположная сторона/прилежащая сторона = 3/4
Чтобы найти гипотенузу, мы используем теорему Пифагораса:
гипотенуза 2 = напротив 2 + рядом 2
H 2 = 3 2 + 4 2
= 6 1 + 5 = 6 1 2
Н = √25 = 5
Теперь cos x = смежная сторона/гипотенуза
cos x = 4/5
Таким образом, значение cos x равно 4/5.
Задача 4. Найдите ∠C (в градусах) и ∠A (в градусах), если ∠B = 45°, BC = 15 дюймов и AC = 12 дюймов.0003 Дано: ∠B = 45°, BC = a = 15 дюймов и AC = b = 12 дюймов. Из закона синусов имеем a/sin A = b/sin B = c/ sin C ⇒ a/sin A = b/sin B ⇒ 15/sin A = 12/sin 45° ⇒ 15/sin A = 12/(1/√2) ⇒ 15/sin A = 12√2 = 16,97 ⇒ sin A = 15/16,97 = 0,8839 ⇒ ∠A = sin -1 (0,8839) = 62,11° Мы знаем, что сумма внутренних углов треугольника равна 18°. Итак, ∠A + ∠B + ∠C = 180° ⇒ 62,11° + 45° + ∠C = 180° ⇒ ∠C = 180° – (62,11° + 45°) = 72,89° Следовательно, ∠A = 62,11° и ∠9 = .8,89 Задача 5. Докажите тождество полууглов функции косинуса. Решение: Тождество половинного угла косинуса: cos (θ/2) = ±√[(1 + cos θ)/2] have, cos 2A = 2 cos 2 A – 1 Теперь замените A на θ/2 с обеих сторон ⇒ cos 2(θ/2) = 2 cos 2 (θ/2) – 1 ⇒ cos θ = 2 cos 2 (θ/2) – 1 ⇒ 2cos 2902 /2) = cos θ + 1 ⇒ cos 2 (θ/2) = (cos θ + 1)/2 ⇒ cos (θ/2) = ±√[(1 + cos θ)/2 ] Отсюда доказано. М. Борна Синус суммы и разности двух углов выглядит следующим образом: Тангенс суммы и разности двух углов sin( α + β ) = sin α cos β + cos α sin β sin( α − β ) = sin α cos β − cos α sin β Косинус суммы и разности двух углов выглядит следующим образом: cos( α + β ) = cos α cos β − sin α sin β cos( α − β ) = cos α cos β + sin α sin β Мы можем доказать эти тождества разными способами. Вот относительно простое доказательство с использованием единичного круга: Доказательство 1 Мы начинаем с единичной окружности (что означает, что она имеет радиус 1) с центром O. Мы строим углы `BOA = alpha` и `AOP = beta`, как показано. Затем мы опускаем перпендикуляр из точки P на ось x в точке T. Точка C является пересечением OA и PT. Затем мы строим линию PR перпендикулярно OA. Наконец, мы опускаем перпендикуляр из R к оси x в S, а другой из R к PT в Q, как показано. Отметим следующее: (1) `/_TPR = alpha`, так как треугольники OTC и PRC подобны. (`/_OTC = /_PRC = 90°` и `/_OCT = /_PCR = 90°-альфа`.) (2) Длина |QT| = |РС| (3) sin (α + β) = |PT| = |PQ| + |QT| = |PQ| + |РС| (4) |PR| = sin (β) (5) В треугольнике PQR |PQ| = |PR| cos (α) (6) Итак, из (4) и (5) |PQ| = sin (β) cos (α). (7) |ИЛИ| = cos (β) (8) В треугольнике OSR |RS| = |ИЛИ| грех (α) (9) Итак, из (7) и (8), |RS| = cos (β) sin (α) (10) Таким образом, из (3), (6) и (9) мы доказали: sin (α + β) = sin (β) cos (α) + cos (β) sin (α) Перестановка дает: sin (α + β) = sin (α) cos (β) + cos (α) sin (β) (11) Из четных и нечетных функций имеем: cos (− β ) = cos( β) и sin (− β ) = −sin(β) (12) Таким образом, заменив β с (− β ), тождество в (10) становится sin ( α − β ) = sin α cos β − cos α sin β [Спасибо Дэвиду Макинтошу за схему приведенного выше доказательства.] Теперь нам нужно доказать cos ( α + β ) = cos α cos β − sin α sin β (13) |ОТ| = cos ( α + β ) (14) В треугольнике ORS имеем: `cos alpha = |OS|/|OR|`. (15) cos (β) = |ИЛИ|, из (7) выше. (16) Из (14) и (15) получаем `cos alpha cos beta= |OS|/|OR|xx|OR| = |ОС|`. (17) В треугольнике QPR имеем `sin alpha = |QR|/|PR|`. (18) sin (β) = |PR|, из (4) выше. (19) Из (17) и (18) получаем `sin alpha sin beta= |QR|/|PR|xx|PR| = |QR|`. (20) Теперь |ОС| − |QR| = |ОТ|. (21) Итак, `cos alpha cos beta — sin alpha sin beta` `= cos(alpha+beta)`. (22) Переставляем, имеем: cos ( α + β ) = cos α cos β − sin α sin β (23) Снова заменяем β на (− β ), и тождество в (22) принимает вид: потому что ( α — β ) = потому что α cos β + sin α sin β Следующее доказательство — стандартное, которое можно найти в большинстве учебников. В нем также используется единичный круг, но оно не такое простое, как первое доказательство. Доказательство 2 Сначала мы докажем тождество косинуса суммы двух углов, а затем покажем, что этот результат можно распространить на все другие заданные тождества. cos (α+β) = cos α cos β − sin α sin β Рисуем окружность радиусом 1 единица с точкой P на окружности в точке (1, 0). Проведем угол α из центра с конечной точкой Q в (cos α, sin α), как показано. [ Q равно (cos α, sin α), потому что гипотенуза равна 1 единице.] Расширим эту идею, нарисовав: a. Угол β с конечными точками при Q (cos α, sin α) и R (cos (α + β), sin (α + β)) б. Угол −β с конечной точкой S (cos (−β), sin (−β)) c. Строки PR и QS , которые эквивалентны по длине. Теперь, используя формулу расстояния из аналитической геометрии, мы имеем: PR 2 = (cos (α + β) − 1) 2 + sin 2 = cos 2 (α + β) − 2 cos (α + β) + 1 + sin 2 (α + β) = 2 − 2cos (α + β) [поскольку sin 2 (α + β) + cos 2 (α + β) = 1] Теперь, используя формулу расстояния на расстоянии QS : QS 2 = (cos α − cos (−β)) 2 + (sin α − sin (−β)) 2 = cos 2 cos α − 2 cos −β) + cos 2 (−β) + sin 2 α − 2sin α sin(−β) + sin 2 (−β) = 2 − 2cos α cos(−β) − 2sin α грех(-β) [начиная с sin 2 α + cos 2 α = 1 и sin 2 (−β) + cos 2 (−2α2 co = 1] .
. 2. Sin, Cos и Tan суммы и разности двух углов
На этой странице…
Доказательства синуса и косинуса сумм и разностей двух углов

Доказательство 1. Использование единичной окружности

Доказательства косинуса

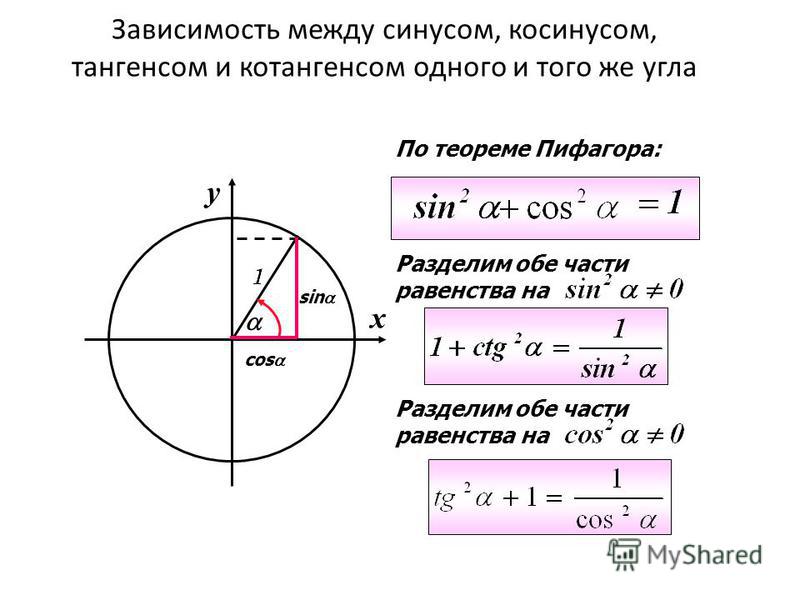 Тем не менее, мы можем многое узнать из следующего доказательства, особенно о том, как работают тригонометрические тождества.
Тем не менее, мы можем многое узнать из следующего доказательства, особенно о том, как работают тригонометрические тождества. Доказательство 2. Использование единичной окружности

потому что β + 2sin α sin β
[поскольку
cos(−β) = cos β (косинус — четная функция) и
sin(−β) = −sinβ (синус — нечетная функция — см.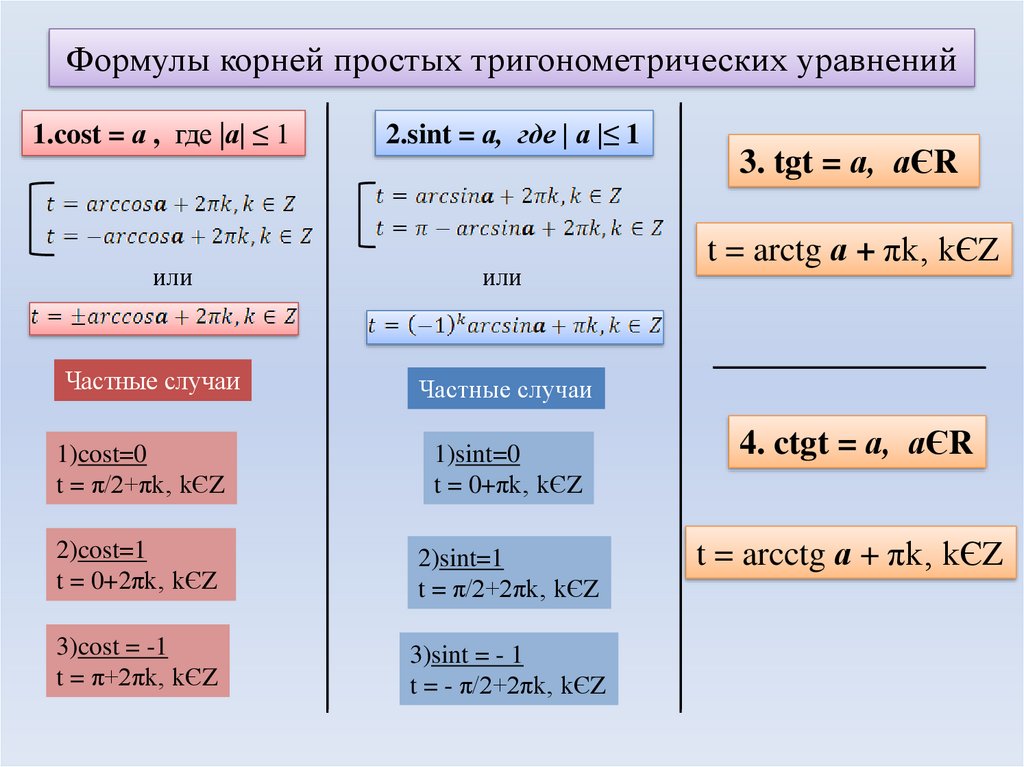 «Четные и нечетные функции» )]
«Четные и нечетные функции» )]
Так как PR = QS , мы можем приравнять два расстояния, которые мы только что нашли:
2 − 2cos (α + β) = 2 − 2cos α cos β + 2sin α sin β
Вычитая 2 с обеих сторон и деля на −2, мы получаем:
cos (α + β) = cos α cos β − sin α sin β
Если мы заменим β на (−β), это тождество станет :
cos (α − β) = cos α cos β + sin α sin β
[поскольку cos(−β) = cos β и sin(−β) = −sinβ]
Синус суммы двух углов
Мы стремимся доказать, что
sin (α + β) = sin α cos β + cos α sin β
Напомним, что (см. фазовый сдвиг)
sin ( θ ) = cos (π/2− θ )
Если θ = α + β, то имеем:
sin (α + β)
= потому что [π/2 — (α + β)]
= потому что [π/2 — α — β)]
Затем мы перегруппируем углы внутри члена косинуса, так как это нам нужно для остальной части доказательства:
cos [π/2 − α − β)] = cos [(π/2 − α) − β]
Используя косинус разности двух углов, который мы только что нашли выше [который сказал
cos (α − β) = cos α cos β + sin α sin β],
имеем:
cos [(π/2 − α) − β]
= cos (π/2 − α) cos (β) + sin (π/2 − α) sin (β)
= sin α cos β + cos α sin β
[Поскольку cos (π/2 − α) = sin α; и sin (π/2 − α) = cos α]
Следовательно:
sin (α + β) = sin α cos β + cos α sin β
Заменив β на (−β), это тождество становится (потому что четных и нечетных функций):
sin (α − β) = sin α cos β − cos α sin β
Мы доказали 4 тождества для синуса и косинуса суммы и разности двух углов.
Резюме:
sin (α + β) = sin α cos β + cos α sin β
sin (α − β) = sin α cos β − cos α sin β
cos (α+β) = cos α cos β − sin α sin β
cos (α − β) = cos α cos β + sin α sin β
Наконец, вот более простое доказательство тождеств с использованием комплексных чисел :
Доказательство 3
Доказательство 3 — Использование комплексных чисел
Экспоненциальная и полярная формы комплексного числа обеспечивают простой способ доказательства основных тригонометрических тождеств.
Предположим, у нас есть 2 комплексных числа, которые мы записываем как:
r 1 e jα = r 1 (cos α + j sin α)
и
r 2 e jβ = r 2 (cos β + j грех β)
Перемножаем эти комплексные числа.
Умножение левых частей:
r 1 e jα × r 2 e jβ = 9 r 56 r 2 e j(α+β)
Мы можем записать этот ответ как:
r 1 r 2 e j(α+β) = r 1 r 2 (cos (α+β) + j sin (α+β)) … (1)
Умножая правые части:
r 1 (cos α + j sin α) × r 2 (cos β + r sin 0 9 0 908 028 90 003 83 1 р 2 (cos α cos β + j cos α sin β + j sin α cos β − sin α sin β)
= r 1 r 2 (cos α cos β − sin α sin β + j (cos α sin β + 2 ) 2)
[так как j 2 = −1]
Теперь приравняем (1) и (2) и разделим обе части на r 1 r 0 : 915
0 3925 912
соз ( α+β) + j sin (α+β) = cos α cos β − sin α sin β + j (cos α sin β + sin α cos β)
Приравнивание действительных частей дает:
cos (α+β) = cos α cos β − sin α sin β
Приравнивание мнимых частей дает:
sin (α+β) = sin α cos β + cos α sin β
Затем мы заменим β на (−β), как и раньше, чтобы получить тождества для sin (α − β) и cos (α − β).
Имеем следующие тождества для тангенса суммы и разности двух углов:
`тангенс(альфа+бета)=(тангенс альфа+тангенс бета)/(1-тангенс альфа\ тангенс бета)`
и
`тангенс (альфа-бета)=(тангенс альфа-тангенс бета)/(1+тангенс альфа\ тангенс бета)`
Доказательство тангенса суммы и разности двух углов
Наше доказательство для них использует тригонометрическое тождество для загара, которое мы встречали ранее.
Доказательство
Случай: `tan(альфа+бета)`
Напомним, что
`tan theta=(sin theta)/(cos theta)`
Итак, полагая θ = α + β и расширяя с помощью наших новых тождеств синуса и косинуса, мы имеем:
`tan(альфа+бета)` `=(sin(альфа+бета))/(cos(альфа+бета))` `=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta- sin alpha sin beta)`
Деление числителя и знаменателя на cos α cos β:
`=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta-sin alpha sin beta)` `-:( cos alpha cos beta)/(cos alpha cos beta`
Упрощение дает нам:
`tan(alpha+beta)=` `(tan alpha+tan beta)/(1-tan alpha\ tan beta)`
Случай: `загар (альфа-бета)`
Замена β на (−β) дает нам
`tan(alpha-beta)=` `(tan alpha-tan beta)/(1+tan alpha\ tan beta)`
[Функция тангенса нечетна, поэтому tan(−β) = − tan β]
Мы доказали тождества двух тангенсов суммы и разности двух углов:
`tan(alpha+beta)=` `(tan alpha+tan beta)/( 1-tan alpha\ tan beta)`
`tan(alpha-beta)=` `(tan alpha-tan beta)/(1+tan alpha\ tan beta)`
Пример 1
Найти точную 9(«o»)`
`=sqrt3/2(1)/sqrt2-1/2(1)/sqrt2`
`=(sqrt3-1)/(2sqrt2)`
Это точное значение для cos 75 o .
Пример 2
Если «sin α = 4/5» (в квадранте I) и «cos β = -12/13» (в квадранте II), оцените «sin(α − β)».
Ответить
Мы используем
sin( α − β ) = sin α cos β − cos α sin β
Сначала нам нужно найти `cos α` и `sin β`.
Если `sin α = 4/5`, то мы можем нарисовать треугольник и найти значение неизвестной стороны по теореме Пифагора (в данном случае 3):
345αОткрыть изображение на новой странице3-4- 5 прямоугольный треугольник
Проделываем то же самое для `cos β = 12/13` и получаем следующий треугольник.
12513βОткрыть изображение на новой странице5-12-13 прямоугольный треугольник
Примечание 1: Мы используем положительное значение «12/13» для расчета требуемого опорного угла относительно «бета».
Примечание 2: Коэффициент синусов положителен как в квадранте I, так и в квадранте II.
Примечание 3: Мы использовали теорему Пифагора, чтобы найти неизвестную сторону, 5.
Теперь о неизвестных соотношениях в вопросе: )
`sin β = 5/13`
(положительно, потому что в квадранте II)
Теперь мы готовы найти требуемое значение sin( α − β ):
`sin(alpha-beta)=` `sin alpha\ cos beta-cos alpha\ sin beta`
`=4/5(-12/13)-3/5(5/13)`
` =(-48-15)/65`
`=(-63)/65`
Это точное значение для sin( α − β ).
Упражнения
1. Найдите точное значение cos 15 o , используя 15 o = 60 o − 45 o
Ответить
Снова используем 30 или -60 9(«o»)`
`=1/2(1)/sqrt2+sqrt3/2(1)/sqrt2`
`=(1+sqrt3)/(2sqrt2)`
2. Если `sin α = 4/5` (в квадранте I) и `cos β = -12/13` (в квадранте II) оценивают `cos(β − α)].`
[Это не то же самое, что пример 2 выше. На этот раз нам нужно найти косинус разности.

 Функция синуса представлена как «sin».
Функция синуса представлена как «sin».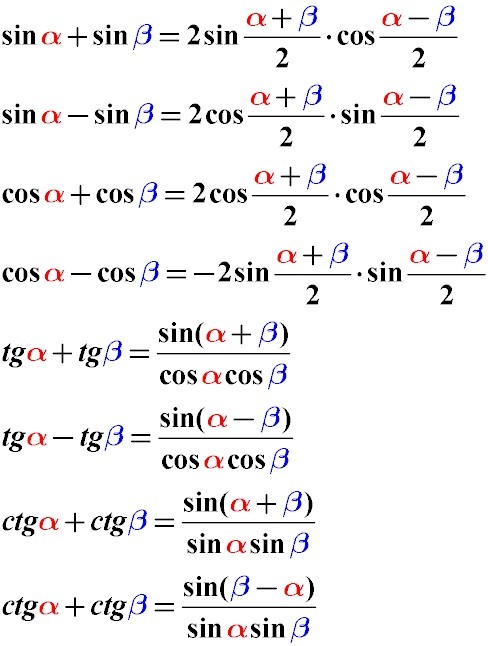
 H.S = R.H.S
H.S = R.H.S