Формулы сложение векторов: Сложение и вычитание векторов

Содержание

Сложение и вычитание векторов. Умножение вектора на число

Высшая математика / Практикум по аналитической геометрии

21.02.201525.11.2015

1. Сложение векторов. Векторы складываются геометрически по правилу параллелограмма или многоугольника.
Правило параллелограмма. Суммой двух векторов

и называют такой третий вектор , выходящий из их общего начала, который служит диагональю параллелограмма, сторонами которого являются сами векторы (рис.1) и обозначают так: .

Рис.1

Правило многоугольника. Чтобы построить сумму любого конечного числа векторов, нужно в конце первого слагаемого вектора построить второй, в конце второго построить третий и т. д. Вектор, замыкающий полученную ломаную линию, представляет собой искомую сумму. Начало его совпадает с началом первого слагаемого вектора, а конец — с концом последнего.

Рис.2

Например, сумма векторов

, , и d получается так (рис.2). Строим векторы

Тогда вектор суммы

Два вектора и , имеющие равные длины, но противоположные направления, называются противоположными векторами (рис.3).

Рис.3

Если вектор

, противоположен вектору , то можно записать:

.
Сумма противоположных векторов равна нуль-вектору:

Сумма векторов удостоверяет:
а) закону переместительности:

б) закону сочетательности:

2. Вычитание векторов. Вычитание двух векторов определяется как действие, обратное сложению.
Разностью двух векторов и называется такой третий вектор , который нужно сложить с вектором , чтобы получить вектор , т.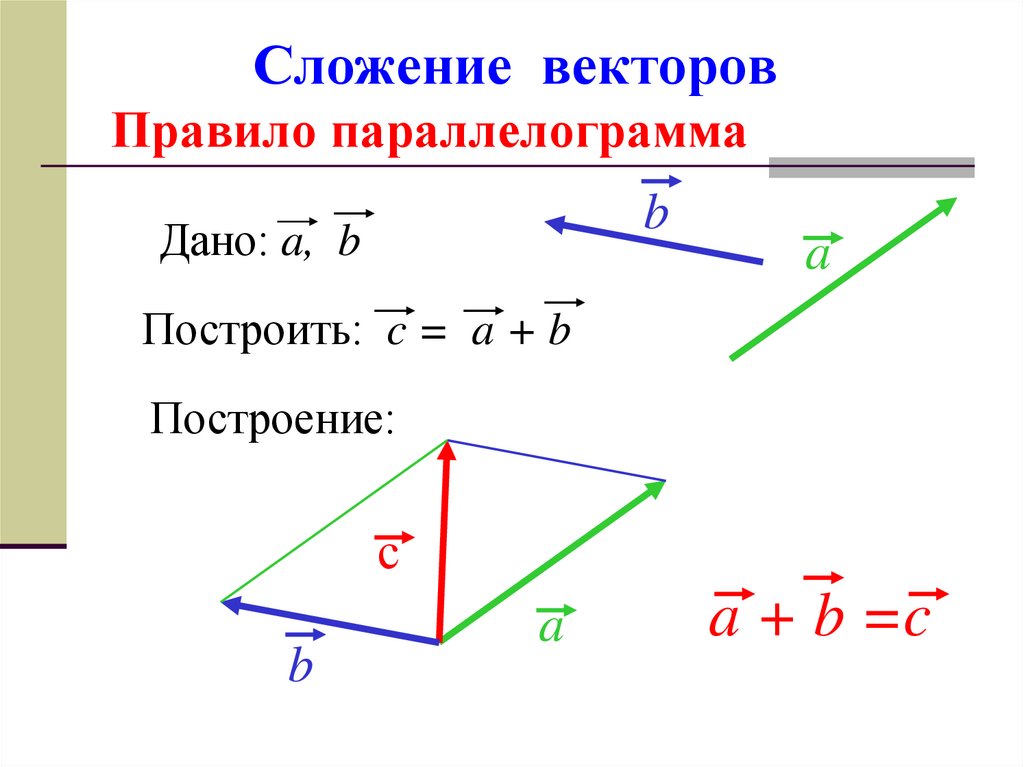 е. , если .
Чтобы из вектора вычесть вектор , нужно отнести их к общему началу и провести вектор из конечной точки вектора-вычитаемого конечную точку вектора-уменьшаемого (рис.4).

Рис.4

То же действие вычитания двух векторов можно произвести иначе.
Чтобы вычесть из вектора вектор , надо прибавить к вектору равный и противоположно направленный вектору вектор (- ).
Построим вектор , длина которого равна длине вектора , а направление его противоположно направлению вектора .
Кроме того, дополним треугольник ABC до параллелограмма АСВВ₁.
Очевидно равно . Следовательно, (рис.4).
Искомая разность

Мы получим следующее равенство:

3. Умножение вектора на скаляр. При умножении вектора на скаляр n получим вектор , коллинеарный с вектором и имеющий длину в n раз больше, чем . Этот новый вектор
имеет одинаковое направление с вектором , если n>0, и противоположное с ним направление, если n

Рис. 5

Если обозначить одноименной буквой с нуликом вверху

вектор длины, равной 1, и того же направления, что и вектор , то из определения умножения вектора на скаляр следует

Единичный вектор направления вектора называется его ортом.

Тегивекторная алгебравекторывычитание векторовразность векторовсложение векторовсумма векторовумножение вектора на число

Сложение и вычитание двух векторов — онлайн калькулятор

В результате сложения двух векторов a и b получается вектор с, все элементы которого равны попарной сумме соответствующих элементов слагаемых векторов. При вычитании тех же векторов все элементы результирующего вектора с равны попарной разности соответствующих элементов.

Нахождение суммы и разности векторов онлайн позволяет обойтись без самостоятельного проведения расчетов.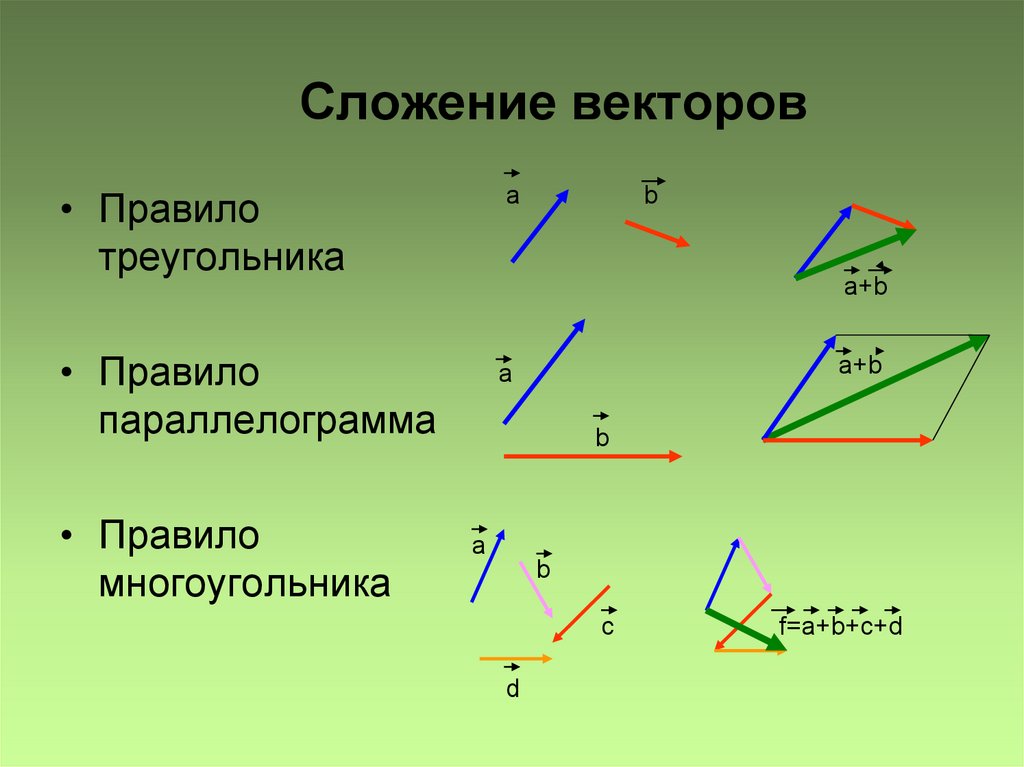 Нужно просто задать векторы (точками или координатами), выбрать действие (сложение или вычитание) и нажать кнопку «рассчитать». После этого онлайн-калькулятор выдаст результат вместе с подробными промежуточными выкладками

Как сложить и вычесть векторы с помощью онлайн-калькулятора

Чтобы сложить или вычесть векторы при помощи онлайн калькулятора, достаточно лишь задать необходимые векторы. Для этого:

Опеделитесь, с какими векторами вы хотите работать. Это могут быть векторы на плоскости или векторы в пространстве.
В рассматриваемом примере, оставим размерность «2». То есть, мы работаем с векторами на плоскости.
Теперь нужно выбрать форму представления векторов: их можно задать координатами либо точками:
Для наглядности, зададим один вектор точками, а второй – координатами.
Теперь в поле «Значение вектора» нужно ввести соответствующие значения. Зададим векторы произвольным образом:
Осталось нажать «Рассчитать» и получить ответ. Отметим, что складываемые и вычитаемые векторы можно также умножать на число. Для наглядности, умножим первый вектор a на 3 и сложим результат с вектором b:

Материалы, которые помогут вам лучше разобраться в теме:

Векторы на плоскости и в пространстве — основные определения
Операции над векторами и их свойства: сложение и умножение
Координаты вектора в декартовой системе координат (ДСК)
Нахождение координат вектора через координаты точек
Векторное произведение — определения, свойства, формулы, примеры и решения
Операции над векторами в прямоугольной системе координат

Ответ:

Решение

Ответ:

list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

Длина вектора. Модуль вектора
Векторное произведение векторов
Умножение вектора на число
Угол между векторами
Смешанное произведение векторов
Скалярное произведение векторов
Определение вектора по двум точкам

Разложение вектора по базису
Проверить являются ли вектора базисом
Ортогональность векторов
Компланарность векторов
Коллинеарность векторов
Проекция вектора на вектор
Площадь треугольника, построенного на векторах

Площадь параллелограмма, построенного на векторах

Как найти сумму и разность векторов без онлайн-калькулятора

Рассмотрим пример с применением формулы для суммы векторов на плоскости.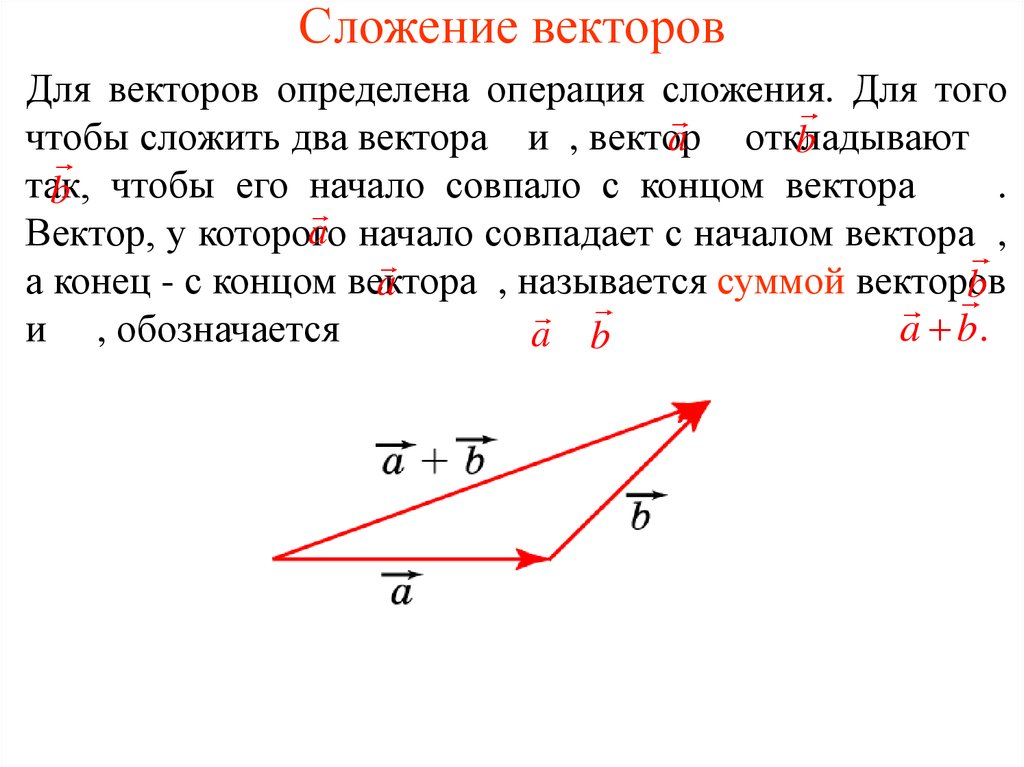 Пусть нужно сложить два вектора: a(3; 5) и b(4; 3). Произведем вычисления:

c→=a→+b→=(ax+bx;ay+by)a→+b→=(3+4;5+3)=(7;8)

Правильность решения можно проверить с помощью онлайн-калькулятора.

Данный сервис будет полезен школьникам и студентам при самостоятельной подготовке к экзаменам и контрольным по векторной алгебре.

Понравился калькулятор? Поделись с друзьями!

Добавление векторов: определение, свойства и методы

Автор Ритеш Кумар Гупта
Последнее изменение 19-10-2022

Сложение векторов: Учащимся крайне необходимо понять свойства векторов, прежде чем выполнять с ними какие-либо математические операции. Векторы можно использовать для выполнения широкого круга математических операций, сложение — одна из таких операций. Результат сложения векторов можно определить, просто сложив два вектора (или равнодействующую). Эта процедура добавления двух или более векторов более сложна, чем скалярное сложение.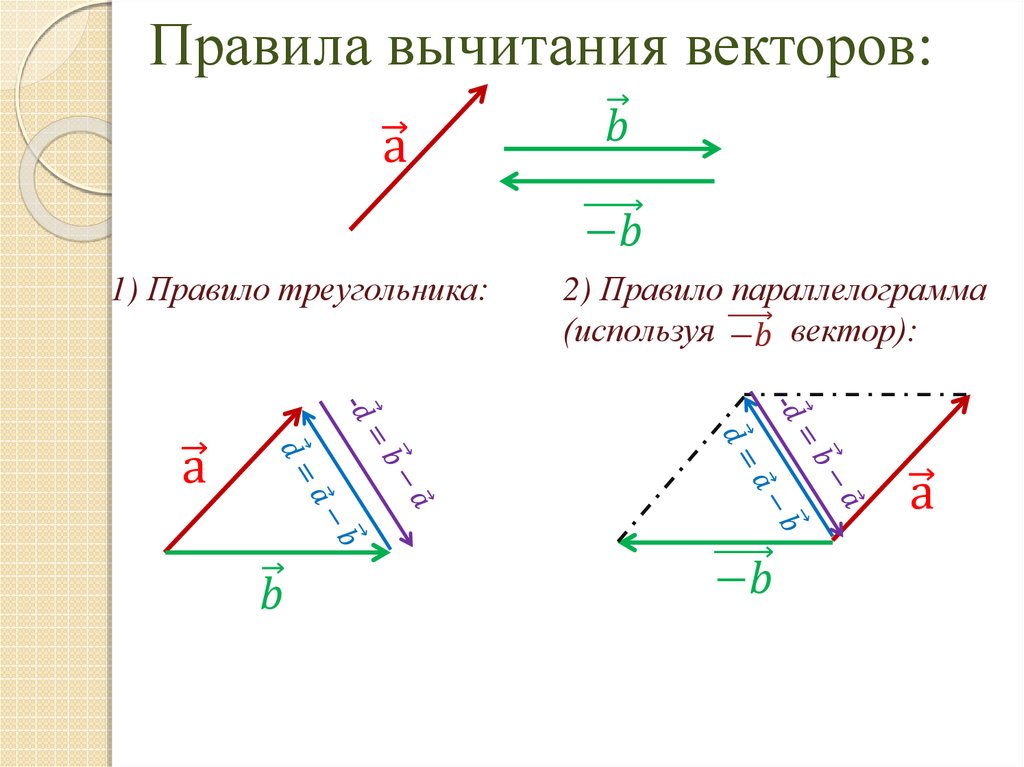

Общее пройденное расстояние в этом случае составляет $20$ миль. Однако смещения нет. Каждое из северных и южных смещений является векторной величиной, а противоположные направления вызывают индивидуальные смещения. Давайте подробно рассмотрим добавление векторов и их свойств на решенных примерах.

Векторы записываются буквами и стрелками над ними и представляются как комбинация направления и величины.

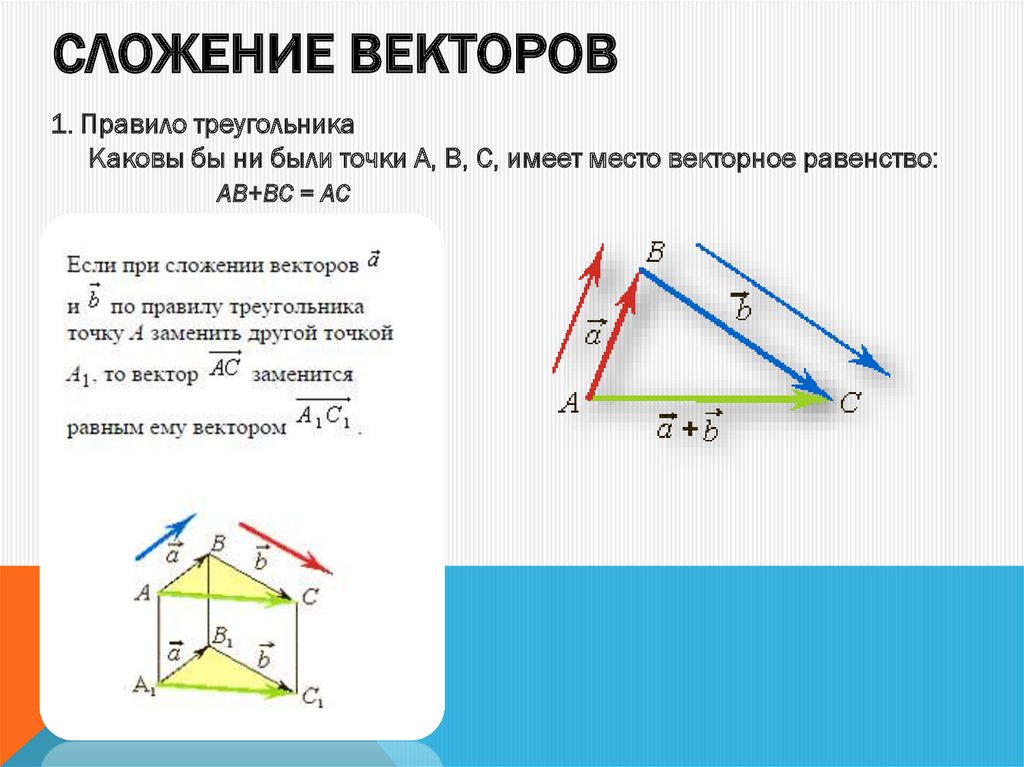
Операция сложения двух или более векторов для получения суммы векторов называется сложением векторов. Сложение векторов осуществляется двумя способами: либо по закону треугольника, либо по закону параллелограмма.
Если два вектора имеют одинаковое направление, сумма их величин в одном и том же направлении равна сумме их направлений.

Если два вектора направлены в противоположные стороны, равнодействующая векторов представляет собой разность величин между двумя векторами и находится в направлении большего вектора. Используя сложение векторов, два вектора, $\overrightarrow x $ и $\overrightarrow y, $ могут быть сложены вместе, и результирующий вектор может быть выражен как $\overrightarrow R = \overrightarrow x + \overrightarrow y . $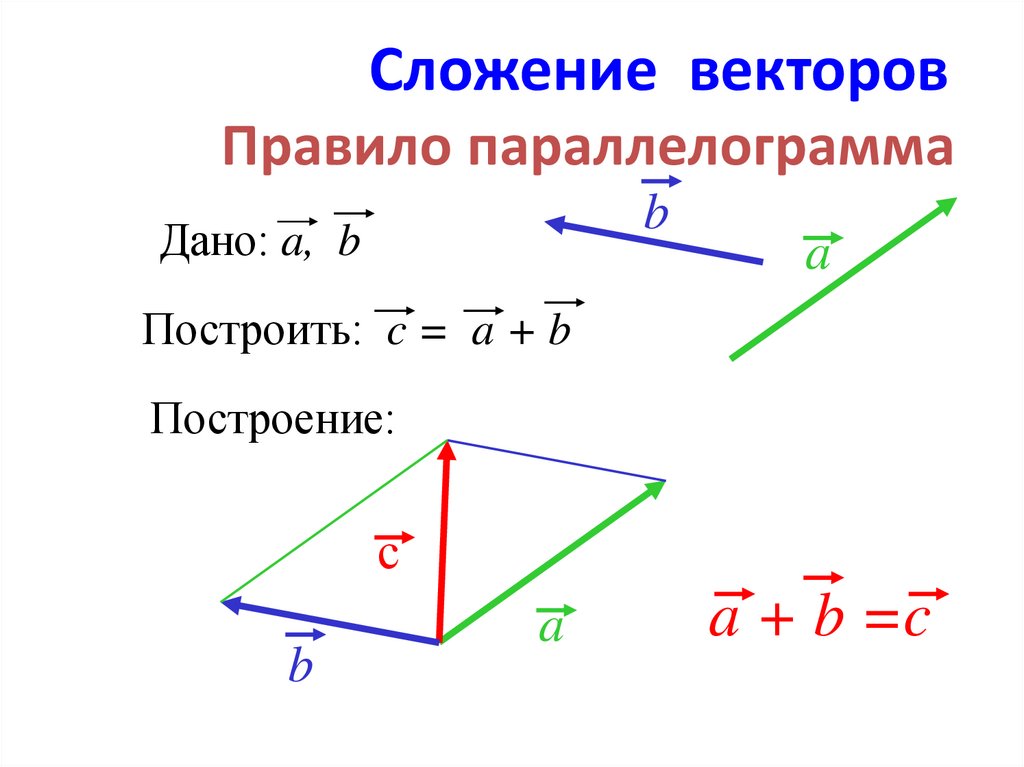

Прежде чем мы сможем узнать о свойствах сложения векторов в математике, мы должны сначала понять требования, которые должны выполняться при сложении векторов.

Ниже приведены требования:
1. Вместе можно объединять только векторы одного типа. Ускорение, например, должно добавляться только к ускорению, а не к перемещению.
2. Мы не можем складывать векторы ни с какими скалярами. то есть мы не можем добавить $2$ с вектором $\overrightarrow a .$

Рассмотрим два вектора $\overrightarrow a $ и $\overrightarrow b $, где $\overrightarrow a = {a_1} i + {a_2}j + {a_3}k$ и $\overrightarrow b = {b_1}i + {b_2}j + {b_3}k.$ Тогда результирующий вектор $\overrightarrow R = \overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1}} \right)i + \left( {{a_2} + {b_2}} \right)j + \left( {{a_3} + {b_3} } \право)к.$

Сложение векторов: свойства

Сложение векторов отличается от сложения алгебраических чисел. Вот некоторые из наиболее важных свойств, о которых следует помнить при сложении векторов:

1. Сложение векторов является коммутативным: это означает, что порядок векторов не влияет на результат сложения. Если два вектора $\overrightarrow a $ и $\overrightarrow b $ сложить вместе, то $\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a $

2. Сложение векторов является ассоциативным: взаимное группирование векторов не влияет на результат при сложении трех или более векторов.
$\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)$

3. Сложение векторов является дистрибутивным: это указывает, что сумма скалярных времен суммы двух векторов равна сумме скалярных времен двух векторов по отдельности.
$м\влево ({\overrightarrow a + \overrightarrow b} \right) = m\overrightarrow a + m\overrightarrow b $

4. Существование идентичности: для любого вектора $\overrightarrow a ,\,\overrightarrow a + \overrightarrow 0 = \overrightarrow a $
Здесь $\overrightarrow 0 $ является аддитивной идентичностью.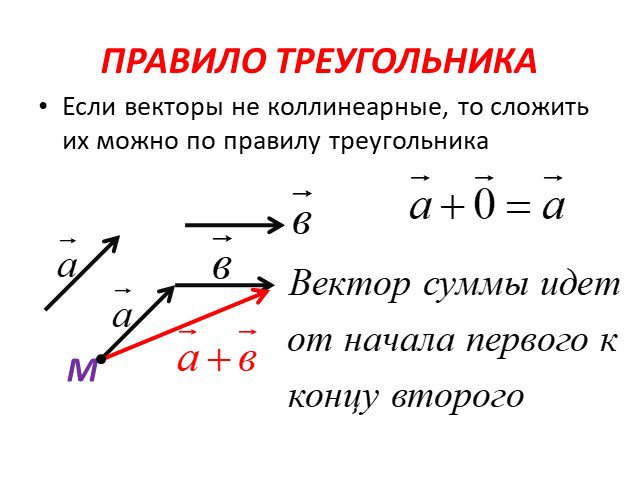

5. Существование обратного: Для любого вектора $\overrightarrow a ,\,\overrightarrow a + \left( { – \overrightarrow a } \right) = \overrightarrow 0 $
Итак, аддитивный обратный существует для каждого вектор.

Добавление векторов: формулы и законы

Добавление векторов осуществляется двумя способами:

1. Треугольный закон сложения векторов : Треугольный закон сложения векторов гласит, что когда два вектора представляются как две стороны треугольника с одинаковым порядком величины и направлением, представляются величина и направление результирующего вектора. по третьей стороне треугольника.

$AB = \overrightarrow a $ и $BC = \overrightarrow b ,$ затем результирующая строка $AC = \overrightarrow a + \overrightarrow b $
Если $a = $ величина $ \overrightarrow а $ 92} + 2\,ab\,\cos\,\theta } \)

2. Параллелограммный закон сложения векторов : Параллелограммный закон сложения векторов утверждает, что если два вектора действуют вдоль двух смежных сторон параллелограмма (с равной длине сторон), оба направлены в сторону от общей вершины, равнодействующая представлена диагональю параллелограмма, проходящей через одну и ту же общую вершину.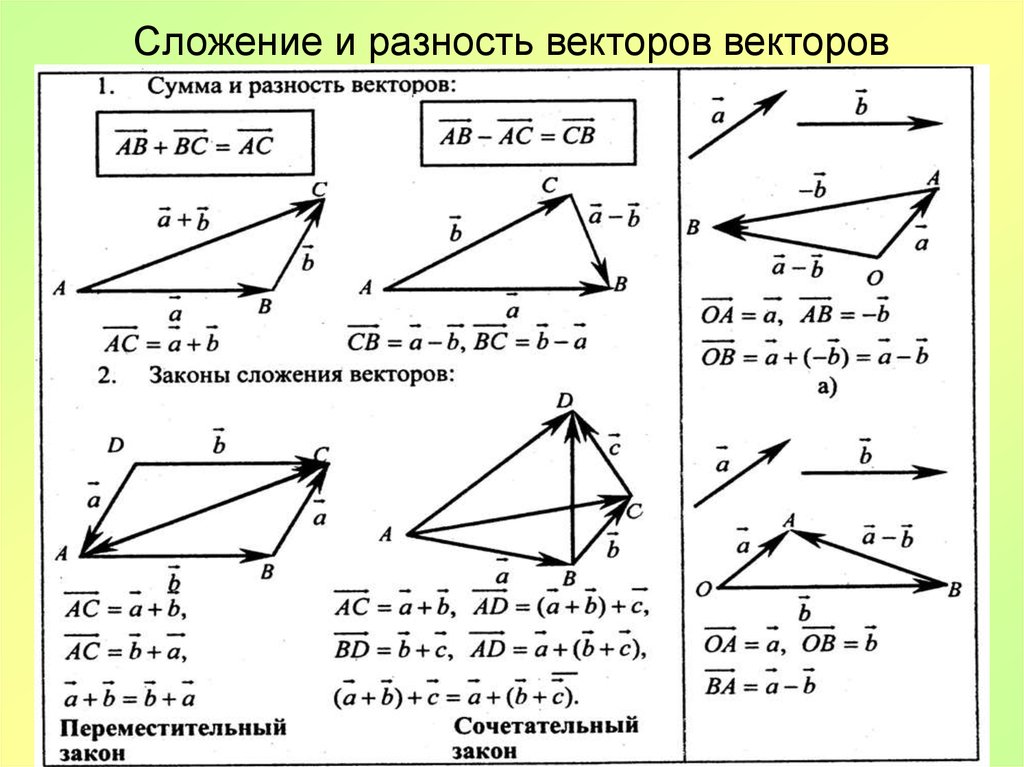

Если $\overrightarrow a $ и $\overrightarrow b $ представляют смежные стороны параллелограмма $ABCD$, как показано на рисунке, то результатом является диагональ $AC$ параллелограмма $ABCD$, проходящий через одну и ту же общую вершину.

Следовательно, мы можем заключить, что треугольные законы сложения векторов и параллелограммные законы сложения векторов эквивалентны.

Решенные примеры – добавление векторов

Давайте разберемся с концепцией добавления векторов примеров с решениями.

Q.1. Если векторы положения точек $A\left( {3,\,4} \right),\,B\left( {5,\, – 6} \right)$ и $C\left( {4,\, – 1} \right)$ являются $\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c $ соответственно, вычислить $\overrightarrow a + 2\overrightarrow b – 3\overrightarrow в.$
Ответ: Пусть $\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c $ являются векторами положения точек $A\left( {3,\,4} \right),\ ,B\left( {5,\, – 6} \right)$ и $C\left( {4,\, – 1} \right). $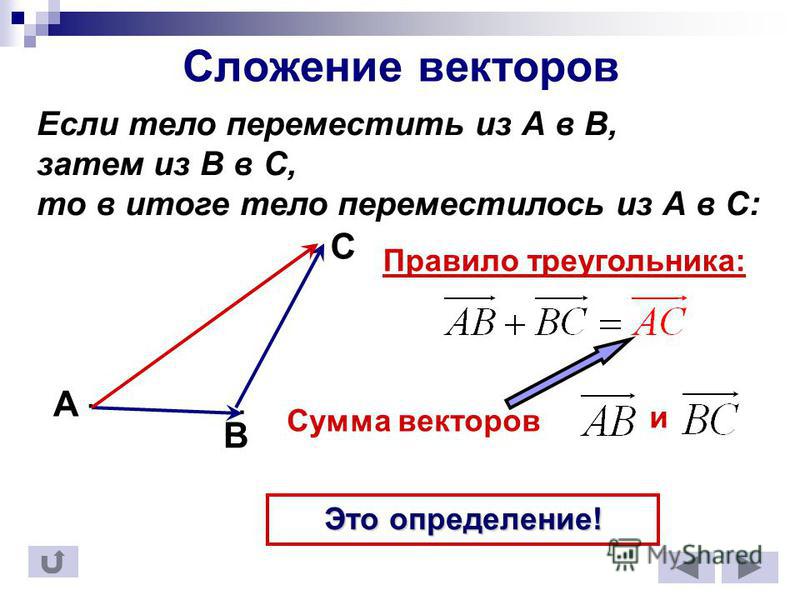
Тогда $\overrightarrow a = 3\ widehat i + 4\widehat j,\,\overrightarrow b = 5\widehat i – 6\widehat j$ и $\overrightarrow c = 4\widehat i – \widehat j$
Следовательно,$\overrightarrow a + 2\overrightarrow b – 3\overrightarrow c = 3\widehat i + 4\widehat j + 2\left( {5\widehat i – 6\widehat j} \right) – 3\left({4\widehat i – \широкая шляпа j }\справа)$ 9{\rm{o}}}} \)
$ = \sqrt {225 + 625 + \frac{{750}}{2}} $
$ = \sqrt {850 + 375} $
\ ( = \sqrt {1225} \)
$=35.$

Q.3. Если $D$ является серединой стороны $BC$ треугольника $ABC$ такого, что $\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {\lambda AD} , $ запишите значение $\lambda .$
Ответ: Дана $D$ — середина стороны $BC$ треугольника $ABC$ такая, что $\overrightarrow { AB} + \overrightarrow {AC} = \overrightarrow {\lambda AD} .$
Пусть $\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c $ являются векторами положения $AB, BC$ и $CA. $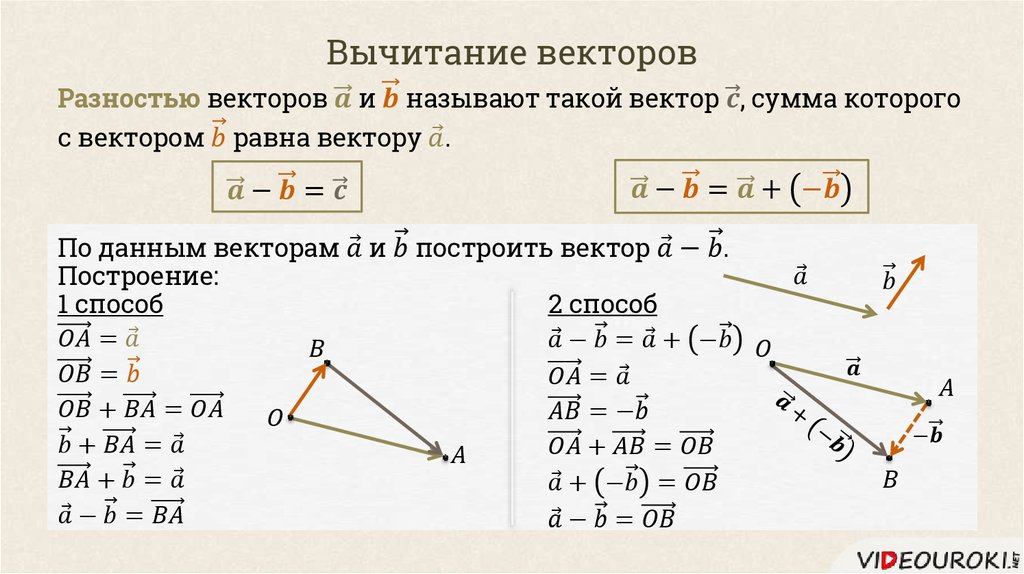
Теперь вектор положения $D $ равно $\frac{{\overrightarrow b + \overrightarrow c}}{2}.$
Тогда $\overrightarrow {AB} = \overrightarrow b — \overrightarrow a $ и $\overrightarrow { AC} = \overrightarrow c – \overrightarrow a $
$\overrightarrow {AD} = \frac{{\overrightarrow b + \overrightarrow c}}}{2} \,- \overrightarrow a $
Теперь мы имеем ,
$\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {\lambda AD} ,$
$ \Rightarrow \overrightarrow b — \overrightarrow a + \overrightarrow c — \overrightarrow a = \lambda \left( {\ frac {{\overrightarrow b + \overrightarrow c}}}{2} — \overrightarrow a} \right )$
$ \Rightarrow \overrightarrow b + \overrightarrow c – 2\overrightarrow a = \lambda \left( {\ frac {{\overrightarrow b + \overrightarrow c – 2\overrightarrow a}}{2}} \ справа)$
$ \стрелка вправо \лямбда = 2$

Q.4. Если $\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c $ являются векторами положения вершин $A, B$ и $C$ соответственно треугольника $ABC,$ напишите значение $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA. } $
Ответ: Даны $\overrightarrow a , \overrightarrow b , \overrightarrow c $ являются векторами положения $A, B$ и $C$ соответственно.
Затем $\overrightarrow {AB} = \overrightarrow b – \overrightarrow a $
$\overrightarrow {BC} = \overrightarrow c – \overrightarrow b $
$\overrightarrow {CA} = \overrightarrow a – \overrightarrow c $
Рассмотрим, $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow b – \overrightarrow a + \overrightarrow c – \overrightarrow b + \overrightarrow a – \ c $
$ = \overrightarrow 0 $

Q.5. Докажите, что сумма трех векторов, определяемых медианами треугольника, направленными из вершин, равна нулю.
Ответ: Пусть $\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c $ являются векторами положения вершин $A, B$ и $C$ соответственно.
Тогда мы знаем, что вектор положения центроида $O$ треугольника равен $\frac{{\overrightarrow a + \overrightarrow b + \overrightarrow c}}{3}. $
Таким образом, сумма трех векторов $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow a – \left( {\ frac {{\overrightarrow a + \overrightarrow b + \overrightarrow c }}{3}} \right) + \overrightarrow b – \left( {\frac{{\overrightarrow a + \overrightarrow b + \overrightarrow c}}{3}} \right) + \overrightarrow c – \left ( {\ frac {{\ overrightarrow a + \ overrightarrow b + \ overrightarrow c}} {3}} \right) $
$ = \ left( {\ overrightarrow a + \ overrightarrow b + \ overrightarrow c} \ right ) — 3 \ влево ( {\ гидроразрыва {{\ overrightarrow a + \ overrightarrow b + \ overrightarrow c}} {3}} \ right) = \ overrightarrow 0 $
Значит, сумма трех векторов, определяемых медианами треугольника, направленными из вершин, равна нулю.

Резюме

В этой статье мы узнали о сложении векторов, их свойствах и примерах. Процедура сложения двух или более векторов отличается от скалярного сложения. Только векторы одного типа могут быть объединены вместе.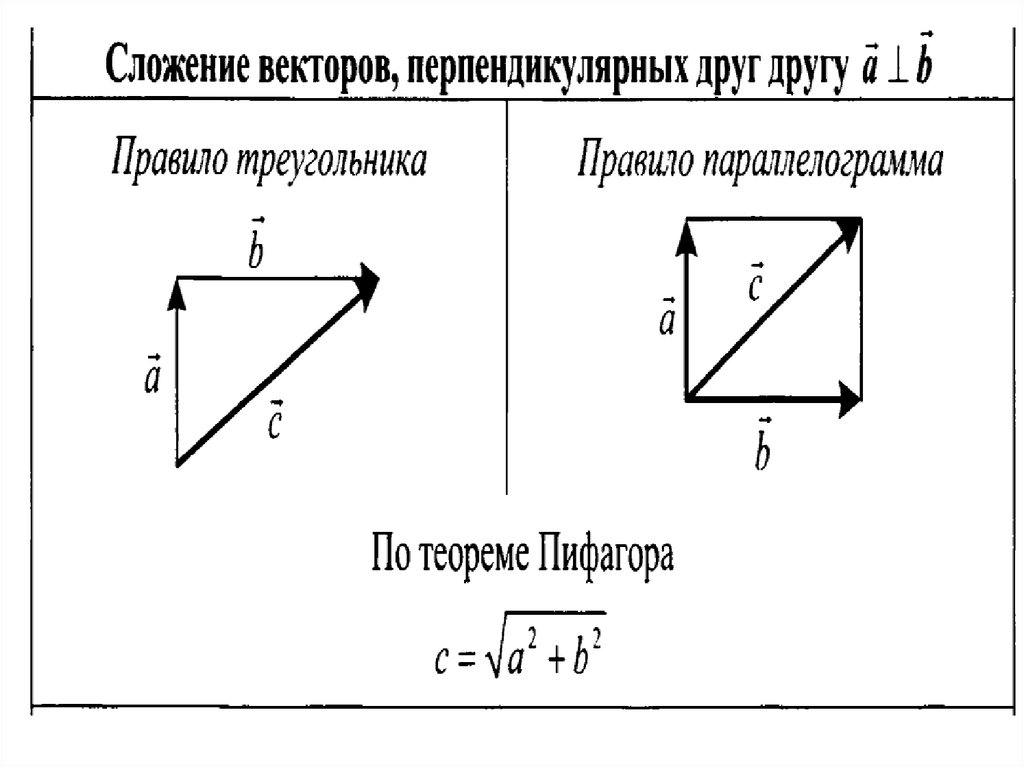 Мы не можем складывать векторы со скалярами. Есть два способа сложения векторов: закон треугольника и закон параллелограмма сложения векторов, которые эквивалентны.

Изучение концепции суммы векторов

Часто задаваемые вопросы (FAQ) – Добавление векторов

Часто задаваемые вопросы, связанные с добавлением векторов, перечислены ниже:

Q.1.1.1.1.1.1. Объясните сложение векторов.
Ответ: Операция сложения двух или более векторов для получения векторной суммы называется сложением векторов. Добавление векторов осуществляется двумя способами: либо по закону треугольника, либо по закону параллелограмма. Когда два вектора располагаются лицом к хвосту, сумма векторов определяется путем рисования вектора от свободного хвоста к свободной голове.

Q.2. Как реализовать сложение векторов?

Ответ: Если два вектора имеют одинаковое направление, сумма их величин в одном и том же направлении равна сумме их направлений.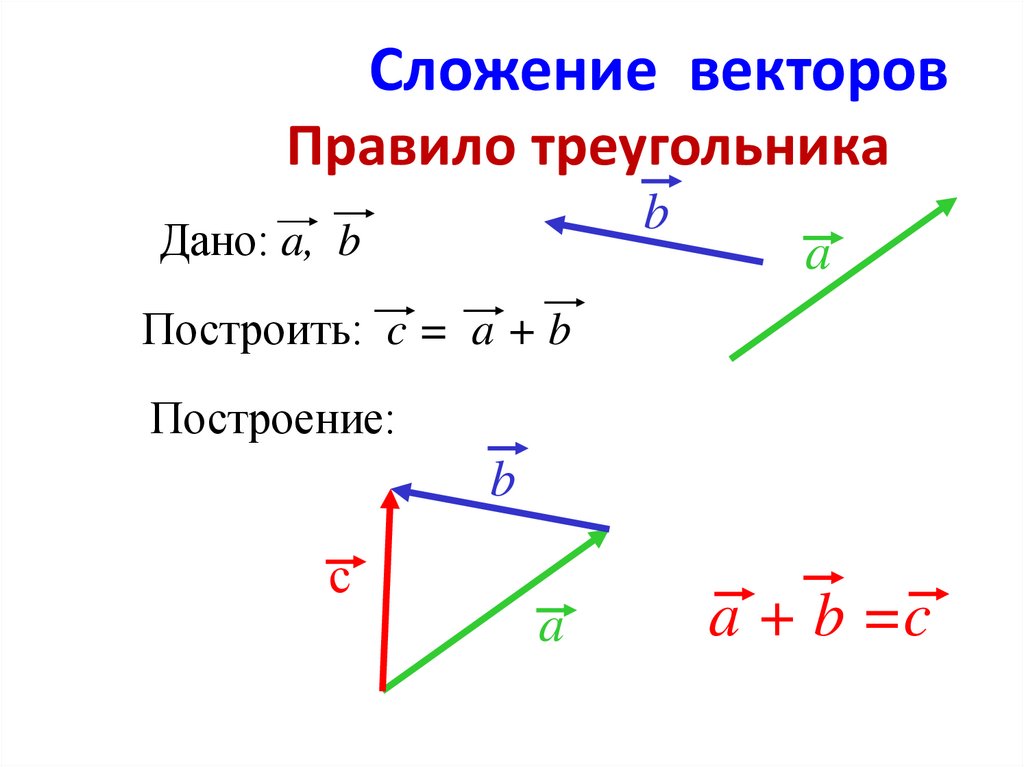

Если два вектора находятся в противоположных направлениях, результирующая векторов представляет собой разность величин между двумя векторами и находится в направлении большего вектора. Во всех остальных случаях для сложения векторов мы используем либо закон треугольника, либо закон параллелограмма.

Q.3. Каковы примеры сложения векторов?
Ответ: Рассмотрим два вектора ${\overrightarrow a}$ и ${\overrightarrow b}$, где $\overrightarrow a = {a_1}\widehat i + {a_2}\widehat j + { a_3}\widehat k$ и $\overrightarrow b = {b_1}\widehat i + {b_2}\widehat j + {b_3}\widehat k.$ Тогда результирующий вектор $\overrightarrow R = \overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1}} \right)\widehat i + \left( {{a_2} + {b_2}} \right)\widehat j + \left( {{a_3} + {b_3}} \right)\widehat k.$

Например:
1. если $\overrightarrow a = \widehat i + 2\widehat j + 3\widehat k$ и \(\overrightarrow b = 4\widehat i + 5\widehat j + 6\widehat k .

\) Тогда результирующий вектор $\overrightarrow R = \overrightarrow a + \overrightarrow b = 5\widehat i + 7\widehat j + 9\widehat k.$
2. Если $\overrightarrow a + \overrightarrow b + \overrightarrow c $ — векторы положения точек $A\left( {3,\,4} \right)\,B\left( {5,\, – 6} \right)$ и $C\left( {4,\, – 1} \right),$ соответственно. Теперь предположим, что нам нужно найти $\overrightarrow a + 2\overrightarrow b – 3\overrightarrow c $
Затем $\overrightarrow a = 3\widehat i + 4\widehat j,\,\overrightarrow b = 5\widehat i – 6\widehat j$ и $\overrightarrow c = 4\widehat i – \widehat j$
Следовательно, $\overrightarrow a + 2\overrightarrow b – 3\overrightarrow c = 3\widehat i + 4\widehat j + 2\left( {5\widehat i – 6\widehat j} \right) — 3\left( {4\widehat i — \widehat j} \right)$
$ = 3\widehat i + 4\widehat j + 10\widehat i — 12\widehat j — 12\widehat i + 3 \широкая шляпа j$
$ = \широкая шляпа i – 5\широкая шляпа j$

Q.4. Для чего используется сложение векторов?
Ответ: Добавление векторов играет важную роль в технике, которая включает силы, электрические поля, магнитные поля, импульс, угловой момент, положение, траектории, поляризацию, плотность тока, намагниченность, скорости, крутящий момент и т.