Формулы сложения синусов и косинусов: Формулы сложения и вычитания тригонометрических функций. Формулы сложения

Сложение синусов и косинусов. Формулы тригонометрии

Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны. А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.

1. Формулы сложения:

косинусы всегда «ходят парами»: косинус-косинус, синус-синус. И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.

Синусы — «смешиваются» : синус-косинус, косинус-синус.

2. Формулы суммы и разности:

косинусы всегда «ходят парами». Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.

Синусы — «смешиваются» :

3.

Формулы преобразования произведения в сумму и разность.

Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому

Когда мы получаем пару синусов? При вычитании косинусов. Отсюда:

«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:

В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется. Принципиален порядок только для второй формулы. Но, чтобы не путаться, для простоты запоминания мы во всех трех формулах в первых скобках берем разность

а во вторых — сумму

Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать. А дают уверенность: если воспользоваться шпаргалкой не удастся, формулы можно легко вспомнить.

Продолжаем наш разговор про наиболее употребляемые формулы в тригонометрии. Важнейшие из них – формулы сложения.

Определение 1

Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.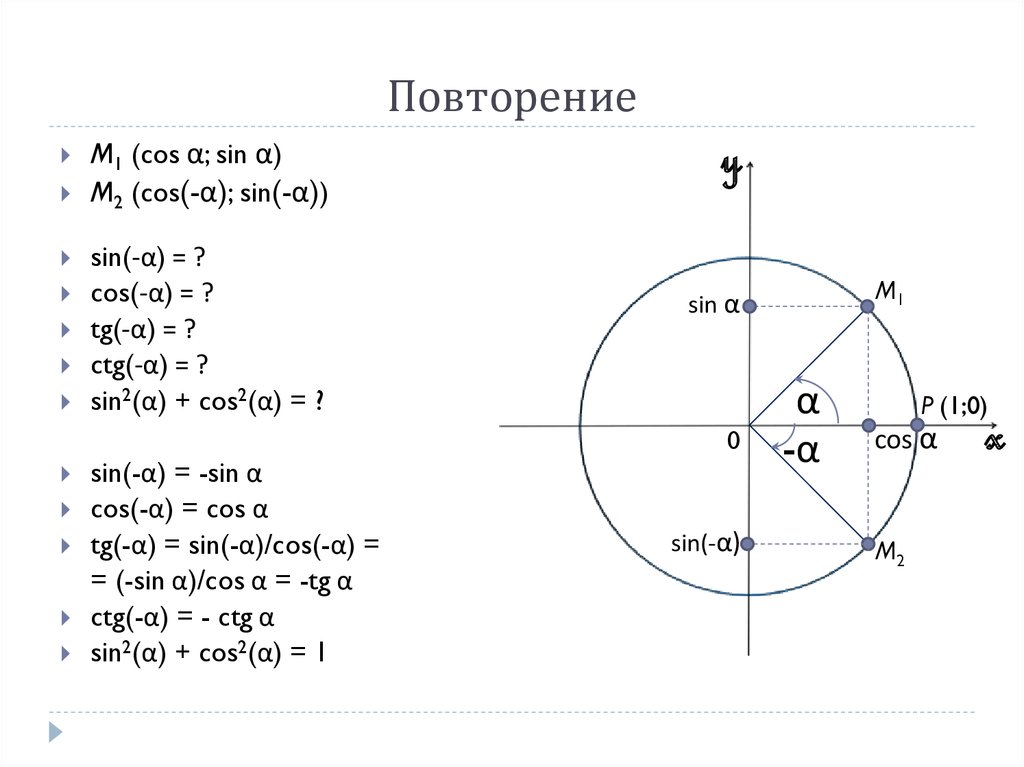

Для начала мы приведем полный список формул сложения, потом докажем их и разберем несколько наглядных примеров.

Yandex.RTB R-A-339285-1

Выделяют восемь основных формул: синус суммы и синус разности двух углов, косинусы суммы и разности, тангенсы и котангенсы суммы и разности соответственно. Ниже приведены их стандартные формулировки и вычисления.

1.Синус суммы двух углов можно получить следующим образом:

Вычисляем произведение синуса первого угла на косинус второго;

Умножаем косинус первого угла на синус первого;

Складываем получившиеся значения.

Графическое написание формулы выглядит так: sin (α + β) = sin α · cos β + cos α · sin β

2. Синус разности вычисляется почти так же, только полученные произведения нужно не сложить, а вычесть друг из друга. Таким образом, вычисляем произведения синуса первого угла на косинус второго и косинуса первого угла на синус второго и находим их разность. Формула пишется так: sin (α — β) = sin α · cos β + sin α · sin β

3. Косинус суммы. Для него находим произведения косинуса первого угла на косинус второго и синуса первого угла на синус второго соответственно и находим их разность: cos (α + β) = cos α · cos β — sin α · sin β

4. Косинус разности: вычисляем произведения синусов и косинусов данных углов, как и ранее, и складываем их. Формула: cos (α — β) = cos α · cos β + sin α · sin β

5. Тангенс суммы. Эта формула выражается дробью, в числителе которой – сумма тангенсов искомых углов, а в знаменателе – единица, из которой вычитается произведение тангенсов искомых углов. Все понятно из ее графической записи: t g (α + β) = t g α + t g β 1 — t g α · t g β

6. Тангенс разности. Вычисляем значения разности и произведения тангенсов данных углов и поступаем с ними схожим образом. В знаменателе мы прибавляем к единице, а не наоборот: t g (α — β) = t g α — t g β 1 + t g α · t g β

7. Котангенс суммы. Для вычислений по этой формуле нам понадобятся произведение и сумма котангенсов данных углов, с которыми мы поступаем следующим образом: c t g (α + β) = — 1 + c t g α · c t g β c t g α + c t g β

8.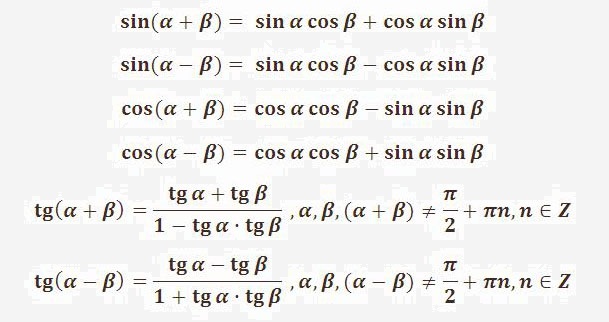 Котангенс разности. Формула схожа с предыдущей, но в числителе и знаменателе – минус, а не плюс c t g (α — β) = — 1 — c t g α · c t g β c t g α — c t g β .

Вы, наверное, заметили, что эти формулы попарно схожи. При помощи знаков ± (плюс-минус) и ∓ (минус-плюс) мы можем сгруппировать их для удобства записи:

sin (α ± β) = sin α · cos β ± cos α · sin β cos (α ± β) = cos α · cos β ∓ sin α · sin β t g (α ± β) = t g α ± t g β 1 ∓ t g α · t g β c t g (α ± β) = — 1 ± c t g α · c t g β c t g α ± c t g β

Соответственно, мы имеем одну формулу записи для суммы и разности каждого значения, просто в одном случае мы обращаем внимание на верхний знак, в другом – на нижний.

Определение 2

Мы можем взять любые углы α и β , и формулы сложения для косинуса и синуса подойдут для них. Если мы можем правильно определить значения тангенсов и котангенсов этих углов, то формулы сложения для тангенса и котангенса будут также для них справедливы.

Как и большинство понятий в алгебре, формулы сложения могут быть доказаны. Первая формула, которую мы докажем, — формула косинуса разности. Из нее потом можно легко вывести остальные доказательства.

Уточним основные понятия. Нам понадобится единичная окружность. Она получится, если мы возьмем некую точку A и повернем вокруг центра (точки O) углы α и β . Тогда угол между векторами O A 1 → и O A → 2 будет равняться (α — β) + 2 π · z или 2 π — (α — β) + 2 π · z (z – любое целое число). Получившиеся вектора образуют угол, который равен α — β или 2 π — (α — β) , или он может отличаться от этих значений на целое число полных оборотов. Взгляните на рисунок:

Мы воспользовались формулами приведения и получили следующие результаты:

cos ((α — β) + 2 π · z) = cos (α — β) cos (2 π — (α — β) + 2 π · z) = cos (α — β)

Итог: косинус угла между векторами O A 1 → и O A 2 → равняется косинусу угла α — β , следовательно, cos (O A 1 → O A 2 →) = cos (α — β) .

Вспомним определения синуса и косинуса: синус — функция угла, равная отношению катета противолежащего угла к гипотенузе, косинус – это синус дополнительного угла. Следовательно, точки

A 1 и A 2 имеют координаты (cos α , sin α) и (cos β , sin β) .

Получим следующее:

O A 1 → = (cos α , sin α) и O A 2 → = (cos β , sin β)

Если непонятно, взгляните на координаты точек, расположенных в начале и конце векторов.

Длины векторов равны 1 , т.к. у нас единичная окружность.

Разберем теперь скалярное произведение векторов O A 1 → и O A 2 → . В координатах оно выглядит так:

(O A 1 → , O A 2) → = cos α · cos β + sin α · sin β

Из этого мы можем вывести равенство:

cos (α — β) = cos α · cos β + sin α · sin β

Таким образом, формула косинуса разности доказана.

Теперь мы докажем следующую формулу – косинуса суммы. Это проще, поскольку мы можем воспользоваться предыдущими расчетами. Возьмем представление α + β = α — (- β) . У нас есть:

cos (α + β) = cos (α — (- β)) = = cos α · cos (- β) + sin α · sin (- β) = = cos α · cos β + sin α · sin β

Это и есть доказательство формулы косинуса суммы.

В последней строчке использовано свойство синуса и косинуса противоположных углов.

Формулу синуса суммы можно вывести из формулы косинуса разности. Возьмем для этого формулу приведения:

вида sin (α + β) = cos (π 2 (α + β)) . Так
sin (α + β) = cos (π 2 (α + β)) = cos ((π 2 — α) — β) = = cos (π 2 — α) · cos β + sin (π 2 — α) · sin β = = sin α · cos β + cos α · sin β

А вот доказательство формулы синуса разности:

sin (α — β) = sin (α + (- β)) = sin α · cos (- β) + cos α · sin (- β) = = sin α · cos β — cos α · sin β
Обратите внимание на использование свойств синуса и косинуса противоположных углов в последнем вычислении.

Далее нам нужны доказательства формул сложения для тангенса и котангенса. Вспомним основные определения (тангенс – отношение синуса к косинусу, а котангенс –наоборот) и возьмем уже выведенные заранее формулы. У нас получилось:

t g (α + β) = sin (α + β) cos (α + β) = sin α · cos β + cos α · sin β cos α · cos β — sin α · sin β

У нас получилась сложная дробь. Далее нам нужно разделить ее числитель и знаменатель на cos α · cos β , учитывая что cos α ≠ 0 и cos β ≠ 0 , получаем:
sin α · cos β + cos α · sin β cos α · cos β cos α · cos β — sin α · sin β cos α · cos β = sin α · cos β cos α · cos β + cos α · sin β cos α · cos β cos α · cos β cos α · cos β — sin α · sin β cos α · cos β

Теперь сокращаем дроби и получаем формулу следующего вида: sin α cos α + sin β cos β 1 — sin α cos α · s i n β cos β = t g α + t g β 1 — t g α · t g β .
У нас получилось t g (α + β) = t g α + t g β 1 — t g α · t g β . Это и есть доказательство формулы сложения тангенса.

Следующая формула, которую мы будем доказывать – формула тангенса разности. Все наглядно показано в вычислениях:

t g (α — β) = t g (α + (- β)) = t g α + t g (- β) 1 — t g α · t g (- β) = t g α — t g β 1 + t g α · t g β

Формулы для котангенса доказываются схожим образом:
c t g (α + β) = cos (α + β) sin (α + β) = cos α · cos β — sin α · sin β sin α · cos β + cos α · sin β = = cos α · cos β — sin α · sin β sin α · sin β sin α · cos β + cos α · sin β sin α · sin β = cos α · cos β sin α · sin β — 1 sin α · cos β sin α · sin β + cos α · sin β sin α · sin β = = — 1 + c t g α · c t g β c t g α + c t g β
Далее:
c t g (α — β) = c t g   (α + (- β)) = — 1 + c t g α · c t g (- β) c t g α + c t g (- β) = — 1 — c t g α · c t g β c t g α — c t g β

Формулы преобразования синусов и косинусов.

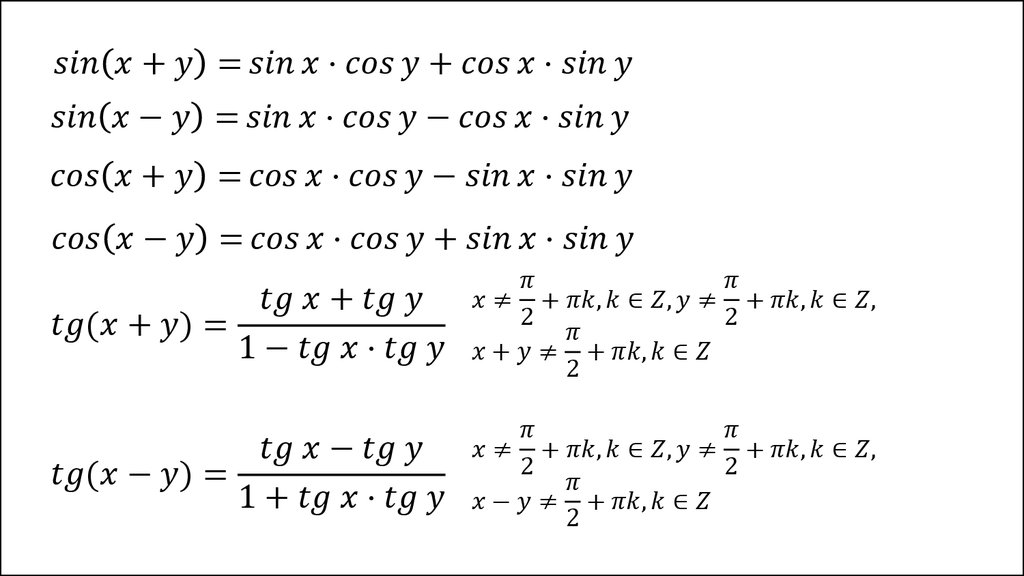Формулы сложения: доказательство, примеры

Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.

В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.

Навигация по странице.

Основные тригонометрические тождества

Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.

Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .

Формулы приведения

Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.

Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .

Формулы сложения

Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.

Формулы двойного, тройного и т.д. угла

Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.

Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .

Формулы половинного угла

Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.

Их вывод и примеры применения можно посмотреть в статье .

Формулы понижения степени

Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов.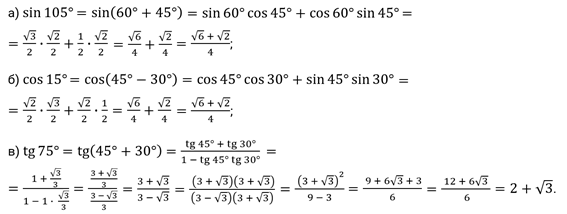 Иными словами, они позволяют понижать степени тригонометрических функций до первой.

Формулы суммы и разности тригонометрических функций

Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.

Формулы произведения синусов, косинусов и синуса на косинус

Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .

Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.

Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.

Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Copyright by cleverstudents

Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.

Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.

tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}

tg \alpha \cdot ctg \alpha = 1

Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha} , а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha} — будет являться котангенсом.

Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .

Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha , которые отличны от \frac{\pi}{2}+\pi z , а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha , отличного от \pi z , z — является целым числом. {2} \alpha = 1 . Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14 .

По условию \frac{\pi}{2}

Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.

ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .

Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

Yandex.RTB R-A-339285-1

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2

Формулы суммы и разности для косинусов

cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2

Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.

Определения формул сумм и разности синусов и косинусов

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.

Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.

Вывод формул суммы и разности синусов и косинусов

Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже

sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β

Также представим сами углы в виде суммы полусумм и полуразностей.

α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим

sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2

Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)

sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу

sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2

Вывод формулы суммы косинусов

cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2

Вывод формулы разности косинусов

cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.

Истоки тригонометрии

Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.

Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.

Начальный этап

Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.

Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.

Сферическая тригонометрия

Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».

Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.

Прямоугольный треугольник

Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.

Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.

Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.

Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.

Определение

Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.

Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.

Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.

Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.

Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.

Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.

Простейшие формулы

В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.

Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.

Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.

Формулы двойного угла и сложения аргументов

Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.

Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.

Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.

Теоремы

Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.

Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.

Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники.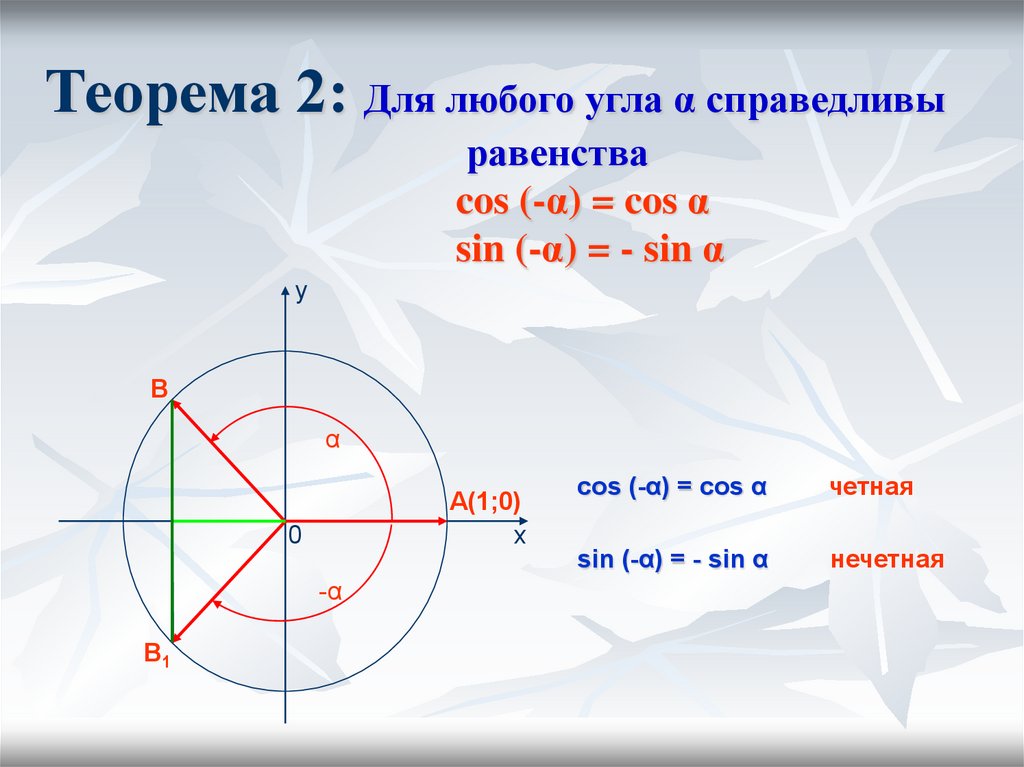 Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.

Ошибки по невнимательности

Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.

Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.

Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.

В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.

Применение

Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.

В заключение

Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.

Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.

Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.

Самые часто задаваемые вопросы

Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.

Какие виды оплаты вы принимаете? Ответ Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.

Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами? Ответ В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.

Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.

Что делать при обнаружении в документе опечаток и ошибок? Ответ Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.

Что нужно сделать, чтобы заказать диплом в вашей компании? Ответ Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.

Последние отзывы

Алексей:

Мне нужно было приобрести диплом для устройства на работу по профессии менеджер. И самое главное, что и опыт, и навыки у меня есть, но без документа я не могу, никуда устроится. Попав на ваш сайт, все-таки решился на покупку диплома. Диплом был выполнен за 2 дня!! Теперь у меня есть работа, о которой я раньше и не мечтал!! Спасибо!

Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.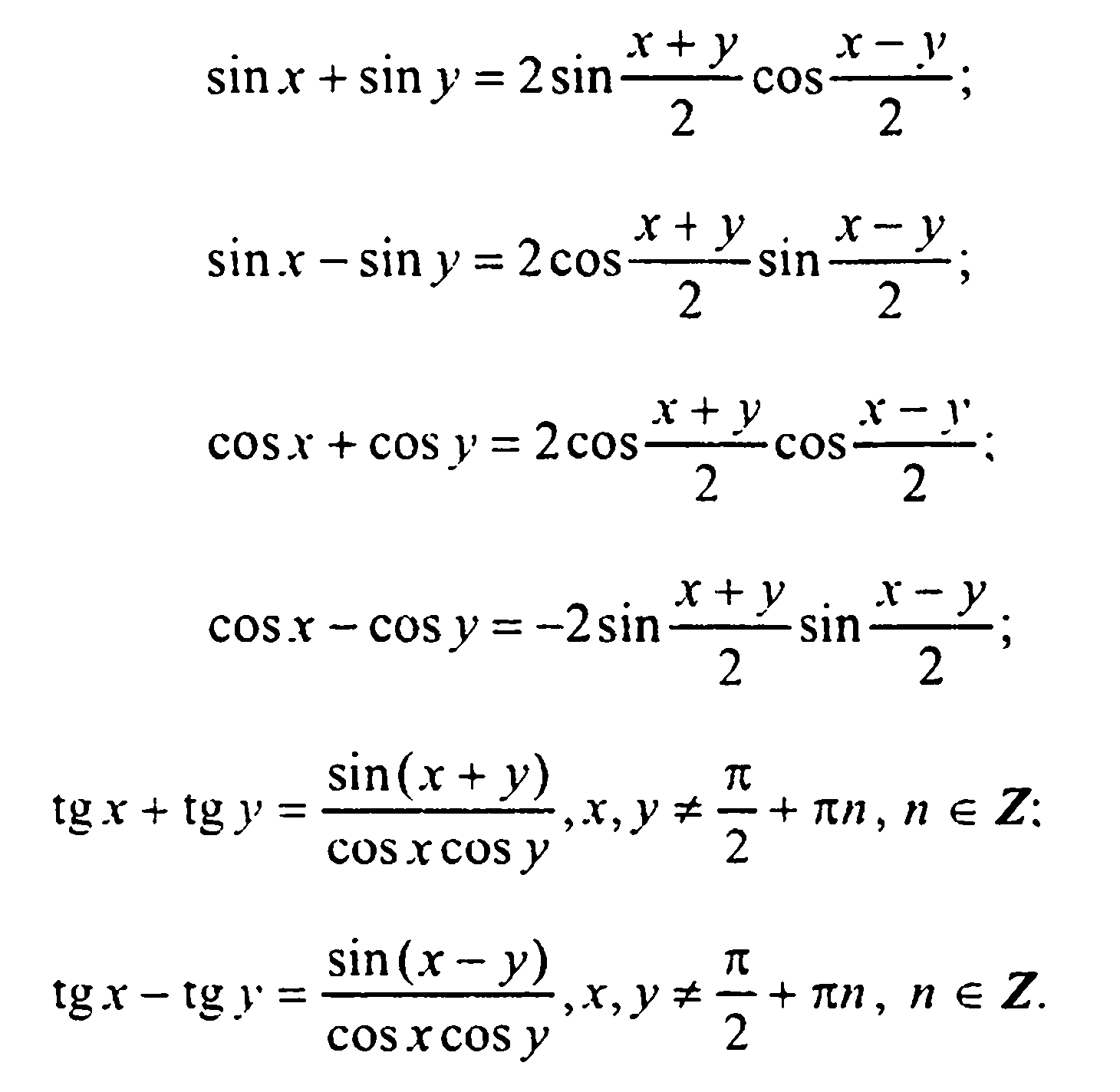
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

375619 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Владимир Александрович Кузьмин

«

Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить. Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии. Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.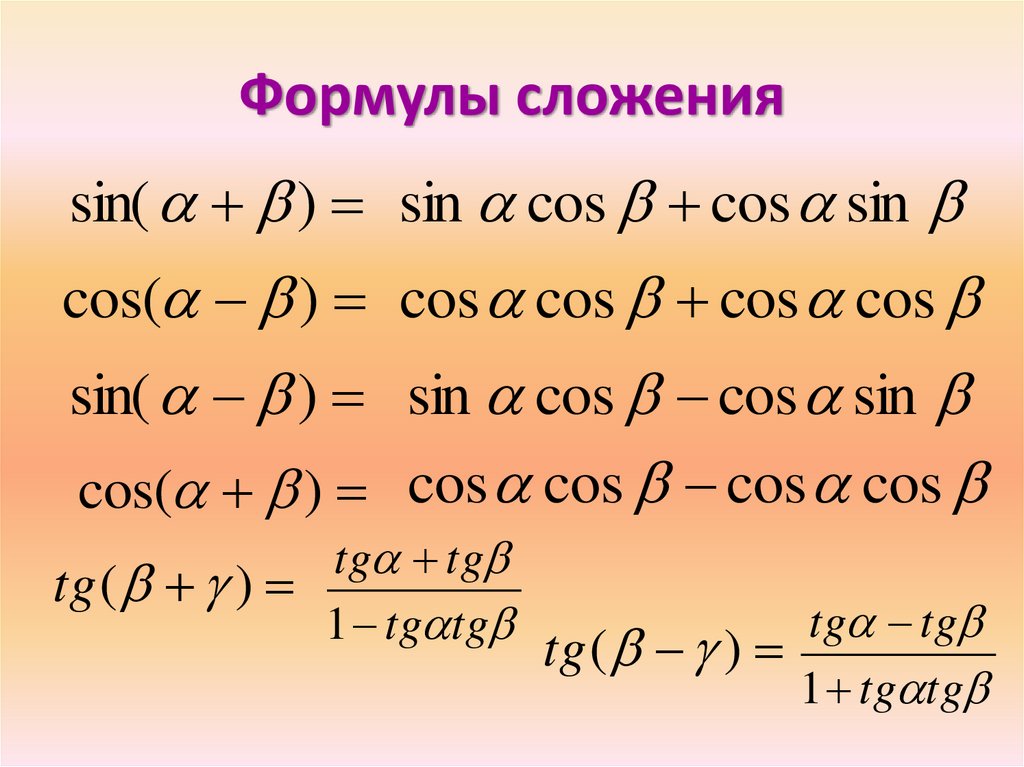 В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!

«

Вячеслав Юрьевич Матыкин

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Клиентам

• Репетиторы по математике
• Репетиторы по русскому языку
• Репетиторы по химии
• Репетиторы по биологии
• Репетиторы английского языка
• Репетиторы немецкого языка

Репетиторам

• Регистрация
• Публичная оферта
• Библиотека
• Бан-лист репетиторов

Партнеры

• ChemSchool
• PREPY. RU
• Class

тригонометрия — Интуиция формулы сложения для синуса и косинуса

Это отличный вопрос, потому что я убежден, что все классные тригонометрические тождества имеют простые пояснительные диаграммы.

В «единично-гипотенузовом» прямоугольном треугольнике $\треугольнике ABC$ (с прямым углом при $C$) катет, противолежащий $A$, имеет длину $\sin A$, а сторона, прилежащая к $A$, имеет длину $ \cos А$. По пропорциональности, если гипотенуза имеет длину $c$, то катет, противоположный $A$, имеет длину $c\;\sin A$, а катет, примыкающий к $A$, имеет длину $c\;\cos A$. Но вы это знаете.

Итак, для построения диаграмм триггерных тождеств,

Везде, где вы видите что-то вроде «этот $\cdot \sin(\text{это})$», вы пытаетесь представить этот термин катетом прямоугольного треугольника, гипотенуза которого равна «этому», а угол, противоположный катету, равен « что». Точно так же представьте «этот $\cdot \cos(\text{это})$» с отрезком , прилегающим к углу «этот» в треугольнике с гипотенузой «этот».

… и везде, где это возможно, использовать теоремы о параллельных прямых и равных углах. 92$ и $\tan\phi = q/p$.

Для левой стороны нам понадобится прямоугольный треугольник с гипотенузой $p$ и еще один с гипотенузой $q$, каждый с острым углом $\theta$. Мы хотим расположить эти треугольники так, чтобы катет, противоположный $\theta$ в $p$-треугольнике, и катет , примыкающий к $\theta$ в $q$-треугольнике, образовывали прямой отрезок, представляющий сумму . их длин. Вот так (с $\theta$, представленным черной точкой, так как я перерабатываю старое изображение):

92$ предполагает, что нам нужно изобразить $r$ как гипотенузу прямоугольного треугольника с катетами $p$ и $q$. По интересному совпадению , угол между гипотенузами нашего $p$-треугольника и $q$-треугольника сам по себе является прямым углом! (Почему?) Таким образом, соединение других концов этих отрезков дает нам $r$.

На самом деле, теперь у нас также есть $\phi$ (белая точка), поскольку $q/p$ явно является отношением «противоположные к смежным» для отмеченного угла.

Чтобы закончить диаграмму, нам нужен прямоугольный треугольник с гипотенузой $r$ и острым углом $\theta+\phi$ (стратегически расположенный так, чтобы левая и правая части тождества были явно равны равно ). Ну, у нас есть прямоугольный треугольник с гипотенузой $r$, но этого недостаточно; углы неправильные. Где мы можем увидеть $\theta+\phi$ (сумма черной точки и белой точки)? Хммм… Посмотрите на верхний левый угол диаграммы: у нас есть угол $\theta$ рядом с и угол $\phi$ … вместе они составляют $\theta+\phi$; и, эй! Они находятся рядом с сегментом $r$! Если бы мы только могли сделать $r$ гипотенузой прямоугольного треугольника с углом $\theta+\phi$.

Это просто: начерти перпендикуляр!

Затем новый (фиолетовый) отрезок напротив $\theta+\phi$ в треугольнике с гипотенузой $r$; он должен иметь длину $r\;\sin(\theta+\phi)$.

Поскольку новый отрезок явно конгруэнтен нижнему отрезку (это противоположные стороны прямоугольника), мы продемонстрировали, что части идентичности триггера равны . Миссия выполнена!

На самом деле мы можем сделать немного немного лучше. Это не круто, что фиолетовый сегмент закрывает другие части диаграммы. Но как мы можем его сдвинуть? Мы нарисовали его, потому что нам нужен был треугольник с $\theta+\phi$ внутри него; чтобы переместить его, нам понадобится еще один такой угол … о, подождите … Обратите внимание, что стороны диаграммы параллельны (перпендикулярны общему отрезку)? и как этот сегмент $r$ является их поперечным ? Хмммм…

Теперь мы можем провести еще один удобный —и не затеняющий— перпендикуляр для представления $r\;\sin(\theta+\phi)$.

Вот вам и схема тождества $p\;\sin\theta + q\;\cos\theta = r\;\sin(\theta+\phi)$.

---

Для формул суммы углов:

$$\begin{align} \sin(\alpha + \beta) &= \sin \alpha\;\cos\beta + \cos\alpha\;\sin\beta \\ \cos(\alpha + \beta) &= \cos \alpha\;\cos\beta — \sin\alpha\;\sin\beta \end{align}$$

нужно немного потрудиться, чтобы понять, как представлять составные продукты. Возьмем, к примеру, $\sin\alpha\;\cos\beta$. Это ситуация «$\text{this}\cdot\sin(\text{that})$» (с «this»$=\cos\beta$ и «that»$=\alpha$) или » $\text{this}\cdot\cos(\text{that})$» ситуация? Это может быть и то, и другое, но давайте предположим первое; это означает, что мы хотели бы, чтобы на нашей диаграмме был прямоугольный треугольник с гипотенуза $\cos\beta$ и острый угол $\alpha$. Но, чтобы создать нашу гипотенузу длины $\cos\beta$, нам нужно, чтобы она была катетом, смежным с $\beta$ в треугольнике с гипотенузой $1$: мы должны сложить один треугольник поверх другого!

Хорошая новость заключается в том, что «другой» катет в (синем) треугольнике с гипотенузой $\cos\beta$ будет иметь длину $\cos\alpha\;\cos\beta$, что удобно, потому что мы понадобится один из них. О, и эй… Другой катет в (розовом) треугольнике с гипотенузой $1$ имеет длину $\sin\beta$, которая может быть гипотенузой удобного нового треугольника с катетами $\cos\alpha\;\sin \beta$ и $\sin\alpha\;\sin\beta$; они нам тоже нужны!

Удобно, мы обнаружили, что создали (внизу слева) угол $\alpha+\beta$. Как и прежде, мы можем опустить простой перпендикуляр, чтобы ограничить этот угол внутри треугольника с гипотенузой $1$; но, как и прежде, мы можем сделать немного лучше:

Это дает нам (белый) треугольник с гипотенузой $1$ и катетами $\sin(\alpha+\beta)$ и $\cos(\alpha+\beta) $, расположенных таким образом, что отрезок sine явно представляет собой сумму двух построенных нами вертикальных отрезков, и что косинус отрезка явно разность отрезков по горизонтали.

С очень небольшой корректировкой мы превращаем диаграмму в иллюстрацию тождеств угловой разности

$$\begin{align} \sin(\alpha-\beta) &= \sin\alpha\;\cos\beta — \cos\alpha\;\sin\beta \\ \cos(\alpha-\beta) &= \cos\alpha\;\cos\beta + \sin\alpha\;\sin\beta \end{align}$$

---

Я призываю вас поискать больше диаграмм тождеств, как в качестве простого упражнения для понимания вашей триггерной системы, так и в качестве попытки определить, что такое тождества на самом деле пытаюсь вам сказать. (Поищите в Интернете «доказательство триггера без слов», и вы увидите, насколько полезными могут быть эти вещи.)

Например, вот простое графическое доказательство закона косинусов, созданное с использованием стратегий построения диаграмм, описанных здесь:

Как только вы начнете думать об исчислении, вы можете подумать о диаграммах для «степенных рядов» синуса и косинуса, секанса и тангенса. (Если вы найдете диаграммы для косеканса и котангенса, дайте мне знать!)

Формулы произведения для суммирования — Что такое формулы произведения для суммирования?

Формулы произведения на сумму используются для выражения произведения функций синуса и косинуса в виде суммы. Они получены из формул суммы и разности тригонометрии. Эти формулы очень полезны при решении интегралов от тригонометрических функций. Давайте изучим произведение, чтобы суммировать формулы вместе с доказательствами и примерами.

Что такое формулы произведения для суммирования?

Формулы произведения на сумму представляют собой набор формул из тригонометрических формул и как мы обсуждали в предыдущем разделе, они выводятся из формул суммы и разности. Вот формулы произведения для суммирования, и вы можете увидеть их вывод под формулами.

Формулы произведения на сумму

Существует 4 формулы произведения на сумму, которые широко используются в качестве тригонометрических тождеств.

1. sin A cos B = (1/2) [ sin (A + B) + sin (A — B)]
2. потому что A sin B = (1/2) [ sin (A + B) — sin (A — B)]
3. cos A cos B = (1/2) [ cos (A + B) + cos (A — B)]
4. sin A sin B = (1/2) [ cos (A — B) — cos (A + B) ]

Вывод формулы произведения на сумму

Мы будем использовать формулы суммы/разности тригонометрии для вывода формулы произведения на сумму. Давайте вспомним формулы суммы и разности sin и cos и присвоим числа каждой из формул суммы/разности.

sin (A + B) = sin A cos B + cos A sin B … (1)
sin (A — B) = sin A cos B — cos A sin B … (2)
cos (A + B) = cos A cos B — sin A sin B … (3)
cos (A — B) = cos A cos B + sin A sin B … (4)

Вывод формулы sin A cos B = (1/2) [ sin (A + B) + sin (A — B) ]:

Складывая уравнения (1) и (2), получаем

sin (A + B) + sin (A — B) = 2 sin A cos B

Разделив обе части на 2,

sin A cos B = (1/2) [ sin (A + B) + sin (A — B)]

Вывод формулы cos A sin B = (1/2) [sin (A + B) — sin (A — B)]:

Вычитание (2) из ​​(1),

sin (A + B) — sin (A — B) = 2, потому что A sin B

Разделив обе части на 2,

, cos A sin B = (1/2) [ sin (A + B) — sin (A – B)]

Вывод формулы cos A cos B = (1/2) [ cos (A + B) + cos (A — B) ]

Складывая уравнения (3) и (4), получаем

cos (A + B) + cos (A — B) = 2 cos A cos B

Деление обеих частей на 2,

cos A cos B = (1/2) [ cos (A + B) + cos (A — B) ]

Вывод формулы sin A sin B = (1/2 ) [ cos (A — B) — cos (A + B) ]

Вычитание (3) из (4),

cos (A — B) — cos (A + B) = 2 sin A sin B

Деление обеих частей на 2,

sin A sin B = (1/2) [ cos (A — B) — cos (A + B) ]

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Забронируйте бесплатный пробный урок

Вы можете увидеть применение формулы произведения для суммирования в разделе ниже.

Примеры формул произведения на сумму

Пример 1: Найдите значение sin 75 ^o  sin 15 ^o  без фактического вычисления значений sin 75 ^{o o}

 

Решение:

Используя одну из формул суммирования произведения,

sin A sin B = (1/2) [ cos (A — B) — cos (A + B) ]

Заменитель A = 75 ^O и B = 15 ^O , мы получаем

SIN 75 ^O SIN 15 ^O = (1/2) [Cos (75 ^O — 15 ^O ) [Cos (75 ^O — 15 ^O ) — cos (75 ^o  + 15 ^o ) ]

= (1/2) [ cos 60 ^o  — cos 90 ^o ]

= (1/2) — [ (1/2) [ (1/2) [ (1/2) [ 0] (из таблицы тригонометрии)

= 1/4

Ответ: sin 75 ^o sin 15 ^o  = 1/4.

Пример 2: Экспресс 2 cos 5x sin 2x как сумма/разность.

Решение:

Используя одну из формул суммирования произведения,

cos A sin B = (1/2) [ sin (A + B) — sin (A — B) ]

Замена A = 5x и B = 2x в приведенной выше формуле,

cos 5x sin 2x = (1/2) [ sin (5x + 2x) — sin (5x — 2x) ]

cos 5x sin 2x = (1/2) [sin 7x — sin 3x]

Умножить обе части на 2,

2 cos 5x sin 2x = sin 7x — sin 3x

Ответ: 2 cos 5x sin 2x = sin 7x — sin 3x.

Пример 3:  Найдите значение интеграла ∫ sin 3x cos 4x dx.

Решение:

Используя одну из формул суммирования произведения,

sin A cos B = (1/2) [ sin (A + B) + sin (A — B)]

Подстановка A = 3x и B = 4x с обеих сторон,

sin 3x cos 4x = (1/2) [ sin (3x + 4x) + sin (3x — 4x) ] = (1/2) [ sin 7x — sin x] (потому что грех (-х) = — грех х).

Теперь мы оценим данный интеграл, используя указанное выше значение.

∫ sin 3x cos 4x dx = ∫ (1/2) [ sin 7x — sin x] dx

= (1/2) [ -cos (7x) / 7 + cos x] + C (с использованием интегрирования подстановкой )

Ответ: ∫ sin 3x cos 4x dx = (1/2) [ -cos (7x) / 7 + cos x] + C.

Часто задаваемые вопросы о формулах произведения для суммирования

?

Формулы произведения для суммирования в тригонометрии — это формулы, которые используются для преобразования произведения тригонометрических функций в сумму тригонометрических функций. Есть 4 важных продукта для суммирования формул.

1. sin A cos B = (1/2) [ sin (A + B) + sin (A — B)]
2. потому что A sin B = (1/2) [ sin (A + B) — sin (A — B)]
3. cos A cos B = (1/2) [ cos (A + B) + cos (A — B)]
4. sin A sin B = (1/2) [ cos (A — B) — cos (A + B) ]

Как получить формулу произведения для суммирования?

Формулы произведения для суммирования получаются с использованием формул суммы и разности, а именно:

• sin (A + B) = sin A cos B + cos A sin B
• sin (A — B) = sin A cos B — cos A sin B
• cos (A + B) = cos A cos B — sin A sin B
• cos (A — B) = cos A cos B + sin A sin B

Добавляя или вычитая две из этих четырех формул, мы можем получить произведение для суммирования формул. Подробное доказательство/вывод формул произведения для суммирования можно найти в статье «Что такое формулы произведения для суммирования?» раздел этой страницы.

Каковы применения формул произведения для суммирования?

Формулы произведения на сумму используются для записи произведения двух тригонометрических функций (sin и cos) в виде суммы. Следовательно, эти формулы полезны при интегрировании, поскольку интегрирование суммы намного проще по сравнению с интегрированием произведения.

Как использовать произведение для суммирования формул?

Вспомним формулы суммирования произведения:

1. sin A cos B = (1/2) [ sin (A + B) + sin (A — B) ]
2. потому что A sin B = (1/2) [ sin (A + B) — sin (A — B)]
3. cos A cos B = (1/2) [ cos (A + B) + cos (A — B)]
4. sin A sin B = (1/2) [ cos (A — B) — cos (A + B) ]

Мы можем использовать одну из этих формул, чтобы найти произведение sin и (или) cos в виде суммы. Например, если нам нужно преобразовать cos 15 ^o  sin 45 ^o в сумму, мы просто применим формулу 2 из приведенного выше списка. Тогда получаем:

cos 15 ^o  sin 45 ^o  = (1/2) [ sin (15 ^o  + 45 ^o ) — sin (15 ^o  — 45 ^o ) ]

= (1/2) [ sin 60 ^o  + sin 30 ^o ] [потому что sin (-x) = — sin x]

= ( ) [ (√3/2) + 1/2] (из таблицы тригонометрии)

= (√3 + 1) / 4

Тождества суммы и разности углов

Тождества суммы и разности углов

---

Мы используем MathJax

Встречаются тригонометрические функции суммы или разности двух углов часто в приложениях. Есть несколько способов подтверждения эти результаты.

Теорема о сумме углов и разности

Следующие тождества верны для всех значений, для которых они определено:

$\sin(A\pm B) = \sin A \cos B \pm \cos A \sin B$

$\cos(A\pm B) = \cos A \cos B \mp \sin A \sin B$

$\tan(A\pm B) = \dfrac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$

$\cot(A\pm B) = \dfrac{\cot A \cot B \mp 1}{\cot B \pm \cot A}$

$\sec(A\pm B) = \dfrac{\sec A \sec B \csc A \csc B}{\csc A \csc B \mp \sec A \sec B}$

$\csc(A\pm B) = \dfrac{\sec A \sec B \csc A \csc B}{\sec A \csc B \pm \csc A \sec B}$

Доказательство: Пусть $P$ будет точкой с координаты   $(1,0)$. Отсчитываем против часовой стрелки от точки $P$, пусть $Q$ — точка, длина дуги которой равна $A$, пусть $R$ — точка, длина дуги которой равна  $A+B$,  и пусть $S$ будет точкой, длина дуги которой равна $-В$. Тогда   $(\cos A,\sin A)$ — координаты точки $Q$, $(\cos(A+B),\sin(A+B))$ — координаты точки $R$, $(\cos(-B),\sin( -B))$   — координаты точки $S$. 92 \end{уравнение*}

Используя симметричное и пифагорейское тождества, это упрощается, чтобы стать формулой суммы углов для косинуса.

Доказательство формулы разности углов для косинус выглядит следующим образом:

\начать{выравнивать} \cos(A-B) &= \cos(A+(-B)) \\ &= \cos A \cos(-B)-\sin A \sin(-B) \\ &= \cos A \cos B + \sin A \sin B \end{выравнивание}

Тогда, используя теорему о кофункциях, мы можем получить формулы для синуса:

\начать{выравнивать} \sin(A \pm B) &= \cos\left( \dfrac{\pi}{2}-(A\pm B)\right) \\ &= \cos\left( \left(\dfrac{\pi}{2}-A\right) \mp B\right) \\ &= \cos\left(\dfrac{\pi}{2}-A\right)\cos B \pm \sin\left(\dfrac{\pi}{2}-A\right)\sin B \\ &= \sin A \cos B \pm \cos A \sin B \end{выравнивание}

По результатам формул синуса и косинуса можно вывести еще четыре формулы. ♦

Формулы также можно вывести с помощью треугольников. Хотя мы ссылаемся на следующий вывод как на доказательство, на самом деле значения углов $A$ и $B$, допускаемые выводом, весьма ограничены, и на самом деле требуется более общее доказательство.

Альтернативное доказательство: Пусть положительный даны углы $A$ и $B$, сумма которых меньше 90 градусов. Построить отрезок $PU$ длины 1. Построить треугольник $TPU$ так, чтобы угол $TPU$ был равен угол $A$, а угол $TUP$ равен дополнению к $A$. Построить описанный прямоугольник $PQRS$ так, что угол $QPT$ равен углу $B$, угол $QPU$ равен сумме углов $A$ и $B$, точка $T$ лежит на сегмент $QR$ и $U$ находятся на сегменте $RS$. Обратите внимание, что угол $RTU$ также равен углу $B$.

Треугольник Соотношения Теорема, имеем:

\начать{выравнивать} \sin(A+B) &= УФ \\ &= RT+QT \\ &= ТУ \cos B + PT \sin B \\ &= \sin A \cos B + \cos A \sin B \end{выравнивание}

Доказательство идентичности суммы углов для косинуса похожий. Тождества разности углов могут быть получены непосредственно с того же рисунка, отождествив угол $A$ с углом $TPS$, а также угол $B$ с углом $TPU$.♦

Существует несколько классов удостоверений, которые непосредственные следствия суммы углов и Теорема о разнице. 92 т}$ $\csc 2t = \dfrac{\sec t \csc t}{2}$

Доказательство: Доказательство двойного формула угла для синуса выглядит следующим образом:

\начать{выравнивать} \sin 2t &= \sin (t+t) \\ &= \sin t \cos t + \cos t \sin t \\ &= 2 \sin t \cos t \end{выравнивание}

Доказательства формул двойного угла для других пять функций похожи.♦

Теорема о снижении мощности

Следующие тождества верны для всех значений, для которых они определено: 92 t = \dfrac{2}{1-\cos 2t}$

Доказательство: формула синуса, начнем с косинуса двойного угол формулу и заменить квадрат косинуса, используя тождество Пифагора. Полученное уравнение можно решить относительно синусоидального квадрата. Доказательства степенных формул для остальных пяти функций похожи.♦

Теорема о половинном угле

Следующие тождества верны для всех значений, для которых они определено:

$\sin\dfrac{t}{2} = \pm\sqrt{\dfrac{1-\cos t}{2}}$	$\cos\dfrac{t}{2} = \pm\sqrt{\dfrac{1+\cos t}{2}}$
$\tan\dfrac{t}{2} = \dfrac{1-\cos t}{\sin t}$	$\cot\dfrac{t}{2} = \dfrac{\sin t}{1+\cos t}$
$\sec\dfrac{t}{2} = \pm\sqrt{\dfrac{2 \sec t}{\sec t+1}}$	$\csc\dfrac{t}{2} = \pm\sqrt{\dfrac{2 \sec t}{\sec t-1}}$

Доказательство: 92 t}{2\sin t\cos t} = \dfrac{\sin t}{\cos t} = \tan t \end{выравнивание}

Подстановка в этот результат дает тангенс Формула половинного угла. Доказательство формулы котангенса аналог.♦

Теорема о произведении суммы

Следующие тождества верны для всех вещественных значений.

$\sin A\sin B=\dfrac12 [(\cos(A-B)-\cos(A+B)]$

$\sin A\cos B=\dfrac12 [(\sin(A+B)+\sin(A-B)]$

$\cos A\cos B=\dfrac12 [(\cos(A+B)+\cos(AB)]$

Доказательство: Расширение и упрощение правая часть каждой формулы с использованием угла Сумма и Теорема о разностях даст левую часть.