Основные тригонометрические формулы. Сумма и разность тригонометрических функций
Содержание
- Тригонометрические функции
- Преобразование суммы тригонометрических функций в произведение
- Основные тригонометрические формулы
- Формулы сложения.
- Список формул
- Список формул сложения
- Формулы понижения степени для квадратов тригонометрических функций
- Сумма аргументов
- Значения тригонометрических функций
- Универсальная тригонометрическая подстановка
- Вывод формул
- Выражение тригонометрических функций через тангенс половинного угла
- Доказательство
- Тригонометрические функции суммы и разности углов
- Примеры применения формул суммы и разности тригонометрических функций
- Формулы тройного угла.
- Формулы приведения.
- Основное тригонометрическое тождество:
- Соотношение между косинусом и тангенсом:
- Тригонометрические функции двойного угла
- Формулы понижения степени для кубов синуса и косинуса
Тригонометрические функции
sin α, cos α
| tg α = | sin α | , α ≠ | π | + πn, n є Z |
| cos α | 2 |
| ctg α = | cos α | , α ≠ π + πn, n є Z |
| sin α |
| sec α = | 1 | , α ≠ | π | + πn, n є Z |
| cos α | 2 |
| cosec α = | 1 | , α ≠ π + πn, n є Z |
| sin α |
Преобразование суммы тригонометрических функций в произведение
| Формула | Название формулы |
| Сумма синусов | |
| Разность синусов | |
| Сумма косинусов | |
| Разность косинусов | |
| Сумма тангенсов | |
| Разность тангенсов |
| Сумма синусов |
| Разность синусов |
| Сумма косинусов |
| Разность косинусов |
| Сумма тангенсов |
| Разность тангенсов |
Основные тригонометрические формулы
sin2 α + cos2 α = 1
tg α · ctg α = 1
| 1 + tg2 α = | 1 |
| cos2 α |
| 1 + ctg2 α = | 1 |
| sin2 α |
Формулы сложения.
sin (α + β) = sin α · cos β + sin β · cos α
sin (α – β) = sin α · cos β – sin β · cos α
cos (α + β) = cos α · cos β – sin α · sin β
cos (α – β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 – tg α · tg β)
tg (α – β) = (tg α – tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β – ctg α)
ctg (α – β) = (ctg α · ctg β – 1) ÷ (ctg β + ctg α)
Список формул
Запишем формулы суммы и разности синусов и косинусов. Как Вы понимаете, их четыре штуки: две для синусов и две для косинусов.
Теперь дадим их формулировки. При формулировании формул суммы и разности синусов и косинусов угол называют полусуммой углов и , а угол – полуразностью. Итак,
- Формула суммы синусов : сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
- Формула разности синусов : разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
- Сумма косинусов : сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы на косинус полуразности этих углов.
- Формула разности косинусов : разность косинусов двух углов равна удвоенному произведению синуса полусуммы на синус полуразности этих углов, взятому со знаком минус.
Стоит отметить, что формулы суммы и разности синусов и косинусов справедливы для любых углов и .
Список формул сложения
Для начала перечислим все формулы сложения, и дадим их формулировки. Для удобства представим их в виде списка:
- Формула синуса суммы – синус суммы двух углов равен сумме произведений синуса первого угла на косинус второго и косинуса первого угла на синус второго.
- Синус разности двух углов – синус разности двух углов равен разности произведений синуса первого угла на косинус второго и косинуса первого угла на синус второго.
- Формула косинуса суммы – косинус суммы двух углов равен разности произведений косинусов этих углов и синусов этих углов.
- Косинус разности – косинус разности двух углов равен сумме произведений косинусов этих углов и синусов этих углов.
- Тангенс суммы .
- Тангенс разности .
- Котангенс суммы .
- Котангенс разности .
Отдавая дань краткости, формулы сложения обычно группируют две в одну, используя знаки плюс минус вида и минус плюс . В таком виде они выглядят так:
Каждая из записанных формул сложения соответствует двум формулам, перечисленным вначале этого пункта. Например, формула отвечает двум формулам: синусу суммы (когда берется верхний знак из ) и синусу разности (когда берется нижний знак из ).
Формулы сложения из таблицы называют соответственно формулами сложения для синуса, косинуса, тангенса и котангенса.
В заключение этого пункта отметим, что формулы сложения для синуса и косинуса справедливы для любых углов и . А формулы сложения для тангенса и котангенса справедливы для всех и , для которых определены входящие в них тангенсы и котангенсы.
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
через косинус двойного угла | |
| Выражение квадрата косинуса через косинус двойного угла | |
| Выражение квадрата тангенса через косинус двойного угла |
| Выражение квадрата синуса через косинус двойного угла |
| Выражение квадрата косинуса через косинус двойного угла |
| Выражение квадрата тангенса через косинус двойного угла |
Сумма аргументов
MM.YYYY» data-percent-format=»10.00%» data-currency-format=»$1,000.00″ data-title=»Сложение аргументов тригонометрических функций» data-view-id=»60_48629″>
Значения тригонометрических функций
| α | 0 | ||||||||||||||||
| α° | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin α | 0 | 1 | 0 | −1 | 0 | ||||||||||||
| cos α | 1 | 0 | −1 | 0 | 1 | ||||||||||||
| tg α | 0 | 1 | − | −1 | 0 | 1 | − | −1 | 0 | ||||||||
| ctg α | − | 1 | 0 | −1 | − | 1 | 0 | −1 | − |
Универсальная тригонометрическая подстановка
| sin α = | 2 tg (α/2) |
| 1 + tg2 (α/2) |
| cos α = | 1 – tg2 (α/2) |
| 1 + tg2 (α/2) |
| tg α = | 2 tg (α/2) |
| 1 – tg2 (α/2) |
| ctg α = | 1 – tg2 (α/2) |
| 2 tg (α/2) |
Вывод формул
Для вывода формул суммы и разности синусов можно использовать формулы сложения, в частности, формулы
синуса суммы ,
синуса разности ,
косинуса суммы и
косинуса разности .
Также нам потребуется представление углов и в виде и . Такое представление правомерно, так как и для любых углов и .
Теперь подробно разберем вывод формулы суммы синусов двух углов вида .
Сначала в сумме заменяем на , а на , при этом получаем . Теперь к применяем формулу синуса суммы, а к – формулу синуса разности:
После приведения подобных слагаемых получаем . В итоге имеем формулу суммы синусов вида .
Для вывода остальных формул нужно лишь проделать аналогичные действия. Приведем вывод формул разности синусов, а также суммы и разности косинусов:
Для разности косинусов мы привели формулы двух видов или . Они эквивалентны, так как , что следует из свойств синусов противоположных углов.
Итак, мы разобрали доказательство всех формул суммы и разности синусов и косинусов.
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
| Выражение синуса угла через тангенс половинного угла | |
| Выражение косинуса угла через тангенс половинного угла | |
| Выражение тангенса угла через тангенс половинного угла |
| Выражение синуса угла через тангенс половинного угла |
| Выражение косинуса угла через тангенс половинного угла |
| Выражение тангенса угла через тангенс половинного угла |
Доказательство
Начнем с доказательства формулы косинуса разности .
Она нам поможет доказать другие формулы сложения.
Перед доказательством стоит озвучить один не очень очевидный факт, который мы используем. Он заключается в следующем. Возьмем единичную окружность. Пусть точки A1 и A2 получены в результате поворота начальной точки A(1, 0) вокруг точки O на углы и соответственно. Тогда угол между векторами и равен либо , либо , где z – любое целое число. Другими словами, угол между указанными векторами равен либо , либо , либо отличается от этих значений на целое число полных оборотов. Приведем графическую иллюстрацию для наглядности.
Более того, формулы приведения позволяют нам записать следующие результаты и . Таким образом, косинус угла между векторами и равен косинусу угла , то есть, . Теперь можно переходить непосредственно к доказательству формулы косинуса разности.
В силу определений синуса и косинуса, точки A1 и A2 имеют координаты и соответственно. Тогда и (при необходимости смотрите координаты векторов через координаты точек их начала и конца).
Длины этих векторов равны единице, так как они равны радиусу единичной окружности.
Теперь запишем скалярное произведение векторов и . С одной стороны имеем , а это же скалярное произведение в координатах имеет вид . Отсюда получаем равенство . Этим доказана формула косинуса разности.
Переходим к доказательству следующей формулы сложения. Формулу косинуса суммы легко доказать, используя уже доказанную формулу и представление вида . Имеем
последний переход возможен в силу свойств синуса и косинуса противоположных углов.
Из формулы косинуса разности легко получить формулу синуса суммы, достаточно лишь обратиться к формуле приведения вида . Так
в последнем переходе мы использовали формулы приведения.
А вот доказательство формулы синуса разности:
в последнем переходе использовалось свойство синуса и косинуса противоположных углов.
Переходим к доказательству формул сложения для тангенса и котангенса. Для этого достаточно вспомнить, что тангенс – это отношение синуса к косинуса, а котангенс – отношение косинуса к синусу, а также применить доказанные выше формулы.
Так . Теперь разделим числитель и знаменатель полученной дроби на , учитывая что и , имеем
после сокращения дробей получаем .
В итоге имеем .
Теперь докажем формулу тангенса разности:
Формулы сложения для котангенса доказываются аналогично формулам сложения для тангенса:
и
Тригонометрические функции суммы и разности углов
sin(α + β) = sin α · cos β + cos α · sin β
sin(α – β) = sin α · cos β – cos α · sin β
cos(α + β) = cos α · cos β – sin α · sin β
cos(α – β) = cos α · cos β + sin α · sin β
| tg(α + β) = | tg α + tg β |
| 1 – tgα · tg β |
| tg(α – β) = | tg α – tg β |
| 1 + tgα · tg β |
| ctg(α + β) = | ctgα · ctg β – 1 |
| ctg β + ctg α |
| ctg(α – β) = | ctgα · ctg β + 1 |
| ctg β – ctg α |
Примеры применения формул суммы и разности тригонометрических функций
Пример.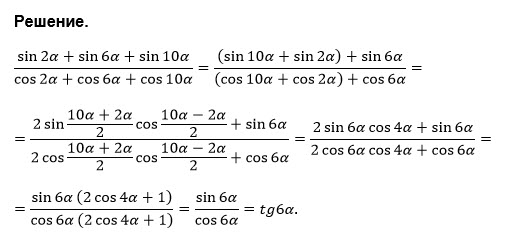
Вычислить точное значение следующего выражения:.
Решение. Так как невозможно найти точное решение ни для , ни для попробуем использовать формулу (7).
Ответ:
Формулы тройного угла.
sin 3α = 3sin α – 4sin³ α
cos 3α = 4cos³ α – 3cos α
tg 3α = (3tg α – tg³ α) ÷ (1 – 3tg² α)
ctg 3α = (3ctg α – ctg³ α) ÷ (1 – 3ctg² α)
Формулы приведения.
Функция / угол в рад. | π/2 – α | π/2 + α | π – α | π + α | 3π/2 – α | 3π/2 + α | 2π – α | 2π + α |
|---|---|---|---|---|---|---|---|---|
sin | cos α | cos α | sin α | – sin α | – cos α | – cos α | – sin α | sin α |
cos | sin α | – sin α | – cos α | – cos α | – sin α | sin α | cos α | cos α |
tg | ctg α | – ctg α | – tg α | tg α | ctg α | – ctg α | – tg α | tg α |
ctg | tg α | – tg α | – ctg α | ctg α | tg α | – tg α | – ctg α | ctg α |
Функция / угол в ° | 90° – α | 90° + α | 180° – α | 180° + α | 270° – α | 270° + α | 360° – α | 360° + α |
Основное тригонометрическое тождество:
sin2α+cos2α=1
Данное тождество − результат применения теоремы Пифагора к треугольнику в единичном тригонометрическом круге.
Соотношение между косинусом и тангенсом:
1/cos2α−tan2α=1 или sec2α−tan2α=1.
Данная формула является следствием основного тригонометрического тождества и получается из него делением левой и правой части на cos2α. Предполагается, что α≠π/2+πn,n∈Z.
Тригонометрические функции двойного угла
sin 2α = 2 sin α · cos α
cos 2α = cos2 α – sin2 α
| tg 2α = | 2 tg α |
| 1 – tg2 α |
| ctg 2α = | ctg2 α – 1 |
| 2 ctg α |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
| Выражение куба синуса через синус угла и синус тройного угла | |
| Выражение куба косинуса через косинус угла и косинус тройного угла |
| Выражение куба синуса через синус угла и синус тройного угла |
| Выражение куба косинуса через косинус угла и косинус тройного угла |
Источники
- https://ru. onlinemschool.com/math/formula/trigonometry_formula/
- https://www.resolventa.ru/spr/trig/formula.htm
- https://www.calc.ru/Trigonometricheskiye-Formuly.html
- http://www.cleverstudents.ru/trigonometry/sum_of_sin_and_cos.html
- http://www.cleverstudents.ru/trigonometry/angle_addition_formulas.html
- https://MicroExcel.ru/summa-raznost-argumentov-trigonometricheskikh-funktsiy/
- https://doza.pro/art/math/geometry/trig-formulas
- https://matworld.ru/trigonometry/summa-i-raznost-trigonometricheskih-funkcij.php
onlinemschool.com/math/formula/trigonometry_formula/определение, примеры решения и свойства
Содержание:
- Формулы тригонометрии и их использование для преобразования тригонометрических выражений
- Тригонометрические выражения
- Формулы сложения и вычитания аргументов
- Формулы приведения
- Соотношения между тригонометрическими функциями одного и того же аргумента
- Формулы двойного аргумента
- Формулы понижения степени
- Преобразование сумм тригонометрических функций в произведение
- Преобразование произведений тригонометрических функций в сумму
- Преобразование выражения к виду .
- Примеры преобразований выражений, содержащих обратные тригонометрические функции
Формулы тригонометрии — это соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом.
Тригонометрические выражения
Выражение, в котором переменная содержится под знаками тригонометрических функций, называют тригонометрическим. Для преобразования тригонометрических выражений используют свойства тригонометрических функций, отмеченные в пп. 100—105, и формулы тригонометрии, указанные ниже в пп. 125—131.
Формулы сложения и вычитания аргументов
Формулы (1)—(4) справедливы для любых Формула (5) верна при отличных от Формула (6) верна при отличных от
Пример 1.
Вычислить sin 75°.
Решение:
Имеем sin 75° = sin (30° + 45°). Воспользовавшись формулой (3) при получим
sin (30° + 45°) = sin 30° cos 45° + cos 30° sin 45°.
Известно, что (см.
п. 99). Значит,
Итак,
Пример 2.
Упростить выражение
Решение:
Воспользуемся для и формулами (3) и (1) и учтем, что
Пример 3.
Вычислить cos 15°.
Решение:
Имеем 15° = 45° — 30°. Воспользовавшись формулой (2) при получим
cos 15° = cos (45° — 30°) = cos 45° cos 30° + sin 45° sin 30° =
Пример 4.
Найти , если .
Решение:
Воспользуемся формулой (5) и учтем, что :
Формулы приведения
Под формулами приведения понимают обычно формулы, сводящие значение тригонометрической функции аргумента вида к функции аргумента .
Пусть, например, нужно вычислить
Имеем:
Аналогично,
Подобным же образом выводятся и остальные формулы приведения. Эти формулы даны в следующей таблице:
Соотношения между тригонометрическими функциями одного и того же аргумента
Если в формуле (2) из п.
125 положить , то получим
откуда, в свою очередь, находим, что
Тождество (2) справедливо при а тождество (3) — при
Равенства (1), (2), (3) связывают между собой различные тригонометрические функции одного и того же аргумента. Известны еще два равенства, связывающие между собой различные тригонометрические функции одного и того же аргумента:
Перемножая эти равенства, получаем равенство
справедливое при
Пример 1.
Известно, что , причем Найти cos t, tg t, ctg t.
Решение:
Из формулы (1) получаем . Подставив вместо sin t его значение, получим
Итак, ; значит, либо
По условию, , т. е. аргумент t принадлежит III четверти. Но в III четверти косинус отрицателен; значит, из двух указанных выше возможностей выбираем одну:
Зная sin t и cos t, находим tg t и ctg t:
Пример 2.
Известно, что , причем . Найти sin t, cos t, tg t.
Peшeние:
Из формулы (3) находим
Подставив вместо ctg t его значение, получим
Итак, .
Значит, либо , либо По условию, Значит, t принадлежит II четверти, а во II четверти синус положителен. Поэтому из двух указанных возможностей выбираем одну:
Для отыскания значения cos t воспользуемся определением котангенса: . Из этого равенства находим
Осталось вычислить значение tg t. Из равенства находим, что . Итак,
Формулы двойного аргумента
Если в формулах (3), (1), (5) из п. 125 положить то получим следующие тождества:
С помощью формул (1), (2) и (3) можно выразить синус, косинус, тангенс любого (допустимого) аргумента через тригонометрические функции вдвое меньшего аргумента. Например, справедливы следующие равенства:
В ряде случаев полезным оказывается использование полученных формул «справа налево», т. е. замена выражения 2 sin t cos t выражением sin 2t (или выражения sin t cos t — выражением , выражения — выражением cos 2t и, наконец, выражения — выражением tg 2t.
Пример:
Упростить выражение tg t — ctg t.
Решение:
Формулы понижения степени
Зная, что (см. n. 128), находим, что
Формулы (1) и (2) называют формулами понижения степени. Они позволяют преобразовывать и в выражения, содержащие первую степень косинуса двойного аргумента. Например, используя формулы (1) и (2), можем получить следующие равенства:
Формулы (1) и (2) используют и «справа налево» для преобразования сумм 1 + cos 2t, 1 — cos 2t в произведения. Например, верны следующие равенства:
Пример 1.
Доказать тождество
Решение:
Знаменатель правой части преобразуем по формуле (1), а числитель — по формуле синуса двойного аргумента (см. п. 128). Получим
Пример 2.
Вычислить , если известно, что .
Решение:
Воспользовавшись тем, что , применим формулы понижения степени. Получим
Преобразование сумм тригонометрических функций в произведение
Пример 1.
Преобразовать в произведение cos 48° — cos 12°.
Решение:
Применив формулу разности косинусов при , получим
Так как , то окончательно получим
cos 48° — cos 12° = — sin 18°.
Пример 2.
Преобразовать в произведение
sin х + cos 2х — sin Зх.
Решение:
Преобразование произведений тригонометрических функций в сумму
Пример:
Преобразовать в сумму произведение sin 43° cos 19°.
Решение:
Воспользовавшись формулой (1) при , получим
Преобразование выражения к виду .
Любое выражение вида можно представить в виде .
Для этого вынесем за скобки выражение :
Ho . Это значит, что точка с координатами удовлетворяет уравнению , т. е. лежит на числовой окружности; поэтому существует такое , что
Обозначив для краткости через А, получаем
Применив к выражению в скобках формулу (2) из п. 125, получим
Числа связаны друг с другом соотношениями:
Например, где
Примеры преобразований выражений, содержащих обратные тригонометрические функции
Пример 1.
Упростить выражение cos (arcsin х), где .
Решение:
Положим arcsin х = у. Тогда sin у = х, . Нужно найти cos у.
Известно, что значит, Но , а на отрезке косинус принимает лишь неотрицательные значения. Поэтому т.е.
Пример 2.
Вычислить .
Решение:
Положим . Тогда
Нужно вычислить
Имеем ; значит,
Так как, далее,
откуда
По условию, значит, а в интервале имеем Итак, т. е.
Пример 3.
Доказать, что для любого х из [- 1; 1] справедливо тождество
Решение:
Вычислим значения синуса левой и правой частей проверяемого равенства:
Синусы, как мы видим, равны, поэтому, чтобы убедиться в справедливости равенства (1), осталось показать, что принадлежат одно-му и тому же промежутку монотонности функции у = sin х (без проверки этого условия можно получить неверный результат, ведь тригонометрические функции могут принимать одинаковые значения и для различных значении аргумента, например )
Имеем Далее, а поэтому Итак, arcsin х и принадлежат одному промежутку монотонности функции у = sin х.
Теперь можно считать, что тождество (1) доказано. Аналогично можно доказать, что
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету «Математика»:
Формулы суммы и разности углов: примеры и методы
На уроке тригонометрии наш учитель математики сказал, что сумма 30° и 40° даст 70°, а сумма sin30° и sin40° не даст sin70° и это вызвало некоторый переполох в классе. Как же тогда сложить и вычесть синусов или косинусов углов ? Далее будет объяснено все, что вам нужно знать о таких операциях.
Какие формулы суммы и разности углов в тригонометрии?
Формулы суммы и разности углов — это уравнения, используемые при выполнении сложения и вычитания тригонометрических тождеств.
В отличие от обычных арифметических операций сложение и вычитание тригонометрических функций имеют другой подход.
Например, cos (45° -15°) не совпадает с cos45° — cos15°. Это становится более сложной задачей, когда в таких арифметических операциях участвуют тригонометрические функции. Итак, для решения этой задачи необходимо вывести формулы.
Знание тригонометрических функций специальных углов, таких как синусы, косинусы и тангенсы 30, 45, 60 и 90 градусов, означает, что сложение или вычитание этих углов может дать другие углы. Например, можно вывести sin15°, поскольку sin15° совпадает с sin(45-30)°. Далее мы будем выводить формулы для решения этих операций.
Доказательство суммы и разности функций косинуса
Разность функций косинуса
Рассмотрим рисунок ниже:
Рисунок 1: Изображение, показывающее использование стандартного положения единичного круга для доказательства разности функций косинуса, — StudySmarter Originals
Рисунок выше взят из стандартного положения единичного круга. Если a — это угол ∠ PON , а b — это угол ∠Q ON , то угол ∠ POQ равен ( a-b ).
Следовательно, — горизонтальная составляющая точки P , а — ее вертикальная составляющая. В то время как горизонтальная составляющая точки Q и — его вертикальная составляющая. Таким образом, чтобы найти расстояние PQ, воспользуемся формулой расстояния между двумя точками.
Где в пункте P , is и в пункте Q , is. Таким образом,
Перестановка уравнения
Помните:
Тогда:
Если угол (A-B ) должны были быть переполнены в стандартную позицию единичного круга из исходного происхождения )0027 O до точки S на рисунке ниже. расстояние PQ на рисунке 1) может быть получено относительно угла (a-b ) и соответствующих точек S ( cos (a-b) , sin (ab) ) и N (1, 0 ).
Использование
Где точка S и N , то
Переставьте и приведите подобные члены
Помните, что
2 9;
Помните, что
Затем
Таким образом,
Решите алгебру, вычитая 2 с обеих сторон уравнения
Разделите по обе стороны на обе стороны
.
0007
Суммирование функций косинуса
Таким образом, подставьте значение b вместо -b в уравнение.
Обратите внимание, что
и
поэтому
Доказательство суммы и разности синусоидальных функций
Изображение прямоугольного треугольника, — StudySmarter Originals
Нарисуйте еще одну прямую, пересекающую A и касающуюся линии BC в точке D, так, чтобы угол BAD был равен β, а угол DAC равен α, как показано ниже.
Проведите линию, перпендикулярную точке D, которая касается линии AB в точке E, как показано ниже.
Из точки E проведите линию, перпендикулярную линии AC, пересекающую линию AD в точке F и пересекающую линию AC в точке G, как показано ниже.
Проведите линию из точки D в точку H на линии EG, перпендикулярную линии EG, как показано ниже.
Обратите внимание, что для каждого последующего шага следует обращаться к рисунку выше.
Поэтому
Использование SOHCATOA
Обратите внимание, что строка EG = EH + HG, поэтому
Отзыв;
прямые HG и DC параллельны и равны.
Таким образом,
Видите, что
Они являются альтернативными углами, потому что линии HD и AC параллельны и пересекаются линией AD.
Примечание ниже
Напомним, что линия AD перпендикулярна линии ED. Поэтому
Зная, что
таким образом
сумма углов треугольника равна 180° см. ниже
Изображение, доказывающее сумму синуса углов, StudySmarter Originals
Из прямоугольного треугольника EDH
Напомним, что
Подставьте значение EH
Между тем, из прямоугольного треугольника AED, используя SOHCAHTOA
Подставляем значение в уравнение
Из прямоугольного треугольника ADC, используя SOHCAHTOA
в уравнение
Глядя на прямоугольный треугольник AED и используя SOHCAHTOA
Подставляем значение в уравнение
Разность его функций
Зная, что
Таким образом, можно получить, заменив β на -β во всем уравнении.
Therefore
Note that
and
therefore
Proving Sum and Difference of Tangent Functions
Summing of tangent functions
Recall that
Therefore
Thus
Разделить каждую единицу в правой части уравнения на cosAcosB
Разница в касательных функциях
Напомним, что
Следовательно,
Таким образом,
Разделите все объекты правой стороны уравнения Cosacosb
SUM и разница в разнице формла.
Ниже вы увидите, как применять формулы суммы и разности.
Найдите значение cos15°
Решение:
Первый шаг — найти наилучшую возможную комбинацию специальных углов, которая даст этот угол. В этом случае 15° можно получить, вычитая 30° из 45°.
Поэтому
отзыв
Следовательно;
Factorize further
Thus
Prove that:
Solution:
knowing that
Therefore
Note that
:
Thus,
Отсюда;
Если человек выходит из точки P в точку R, которая находится в 20 км строго к востоку от P, то он идет в точку S к северу от R. Найдите расстояние от R до S, если S составляет 75 градусов северо-востока. P без использования калькуляторов или математических таблиц.
Решение:
Нас просят рассчитать расстояние RS. Using SOHCAHTOA
Note that
Therefore
Where
and
Then
Multiply the numerator and denominator by
Thus
Sum and Формулы разности углов — основные выводы
- Сумма и разность тригонометрических функций не вычисляются прямым арифметическим методом.
- Формула суммы и разности синуса
- Формула суммы и разности косинуса
- Формула суммы и разности тангенса
Решение тригонометрических уравнений алгебраическими методами
Горячая математика Уравнение, которое содержит
тригонометрические функции
называется тригонометрическое уравнение .
Пример:
грех 2 Икс + потому что 2 Икс знак равно 1 2 грех Икс − 1 знак равно 0 загар 2 2 Икс − 1 знак равно 0
Чтобы решить тригонометрическое уравнение, мы используем правила алгебры, чтобы изолировать тригонометрическую функцию по одну сторону от знака равенства. Затем мы используем наши знания о значениях тригонометрических функций для решения переменной.
Когда вы решаете тригонометрическое уравнение, которое включает только одно тригонометрическое выражение, начните с выделения выражения.
Когда тригонометрические функции не могут быть объединены в одной части уравнения, попробуйте разложить уравнение на множители, а затем применить
свойство нулевого продукта
решить уравнение.
Если уравнение имеет квадратную форму, по возможности, первый фактор. Если это невозможно, примените
квадратичная формула
решить уравнение.
Пример :
Решать 2 грех Икс − 1 знак равно 0 .
Чтобы решить уравнение, начнем с того, что перепишем его так, чтобы sin Икс изолирован с левой стороны. Итак, сначала добавьте 1 в каждую сторону, а затем разделить каждую сторону на 2 .
2 грех Икс знак равно 1 грех Икс знак равно 1 2
С
грех
Икс
имеет период
2
π
, сначала найдем все решения в интервале
[
0
,
2
π
]
.