Задачи на сопротивление цепи – Решение задач на закон Ома для участка и полной цепи

Решение задач на закон Ома для участка и полной цепи

Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.

Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Формула закона Ома для участка цепи:

Формула закона Ома для полной цепи:

Задача 1

Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.

Дано  U = 220 В I = 1,2 А	Решение Согласно закону Ома для участка цепи:
Найти R — ?
Ответ: R = 183,3 Ом.

Задача 2

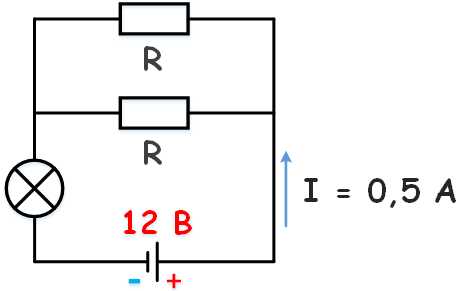
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Дано  E = 12 В I = 0,5 А Rл = Rр/2 Rр = 10 Ом	Решение Найдем экв. сопротивление двух параллельно соединённых резисторов: Сопротивление лампочки: Согласно закону Ома для полной цепи:
Найти r — ?
Ответ: r = 14 Ом.

Задача 3

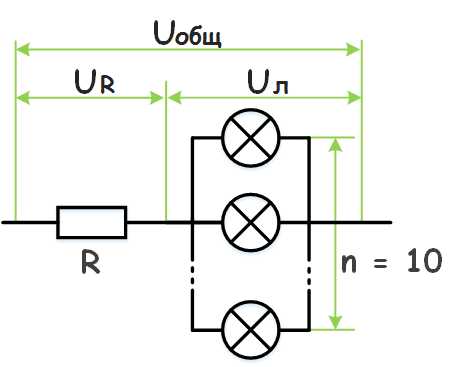
К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.

Дано  Uобщ = 10 В Rр = 2 Ом Rл = 10 Ом	Решение Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи: При последовательном соединении ток в цепи общий: Выразим Uл через Uобщ: Найдем Rэкв: Окончательно получим:
Найти Uл — ?
Ответ: Uл = 4 В.

Задача 4

Как определить длину мотка медной проволоки, не разматывая его?

Решение:

Для решения данной задачи необходимо воспользоваться формулой:

отсюда длина проволоки

В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.

Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив  диаметр проволоки и по формуле Πr² вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.

Задача 5

Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?

Решение:

При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I₁ и I₂ проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.

Просмотров: 9578

electroandi.ru

ФИЗИКА: ЗАДАЧИ на Закон Ома с решениями

Задачи на Закон Ома с решениями

Формулы, используемые на уроках «Задачи на Закон Ома».

Название величины	Обозначение	Единица измерения	Формула
Сила тока	I	А	I = U / R
Напряжение	U	В	U = IR
Сопротивление	R	Ом	R = U/I

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.  Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?

---

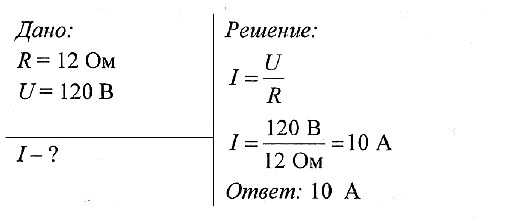
Задача № 2.  Сопротивление проводника 6 Ом, а сила тока в нем 0,2 А. Определите напряжение на концах проводника.

---

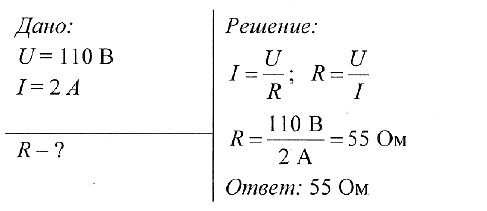
Задача № 3.  Определите сопротивление проводника, если при напряжении 110 В сила тока в нем 2 А.

---

Задача № 4.  По графикам зависимости силы тока от напряжения определите сопротивление каждого проводника. 

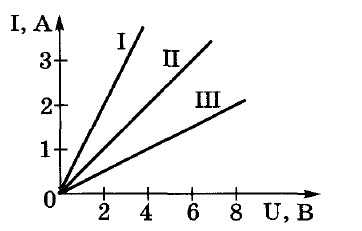
Решение:

 

---

Задача № 5.  Чему равна сила тока в электрической лампе карманного фонаря, если сопротивление нити накала 16,6 Ом и лампа подключена к батарейке напряжением 2,5 В?

 

---

Задача № 6.  Электрический утюг включен в сеть с напряжением 220 В. Какова сила тока в нагревательном элементе утюга, если сопротивление его равно 48,4 Ом?

---

Задача № 7.  При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?

---

Задача № 8.  Чему равно сопротивление спирали электрической лампы в рабочем состоянии, у которой на цоколе написано 6,3 В, 0,22 А?

---

Задача № 9.  Показание вольтметра, присоединенного к горящей электрической лампе накаливания, равно 120 В, а амперметра, измеряющего силу тока в лампе, 0,5 А. Чему равно сопротивление лампы? Начертите схему включения лампы, вольтметра и амперметра.

---

Задача № 10.   ОГЭ  Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения U_R на внешнем участке и падение напряжения U_r на внутреннем участке цепи.

 

---

Краткая теория для решения Задачи на Закон Ома.

 

---

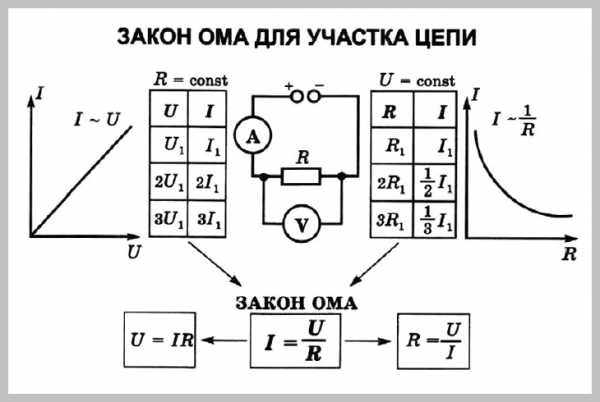
Это конспект по теме «ЗАДАЧИ на Закон Ома». Выберите дальнейшие действия:

 

ЗАДАЧИ на Закон Ома с решениями

3.9 (77.78%) 9 vote[s]

uchitel.pro

«Электрическое сопротивление. Закон Ома». Видеоурок. Физика 8 Класс

Тема: Электромагнитные явления

Урок: Решение задач на тему “Электрическое сопротивление. Закон Ома”

На предыдущих уроках мы говорили, что сила тока зависит от напряжения и сопротивления проводника. Также мы выяснили, что сопротивление проводника зависит от его геометрических размеров и материала, из которого он сделан. На этом уроке будут рассмотрены задачи, связанные именно с этими двумя положениями.

Первая формула, которая понадобится для решения задач, – закон Ома для участка цепи:

Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Сила тока измеряется в Амперах (I=[А]), напряжение – в Вольтах (U=[В]), сопротивление – в Омах (R=[Ом]). Тогда из закона Ома можно сказать, что .

Еще одна формула, которая нам понадобится, – формула зависимости сопротивления проводника от его параметров:

Сопротивление проводника равно его удельному сопротивлению, умноженному на дробь, где в числителе – длина проводника, в знаменателе – площадь поперечного сечения проводника. При этом сопротивление измеряется в Омах (R=[Ом]), длина – в метрах (l=[м]). В единицах измерения СИ (система интернациональная) площадь измеряется в метрах квадратных, но поскольку сечение провода невелико, то имеет смысл измерять площадь поперечного сечения в миллиметрах квадратных (S=[м²]=[мм²]). Удельное сопротивление, как правило, определяется по таблицам: зная материал, из которого сделан проводник, можно определить его удельное сопротивление. Единицы измерения удельного сопротивления:

Первая запись единиц измерения используется для удобства (), а в таблицах значение обычно подается в виде второй записи (). Можно увидеть, что записи эквивалентны, т. к. если перевести миллиметры в метры, то метры сократятся.

Рассмотрим следующую задачу: надо определить силу тока в проводнике, длина которого 100 м, а сечение этого проводника – 0,5 мм².

Этот проводник выполнен из меди и включен в цепь таким образом, что на его концах наблюдается напряжение 6,8 В. Стоит отметить, что в задаче дан материал, из которого сделан проводник. Значит, можно узнать значение удельного сопротивления из таблицы.

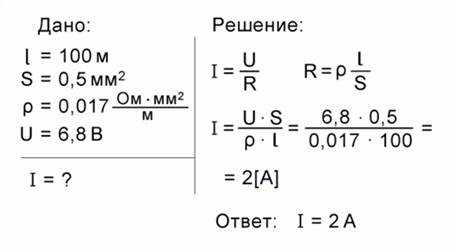
Рис. 1. Решение задачи №1

Сначала следует записать краткое условие задачи. На рис. 1. слева от вертикальной черты показано, как это нужно сделать. Значение длины (l=100 м), площади поперечного сечения (S=0,5 мм²) и напряжения (U=6,8 В) дано в условии. Значение удельного сопротивления меди () мы взяли из таблицы. Под горизонтальной чертой на рис. 1 написано, что нужно найти в задаче – силу тока.

Для решения задачи запишем закон Ома для участка цепи: . Также нам потребуется выражение для сопротивления проводника: . Далее постараемся записать решение в общем виде, то есть выражение для сопротивления мы подставим в закон Ома. Поскольку R в законе Ома стоит в знаменателе, то ρ и l окажутся в знаменателе, S перейдет в числитель. Получаем:

Теперь подставим значения данных величин:

Ответ: I=2A.

Это можно понять так: если подключить амперметр последовательно к данному проводнику, то он покажет значение 2А. Стоит обратить внимание, что ничего сложного в таких задачах нет. Стоит только разобраться, какие величины куда подставить. Обычно такие задачи в дальнейшем будут использоваться как составная часть более сложных задач.

В предыдущей задаче мы находили значение силы тока. Но эту характеристику можно измерить соответствующим прибором – амперметром. Поэтому, как правило, есть другие задачи, в которых требуется найти характеристики проводника. Если мы хотим сделать какое-то сопротивление, то мы должны знать эти характеристики проводника: длину, площадь сечения, материал. Решая такие задачи, мы сможем их найти, зная силу тока и напряжение.

Рассмотрим пример именно такой задачи. По вольфрамовой проволоке протекает электрический ток. Длина проволоки – 4 м, сила тока составляет 0,05 А. Напряжение, под которым находится данный проводник, составляет 5 В. Необходимо определить величину площади поперечного сечения.

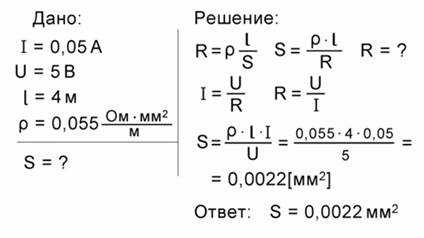
Рис. 2. Решение задачи №2

Как и в первом случае, запишем краткое условие задачи (рис. 2, слева от вертикальной черты). Нам даны сила тока I=0,05 А, напряжение U=5 В и длина проволоки l=4 м. Значение удельного сопротивления вольфрама  можно найти из таблицы. Под горизонтальной чертой написано то, что требуется найти: S, площадь поперечного сечения проволоки.

Как и в предыдущей задаче запишем две формулы. Первая – это формула для вычисления сопротивления проводника: . Отсюда можно выразить площадь сечения проводника:

Из этого уравнения мы не сможем сразу найти сечение, поскольку нам неизвестно сопротивление. Для его определения потребуется вторая формула – закон Ома для участка цепи: . Из него можно выразить значение сопротивления всей проволоки:

Подставив это выражение в формулу для площади сечения, получим:

Получаем дробь, где в числителе стоит произведение трех величин: удельного сопротивления, длины проводника и силы тока, а в знаменателе стоит только напряжение. Подставим численные значения:

Получаем ответ: площадь поперечного сечения проволоки . Как видим, сечение проволоки невелико, то есть проволока будет очень тонкой.

Стоит отметить, что для решения конкретных технических задач, подобных решенной ранее, обычно используются данные, которые получают при помощи приборов. Например, имеется катушка с намотанным на нее проводником. Требуется измерить, например, длину этого проводника. Разматывать катушку не имеет смысла, поскольку провод может быть очень длинным. Как же тогда поступить?

Рис. 3. Схема для измерения длины проводника в катушке

По небольшому образцу такого провода измеряют площадь его сечения. По внешнему виду проводника можно определить материал, из которого он сделан, а значит, и узнать его удельное сопротивление. Далее катушку (обозначена желтым цветом на рис. 3) подключают к источнику тока и при помощи амперметра и вольтметра определяют напряжение на этой катушке и силу тока, протекающего по проводнику, который намотан на эту катушку. В результате получаем задачу, похожую на ту, что мы решали ранее, но найти надо длину проводника. Используя формулу для сопротивления и закон Ома, получим:

В заключение стоит сказать, что такие задачи не являются трудными, но достаточно показательны. Из большого количества величин, данных в задаче, можно легко получить значение требуемой величины.

 

Список литературы

1. Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
2. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
3. Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети интернет

1. Фестиваль педагогических идей «Открытый урок» (Источник).
2. ПроШколу.ру (Источник).
3. Электрознайка (Источник).

 

Домашнее задание

1. Стр. 106–108: вопросы № 1–4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
2. Длина и площадь поперечного сечения алюминиевого и железного проводов одинаковые. На них подается одинаковое напряжение. В каком из проводов сила тока будет больше?
3. Можно ли вычислить напряжение в проводнике, зная силу тока в нем, его длину и площадь сечения, но не зная, из какого материала он сделан?
4. Для уменьшения потерь энергии соединительные провода делают так, чтобы ток в них был как можно меньше. Для этого их должны делать большего или меньшего диаметра?

interneturok.ru

Урок решения задач по теме «Закон Ома для участка цепи, последовательное и параллельное соединения»

Разделы: Физика

---

Цель урока: Закрепить изученный материал путем решения задач.

Задачи:

Образовательные:

• Научить учащихся решать задачи на последовательное и параллельное соединение проводников;
• Углубить и расширить знания о данных видах соединения проводников;
• Научить определять силу тока, напряжение, сопротивление при последовательном и параллельном соедини проводников;
• Научить решать задачи на смешанное соединение проводников;
• Научить учащихся разбираться в схемах электрических цепей.

Воспитательные:

• Развить личные качества учащихся: аккуратность, внимание, усидчивость;
• Воспитывать культуру общения при работе в группах.

Развивающие:

• Продолжить развитие навыков решения задач на данную тему;
• Продолжить развитие умений анализировать условия задач и ответов, умений делать выводы, обобщения;
• Продолжить развитие памяти, творческих способностей.

План урока

№	Этап	Время	Метод
	Организационный момент	2 мин	Словесный
I	Актуализация знаний	5 мин	Письменная работа в парах
II	Вводная часть	2 мин	Слово учителя, опрос учащихся
III	Решение задач	45-50 мин	Работа учителя, учащихся у доски
IV	Работа учащихся в группах	20 мин	Групповой работы, устный, письменный
V	Итог урока	1-2 мин	Словесный метод

Оформление класса: Проектор с экраном, доска с мелом. Раздаточный материал.

Слайд 1 включен в начале урока. Урок начинается с физического диктанта.

I. Актуализация знаний.

На слайде физический диктант. (Слайд 2). Учащимся выдается таблица для заполнения.

1. Заполнить двенадцать ячеек таблицы на карточке:

Ученый	Физическая величина	Формула	Единица измерения
1	2	3	4
5	6	7	8
9	10	11	12
Выполнил ______________ Проверил __________ Оценка__________

2. После заполнения таблиц учащиеся меняют карточками с соседом по парте, проверяют вместе с учителем и выставляют оценку:

Кол-во ошибок	1	2-3	4-6	7 и более
Оценка	5	4	3	2

II. Вводное слово.

Сегодня на уроке мы с вами будем решать задачи на закон Ома, на последовательное и параллельное соединение проводников. (Слайд 3).

Запишите тему урока. (Слайд 4).

Для этого вспомним формулы и законы, которые нам пригодятся при решении задач.

III. Решение задач.

(3 ученика выходят к доске и записывают: первый закон Ома и выражает и него напряжение и сопротивление; второй – формулы справедливые для последовательного соединения; третий – формулы справедливые для последовательного соединения).

Задача 1. Для начала решим устную задачу на запоминание закона Ома. (Слайд 5)

a) U = 20B,R=10Om,I-?
б) I=10A,R = 5Om, R-?
в) I = 5A,U=15B,R-?

Ответ: а) I = 2А; б) U= 50 Ом; в) R = 3 Ом.

Задача 2. (Решает учитель с использованием презентации) Слайд 6.

Рассчитать силу тока, проходящую по медному проводу длиной 100м, площадью поперечного сечения 0,5мм², если к концам провода приложено напряжение 6,8B.

Дано:

I=100м
S=0,5мм²
U=6,8В

I-?

Решение:

Ответ: Сила тока равна 2А.

Вопросы: Что известно из условия задачи? Какую величину необходимо определить? По какому закону будем определять силу тока? Какие величины нам неизвестны для нахождения силы тока и как их найти? ( – берется из таблицы). Теперь найдем R и полученное значение подставим в формулу для нахождения силы тока. (Перевод S в м² не нужно делать, т.к. в единицах измерения плотности тоже присутствуют тоже мм²)

Задача 3. (Решает у доски сильный ученик) Условия задачи Слайд 7.

В электрическую цепь включены последовательно резистор сопротивлением 5 Ом и две электрические лампы сопротивлением 500 Ом. Определите общее сопротивление проводника.

Дано:

R_AB=5 Ом
R_BC=500 Ом
R_CD=500 Ом

R_AD-?

Решение:

Ответ: Общее сопротивление проводника равно 1005 Ом.

Вопросы: Какие элементы цепи нам даны? Как найти общее сопротивление?

Задача 4. (Класс делится на 2 группы, каждая из которой решает задачу своим способом (одни находя силу тока используя закон Ома, вторые используя формулу параллельного соединения). Затем по одному представителю пишут решения на доске) Условия задачи Слайд 8.

Два резистора сопротивлением r ₁ = 5 Ом и r₂= 30 Ом включены, как показано на рисунке, к зажимам источника тока напряжением 6В. Найдите силу тока на всех участках цепи.

Дано:

r₁=5 Ом
r₂=30 Ом
U=6B

I₀-?

Решение:

Ответ: Сила тока на всех участках цепи равна 1,4 А.

Вопросы: Какой тип соединения рассматривается в задаче? Что известно из условия? Какие величины необходимо найти? Как найти I₀? Что для этого неизвестно? Как найти I ₁ и I₂?

Второй способ решения данной задачи:

Дано:

r₁=5 Ом
r₂=30 Ом
U=6B

I₀-?

Решение:

Ответ: Сила тока на всех участках цепи равна 1,4А.

Вопросы: Какой тип соединения рассматривается в задаче? Что известно из условия? Какие величины необходимо найти? По какой формуле будем находить общий ток в цепи? Какая величина нам неизвестна при нахождении силы тока и как ее найти?

Задача 5. (Решает ученик, можно вызвать два ученика по очереди). Определите полное сопротивление цепи и токи в каждом проводнике, если проводники соединены так, как показано на рисунке, а r₁=1 Ом, r₂=2 Ом, r₃= 3 Ом, U_AC = 11В. Условие задачи Слайд 9.

Дано:

r₁=1 Ом
r₂=2 Ом
r₃=3 Ом
U_AB=11B

R_AC-?
I₁-?
I₂-?
I₃-?

Решение:

Ответ: R_АС =2,2 Ом, I₁=2A, I₂=3 А, I₃=2A.

Вопросы: Какие типы соединения изображены на рисунке? Что нужно определить? Как найти полное сопротивление и величины в него входящие? Как найти силу тока в цепи? Как определить I₁ и 1₂? Как определить U_BC?

Задача 6. Условия задачи Слайд 10. (Вопросы 1,2,5 решаются устно. 3,4 – два ученика).

1. Какому значению силы тока и напряжения соответствует точка А?
2. Какому значению силы тока и напряжения соответствует точка В?
3. Найдите сопротивление в точке А и в точке В.
4. Найдите по графику силу тока в проводнике при напряжении 8 В и вычислите сопротивление в этом случае.
5. Какой вывод можно проделать по результатам задачи?

Ответ:

1. Сила тока = 0,4 А, напряжение – 4В.
2. Сила тока = 0,6 А, напряжение – 6В.
3. Сопротивление в т.А – 10 Ом, в т.В – 10 Ом.
4. Сила тока = 0,8А, сопротивление – 10 Ом.
5. При изменении силы тока и напряжения на одинаковую величину, сопротивление остается постоянным.

IV. Самостоятельная работа в группах.

Учащиеся делятся на 4 группы и каждой группе дается карточка с заданием.

Учитель объясняет критерии выставления оценок:

Во время работы в группах ведется наблюдение за более и менее активными участниками группы. Соответственно это будет влиять на более или менее высокую оценку при проверке записей в тетради, также будет учитываться уровень сложности решенных задач. Тетради с записями сдаются в конце урока. Время для решения задач ограниченное.

Задание 1. Слайд 11. (8 мин.)

Вопросы к карточкам:

1. Перечислите все элементы цепи.
2. Какие виды соединения используются?
3. Рассчитайте напряжение на лампе.
4. Рассчитайте напряжение на реостате.
5. Рассчитайте силу тока на всем участке цепи.

Задание 2. Слайд 12. (4 мин.)

Определить общее сопротивление в цепи.

R₁ = 2 Ом, R₂ = 102 Ом, R ₃ = 15 Ом, R₄ = 4 Ом.

Задание 3. Слайд 13. (3 мин.)

Определите силу тока I при заданных U и R.

Группа	R, Ом	U, В	I, А
I	2	55	?
II	14,2	87,4	?
III	21	100	?
IV	0,16	0,28	?

Задание 4. Слайд 14. (5 мин)

Моток проволоки имеет сопротивление R и длину l .

Вычислить площадь поперечного сечения S.

Группа	Материал	Параметры
		Сопротивление	Длина проводника	Удельное сопротивление
		R, Ом	l, мм2	p, Ом·мм2/м
I	Медь	0,83	33,9	1,7·10-2
II	Алюминий	16,1	83,1	2,8·10-2
III	Серебро	0,39	0,234	1,6·10-2
IV	Сталь	23,2	3,06	12·10-2

После выполнения заданий группами, тетради сдаются учителю.

V. Итог урока.

На сегодня все. Мы с вами научились решать задачи на последовательное и параллельное соединение проводников, закрепили знания о законе Ома для участка цепи.

Домашнее задание. Повторить все формулы и физические величины.

2.04.2010

xn--i1abbnckbmcl9fb.xn--p1ai

Решение задач на расчет электрического сопротивления с помощью моделей

Разделы: Физика

---

Цели: обучающая: систематизировать знания и умения учащихся решать задачи ан расчет эквивалентных сопротивлений с помощью моделей, каркасов и т.д.

Развивающая: развитие навыков логического мышления абстрактного мышления, умений заменять схемы эквивалентности, упрощать расчет схем.

Воспитательная: воспитание чувства ответственности, самостоятельности , необходимости навыков приобретенных на уроке в будущем

Оборудование: проволочный каркас куба, тетраэдера, сетки бесконечной цепочки сопротивлений.

ХОД УРОКА

Актуализация:

1. Учитель: “Вспомним последовательное соединение сопротивлений”.

Учащиеся на доске зарисовывают схему.

и записывают

R_эк=n*R

U_об=U₁+U₂

Y_об=Y₁=Y₂

Учитель: вспомним параллельное соединение сопротивлений.

Учащийся на доске зарисовывает элементарную схему:

 U_об=U₁+U₂

Y_об=Y₁=Y₂

; длядля n равных

Учитель: А теперь будем решать задачи на расчет эквивалентного сопротивления участок цепи представлен в виде геометрической фигуры, либо металлической сетки.

Задача № 1

Проволочный каркас в виде куба, рёбра которого представляют равные сопротивления R. Рассчитать эквивалентное сопротивление между точками А и В. Чтобы рассчитать эквивалентное сопротивление данного каркаса необходимо заменить эквивалентной схемой. Точки 1, 2, 3 имеют одинаковый потенциал, их можно соединить в один узел. А точки (вершины) куба 4, 5, 6 можно соединить в другой узел по той же причине. Учащиеся имеют на каждой парте такую модель. После выполнения описанных действий зарисовывают эквивалентную схему.

 

На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно для последовательного соединения сопротивлений имеем:

Задача № 2

Рассчитать R_ЭКВ. этого же куба, если куб включён в цепь в точках 2 и 4.

По тому же принципу потенциалы точек А и 6 равны, В и 3 равны. Учащиеся совмещают эти точки на своей модели и получают эквивалентную схему:

Расчёт эквивалентного сопротивления такой цепи прост

Задача № 3

Эта же модель куба, с включением в цепь между точками 2 и В. Учащиеся соединяют точки с равными потенциалами 1 и 3; 6 и 4. Тогда схема будет выглядеть так:

Точки 1,3 и 6,4 имеют равные потенциалы, и ток по сопротивлениям между этими точками не потечёт и схема упрощается до вида; эквивалентное сопротивление которой рассчитывается так:

Задача № 4

Равносторонняя треугольная пирамида, ребро которой имеет сопротивление R. Рассчитать эквивалентное сопротивление при включении в цепь.

Точки 3 и 4 имеют равный потенциал, поэтому по ребру 3,4 ток не потечёт. Учащиеся убирают его.

Тогда схема будет выглядеть так:

либо

Эквивалентное сопротивление рассчитывается так:

Задача № 5

Металлическая сетка с сопротивлением звена равном R. Рассчитать эквивалентное сопротивление между точками 1 и 2.

В точке 0 можно звенья отделить, тогда схема будет иметь вид:

- сопротивление одной половины симметричной по 1-2 точкам. Параллельно ей такая же ветвь, поэтому

Задача № 6

Рассчитать эквивалентное сопротивление проволочной звезды с сопротивлением каждого звена R, включённой в цепь между точками 1 и 2.

 Звезда состоит из 5-и равносторонних треугольников, сопротивление каждого.

Между точками 1 и 2 один треугольник параллелен четырём, последовательно соединенным между собой

Имея опыт расчёта эквивалентного сопротивления проволочных каркасов можно приступить к расчету сопротивлений цепи, содержащий бесконечное число сопротивлений. Например:

 Если отделить звено

от общей схемы, то схема не изменится, тогда  можно представить ввиде

или ,

решаем данное уравнение относительно R_экв.

Итог урока: мы научились абстрактно представлять схемы участков цепи, заменять их эквивалентными схемами, которые позволяют легко рассчитать эквивалентное сопротивление.

На дом:

Рассчитать эквивалентное сопротивление проволочного каркаса из двух окружностей с радиусами r₁ и r_2, r₂₌2r₁ между точками А и В. Сопротивление единицы длинны проволоки?

Указание: Эту модель представить в виде:

21.03.2008

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников»

Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников»

«Физика — 10 класс»

При решении задач на применение закона Ома необходимо учитывать, что при последовательном соединении проводников сила тока во всех проводниках одинакова, а при параллельном их соединении напряжение одинаково на всех проводниках.

Задача 1.

Параллельно амперметру, имеющему сопротивление R_а = 0,5 Ом, подсоединён медный провод длиной l = 0,4 м и диаметром d = 0,001 м. Удельное сопротивление меди ρ = 1,7 • 10^-8 Ом • м. Определите полную силу тока в цепи, если амперметр показывает силу тока I_а = 0,2 А.

Р е ш е н и е.

Так как амперметр и провод подключены параллельно, то напряжение на амперметре равно напряжению на проводе:

I_аR_а = I_nR_n.

Определим сопротивление провода:

Тогда

Полная сила тока в цепи

Задача 2.

На рисунке 15.7 все сопротивления резисторов равны R. Определите эквивалентное сопротивление цепи.

Чему равна полная сила тока в цепи, если на клеммы 1, 2 подано напряжение U?

Р е ш е н и е.

Трудно определить, как соединены резисторы R1 и R3 — последовательно или параллельно. В подобных схемах всегда нужно искать резисторы, соединения которых очевидны. Так, очевидно, что резисторы 7?5 и R6 соединены последовательно. Значит, R_5,6 = R₅ + R₆ = 2R. Эквивалентный резистор сопротивлением R_5,6 соединён с резистором R₄ параллельно. Следовательно,

Эквивалентный резистор сопротивлением R_4-6, в свою очередь, соединён последовательно с резистором R₃:

R_3-6 = R₃ + R_4-6 = R + (2/3)R = (5/3)R,

а эквивалентный резистор сопротивлением R_3-6 — параллельно с резистором R₂:

И наконец, эквивалентный резистор R_2-6 соединён последовательно с резистором R₁, так что

R_экв = R_2-б + R = (5/8)R + R = (13/8)R.

Из закона Ома следует, что сила тока

Задача 3.

К участку цепи с напряжением U через резистор сопротивлением R подключены параллельно десять лампочек, имеющих одинаковое сопротивление r.

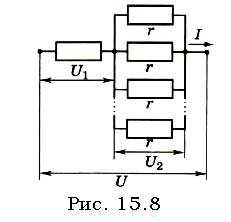
Определите напряжение на каждой лампочке.

Р е ш е н и е.

Начертим схему цепи (рис. 15.8). Очевидно, что напряжение на каждой лампочке будет одинаково, так как они соединены параллельно.
Резистор сопротивлением R и участок цепи с лампочками соединены последовательно,
следовательно, U = U₁ + U₂ = IR + IR_экв.
Запишем закон Ома для каждого из участков цепи:
откуда или
Решив это уравнение относительно U₂,
получим
Найдём эквивалентное сопротивление участка цепи с лампочками из соотношения

откуда

Окончательно получим

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика

Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

class-fizika.ru

Рекомендации по решению нетрадиционных задач на расчет электрических цепей постоянного тока

Разделы: Физика

---

Введение

Решение задач — неотъемлемая часть обучения физике, поскольку в процессе решения задач происходит формирование и обогащение физических понятий, развивается физическое мышление учащихся и совершенствуется их навыки применения знаний на практике.

В ходе решения задач могут быть поставлены и успешно реализованы следующие дидактические цели:

• Выдвижение проблемы и создание проблемной ситуации;
• Обобщение новых сведений;
• Формирование практических умений и навыков;
• Проверка глубины и прочности знаний;
• Закрепление, обобщение и повторение материала;
• Реализация принципа политехнизма;
• Развитие творческих способностей учащихся.

Наряду с этим при решении задач у школьников воспитываются трудолюбие, пытливость ума, смекалка, самостоятельность в суждениях, интерес к учению, воля и характер, упорство в достижении поставленной цели. Для реализации перечисленных целей особенно удобно использовать нетрадиционные задачи.

§1. Задачи по расчету электрических цепей постоянного тока

По школьной программе на рассмотрение данной темы очень мало отводится времени, поэтому учащиеся более или менее успешно овладевают методами решения задач данного типа. Но часто такие типы задач встречаются олимпиадных заданиях, но базируются они на школьном курсе.

К таким, нестандартным задачам по расчету электрических цепей постоянного тока можно отнести задачи, схемы которых:

1) содержат большое число элементов – резисторов или конденсаторов;

2) симметричны;

3) состоят из сложных смешанных соединений элементов.

В общем случае всякую цепь можно рассчитать, используя законы Кирхгофа. Однако эти законы не входят в школьную программу. К тому же, правильно решить систему из большого числа уравнений со многими неизвестными под силу не многим учащимся и этот путь не является лучшим способом тратить время. Поэтому нужно уметь пользоваться методами, позволяющими быстро найти сопротивления и емкости контуров.

§2. Метод эквивалентных схем

Метод эквивалентных схем заключается в том, что исходную схему надо представить в виде последовательных участков, на каждом из которых соединение элементов схемы либо последовательно, либо параллельно. Для такого представления схему необходимо упростить. Под упрощением схемы будем понимать соединение или разъединение каких-либо узлов схемы, удаление или добавление резисторов, конденсаторов, добиваясь того, чтобы новая схема из последовательно и параллельно соединенных элементов была эквивалентна исходной.

Эквивалентная схема – это такая схема, что при подаче одинаковых напряжений на исходную и преобразованную схемы, ток в обеих цепях будет одинаков на соответствующих участках. В этом случае все расчеты производятся с преобразованной схемой.

Чтобы начертить эквивалентную схему для цепи со сложным смешанным соединением резисторов можно воспользоваться несколькими приемами. Мы ограничимся рассмотрением в подробностях лишь одного из них – способа эквипотенциальных узлов.

Этот способ заключается в том, что в симметричных схемах отыскиваются точки с равными потенциалами. Эти узлы соединяются между собой, причем, если между этими точками был включен какой-то участок схемы, то его отбрасывают, так как из-за равенства потенциалов на концах ток по нему не течет и этот участок никак не влияет на общее сопротивление схемы.

Таким образом, замена нескольких узлов равных потенциалов приводит к более простой эквивалентной схеме. Но иногда бывает целесообразнее обратная замена одного узла

несколькими узлами с равными потенциалами, что не нарушает электрических условий в остальной части.

Рассмотрим примеры решения задач эти методом.

З а д а ч а №1

Рассчитать сопротивление между точками А и В данного участка цепи. Все резисторы одинаковы и их сопротивления равны r.

Решение:

В силу симметричности ветвей цепи точки С И Д являются эквипотенциальными. Поэтому резистор между ними мы можем исключить. Эквипотенциальные точки С и Д соединяем в один узел. Получаем очень простую эквивалентную схему:

Сопротивление которой равно:

RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.

З а д а ч а № 2

Решение:

В точках F и F` потенциалы равны, значит сопротивление между ними можно отбросить. Эквивалентная схема выглядит так:

Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны между собой и равны R1:

1/R1=1/2r+1/r=3/2r

R1=2/3*r

С учетом этого получается новая эквивалентная схема:

Ее сопротивление и сопротивление исходной цепи RАВ равно:

1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r

RАВ=(7/6)*r.

З а д а ч а № 3.

Решение:

Точки С и Д имеют равные потенциалы. Исключением сопротивление между ними. Получаем эквивалентную схему:

Искомое сопротивление RАВ равно:

1/RАВ=1/2r+1/2r+1/r=2/r

RАВ=r/2.

З а д а ч а № 4.

Решение:

Как видно из схемы узлы 1,2,3 имеют равные потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют тоже равные потенциалы- соединим их в узел 2. Получим такую эквивалентную схему:

Сопротивление на участке А-1, R 1-равно сопротивлению на участке 2-В,R3 и равно:

R1=R3=r/3

Сопротивление на участке 1-2 равно: R2=r/6.

Теперь получается эквивалентная схема:

Общее сопротивление RАВ равно:

RАВ= R1+ R2+ R3=(5/6)*r.

З а д а ч а № 5.

Решение:

Точки C и F-эквивалентные. Соединим их в один узел. Тогда эквивалентная схема будет иметь следующий вид:

Сопротивление на участке АС:

Rас=r/2

Сопротивление на участке FN:

R_FN =

Сопротивление на участке DB:

R_DB =r/2

Получается эквивалентная схема:

Искомое общее сопротивление равно:

R_AB= r.

Задача №6

Решение:

Заменим общий узел О тремя узлами с равными потенциалами О, О₁ , О₂. Получим эквивалентную систему:

Сопротивление на участке ABCD:

R₁=(3/2)*r

Сопротивление на участке A`B`C`D`:

R₂= (8/3)*r

Сопротивление на участке ACВ

R₃ = 2r.

Получаем эквивалентную схему:

Искомое общее сопротивление цепи R_AB равно:

R_AB= (8/10)*r.

Задача №7.

Решение:

“Разделим” узел О на два эквипотенциальных угла О₁ и О₂. Теперь схему можно представить, как параллельные соединение двух одинаковых цепей. Поэтому достаточно подробно рассмотреть одну из них:

Сопротивление этой схемы R₁ равно:

R₁ = 3r

Тогда сопротивление всей цепи будет равно:

R_AB = (3/2)*r

З а д а ч а №8

Решение:

Узлы 1 и 2 – эквипотенциальные, поэтому соединим их в один узел I. Узлы 3 и 4 также эквипотенциальные – соединимих в другой узел II. Эквивалентная схема имеет вид:

Сопротивление на участке A- I равно сопротивлению на участке B- II и равно:

R_I =

Сопротивление участка I-5-6- II равно:

R_II = 2r

Cопротивление участка I- II равно:

R_III =

Получаем окончательную эквивалентную схему:

Искомое общее сопротивление цепи R_AB=(7/12)*r.

З а д а ч а №9

В ветви ОС заменим сопротивление на два параллельно соединенных сопротивления по 2r. Теперь узел С можно разделить на 2 эквипотенциальных узла С₁ и С₂. Эквивалентная схема в этом случае выглядит так:

Сопротивление на участках ОС_IB и DC_IIB одинаковы и равны, как легко подсчитать 2r. Опять чертим соответствующую эквивалентную схему:

Сопротивление на участке AOB равно сопротивлению на участке ADB и равно (7/4)*r. Таким образом получаем окончательную эквивалентную схему из трех параллельно соединенных сопротивлений:

Ее общее сопротивление равно R_AB= (7/15)*r

З а д а ч а № 10

Точки СОD имеют равные потенциалы – соединим их в один узел О^I .Эквивалентная схема изображена на рисунке :

Сопротивление на участке А О^I равно . На участке О^IВ сопротивление равно .Получаем совсем простую эквивалентную схему:

ЕЕ сопротивление равно искомому общему сопротивлению

R_AB=(5/6)*r

Задачи № 11 и № 12 решаются несколько иным способом, чем предыдущие. В задаче №11 для ее решения используется особое свойство бесконечных цепей, а в задаче № 12 применяется способ упрощения цепи.

Задача № 11

Решение

Выделим в этой цепи бесконечно повторяющееся звено, оно состоит в данном случае из трех первых сопротивлений. Если мы отбросим это звено, то полное сопротивление бесконечной цепи R не измениться от этого , так как получится точно такая же бесконечная цепь. Так же ничего не измениться, если мы выделенное звено подключим обратно к бесконечному сопротивлению R, но при этом следует обратить внимание , что часть звена и бесконечная цепь сопротивлением R соединены параллельно. Таким образом получаем эквивалентную схему :

Получается уравнения

R_AB=2ч +

R_AB = R

Решая систему этих уравнений, получаем:

R=ч (1+ ).

§3. Обучение решению задач по расчету электрических цепей способом эквипотенциальных узлов

Задача – это проблема, для разрешения которой ученику потребуются логические рассуждения и выводы. Строящиеся на основе законов и методов физики. Таким образом, с помощью задач происходит активизация целенаправленного мышления учащихся.

В то же время. Теоретические знания можно считать усвоенными только тогда, когда они удачно применяются на практике. Задачи по физике описывают часто встречающиеся в жизни и на производстве проблемы, которые могут быть решены с помощью законов физики и, если ученик успешно решает задачи, то можно сказать, что он хорошо знает физику.

Для того, чтобы ученики успешно решали задачи, недостаточно иметь набор методов и способов решения задач, необходимо еще специально учить школьников применению этих способов.

Рассмотрим план решения задач по расчету электрических цепей постоянного тока методом эквипотенциальных узлов.

1. Чтение условия.
2. Краткая запись условия.
3. Перевод в единицы СИ.
4. Анализ схемы:
1. установить, является ли схема симметричной;
2. установить точки равного потенциала;
3. выбрать, что целесообразнее сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов;
4. начертить эквивалентную схему;
5. найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом участке по законам последовательного и параллельного соединения;
6. начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями;
7. пункты 5 и 6 повторять до тех пор, пока не останется одно сопротивление, величина которого и будет решением задачи.
5. Анализ реальности ответа.

Подробнее об анализе схемы

а) установить, является ли схема симметричной.

Определение. Схема симметрична, если одна ее половина является зеркальным отражением другой. Причем симметрия должна быть не только геометрической, но должны быть симметричны и численные значения сопротивлений или конденсаторов.

Примеры:

1)

Схема симметричная, так как ветви АСВ и АДВ симметричны геометрически и отношение сопротивления на одном участке АС:АД=1:1 такое же, как и на другом участке СД:ДВ=1:1.

2)

Схема симметричная, так как отношение сопротивлений на участке АС:АД=1:1 такое же, как и на другом участке СВ:ДВ=3:3=1:1

3)

Схема не симметрична, так как отношения сопротивлений численно

не симметричны -1:2 и 1:1.

б) установить точки равных потенциалов.

Пример:

Из соображений симметрии делаем вывод, что в симметричных точках потенциалы равны. В данном случае симметричными точками являются точки С и Д. Таким образом, точки С и Д – эквипотенциальные точки.

в) выбрать, что целесообразно сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов.

Мы видим в этом примере, что между точками равных потенциалов С и Д включено сопротивление, по которому ток не будет течь. Следовательно, мы можем отбросить это сопротивление, а точки С и Д соединить в один узел.

г) начертить эквивалентную схему.

Чертим эквивалентную схему. При этом получаем схему с соединенными в одну точку точками С и Д.

д) найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом таком участке по законам последовательного и параллельного соединения.

Из полученной эквивалентной схемы видно, что на участке АС мы имеем два параллельно соединенных резистора. Их общее сопротивление находится по закону параллельного соединения:

1/ Rобщ=1/R1+1/R2+1/R3+…

Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.

На участке СВ картина аналогичная:

1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.

е)начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями.

Чертим эквивалентную схему подставляя в нее рассчитанные сопротивления участков RAC и RCB:

ж)пункты д) и е) повторять до тех пор, пока останется одно сопротивление, величина которого и будет решением задачи.

Повторяем пункт д): на участке АВ имеем два последовательно соединенных сопротивления. Их общее сопротивление находим по закону последовательного соединения:

Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Повторяем пункт е): чертим эквивалентную схему:

Мы получили схему с одним сопротивлением, величина которого равна сопротивлению исходной схемы. Таким образом, мы получили ответ RAB = r.

Далее, для проверки усвоения данного материала можно учащимся предложить задания для самостоятельной работы, взятые из дидактического материала. (см. приложение)

Литература

1. Балаш. В.А. задачи по физике и методы их решения. - М: Просвещение,1983.
2. Лукашик В.И. Физическая олимпиада.- М: Просвещение, 2007
3. Усова А.В., Бобров А.А. Формирование учебных умений и навыков учащихся на уроках физики.- М: Просвещение,1988
4. Хацет А. Методы расчета эквивалентных схем //Квант.
5. Чертов А. Г. Задачник по физике. – М.: Высшая школа,1983
6. Зиятдинов Ш.Г., Соловьянюк С.Г. (методические рекомендации) г. Бирск,1994г
7. Марон А.Е., Марон Е.А. Физика. Дидактические материалы. Москва, “Дрофа”, 2004г

24.03.2012

xn--i1abbnckbmcl9fb.xn--p1ai

No related posts.