Методика решения задач по химии на изменение концентрации раствора
В задачах, связанных с добавлением к раствору определенного количества растворителя или растворенного вещества, необходимо сначала рассчитать массу растворенного вещества в исходном растворе, а затем использовать ее для дальнейших вычислений. Условие каждой задачи для большей наглядности лучше изобразить в виде рисунка.
Задача 1.
К 180,0 г 8% -ного раствора хлорида натрия добавили 20 г NaС1. Массовая доля хлорида натрия в образовавшемся растворе равна ….% (запишите число с точностью до десятых).
Дано:
масса исходного раствора: mисх.р-ра = 180 г;
массовая доля NaС1 в исходном растворе: (NaС1)в исх р-ре = 8%;
масса добавленной соли NaС1: m(NaСl)добавл = 20 г.
Найти:
массовую долю соли в конечном растворе: (NaС1)в кон/ р-ре
Решение:
Условие задачи удобно отобразить в виде рисунка:
1. Находим массу NaСl в исходном растворе:
2. Масса NaС1 в конечном растворе представляет собой сумму:
m(NаС1)в кон.р.ре = m(NаС1)в исх. р.ре + m(NаС1)добавл. = 14,4+ 20 = 34,4 г.
3. Массу добавленной соли учитываем и в массе конечного раствора:
mкон. р-ра = mисх. р-ра + m(NаС1)добавл. = 180 + 20 = 200 г.
4. Полученные данные позволяют определить массовую долю в конечном растворе:
Ответ: (NaС1)в исх р-ре = 17,2%.
Задача, в которой добавляется некоторое количество воды к порции раствора известной концентрации, решается по тому же алгоритму.
В задаче на смешение двух растворов требуется проводить немного большее количество расчетов. В этом случае необходимо вычислить массу растворенного вещества в каждом из
исходных растворов.
Задача 2.
Смешали 200 г 20%-ного раствора NаОН с 218 мл 10%-ного раствора того же вещества (p = 1,11 г/мл). Массовая доля щелочи в полученном растворе. …% (Запишите число с точностью до десятых).
Дано:
масса первого раствора NаОН: m1 исх р-ра = 200 г;
массовая доля NаОН в первом р-ре: со(МаОН) в 1 исх р-ре = 20% ;
объем второго раствора NаОН: V2исх.р-ра = 218 мл;
массовая доля NаОН во втором р-ре: (NаОН) во 2 исх. р-ре = 10% ;
плотность второго исходного раствора: р2 исх. р.р=1,11 г/мл.
Найти: массовую долю NаОН в конечном р-ре: (NаОН)в кон р-ре
Решение:
Условие задачи удобно отобразить в виде рисунка:
При решении данной задачи необходимо определить массу NаОН в каждом из исходных растворов. Далее найти суммарную массу конечного раствора и массу NаОН в нем. После этого вычисляем искомую величину.
Схематично алгоритм решения можно отразить так:
1. Находим массу NаОН в первом исходном растворе:
2. Находим массу второго исходного раствора:
m2 исх. р-ра = V2 исх. р-ра. p 2 исх. р-ра = 218 . 1,11 = 242 г.
3. Находим массу NаОН во втором исходном растворе:
m(NaOH)в кон. р-ре = m(NaOH)в 1 исх. р-ре + m(NaOH)во 2 исх. р-ре = 40 + 24,2 = 64,2 г.
5. Находим массу конечного раствора:
mкон. р-ра = m1 исх. р-ра + m2 исх. р-ра = 200 + 242 = 442 г.
6. Находим массовую долю NаОН в конечном растворе:
Округляем полученное значение до десятых.
Ответ: (NaOH)в кон.р-ре = 14,5%.
В задаче на выпаривание масса раствора уменьшается обычно за счет удаления растворителя. При этом масса растворенного вещества остается прежней, что приводит к увеличению концентрации.
Задача 3.
Определите массу воды, которую необходимо выпарить из 2 л 10% раствора NаОН (р = 1,11 г/мл) для повышения массовой доли NаОН в нем до 15% . Ответ: … г (запишите число с точностью до целых).
Дано:
объем исходного раствора: Vисх. р-ра = 2 л;
плотность исходного раствора: рисх р-ра =1,11 г/мл;
массовая доля NаОН в исходном р-ре: (NаОН)в исх р.ре = 10% ;
массовая доля NаОН в конечном р-ре:(NаОН)в кон р-ре = 15%
Найти: массу испарившейся воды: m(Н2О)испарили = ?
Решение:
При выпаривании водного раствора NаОН улетучиваться будет только вода. Масса NаОН будет одинаковой как в исходном, так и в конечном растворе.
Схематично алгоритм решения можно представить следующим образом:
1. Найдем массу исходного раствора:
m исх. р-ра = V исх. р-ра. рисх. р-ра
V исх. р-ра = 2 л = 2000 мл
m
2. Найдем массу NаОН в исходном растворе:
3. Определим массу конечного раствора:
4. Уменьшение массы раствора произошло только из-за испарения воды, следовательно, по разнице масс исходного и конечного растворов можно найти массу улетучившейся воды:
m(Н2О)испарилось = mисх р-ра – mкон. р-ра = 2220 — 1480 = 740 г.
Ответ: m(Н2О)испарилось = 740 г.
В условиях некоторых задач предполагается выведение из раствора в виде газа легколетучего растворенного вещества (например МН3; НС1; Н2S или растворенного в воде органического вещества). Для решения таких задач необходимо считать неизменной массу растворителя (воды).
Задача 4.
При нагревании 200 г 25%-ного раствора аммиака 20 г этого вещества улетучилось. Массовая доля аммиака в растворе после нагревания равна… % (запишите число с точностью до десятых).
Дано:
масса исходного раствора: mисх р-ра = 200 г;
массовая доля NН3 в исходном растворе: (NН3)в исх. р-ре = 25% ;
масса улетучившегося аммиака: m(NН3)улетучилось = 20 г.
Найти: массовую долю NH3 в конечном р-ре: (NН3)в кон. р ре =?
Решение:
Схематично алгоритм решения можно представить следующим образом:
1. Находим массу NН3 в исходном растворе:
2. Находим массу NН3 в конечном растворе:
m(NH3) в кон. р-ре = m(NH3) в исх. р-ре — m(NН3)улетело = 50 — 20 = 30 г.
Находим массу конечного раствора1:
mкон р-ра = mисх р-ра — m(NН3)улетучилось = 200 — 20 = 180 г.
4. Находим массовую долю аммиака в конечном растворе:
Округляем значение, согласно требованию условия, и получаем: (NН3)в кон. р-ре = 16,7% .
Ответ: (NН3)в кон. р-ре = 16,7% .
Комментарии: 1При решении данной задачи учащиеся часто забывают найти массу
конечного раствора. После определения массы оставшегося аммиака они для нахождения массовой доли NH3 в конечном растворе ошибочно делят массу оставшегося NH3 на массу исходного раствора.
Избежать этой распространенной ошибки помогают комментарии каждой записанной величины. Например, следует записывать mкон. р-ра, а не mр-ра ; m(NH3)в кон. р-ре, а не m(NH3).
Источник:
ЕГЭ. Химия. Расчетные задачи в тестах ЕГЭ. Части А, В, С / Д.Н. Турчен. — М.: Издательство «Экзамен», 2009. — 399 [1]с. (Серия «ЕГЭ. 100 баллов»). I8ВN 978-5-377-02482-8.
buzani.ru
Решение задач на растворы
Разделы: Математика, Химия
Цели урока: Рассмотреть алгоритм решения задач на растворы: познакомиться с приемами решения задач в математике и химии, рассмотреть биологическое значение воды как универсального растворителя, развить практические умения решать задачи, расширить знания учащихся о значении этих веществ в природе и деятельности человека, сформировать целостную картину о взаимосвязи предметов в школе.
Ход урока
Организационный момент
Учитель математики: Здравствуйте! Сегодня мы проводим необычный урок – урок на перекрестке наук математики и химии.
Учитель химии: Здравствуйте, ребята! Мы с вами увидим, как математические методы решения задач помогают при решении задач по химии.
А чтобы сформулировать тему урока, давайте проделаем небольшой эксперимент.
(Наливаю в 2 хим. стакана воду, добавляю в оба одинаковое количество сульфата меди.) Что получилось? (Растворы). Из чего состоит раствор? (Из растворителя и растворённого вещества). А теперь добавим в один из стаканов ещё немного сульфата меди. Что стало с окраской раствора? (Он стал более насыщенным). Следовательно, чем отличаются эти растворы? (Массовой долей вещ-ва).
Учитель математики: А с математической точки зрения – разное процентное содержание вещества.
Итак, тема урока “Решение задач на растворы”.
Цель урока: Рассмотреть алгоритм решения задач на растворы, познакомить с приемами решения задач в математике и химии, расширить знания о значении этих растворов в быту, сформировать целостную картину о взаимосвязи предметов в школе.
Девиз: “Только из союза двух работающих вместе и при помощи друг друга рождаются великие вещи” Антуан де Сент-Экзюпери.
Учитель математики: Для урока необходимо повторить понятие процента.
– Что называют процентом? (1/100 часть числа).
– Выразите в виде десятичной дроби 17%, 40%, 6%.
– Выразите в виде обыкновенной дроби 25%, 30%, 7%.
– Установите соответствие:
| 40% | 1/4 |
| 25% | 0,04 |
| 80% | |
| 4% | 4/5 |
Одним из основных действий с процентами – нахождение % от числа.
Как найти % от числа? (% записать в виде дроби, умножить число на эту дробь.)
– Найти 10% от 30 (10%=0,1 30·0,1=3).
– Вычислите:
1) 20% от 70;
2) 6% от 20;
3) х% от 7.
Учитель химии
– Что такое раствор? (Однородная система, состоящая из частиц растворенного вещества, растворителя и продуктов их взаимодействия.)
– Приведите примеры растворов, с которыми вы встречаетесь в повседневной жизни. (уксус, нашатырный спирт, раствор марганцовки, перекись водорода и др.)
– Какое вещество чаще всего используется в качестве растворителя? (Вода)
Часто понятие “раствор” мы связываем, прежде всего, с водой, с водными растворами. Есть и другие растворы: например спиртовые раствор йода, одеколона, лекарственные настойки.
Хотя именно вода является самым распространённым соединением и “растворителем” в природе.
3/4 поверхности Земли покрыто водой.
Человек на 70% состоит из воды.
В сутки человек выделяет 3 литра воды и столько же нужно ввести в организм.
Овощи – 90% воды содержат (рекордсмены — огурцы - 98%)
Рыба 80% (рекордсмен у животных – медуза 98%)
Хлеб – 40%
Молоко – 75%
– Что такое массовая доля растворенного вещества? (Отношение массы растворенного вещества к общей массе раствора.)
– Вспомните формулу для вычисления массовой доли растворенного вещества и производные от нее (w = m (р.в.)/m (р-ра ) ; m (р.в.)= m (р-ра) · w ; m (р-ра) = m (р.в.)/ w )
– По какой формуле можно рассчитать массу раствора? (m(р-ра) = m (р.в.) + m (р-ля)).
Учитель химии предлагает решить учащимся задачу:
Задача №1. Перед посадкой семена томатов дезинфицируют 15%-ным раствором марганцовки. Сколько г марганцовки потребуется для приготовления 500 г такого раствора? (Ответ: 40 г.)
Учитель математики.
– Давайте посмотрим на эту задачу с точки зрения математики. Какое правило на проценты вы применили при решении этой задачи? (Правило нахождения процента от числа.)
15% от 500;
500·0,15=75 (г) – марганцовки.
Ответ: 75 г.
– Как видите, задачи, которые вы встречаете на химии, можно решать на уроках математики без применения химических формул.
Задачам на растворы в школьной программе уделяется очень мало времени, но эти задачи встречаются на экзаменах в 9 и 11 классах. В этом году на экзамене в 9 классе была задача на смешивание растворов, и она оценивалась в 6 баллов.
Задача №2. При смешивании 10%-го и 30%-го раствора марганцовки получают 200 г 16%-го раствора марганцовки. Сколько граммов каждого раствора взяли?
Можно ли решить эту задачу так быстро?
О чем говорится в этой задаче? (о растворах)
Что происходит с растворами? (смешивают)
Решение:
| Раствор | %-е содержание | Масса раствора (г) | Масса вещества (г) |
1 раствор |
10% = 0,1 |
х |
0,1х |
Смесь |
16% = 0,16 |
200 |
0,16 · 200 |
0,1х + 0,3(200-х) = 0,16 · 200
0,1х + 60 – 0,3х = 32
-0,2х = -28
х = 140
140 (г) – 10% раствора
200 – 140 = 60 (г) — 30% раствора.
Ответ: 140 г, 60 г.
Учитель математики. Рассмотрим еще один раствор – это уксусная кислота. Водный раствор уксусной кислоты, полученный из вина (5-8%) называют винным уксусом. Разбавленный (6-10%) раствор уксусной кислоты под названием “столовый уксус” используется для приготовления майонеза, маринадов и т.д. Уксусная эссенция 80% раствор. Ее нельзя применять без разбавления для приготовления пищевых продуктов. “Столовый уксус”, используют для приготовления маринадов, майонеза, салатов и других пищевых продуктов. Очень часто при приготовлении блюд под руками оказывается уксусная эссенция. Как из нее получить столовый уксус. Поможет следующая задача.
Задача №3. Какое количество воды и 80%-го раствора уксусной кислоты следует взять для того, чтобы приготовить 200 г столового уксуса (8%-ый раствор уксусной кислоты.)
Решение:
Раствор |
%-е содержание |
Масса раствора (г) |
Масса вещества (г) |
Уксусная кислота |
80%=0,8 |
х |
0,8х |
Смесь |
8%=0,08 |
200 |
0,08 · 200 |
0,8х = 0,08 · 200
0,8х = 16
х = 16 : 0,8
х = 20
20 (г) – уксусной кислоты
200 – 20 = 180 (г) – воды.
Ответ: 20 г, 180 г.
Учитель химии. А сейчас мы решим экспериментальную задачу.
Приготовить 20 г 5%-го раствора поваренной соли. (Расчётная часть). Затем выполняем практическую часть. (Напомнить правила Т-Б).
2. Экспериментальная часть (Соблюдать правила техники безопасности).
- Уравновесить весы.
- Взвесить необходимое количество соли.
- Отмерить мерным цилиндром воду.
- Смешать воду и соль в стакане.
Учитель математики. Проведем проверочную работу, в которую включили задачи из сборника для подготовке к экзаменам в 9-м классе.
Проверочная работа
| При смешивании 15%-го и 8% -го раствора кислоты получают 70 г 10%-го раствора кислоты. Сколько граммов каждого раствора взяли? | При смешивании 15%-го и 60% -го раствора соли получают 90 г 40%-го раствора соли. Сколько граммов каждого раствора взяли? |
| 1р 15% = 0,15 х 0,15х |
1р 15%=0,15 х 0,15х |
| 2р 8% = 0,08 70 — х 0,08(70 — х) |
2р 60% = 0,6 90 — х 0,6(90 — х) |
| см 10% = 0,1 70 0,1 · 70 |
3р 40% = 0,4 90 0,4 · 90 |
| 0,15х + 0,08(70 — х) = 0,1 · 70 0,15х + 5,6 — 0,08х = 7 0,07х = 7 — 5,6 0,07х = 1,4 х = 1,4:0,07 х = 20 20(г) – 15%-го раствора. 70 – 20 = 50 (г) — 8% раствора Ответ: 20 гр., 50 г. |
0,15х + 0,6(90 — х) = 0,4 · 90 0,15х + 54 — 0,6х = 36 -0,45х = 36 — 54 -0,45х =-18 х = 18 : 0,45 х = 40 40 (г) -15% раствора. 90 — 40 = 50 (г) — 60% раствора. Ответ: 40 гр., 50 г. |
Подведение итогов урока
Учитель химии.
– Посмотрите на содержание всех решенных сегодня задач. Что их объединяет? (Задачи на растворы.)
– Действительно, во всех задачах фигурируют водные растворы; расчеты связаны с массовой долей растворенного вещества; и если вы обратили внимание, задачи касаются разных сторон нашего быта.
Учитель математики.
– Посмотрите на эти задачи с точки зрения математики. Что их объединяет? (Задачи на проценты.)
При решении всех этих задач мы используем правило нахождения процента от числа.
Оценки за урок.
Домашнее задание.
Важное место в рационе питания человека, а особенно детей занимает молоко и молочные продукты. Решим такую задачу:
Задача №1. Какую массу молока 10%-й жирности и пломбира 30%-й жирности необходимо взять для приготовления 100 г 20%-го новогоднего коктейля?
Решение:
%-е содержание |
Масса раствора (г) |
Масса вещества (г) |
|
Молоко |
10% = 0,1 |
х |
0,1х |
Коктейль |
20% = 0,2 |
100 |
0,2 · 100 |
0,1х + 0,3(100-х) = 0,2 · 100
0,1х + 30 – 0,3х = 20
-0,2х = -10
х = 50
50(г) – молока
100 – 50 = 50(г) – пломбира.
Ответ:50 г молока, 50 г пломбира.
Задача №3. Для засола огурцов используют 7% водный раствор поваренной соли (хлорида натрия NaCl). Именно такой раствор в достаточной мере подавляет жизнедеятельность болезнетворных микроорганизмов и плесневого грибка, и в то же время не препятствует процессам молочнокислого брожения. Рассчитайте массу соли и массу воды для приготовления 1 кг такого раствора?
Рефлексия. (Синквейн)
Раствор
Разбавленный, водный
Растворять, смешивать, решать
Растворы широко встречаются в быту.
Смеси
Наш урок подошел к концу. Сейчас каждый из вас оставит на парте тот смайлик, какое настроение вы приобрели на уроке.
Спасибо за урок!
Процент
Лист к уроку
Презентация
6.01.2013
xn--i1abbnckbmcl9fb.xn--p1ai
Задачи на растворы и методы их решения
Решение задач на растворы является важным разделом курса химии в современной школе. У многих ребят возникают определенные затруднения при проведении вычислений, связанные с отсутствием представлений о последовательности выполнения задачи. Проанализируем некоторые термины, которые включают в себя задачи на растворы по химии, и приведем примеры готовых решений.

Процентная концентрация
Задачи предполагают составление и решение пропорции. Учитывая, что выражается этот вид концентрации в массовых долях, можно определить содержание вещества в растворе.
Упомянутая величина является количественной характеристикой раствора, предложенного в задаче. В зависимости от типа задания, необходимо определять новую процентную концентрацию, рассчитывать массу вещества, вычислять объем раствора.

Молярная концентрация
Некоторые задачи на концентрацию растворов связаны с определением количества вещества в объеме растворителя. Единицами измерения такой величины является моль/л.
В школьной программе задания такого вида встречаются только на старшей ступени обучения.

Особенности задач на растворы
Приведем некоторые задачи на растворы по химии с решением, чтобы показать последовательность действий при их разборе. Для начала заметим, что можно делать рисунки, чтобы понять суть процессов, описываемых в предложенном задании. При желании можно оформлять задачу и в виде таблицы, в которой будут поставлены исходные и искомые величины.

Задача 1
В емкость, содержащую 5 литров 15%-раствора соли, влили семь литров воды. Определите процентную концентрацию вещества в новом растворе.
Для того чтобы определить искомую величину, обозначим ее через Х. Через пропорцию вычислим количественное содержание вещества в первом растворе: если 5 умножить на 0,15, получаем 0,75 грамма.
Далее вычисляем массу нового раствора, учитывая, что влили 7 литров воды, и получаем 12 граммов.
Находим содержание в процентах поваренной соли в полученном растворе исходя из определения данной величины, получаем: (0,75 : 12) х 100% = 6,25%
Приведем еще один пример задания, связанного с использованием при расчетах математической пропорции.
Задача 2
Сколько по массе меди необходимо добавить к куску бронзы, имеющему массу 8 килограммов, содержащему 13 процентов чистого металла, чтобы увеличить процентное содержание меди до 25 %.
Такие задачи на растворы сначала требуют определить массу чистой меди в исходном сплаве. Для этого можно воспользоваться математической пропорцией. В результате получается, что масса составляет: 8 х 0,13 = 1,04 кг
Искомую величину возьмем за х (граммов), тогда в новом сплаве получим ее значение (1,04 + х) килограммов. Выразим массу получаемого сплава, получаем: (8 + х) килограммов.
В задаче содержание металла в процентах в новом сплаве составляет 25 процентов, можно составить математическое уравнение.
Разнообразные задачи на растворы включают в тестовые задания для проверки уровня предметных знаний выпускников одинадцатых классов. Приведем некоторые условия и решения заданий такого типа.

Задача 3
Определите объем (при нормальных условиях) газа, который был собран после введения 0,3 моль чистого алюминия в 160 миллилитрах теплого 20% раствора едкого калия (1,19 г/мл).
Последовательность проведения расчетов в данной задаче:
- Сначала необходимо определить массу раствора.
- Далее вычисляется количество щелочи.
- Полученные параметры сравниваются между собой, определяется недостача. Последующие вычисления проводят по веществу, взятому в недостаточном количестве.
- Пишем уравнение реакции, происходящей между исходными веществами, расставляем стереохимические коэффициенты. Проводим вычисления по уравнению.
Масса раствора щелочи, используемой в задаче, составляет 160 х 1,19 = 190,4 г.
Масса вещества составит 38,08 грамма. Количество взятой щелочи — 0,68 моль. В условии сказано, что количество алюминия 0,3 моль, следовательно, в недостатке присутствует именно этот металл.
Последующие вычисления осуществляем именно по нему. Получается, что объем газа составит 0,3 х 67,2/2 = 10,08 л.
Задачи на растворы такого типа у выпускников вызывают максимальные затруднения. Причина в неотработанности последовательности действий, а также в отсутствии сформированных представлений об основных математических вычислениях.

Задача 4
Задачи по теме «Растворы» могут включать и определение чистого вещества при заданном процентном содержании примесей. Приведем пример подобного задания, чтобы у ребят не возникало сложностей с его выполнением.
Вычислите объем газа, полученного при воздействии концентрированной серной кислоты на 292,5 г соли с 20% примесей.
Последовательность действий:
- Учитывая, что в условии задачи говорится о наличии 20 процентов примесей, необходимо определить содержание вещества по массе (80 %).
- Прописываем уравнение химической реакции, расставляем стереохимические коэффициенты. Проводим вычисления объема выделяющегося газа, используя молярный объем.
Масса вещества, исходя из того, что есть примеси, получается 234 грамма. А при проведении вычислений по данному уравнению, получим, что объем будет равен 89,6 литров.

Задача 5
Какие еще предлагаются в школьной программе по химии задачи на растворы? Приведем пример задания, связанного с необходимостью вычисления массы продукта.
Сульфид свинца (II), имеющий массу 95,6 г, взаимодействует с 300 миллилитрами 30%-раствора перекиси водорода (плотность 1,1222 г/мл). Продукт реакции составляет (в граммах) …
Порядок решения задачи:
- Растворы веществ переводим через пропорции в массу.
- Далее определяем количество каждого исходного компонента.
- После сравнения полученных результатов, выбираем то вещество, которое взято в недостаточном количестве.
- Вычисления проводим именно по веществу, взятому в недостатке.
- Составляем уравнение химического взаимодействия и вычисляем массу неизвестного вещества.
Вычислим раствор перекиси, он составляет 336,66 грамма. Масса вещества будет соответствовать 100,99 грамма. Вычислим количество моль, оно составит 2,97. Сульфида свинца будет 95,6 /239 =0,4 моль, (он содержится в недостатке).
Составляем уравнение химического взаимодействия. Определяем по схеме искомую величину и получаем 121,2 граммов.
Задача 6
Найти количество газа (моль), которое можно получить при термическом обжиге 5,61 кг сульфида железа (II), имеющего степень чистоты 80%.
Порядок действий:
- Вычисляем массу чистого FeS.
- Записываем уравнение химического взаимодействия его с кислородом воздуха. Проводим вычисления по реакции.
По массе чистое вещество составит 4488 г. Количество определяемого компонента будет 51 литр.
Задача 7
Из 134,4 литров (при нормальных условиях) оксида серы (4) приготовили раствор. К нему прилили 1,5 литра 25%-раствора едкого натра (1,28 г/мл). Определите массу получившейся соли.
Алгоритм вычислений:
- Рассчитываем массу раствора щелочи по формуле.
- Находим массу и число моль едкого натра.
- Вычисляем эту же величину для оксида серы (4).
- По соотношению полученных показателей определяем состав образующейся соли, определяем недостаток. Расчеты проводим по недостатку.
- Записываем химическую реакцию с коэффициентами, вычисляем массу новой соли по недостатку.
В итоге у нас получается:
- раствор щелочи составит 1171,875 грамма;
- по массе гидроксида натрия составит 292,97 грамма;
- в молях данного вещества содержится 7,32 моль;
- анологично вычисляем для оксида серы (4), получаем 6 моль;
- в результате взаимодействия будет образовываться средняя соль;
- получаем 756 граммов.
Задача 8
К 100 граммам 10%-раствора хлорида аммония прилили 100 г 10%-раствора нитрата серебра. Определите массу (в граммах) осадка.
Алгоритм вычислений:
- Вычисляем массу и количество вещества хлорида аммония.
- Рассчитываем массу и количество вещества соли — нитрата серебра.
- Определяем, какое из исходных веществ было взято в недостаточном количестве, проводим по нему расчеты.
- Записываем уравнение происходящей реакции, проводим по ней расчеты массы осадка.
Холрида аммония по массе будет 10 г, по количеству — 0,19 моль. Нитрата серебра взято 10 граммов, что составляет 0,059 моль. При вычислениях по недосттаку, получим массу соли 8,46 грамма.
Для того чтобы справиться со сложными заданиями, которые предлагаются на выпускных экзаменах в девятом и одиннадцатом классе (по курсу неогранической химии), необходимо владеть алгоритмами и иметь определенные вычислительные навыки. Кроме того, важно владеть технологией составления химических уравнений, уметь расставлять коэффициенты в процессе.
Без таких элементарных умений и навыков даже самая простая задача на определение процентной концентрации вещества в растворе либо смеси, покажется выпускнику трудным и серьезным испытанием.
fb.ru
Задача на растворы.
Задание B13 (№ 99572) из Открытого банка заданий для подготовки к ЕГЭ по математике:
Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
В задачах на сплавы и растворы используется одна единственная формула:
%, где
P — процентное содержание чистого вещества в сплаве или растворе,
m — масса чистого вещества
M — масса сплава или раствора.
Задачи на сплавы и растворы удобно решать с помощью таблицы. Порядок заполнения таблицы такой:
1. Сначала решаем, какую величину мы примем за неизвестное, и заполняем тот столбец таблицы, в котором речь идет об этой величине.
2. Заполняем тот столбец, параметры которого даны.
3. Параметры третьего столбца выражаем через параметры первых двух.
Поясню алгоритм решения задачи на сплавы и растворы на примере данной задачи.
1. Поскольку в условии масса первого раствора не указана, примем ее за х. Масса второго раствора равна массе первого и тоже равна х. После того, как растворы смешали, мы получила раствор, масса которого равна 2х.
Начнем заполнять таблицу:
2. В условии задачи дано процентное содержание вещества в каждом растворе. Внесем эти условия в соответствующий столбец таблицы:
3. Параметры второго столбца, то есть массу чистого вещества выразим через параметры первых двух. Для этого воспользуемся формулой:
:
Процентное содержание вещества в получившемся растворе равно
массе вещества:
разделить
на массу раствора: ,
и умножить на 100%
Получим:
%%
Ответ: 17%.
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачатьFirefox
ege-ok.ru
Интегрированный урок математики и химии по теме «Решение задач на процентную концентрацию, сплавы и растворы»
Разделы: Математика, Химия
Цели урока:
1. Обобщить и закрепить теоретический материал из курса математики и химии:
А) выражение процентов в виде десятичных дробей;
Б) выражение десятичных дробей в процентах;
В) понятия: растворы, примесь, сплав, а также концентрация растворов (процентное содержание растворенного вещества в растворителе).
2. Показать и раскрыть суть способа решения задач на “Конверт Пирсона”, закрепить навыки решения расчетных задач по математике и по химии.
3. Развивать познавательный интерес, реализуя межпредметные связи курсов математики и химии.
Тип урока: Интегрированный урок с химией.
Оборудование урока:
- карточки с заданиями для самостоятельной работы;
- карточки с дифференцированными домашними заданиями.
Учителя:
- математики – Яковлева Н.С.
- химии – Семенова А.П.
Ход урока
I. Организационный момент:
— сообщение темы, цели урока
— ознакомить учащихся с планом урока.
II. Повторение основных понятий (устно)
- Выразить проценты в виде десятичных дробей;
- Запишите в процентах десятичные дроби;
- Назовите целую и дробные части числа.
III.Фронтальная письменная работа
Учитель химии:
Задача №1:
К 60 г. соли добавили 100 г. воды. Определите содержание соли в растворе (содержимость соли в %).
Решение:
— найдем массу всего раствора: 60+100=160 (г)
— отсюда находим содержание соли в %: 150 г. -100%
60 г. – х
х=60*100/150=40%
Ответ: в растворе 40% соли
Задача №2
К 200г. 20% раствору соли добавили 60г. соли. Найдите концентрацию раствора.
Решение:
1) Находим массу соли в первом растворе:
200г. – 100%
х – 20%
х= 200*20/100 = 40г. соли
2) Найдем всю массу соли: 40+60=100г. соли во всем растворе
3) Находим массу нового раствора: 200+60=260г.
4) Найдем % концентрацию соли в конечном растворе:
260 – 100%
100 – у
у=100*100/260=38,46%
Ответ: в новом растворе содержимость соли будет 38,46%.
Учитель химии:
Ребята, давайте вспомним алгоритм решения задач на “примеси”, “сплавы”, “растворы”.
- Если дана масса примеси в условии задачи, то отнимем массу или объем примеси от всей массы (объема) вещества, содержащего примесь.
- По необходимости составляет уравнение реакции.
- Далее решаем как обычную задачу на составление пропорции.
Для решения задач на смеси растворов применяется метод называемый “конверт Пирсона”.
Сущность этого приема состоит в том, что по диагоналям из большей величины массовой доли растворенного вещества (в %) вычитают меньшую:
где а – большая массовая доля I раствора,
в — меньшая массовая доля II раствора,
с — искомая массовая доля (%) растворенного вещества в растворе.
Задача №3.
Смешали 30% и 10% растворы соленой кислоты и получили 600г. 15% раствора. Сколько граммов каждого вещества взяли?
Решение: (учитель химии) “Конверт Пирсона”:
| 30% | 5% | 3 – 450г. | ||
| 600г. | 15% | 5 | ||
| 10% | 15% | 1 – 150г. |
600 : (1+3) = 150г. — 10% раствор.
150*3 = 450г. — 30% раствор.
(учитель математики) Алгебраический:
I раствор – х (г) — 30% кислота — 0,3х
II раствор – у (г) — 10% кислота — 0,1у
Смесь: 600(г) – 15% кислота = > 0,15*600=90(г)
0,15*600=90(г) – кислоты содержит смесь
тогда:
0,3х+0,1у=90
х+у=600
у=450
х=150
Ответ: 150(г) и 450(г)
Задача №4.
(Половина класса решают алгебраическим, другая – применяя “Конверт Пирсона”).
Как приготовить 630 г. 36% раствор из 9% и 72% растворов?
Решение: “Конверт Пирсона”
9% 36 4-360(г) 630(г) 36% 9 72% 27 3-270(г)
1) 36-9=27, 72-36=36.
2) НОД (36;27) = 9.
3) 36:9=4 (массовой части 9% раствора),
27:9=3 (массовой части 72% раствора).
4) 630:(3+4)=90(г) раствора с соответственно на одну массовую часть раствора
5) 90*4=360(г) – 9% раствор,
90*3=270(г) – 72% раствор.
Алгебраический:
I раствор – х(г) – 9% — 0,9х
II раствор – у(г) – 72% — 0,72у
630(г)-36% — 0,36*630=226,80 (г)
х+у=630 => у=630-х
0,09х+0,72у=226,80
0,09х+0,72(630-х)=226,80
0,09х+453,6-0,72х=226,80
453,6-226,80=0,72х-0,09х
226,8=0,63х
х=360(г) – 9% раствор
630-360=270(г) – 72% раствор
Ответ:
1 раствор- 9% и весит 360 г,
11 раствор — 72% — 270 г.
Задача №5. (учитель математики)
Имеется два сплава золота и серебра. В одном количества этих металлов находится в отношении 2:3, а в другом – 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро были бы в отношении 5:11?
Решение: (Удобно составлять следующую таблицу).
| Взято (кг) | Отношение золота к серебру | Отношения веса золота к весу сплава | Взяли золота (кг) | |
| 1 сплав | Х | 2:3 | 2:5 | 2/3 Х |
| 2 сплав | 8 – Х | 3:7 | 3:10 | 3/10 (8 – Х) |
| новый | 8 | 5:11 | 5:16 | 2/3 Х+3/10 (8 – Х) |
(2/3 Х+3/10 (8 – 10)) : 8=5/16
Отсюда находим, что х=1
1кг. взяли из 1сплава, 7кг. – 2 сплав.
Ответ: 1 (кг) и 7 (кг).
IV. Самостоятельная работа (Раздаются карточки)
Задача №1
Найдите концентрацию всего раствора, если к 200(г) 40% раствору добавили 300(г) 50% раствора этого вещества.
Решение: (удобно решать алгебраическим способом).
1. Найдем массу соли в каждом растворе:
I раствор – 200(г) – 40% — 200*0,40=80(г) соли .
II раствор – 300(г) – 50% — 300*0,50=150(г) соли.
Смесь: 500(г) — ? —
2. Найдем концентрацию всего раствора:
500(г) – 100%
230(г) — х-?
х=230*100:500=46% — соли содержится в новом растворе
Ответ: 46%
Задача №2.
Нужно приготовить 25% раствор серной кислоты, смешав 76% и 15% растворы. Сколько надо взять каждого раствора?
Решение: “Конверт Пирсона”:
76% 10 част. 76% раст. 25% 15% 51 част. 15% раст.
Ответ:
10 частей – 76% раствора
15 частей — 15% раствора.
Задача №3.
Сплав меди и цинка содержал меди на 640 г больше, чем цинка. После того как из сплава выделили 6/7, содержащейся в нем меди и 60% цинка, масса сплава оказалась равной 200г. Сколько весил сплав первоначально?
Решение:
| Было: | х(г) цинка —————— | Осталось: 1- 0,6 = 0,4 части цинка, |
| х + 640 г меди ————- | 1 — 6/7 = 1/7 часть меди. |
Сплав: 2
00 = 0,4 х + 1/7(х + 640)
Отсюда х = 200.
Значит, первоначально, было 200(г) цинка, 840 (г) меди, а масса сплава равна 200 + 840 = 1 кг 40 г.
Ответ: Сплав весил 1 кг 40 г.
Проверка:
(Открывается задняя сторона доски, ребята проверяют результаты работы своих соседей, совместно с учителями выставляют оценки)
V. Раздаются карточки с заданиями для самостоятельного решения на дом:
(задание дифференцированное, учащиеся сами выбирают, первые 3 задачи легкие, последние 4 - посложнее)
1. К раствору, содержащему 40г. Соли, добавили 200г. воды, в результате чего концентрация уменьшилось на 10%. Сколько воды содержал раствор и каково его процентное содержание?
Ответ: 160 г. воды и 20%
2. Имеется 2 слитка серебра с оловом. В первом слитке имеется 360г. серебра и 40г. олова. Во втором слитке – 450г. серебра и 150г. олова. Сколько взяли от каждого, если масса нового слитка 200г. и содержится в нем 81% серебра?
Ответ: 80 г. и 120г.
3. Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла из этих сортов, чтобы получить 140 тонн стали, содержащей 30% никеля?
Ответ: 1 сорт – 40(т) и 2 сорт – 100(т)
4. Имеется два раствора 30% и 3% перекиси водорода, нужно смешать их, чтобы получилось 12% раствор. Как их нужно взять в массовом отношении?
Ответ: 3% раствор нужно взять в 2 раза больше.
5. Имеется 2 слитка сплава золота и меди. В первом слитке содержится 230г. золота и 20г. меди, а во втором – 240г. золота и 60г. меди. От каждого слитка взяли по кусочку, сплавили их и получилось 300г. сплава, в которых 84% золота. Определить массу кусочка, взятого от первого слитка.
Ответ: от 1 слитка взяли 100 (г) золота.
6. Если смешать 6 кг и 2 кг растворов серной кислоты разной концентрации, то получается 12% раствор кислоты. При смешивании двух одинаковых масс, тех же растворов, получается 15% раствор. Определить первоначальную концентрацию каждого раствора.
Ответ: 10% и 20%.ъ
7. Два куска латуни имеют массу 30 кг, первый кусок содержит 5кг чистой меди, а второй – 4кг. Сколько процентов меди содержит первый кусок, если второй содержит меди на 15% больше, чем первый?
VI. Подведение итогов урока.
VII. Выставление оценок.
VIII. Домашнее задание.
Учитель математики:
На следующем уроке сдача зачета №5 и защита домашней работы.
2.04.2008
xn--i1abbnckbmcl9fb.xn--p1ai
Задачи по химии на тему «Растворы»
Выполнила студентка гр.ВХМС-31 Боякова Алена
Условия задач по теме «Растворы» (5 задач)
Требуется приготовить 1 кг 15%-го раствора аммиака. Сколько нужно взять для этого 25%-го раствора аммиака и воды?
К 80 г раствора соли неизвестной концентрации прибавили 40 г воды. Вычислите массовую долю соли в исходном растворе, если после разбавления она стала равной 18%.
Из 400 г 20%-го раствора соли упариванием удалили 100 г воды. Чему стала равна массовая доля соли в полученном растворе?
В результате упаривания 450 г 10%-го раствора хлорида кальция его массовая доля увеличилась вдвое. Вычислите массу испарившейся воды.
Имеются два раствора аммиака с массовой долей 25% и 5%. Сколько граммов каждого раствора надо взять, чтобы получить 125 г 10%-го раствора аммиака?
Пример решенной задачи по теме растворы:
Задача для примера решения
Сколько граммов воды надо испарить из 800 г 15%-го раствора вещества, чтобы увеличить его массовую долю на 5%?
ДАНО:
ω(в-ва)=15%=0,15
m(p-pa)=800г
ω'(в-ва)=(15+5)%=20%=0,2
НАЙТИ:
mисп.(H2O)=?
РЕШЕНИЕ:
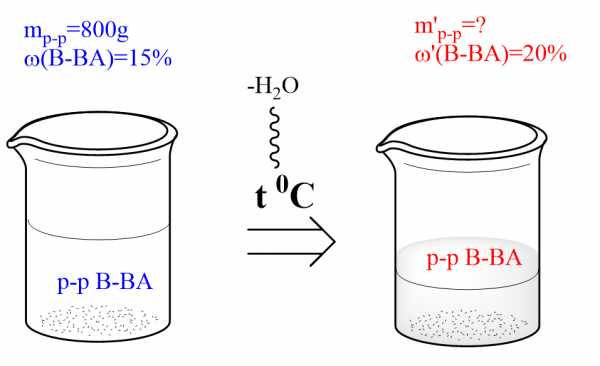
1)Найдем массу растворенного вещества в исходном растворе:
m(в-ва)=ω(в-ва)⋅m(p−pa)=0,15⋅800г=120г
2) Поскольку испаряется только вода, масса вещества остается неизменной: m(в-ва) = m'(в-ва)=120г
3) Зная массу растворенного вещества и его массовую долю, найдем массу полученного раствора:
m′(р-ра)=m(в-ва))ω(в-ва)=120г0,2=600г
Масса испаренной воды — разность масс полученного и исходного растворов:
mисп.(h3O)= m(р-ра) — m'(р-ра) = 800г — 600г = 200г
ОТВЕТ: необходимо испарить 200г воды
Список используемой литературы:
1. И.Г. Хомченко «Сборник задач и упражнений по химии для средней школы»
Москва. Новая волна – 2008г.
2. ЕГЭ – Химия 2011 под редакцией А.А. Ковериной. Москва Национальное образование
2011 г.
infourok.ru
Методика решения задач на растворы с применением правила креста
ТРУСКОВ А.А.
учитель химии магистральнинской средней школы № 2
(пос. Магистральный, Казачинско-Ленский р-н, Иркутская обл.) Многие важные вопросы изучения курса химии по ряду причин исключены из школьной программы. Среди них закон эквивалентов, разные способы выражения концентрации растворов, правило креста и многие другие. Однако на факультативных занятиях, при подготовке ребят к олимпиадам без них не обойтись. Да и в жизни ребятам они пригодятся, особенно тем, кто свяжет будущую профессию с химией (заводские лаборатории, аптеки, научно-исследовательская работа, да и просто химия в быту).
Особенно трудно в этом отношении молодым учителям – у них нет той массы дополнительной литературы, которую накопили старые учителя за десятки лет работы в школе, а что издает современная книгопечатная отрасль промышленности – известно всем. Поэтому предлагаемая методика решения задач на растворы с применением правила креста, думается, хоть сколько-то поможет молодым коллегам в этом деле.
«Конверт Пирсона»
Очень часто в лабораторной практике и при решении олимпиадных задач приходится встречаться со случаями приготовления растворов с определенной массовой долей растворенного вещества, смешением двух растворов разной концентрации или разбавлением крепкого раствора водой. В некоторых случаях можно провести достаточно сложный арифметический расчет. Однако это малопродуктивно. Чаще для этого лучше применить правило смешения (диагональную модель «конверта Пирсона», или, что то же самое, правило креста).
Допустим, нужно приготовить раствор определенной концентрации, имея в распоряжении два раствора с более высокой и менее высокой концентрацией, чем нужно нам. Тогда, если обозначить массу первого раствора через m1, а второго – через m2, то при смешивании общая масса смеси будет слагаться из суммы этих масс. Пусть массовая доля растворенного вещества в первом растворе – ω1, во втором – ω2, а в их смеси – ω3. Тогда общая масса растворенного вещества в смеси будет слагаться из масс растворенного вещества в исходных растворах:
m1•ω1 + m2•ω2 = ω3(m1 + m2).
Отсюда
m1(ω1 – ω3) = m2(ω3 – ω2),
m1/m2 = (ω3 – ω2)/(ω1 – ω3).
Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворенного вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.
При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешении. При расчетах записывают одну над другой массовые доли растворенного вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
Для пояснения этого правила сначала решим простейшую задачу.
ЗАДАЧА 1
Определите концентрацию раствора, полученного при слиянии 150 г 30%-го и 250 г 10%-го растворов какой-либо соли.
Дано:
m1 = 150 г,
m2 = 250 г,
ω1 = 30%,
ω2 = 10%.
Найти:
ω3.
Решение
►1-й способ (метод пропорций).
Общая масса раствора:
m3 = m1 + m2 = 150 + 250 = 400 г.
Массу вещества в первом растворе находим методом пропорций, исходя из определения: процентная концентрация раствора показывает, сколько граммов растворенного вещества находится в 100 г раствора:
100 г 30%-го р-ра – 30 г в-ва,
150 г 30%-го р-ра – х г в-ва,
х = 150•30/100 = 45 г.
Для второго раствора составляем аналогичную пропорцию:
100 г 10%-го р-ра – 10 г в-ва,
250 г 10%-го р-ра – y г в-ва,
y = 250•10/100 = 25 г.
Следовательно, 400 г нового раствора содержит 45 + 25 = 70 г растворенного вещества.
Теперь можно определить концентрацию нового раствора:
400 г р-ра – 70 г в-ва,
100 г р-ра – z г в-ва,
z = 100•70/400 = 17,5 г, или 17,5%.
►2-й способ (алгебраический).
m1•ω1 + m2•ω2 = ω3(m1 + m2).
Отсюда
ω3 = (m1•ω1 + m2•ω2)/(m1 + m2).
В результате находим:
ω3 = (150•30 + 250•10)/(150 + 250) = 17,5%.
►3-й способ (правило креста).
(ω3 – 10)/(30 – ω3) = 150/250.
Тогда
(30 – ω3)•150 = (ω3 – 10)•250,
4500 – 150ω3 = 250ω3 – 2500,
4500 – 2500 = 250ω3 – 150ω3,
7000 = 400ω3, ω3 = 7000/400 = 17,5%.
Ответ. При слиянии взятых растворов получится новый раствор с концентрацией ω3 = 17,5%.
Теперь решим задачи посложнее.
ЗАДАЧА 2
Определите, сколько нужно взять 10%-го раствора соли и 30%-го раствора этой же соли для приготовления 500 г 20%-го раствора.
Дано:
ω1 = 10%,
ω2 = 30%,
ω3 = 20%,
m3 = 500 г.
Найти:
m1, m2.
Решение
Используем правило креста.
Для приготовления 500 г 20%-го раствора соли нужно взять по 10 частей растворов исходных концентраций.
Проверим правильность нашего решения, учитывая, что 1 часть равна 500/(10 + 10) = 25 г.
250 г 10%-го р-ра – х г соли,
100 г 10%-го р-ра – 10 г соли,
х = 250•10/100 = 25 г.
250 г 30%-го р-ра – y г соли,
100 г 30%-го р-ра – 30 г соли,
y = 250•30/100 = 75 г.
m(р-ра) = 250 + 250 = 500 г.
m(соли) = 25 + 75 = 100 г.
Отсюда находим ω3:
500 г р-ра – 100 г соли,
100 г р-ра – ω3 г соли,
ω3 = 100•100/500 = 20 г, или 20%.
Ответ. Для приготовления 500 г 20%-го раствора нужно взять исходные растворы по 250 г
(m1 = 250 г, m2 = 250 г).
ЗАДАЧА 3
Определите, сколько нужно взять растворов соли 60%-й и 10%-й концентраций для приготовления 300 г раствора 25%-й концентрации.
Дано:
ω1 = 60%,
ω2 = 10%,
ω3 = 25%,
m3 = 300 г.
Найти:
m1, m2.
Решение
Масса одной части: 300/50 = 6 г.
Тогда
m1 = 6•15 = 90 г, m2 = 6•35 = 210 г.
Проверим правильность решения.
100 г 60%-го р-ра – 60 г соли,
90 г 60%-го р-ра – х г соли,
х = 54 г.
100 г 10%-го р-ра – 10 г соли,
210 г 30%-го р-ра – y г соли,
y = 21 г.
m(соли) = 54 + 21 = 75 г.
Находим концентрацию нового раствора:
300 г р-ра – 75 г соли,
100 г р-ра – z г соли,
z = 100•75/300 = 25 г, или 25%.
Ответ. m1 = 90 г, m2 = 210 г.
Теперь перейдем к еще более сложным задачам.
ЗАДАЧА 4
Определите массу раствора Nа2СО3 10%-й концентрации и массу сухого кристаллогидрата Na2CO3•10H2O, которые нужно взять для приготовления 540 г раствора 15%-й концентрации.
Дано:
ω1 = 10%,
ω3 = 15%,
m3 = 540 г.
Найти:
m1, m2.
Решение
►1-й способ (через систему уравнений с двумя неизвестными).
Определяем массу соли Na2CO3 в 540 г 15%-го раствора:
100 г 15%-го р-ра – 15 г соли,
540 г 15%-го р-ра – z г соли,
z = 540•15/100 = 81 г.
Cоставляем систему уравнений:
Находим молярную массу:
Избавляемся от лишних неизвестных:
m2 = 286y/106;
100 г 10%-го р-ра – 10 г соли,
m1 г 10%-го р-ра – х г соли,
m1 = 100х/10 = 10х.
Подставляем m2 и m1 в систему уравнений:
С учетом того, что х = 81 – y, избавляемся от второго неизвестного:
10(81 – y) + 286y/106 = 540.
Отсюда
y = 270/7,3 = 37 г.
Тогда m2 = 286y/106 = 2,7•37≈100 г – это масса необходимого количества кристаллогидрата Na2СО3•10H2O.
Далее находим: х = 81 – y = 81 – 37 = 44 г – это масса соли из 10%-го раствора.
Находим массу 10%-го раствора:
100 г 10%-го р-ра – 10 г соли,
m1 г 10%-го р-ра – 44 г соли,
m1 = 100•44/10 = 440 г.
Видно, что так можно решить данную задачу – способ надежный, но, к сожалению, достаточно длинный, громоздкий и сложный. Им успешно могут воспользоваться учащиеся с достаточно развитым логическим мышлением. Для других он будет сложноват.
►2-й способ (правило креста).
Допустим, что Na2СО3•10H2O – это «сухой раствор» (ведь он же содержит воду). Тогда найдем его «концентрацию»:
286 г – 106 г соли,
100 г – х г соли,
х = 100•106/286 = 37 г, или 37%.
Применяем правило креста.
Находим массу одной части и массы веществ:
540/27 = 20 г,
m1 = 20•22 = 440 г, m2 = 20•5 = 100 г.
Ответ. Для приготовления 540 г раствора Na2CO3 15%-й концентрации необходимо взять 440 г 10%-го раствора и 100 г кристаллогидрата.
Таким образом, применение правила креста удобнее и проще при решении подобных задач. Этот способ более экономичен по времени и менее трудоемок.
Правило креста можно применять и в тех случаях, когда нужно получить раствор меньшей концентрации путем разбавления водой более концентрированного раствора или получить более концентрированный раствор путем добавления к исходному раствору сухой смеси. Рассмотрим это на примерах.
ЗАДАЧА 5
Сколько воды нужно добавить к 250 г раствора соли для понижения его концентрации с 45% до 10%?
Дано:
ω1 = 45%,
ω3 = 10%,
m1 = 250 г.
Найти:
m2.
Решение
Принимаем, что концентрация для добавляемой воды – ω2 = 0%. Используем правило креста.
Определяем массу одной части через первый раствор: 250/10 = 25 г.
Тогда масса необходимой воды равна:
m2 = 25•35 = 875 г.
Проверим правильность решения.
Масса нового раствора:
m3 = 250 + 875 = 1125 г.
Масса соли в исходном растворе:
250 г 45%-го р-ра – х г соли,
100 г 45%-го р-ра – 45 г соли,
х = 250•45/100 = 112,5 г.
Находим ω3:
1125 г р-ра – 112,5 г соли,
100 г р-ра – y г соли,
y = 100•112,5/1125 = 10 г, или 10%.
Ответ. m2 = 875 г.
ЗАДАЧА 6
Сколько сухой соли нужно добавить к 250 г раствора 10%-й концентрации для ее увеличения до 45%?
Дано:
ω1 = 10%,
m1 = 250 г,
ω3 = 45%.
Найти:
m(с. с.).
Решение
Принимаем, что сухая соль – это раствор с ω2 = 100%. Используем правило креста.
Определяем массу одной части через первый раствор: 250/55 = 4,5 г.
Определяем массу сухой соли:
m(с. с.) = 4,5•35 = 158 г.
Проверяем правильность решения.
Масса нового раствора:
m3 = 250 + 158 = 408 г.
Масса соли в исходном растворе:
100 г 10%-го р-ра – 10 г соли,
250 г 10%-го р-ра – х г соли,
х = 250•10/100 = 25 г.
Общая масса соли в новом растворе:
25 + 158 = 183 г.
Концентрация нового раствора:
408 г р-ра – 183 г соли,
100 г р-ра – y г соли,
y = 100•183/408 = 45 г, или 45%.
Ответ. m(с. с.) = 158 г.
Думается, что опытный учитель всегда найдет несколько способов решения любой задачи. Но как учила меня моя первая учительница по химии Клавдия Макаровна в школе № 17 г. Иркутска, так и я стараюсь учить своих учеников: всегда глубоко продумывать и понимать химическую сущность задачи и находить наиболее рациональный способ ее решения, а не просто подгонять под ответ в конце учебника.
Средняя оценка
(10 голосов)
art-con.ru
