Формулы сокращенного умножения для кубов: Перечислите формулы сокращённого умножения. — ответ на Uchi.ru

Какое тождество называют формулой разности кубов. Формулы сокращенного умножения

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть а, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a 2 — b 2 = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у) 2 + (х + у) 2

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки .

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения .

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку .

Вспомним, как выглядит формула разности кубов.

a 3 − b 3 = (a − b)(a 2 + ab + b 2)

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a 2 + ab + b 2) = a 3 − b 3

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «27а 3 » — это «(3а) 3 », значит, для формулы разности кубов вместо «a » мы используем «3a ».

Используем формулу разности кубов. На месте «a 3 » у нас стоит «27a 3 », а на месте «b 3 », как и в формуле, стоит «b 3 ».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов «», только вместо «a » стоит «x », а на месте «b » стоит «1 ».

Используем для «(x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить «(y 2 − 1)(y 4 + y 2 + 1) » с правой частью формулы разности кубов
«a 3 − b 3 = (a − b)(a 2 + ab + b 2) », то можно понять, что на месте «a » из первой скобки стоит «y 2 , а на месте «b » стоит «1 ».

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа.

В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. 2\right)\]

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки .

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения .

Рекомендуем каждую формулу прописать не менее 12 раз.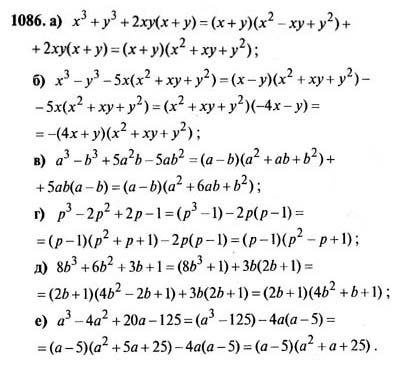 Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку .

Вспомним, как выглядит формула разности кубов.

a 3 − b 3 = (a − b)(a 2 + ab + b 2)

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a 2 + ab + b 2) = a 3 − b 3

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «27а 3 » — это «(3а) 3 », значит, для формулы разности кубов вместо «a » мы используем «3a ».

Используем формулу разности кубов. На месте «a 3 » у нас стоит «27a 3 », а на месте «b 3 », как и в формуле, стоит «b 3 ».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов «», только вместо «a » стоит «x », а на месте «b » стоит «1 ».

Используем для «(x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить «(y 2 − 1)(y 4 + y 2 + 1) » с правой частью формулы разности кубов
«a 3 − b 3 = (a − b)(a 2 + ab + b 2) », то можно понять, что на месте «a » из первой скобки стоит «y 2 , а на месте «b » стоит «1 ».

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть а, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a 2 — b 2 = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у) 2 + (х + у) 2

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Схемы сокращенного умножения.

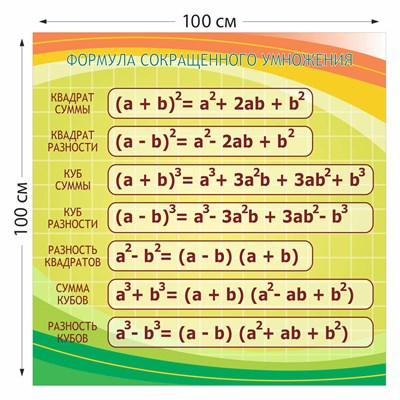Формулы сокращенного умножения

Формулы сокращенного умножения (ФСО) нужны для того, чтобы умножать и возводить числа, выражения, в том числе многочлены. То есть с помощью формул можно работать с числами гораздо быстрее и проще. Таким образом, из сложного уравнения можно составить обычное уравнение, что упростит задачу.

Таблица с формулами сокращенного умножения

Наименование	Формула	Как читать
Сумма в квадрате		Квадрат первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения.
Квадрат разницы		Квадрат разницы между двумя выражениями равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Куб суммы		Куб разности двух выражений равен кубу первого выражения плюс утроенное произведение первого выражения в квадрате на второе выражение плюс утроенное произведение первого выражения на второе в квадрате плюс второе выражение в кубе.
Разностный куб		Куб разности двух величин равен первому выражению в кубе минус утроенное произведение первого выражения в квадрате на второе выражение плюс утроенное произведение первого выражения на второе в квадрате минус второе выражение в кубе.
Разность квадратов		Разность квадратов первого и второго выражений равна произведению разности двух выражений на их сумму.
Сумма кубов		Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.
Разность кубиков		Произведение разности двух выражений на неполный квадрат суммы равно разности их кубов.

Обратите внимание на первые четыре формулы. Благодаря им можно возвести в квадрат или возвести в куб сумму (разность) двух выражений. Что касается пятой формулы, то ее необходимо применять для краткого умножения разности или суммы двух выражений.

Последние две формулы (6 и 7) используются для умножения суммы обоих выражений на их неполный квадрат разности или суммы.

Приведенные выше формулы довольно часто требуются на практике. Именно поэтому желательно знать их наизусть.

Если вам попадется пример, разлагающий многочлен на множители, то во многих случаях нужно переставить левую и правую части.

Например, возьмем ту же самую первую формулу:

и положим левую часть к правой, а правую к левой:

Ту же процедуру можно проделать и с остальными формулами.

Доказательство ФСО

Остановимся на доказательствах приведенных формул умножения. Это несложно. Вам просто нужно открыть скобки. Рассмотрим первую формулу — квадрат суммы: .

Шаг первый.

Возведем a + b во вторую степень. Для этого не будем трогать степень, а проведем банальное умножение: = x.

Шаг второй. Теперь раскроем скобки: х+х.

Шаг третий … Раскройте скобки: х + х + х + х.

Шаг четвертый … Умножаем, не забывая про знаки: х+х+.

Шаг пятый … Упростим выражение:.

Таким же образом можно доказать абсолютно любую формулу сокращенного умножения.

Примеры и решения с использованием FSO

Обычно эти семь формул используются, когда вам нужно упростить выражение, чтобы решить уравнение или даже общий пример.

Пример 1

Упражнение

Упростим выражение:

Как видите, первая формула сокращенного умножения — Квадрат суммы — подходит для этого примера.

Решение

На основе первой формулы пример необходимо разложить на множители. Для этого смотрим в формулу и подставляем вместо букв цифры. В нашем случае «а» — 3х, а «б» — 5:9.0005

Читаем правую часть и записываем результат. Получаем:

В примере нужно умножить все, что умножается и сразу получаем ответ:

Конечно, есть и примеры с дробями. Но, если вы научитесь решать простые примеры, то и других типов вы не будете бояться.

Пример 2

Упражнение

Упростите выражение

Решение

= — x x + =

Удвоенное произведение этих выражений равно -, что совпадает со вторым членом трехчлена (со знаком плюс), а значит,

Итак, как видите, ничего сложного в примерах нет. Главное знать формулы, где их можно применить, а где можно обойтись без них.

Справочные источники

1. Арефьева И. Г., Пирютко О. Н. Алгебра: учеб. пособие для 7 класса учреждений общего среднего образования: Минск «Народная асвета», 2017. — 304 с.
2. Никольский С.М., Потапов М.К. Алгебра 7 класс: М: 2015 — 287 с.
3. Рубин А.Г., Чулков П.В. Алгебра. 7-й класс. Москва: 2015. — 224 с.

БСС — формулы сокращенного умножения по алгебре для 7 класса с примерами обновлено: 22 ноября 2019 автором: Научные Статьи.Ру

На предыдущем уроке мы разобрались с факторингом. Мы освоили два метода: вынос общего множителя за скобки и группировку. В этом уроке следующий мощный способ: формулы сокращенного умножения … Короче — пох.

Формулы сокращенного умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) необходимы во всех разделах математики. Они используются при упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т. д. и т. п. Словом, есть все основания иметь с ними дело. Понять, откуда они берутся, зачем нужны, как их запомнить и как применять.

Понятно?)

Откуда берутся формулы сокращенного умножения?

Равенства 6 и 7 записываются не очень привычным образом. Как бы наоборот. Это сделано специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее откуда ФСО.

Они получаются от умножения.) Например:

(a + b) 2 = (a + b) (a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2

Вот и все, никаких научных фокусов. Мы просто умножаем скобки и даем похожие. Вот и получается всех формул сокращенного умножения. Сокращенное умножение связано с тем, что в самих формулах нет умножения скобок и слепка однотипных. Сокращено.) Сразу выдается результат.

ФСО нужно знать наизусть. Без первой тройки о тройке и мечтать нельзя, без остальных — о четверке и пятерке.)

Зачем нужны формулы сокращенного умножения?

Есть две причины учиться, даже запоминать эти формулы. Во-первых, готовый ответ на машине резко снижает количество ошибок. Но это не основная причина. А вот второй…

Если вам нравится этот сайт…

Кстати, у меня для вас есть еще парочка интересных сайтов.)

Вы можете попрактиковаться в решении примеров и узнать свой уровень. Мгновенное проверочное тестирование. Учимся — с интересом!)

вы можете ознакомиться с функциями и производными.

Выражение ( a + b ) 2 есть квадрат суммы числа a и b . .. По определению степени выражение ( a + b a 8 8 + б )( а + б ). Следовательно, из квадрата суммы можно сделать вывод, что

( a + b ) 2 = ( a + b )( a + b ) = a 2 + ab + ab + b 2 = a 2 + 2 ab + b 2 ,

то есть квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

формула квадрата суммы

( а + б ) 2 = а 2 + 2 аб + б 2

Многочлен a 2 + 2 ab + b 2 называется разложением квадрата суммы.

Поскольку a и b обозначают любые числа или выражения, то правило дает нам возможность сокращенным способом возводить в квадрат любое выражение, которое можно рассматривать как сумму двух членов.

Пример. Квадратное выражение 3 x 2 + 2 ху .

Решение: чтобы не делать дополнительных преобразований воспользуемся формулой квадрата суммы. Мы должны получить сумму квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(3 x 2 + 2 xy ) 2 = (3 x 2) 2 + 2 (3 x 2 2 xy ) + (2 xy ) 0 2 900

Теперь, используя правила умножения и возведения в степень одночленов, упростим полученное выражение:

(3 x 2) 2 + 2 (3 x 2 2 xy ) + (2 xy ) 2 = x 4 + 12 x 3 y + 4 + x 3 y + 4 + 4 x 3 y + 4 + 4 x 3 y + 4 + x 3 x + 4 + x 3 x + 4 + x 3 . 2 г 2

Квадрат разницы

Выражение ( a — b ) 2 равно разности в квадрате чисел a и b . .. Выражение ( a — b ) 2 есть произведение двух полиномов ( a — b ) 9017 б )( а — б ). Следовательно, из квадрата разности можно сделать вывод, что

( A — B ) 2 = ( A — B ) ( A — B ) = A 2 — AB ) = A 2 — AB ). а 2 — 2 аб + б 2 ,

то есть квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа.

Из правила следует, что общая формула квадратов разности без промежуточных преобразований будет выглядеть так:

( а — б ) 2 = а 2 — 2 аб + б 2

Многочлен a 2 — 2 ab + b 2 называется разложением квадрата разности.

Это правило применяется к сокращенному возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.

Пример. Представьте квадрат разности в виде трех членов:

(2 и 2 — 5 и 2) 2

Решение: по формуле квадрата разности находим:

(2 a 2 — 5 ab 2) 2 = (2 a 2) 2 — 2(2 a 2 5 ab 2) + (5 ab 902) 2

Теперь преобразуем выражение в стандартный полином:

(2 а 2) 2 — 2(2 а 2 5 аб 2) + (5 аб 2) 2 = 4 а 4 — 20 а 3 б 7 7 19178 91 + 20 б 4

Разность квадратов

Выражение a 2 — b 2 есть разность квадратов чисел a и b … Выражение a 2 — b 2 есть сокращенный способ умножения двух чисел на сумму двух чисел их разница:

( A + B ) ( A — B ) = A 2 + AB — AB — B 2 = AB — B 2 = AB — B 2 =

7 B B — AB — B .

то есть произведение суммы двух чисел на их разность равно разности квадратов этих чисел.

Из правила следует, что общая формула разности квадратов выглядит так:

и 2 — б 2 = ( а + б )( а — б )

Это правило касается сокращенного умножения выражений, которые можно представить: одно как сумму двух чисел, а другое как разность этих же чисел.

Пример. Преобразовать произведение в бином:

(5 и 2 + 3)(5 и 2 — 3)

Решение:

(5 a 2 + 3)(5 a 2 — 3) = (5 и 2) 2 — 3 2 = 25 и 4 — 9

В примере мы применили формулу разности квадратов справа налево, то есть нам дали формулу правой части, и мы преобразовали ее в левую:

( a + b )( a — b ) = a 2 — b 2

На практике все три рассмотренные формулы применяются как слева направо, так и справа налево в зависимости от ситуации.

Для упрощения алгебраических многочленов существует формулы сокращенного умножения … Их не так много и запомнить их легко, но запомнить их нужно. Обозначения, которые используются в формулах, могут иметь любую форму (числовую или полиномиальную).

Первая формула сокращенного умножения называется разностью квадратов . Она заключается в том, что из квадрата одного числа вычитается квадрат второго числа, который равен величине разности между этими числами , а также их продукт.

а 2 — б 2 = (а — б) (а + б)

Разберем для наглядности:

22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9a 2 — 4b 2 c 2 = (3a — 2bc) (3a + 2bc)

Вторая формула примерно сумма квадратов … Звучит так, сумма двух величин в квадрате равна квадрату первой величины, к ней прибавляется удвоенное произведение первой величины на вторую, к ним прибавляется квадрат второй величины.

(а + b) 2 = а 2 + 2ab + b 2

Благодаря этой формуле становится намного проще вычислять квадрат большого числа без использования компьютеров.

Так например: квадрат 112 будет
1) В начале разложим 112 на числа, квадраты которых нам знакомы
112 = 100 + 12
2) Полученное в скобки заносим в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

Третья формула — квадратная разность … Которая утверждает, что два вычитаемых значения в квадрате равны тому факту, что из первого значения в квадрате мы вычитаем двойное произведение первого значения, умноженного на второй, добавляя к ним квадрат второго значения.

(а + b) 2 = а 2 — 2ab + b 2

где (a — b) 2 равно (b — a) 2. Чтобы доказать это, (a-b) 2 = a 2 -2ab + b 2 = b 2 -2ab + a 2 = (b-a) 2

Четвертая формула сокращенного умножения называется куб сумма … Что звучит так: два слагаемых значения в кубе равны кубу 1 значения, тройное произведение 1 значения в квадрате, умноженное на 2-е значение, к ним прибавляется тройное произведение числа 1 значение, умноженное на квадрат 2 значений, плюс второе значение в кубе.

(а + б) 3 = а 3 + 3а 2 б + 3аб 2 + б 3

Пятый, как вы уже поняли, называется куб разности … Который находит разности между величинами, так как из первого обозначения в кубе вычитаем тройное произведение первого обозначения в квадрате умноженное на второе , к ним прибавляется тройное произведение первого обозначения, умноженное на квадрат второго обозначения, минус второе обозначение в кубе.

(а-б) 3 = а 3 — 3а 2 б + 3аб 2 — б 3

Называется шестой — сумма кубов … Сумма кубов равна произведению двух слагаемых, умноженному на неполный квадрат разности, так как в середине нет удвоенного значения.

а 3 + b 3 = (а + b) (а 2 -ab + b 2)

Другими словами, сумму кубов можно назвать произведением в двух скобках.

Седьмой и последний называется разность кубиков (его легко спутать с формулой куба разности, но это разные вещи). Разница между кубиками равна произведению разности двух значений, умноженной на неполный квадрат суммы, так как в середине нет удвоенного значения.

а 3 — б 3 = (а-б) (а 2 + аб + б 2)

А так формул сокращенного умножения всего 7, они похожи между собой и легко запоминаются, главное не запутаться в знаках. Они также предназначены для использования в обратном порядке, и в учебниках собрано довольно много таких заданий. Будьте осторожны, и у вас все получится.

Если у вас есть вопросы по формулам, обязательно пишите их в комментариях. Мы будем рады ответить Вам!

Если вы в декретном отпуске, но хотите зарабатывать. Просто перейдите по ссылке Интернет-бизнес с Oriflame. Там все очень подробно написано и показано. Это будет интересно!

Математические выражения (формулы) Сокращенное умножение (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) чрезвычайно незаменимы во многих областях из точных наук. Эти 7 символьных обозначений незаменимы для упрощения выражений, решения уравнений, умножения многочленов, сокращения дробей, решения интегралов и многого другого. А это значит, что будет очень полезно понять, как они получаются, для чего нужны, а главное, как их запомнить, а затем применить. Затем применяя формулы сокращенного умножения на практике, самое сложное будет посмотреть что такое NS и что у вас есть. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.

И так они:

Первые х 2 — 2 = (x — y) (x + y) .Для вычисления разности квадратов два выражения надо умножить на разности этих выражений на их суммы.

Второй (х + у) 2 = х 2 + 2ху + у 2 … Чтобы найти квадрат суммы двух выражений, нужно прибавить удвоенное произведение первого выражения к второе плюс квадрат второго выражения к квадрату первого выражения.

Третье (x — y) 2 = x 2 — 2xy + y 2 … Чтобы вычислить квадрат разницы двух выражений, нужно вычесть удвоенное произведение первого выражения на второе плюс квадрат второго выражения из квадрата первого выражения.

Четвертый (x + y) 3 = x 3 + 3x 2 y + 3x 2 + y 3. Чтобы вычислить куб суммы двух выражений, нужно прибавить к кубу первого выражения тройное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Пятый (х — у) 3 = х 3 — 3х 2 у + 3х 2 — at 3 … Для вычисления куба разности двух выражений необходимо из куба первого выражения вычесть утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

Шестое x 3 + at 3 = (x + y) (x 2 — xy + y 2) Чтобы вычислить сумму кубов двух выражений, нужно перемножить суммы первого и вторых выражений неполным квадратом разности этих выражений.

Седьмая x 3 — at 3 = (x — y) (x 2 + xy + y 2) Для выполнения вычисления кубики разности два выражения, разница между первым и вторым выражением должна умножить на неполный квадрат суммы этих выражений.

Нетрудно запомнить, что все формулы применяются для выполнения расчетов и в обратном направлении (справа налево).

Существование этих закономерностей было обнаружено около 4 тысяч лет назад. Их широко использовали жители древнего Вавилона и Египта. Но в те времена их выражали словесно или геометрически и не использовали буквы в расчетах.

Давайте проанализируем доказательство квадрата суммы (a + b) 2 = a 2 + 2ab + b 2.

Первым эту математическую закономерность доказал древнегреческий ученый Евклид, работавший в Александрии в 3 веке до н. Эллада . Широко употребляли не «а 2», а «квадрат на отрезке а», не «аб», а «прямоугольник, заключенный между отрезками а и Ь». 92$.

Для этого запомните следующее правило:

Если к выражению прибавить любой одночлен и вычесть такой же одночлен, то получим правильное тождество.

Добавим к нашему выражению и вычтем из него моном $ab$:

В сумме получим:

То есть разность квадратов двух мономов равна произведению их разности на их сумму . 2$ 92\справа)\]

Формулы или правила сокращенного умножения используются в арифметике, а точнее в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами формулы выведены из существующих в алгебре правил умножения нескольких многочленов.

Использование этих формул обеспечивает достаточно оперативное решение различных математических задач, а также способствует упрощению выражений. Правила алгебраических преобразований позволяют производить некоторые манипуляции с выражениями, следуя которым можно получить выражение в левой части равенства, которое в правой части, или преобразовать правую часть равенства (чтобы получить выражение в слева после знака равенства).

Формулы сокращенного умножения удобно знать по памяти, так как они часто используются при решении задач и уравнений. Основные формулы, включенные в этот список, и их названия приведены ниже.

квадрат суммы

Чтобы вычислить квадрат суммы, нужно найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения это правило записывается так: (a + c)² = a² + 2ac + c².

Квадрат разности

Для вычисления квадрата разности нужно вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с обратным знаком ) и квадрат второго числа. В виде выражения это правило выглядит так: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел в квадрате равна произведению суммы этих чисел на их разность. В виде выражения это правило выглядит так: а² — с² = (а + с) (а — с).

куб суммы

Для вычисления куба суммы двух слагаемых необходимо вычислить сумму, состоящую из куба первого слагаемого, тройного произведения квадрата первого слагаемого на второе, утроенное произведение первого члена на квадрат второго и куб второго члена. В виде выражения это правило выглядит так: (a + c)³ = a³ + 3a²c + 3ac² + c³.

Сумма кубов

Согласно формуле равна произведению суммы этих слагаемых на их неполный квадрат разности. В виде выражения это правило выглядит так: а³ + с³ = (а + с) (а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образуется при сложении двух кубиков. Известны только величины их сторон.

Если значения сторон малы, то легко произвести расчеты.

Если длины сторон выражены громоздкими числами, то в этом случае проще применить формулу «Суммы кубов», что значительно упростит расчеты.

куб разности

Выражение для кубической разности звучит так: как сумму третьей степени первого члена утроить отрицательное произведение квадрата первого члена на второй утроить произведение первого члена на квадрат второго и отрицательный куб второго члена. В виде математического выражения куб разности выглядит так: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов только одним знаком. Таким образом, разность кубов представляет собой формулу, равную произведению разности этих чисел на их неполный квадрат суммы. В виде разность кубов выглядит так: а 3 — с 3 = (а — с) (а 2 + ас + с 2).

Пример. Необходимо рассчитать объем фигуры, который останется после вычитания желтой объемной фигуры, которая также является кубом, из объема синего куба. Известен только размер стороны малого и большого куба.

Если значения сторон небольшие, то расчеты достаточно просты. А если длины сторон выражены значащими числами, то стоит воспользоваться формулой под названием «Разность кубов» (или «Разностный куб»), которая значительно упростит расчеты.

В предыдущих уроках мы рассмотрели два способа разложения полинома на множители: вынос общего множителя за скобки и метод группировки.

В этом уроке мы рассмотрим другой способ разложения многочлена на множители с использованием формул сокращенного умножения .

Мы рекомендуем писать каждую формулу не менее 12 раз. Для лучшего запоминания запишите все формулы сокращенного умножения для себя на небольшой шпаргалке.

Вспомните, как выглядит формула разности кубов.

а 3 — б 3 = (а — б) (а 2 + аб + б 2)

Формулу разности кубов не очень легко запомнить, поэтому рекомендуем использовать особый способ ее запоминания.

Важно понимать, что любая формула сокращенного умножения работает и в обратную сторону.

(а — б) (а 2 + аб + б 2) = а 3 — б 3

Рассмотрим пример. Необходимо факторизовать разность кубов.

Обратите внимание, что «27a 3» — это «(3a) 3», а это значит, что для формулы разности кубов вместо «a» мы используем «3a».

Используем формулу разности кубов. На месте «а 3» имеем «27а 3», а на месте «б 3», как и в формуле, «б 3».

Применение разности кубов в обратном порядке

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов по формуле сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1) (x 2 + x + 1)» напоминает правую часть формулы разности кубов «», только вместо «a» стоит «x», и вместо «б» стоит «1».

Для «(x − 1)(x 2 + x + 1)» используем формулу разности кубов в обратном направлении.

Рассмотрим более сложный пример. Требуется упростить произведение многочленов.

Если мы сравним «(y 2 − 1)(y 4 + y 2 + 1)» с формулами разности правого куба,
« a 3 − b 3 = (a − b)(a 2 + ab + b 2)” , то можно понять, что на месте «а» из первой скобки стоит «у 2», а на месте «б» стоит «1».

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрат суммы и квадрат разности двух выражений; разность квадратов двух выражений; куб суммы и куб разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители и приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть a, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго плюс квадрат второго выражения.

(а + b) 2 = а 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения и второго плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.

а 2 — б 2 = (а — б) (а + б)

4. куб суммы двух выражений равен кубу первого выражения плюс умноженному на три квадрата первого выражения умноженному на второе плюс умноженному на три произведению первого выражения на квадрат второго плюс умноженному на куб второе выражение.

(а + б) 3 = а 3 + 3а 2 б + 3аб 2 + б 3

5. куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.