Формулы статистики: формулы по статистике

Содержание

просто о сложных формулах / Хабр

Статистика вокруг нас

Статистика и анализ данных пронизывают практически любую современную область знаний. Все сложнее становится провести границу между современной биологией, математикой и информатикой. Экономические исследования и регрессионный анализ уже практически неотделимы друг от друга. Один из известных методов проверки распределения на нормальность — критерий Колмогорова-Смирнова. А вы знали, что именно Колмогоров внес огромный вклад в развитие математической лингвистики?

Еще будучи студентом психологического факультета СПбГУ, я заинтересовался когнитивной психологией. Кстати, Иммануил Кант не считал психологию наукой, так как не видел возможности применять в ней математические методы. Мои текущие исследования посвящены моделированию психических процессов, и я надеюсь, что такие направления в современной когнитивной психологии, как вычислительные и коннективисткие модели, смягчили бы его отношение!

Конечно, статистика применяется далеко за пределами научных лабораторий: в рекламе, маркетинге, бизнесе, медицине, образовании и т.

д. Но, что самое интересное, базовые знания анализа данных крайне полезны и в повседневной жизни. Например, думаю, все вы знакомы с понятием среднего арифметического. Среднее значение очень часто используется в СМИ при обсуждении различных социально-экономических показателей — доходов, уровня безработицы и т.д. В 2005 году британские СМИ писали о том, что средний уровень дохода населения не только не возрос, но снизился на 0,2 % по сравнению с предыдущим годом. Мелькали заголовки «Доходы населения снизились впервые с 1990 года». Некоторые политики даже использовали этот факт, критикуя действующее правительство. Однако, важно понимать, что среднее арифметическое — хороший показатель, когда наш признак имеет симметричное распределение (богатых столько же, сколько бедных). Реальное же распределение доходов имеет скорее следующий вид:

Распределение имеет явно выраженную асимметрию: очень состоятельных людей заметно меньше, чем представителей среднего класса. Это приводит к тому, что в данном случае банкротство одного из миллионеров может значительно повлиять на этот показатель.

Гораздо информативнее использовать значение медианы для описания таких данных. Медиана — это значение зарплаты, которое находится в самой середине распределения доходов (50% всех наблюдений меньше медианы, 50% — больше). И, как ни удивительно, медиана дохода в 2005 году в Великобритании, в отличие от среднего значения, продолжила свой рост. Таким образом, если вы знаете о различных типах распределения и различных мерах центральной тенденции (среднее и медиана), то вас не так просто ввести в заблуждение в таких случаях, как описаны в примере.

Черный ящик статистического анализа

Как мы уже выяснили, чем бы вы ни планировали заниматься, вероятность столкнуться с курсом «математическая статистика в вашей области» постепенно приближается к единице. Однако, часто занятия по введению в статистику не вызывают восторга у студентов нетехнических факультетов. Через несколько занятий выясняется, что такие базовые понятия, как, например, корреляция представляют собой нечто следующее:

И, отчаявшись досконально разобраться с происхождением этих сумм и квадратных корней, студент может начать воспринимать статистику следующим образом: «если r > 0, то положительная связь, а если меньше 0, то отрицательная»; «если p уровень значимости меньше 0. 05 — то хорошо, если от 0.05 до 0.1 — то не очень хорошо, а если больше 0.1 — то плохо». Помогая студентам готовиться к экзамену, не раз сталкивался с такими заклинаниями! Также, разумеется, никто не рассчитывает все эти показатели вручную, и используя, например, SPSS, можно за секунду загуглить пошаговую инструкцию «как сравнить два средних».

Жмем сюда
Снимаем/ставим галочки тут
p < 0.05 —> profit

Статистический анализ начинает напоминать черный ящик: на вход подаются данные, на выход — таблица основных результатов и значение p-уровня значимости (p-value), который и расставит все точки над i.

О чем нам, собственно, говорит p-value?

Предположим, мы решили выяснить, существует ли взаимосвязь между пристрастием к кровавым компьютерным играм и агрессивностью в реальной жизни. Для этого были случайным образом сформированы две группы школьников по 100 человек в каждой (1 группа — фанаты стрелялок, вторая группа — не играющие в компьютерные игры).

В качестве показателя агрессивности выступает, например, число драк со сверстниками. В нашем воображаемом исследовании оказалось, что группа школьников-игроманов действительно заметно чаще конфликтует с товарищами. Но как нам выяснить, насколько статистически достоверны полученные различия? Может быть, мы получили наблюдаемую разницу совершенно случайно? Для ответа на эти вопросы и используется значение p-уровня значимости (p-value) — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет. Иными словами, это вероятность получить такие или еще более сильные различия между нашими группами, при условии, что, на самом деле, компьютерные игры никак не влияют на агрессивность. Звучит не так уж и сложно. Однако, именно этот статистический показатель очень часто интерпретируется неправильно.

А теперь несколько примеров про p-value

Итак, мы сравнили две группы школьников между собой по уровню агрессивности при помощи стандартного t-теста (или непараметрического критерия Хи — квадрат более уместного в данной ситуации) и получили, что заветный p-уровень значимости меньше 0.

05 (например 0.04). Но о чем в действительности говорит нам полученное значение p-уровня значимости? Итак, если p-value — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет, то какое, на ваш взгляд, верноеутверждение:

Компьютерные игры — причина агрессивного поведения с вероятностью 96%.
Вероятность того, что агрессивность и компьютерные игры не связаны, равна 0.04.
Если бы мы получили p-уровень значимости больше, чем 0.05, это означало бы, что агрессивность и компьютерные игры никак не связаны между собой.
Вероятность случайно получить такие различия равняется 0.04.

Все утверждения неверны.

Если вы выбрали пятый вариант, то абсолютно правы! Но, как показывают многочисленные исследования, даже люди со значительным опытом в анализе данных часто некорректно интерпретируют значение p-value (например, можно посмотреть эту интересную статью).

Давайте разберем все ответы по порядку:

Первое утверждение — пример ошибки корреляции: факт значимой взаимосвязи двух переменных ничего не говорит нам о причинах и следствиях. Может быть, это более агрессивные люди предпочитают проводить время за компьютерными играми, а вовсе не компьютерные игры делают людей агрессивнее.
Это уже более интересное утверждение. Все дело в том, что мы изначально принимаем за данное, что никаких различий на самом деле нет. И, держа это в уме как факт, рассчитываем значение p-value. Поэтому правильная интерпретация: «Если предположить, что агрессивность и компьютерные игры никак не связаны, то вероятность получить такие или еще более выраженные различия составила 0.04».

А что делать, если мы получили незначимые различия? Значит ли это, что никакой связи между исследуемыми переменными нет? Нет, это означает лишь то, что различия, может быть, и есть, но наши результаты не позволили их обнаружить.
Это напрямую связано с самим определением p-value. 0.04 — это вероятность получить такие или еще более экстремальные различия. Оценить вероятность получить именно такие различия, как в нашем эксперименте, в принципе невозможно!

Вот такие подводные камни могут скрываться в интерпретации такого показателя, как p-value. Поэтому очень важно понимать механизмы, заложенные в основании методов анализа и расчета основных статистических показателей.

Онлайн-курс по основам статистики: сложные формулы несложным языком

Сейчас я пишу диссертацию на факультете психологии СПбГУ и преподаю статистику биологам в Институте биоинформатики. Основываясь на курсе читаемых лекций и собственного исследовательского опыта, возникла идея создать онлайн-курс по введению в статистику на русском языке для всех желающих, необязательно биоинформатиков или биологов.

Существует много хороших онлайн-курсов по анализу данных и статистике (например, такой, такой, или такой), но практически все они на английском языке. Надеюсь, что курс будет полезен для тех, кто только знакомится с основами статистики. В нем я стараюсь в максимально доступной форме разобрать основные идеи и методы анализа данных, уделяя особое внимание самой идее статистической проверки гипотез и интерпретации получаемых результатов. В качестве примеров будут задачи из различных областей: от биоинформатики до социологии. Курс бесплатный и все его материалы останутся открытыми после окончания, начинается 15 февраля.

Полезные материалы

Если вы знаете какие-либо полезные курсы или материалы по введению в статистику — делитесь в комментариях!

Основные статистические функции в Excel: использование, формулы

Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.

Использование статистических функций
- СРЗНАЧ
- МАКС
- МИН
- СРЗНАЧЕСЛИ
- МЕДИАНА
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
Заключение

Использование статистических функций

Смотрите также: “Основные математические функции в Excel: использование, формулы”

Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.

Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:

Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
Используем сочетание клавиш Shift+F3.

Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.

Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.

На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.

Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.

Давайте теперь рассмотрим наиболее популярные функции.

СРЗНАЧ

Смотрите также: “Как посчитать среднее значение в Excel: формула, функции, инструменты”

Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:

=СРЗНАЧ(число1;число2;…)

В качестве аргументов функции можно указать:

конкретные числа;
ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
диапазон ячеек – указывается вручную или путем выделения в таблице.
переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.

МАКС

Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:

=МАКС(число1;число2;…)

В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.

МИН

Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:

=МИН(число1;число2;…)

Аргументы функции заполняются так же, как и для оператора МАКС.

СРЗНАЧЕСЛИ

Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:

=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)

В аргументах указываются:

Диапазон ячеек – вручную или с помощью выделения в таблице;
Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
Диапазон_усреднения – не является обязательным аргументом для заполнения.

МЕДИАНА

Оператор находит медиану заданного диапазона значений. Синтаксис функции:

=МЕДИАНА(число1;число2;…)

В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.

НАИБОЛЬШИЙ

Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:

=НАИБОЛЬШИЙ(массив;k)

Аргумента функции два: массив и номер позиции – K.

Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.

НАИМЕНЬШИЙ

Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:

=НАИМЕНЬШИЙ(массив;k)

МОДА.ОДН

Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:

=МОДА.ОДН(число1;число2;…)

В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.

Для вертикальных массивов, также, используется функция МОДА.НСК.

СТАНДОТКЛОН

Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:

СТАДНОТКЛОН.В – находит стандартное отклонение выборки
СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности

Формулы функций выглядят следующим образом:

=СТАДНОТКЛОН.В(число1;число2;…)
=СТАДНОТКЛОН.Г(число1;число2;…)

СРГЕОМ

Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:

=СРГЕОМ(число1;число2;…)

Заключение

В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.

Смотрите также:

Почему Эксель не считает формулу: что делать
Сортировка и фильтрация данных в Excel

Формулы статистики

На этой веб-странице перечислены формулы статистики, используемые в Stat Trek учебники. Каждая формула ссылается на веб-сайт страница, которая объясняет, как использовать формулу.

Параметры

Среднее значение населения = μ = ( Σ X _i ) / N
Стандартное отклонение населения = σ = sqrt [ Σ ( X _i — мк) ²/Н]
Дисперсия населения = о ² = Σ ( X _i — мк) ² / N
Дисперсия доли населения = σ _P ² = PQ / n
Стандартизированная оценка = Z = (X — μ) / σ
Коэффициент корреляции населения = ρ = [ 1 / N ] * Σ { [ (X _i — μ _X ) / σ _x ] * [ (Y _i — μ _Y ) / σ _г] }

Статистика

Если не указано иное, в этих формулах предполагается простая случайная выборка.

Среднее значение выборки = х = ( Σ х _i ) / n
Стандартное отклонение выборки = s = sqrt [ Σ ( x _i — х) ² / (n-1)]
Выборочная дисперсия = с ² = Σ ( х _i — х) ² / (п-1)
Дисперсия доли выборки = с _р ² = pq / (n — 1)
Доля объединенной выборки = p = (p ₁ * n ₁ + p ₂ * n ₂ ) / (n ₁ + n ₂ )
Стандартное отклонение объединенной выборки = с _р = sqrt [ (n ₁ — 1) * s ₁ ² + (п ₂ — 1) * с ₂ ² ] / (n ₁ + n ₂ — 2) ]
Коэффициент корреляции выборки = г = [ 1 / (п — 1) ] * Σ { [ (х _я — х) / с _x ] * [ (у _я — у) / с _г ] }

Корреляция

Корреляция Пирсона продукт-момент = r = Σ (xy) / sqrt [ ( Σ x ² ) * ( Σ y ² ) ]
Линейная корреляция (выборочные данные) = r = [ 1 / (n — 1) ] * Σ { [ (x _i — x) / с _x ] * [ (y _i — y) / с _y ] }
Линейная корреляция (данные населения) = ρ = [ 1 / N ] * Σ { [ (X _i — μ _X ) / σ _x ] * [ (Y _i — μ _Y ) / σ _y ] 1 }

Простая линейная регрессия

Линия простой линейной регрессии: ŷ = b ₀ + b ₁ x
Коэффициент регрессии = б ₁ = Σ [ (х _i — х) (у _я — у) ] / Σ [ (х _я — х) ² ]
Пересечение наклона регрессии = б ₀ = у — б ₁ * х
Коэффициент регрессии = б ₁ = г * (с _у / с _х )
Стандартная ошибка наклона регрессии = с _{б ₁} = sqrt [ Σ(y _i — ŷ _i ) ² / (п — 2) ] / sqrt [ Σ(x _я — х) ² ]

Подсчет

п факториал: н! = п * (п-1) * (п — 2) * . . . * 3 * 2 * 1. По соглашению, 0! = 1,
Перестановки n вещей, взятых r за один раз: _n P _r = n! / (н — р)!
Комбинации из n вещей, взятых r за один раз: _n C _r = n! / г!(п — г)! = _n P _r / r!

Вероятность

Правило добавления: Р (А ∪ В) = Р(А) + Р(В) — Р(А ∩ В)
Правило умножения: Р (А ∩ В) = Р(А) Р(В|А)
Правило вычитания: P(A’) = 1 — P(A)

Случайные величины

В следующих формулах X и Y являются случайными величинами, а a и b являются константами.

Ожидаемое значение X = E (X) = μ _x = Σ [ x _i * P (x _i ) ]
Дисперсия X = Var(X) = σ ² = Σ [ х _i — E(x) ] ² * P(x _i ) = Σ [ x _i — μ _x ] ² * P(x _i )
Нормальная случайная величина = z-оценка = z = (X — μ)/σ
Статистика хи-квадрат = Χ ² = [ ( n — 1 ) * с ² ] / σ ²
f статистика = ф = [ с ₁ ² /σ ₁ ² ] / [ с ₂ ² /σ ₂ ² ]
Ожидаемое значение суммы случайных величин = Е(Х + Y) = Е(Х) + Е(Y)
Ожидаемое значение разницы между случайными величинами = Е(Х — У) = Е(Х) — Е(У)
Дисперсия суммы независимых случайных величин = Вар(Х + Y) = Вар(Х) + Вар(Y)
Дисперсия разности между независимыми случайными величинами = Вар(Х — Y) = Вар(Х) + Вар(Y)

Распределение проб

Среднее выборочное распределение среднего = μ _x = мк
Среднее выборочное распределение доли = мк _р = Р
Стандартное отклонение пропорции = σ _р = sqrt[P * (1 — P)/n] = sqrt(PQ/n)
Стандартное отклонение среднего = σ _x = σ/sqrt(n)
Стандартное отклонение разности выборочных средних = σ _d = sqrt[ (σ ₁ ² / n ₁ ) + (σ ₂ ² / п ₂) ]
Стандартное отклонение разницы пропорций выборки = σ _d = sqrt{ [P ₁ (1 — P ₁ ) / номер ₁ ] + [P ₂ (1 — P ₂) / № ₂ ] }

Стандартная ошибка

Стандартная ошибка пропорции = SE _p = с _р = sqrt[p * (1 — p)/n] = sqrt(pq/n)
Стандартная ошибка разности пропорций = SE _p = с _р = sqrt{ p * ( 1 — p ) * [ (1/n ₁ ) + (1/n ₂ ) ] }
Стандартная ошибка среднего = SE _x = с _х = с/кв (n)
Стандартная ошибка разности выборочных средних = SE _д = с _д = sqrt[ (s ₁ ² / п ₁ ) + (с ₂ ² / номер ₂ ) ]
Стандартная ошибка разности парных выборочных средних = SE _д = с _д = { квт [ (Σ(d _i — d) ² / (n — 1) ] } / sqrt(n)
Стандартная ошибка объединенной выборки = с _{объединено} = sqrt [ (n ₁ — 1) * s ₁ ² + (n ₂ — 1) * с ₂ ² ] / (n ₁ + n ₂ — 2) ]
Стандартная ошибка разности пропорций выборки = с _д = sqrt{ [p ₁ (1 — p ₁ ) / п ₁ ] + [p ₂ (1 — p ₂ ) / номер ₂ ] }

Дискретные распределения вероятностей

Биномиальная формула: P(X = x) = б( х ; н, Р ) = _n C _x * P ^x * (1 — P) ^{n — x} = _n C _x * P ^x * Q ^{n — x}
Среднее биномиального распределения = μ _x = n * P
Дисперсия биномиального распределения = σ _x ² = n * P * ( 1 — P )
Отрицательная биномиальная формула: P(X = x) = b*( x ; r, P ) = _x-1 C _r-1 * Р ^р * (1 — Р) ^{х — р}
Среднее отрицательного биномиального распределения = μ _x = rQ / P
Дисперсия отрицательного биномиального распределения = σ _x ² = р * К/П ²
Геометрическая формула: P(X = x) = g( x ; P ) = P * Q ^{x — 1}
Среднее геометрическое распределение = мк _х = Q / P
Дисперсия геометрического распределения = σ _x ² = В/П ²
Гипергеометрическая формула: P(X = x) = ч( x ; N , н , к ) = [ _k C _x ] [ _N-k C _n-x ] / [ _Н С _Н ]
Среднее значение гипергеометрического распределения = мк _х = n * k / N
Дисперсия гипергеометрического распределения = σ _x ² = п * к * ( Н — к ) * ( Н — п ) / [Н ² * ( Н — 1 ) ]
Формула Пуассона: P( x; µ ) = (e ^-µ) (µ ^x) / x!
Среднее значение распределения Пуассона = мк _х = мк
Дисперсия распределения Пуассона = σ _x ² = μ
Полиномиальная формула: P = [ n! / ( п ₁ ! * п ₂ ! * . .. п _к ! )] * ( стр. ₁ ^{п ₁} * p ₂ ^{n ₂} * . . . * p _k ^{n _k} )

Линейные преобразования

Для следующих формул предположим, что Y является линейное преобразование случайной величины X, определяемой уравнением: Y = aX + b.

Среднее линейного преобразования = E(Y) = У = аХ + б.
Дисперсия линейного преобразования = Var(Y) = а ² * Вар(Х).
Стандартизированная оценка = z = (x — μ _x) / σ _x.
t статистика = t = (x — μ _x) / [s/sqrt(n)].

Оценка

Доверительный интервал: Выборочная статистика + Критическое значение * Стандартная ошибка статистики
Погрешность = (Критическое значение) * (Стандартное отклонение статистики)
Погрешность = (Критическое значение) * (Стандартная ошибка статистики)

Проверка гипотез

Стандартизированная тестовая статистика = (Статистика — Параметр) / (Стандартное отклонение статистики)
Одновыборочный z-тест для пропорций: z-оценка = z = (p — P ₀) / sqrt (p * q / n)
Двухвыборочный z-тест для пропорций: z-оценка = z = z = [(p ₁ — p ₂ ) — d ] / SE
Одновыборочный t-критерий для средних: t статистика = t = (x — μ) / SE
Двухвыборочный t-критерий для средних: t статистика = t = [ (x ₁ — х ₂ ) — д ] / SE
Стьюдентный критерий с согласованной выборкой для средних значений: t статистика = t = [ (x ₁ — х ₂ ) — Д ] / SE = (д — Д) / SE
Статистика критерия хи-квадрат = Χ ² = Σ[ (Наблюдается — Ожидается) ² / Ожидается ]

Степени свободы

Правильная формула для степеней свободы (DF) зависит от ситуации (характер тестовой статистики, количество образцов, исходные предположения и др. ).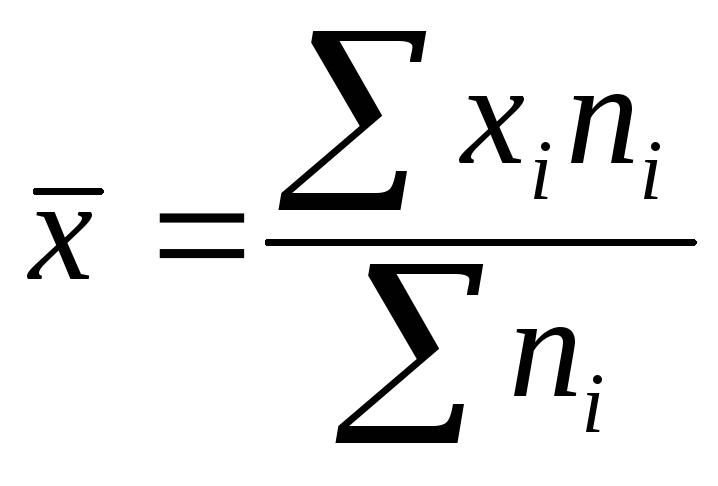

Одновыборочный t-критерий: ДФ = п — 1
Двухвыборочный t-критерий: ДФ = (s ₁ ² /n ₁ + с ₂ ² /n ₂ ) ² / { [ (с ₁ ² / п ₁ ) ² / (n ₁ — 1) ] + [ (с ₂ ² / п ₂ ) ² / (n ₂ — 1) ] }
Двухвыборочный t-критерий, объединенная стандартная ошибка: ДФ = п ₁ + п ₂ — 2
Простая линейная регрессия, тестовый наклон: ДФ = n — 2
Хи-квадрат критерия согласия: ДФ = к — 1
Критерий хи-квадрат на однородность: ДФ = (г — 1) * (с — 1)
Тест хи-квадрат на независимость: ДФ = (г — 1) * (с — 1)

Размер выборки

Ниже первые две формулы находят наименьшие размеры выборки. требуется для достижения фиксированной погрешности, используя простой случайная выборка. Третья формула распределяет выборку по стратам на основе пропорционального плана. четвертая формула, распределение Неймана, использует стратифицированную выборку для минимизировать дисперсию при фиксированном размере выборки. И последняя формула, оптимальное распределение, использует стратифицированную выборку для минимизации дисперсии, при фиксированном бюджете.

Среднее значение (простая случайная выборка): n = {z ² * σ ² * [Н/(Н-1)]} / {МЕ ² + [ z ² * σ ² / (N — 1) ] }
Доля (простая случайная выборка): n = [(z ² * p * q) + ME ²] / [ME ² + з ² * п * к/н ]
Пропорциональная стратифицированная выборка: п _ч = ( N _ч / N ) * n
Распределение Неймана (стратифицированная выборка): n _ч = n * ( N _ч * σ _ч ) / [ Σ ( N _я * σ _я ) ]
Оптимальное распределение (стратифицированная выборка):
n _h = n * [( N _h * σ _h ) / sqrt( c _h ) ] / [ Σ ( N _я * σ _я ) / кврт( с _и )]

Базовые формулы статистики — Cuemath

Статистика — это раздел математики, который имеет дело с числами и анализом данных. Статистика — это наука о сборе, анализе, интерпретации, представлении и организации данных.

Короче говоря, статистика имеет дело со сбором, классификацией, упорядочиванием и представлением собранных числовых данных простыми и понятными способами. Статистика интерпретирует различные результаты и возможности прогноза. Существуют различные основные формулы статистики, которые помогают нам иметь дело с фактами, наблюдениями и информацией, которые представлены только в виде числовых данных. С помощью статистики мы можем найти различные меры центральных тенденций и отклонения значений данных от центра. Давайте изучим основные формулы статистики вместе с несколькими решенными примерами. 9{2}}{н}} \\
\хлайн
\end{массив}\)

где
x = данные наблюдений
\(\bar{x}\) = Среднее
n = общее количество наблюдений

Решенные примеры с использованием формулы базовой статистики

Пример 1: Возраст учащихся = {14,15,16,15,17,15,18}
Найдите режим.