формулировки, доказательства, примеры, формулы степеней
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Свойства степени с натуральным показателем
Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:
Определение 11. Главное свойство степени: am·an=am+n
Можно обобщить до: an1·an2·…·ank=an1+n2+…+nk.
2. Свойство частного для степеней, имеющих одинаковые основания: am:an=am−n
3.
Равенство можно расширить до: (a1·a2·…·ak)n=a1n·a2n·…·akn
4. Свойство частного в натуральной степени: (a:b)n=an:bn
5. Возводим степень в степень: (am)n=am·n,
Можно обобщить до:(((an1)n2)…)nk=an1·n2·…·nk
6. Сравниваем степень с нулем:
- если a>0, то при любом натуральном n, an будет больше нуля;
- при a, равном 0, an также будет равна нулю;
- при a<0 и таком показателе степени, который будет четным числом 2·m, a2·m будет больше нуля;
- при a <0 и таком показателе степени, который будет нечетным числом 2·m−1, a2·m−1 будет меньше нуля.
7. Равенство an<bn будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.
8. Неравенство am>an будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными.
Далее мы разберем каждое свойство подробно и попробуем привести доказательства.
1. Начнем с основного свойства степени: равенство am·an=am+n будет верным при любых натуральных m и n и действительном a. Как доказать это утверждение?
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
Это можно сократить до (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.
Разберем конкретный пример, подтверждающий это.
Пример 1Итак, у нас есть две степени с основанием 2. Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 22·23=22+3=25 Вычислим значения, чтобы проверить верность этого равенства.
У нас получилось равенство: 22·23=22+3=25 Вычислим значения, чтобы проверить верность этого равенства.
Выполним необходимые математические действия: 22·23=(2·2)·(2·2·2)=4·8=32 и 25=2·2·2·2·2=32
В итоге у нас вышло: 22·23=25. Свойство доказано.
В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n1, n2 и др. буквой k, мы получим верное равенство:
an1·an2·…·ank=an1+n2+…+nk.
Пример 2Пример с конкретными числами (легко посчитать самостоятельно): (2,1)3·(2,1)3·(2,1)4·(2,1)7=(2,1)3+3+4+7=(2,1)17.
2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство am:an=am−n, которое справедливо при любых натуральным m и n (причем m больше n) ) и любом отличном от нуля действительном a.
Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0n=0). Условие, чтобы число m обязательно было больше n, нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m, мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
am−n·an=a(m−n)+n=am
Из него можно вывести: am−n·an=am
Вспомним про связь деления и умножения. Из него следует, что am−n– частное степеней am и an. Это и есть доказательство второго свойства степени.
Пример 3Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π: π5:π2=π5−3=π3
3. Следующим мы разберем свойство степени произведения: (a·b)n=an·bn при любых действительных a и b и натуральном n.
Следующим мы разберем свойство степени произведения: (a·b)n=an·bn при любых действительных a и b и натуральном n.
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
Вспомнив свойства умножения, запишем: . Это значит то же самое, что и an·bn.
Пример 4Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
(a1·a2·…·ak)n=a1n·a2n·…·akn
Пример 5С конкретными числами получим следующее верное равенство: (2·(-2,3)·a)7=27·(-2,3)7·a
4. После этого мы попробуем доказать свойство частного: (a:b)n=an:bn при любых действительных a и b, если b не равно 0, а n – натуральное число.
Для доказательства можно использовать предыдущее свойство степени. Если (a:b)n·bn=((a:b)·b)n=an , а (a:b)n·bn=an, то из этого выходит, что (a:b)n есть частное от деления an на bn.
Пример 6Подсчитаем пример: 312:-0. 53=3123:(-0,5)3
53=3123:(-0,5)3
5. Далее мы поговорим о свойстве возведения степени в степень: (am)n=am·n для любого действительного a и любых натуральных n и m.
Пример 7Начнем сразу с примера: (52)3=52·3=56
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:
Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p, q, r, s, то верно будет:
apqys=ap·q·y·s
Пример 8Добавим конкретики: (((5,2)3)2)5=(5,2)3·2·5=(5,2)30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Для начала сравним степень с нулем. Почему an>0 при условии, что а больше 0?
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени an с положительным основанием и натуральным показателем это будет верно.
А что же такое степень, как не результат умножения чисел? Тогда для любой степени an с положительным основанием и натуральным показателем это будет верно.
35>0, (0,00201)2>0 и 3491351>0
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Пример 10Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2·m, где m – натуральное число.
Тогда:
Вспомним, как правильно умножать отрицательные числа: произведение a·a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a2·m также положительны.
Пример 11Например, (−6)4>0, (−2,2)12>0 и -296>0
А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2·m−1.
Тогда
Все произведения a·a, согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a, то конечный результат будет отрицателен.
Тогда получим: (−5)3<0, (−0,003)17<0 и -111029<0
7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).
Как это доказать?
an<bn– неравенство, представляющее собой произведение левых и правых частей nверных неравенств a<b. Вспомним основные свойства неравенств справедливо и an<bn.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 12Например, верны неравенства: 37<(2,2)7 и 3511124>(0,75)124
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Для начала нам нужно убедиться, что am<an при условии, что m больше, чем n, и а больше 0, но меньше 1.Теперь сравним с нулем разность am−an
Вынесем an за скобки, после чего наша разность примет вид an·(am−n−1). Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m−n>0, тогда am−n−1–отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
У нас вышло, что am−an<0 и am<an. Свойство доказано.
Осталось привести доказательство второй части утверждения, сформулированного выше: am>a справедливо при m>n и a>1. Укажем разность и вынесем an за скобки: (am−n−1).Степень an при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a>1 степень am−n больше единицы. Выходит, am−an>0 и am>an, что нам и требовалось доказать.
Пример с конкретными числами: 37>32
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
Определение 21. am·an=am+n
2. am:an=am−n
3. (a·b)n=an·bn
4. (a:b)n=an:bn
5. (am)n=am·n
6. an<bn и a−n>b−n при условии целого положительного n, положительных a и b, a<b
7. am<an, при условии целых m и n, m>n и 0<a<1, при a>1 am>an.
Если основание степени равно нулю, то записи am и an имеют смысл только лишь в случае натуральных и положительных m и n. В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (ap)q=ap·q, (a−p)q=a(−p)·q, (ap)−q=ap·(−q) и (a−p)−q=a(−p)·(−q)
Условия: p=0 или натуральное число; q– аналогично.
Если значения p и q больше 0, то у нас получится (ap)q=ap·q. Схожее равенство мы уже доказывали раньше. Если p=0, то:
(a0)q=1q=1 a0·q=a0=1
Следовательно, (a0)q=a0·q
Для q=0 все точно так же:
(ap)0=1 ap·0=a0=1
Итог: (ap)0=ap·0.
Если же оба показателя нулевые, то (a0)0=10=1 и a0·0=a0=1, значит, (a0)0=a0·0.
Далее разберем равенство (a−p)q=a(−p)·q. Согласно определению степени с целым отрицательным показателем имеем a-p=1ap, значит, (a-p)q=1apq.
Вспомним доказанное выше свойство частного в степени и запишем:
1apq=1qapq
Если 1p=1·1·…·1=1 иapq=ap·q, то 1qapq=1ap·q
Эту запись мы можем преобразовать в силу основных правил умножения в a(−p)·q.
Так же: ap-q=1(ap)q=1ap·q=a-(p·q)=ap·(-q).
И (a-p)-q=1ap-q=(ap)q=ap·q=a(-p)·(-q)
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Доказательство предпоследнего свойства: вспомним, a−n>b−n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b.
Тогда неравенство можно преобразовать следующим образом:
1an>1bn
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
1an-1bn=bn-anan·bn
Вспомним, что в условии a меньше b, тогда, согласно определению степени с натуральным показателем: — an<bn, в итоге: bn−an>0.
an·bn в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь bn-anan·bn, которая в итоге также дает положительный результат. Отсюда 1an>1bn откуда a−n>b−n, что нам и нужно было доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Определение 31. am1n1·am2n2=am1n1+m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 ( свойство произведения степеней с одинаковыми основаниями).
2.am1n1:bm2n2=am1n1-m2n2 , если a>0 (свойство частного).
3. a·bmn=amn·bmn при a>0 и b>0, а если m1n1>0 и m2n2>0, то при a≥0 и (или) b≥0 (свойство произведения в дробной степени).
4. a:bmn=amn:bmn при a>0 и b>0, а если mn>0, то при a≥0 и b>0 (свойство частного в дробной степени).
5. am1n1m2n2=am1n1·m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 (свойство степени в степени).
6. ap<bp при условии любых положительных a и b, a<b и рациональном p при p>0; если p<0 — ap>bp (свойство сравнения степеней с равными рациональными показателями).
7. ap<aq при условии рациональных чисел p и q, p>q при 0<a<1; если a>0 – ap>aq
Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.
Согласно тому, что из себя представляет степень с дробным показателем, получим:
am1n1=am1n1 и am2n2=am2n2, следовательно, am1n1·am2n2=am1n1·am2n2
Свойства корня позволят нам вывести равенства:
am1·m2n1·n2·am2·m1n2·n1=am1·n2·am2·n1n1·n2
Из этого получаем: am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Преобразуем:
am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Показатель степени можно записать в виде:
m1·n2+m2·n1n1·n2=m1·n2n1·n2+m2·n1n1·n2=m1n1+m2n2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
am1n1: am2n2=am1n1: am2n2=am1·n2:am2·n1n1·n2==am1·n2-m2·n1n1·n2=am1·n2-m2·n1n1·n2=am1·n2n1·n2-m2·n1n1·n2=am1n1-m2n2
Доказательства остальных равенств:
a·bmn=(a·b)mn=am·bmn=amn·bmn=amn·bmn;(a:b)mn=(a:b)mn=am:bmn==amn:bmn=amn:bmn;am1n1m2n2=am1n1m2n2=am1n1m2n2==am1m2n1n2=am1·m2n1n2==am1·m2n2·n1=am1·m2n2·n1=am1n1·m2n2
Следующее свойство: докажем, что для любых значений a и b больше 0, если а меньше b, будет выполняться ap<bp, а для p больше 0 — ap>bp
Представим рациональное число p как mn. При этом m–целое число, n–натуральное. Тогда условия p<0 и p>0 будут распространяться на m<0 и m>0. При m>0 и a<b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство am<bm.
Используем свойство корней и выведем: amn<bmn
Учитывая положительность значений a и b, перепишем неравенство как amn<bmn. Оно эквивалентно ap<bp.
Таким же образом при m<0 имеем a am>bm, получаем amn>bmn значит, amn>bmn и ap>bp.
Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 ap<aq, а при a>0 будет верно ap>aq.
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m1n и m2n
Здесь m1 и m2 – целые числа, а n – натуральное. Если p>q, то m1>m2 (учитывая правило сравнения дробей). Тогда при 0<a<1 будет верно am1<am2, а при a>1 – неравенство a1m>a2m.
Их можно переписать в следующем виде:
am1n<am2nam1n>am2n
Тогда можно сделать преобразования и получить в итоге:
am1n<am2nam1n>am2n
Подводим итог: при p>q и 0<a<1 верно ap<aq, а при a>0– ap>aq.
Основные свойства степеней с иррациональными показателями
На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):
Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):
1. ap·aq=ap+q
2. ap:aq=ap−q
3. (a·b)p=ap·bp
4. (a:b)p=ap:bp
5. (ap)q=ap·q
6. ap<bp верно при любых положительных a и b, если a<b и p – иррациональное число больше 0; если p меньше 0, то ap>bp
7. ap<aq верно, если p и q– иррациональные числа, p<q, 0<a<1; если a>0, то ap>aq.
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a>0 обладают теми же свойствами.
Свойства степени с натуральным показателем. Примеры с решениями
Возведение произведения в степень
Выражение (ab)n является степенью произведения множителей a и b. Это выражение можно представить в виде произведения степеней anbn. Докажем это на примере.
Это выражение можно представить в виде произведения степеней anbn. Докажем это на примере.
По определению степени:
Раскрываем скобки, а затем, используя переместительный закон умножения, переставляем сомножители так, чтобы одинаковые буквы стояли рядом:
Группируем отдельно множители a и множители b и получаем:
Воспользовавшись определением степени, находим:
Следовательно, формула возведения произведения в степень будет выглядеть так:
(ab)n = anbn.
Свойство степени произведения распространяется на степень произведения двух и более множителей:
(3a2b)2 = 9a4b2.
Отсюда следует правило:
Чтобы возвести произведение в степень, можно отдельно возвести в эту степень каждый множитель и полученные результаты перемножить.
Возведение частного в степень
Для возведения в степень частного надо возвести в степень отдельно делимое и делитель.
Если говорить иначе, то степень частного равна частному степеней:
Так как частное в алгебре часто записывается в виде дроби (знак деления заменяется дробной чертой), то правило возведения частного в степень можно переформулировать так, чтобы оно подходило и для дробей:
Чтобы возвести дробь в степень надо возвести в эту степень отдельно её числитель и знаменатель.
Общая формула возведения в степень частного будет выглядеть так:
Возведение степени в степень
Для возведения степени числа в степень, надо перемножить показатели степеней, а основание оставить без изменений.
Например, нам нужно возвести 72 в третью степень:
(72)3.
Чтобы нам не возводить 7 сначала во вторую степень, а после этого ещё в третью, вспоминаем, что степень числа это сокращённая форма умножения одинаковых сомножителей, а это значит, что:
(72)3 = 72 · 72 · 72 = 72+2+2 = 72·3 = 76.
Следовательно, при возведении степени в степень показатели степеней перемножаются.
Общая формула возведения степени в степень:
(ax)y = axy.
Примеры на свойства степеней
Пример 1. Выполните действия:
а) (x5)3;
б) 2(n3)5;
в) -4(a4)2.
Решение:
а) (x5)3 = x5 · 3 = x15;
б) 2(n3)5 = 2n3 · 5 = 2n15;
в) -4(a4)2 = -4a4 · 2 = -4a8.
Пример 2. Возведите в степень:
а) (-2mn)4;
б) (3bc)3;
в) (-6a4b)2.
Решение:
а) (-2mn)4 = (-2)4 · m4 · n4 = 16m4n4;
б) (3bc)3 = 33 · b3 · c3 = 27b3c3;
в) (-6a4b)2 = (-6)2 · (a4)2 · b2 = 36 · a8 · b2 = 36a8b2.
Пример 3. Возведите дробь в степень:
Решение:
| а) ( | 2a | )2 = | (2a)2 | = | 4a2 | ; |
| 5 | 52 | 25 |
| б) (- | xy | )5 = — | (xy)5 | = — | x5y5 | ; |
| z | z5 | z5 |
| в) ( | a2b | )3 = | (a2b)3 | = | (a2)3 · b3 | = | a6b3 | . |
| 2c3 | (2c3)3 | 23 · (c3)3 | 8c9 |
| 1. |
Умножение степеней
Сложность: лёгкое |
1 |
2.
|
Степень в степени
Сложность: лёгкое |
1 |
| 3. |
Возведение степени в степень (буквы)
Сложность: лёгкое |
2 |
4.
|
Степень в степени (основание)
Сложность: лёгкое |
2 |
| 5. |
Степень в степени (показатель степени)
Сложность: лёгкое |
2 |
6.
|
Произведение трёх степеней
Сложность: лёгкое |
2 |
| 7. |
Произведение степеней (основание — бином)
Сложность: лёгкое |
1 |
8.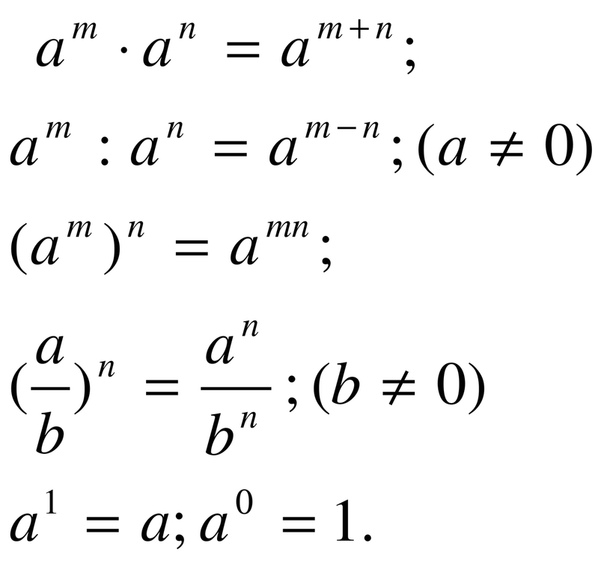
|
Частное трёх степеней
Сложность: лёгкое |
2 |
| 9. |
Произведение степеней с одинаковыми основаниями (буквы)
Сложность: лёгкое |
3 |
10.
|
Произведение двух степеней (числа)
Сложность: лёгкое |
2 |
| 11. |
Частное двух степеней (отрицательное основание)
Сложность: лёгкое |
2 |
12.
|
Возведение степени в степень (числа)
Сложность: лёгкое |
2 |
| 13. |
Частное двух степеней (дробь)
Сложность: лёгкое |
3 |
14.
|
Частное двух степеней (отрицательные смешанные числа)
Сложность: лёгкое |
1 |
| 15. |
Произведение степеней с одним основанием (числа)
Сложность: среднее |
3 |
16.
|
Произведение отрицательных и противоположных степеней
Сложность: среднее |
5 |
| 17. |
Уравнение (частное степеней, целые числа)
Сложность: среднее |
3 |
18.
|
Дробь (буквы)
Сложность: среднее |
2 |
| 19. |
Произведение степени и степени в степени
Сложность: среднее |
2 |
20.
|
Деление и умножение степеней
Сложность: среднее |
3 |
| 21. |
Произведение двух дробей
Сложность: среднее |
2 |
22.
|
Произведение степеней в степени
Сложность: среднее |
3 |
| 23. |
Частное степени в степени и степени
Сложность: среднее |
2 |
24.
|
Умножение и деление степеней
Сложность: среднее |
1 |
| 25. |
Вычисление выражения со степенями
Сложность: среднее |
1 |
Свойства степени с целым показателем
Степень с целым показателем
Первый урок посвящен понятию обыкновенной степени с целым показателем — это математическая операция, в ходе которой число многократно умножается на само себя. 0=3*1=3; $$
В этом случае необходимо привести все степени к одинаковому основанию. Замечаем, что \(15\) раскладывается, как произведение 3 и 5, получим одинаковые основания и применим формулы №1,№3.
0=3*1=3; $$
В этом случае необходимо привести все степени к одинаковому основанию. Замечаем, что \(15\) раскладывается, как произведение 3 и 5, получим одинаковые основания и применим формулы №1,№3.
7.1.1. Степень с целым показателем.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 1k. Опубликовано
I. Определение. (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:
Примеры. Вычислить:
Решение.
II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:
Примеры. Вычислить:
Вычислить:
Решение.
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.
Примеры на все свойства степени.
Упростить:
Решение.
При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
Пример 8 ) решаем так же, как решали пример 7) вторым способом.
В примере 9) представим 73как 72∙7, а степень 45как 43∙42, а затем сократим дробь на (72∙43).
В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).
Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи
Оглавление:
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению. ..
..
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению. ..
..
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению. ..
..
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):
е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению. ..
..
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению. ..
..
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа «Все главные формулы по школьной математике»:
К оглавлению…
Конспект урока «Свойства степени с натуральным показателем»
Конспект урока.
«Свойства степени с натуральным показателем»
Учитель
Патракова Л. В.
2018г.
1. | Патракова Лариса Васильевна |
2. Место работы | МБОУ школа № 5 г.о. Кинешма |
3. Должность | Учитель |
4. Предмет | Алгебра |
5. Класс | 7 |
6. Тема урока | «Свойства степени с натуральным показателем». 1 урок |
7. Базовый учебник | Г.В. Дорофеев, С. Алгебра 7 класс, «Просвещение», 2017г. |
Цели урока: познакомить учащихся со свойствами степени с натуральным показателем; владеть правилами выполнения действий над степенями; обеспечить условия для развития умений работы с источниками учебной информации, выделять главное и второстепенное.
Задачи:
Образовательные (формирование познавательных УУД): изучить свойства степени (умножение, деление, возведение степени в степень) с натуральным показателем; научить выполнять действия на применение правил; совершенствование вычислительных навыков.
Развивающие (формирование регулятивных УУД): развивать умения наблюдать, сравнивать, анализировать, делать выводы, развивать устную математическую речь.
Воспитательные (формирование коммуникативных и личностных УУД): формировать трудолюбие, внимательность, активность, умение слушать мнения других, участвовать в коллективном обсуждении проблем, воспитывать самостоятельность.
Тип урока: Урок «открытия» нового знания.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Используемые технологии: проблемное обучение, обучение в сотрудничестве, личностно-ориентированное обучение, коммуникативные и здоровьесберегающие технологии.
Необходимое оборудование: компьютер, проектор, экран, учебники по алгебре, карточки.
Сценарий урока.
1.Организационный момент.
Здравствуйте, ребята!
Начинаем наш урок, тему которого узнаем чуть позже.
Перед тем, как приступить к работе вспомним: какие правила мы должны соблюдать на уроке? Ответы детей. Учитель выслушивает ответы учеников: (Слушать, слышать друг друга, дополнять, исправлять, помогать)
-Запишем в тетрадях число, «Классная работа».
— Скажите, что нового вы узнали на предыдущих уроках? (ответы учеников)
Сегодня эпиграфом нашего урока станут слова М. В.Ломоносова
В.Ломоносова
«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»
-Где особенно часто используют степени, в каких науках? (Проверка домашнего задания найти дополнительный материал)
2.Актуализация опорных знаний.
Устная работа. (Слайд)
-Что называют степенью числа?
-Привести примеры.
-Назвать основание и показатель степени (Слайд)
-Любым ли числом может быть основание? Привести примеры.
-Всегда ли степень с отрицательным основанием, есть число отрицательное? -Сформулируйте определение. Приведите примеры.
— Что называют степенью числа с показателем 1?
Выполним вычисления и узнаем тему нашего урока (карточка 1 и 2)
ме | ой | ре | пе | св | к | да | ни | ва | нет | ра | ст | ро | см | сте | с | нь |
-36 | 25 | 12 | 81 | 16 | 8 | 4,5 | 7,9 | 10 | 7 | -6 | 9 | 6 | -9 | -8 | 36 | 1 |
|
сте | зате | нату | лем | пени | раль | ный | с | пока | ным |
-12 | 103 | 16 384 | 3026 | 10 609 | 59 049 | 177147 | 36 | 121 | 531 441 |
Запишем в тетради тему нашего урока: «Свойства степени». Название целей и задач урока.
Название целей и задач урока.
3. Освоение нового учебного материала.
Скажите, в чем возникла трудность при выполнении заданий второй части?
Работа в группах.
Карточка 3. ( см приложение)
-Вам сейчас предстоит изучить карточки, проанализировать, обобщить материал, сделать выводы, и после этого вы сможете вычислить примеры в которых у вас возникли затруднения. (См Инструкцию к карточке №3.)
-Посмотрите на образец решения примеров.
-Сформулируйте свойства степеней.
Работа с учебником.
Что написано в учебнике про деление степеней (какая неточность написана в карточке), Что надо запомнить и как исправить? Обязательно ли чтобы основание ≠0? Как вы думаете, почему?
Докажите, на примере почему
Запишите формулы в тетрадь.
4. Закрепление учебного материала.
Устная работа на применение формул по цепочке. Выполните номера из учебника и дайте определение, которое использовали при решение примеров 524,530,557, 540.
Физкультминутка. https://www.youtube.com/watch ?v=SAWr-KZhD0E
Проговаривание свойств степеней.
Карточка 4. ( см приложение)
Выполните задание №1, №2, №3.
Те ученики, которые быстро справились с заданием выполняют №4.
Запишите ответы в тетрадь. После того, как задание выполнено, ученики меняются тетрадями и проверяют тетради одноклассников, отмечая правильно решенные примеры знаком «+» (проверяя решения по слайду)
Объяснение трудных моментов, повторение правил, работа в группах.
Обратимся к таблицам и попробуем решить задание, с которым мы не смогли справиться в начале урока.
; ; ; ; ; .
Степень числа «3» мы можем найти в учебнике? Кто уже видел этот номер, подскажите остальным (№549)?
-Мы можем полностью озвучить тему нашего урока.
-Как она будет звучать?
-Что значит натуральная степень?
-Натуральное число?
-Какие свойства мы выучили?
-Сформулируйте свойства степеней.
Можно ли умножать или делить степени с разными основаниями?
Какое обязательное условие?
Выполним устно: , , ? (Слайд)
— Что надо сделать, чтобы применить выученные правила?
Выполнить на доске и в тетрадях №549, 548.
5.Задание на дом.
1.В тетрадь «Справочный материал» записать формулы и свойства степеней (опорные сигналы), выписать степени чисел «2», «3» с показателями от 1 до 15. (П 6.1, 6.2 )
2.Зашифровать фразу или слово, используя выражения со степенями + №537
или выполнить №№ 525, 529, 537, 536.
6. Подведение итогов урока. Рефлексия.
-Что мы изучали сегодня на уроке?
-Какие свойства степени мы выучили?
— Сформулируйте свойства степеней.
— Можно ли умножать или делить степени с разными основаниями?
Оцени свою работу:
— Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно.
— Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно.
— У меня не было желания работать. Сегодня не мой день.
Приложение
карточка 3.
Инструкция к карточке №3.
1.Повтори определение степени, вспомни, где записывается основание степени и показатель степени. (если забыл, можешь использовать карточки 1.1 и 1.2)
2. Внимательно прочитай определение 1. «Как умножать степени с одинаковым основанием», посмотри на схему- рисунок и запомни, что нужно сделать.
3. Посмотри на решение примеров. Выясни, как получается ответ.
4. Внимательно читай определение 2. Изучив схему-рисунок дополни определение необходимыми словами.
5. Посмотри на решение примеров. Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
6. Внимательно читай начало определения 3, изучив схему-рисунок дополни определение необходимыми словами.
7. Посмотри на решение примеров. Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
8. Повтори все определения еще раз.
9.Обрати внимания на перечеркнутые свойства, сделай вывод, проверь на примерах. Возьми основание равное 2, а затем 3.
Карточка 4.
В работе использован учебник Г.В. Дорофеева «Алгебра-7»
В работе использованы картинки.
https://www.google.ru/search ?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgrc=bDOXOOLse5BjdM:
https://www.google.ru/search?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgdii=KD3ROdzdl3-zpM:&imgrc=5JGazRRLNnZdYM:
https://www. google.ru/search?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgrc=5JGazRRLNnZdYM:
google.ru/search?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgrc=5JGazRRLNnZdYM:
Карточка1
Карточка №2
Карточка №4
Карточка №5
Карточка №6
Карточка №3
Карточка 7.
Карточка №1.1
Карточка №1.2
Инструкция к карточке №3
DOCX / 11.98 Кб
Пояснительная записка к карточкам
DOCX / 13.12 Кб
Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция
В евклидовой геометрии четырехугольник — это четырехугольная двумерная фигура, сумма внутренних углов которой равна 360 °. Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников.
Итак, каковы свойства четырехугольника? Четырехугольники обладают двумя свойствами:
- Четырехугольник должен быть замкнутой формы с 4-мя сторонами
- Сумма всех внутренних углов четырехугольника составляет 360 °
В этой статье вы получите представление о 5 типах четырехугольников и познакомитесь с их свойствами четырехугольников.
Это то, что вы прочитаете в статье:
Вот видео, объясняющее свойства четырехугольника:
На приведенной ниже схеме показан четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов составляет 360 °.
Таким образом, A + ∠B + ∠C + ∠D = 360 °
Различные виды четырехугольников
Существует 5 типов четырехугольников в зависимости от их формы. Эти 5 четырехугольников:
- Прямоугольник
- Квадрат
- Параллелограмм
- Ромб
- Трапеция
Давайте подробно обсудим каждый из этих 5 четырехугольников:
Вот вопросы, которые научат вас применять свойства всех пяти четырехугольников, которые вы узнаете в этой статье.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами. Таким образом, все углы в прямоугольнике равны (360 ° / 4 = 90 °). Причем противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.
Свойства прямоугольников
Прямоугольник имеет три свойства:
- Все углы прямоугольника равны 90 °
- Противоположные стороны прямоугольника равны и параллельны
- Диагонали прямоугольника делят друг друга пополам
Формула прямоугольника — Площадь и периметр прямоугольника
Если длина прямоугольника L, а ширина B, то
- Площадь прямоугольника = длина × ширина или L × B
- Периметр прямоугольника = 2 × (L + B)
Эти практические вопросы помогут вам закрепить свойства прямоугольников
Планируете ли вы поступить в бизнес-школу США? Позвольте нам помочь вам пройти первый этап процесса i.
е., сдавая GMAT. Пройдите бесплатный тест GMAT, чтобы понять свой базовый результат, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Площадь
Квадрат — четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.
Объекты квадрата
Чтобы четырехугольник стал квадратом, он должен обладать определенными свойствами. Вот три свойства квадратов:
- Все углы квадрата равны 90 °
- Все стороны квадрата равны и параллельны друг другу
- Диагонали делят друг друга перпендикулярно пополам
Формула квадрата — Площадь и периметр квадрата
Если сторона квадрата — «а», тогда
- Площадь квадрата = a × a = a²
- Периметр квадрата = 2 × (a + a) = 4a
Эти практические вопросы помогут вам закрепить свойства квадратов
Если вы наберете Q50-51 за GMAT, вы сможете набрать 700+ баллов за GMAT.
Почему бы вам не начать подготовку к GMAT с помощью наших бесплатных подготовительных ресурсов и не начать свой путь к получению Q50-51 на GMAT. Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50.
Параллелограмм
Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, у него две пары параллельных сторон. Причем противоположные углы в параллелограмме равны, а его диагонали делят друг друга пополам.
Свойства параллелограмма
Четырехугольник, удовлетворяющий перечисленным ниже свойствам, будет классифицирован как параллелограмм.Параллелограмм имеет четыре свойства:
- Противоположные углы равны
- Противоположные стороны равны и параллельны
- Диагонали делят друг друга пополам
- Сумма любых двух смежных углов равна 180 °
Формулы параллелограмма — Площадь и периметр параллелограмма
Если длина параллелограмма равна «l», ширина — «b», а высота — «h», тогда:
- Периметр параллелограмма = 2 × (l + b)
- Площадь параллелограмма = l × h
Эти практические вопросы помогут вам закрепить свойства параллелограмма
Ромб
Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу. Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», так как он похож на ромб в игральных картах.
Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», так как он похож на ромб в игральных картах.
Свойства ромба
Ромб — это четырехугольник, обладающий следующими четырьмя свойствами:
- Противоположные углы равны
- Все стороны равны и противоположные стороны параллельны друг другу
- Диагонали делят друг друга перпендикулярно
- Сумма любых двух смежных углов составляет 180 °
Формулы ромба — Площадь и периметр ромб
Если сторона ромба — это, то периметр ромба = 4a
Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Эти практические вопросы помогут вам закрепить свойства ромба
Трапеция
Трапеция (в США ее называют трапецией) — это четырехугольник, у которого есть только одна пара параллельных сторон.Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.
Свойства трапеции
Трапеция — это четырехугольник, в котором одно свойство:
- Только одна пара противоположных сторон параллельна друг другу
Формулы трапеции — Площадь и периметр трапеции
Если высота трапеции « h» (как показано на диаграмме выше), то:
- Периметр трапеции = Сумма длин всех сторон = AB + BC + CD + DA
- Площадь трапеции = ½ × (Сумма длин параллельных сторон) × h = ½ × (AB + CD) × h
Эти практические вопросы помогут вам закрепить свойства трапеции
Свойства четырехугольника
В таблице ниже суммированы все свойства четырехугольников, которые мы изучили до сих пор:
| Свойства четырехугольника | Прямоугольник | Квадрат | Параллелограмм | Ромб | Трапеция | ||||||
| Все стороны равны | ✖ | 902 902 902 902 ✔ | 2 902 902 902 ✔2 902 Стороны равны✔ | ✔ | ✔ | ✔ | ✖ | ||||
| Противоположные стороны параллельны | ✔ | ✔ | ✔ | 902✔ | ✔ | ✔ | ✖ | ✖ | ✖ | ||
| Противоположные углы равны | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ двух смежных углов | ✔ | ✔ | ✔ | ✔ | ✖ |
| Разделить пополам | ✔ 9022 0 | ✔ | ✔ | ✔ | ✖ | ||||||
| Перпендикулярно пополам | ✖ | ✔ | ✖ | ✔ | 0 ✖3✔ | 0 ✖3
Важные формулы четырехугольника
В таблице ниже приведены формулы площади и периметра четырехугольников различных типов:
| Формулы четырехугольника | Прямоугольник | Квадрат | Параллелограмм | Ромб | Ромб 902 902 902 9019 9019 9035 902 902 902 902 902 902
Дополнительная литература: Четырехсторонние вопросыПопрактикуемся в применении свойств четырехугольника на следующих типовых вопросах: Вопрос 1 Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров.
РешениеШаг 1: Дано
Шаг 2: найти
Шаг 3: подход и разработка Забор можно строить только вокруг внешней стороны сада.
Следовательно, необходимая длина забора — 50 метров. Следовательно, вариант E — правильный ответ. Вопрос: 2Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стены — 1,5 доллара за квадратный метр. Если стена 25 метров в длину и 18 метров в ширину, то какова общая стоимость покраски стены?
РешениеШаг 1: Дано
Шаг 2: найти
Шаг 3: подход и разработка
Следовательно, правильный ответ — вариант E. Мы надеемся, что к настоящему времени вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти концепции для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить доступ бесплатно, зарегистрировавшись здесь. Вот еще несколько статей по математике:
Часто задаваемые вопросыКакие бывают четырехугольники?Существует 5 типов четырехугольников: прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб. Где я могу найти несколько практических вопросов по четырехугольникам?В этой статье вы можете найти несколько практических вопросов о четырехугольниках. Какова сумма внутренних углов четырехугольника?Сумма внутренних углов четырехугольника равна 360 °. Математические формулы, практические вопросы и примеры по недвижимости Математика по недвижимости — важная часть экзамена по недвижимости и важная концепция, которую необходимо понять, чтобы сделать успешную карьеру в сфере недвижимости. Сколько стоит математика на экзамене по недвижимости?Независимо от того, в каком штате вы хотите получить лицензию на недвижимость, вы можете ожидать, что на экзамене вы увидите вопросы по математике. Хотя количество вопросов по математике на экзамене варьируется от штата к штату, общее количество вопросов, связанных с математикой, составляет где-то между 10-15%. Как математика используется в недвижимости? Хотя вам, возможно, не придется использовать математику каждый день в качестве агента по недвижимости, вы должны быть готовы к возникновению проблем, требующих глубокого понимания концепций математики в сфере недвижимости.Примеры математических понятий, которые должны знать агентов по недвижимости, следующие: .
Сложная ли математика в сфере недвижимости? Математика недвижимости — это НЕ сложно. Многие студенты боятся изучать математику и использовать математику в своей карьере, однако математика в сфере недвижимости не является сложной задачей, и вам нужно усвоить лишь несколько концепций. Чем больше практики и времени потратите на понимание математических задач и понятий, которые вы можете увидеть, тем лучше вы будете сдавать экзамен и на протяжении всей своей карьеры. Математические определения недвижимостиСловарь основных арифметических навыков
Узнайте больше об основах математики в сфере недвижимости в нашем курсе «Принципы в сфере недвижимости». Преобразование единиц измерения Умение понимать размеры поможет вам заложить прочную основу для того, чтобы стать экспертом на протяжении всей вашей карьеры в сфере недвижимости. Преобразование линейных измерений
Измерения площади Размеры площади даны в различных единицах.
Измерение объема Как и в случае с другими средствами измерения предметов, объем пространства или объекта может быть выражен множеством различных способов.
Диаграмма кубических футов Пример задачи измеренияВашему клиенту необходимо арендовать климат-контроль, застрахованный и таможенный склад на 6 месяцев для хранения 500 поддонов строительных инструментов от крупнейшего производителя инструментов в Китае, каждый полный поддон имеет высоту 4 фута на 5 футов 8 футов и все термоусадочные. завернутый в промышленный пластик.Единственная доступная площадь в городе сдается за 22,5 цента за кубический фут в месяц. Сколько стоит место?
Дроби, десятичные дроби и процентыДроби Дробь — это часть чего-то. Десятичные знакиДроби также выражаются десятичными знаками. Дробь ¼ может быть выражена как 0,25, дробь ½ также выражается как 0,5, ¾ как 0,75 и так далее. Как преобразовать дробь в десятичную? Просто разделив верхнее число (числитель) на нижнее число (знаменатель). Чтобы преобразовать ¾ в эквивалентную десятичную дробь: 3 ÷ 4 = 0,75 Как агент по недвижимости или РИЭЛТОР® и на экзамене на лицензию вы будете использовать калькулятор, а не карандаш и бумагу, поэтому вы почти всегда обнаружите, что перед вычислениями проще переводить дроби в десятичные. Калькуляторы основаны на десятичных точках, а не на дробях. Вы можете ввести 1,25 на калькуляторе; вы не можете ввести 1 ¼. В процентахПроцент — это выражение, означающее на сотню или на сотку.Следовательно, если вы говорите «3%», вы говорите, что измеряемый элемент был разделен на 100 частей, а часть, которую вы описываете, состоит из трех из этих 100 частей. Расположение десятичной точки в номере важно:
Решение проблем в процентахЕсть три формулы, которые важны для решения всех процентных задач.
Еще один способ запомнить эти формулы — подумать:
Метод Т-образной балкиМногие студенты, изучающие недвижимость, не чувствуют себя комфортно с 3 формулами, используемыми для решения процентных задач, поэтому другой способ приблизиться к этому — визуализировать букву «Т», буква «Т» будет представлять взаимосвязь между ЧАСТЬ, ИТОГО и СТАВКА. Этот метод известен как метод Т-образного стержня. Используя метод Т-образного стержня, вставьте известные фигуры в правильные места внутри круга.Умножьте, если линия между цифрами вертикальная, чтобы получить неизвестное, и разделите, если линия между цифрами горизонтальная, чтобы получить неизвестное. При делении всегда сначала вводите ЧАСТЬ в калькулятор. Математика недвижимости, метод Т-образного стержня Математические формулы для недвижимости Математические формулы — важный компонент для сдачи экзамена и становления успешным брокером по недвижимости или торговым агентом. Соотношение кредита к стоимости (LTV)Коэффициент LTV = APV ÷ MA APV = Оценочная стоимость недвижимости Формула простого процентаА = P (1 + RT) A = Общая начисленная сумма (основная сумма + проценты) Множитель валовой ренты Множитель валовой арендной платы = Цена собственности ÷ Годовой валовой доход от аренды Калькулятор множителя валовой ренты Формулы налога на имущество Ставка налога на имущество = Оценочная стоимость × Миллионная ставка Формулы дисконтных баллов дисконтных балла = предоплата Формула «Практическое правило ипотечного кредитования» (правило 28/36) Расходы на жилье для получения большинства ссуд = Валовой ежемесячный или годовой доход ×. ПроецированиеПроецирование — это название, которое мы даем справедливому разделению затрат и выгод финансовой операции. В контексте недвижимости мы имеем дело с большими числами и разделяем такие вещи, как налоги на недвижимость, сборы ассоциации домовладельцев, арендная плата, выплачиваемая арендаторами, и так далее, но концепция остается той же. Вопрос в том, кто за что платит, и процесс пропорционального распределения помогает принять это решение. При закрытии различные позиции распределяются пропорционально, и некоторые комиссии часто распределяются между покупателем, продавцом и брокерами.Другими словами, общая сумма должна быть пропорционально распределена или распределена в соответствии с пропорциональным распределением, как и упомянутые выше файлы cookie. Типичные статьи расходов, подлежащие пропорциональному распределению, включают налоги на недвижимость, ежемесячные проценты, подлежащие уплате при получении займов, арендную плату и сборы домовладельцев. Распределение процентов по ссудамПроценты почти всегда выплачиваются в просрочку (выплачиваются в конце периода). Другими словами, когда вы вносите платеж по ипотеке первого числа месяца, вы платите процентную часть за предыдущий месяц. Проценты по новой ссуде рассчитываются путем умножения основной суммы остатка на процентную ставку и последующего деления на 365 дней. Пример пропорционального распределения процентов по ссудеПокупатель получает новый заем в размере 150 000,00 долларов США под 8% годовых.
Пришло время начать практиковатьПринципы в сфере недвижимости — Глава 8: Обзор математики в сфере недвижимости Сводное видео Автор и издатель: VanEd Иллюстративная математикаИллюстративная математика7 класс
7.RP. 7 класс — Соотношения и пропорциональные отношения7.RP.A. Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.7.RP.A.1. Вычислите удельные скорости, связанные с соотношением долей, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит 1/2-долларовую милю за каждый 1/4-долларовый час, вычислите удельную скорость как сложную долю $ \ frac {1/2} {1/4} $ миль в час, что эквивалентно 2 $ милям. в час.7. RP.A.2. Признать и представить пропорциональные отношения между количествами. RP.A.2. Признать и представить пропорциональные отношения между количествами.7.RP.A.2.a. Решите, находятся ли две величины в пропорциональном отношении, например, проверив эквивалентные отношения в таблице или построив график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.7.RP.A.2.b. Определите константу пропорциональности (единицу измерения) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.7.RP.A.2.c. Изобразите пропорциональные отношения уравнениями. Например, если общая стоимость $ t $ пропорциональна количеству $ n $ товаров, купленных по постоянной цене $ p $, соотношение между общей стоимостью и количеством товаров может быть выражено как $ t = pn $.7.RP.A.2.d. Объясните, что означает точка $ (x, y) $ на графике пропорциональной зависимости в терминах ситуации, уделяя особое внимание точкам $ (0, 0) $ и $ (1, r) $, где $ r $ это удельная ставка. 7.RP.A.3. Используйте пропорциональные отношения для решения многоступенчатых соотношений и процентных задач. Примеры: простые проценты, налог, наценки и уценки, чаевые и комиссии, сборы, увеличение и уменьшение процентов, ошибка в процентах.
7.NS. 7 класс — Система счисления7.NS.A. Применяйте и расширяйте предыдущие представления об операциях с дробями для сложения, вычитания, умножения и деления рациональных чисел.7.NS.A.1. Применяйте и расширяйте предыдущие представления о сложении и вычитании для сложения и вычитания рациональных чисел; представляют собой сложение и вычитание на горизонтальной или вертикальной числовой линейной диаграмме.7.NS.A.1.a. Опишите ситуации, в которых противоположные количества объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что его две составляющие заряжены противоположно. 7.NS.A.1.b. Под $ p + q $ понимается число, расположенное на расстоянии $ | q | $ от $ p $ в положительном или отрицательном направлении в зависимости от того, положительное или отрицательное значение $ q $. Докажите, что сумма числа и его противоположности равна 0 (аддитивно противоположны). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.7.NS.A.1.c. Под вычитанием рациональных чисел понимается добавление аддитивного обратного, $ p — q = p + (-q) $. Покажите, что расстояние между двумя рациональными числами на числовой прямой является абсолютной величиной их разницы, и примените этот принцип в контексте реального мира.7.NS.A.1.d. Применяйте свойства операций как стратегии для сложения и вычитания рациональных чисел.7. NS.A.2. Применяйте и расширяйте предыдущие представления об умножении и делении, а также о дробях для умножения и деления рациональных чисел. NS.A.2. Применяйте и расширяйте предыдущие представления об умножении и делении, а также о дробях для умножения и деления рациональных чисел.7.NS.A.2.a. Поймите, что умножение расширяется от дробей до рациональных чисел, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $ (- 1) (- 1) = 1 $ и правилам умножения со знаком. числа.Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.7.NS.A.2.b. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если $ p $ и $ q $ — целые числа, то $ — (p / q) = (-p) / q = p / (- q) $. Интерпретируйте частные рациональных чисел, описывая контексты реального мира.7.NS.A.2.c. Применяйте свойства операций как стратегии умножения и деления рациональных чисел.7.NS.A.2.d. Преобразуйте рациональное число в десятичное с помощью длинного деления; знайте, что десятичная форма рационального числа оканчивается нулями или в конечном итоге повторяется.7.NS.A.3. Решайте реальные и математические задачи, используя четыре операции с рациональными числами.
7.EE. 7 класс — Выражения и уравнения7.Э.А. Используйте свойства операций для создания эквивалентных выражений.7.EE.A.1. Применяйте свойства операций как стратегии для сложения, вычитания, разложения и расширения линейных выражений с рациональными коэффициентами.7.EE.A.2. Поймите, что переписывание выражения в разных формах в контексте проблемы может пролить свет на проблему и на то, как соотносятся количества в ней. Например, $ a + 0,05a = 1.05a $ означает, что «увеличить на $ 5 \% $» — это то же самое, что «умножить на $ 1.05 $. »7. EE.B. Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения. EE.B. Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.7.EE.B.3. Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически. Применяйте свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки.Например: если женщина, зарабатывающая $ \ $ 25 $ в час, получает прибавку в $ 10 \% $, она будет получать дополнительную $ \ frac {1} {10} $ из своей зарплаты в час, или $ \ $ 2.50 $, за новая зарплата $ 27,50 $. Если вы хотите разместить полотенцесушитель длиной $ 9 \ frac34 $ дюймов в центре двери шириной $ 27 \ frac12 $ дюймов, вам нужно будет разместить планку на расстоянии примерно 9 $ дюймов от каждого края; эту оценку можно использовать как проверку точного вычисления. 7.EE.B.4. Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения проблем, рассуждая о величинах.7.EE.B.4.a. Решите задачи со словами, приводящие к уравнениям вида $ px + q = r $ и $ p (x + q) = r $, где $ p $, $ q $ и $ r $ — конкретные рациональные числа. Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определив последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника составляет 54 доллара за см. Его длина — 6 $ см. Какая у него ширина?7.EE.B.4.b. Решите проблемы со словами, приводящие к неравенствам вида $ px + q> r $ или $ px + q
7.G. 7 класс — Геометрия7. Г.А. Рисуйте, конструируйте и описывайте геометрические фигуры и описывайте отношения между ними.7.G.A.1. Решение проблем, связанных с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей на основе масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе.7.G.A.2. Нарисуйте (от руки, линейкой и транспортиром, а также техникой) геометрические фигуры в заданных условиях.Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.7.G.A.3. Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид. 7. г. Решайте реальные и математические задачи, касающиеся измерения угла, площади, площади поверхности и объема.7.G.B.4. Знать формулы площади и окружности круга и использовать их для решения задач; дают неформальный вывод отношения между окружностью и площадью круга.7.G.B.5. Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла на фигуре.7.G.B.6. Решайте реальные и математические задачи, связанные с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
7.SP. 7 класс — Статистика и вероятность7.SP.A. Используйте случайную выборку, чтобы делать выводы о популяции. 7.SP.A.1. Поймите, что статистику можно использовать для получения информации о совокупности, исследуя ее выборку; Обобщения о генеральной совокупности из выборки действительны только в том случае, если выборка является репрезентативной для этой генеральной совокупности.Поймите, что случайная выборка имеет тенденцию давать репрезентативные выборки и поддерживать достоверные выводы.7.SP.A.2. Используйте данные из случайной выборки, чтобы сделать выводы о популяции с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы измерить вариации оценок или прогнозов. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; прогнозировать победителя школьных выборов на основе данных случайно выбранных опросов.Оцените, насколько далеко может быть оценка или прогноз.7.SP.B. Сделайте неформальные сравнительные выводы о двух популяциях. 7.SP.B.3. Неформально оцените степень визуального перекрытия двух распределений числовых данных с аналогичной изменчивостью, измеряя разницу между центрами, выражая ее как кратное от меры изменчивости. Например, средний рост игроков в баскетбольной команде на 10 см больше, чем средний рост игроков в футбольной команде, что примерно в два раза больше вариабельности (среднего абсолютного отклонения) в любой команде; на точечной диаграмме различие между двумя распределениями высот заметно.7.SP.B.4. Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух популяциях. Например, решите, являются ли слова в главе учебника по естествознанию для седьмого класса обычно длиннее, чем слова в главе учебника по естествознанию для четвертого класса.7.SP.C. Исследуйте случайные процессы, а также разрабатывайте, используйте и оценивайте вероятностные модели. 7.SP.C.5. Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность того, что событие произойдет. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие.7.SP.C.6. Оцените вероятность случайного события, собрав данные о случайном процессе, который его производит, и наблюдая за его относительной частотой в долгосрочном периоде, и спрогнозируйте приблизительную относительную частоту с учетом вероятности.Например, бросая кубик с числами 600 раз, предположите, что число 3 или 6 будет брошено примерно 200 раз, но, вероятно, не ровно 200 раз.7.SP.C.7. Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности модели с наблюдаемыми частотами; если согласие плохое, объясните возможные источники расхождения. Сравните вероятности модели с наблюдаемыми частотами; если согласие плохое, объясните возможные источники расхождения.7.SP.C.7.a. Разработайте единую вероятностную модель, назначив равную вероятность всем исходам, и используйте модель для определения вероятностей событий.Например, если ученик выбран случайным образом из класса, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка.7.SP.C.7.b. Разработайте вероятностную модель (которая может быть неоднородной), наблюдая за частотами в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что вращающийся пенни упадет орлом вверх или брошенный бумажный стаканчик упадет открытым концом вниз. Являются ли результаты для вращающегося пенни одинаково вероятными на основе наблюдаемых частот?7.SP.C.8. Найдите вероятности сложных событий, используя организованные списки, таблицы, древовидные диаграммы и моделирование. Найдите вероятности сложных событий, используя организованные списки, таблицы, древовидные диаграммы и моделирование.7.SP.C.8.a. Поймите, что, как и в случае с простыми событиями, вероятность составного события — это доля результатов в пространстве выборки, для которых возникает составное событие.7.SP.C.8.b. Представляйте образцы пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы.Для события, описываемого повседневным языком (например, «катящиеся двойные шестерки»), определите результаты в пространстве выборки, которые составляют событие.7.SP.C.8.c. Разработайте и используйте моделирование для генерации частот для сложных событий. Например, используйте случайные цифры в качестве инструмента моделирования, чтобы приблизиться к ответу на вопрос: если 40% доноров имеют кровь типа A, какова вероятность того, что потребуется по крайней мере 4 донора, чтобы найти одного с кровью типа A?Бесплатные рабочие листы по линейным уравнениям (6-9 классы, предалгебра, алгебра 1)Вы здесь: Главная → Рабочие листы → Линейные уравненияЗдесь вы найдете неограниченное количество распечатываемых рабочих листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Вы можете настроить рабочие листы, включив в них одношаговые, двухэтапные или многоступенчатые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Рабочие листы подходят к курсам предварительной алгебры и алгебры 1 (6-9 классы). Вы можете выбрать из СЕМЬ основных типов уравнений, от простых до сложных, описанных ниже (например, одношаговые уравнения, переменные с обеих сторон или необходимость использования свойства распределения). Настройте рабочие листы, используя генератор ниже. Основные инструкции к рабочим листам Каждый рабочий лист генерируется случайным образом и поэтому уникален. Вы можете создавать рабочие листы либо в формате html, либо в формате PDF — и то, и другое легко распечатать.Чтобы получить рабочий лист PDF, просто нажмите кнопку с названием « Создать PDF » или « Создать рабочий лист PDF ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Просмотреть в браузере » или « Сделать html-лист ». Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе. Иногда сгенерированный рабочий лист не совсем то, что вам нужно.Просто попробуйте еще раз! Чтобы получить другой рабочий лист с теми же параметрами:
Рабочие листы готовыеСм. Также ТакжеРабочие листы для упрощения выражений Рабочие листы для вычисления выражений с переменными Рабочие листы для написания выражений с переменными из словесных выражений Рабочие листы для линейных неравенств Ключ к учебным пособиям по алгебре Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй.Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 вводят рациональные числа и выражения. Книги 8-10 охватывают реальную систему счисления. => Узнать больше Введение, формула, свойства, решаемые примеры и часто задаваемые вопросыЧто такое полукруг?
Пунктирными линиями обозначена окружность. Что вы подразумеваете под периметром полукруга?
где, R = радиус полукруга. π = Константа с именем Пи, приблизительно равная 3.2} \]. Что вы имеете в виду под окружностью полукруга?где, R = радиус полукруга. Π = Константа с именем Пи, приблизительно равная 3,142. Единица измерения длины полукруга — м или см. Что вы подразумеваете под углом, вписанным в полукруг?
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Периметр формулы полукруга | \ [R \ left ({\ pi — 2} \ right) \] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формула окружности полукруга | \ [2 \ pi R \] |
ВОПРОСЫ
Вопрос 1
Диаметр полукруга составляет 100 метров. Найдите периметр полукруга по формуле полукруга.
Найдите периметр полукруга по формуле полукруга.
Решение
Перечислим данную информацию,
Диаметр = 100 м
Периметр =?
Формула для вычисления периметра полукруга: \ [R \ left ({\ pi — 2} \ right) \]
Нам нужно R для вычисления периметра полукруга,
\ [Radius = \ frac { {Диаметр}} {2} = \ frac {{100}} {2} = 50 {\ text {}} метр \]
\ [\ Pi = 3.142 \]
Таким образом, периметр = 50 (3,142 + 2) = 257,1 см.
Вопрос 2
Школьная баскетбольная площадка Рии состоит из двух полукругов на каждом конце. Полукруги имеют радиус 6 футов. Каков периметр одного полукруга корта?
Решение
Перечислим данную информацию,
Радиус = 6 футов
\ [\ Pi = 3,142 \].
Периметр =?
Формула для вычисления периметра полукруга: \ [R \ left ({\ pi — 2} \ right) \]
Следовательно, периметр полукруга на одном конце площадки равен 6 (3. 142 + 2) = 30,72 см
142 + 2) = 30,72 см
Вопрос 3
Окружность, показанная ниже на рисунке 2.1, имеет диаметр 8 см. Найдите следующее:
Решение
Перечислим данную информацию,
Диаметр = 8 см
Периметр =?
Площадь =?
Используя формулу периметра полукруга, то есть \ [R \ left ({\ pi — 2} \ right) \]
Нам нужно R для вычисления периметра,
\ [Radius = \ frac {{Диаметр}] } {2} = \ frac {8} {2} = 8 {\ text {}} см \]
\ [\ Pi = 3.2} \]
Вопрос 5
Найдите длину окружности полукруга диаметром 7 см.
Решение
Перечислим данную информацию,
Диаметр = 7 см
Окружность =?
\ [Радиус = \ frac {{Диаметр}} {2} = \ frac {7} {2} = 3,5 {\ text {}} см \]
\ [\ Pi = 3.142 \]
Окружность круг = \ [2 \ пи \ раз R \]
Следовательно, окружность круга = \ [3. 142 \; \ times 3,5 \ times 2 = {\ text {}} 21.944 {\ text {}} см \]
142 \; \ times 3,5 \ times 2 = {\ text {}} 21.944 {\ text {}} см \]
Вопрос 6
У Джорджа есть сад перед его домом, имеющий форму круга диаметром 10 ярдов. Джордж хочет ограждать ровно половину сада. Найдите периметр части, которую он хочет ограждать.
Решение
Перечислим данную информацию,
Диаметр = 10 см
Периметр =?
Формула для вычисления периметра полукруга: \ [R \ left ({\ pi + 2} \ right) \]
Нам нужно R для вычисления периметра,
\ [Radius = \ frac {{Диаметр }} {2} = \ frac {{10}} {2} = 5 {\ text {}} см \]
\ [\ Pi = 3.142 \]
Следовательно, периметр = 5 (3,142 + 2) = 25,71 см
Стандартные математические стандарты седьмого класса Common Core
7.Соотношение цены и пропорции
7.
 RP.A Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.
RP.A Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.7.RP.A.1 Вычислить удельные скорости, связанные с соотношениями долей, включая соотношения длин, площадей и других величин, измеренных в одинаковых или разных единицах.
7.RP.A.2 Распознавать и представлять пропорциональные отношения между количествами.
7.RP.A.2a Решите, находятся ли две величины в пропорциональной зависимости, например, проверив эквивалентные отношения в таблице или построив график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
7.RP.A.2b. Определите константу пропорциональности (удельная ставка) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.
7.
 RP.A.2c Изобразите пропорциональные отношения уравнениями.
RP.A.2c Изобразите пропорциональные отношения уравнениями.7.RP.A.2d Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, уделяя особое внимание точкам (0, 0) и (1, r), где r это удельная ставка.
7.RP.A.3 Используйте пропорциональные отношения для решения многоступенчатых соотношений и процентных задач.
7.NS Система счисления
7.NS.A Применяйте и расширяйте предыдущие представления об операциях с дробями для сложения, вычитания, умножения и деления рациональных чисел.
7.NS.A.1 Применять и расширять предыдущие представления о сложении и вычитании для сложения и вычитания рациональных чисел; представляют собой сложение и вычитание на горизонтальной или вертикальной числовой линейной диаграмме.

7.NS.A.1a Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0.
7.NS.A.1b Под p + q понимается число, расположенное на расстоянии | q | от p, в положительном или отрицательном направлении, в зависимости от того, является ли q положительным или отрицательным. Докажите, что сумма числа и его противоположности равна 0 (аддитивно противоположны). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
7.NS.A.1c Под вычитанием рациональных чисел понимается добавление обратного аддитивного числа, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой является абсолютной величиной их разницы, и примените этот принцип в контексте реального мира.
7.NS.A.1d Применяйте свойства операций как стратегии для сложения и вычитания рациональных чисел.

7.NS.A.2 Применяйте и расширяйте предыдущие представления об умножении, делении и дробях для умножения и деления рациональных чисел.
7.NS.A.2a Поймите, что умножение расширяется от дробей до рациональных чисел, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (-1) (- 1) = 1 и правила умножения чисел со знаком. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
7.NS.A.2b Поймите, что целые числа можно делить, при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом.Если p и q целые числа, то — (p / q) = (-p) / q = p / (- q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
7.
 NS.A.2c Применяйте свойства операций как стратегии умножения и деления рациональных чисел.
NS.A.2c Применяйте свойства операций как стратегии умножения и деления рациональных чисел.7.NS.A.2d Преобразование рационального числа в десятичное с помощью длинного деления; знайте, что десятичная форма рационального числа оканчивается нулями или в конечном итоге повторяется.
7.NS.A.3 Решение реальных и математических задач, включающих четыре операции с рациональными числами.
- Завершите уравнения сложения и вычитания с целыми числами (7-C.13)
- Сложение и вычитание целых чисел: задачи со словами (7-C.14)
- Полные уравнения умножения и деления с целыми числами (7-C.22)
- Сложить, вычесть, умножить и разделить целые числа (7-C.23)
- Сложение и вычитание десятичных знаков: проблемы со словами (7-E.
 2)
2) - Умножение десятичных и целых чисел: проблемы со словами (7-E.4)
- Разделите десятичные дроби на целые числа: проблемы со словами (7-E.6)
- Сложение, вычитание, умножение и деление десятичных знаков: проблемы со словами (7-E.8)
- Сложение и вычитание дробей: задачи со словами (7-G.2)
- Сложение и вычитание смешанных чисел: задачи со словами (7-G.4)
- Умножение дробей и смешанных чисел: задачи со словами (7-G.11)
- Разделите дроби и смешанные числа: задачи со словами (7-G.14)
- Сложение, вычитание, умножение и деление дробей и смешанных чисел: проблемы со словами (7-G.16)
- Сложить, вычесть, умножить и разделить денежные суммы: задачи со словами (7-M.
 1)
1) - Прайс-листы (7-M.2)
- Оценка для решения задач со словами (7-N.1)
7.EE Выражения и уравнения
7.EE.A Используйте свойства операций для создания эквивалентных выражений.
7.EE.A.1 Применяйте свойства операций как стратегии для сложения, вычитания, разложения и расширения линейных выражений с рациональными коэффициентами.
7.EE.A.2 Поймите, что переписывание выражения в различных формах в контексте проблемы может пролить свет на проблему и на то, как соотносятся количества в ней.
7.EE.B Решение реальных и математических задач с помощью числовых и алгебраических выражений и уравнений.
7.
 EE.B.3 Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически.Применяйте свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки.
EE.B.3 Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически.Применяйте свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки.7.EE.B.4. Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения проблем, рассуждая о величинах.
7.EE.B.4a Решите задачи со словами, приводящие к уравнениям вида px + q = r и p (x + q) = r, где p, q и r — конкретные рациональные числа. Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определив последовательность операций, используемых в каждом подходе.
7.
 EE.B.4b Решите проблемы со словами, приводящие к неравенствам вида px + q> r или px + q.
EE.B.4b Решите проблемы со словами, приводящие к неравенствам вида px + q> r или px + q.
7.G геометрия
7.G.A. Рисуйте, конструируйте и описывайте геометрические фигуры и описывайте отношения между ними.
7.G.A.1. Решение задач, связанных с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей на основе масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе.
7.G.A.2 Нарисуйте (от руки, линейкой, транспортиром и технологией) геометрические фигуры в заданных условиях.Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
7.
 G.A.3. Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.
G.A.3. Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.
7.G.B Решение реальных и математических задач, связанных с измерением угла, площади, площади поверхности и объема.
7.G.B.4 Знать формулы площади и длины окружности и использовать их для решения задач; дают неформальный вывод отношения между окружностью и площадью круга.
7.G.B.5 Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла на фигуре.
7.G.B.6 Решение реальных и математических задач, касающихся площади, объема и площади поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.

7.SP Статистика и вероятность
7.SP.A Используйте случайную выборку, чтобы делать выводы о совокупности.
7.SP.A.1 Понимать, что статистику можно использовать для получения информации о совокупности, исследуя ее выборку; Обобщения о генеральной совокупности из выборки действительны только в том случае, если выборка является репрезентативной для этой генеральной совокупности.Поймите, что случайная выборка имеет тенденцию давать репрезентативные выборки и поддерживать достоверные выводы.
7.SP.A.2 Используйте данные случайной выборки, чтобы сделать выводы о популяции с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы измерить вариации оценок или прогнозов.
7.
 SP.B Сделайте неформальные сравнительные выводы о двух популяциях.
SP.B Сделайте неформальные сравнительные выводы о двух популяциях.7.SP.B.3 Неформально оценить степень визуального перекрытия двух распределений числовых данных с аналогичной изменчивостью, измерив разницу между центрами, выразив ее как кратное от меры изменчивости.
7.SP.B.4 Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух популяциях.
- Вычислить среднее значение, медианное значение, режим и диапазон (7-CC.1)
- Интерпретируйте диаграммы и графики, чтобы найти среднее значение, медиану, режим и диапазон (7-CC.2)
- Среднее значение, медиана, мода и диапазон: найдите недостающее число (7-CC.3)
- Изменения среднего, медианного значения, режима и диапазона (7-CC.4)
7.SP.C Исследование случайных процессов, разработка, использование и оценка вероятностных моделей.
7.SP.C.5 Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность того, что событие произойдет. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие.
7.SP.C.6 Приблизить вероятность случайного события, собрав данные о случайном процессе, который его вызывает, и наблюдая его долгосрочную относительную частоту, и спрогнозировать приблизительную относительную частоту с учетом вероятности.
7.SP.C.7 Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности модели с наблюдаемыми частотами; если согласие плохое, объясните возможные источники расхождения.
7.SP.C.7a Разработайте единую вероятностную модель, назначив равную вероятность всем исходам, и используйте модель для определения вероятностей событий.
7.SP.C.7b Разработайте вероятностную модель (которая может быть неоднородной), наблюдая за частотами в данных, полученных в результате случайного процесса.
7.SP.C.8 Найдите вероятности сложных событий, используя организованные списки, таблицы, древовидные диаграммы и моделирование.
7.SP.C.8a Поймите, что, как и в случае с простыми событиями, вероятность составного события — это доля исходов в пространстве выборки, для которых возникает составное событие.
7.SP.C.8b. Представьте образцы пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы. Для события, описываемого повседневным языком (например, «катящиеся двойные шестерки»), определите результаты в пространстве выборки, которые составляют событие.
7.SP.C.8c Разработайте и используйте моделирование для генерации частот для сложных событий.
Общие основные государственные стандарты © Copyright 2010.Центр передового опыта Национальной ассоциации губернаторов и Совет директоров государственных школ. Все права защищены.
Какие формулы приведены в разделе SAT Math?
Подготовка к SAT может стать стрессом как для учащихся, так и для родителей. В конце концов, результаты SAT могут иметь огромное влияние на будущий успех старшеклассника, влияя на его способность поступать в лучшие колледжи и даже выигрывать гранты и стипендии.Из-за того, что так много предстоит изучить как по чтению, так и по математике, семьи часто остаются ошеломленными и не понимают, с чего начать.
Хотя репетиторство по SAT может помочь облегчить бремя, учащиеся также должны самостоятельно покопаться, чтобы определить, какую информацию они делают и не должны запоминать перед важным днем. Прочтите, чтобы узнать, какие формулы предлагаются студентам в разделе SAT Math, чтобы ваш ученик не тратил время на запоминание информации, доступной им во время экзамена.
Подготовка к SAT Math РазделМатематический раздел теста SAT предназначен для оценки понимания учащимися тех математических понятий, которые с наибольшей вероятностью могут возникнуть в колледже. Текущий экзамен охватывает три различных области математики: сердце алгебры, решение проблем и анализ данных и переход к продвинутой математике. Цель состоит в том, чтобы определить, могут ли учащиеся применить то, чему они научились в средней школе, для решения реальных задач с помощью комбинации вопросов с множественным выбором и вопросов с сеткой ответов.
Несмотря на то, что SAT предназначен для измерения того, что учащиеся уже знают, им не нужно запоминать все математические концепции и формулы, чтобы добиться успеха. Совет колледжа перечисляет 12 наиболее часто используемых геометрических формул в каждом разделе SAT Math, поэтому подросткам не нужно беспокоиться о том, чтобы запомнить их все. Вместо этого старшеклассники должны посвятить драгоценную память тем формулам алгебры и тригонометрии, которые не указаны на экзамене, и привыкнуть к знанию, где и когда использовать все вышеперечисленное.
Математические формулы в SATГотовитесь к SAT? Следующие 12 геометрических формул перечислены в разделах SAT Math:
1. Площадь кругаА = πr²
Эта формула показывает, что площадь круга равна π (или 3,14159…), умноженному на значение радиуса круга (r) в квадрате. Радиусом называется любая прямая линия, проведенная от центральной точки круга до края.
2. Окружность кругаC = πd или 2πr
Используемая для вычисления длины окружности или окружности, эта формула показывает, что C равно значению π (или 3,14159…), умноженному на диаметр (d). Диаметр относится к линии, которая делит окружность пополам через середину.
3. Площадь прямоугольникаA = lw
Площадь прямоугольника равна его длине (l), умноженной на его ширину (w).
4. Площадь треугольникаA = 1/2 bh
Найдите площадь треугольника, умножив длину основания (b) на длину высоты (h), а затем умножив полученную сумму на 1/2.
5. Теорема Пифагораa² + b² = c²
Важная формула для решения геометрических задач, теорема Пифагора, показывает, что для прямоугольного треугольника сумма квадратов двух меньших сторон равна квадрату большей стороны, известной как гипотенуза.

_5-1200x800.jpg) ФИО
ФИО Б. Суворова и др.
Б. Суворова и др.
 е., сдавая GMAT. Пройдите бесплатный тест GMAT, чтобы понять свой базовый результат, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
е., сдавая GMAT. Пройдите бесплатный тест GMAT, чтобы понять свой базовый результат, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub. Почему бы вам не начать подготовку к GMAT с помощью наших бесплатных подготовительных ресурсов и не начать свой путь к получению Q50-51 на GMAT. Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50.
Почему бы вам не начать подготовку к GMAT с помощью наших бесплатных подготовительных ресурсов и не начать свой путь к получению Q50-51 на GMAT. Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50.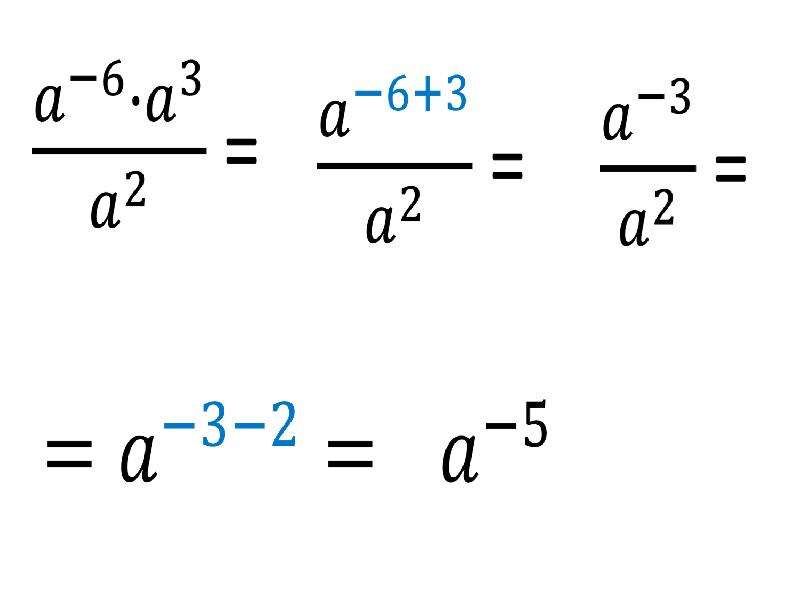

 Мы — самая обсуждаемая компания по подготовке к GMAT на gmatclub: мы получили более 2060 отзывов.
Мы — самая обсуждаемая компания по подготовке к GMAT на gmatclub: мы получили более 2060 отзывов.  Если вы станете экспертом по математике и сможете решать математические задачи по недвижимости, это поможет вам выделиться на рынке и стать лучшим агентом по недвижимости, а также значительно упростит сдачу экзамена по недвижимости.
Если вы станете экспертом по математике и сможете решать математические задачи по недвижимости, это поможет вам выделиться на рынке и стать лучшим агентом по недвижимости, а также значительно упростит сдачу экзамена по недвижимости.

 Например, в дроби 3/5 знаменатель 5. В числе 125 3/5 знаменатель 5. Этот термин относится только к нижнему числу дроби, а не к остальной части числа.
Например, в дроби 3/5 знаменатель 5. В числе 125 3/5 знаменатель 5. Этот термин относится только к нижнему числу дроби, а не к остальной части числа.
 Это упрощает сложение, вычитание и сравнение дробей.
Это упрощает сложение, вычитание и сравнение дробей.
 Ниже приведен список измерений и преобразований, которые вам нужно будет освоить.
Ниже приведен список измерений и преобразований, которые вам нужно будет освоить. Следующие формулы освежат ваши знания об этих единицах.
Следующие формулы освежат ваши знания об этих единицах.
 Дроби говорят нам, на сколько частей делится целое, а также с какими частями мы работаем.Например, в дроби ¼ нижнее число, называемое знаменателем, говорит нам, что предмет был разделен на 4 части; верхнее число, называемое числителем, говорит нам, что мы работаем с 1 из этих 4 частей.
Дроби говорят нам, на сколько частей делится целое, а также с какими частями мы работаем.Например, в дроби ¼ нижнее число, называемое знаменателем, говорит нам, что предмет был разделен на 4 части; верхнее число, называемое числителем, говорит нам, что мы работаем с 1 из этих 4 частей.

 Помните, что практика ведет к совершенству, поэтому чем больше времени вы потратите на запоминание этих формул, тем лучше вам будет.
Помните, что практика ведет к совершенству, поэтому чем больше времени вы потратите на запоминание этих формул, тем лучше вам будет. 28
28
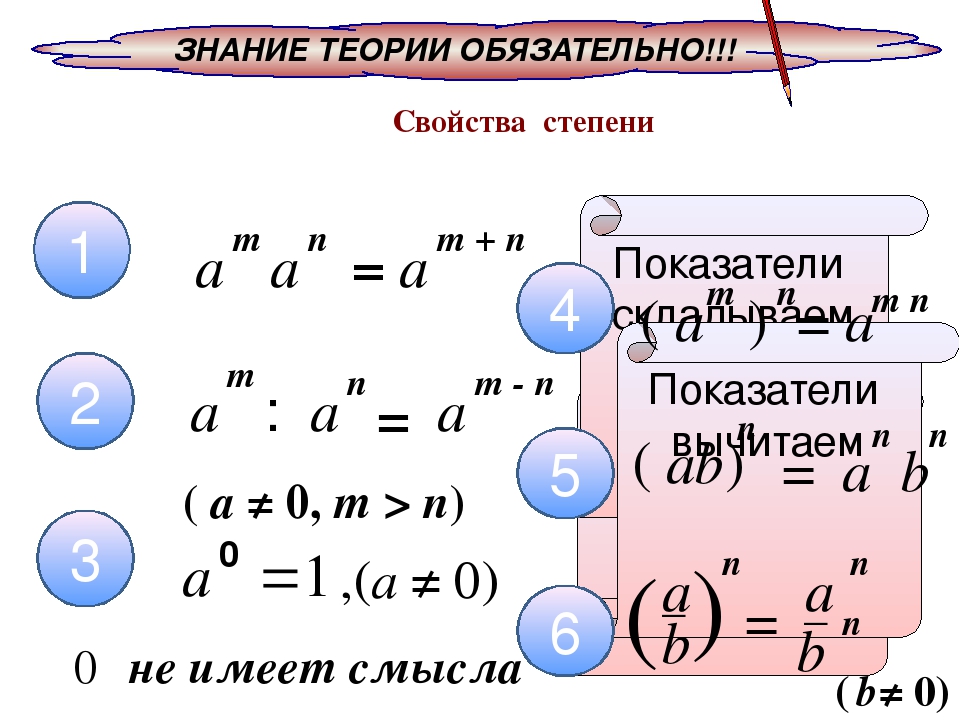 Таким образом, в июле Покупатель будет владеть недвижимостью в течение 17 дней.
Таким образом, в июле Покупатель будет владеть недвижимостью в течение 17 дней.

 Ключ ответа генерируется автоматически и помещается на вторую страницу файла.
Ключ ответа генерируется автоматически и помещается на вторую страницу файла.

 RP.A Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.
RP.A Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач. RP.A.2c Изобразите пропорциональные отношения уравнениями.
RP.A.2c Изобразите пропорциональные отношения уравнениями.

 NS.A.2c Применяйте свойства операций как стратегии умножения и деления рациональных чисел.
NS.A.2c Применяйте свойства операций как стратегии умножения и деления рациональных чисел. 2)
2) 1)
1) EE.B.3 Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически.Применяйте свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки.
EE.B.3 Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически.Применяйте свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки. EE.B.4b Решите проблемы со словами, приводящие к неравенствам вида px + q> r или px + q.
EE.B.4b Решите проблемы со словами, приводящие к неравенствам вида px + q> r или px + q. G.A.3. Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.
G.A.3. Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.
 SP.B Сделайте неформальные сравнительные выводы о двух популяциях.
SP.B Сделайте неформальные сравнительные выводы о двух популяциях.