Формулы сложения и вычитания для тангенса и котангенса
Формула сложения касательной
На предыдущей странице мы получили тождества сложения для синуса и косинуса:
\[\ грех \ влево ( {\ альфа + \ бета } \ вправо) = \ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета , \]
\[\cos \left( {\alpha + \beta} \right) = \cos \alpha \cos \beta — \sin \alpha \sin \beta .\]
Предположим теперь, что \(\cos \left( {\alpha + \beta } \right) \ne 0,\) или \(\alpha + \beta \ne \frac{\pi }{2} + \pi n ,\) \(n \in \mathbb{Z}.\) Кроме того, пусть также \(\cos \alpha \ne 0\) и \(\cos \beta \ne 0,\), т. е. \(\ alpha, \beta \ne \frac{\pi }{2} + \pi n,\) \(n \in \mathbb{Z},\), так что мы можем разделить на \(\cos\alpha\cos\ бета.\)
Тогда формула сложения тангенсов будет равна
\[\require{cancel} \tan \left({\alpha + \beta} \right) = \frac{{\sin \left({\alpha + \beta} \right)}}{{\cos\ слева ( {\ альфа + \ бета } \ справа)}} = \ гидроразрыва {{\ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета}} {{\ соз \ альфа \ соз \ бета — \ грех \ альфа \ грех \ бета}} = \ гидроразрыва {{\ гидроразрыва {{\ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета}} {{\ соз \ альфа \ соз \ бета}}} }{{\ frac {{\ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta}} {\ cos \ alpha \ cos \ beta}}}} = \ frac {{\ frac {{\ sin \alpha \cancel{\cos\beta}}}{{\cos\alpha\cancel{\cos\beta}}} + \frac{{\cancel{\cos\alpha}\sin\beta}}{{ \cancel{\cos\alpha}\cos\beta}}}}{{\frac{\cancel{\cos\alpha\cos\beta}}}{\cancel{\cos\alpha\cos\beta}} — \ frac {{\ sin \ alpha \ sin \ beta}} {{\ cos \ alpha \ cos \ beta}}}} = \ frac {{\ tan \ alpha + \ tan \ beta}} {{1 — \ tan \ альфа\тангенс\бета}}.
Следовательно,
\[\tan\left( {\alpha + \beta} \right) = \frac{\tan\alpha + \tan\beta}{1 — \tan\alpha\tan\beta}\]
Формула вычитания касательной
Функция тангенса нечетная:
\[\ тан \ влево ( { — \ бета } \ вправо) = \ гидроразрыва {{\ грех \ влево ( { — \ бета } \ вправо)}} {{\ соз \ влево ( { — \ бета } \ вправо )}} = \ frac {{ — \ sin \ beta }} {{\ cos \ beta }} = — \ tan \ beta .\]
Заменяя \(\beta \to -\beta\) в формуле сложения тангенсов, получаем формулу вычитания тангенсов:
\[\ tan \left( {\alpha — \beta} \right) = \frac{{\tan \alpha + \tan \left({ — \beta} \right)}}{{1 — \tan \ alpha \tan \left( { — \beta } \right)}} = \frac{{\tan \alpha — \tan \beta}}{{1 + \tan \alpha \tan \beta }}.\]
Таким образом,
\[\tan\left( {\alpha — \beta} \right) = \frac{\tan\alpha — \tan\beta}{1 + \tan\alpha\tan\beta}\]
Формула сложения котангенса
Аналогичным образом мы можем установить тождество сложения для котангенса.
Пусть \(\sin \left( {\alpha + \beta } \right) \ne 0,\), то есть \(\alpha + \beta \ne \pi n,\) \(n \in \mathbb {Z}.\) Мы также предполагаем, что \(\sin\alpha \ne 0\) и \(\sin\beta \ne 0,\) или \(\alpha ,\beta \ne \pi n,\) \(n \in \mathbb{Z},\), так что мы можем разделить на \(\sin\alpha\sin\beta.\)
Тогда у нас есть
\[\ кроватка \ влево ( {\ альфа + \ бета} \ вправо) = \ гидроразрыва {{\ соз \ влево ( {\ альфа + \ бета} \ вправо)}}} {{\ грех \ влево ( {\ альфа + \ beta } \ right)}} = \ frac {{\ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta}} {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ бета}} = \ гидроразрыва {{\ гидроразрыва {{\ соз \ альфа \ соз \ бета — \ грех \ альфа \ грех \ бета}} {{\ грех \ альфа \ грех \ бета}}}} {{\ гидроразрыва {{\ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета}} {{\ грех \ альфа \ грех \ бета}}}} = \ гидроразрыва {{\ гидроразрыва {{\ соз \ альфа \ соз \beta}}{{\sin\alpha\sin\beta}} — \frac{\cancel{\sin\alpha\sin\beta}}{\cancel{\sin\alpha\sin\beta}}}}{ {\ гидроразрыва {{\ отмена {\ грех \ альфа} \ соз \ бета}} {{\ отмена {\ грех \ альфа} \ грех \ бета}} + \ гидроразрыва {{\ соз \ альфа \ отмена {\ грех \ бета} }}{{\sin \alpha \cancel{\sin\beta} }}}} = \frac{{\cot \alpha \cot \beta — 1}}{{\cot \beta + \cot\alpha }}.
Мы получили следующий результат:
\[\cot\left( {\alpha + \beta} \right) = \frac{\cot\alpha\cot\beta — 1}{\cot\alpha + \cot\beta}\]
Котангенс суммы двух углов также может быть выражен через тангенсы:
\[\cot\left( {\alpha + \beta} \right) = \frac{1 — \tan\alpha\tan\beta}{\tan\alpha + \tan\beta}\]
Формула вычитания котангенса
Сначала заметим, что функция котангенса нечетна:
\[\ кроватка \ влево ( { — \ альфа } \ вправо) = \ гидроразрыва {{\ соз \ влево ( { — \ альфа } \ вправо)}} {{\ грех \ влево ( { — \ альфа} \ вправо )}} = \frac{{\cos \alpha}}{{ — \sin \alpha}} = — \cot \alpha .\]
Теперь мы можем легко вывести формулу вычитания котангенса. Получается заменой \(\beta\to-\beta\) в формуле сложения котангенсов:
\[\ раскладушка \ влево ({\ альфа — \ бета} \ справа) = \ гидроразрыва {{\ раскладушка \ альфа \ раскладушка \ влево ( { — \ бета} \ справа) — 1}} {{\ раскладушка \ альфа + \cot \left( { — \beta } \right)}} = \frac{{ — \cot \alpha \cot \beta — 1}}{{\cot \alpha — \cot \beta}} = \frac {{\cot \alpha \cot \beta + 1}}{{\cot \beta — \cot \alpha}}.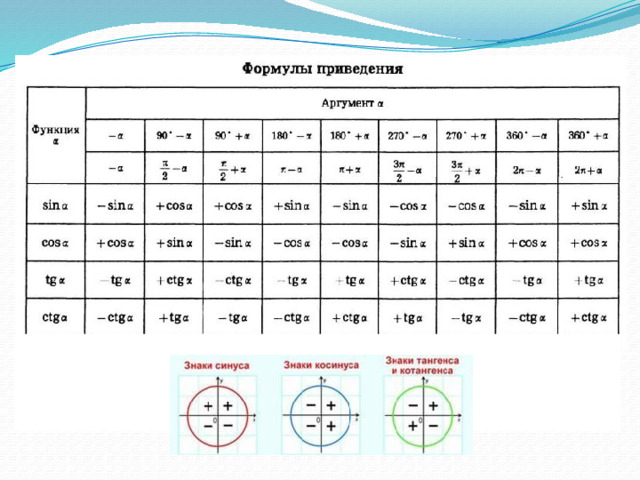 \]
\]
Итак, у нас есть
\[\cot\left( {\alpha — \beta} \right) = \frac{\cot\alpha\cot\beta + 1}{\cot\beta — \cot\alpha}\]
В терминах тангенсов формула вычитания котангенса имеет вид
\[\cot\left( {\alpha — \beta} \right) = \frac{1 + \tan\alpha\tan\beta}{\tan\alpha — \tan\beta}\]
См. решенные проблемы на стр. 2.
комплексный тангенс и котангенс
Функция тангенса и котангенса для комплексных значений z определяется уравнениями
| tanz:=sinzcosz,cotz:=coszsinz. |
Используя формулы Эйлера (http://planetmath.org/ComplexSineAndCosine), также можно определить
| tanz:=-ieiz-e-izeiz+e-iz,cotz:=ieiz+e-izeiz-e-iz. | (1) |
Формулы вычитания косинуса и синуса (http://planetmath.org/ComplexSineAndCosine) дают добавку между котангенсом и тангенсом:
кроватка(π2-z)=cos(π2-z)sin(π2-z)=cosπ2cosz+sinπ2sinzsinπ2cosz-cosπ2 sinz=sinzcosz=tanz. |
Таким образом, свойства тангенса легко выводятся из соответствующих свойств котангенса.
Из-за тождественного уравнения cos2z+sin2z=1 косинус и синус не обращаются в нуль одновременно, поэтому их частное cotz конечно во всех конечных точках z комплексной плоскости, кроме нулей z=n π (n=0,±1,±2,…) sinz, где cotz обращается в бесконечность. Мы увидим, что эти кратные π являются простыми полюсами cotz.
Если перейти от z к z + π, то и cosz, и sinz меняют знаки (ср. антипериодическая функция), и поэтому их частное остается неизменным. Соответственно, π — это период cotz. Но если ω — произвольный период cotz, мы имеем cot(z+ω)=cotz, и особенно z=0 дает cotω=∞; то (1) говорит, что eiω=e-iω, т.е. e2iω=1. Поскольку простой период комплексной показательной функции равен 2iπ, последнее уравнение справедливо только для значений ω=nπ (n=0,±1,±2,…). Таким образом, мы показали, что простой период cotz равен π.
Мы знаем, что
| sinzz=sinz-sin0z→cos0=1 as z→0; |
поэтому
zcotz=zsinz⋅cosz→1⋅cos0=1 as z→0.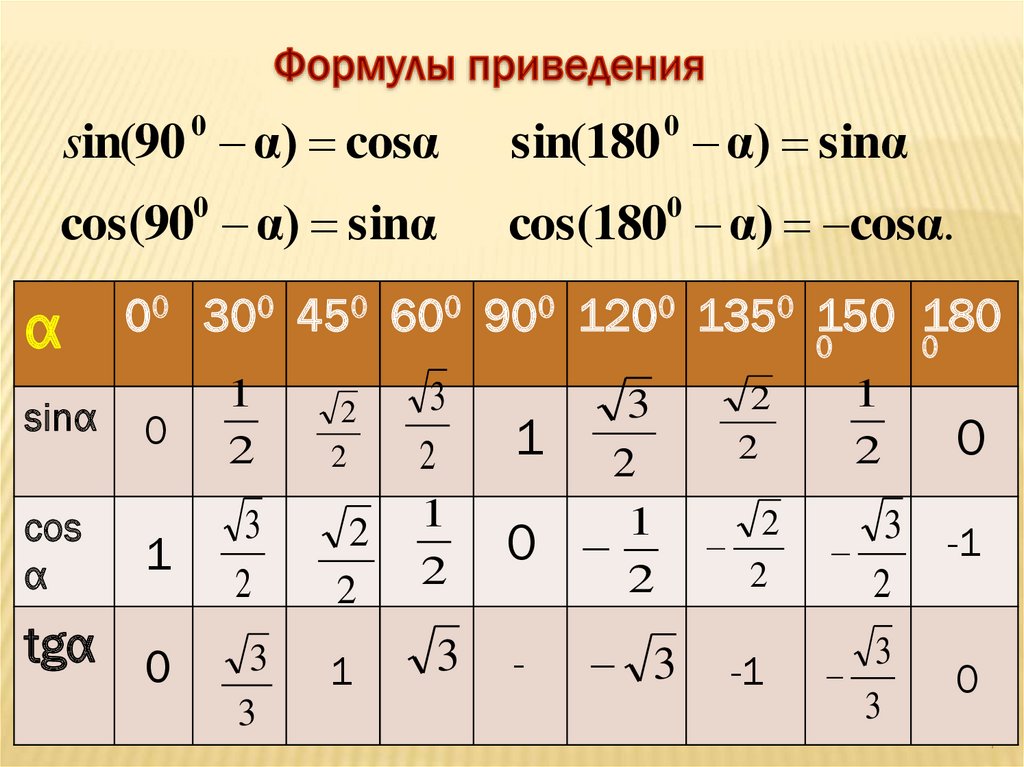 |
Этот результат вместе с
| раскладушкаz→∞ ас z→0, |
означает, что z=0 является простым полюсом cotz.
Из-за периодичности cotz имеет простые полюса в точках z=0,±π,±2π,…. Так как есть производная
| dcotzdz=-1sin2z, |
cotz голоморфна во всех конечных точках, кроме тех полюсов, которые накапливаются только в точке z=∞. Таким образом, котангенс является мероморфной функцией. То же самое относится, естественно, и к функции тангенса.
Как и все мероморфные функции, котангенс может быть выражен в виде ряда с членами частичной дроби (http://planetmath.org/PartialFractionsOfExpressions) вида ajk(z-pj)k, где pj — полюса — см. эту запись (http://planetmath.org/ExamplesOfInfiniteProducts).
Действительные (http://planetmath.org/CmplexFunction) и мнимые части тангенса и котангенса видны из формул
| tan(x+iy)=sinxcosx+isinycoshycos2x+sinh3y, |
| кроватка(x+iy)=sinxcosx-isinycoshysin2x+sinh3y, |
, который может быть получен из (1) путем замены z:=x+iy
(х, у∈ℝ).