диагоналей, углов, оснований, высоты и тд
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Свойства равнобедренной (равнобокой) трапеции
В данной публикации мы рассмотрим определение и основные свойства равнобедренной трапеции.
Напомним, трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны, т.е. AB = CD.
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
Свойство 1
Углы при любом из оснований равнобедренной трапеции равны.
- ∠DAB = ∠ADC = α
- ∠ABC = ∠DCB = β
Свойство 2
Сумма противоположных углов трапеции равняется 180°.
Для рисунка выше: α + β = 180°.
Свойство 3
Диагонали равнобедренной трапеции имеют одинаковую длину.
AC = BD = d
Свойство 4
Высота равнобедренной трапеции BE, опущенная на основание большей длины AD, делит его на два отрезка: первый равняется половине суммы оснований, второй – половине их разности.
Свойство 5
Отрезок MN, соединяющий середины оснований равнобокой трапеции, перпендикулярен этим основаниям.
Прямая, проходящая через середины оснований равнобедренной трапеции, называется ее осью симметрии.
Свойство 6
Вокруг любой равнобедренной трапеции можно описать окружность.
Свойство 7
Если сумма оснований равнобокой трапеции равно удвоенной длине ее боковой стороны, в нее можно вписать окружность.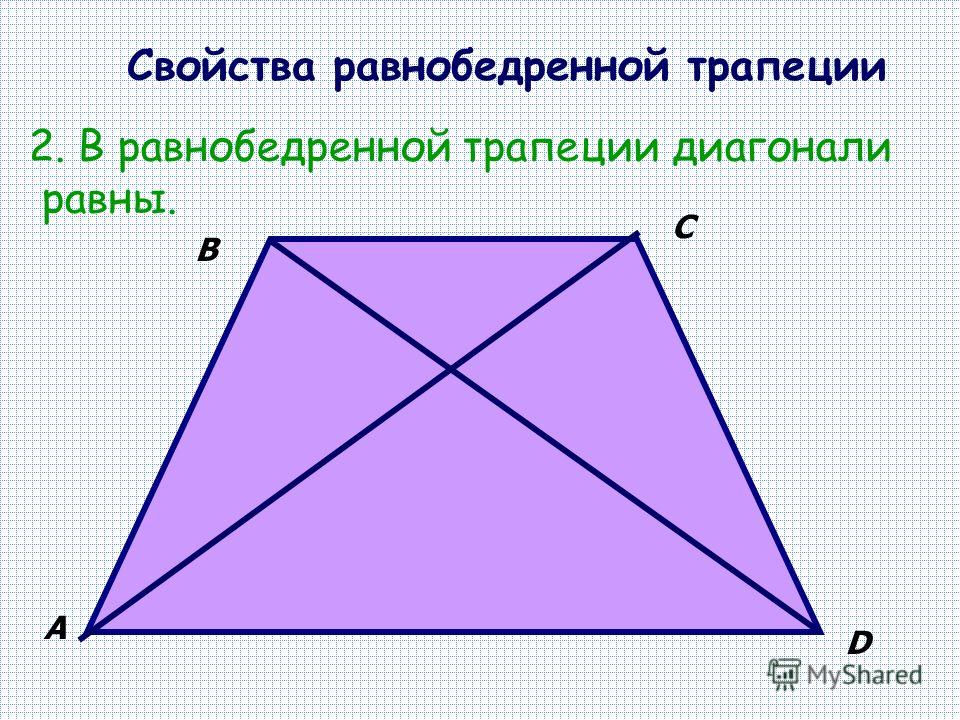
Радиус такой окружности равняется половине высоты трапеции, т.е. R = h/2.
Примечание: остальные свойства, которые применимы ко всем видам трапеций, приведены в нашей публикации – “Что такое трапеция: определение, виды, свойства”.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Найти высоту равнобедренной трапеции если известны основания.
 Особенности равнобедренной трапеции. Как быть, если известны координаты вершин трапеции
Особенности равнобедренной трапеции. Как быть, если известны координаты вершин трапецииГеометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Найти высоту произвольной трапеции
Базируясь на исходных данных, определение высоты фигуры возможно несколькими способами.
Известна площадь
Если длина параллельных сторон известна, а также указана площадь фигуры, то для определения искомого перпендикуляра можно воспользоваться следующим соотношением:
S=h*(a+b)/2,
h – искомая величина (высота),
S – площадь фигуры,
a и b – стороны, параллельные друг другу.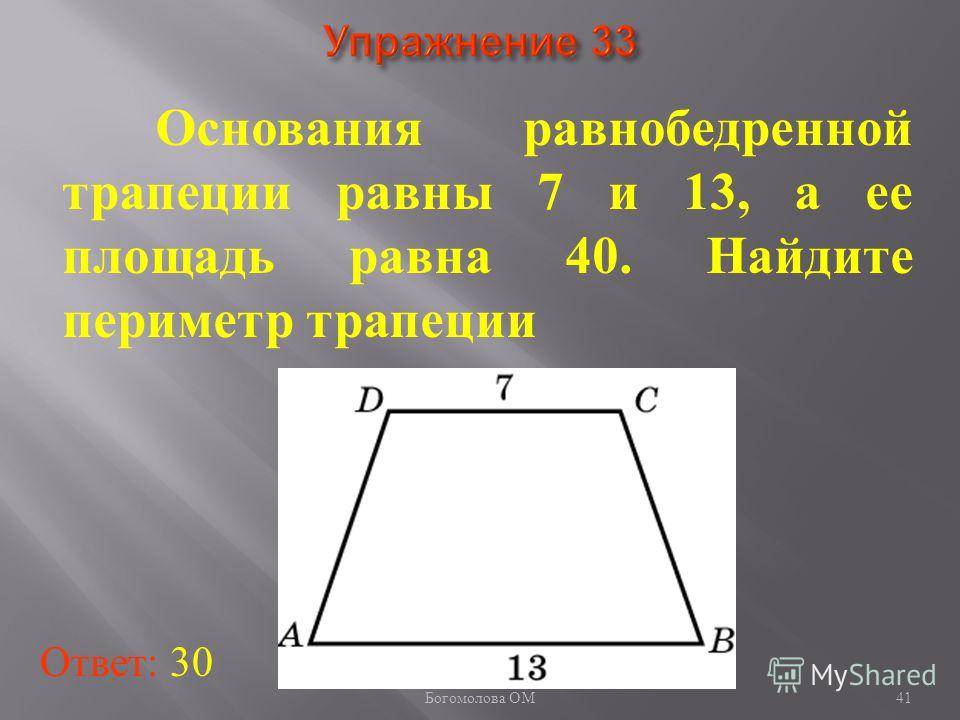
Из приведенной формулы следует, что h=2S/(a+b).
Известна величина средней линии
Если среди исходных данных помимо площади трапеции (S) известна, и длина ее линии средины (l), то для вычислений пригодится другая формула. Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Исходя из свойства трапеции l=(a+b)/2,
l – линия средины,
a, b – стороны-основания четырехугольника.
Поэтому h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В данном случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, воспользуйтесь ею для двух получившихся прямоугольных треугольников. Итоговое выражение будет иметь вид:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d – 2 другие стороны.
Углы в основании
При наличии данных об углах при основании, воспользуйтесь тригонометрическими функциями.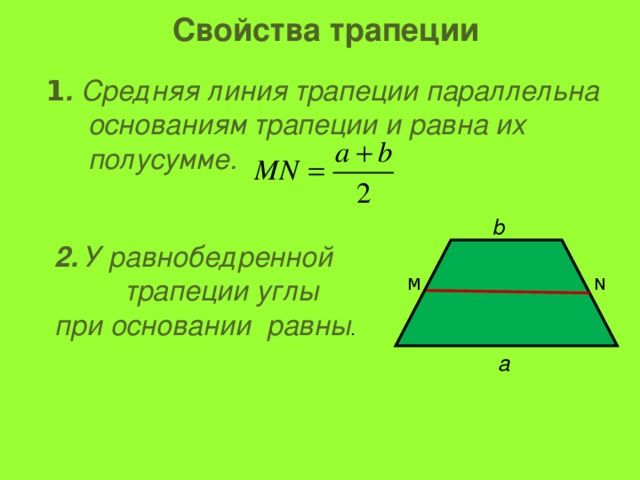
h = c* sinα = d*sinβ,
α и β – углы в основании четырехугольника,
c и d – его боковые стороны.
Диагонали фигуры и углы, которые пересекаясь они образуют
Длина диагонали – длина отрезка, соединяющего противоположные вершины фигуры. Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1*d2)/2l sinφ,
a и b – стороны-основания фигуры,
d1 и d2 – диагонали трапеции,
γ и φ – углы между диагоналями.
Высота фигуры и радиус окружности, которая в нее вписана
Как следует из определения такого рода окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Поэтому расстояние между ними – диаметр – искомая высота фигуры. А так как диаметр – удвоенный радиус, то:
h = 2 * r,
r – радиус окружности, которую вписали в данную трапецию.
Найти высоту равнобедренной трапеции
- Как и следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее боковых сторон.
 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:
h = c* sinα,
h = с * tgα *cosα = с * tgα * (b — a)/2c = tgα * (b-a)/2,
α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.
- Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.
По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — &alpha- и &beta-. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin &alpha-.
В этом выражении можно легко заменить &alpha- на &beta-. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * &radic- {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — &gamma-, можно воспользоваться такой формулой:
S = (4 * r 2) / sin &gamma-.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * &radic- {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.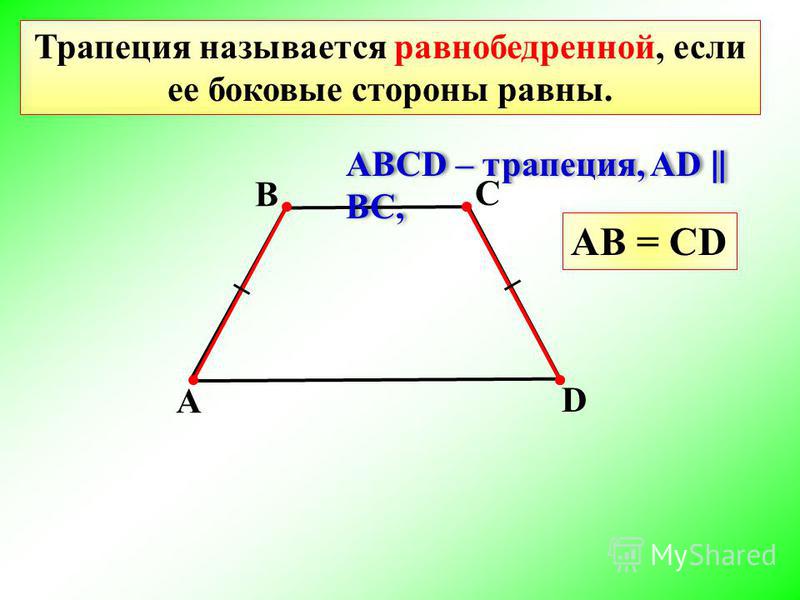
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5- 7), В(8- 7), С(10- 1), Д(1- 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = &radic-{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна &radic-{(8-5) 2 + (7-7) 2 } = &radic-9 = 3. Нижнее — СД = &radic- {(10-1) 2 + (1-1) 2 } = &radic-81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5- 1), пусть это будет точка Н. Длина отрезка АН получится равной &radic-{(5-5) 2 + (7-1) 2 } = &radic-36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.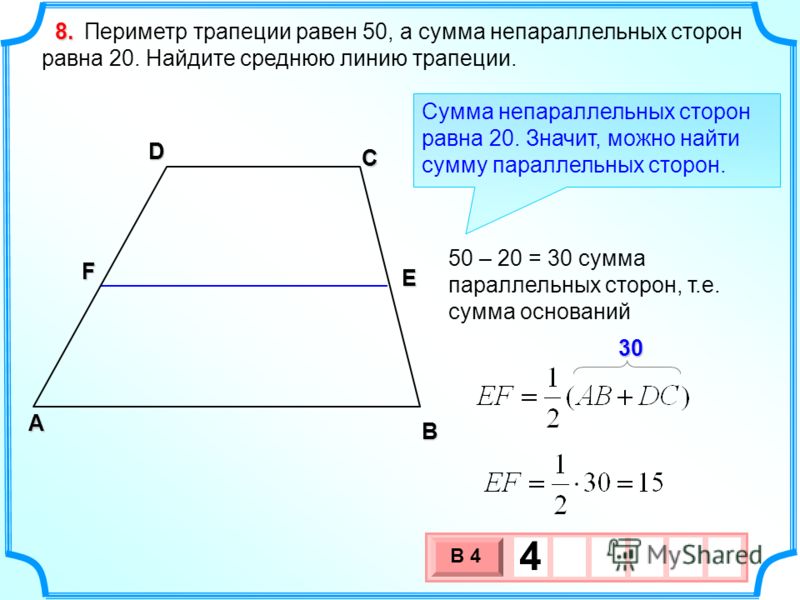
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º- = 18/2 * ½- = 4,5 (дм 2). Задача решена.
Ответ: площадь трапеции равна 4,5 дм 2 .
№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ: S = 20 см 2 .
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º-. Нужно вычислить ее площадь.
Нужно вычислить ее площадь.
Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º-, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ: Искомая площадь равна 45 см 2 .
№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т- вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь
Ответ : х = &radic- {(а 1 2 + 5 а 2 2) / 6}.
ДРУГОЕ
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их…
Их…
Математика — школьный предмет, который изучается всеми, независимо от профиля класса. Однако она не всеми любима. Порой…
Математика — это удивительная наука. Однако такая мысль приходит только тогда, когда ее понимаешь. Чтобы этого достичь,…
Школьная программа предусматривает обучение детей геометрии с раннего возраста. Одно из самых базовых знаний этой…
Периметр любого треугольника — это длина линии, ограничивающей фигуру. Чтобы его вычислить, нужно узнать сумму всех…
Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от…
После изучения темы про прямоугольные треугольники ученики часто выбрасывают из головы всю информацию о них. В том…
Часто ученики возмущенно спрашивают: «Как мне в жизни это пригодится?». На любую тему каждого предмета. Не…
Самый простой многоугольник, который изучается в школе — это треугольник. Он более понятен для учащихся и встречает…
На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть…
Найти площадь равностороннего треугольника можно по любой формуле для произвольной фигуры данного типа или…
Часто на просторах интернета можно найти насмешки по поводу того, как знания по математике — интегралы, дифференциалы,…
В нашей жизни очень часто приходится сталкиваться с применением геометрии на практике, например, в строительстве. Среди наиболее часто встречающихся геометрических фигур есть и трапеция. И для того, чтобы проект был успешным и красивым, необходим правильный и точный расчет элементов для такой фигуры.
Среди наиболее часто встречающихся геометрических фигур есть и трапеция. И для того, чтобы проект был успешным и красивым, необходим правильный и точный расчет элементов для такой фигуры.
Что собой представляет выпуклый четырехугольник, который имеет пару параллельных сторон, именуемых основаниями трапеции. Но есть еще две другие стороны, соединяющие эти основания. Их называют боковыми. Один из вопросов, касающийся данной фигуры, это: «Как найти высоту трапеции?» Сразу необходимо обратить внимание, что высота — это отрезок, определяющий расстояние от одного основания до другого. Существует несколько способов для определения этого расстояния, в зависимости от известных величин.
1. Известны величины обоих оснований, обозначим их b и k, а так же площадь данной трапеции. Используя известные величины, найти высоту трапеции в этом случае очень легко. Как известно из геометрии, вычисляется, как произведение половины суммы оснований и высоты. Из этой формулы можно легко вывести искомую величину.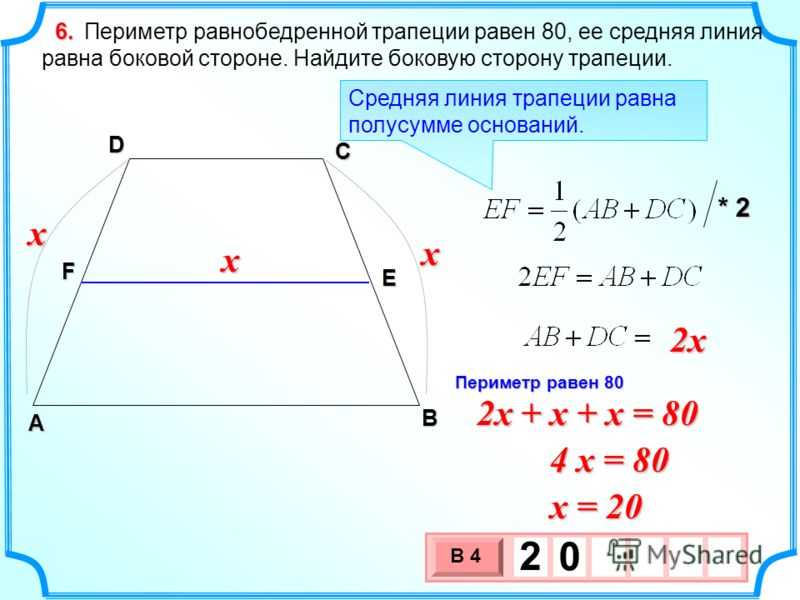 Для этого необходимо площадь разделить на половину суммы оснований. В виде формул это будет выглядеть так:
Для этого необходимо площадь разделить на половину суммы оснований. В виде формул это будет выглядеть так:
S=((b+k)/2)*h, отсюда h=S/((b+k)/2)=2*S/(b+k)
2. Известна длина средней линии, обозначим ее d, и площадь. Для тех, кто не знает, средней линией называю расстояние между серединами боковых сторон. Как найти высоту трапеции в этом случае? Согласно свойству трапеции, средняя линия соответствует половине суммы оснований, то есть d=(b+k)/2. Опять же прибегаем к формуле площади. Заменив половину суммы оснований на величину средней линии, получим следующее:
Как видим из полученной формулы очень легко вывести высоту. Разделив площадь на величину средней линии, мы найдем искомую величину. Запишем это формулой:
3. Известна длина одной боковой стороны (b) и угол, образующийся между этой стороной и наибольшим основанием. Ответ на вопрос, как найти высоту трапеции, есть и в этом случае. Рассмотрим трапецию ABCD, где AB и CD являются боковыми сторонами, причем AB=b. Наибольшим основанием является AD.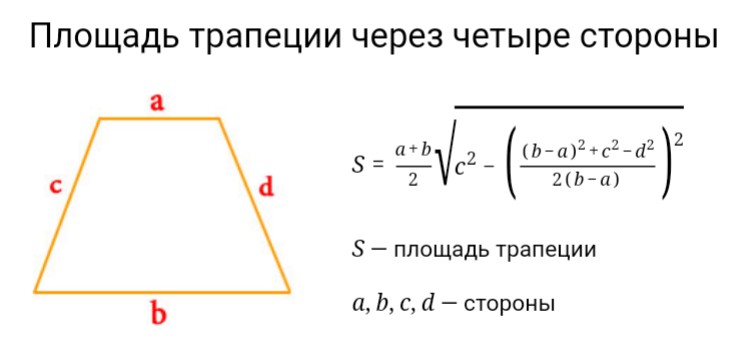 Угол, образованный AB и AD обозначим α. Из точки B опустим высоту h на основание AD. Теперь рассмотрим полученный треугольник ABF, который является прямоугольным. Сторона AB является гипотенузой, а BF-катетом. Из свойства прямоугольного треугольника отношение значения катета и значению гипотенузы соответствует синусу угла, противолежащего катету (BF). Поэтому, исходя из вышеизложенного, для вычисления высоты трапеции перемножаем значение известной стороны и синус угла α. В виде формулы это выглядит следующим образом:
Угол, образованный AB и AD обозначим α. Из точки B опустим высоту h на основание AD. Теперь рассмотрим полученный треугольник ABF, который является прямоугольным. Сторона AB является гипотенузой, а BF-катетом. Из свойства прямоугольного треугольника отношение значения катета и значению гипотенузы соответствует синусу угла, противолежащего катету (BF). Поэтому, исходя из вышеизложенного, для вычисления высоты трапеции перемножаем значение известной стороны и синус угла α. В виде формулы это выглядит следующим образом:
4. Аналогично рассматривается случай, если известны размер боковой стороны и угол, обозначим его β, образующийся между этой стороной и меньшим основанием. При решении такой задачи величина угла между известной боковой стороной и проведенной высотой будет 90°- β. Из свойства треугольников — отношение длины катета и гипотенузы соответствует косинусу угла, расположенного между ними. Из этой формулы легко вывести величину высоты:
h = b *cos(β-90°)
5. Как найти высоту трапеции, если известен лишь радиус вписанной окружности? Из определения окружности, она касается одной точкой каждого основания. Кроме того, эти точки находятся на одной линии с центром окружности. Из этого следует, что расстояние между ними является диаметром и, в то же время, высотой трапеции. Выглядит так:
Кроме того, эти точки находятся на одной линии с центром окружности. Из этого следует, что расстояние между ними является диаметром и, в то же время, высотой трапеции. Выглядит так:
6. Часто встречаются задачи, в которых необходимо найти высоту равнобедренной трапеции. Напомним, что трапеция, имеющая равные боковые стороны, называется равнобедренной. Как найти высоту равнобедренной трапеции? При перпендикулярных диагоналях высота равна половине суммы оснований.
Но, что делать, если диагонали не перпендикулярны? Рассмотрим равнобедренную трапецию ABCD. Согласно ее свойствам, основания параллельны. Из этого следует, что углы при основаниях также будут равны. Проведем две высоты BF и CM. Исходя из вышесказанного, можно утверждать, что треугольники ABF и DCM равны, то есть AF= DM = (AD — BC)/2 = (b-k)/ 2. Теперь, исходя из условия задачи, определимся с известными величинами, а уж потом находим высоту, учитывая все свойства равнобедренной трапеции.
Математическая задача: Равнобедренная трапеция — вопрос № 7395, алгебра
Вычислите площадь равнобедренной трапеции ABCD, если a = 10см, b = 5см, c = 4см.
Правильный ответ:
S = 28 см 2Пошаговое объяснение:
a=10 см b=5 см c=4 см x=(a−c)/2=(10− 4)/2=3 см h=b2−x2
=52−32
=4 см S=2a+c⋅ h=210+4⋅ 4=28 см2
Вы нашли ошибка или неточность? Смело звоните по номеру
пишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
Расчет равнобедренного треугольника.
См. также наш калькулятор тригонометрического треугольника.
- 0037
- Площадь формы
- Треугольник
- Трапезиоид
Оценка слов Проблема:
- Практика для 14 -летнего ребенка
Мы поощряем вас к тому, чтобы посмотреть это тусовное видео по этой математике: видео: видео 2
3.
- Равнобедренная
Равнобедренная трапеция ABCD ABC = 12 угол ABC = 40° b=6. Вычислите окружность и площадь. - Внутренние углы IST
Определить внутренние углы равнобедренной трапеции ABCD /а, с — основания/ и если: альфа:гамма = 1:3 - Вычислить 48073
Вычислить площадь равнобедренной трапеции ABCD, если a = 14 см, c = 8 см, а величина угла DAB равна 52°. - Трапеция — пересечение диагоналей
В ABCD длина трапеции AB = 8 см, высота трапеции 6 см, расстояние пересечения диагоналей от AB 4 см. Вычислите площадь трапеции. - Высота — 6183
В равнобедренной трапеции ABCD длина основания а = 10 см, с = 6 см, длина плеча 4 см. Вычислите его высоту — результат округлите до десятых. - Равнобедренная трапеция
Равнобедренная трапеция ABCD, AB||CD определяется как |CD| = c = 12 см, высота v = 16 см и |CAB| = 20°. Вычислите площадь трапеции. - Трапеция
Трапеция получается путем разрезания вершины прямоугольного равнобедренного треугольника. Основание трапеции 10 см, вершина 5 см. Найдите площадь трапеции.
Основание трапеции 10 см, вершина 5 см. Найдите площадь трапеции. - Параметры: 36691
Рассчитайте длину плеч и площадь равнобедренной трапеции, если известны следующие параметры: o = 20 см a = 10 см, c = 4 см h = 2 см - Основания
Основания равнобедренной трапеции ABCD имеют длину 10 см и 6 см. Его плечи образуют угол α = 50˚ с более длинным основанием. Вычислите длину окружности и площадь трапеции ABCD. - Равнобедренная 5666
В равнобедренной трапеции ABCD вычислите длину недостающей стороны «а» и ее площади. Сторона b = d = 50 см, c = 20 см, высота = 48 см. - Трапециевидное основание
Рассчитайте поверхность и объем четырехугольной призмы с трапециевидным основанием, где a = 7 см, b = 4 см, c = 5 см, d = 4 см, высота трапеции v = 3,7 см и высота призмы h = 5 см. - трапеция 3428
Дана трапеция ABCD с основаниями AB, CD. Пусть K — середина стороны AB, а точка L — середина стороны CD. Площадь треугольника ALB равна 15 см 2 , а площадь треугольника DKC равна 10 см². Вычислите площадь трапеции ABCD.
Вычислите площадь трапеции ABCD. - Трапеция
Найдите высоту трапеции ABCD, площадь которой 77,5 см², а длина основания 16 см и 15 см. - Окружность 2598
Рассчитайте длину окружности и площадь параллелограмма ABCD, если a = 72 см и v = 4,3 см b = 6 см - Равнобедренная 7929
ABCD Равнобедренная трапеция. A = 6см, e = 7см и угол дельты = 105°. Подсчитайте оставшиеся страницы. - Диагонали трапеций
Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. - Подобие 30821
Дан квадрат ABCD со стороной а = 5,3см. Определите размер стороны подобного квадрата, если коэффициент подобия k = 3 см. Вычислите площадь и периметр увеличенного квадрата
Формула площади трапеции: определение, типы, свойства, площадь
- Автор Гурудат
- Последнее изменение 24-01-2023
Трапеция представляет собой четырехугольник с одним набором параллельных сторон (оснований) и непараллельных сторон (катетов). Количество единичных квадратов, которые могут быть вписаны в Площадь трапеции , измеряется в квадратных единицах как \(см2, м2, дюйм2\) и т. д.
Количество единичных квадратов, которые могут быть вписаны в Площадь трапеции , измеряется в квадратных единицах как \(см2, м2, дюйм2\) и т. д.
Трапеция или трапеция – это четырехугольник, определяемый как фигура с четырьмя стороны и один набор параллельных сторон. Параллельные стороны называются основаниями, а непараллельные стороны называются катетами трапеции.
Линия, соединяющая середины непараллельных сторон трапеции, называется серединой отрезка.
Изучите все концепции площади трапеции
Проверьте выше различные типы изображений трапеций, где стрелка представляет параллельную сторону. На всех трех изображениях мы видим, что две стороны параллельны друг другу, тогда как две другие стороны не параллельны
Если мы проведем отрезок между двумя непараллельными сторонами, трапеция будет разделена на две части. неравные части.
Равнобедренная трапеция
Мы изучили понятие равнобедренных треугольников, где две стороны треугольника равны, и углы, противоположные равным сторонам, также равны. Точно так же у нас есть равнобедренная трапеция, у которой две непараллельные стороны равны и образуют равные углы при одном из оснований. Мы можем увидеть пример этого на приведенном ниже рисунке. Ее еще называют равнобедренной трапецией.
Точно так же у нас есть равнобедренная трапеция, у которой две непараллельные стороны равны и образуют равные углы при одном из оснований. Мы можем увидеть пример этого на приведенном ниже рисунке. Ее еще называют равнобедренной трапецией.
Прямоугольная трапеция
Прямоугольная трапеция (также называемая прямоугольной) имеет два смежных прямых угла. Правильные трапеции используются в правиле трапеций для вычисления площадей под кривой. Острая трапеция имеет два смежных острых угла на более длинном ребре основания, а тупая трапеция имеет по одному острому и одному тупому углу на каждом основании. 9\цирк }\).
Площадь трапеции можно вычислить, используя длины двух ее параллельных сторон и высоту между ними.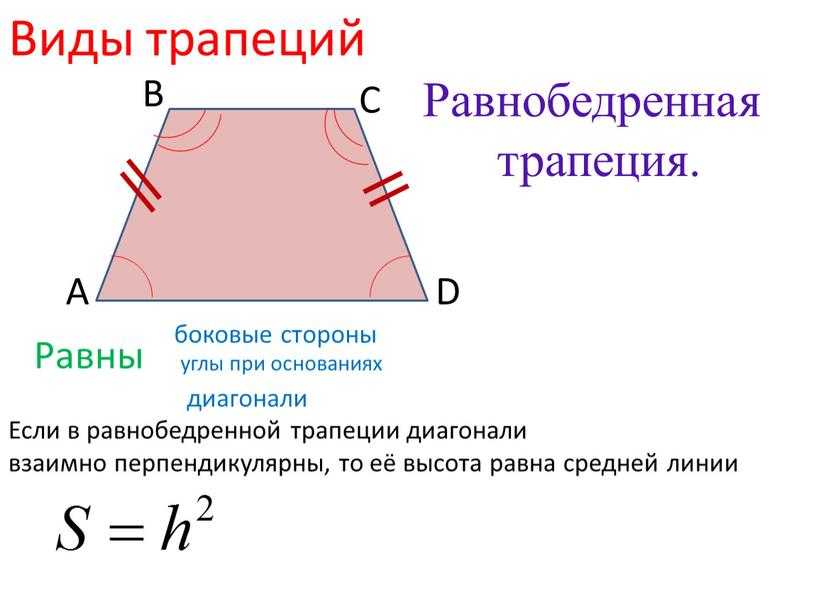 Формула для расчета площади \((A)\) трапеции с использованием основания и высоты имеет следующий вид:
Формула для расчета площади \((A)\) трапеции с использованием основания и высоты имеет следующий вид:
\(A = \frac{1}{2}(a + b) \times h\)
где \(a\) и \(b\) — длины параллельных сторон трапеции, а \(h\) — высота.
Вывод формулы площади трапеции
Пусть \(ABCD\) будет трапецией, две параллельные стороны которой \(AB\) и \(CD\), а \(AD\) и \(BC\) его непараллельные стороны.
Пусть \(DL=h\) высота трапеции \(ABCD. AC\), делящей трапецию на два треугольника \(ABC\) и \(ACD\).
Следовательно, площадь трапеции \(ABCD = {\text{Площадь}}\,{\текст{из}}\,\Delta ABC + {\text{Площадь}}\,{\текст{из}}\, ACD\) …(I)
Так как \(h\) высота трапеции \(ABCD\). Следовательно, это также высота \(\Delta ABC\) и \(\Delta ACD\).
Следовательно, площадь \(\Delta ABC = \frac{1}{2} \times AB \times h\)
и площадь \(\Delta ACD = \frac{1}{2} \times DC \times h\)
Подставляя эти значения в (i), получаем
Площадь трапеции \(ABCD = \left( {\frac{1}{2} \times AB \times h} \right) + \ слева ( {\ гидроразрыва {1} {2} \ раз DC \ раз ч} \ справа) \)
\ ( = \ гидроразрыва {1} {2} \ раз (AB + DC) \ раз ч \)
\(= \frac{1}{2} \times \left( {{\rm{Сумма\;\;параллельных\;сторон}}} \right) \times \left( {\rm{расстояние\ ;между\;параллельными\;сторонами}}} \right)\)
Следовательно, площадь трапеции равна половине произведения суммы параллельных сторон на высоту.
Площадь трапеции с помощью двух трапеций
Чтобы вывести формулу площади трапеции с использованием параллелограмма, мы рассмотрим две одинаковые трапеции, каждая с основаниями \(a\) и \(b\) и высотой \(h\ ). Пусть \(A\) – площадь каждой трапеции. Представьте, что вторая трапеция перевернута вверх дном, как показано на рисунке ниже.
Соединяя две трапеции, мы получаем
Мы можем видеть, что новая фигура, полученная при соединении двух трапеций, представляет собой параллелограмм, основание которого \(a+ b\) и высота \(h\). Мы знаем, что
Площадь параллелограмма \( = {\rm{основание}} \times {\rm{высота}}\)
Площадь приведенного выше параллелограмма равна,\(A + A = 2A\).
Следовательно, \(2{\rm{}}A = (a + b){\rm{}}h\)
\(\Rightarrow A = \frac{1}{2}(a + b) \times h\)
Таким образом, мы получили площадь трапеции.
Трапециевидная призма
Трехмерное твердое тело, состоящее из двух трапеций на противоположных гранях, соединенных четырьмя параллелограммами, называемыми боковыми гранями, называется трапециевидной призмой.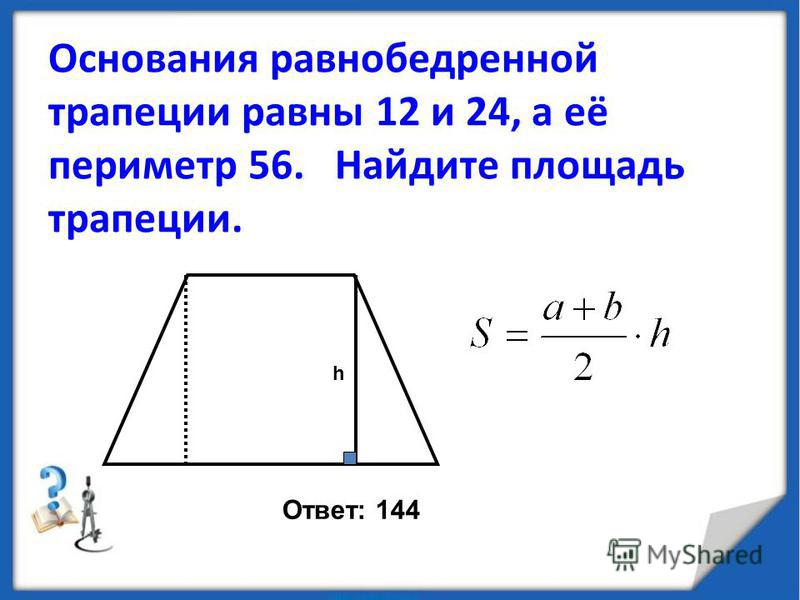
Если \(a,b\) — стороны основания, \(h\) — высота, а \(l\) — длина. Тогда объем трапециевидной призмы равен
\(V = \frac{1}{2}(a + b) \times h \times l\)
Площадь поверхности трапециевидной призмы \( = 2 \times {\rm{площадь\;основания}} + {\rm{боковая\;поверхность\;площадь}}\)
\( = 2 \times \frac{1}{2}(a + b)h + (a \times l) + (b \times l) + (c \times l) + (d \times l)\ )
\( = h(a + b) + l(a + b + c + d)\)
Следовательно, общая площадь поверхности трапециевидной призмы равна \(h(a + b) + l(a + б + в + г)\)
Решаемые примеры
Q.1. Найдите площадь трапеции, параллельные стороны которой имеют длины \({\rm{10\,см}}\) и \({\rm{12\,см}}\), а расстояние между ними равно \( {\rm{4\,cm}}\)
Ответ: Мы знаем, что площадь трапеции 92}\), а длина параллельных сторон равна \(30\;{\rm{см}}\) и \(14\;{\rm{см}}\) соответственно.
Мы знаем, что площадь трапеции
\( = \frac{1}{2} \times \left( {\rm{sum\;of\;\;параллельных\;сторон}}} \right) \times \left( {{\rm{Расстояние\;между\;параллельными\;сторонами}}} \right)\)
\( \Rightarrow 440 = \frac{1}{2} \times (30 + 14) \times h\)
\( \Rightarrow h = \frac{{440 \times 2}}{{44}}\;{\rm{cm}}\)
\( \Rightarrow h = 10 \ раз 2\;{\rm{см}}\)
\( \Rightarrow h = 20\;{\rm{см}}\) 92}\)
Мы знаем, что площадь трапеции
\( = \frac{1}{2} \times \left( {\rm{sum\;of\;\;параллельных\;сторон}} } \right) \times \left( {{\rm{Расстояние\;между\;\;параллельными\;сторонами}}} \right)\)
\( \Rightarrow 480 = \frac{1}{2} \times (AB + CD) \times AL\)
\( \Rightarrow 480 = \frac{1}{2} \times (20 + CD) \times 15\)
\( \Rightarrow 20 + CD = \frac {{480 \times 2}}{{15}}\)
\( \Стрелка вправо 20 + CD = 32 \times 2\)
\( \Стрелка вправо 20 + CD = 64\)
\( \Стрелка вправо CD = 44 \;{\rm{см}}\) 92}\).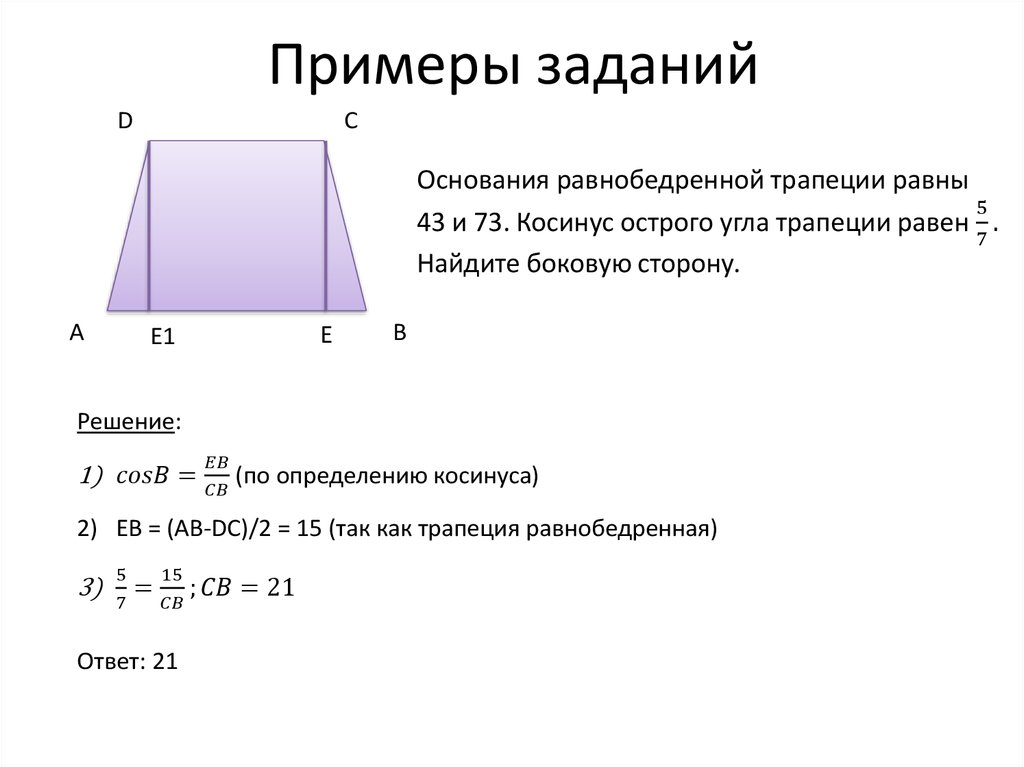
Мы знаем, что площадь трапеции
\( = \frac{1}{2} \times \left( {\rm{sum\;of\;\;параллельных\;сторон}}} \right) \times \left( {{\rm{Расстояние\;между\;\;параллельными\;сторонами}}} \right)\)
\( \Rightarrow 0.55 = \frac{1}{2} \times \left ( {\rm{сумма\;из\;\;параллельных\;сторон}}} \right) \times \left( {\rm{Расстояние\;между\;параллельными\;сторонами}} } \right)\)
\( \Rightarrow \frac{1}{2} \times \left( {\rm{сумма\;\;параллельных\;сторон}}} \right) \times \фракция {{11}}{{100}} = 0,55\) 92}\)
Мы знаем, что площадь трапеции
\( = \frac{1}{2} \times \left( {\rm{sum}}\,{\rm{of}}\,{ \rm{the}}\,{\rm{параллельно}}\,{\rm{стороны}}} \right) \times \left( {{\rm{Расстояние}}\,{\rm{между}} \,{\rm{the}}\,{\rm{параллельно}}\,{\rm{стороны}}} \right)\)
\( \Rightarrow 105 = \frac{1}{2} \times \left( {\rm{sum}}\,{\rm{of}}\,{\rm{the}}\,{\rm{параллельно}}\,{\rm{стороны}}} \right ) \times 7\)
\( \Стрелка вправо 105 = \frac{1}{2} \times (x + 6 + x) \times 7\)
\( \Стрелка вправо 2x + 6 = \frac{{105 \ раз 2}}{7}\)
\( \Стрелка вправо 2x + 6 = 30\)
\( \Стрелка вправо 2x = 24\)
\( \Стрелка вправо x = 12\;{\rm{см}}\)
Следовательно, длина параллельных сторон равны \(12\,{\rm{cm}}\) и \(\left({12 + 6} \right)\,{\rm{cm = 18}}\,{\rm{cm}}\ )
В приведенной выше статье мы изучили определение трапеции, свойства трапеции и формулу для нахождения площади трапеции.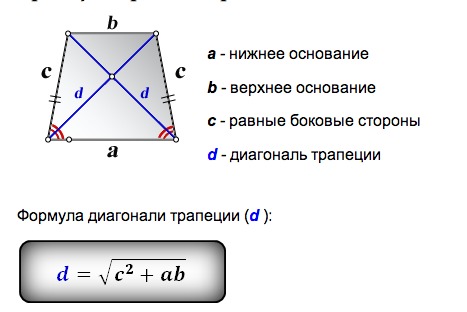 Также мы вывели формулу площади трапеции с помощью треугольников и с помощью двух трапеций. 9\цирк }\).
Также мы вывели формулу площади трапеции с помощью треугольников и с помощью двух трапеций. 9\цирк }\).
2. У трапеции две параллельные стороны и две непараллельные стороны.
3. Диагонали равнобедренной трапеции пересекаются пополам.
4. Длина среднего отрезка равна половине суммы параллельных оснований трапеции.
5. Две пары смежных углов трапеции, образованных между параллельными сторонами, и одна из непараллельных сторон являются дополнительными.
Q.2. Какие формулы площади и периметра трапеции?
Ответ: Площадь трапеции равна
\( = \frac{1}{2} \times \left( {\rm{sum\;of\;\;параллельных\;сторон}}} \right ) \times \left( {{\rm{Расстояние\;между\;\;параллельными\;сторонами}}} \right)\) и периметром трапеции \(=a+b+c+d\)
Где \(a, b, c\) и \(d\) — длины сторон трапеции.
Q.3. Каково соотношение диагоналей трапеции?
Ответ: Диагонали равнобедренной трапеции делят друг друга пополам.

 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции. Основание трапеции 10 см, вершина 5 см. Найдите площадь трапеции.
Основание трапеции 10 см, вершина 5 см. Найдите площадь трапеции.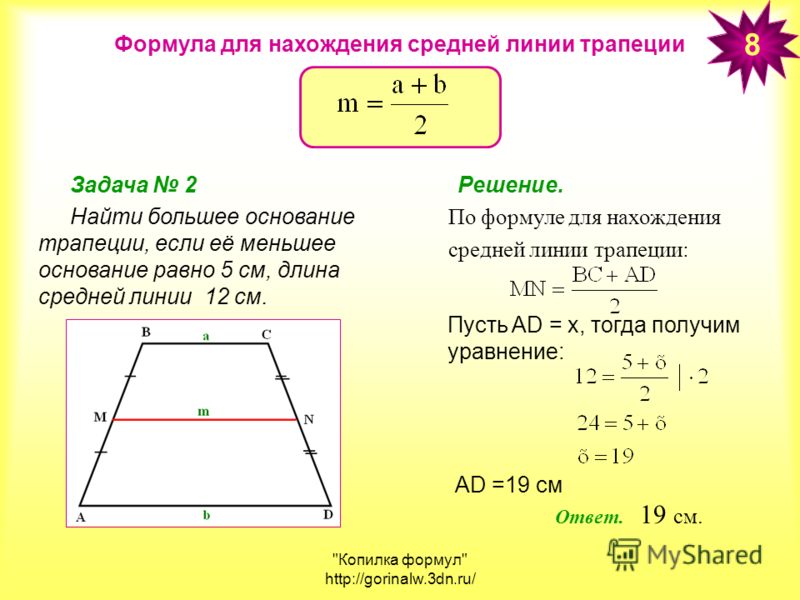 Вычислите площадь трапеции ABCD.
Вычислите площадь трапеции ABCD.