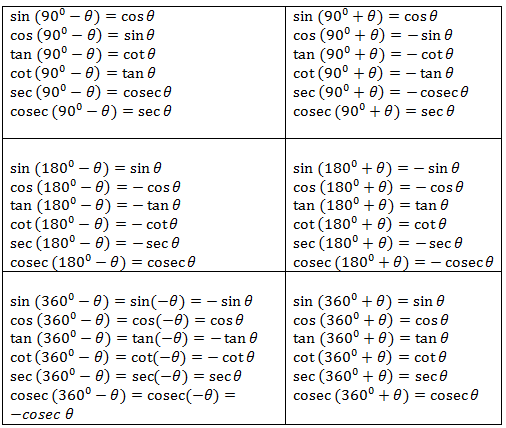Что такое sin cos: Синус, косинус, тангенс и котангенс

Использование функций Sincos в C

Функции «sin()» и «cos()» очень часто используются при работе с углами в математике. Точно так же при выполнении математических вычислений в программировании, связанных с геометрией или тригонометрией, эти функции оказываются очень полезными. Язык программирования C также реализует эти функции в своем заголовочном файле «math.h». После включения этого заголовочного файла в код C программисты могут удобно использовать эти функции для вычисления тригонометрических отношений. В этом руководстве мы попытаемся изучить использование функций «sin()» и «cos()» языка программирования C.

Содержание

1. Использование функций Sin и Cos в C
2. Пример 1: Нахождение синуса и косинуса положительного угла в радианах
3. Пример 2: Нахождение синуса и косинуса отрицательного угла в радианах
4. Пример 3: Нахождение синуса и косинуса «0» угла в радианах
5. Пример 4: Нахождение синуса и косинуса заданного угла в градусах
6. Пример 5: Нахождение синуса и косинуса угла в градусах, предоставленных во время выполнения
7. Вывод

Использование функций Sin и Cos в C

Использование функций синуса и косинуса языка программирования C показано в следующих пяти примерах:

Пример 1: Нахождение синуса и косинуса положительного угла в радианах

Для нахождения синуса и косинуса положительного угла в радианах на языке программирования C вам нужно будет реализовать код, показанный ниже:

В эту программу мы включили заголовочный файл «math. h», содержащий реализацию функций «sin()» и «cos()», вместе с заголовочным файлом «stdio.h». Затем мы определили переменную с плавающей запятой «x» и присвоили ей положительный угол «90». После этого мы определили две другие переменные с плавающей запятой для хранения результатов функций «sin()» и «cos()» соответственно. Наконец, мы использовали операторы «printf» для отображения значений функций «sin()» и «cos()» на терминале, за которыми следует оператор «return 0».

Для компиляции этого скрипта мы использовали следующую команду:

$ gcc sincos.c –o sincos –lm

Мы использовали параметр «-lm» в этой команде, чтобы связать заголовочный файл «math.h» с скомпилированной программой. Без этого вы не сможете скомпилировать этот скрипт.

Затем для выполнения этого скрипта мы использовали команду, показанную ниже:

$ ./sincos

Результаты синуса и косинуса предоставленного положительного угла в радианах показаны на следующем изображении:

Пример 2: Нахождение синуса и косинуса отрицательного угла в радианах

Для нахождения синуса и косинуса отрицательного угла в радианах на языке программирования C вам нужно будет реализовать код, показанный ниже:

В эту программу мы включили заголовочный файл «math. h», содержащий реализацию функций «sin()» и «cos()», вместе с заголовочным файлом «stdio.h». Затем мы определили переменную с плавающей запятой «x» и присвоили ей отрицательный угол «-90». После этого мы определили две другие переменные с плавающей запятой для хранения результатов функций «sin()» и «cos()» соответственно. Наконец, мы использовали операторы «printf» для отображения значений функций «sin()» и «cos()» на терминале, за которыми следует оператор «return 0».

Результаты синуса и косинуса заданного отрицательного угла в радианах показаны на следующем изображении:

Пример 3: Нахождение синуса и косинуса «0» угла в радианах

Для нахождения синуса и косинуса угла «0» в радианах на языке программирования C вам нужно будет реализовать код, показанный ниже:

В эту программу мы включили заголовочный файл «math.h», содержащий реализацию функций «sin()» и «cos()», вместе с заголовочным файлом «stdio.h». Затем мы определили плавающую переменную «x» и присвоили ей угол «0». После этого мы определили две другие переменные с плавающей запятой для хранения результатов функций «sin()» и «cos()» соответственно. Наконец, мы использовали операторы «printf» для отображения значений функций «sin()» и «cos()» на терминале, за которыми следует оператор «return 0».

Результаты синуса и косинуса угла «0» в радианах показаны на следующем изображении:

Пример 4: Нахождение синуса и косинуса заданного угла в градусах

Для нахождения синуса и косинуса заданного угла в градусах на языке программирования C вам нужно будет реализовать код, показанный ниже:

В эту программу мы включили заголовочный файл «math.h», содержащий реализацию функций «sin()» и «cos()», вместе с заголовочным файлом «stdio.h». Кроме того, мы также определили переменную «PI». Затем мы определили переменную с плавающей запятой «x» и присвоили ей положительный угол «90». После этого мы определили плавающую переменную «градусы» и присвоили ей значение «PI/180». Затем мы определили две другие переменные с плавающей запятой для хранения результатов функций «sin()» и «cos()» соответственно, но на этот раз результаты также умножаются на переменную «степень». Наконец, мы использовали операторы «printf» для отображения значений функций «sin()» и «cos()» на терминале, за которыми следует оператор «return 0».

Результаты синуса и косинуса предоставленного угла в градусах показаны на следующем изображении:

Пример 5: Нахождение синуса и косинуса угла в градусах, предоставленных во время выполнения

Для нахождения синуса и косинуса угла в градусах, предоставленных во время выполнения на языке программирования C, вам нужно будет реализовать код, показанный ниже:

В эту программу мы включили заголовочный файл «math.h», содержащий реализацию функций «sin()» и «cos()», вместе с заголовочным файлом «stdio.h». Кроме того, мы также определили переменную «PI». Затем мы определили переменную с плавающей запятой «x» и попросили пользователя ввести ее значение, отобразив сообщение на терминале. После этого мы определили плавающую переменную «градусы» и присвоили ей значение «PI/180». Затем мы определили две другие переменные с плавающей запятой для хранения результатов функций «sin()» и «cos()» соответственно, но на этот раз результаты также умножаются на переменную «степень». Наконец, мы использовали операторы «printf» для отображения значений функций «sin()» и «cos()» на терминале, за которыми следует оператор «return 0».

После выполнения этого кода пользователю было предложено ввести угол по своему выбору, как показано на изображении ниже:

Результаты синуса и косинуса угла, предоставленные пользователем во время выполнения в градусах, показаны на следующем изображении:

Вывод

С помощью этого руководства мы стремились научить вас использовать функции «sin()» и «cos()» языка программирования C. Для этого мы поделились с вами пятью различными примерами, в которых мы использовали эти функции. Мы рассчитали эти значения для положительных, отрицательных и нулевых углов соответственно. Более того, мы также научили вас вычислять эти значения в градусах, а не в радианах, поскольку эти функции по умолчанию возвращают результаты в радианах в языке программирования C. Мы также объяснили, как можно взять угол, синус и косинус которого найдены пользователем во время выполнения. Изучив эти различные варианты, вы можете уверенно использовать функции «sin()» и «cos()» в языке программирования C в Linux.

любой язык — Какой алгоритм вычисления sin или cos используется в современных языках?

Вопрос задан 7 лет 3 месяца назад

Изменён 7 лет 3 месяца назад

Просмотрен 4k раз

Мне интересно, каким образом, например, реализован этот алгоритм в math.h:

Если разложение в ряд, то какое, и сколько элементов?
Если таблица, то на сколько элементов?
Есть ли какие-либо альтернативные варианты, которые я не привёл?

Интересует не конкретно math.h, а больше методы расчёта этих функций, используемые в библиотеках языков программирования.

• алгоритм
• любой-язык

3

В современных алгоритмах вычисления трансцендентных функций творится полная жесть.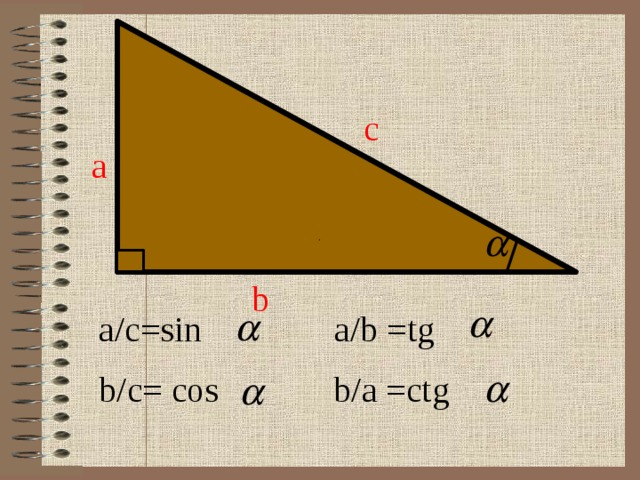

Там используется не один алгоритм, а целое семейство, и в зависимости от входного значения, возможностей аппаратуры, необходимой точности и других параметров подбирается наиболее подходящий.

Начнём с того, что вычисление синусов поддерживается на уровне железа. Но есть нюанс, что аппаратная инструкция не отличается точностью, поэтому на неё часто не полагаются.

Большинство трансцендентных функций использует многочлены Чебышева (но не все, например, вычисление корня). А вот какие конкретно — зависит от условий. Операции сложения, умножения и деления и др. в зависимости от железа могут присутствовать, а могут нет, и у них может быть разная скорость. В зависимости от этого подбирается способ вычисления (с делением или без). Дальше смотрим на необходимую точность, и подбираем подходящие многочлены. Далее могут применяться хитрости с интерполяцией, чтобы сэкономить на сложности многочленов.

Какие конкретно многочлены и при каких условиях используются — смотрите сорцы.

Информация основана на ответе на вопрос How does C compute sin() and other math functions?, автор Donald Murray. По ссылке вы найдёте больше подробностей.

Что касается Java, C#, PHP и остальных высокоуровневых языков, то в конечном счёте они вызывают низкоуровневые заоптимизированные десятилетиями низкоуровневые реализации на C, которые и выполняют всё это шаманство. Как правило, лезть туда не надо. Это одни из самых проверенных временем алгоритмов.

7

Матфункции в Java реализуются не на Java в чистом виде, а вызовом нативных функций Си. Какой бы альтернативный вариант вы не использовали, крайне сомнительно, что он будет быстрее. А конкретная реализация зависит от платформы на которой запущена JVM.

1

Есть справочник по спецфункциям под ред. Абрамовиц, Стиган. По сути — стандарт США. Прописанные в нём формулы заточены либо под абсолютную, либо под относительную ошибку.

Скажем, в районе нуля функцию sinc x = sin x / x выражают через экономизированные представления рядов Тейлора. Экономизация состоит в замене степеней x на их выражения через полиномы Чебышёва P_n = cos(n arccos x), которые в силу своей синуисоидальной природы стабилизируют абсолютную ошибку (поскольку первый отброшенный полином — это косинус). Синус получают как x*sinc x, и поэтому у него стабилизирована относительная ошибка.

Надо понимать, что речь шла о некоторой окрестности нуля. На дпугих интервалах могут быть использованы другие методы.
Косинус как функция самостоятельного значения не имеет, поскольку даже в школе рассказывают, как из синуса угла 0-90 можно линейными операциями получить и синус, и косинус любого угла.

Но есть и специализированные алгоритмы для табулирования синуса и косинуса. Например, в самой популярной модификации Кули-Тьюки алгоритма быстрого (дискретного) преобразования Фурье на массивах с размерностью степени двойки востребованы синусы и косинусы аргумента pi / 2^k. Такие таблицы обычно вычисляют рекуррентно, с использованием формул для половинного аргумента.

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Предварительное исчисление алгебры

— Что НА САМОМ ДЕЛЕ делают cos и sin?

Задавать вопрос

спросил 8 лет, 4 месяца назад

Изменено 6 лет, 8 месяцев назад

Просмотрено 3к раз

$\begingroup$

Мне очень трудно понять, что делают sin и cos, когда вы вводите данные в калькулятор.

Что я о них понимаю

1) Оба они, по сути, находят максимальное и минимальное значения для соответствующих осей. потому что это х, а синус это у.

— это имеет ИДЕАЛЬНЫЙ смысл. Ура!

2) Вы можете найти, каковы другие длины треугольника. (value(sin(theta)) (value(cos(theta)) **я понимаю, что в большинстве случаев тета должна быть в радианах.

— это понятно. Ура!

Итак, что, черт возьми, происходит, когда вы вводите sin($\pi$/6). Как это равно 1/2? Я понимаю, что в основном синус $\pi$/6 (y min и max) будет 1/2, хорошо, но почему? когда вы делаете cos(0), x = 1, потому что r = 1 (почему r = 1?). Вот тут я в замешательстве. Опять же, я могу сделать это на калькуляторе, но я программист, и если что-то не имеет смысла, у меня кружится голова, и мне нужно понять, что происходит.

• алгебра-предварительное исчисление
• тригонометрия

$\endgroup$

5

$\begingroup$

Если вы нарисуете единичную окружность (окружность радиуса $1$ с центром в начале координат) в плоскости $XY$ и начнете с $0$ радиан (т.