Формулы треугольники: Все формулы для треугольника

2=m*n\)
\( r=\frac{a+b−c}{2}\)- радиус вписанной окружности
\( sin α=a/c\)
\( tan α=a/b\)
\( cot α=b/a\)

Формулы площади

полупериметр \(p=\frac{a+b+c}{2}\)

Площадь треугольника
\(S=\frac{ ch_c}{2}\)
\(S=\frac{ab sin γ}{2}\)
\(S=\sqrt{p(p−a)(p−b)(p−c)}\)
\(S=pr \)

где \(r\) радиус треугольника вписанной окружности
\(S=\frac{abc}{ 4R}\)

где — R-радиус описанной окружности

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Ринат Фарагатович Шаймарданов

Репетитор по математике

Стаж (лет)

Образование:

Уфимский авиационный институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Повышение успеваемости по физике 7-11 класс, подготовка к ВПР, ОГЭ и ЕГЭ. Ответственно подхожу к делу, стараюсь объяснять законы физики на примерах из окружающего нас мира.

Оксана Ростиславна Гришина

Репетитор по математике

Стаж (лет)

Образование:

Южный федеральный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике для 2-9 классов. Подготовка к ОГЭ и олимпиадам, теория вероятности и статистики. Математика занимает неотъемлемую часть моей жизни! Наличие собственной методической разработки по предмету позволяет мне развивать у ребят активные учебно-познавательные умения, а использование инновационной педагогической технологии «Перевернутый класс» обеспечивает понимание каждым ребенком ценности образования, внутренней мотивации и ответственности за свое обучение.

В результате, мы получаем высокое качество знаний и достойные результаты на экзаменах.

Анастасия Сергеевна Роствинская

Репетитор по математике

Стаж (лет)

Образование:

Нижегородский Государственный Технический университет имени Р. Е. Алексеева

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по химии для 7-9 классов. Подготовка к ОГЭ. Я занимаюсь репетиторством уже 3 года, являюсь именным стипендиатом от крупной компании Теплоэнерго, так же победитель конкурса Профстажировки 2.

0 2019 и 2021 года, уже со второго курса написала 2 статьи по химическим технологиям, университет закончила с аттестатом отличия. Мои ученики с достоинством сдали ОГЭ и уже закончили школу. Так же я оказывала помощь студентам младших курсов.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Площади

Формулы для площади треугольника

Вывод формул для площади произвольного треугольника

Вывод формул для площади равностороннего (правильного) треугольника

Вывод формул для площади прямоугольного треугольника

Формулы для площади треугольника

Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.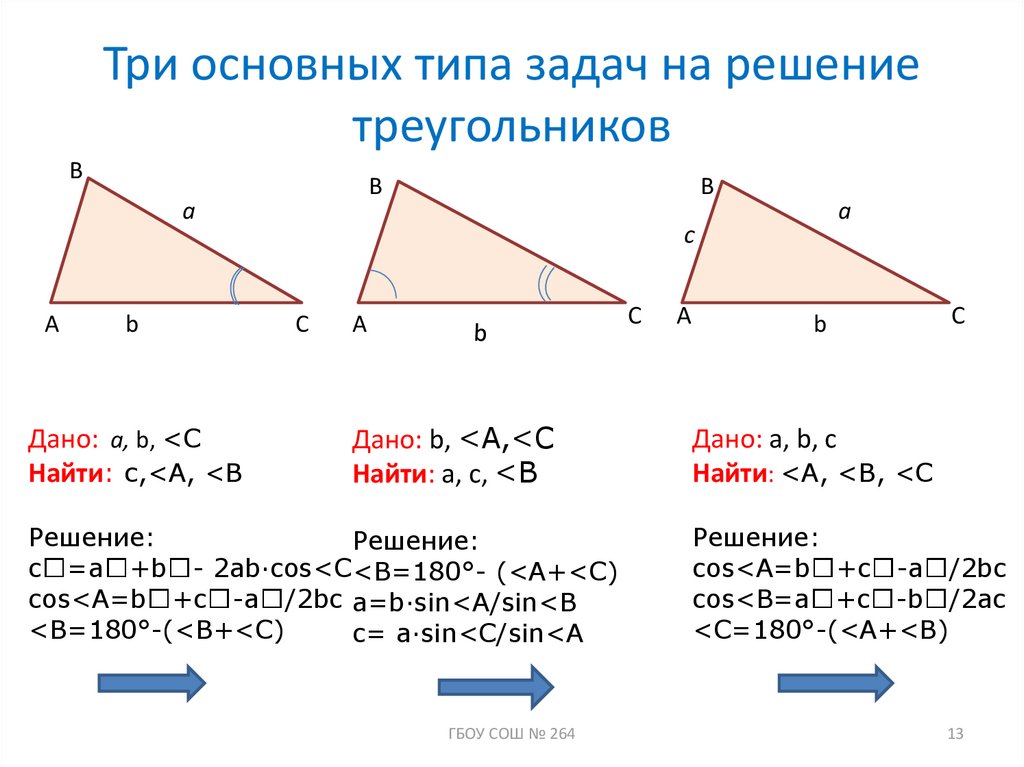

Фигура	Рисунок	Формула площади	Обозначения
Произвольный треугольник		Посмотреть вывод формулы	a – любая сторона, h_a – высота, опущенная на эту сторону
		Посмотреть вывод формулы	a и b – две любые стороны, С – угол между ними
		. Посмотреть вывод формулы Герона	a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона»
		Посмотреть вывод формулы	a – любая сторона, B, С – прилежащие к ней углы
		Посмотреть вывод формулы	a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр
		Посмотреть вывод формулы	a, b, c – стороны, R – радиус описанной окружности
		S = 2R² sin A sin B sin C Посмотреть вывод формулы	A, B, С – углы, R – радиус описанной окружности
Равносторонний (правильный) треугольник		Посмотреть вывод формулы	a – сторона
		Посмотреть вывод формулы	h – высота
		Посмотреть вывод формулы	r – радиус вписанной окружности
		Посмотреть вывод формулы	R – радиус описанной окружности
Прямоугольный треугольник		Посмотреть вывод формулы	a и b – катеты
		Посмотреть вывод формулы	a – катет, φ – прилежащий острый угол
		Посмотреть вывод формулы	a – катет, φ – противолежащий острый угол
		Посмотреть вывод формулы	c – гипотенуза, φ – любой из острых углов

Произвольный треугольник
	где a – любая сторона, h_a – высота, опущенная на эту сторону Посмотреть вывод формулы
	где a и b – две любые стороны, С – угол между ними Посмотреть вывод формулы
	. где a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона» Посмотреть вывод формулы Герона
	где a – любая сторона, B, С – прилежащие к ней углы Посмотреть вывод формулы
	где a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр Посмотреть вывод формулы
	где a, b, c – стороны, R – радиус описанной окружности Посмотреть вывод формулы
	S = 2R² sin A sin B sin C где A, B, С – углы, R – радиус описанной окружности Посмотреть вывод формулы
Равносторонний (правильный) треугольник
	где a – сторона Посмотреть вывод формулы
	где h – высота Посмотреть вывод формулы
	где r – радиус вписанной окружности Посмотреть вывод формулы
	где R – радиус описанной окружности Посмотреть вывод формулы
Прямоугольный треугольник
	где a и b – катеты Посмотреть вывод формулы
	где a – катет, φ – прилежащий острый угол Посмотреть вывод формулы
	где a – катет, φ – противолежащий острый угол Посмотреть вывод формулы
	где c – гипотенуза, φ – любой из острых углов Посмотреть вывод формулы

Произвольный треугольник

где
a – любая сторона,

h_a – высота, опущенная на эту сторону

Посмотреть вывод формулы

где
a и b – две любые стороны,
С – угол между ними

Посмотреть вывод формулы

где
a, b, c – стороны,
p – полупериметр

Формулу называют «Формула Герона»

Посмотреть вывод формулы Герона

где
a – любая сторона,
B, С – прилежащие к ней углы

Посмотреть вывод формулы

где
a, b, c – стороны,
r – радиус вписанной окружности,
p – полупериметр

Посмотреть вывод формулы

где
a, b, c – стороны,
R – радиус описанной окружности

Посмотреть вывод формулы

S = 2R² sin A sin B sin C

где
A, B, С – углы,
R – радиус описанной окружности

Посмотреть вывод формулы

Равносторонний (правильный) треугольник

где
a – сторона

Посмотреть вывод формулы

где
h – высота

Посмотреть вывод формулы

где
r – радиус вписанной окружности

Посмотреть вывод формулы

где
R – радиус описанной окружности

Посмотреть вывод формулы

Прямоугольный треугольник

где
a и b – катеты

Посмотреть вывод формулы

где
a – катет,
φ – прилежащий острый угол

Посмотреть вывод формулы

где
a – катет,
φ – противолежащий острый угол

Посмотреть вывод формулы

где
c – гипотенуза,
φ – любой из острых углов

Посмотреть вывод формулы

Вывод формул для площади произвольного треугольника

Утверждение 1. Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а h_a – высота, опущенная на эту сторону.

Доказательство.

Рис. 1

Достроив треугольник ABC до параллелограммапараллелограмма ABDC (рис. 1), получим

что и требовалось доказать.

Утверждение 2. Площадь треугольника можно найти по формуле

где a и b – две любые стороны треугольника, а С – угол между ними.

Доказательство.

Рис. 2

Поскольку

h_a = b sin C ,

то, в силу утверждения 1, справедлива формула

что и требовалось доказать.

Утверждение 3. Площадь треугольника можно найти по формуле

где a – любая сторона треугольника, а B, С – прилежащие к ней углы.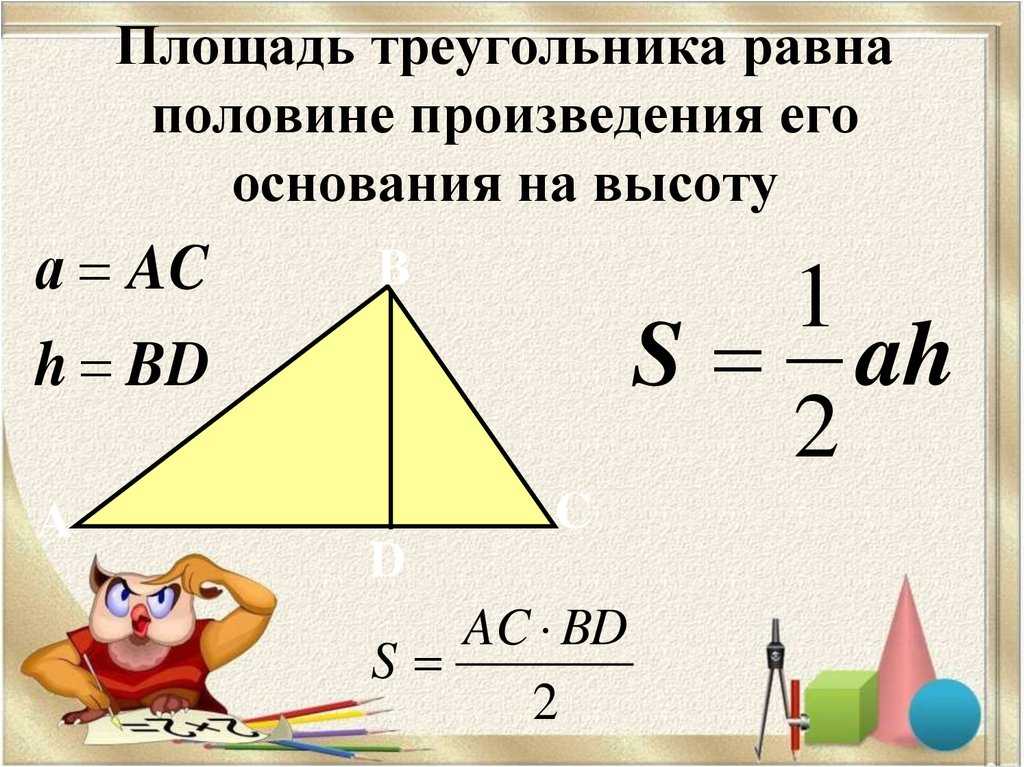

Замечание. Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.

Доказательство.

Рис. 3

Поскольку (рис.3)

x = h_actg C , y = h_actg B ,

то

a = x + y =
= h_actg C + h_actg B =
= h_a( ctg C + ctg B) .

Следовательно,

Поэтому

что и требовалось доказать.

Утверждение 4. Площадь треугольника можно найти по формуле

где a, b, c – стороны треугольника, а r – радиус вписанной окружности.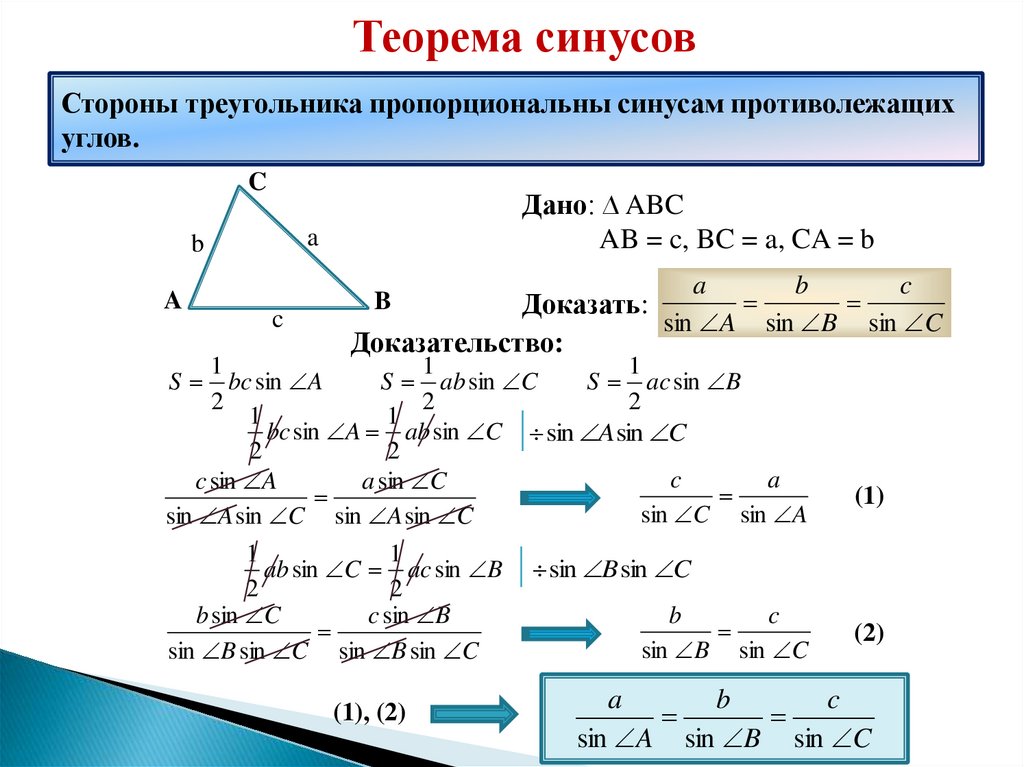

Доказательство.

Рис. 4

Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим

что и требовалось доказать.

Утверждение 5. Площадь треугольника можно найти по формуле

где a, b, c – стороны треугольника, а R – радиус описанной окружности.

Доказательство.

Рис. 5

В силу теоремы синусов справедливо равенство

Следовательно,

Поэтому

что и требовалось доказать.

Утверждение 6. Площадь треугольника можно найти по формуле:

S = 2R² sin A sin B sin C ,

где A, B, С – углы треугольника, а R – радиус описанной окружности.

Доказательство.

Рис. 6

В силу теоремы синусов справедливо равенство

Поэтому

a = 2R sin A ,
b = 2R sin B ,
c = 2R sin C ,

В силу утверждения 5

что и требовалось доказать.

Вывод формул для площади равностороннего треугольника

Утверждение 7.

Если a – сторона равностороннего треугольника, то его площадь

Если h – высота равностороннего треугольника, то его площадь

Если r – радиус вписанной в равносторонний треугольник окружности, то его площадь

Если R – радиус описанной около равностороннего треугольника окружности, то его площадь

Доказательство.

Рассмотрим рисунок 7.

Рис. 7

В силу утверждения 2

Рассмотрим рисунок 8.

Рис. 8

Поскольку

то

Рассмотрим рисунок 9.

Рис. 9

Поскольку у равностороннего треугольника центр вписанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство h = 3r. Следовательно,

Рассмотрим рисунок 10.

Рис. 10

Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство Следовательно,

Доказательство утверждения 7 завершено.

Вывод формул для площади прямоугольного треугольника

Утверждение 8.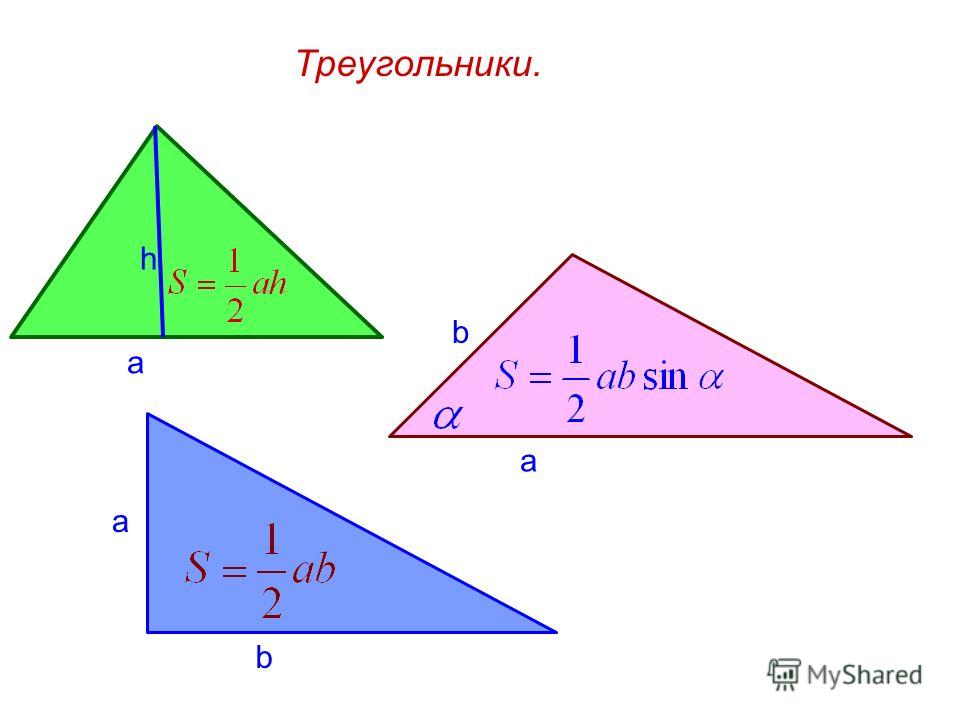

Если a и b – катеты прямоугольного треугольника, то его площадь

Если a – катет прямоугольного треугольника, а φ – прилежащий к этому катету острый угол, то площадь прямоугольного треугольника

Если a – катет прямоугольного треугольника, а φ – противолежащий этому катету острый угол, то площадь прямоугольного треугольника

Если c – гипотенуза прямоугольного треугольника, а φ – острый угол, то площадь прямоугольного треугольника

Доказательство.

Рассмотрим рисунок 11.

Рис. 11

В силу утверждения 2

Рассмотрим рисунок 12.

Рис. 12

Поскольку

b = a tg φ ,

то

Рассмотрим рисунок 13.

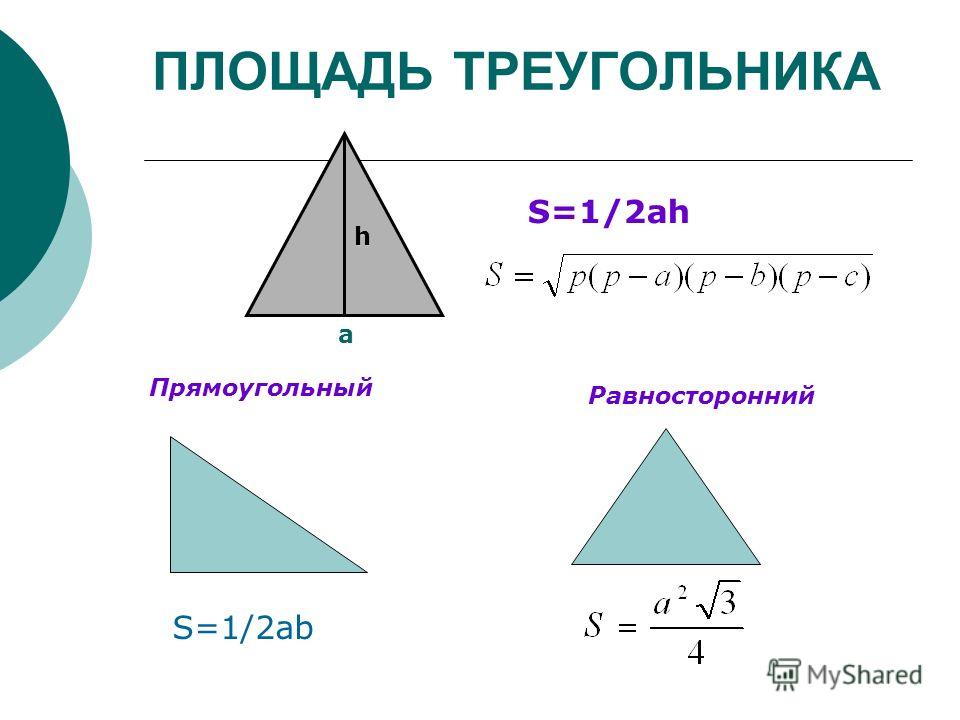Рис. 13

Поскольку

b = a ctg φ ,

то

Рассмотрим рисунок 14.

Рис. 14

Поскольку

a = c cos φ ,
b = c sin φ ,

то

Доказательство утверждения 8 завершено.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Площадь треугольника

Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.

Таблица с формулами площади треугольника (в конце страницы)

Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)

— Вычисления (показано) (скрыто)

— примечания (показано) (скрыто)

Для всех треугольников

Площадь треугольника по основанию и высоте

Сторона a

Высота h

Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по двум сторонам и углу между ними

Сторона a

Сторона b

Угол α° между сторонами a и b

Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по радиусу вписанной окружности и трем сторонам

Сторона a

Сторона b

Сторона c

Радиус r вписанной окружности

Площадь треугольника по радиусу описанной окружности и трем сторонам

Сторона a

Сторона b

Сторона c

Радиус R описанной окружности

Площадь треугольника по формуле Герона

Полупериметр:

Сторона a

Сторона b

Сторона c

Площадь произвольного треугольника по стороне и двум прилежащим углам

Сторона a

Угол β°

Угол α°

Для равнобедренных треугольников

Площадь равнобедренного треугольника по боковым сторонам и основанию

Сторона a (a = b)

Сторона c

Площадь равнобедренного треугольника по боковым сторонам и углу между ними

Боковая сторона a (a = b)

Угол α° между боковыми сторонами

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними

Боковая сторона a (a = b)

Основание треугольника c

Угол β° между основанием и стороной

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами

Основание треугольника c

Угол α° между боковыми сторонами

Для равносторонних треугольников

Площадь равнобедренного треугольника по высоте и основанию

Основание треугольника c

Высота h

Площадь равностороннего треугольника по стороне

Сторона a (a = b = c)

Площадь равностороннего треугольника по высоте

Высота h

Площадь равностороннего треугольника по радиусу вписанной окружности

Радиус r вписанной окружности

Площадь равностороннего треугольника по радиусу описанной окружности

Радиус R описанной окружности

Для прямоугольных треугольников

Площадь прямоугольного треугольника по двум катетам

Катет a

Катет b

Площадь прямоугольного треугольника через гипотенузу и угол

Сторона c

Угол α

Площадь прямоугольного треугольника через катет и угол

Сторона b

Угол α

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Отрезок d

Отрезок e

Площадь прямоугольного треугольника через гипотенузу и вписанную окружность

Сторона с

Радиус r

Площадь прямоугольного треугольника по формуле Герона

Полупериметр:

Сторона a

Сторона b

Сторона c

Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.

Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.

В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.

Таблица с формулами площади треугольника

	исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
Для всех треугольников
1	основание и высота
2	две стороны и угол между ними
3	радиус вписанной окружности и три стороны
4	радиус описанной окружности и три стороны
5	три стороны (по формуле Герона)		где
6	сторона и два прилежащих угла
Для равнобедренных треугольников
7	боковые стороны и основание
8	боковые стороны и угол между ними
9	боковые стороны, основание и угол между боковыми сторонами и основанием
10	основание и угол между боковыми сторонами
11	высота и основание
Для равносторонних треугольников
12	сторона
13	высота
14	радиус вписанной окружности
15	радиусу описанной окружности
Для прямоугольных треугольников
16	два катета
17	гипотенуза и угол
18	катет и угол
19	отрезки, на которые делит гипотенузу вписанная окружность
20	гипотенуза и радиус вписанной окружности
21	три стороны (по формуле Герона)		где

Определения

Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Скачать формулы площади треугольника в виде картинки

Справочник репетитора по математике. Формулы, теоремы и свойства треугольников. Виртуальный онлайн репетитор. — Колпаков Александр Николаевич

Теоретичесикие шпаргалки по элементарной геометрии для занятий с репетитором по математике. Базовый школьный уровень. Свойства элементов треугольника. В помощь для решению задач по всему курсу планиметрии. Для тренировки решения задач С4 на ЕГЭ по математике.

1) Определение тригонометрических функций острого угла в прямоугольном треугольнике и теорема Пифагора

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов, то есть

2) Формулы площади треугольника

где (Формула Герона)

, где r- вписанной окружности

, где R — радиус описанной окружности

3) Подобие треугольников

Определение: два треугольника называются подобными, если у них соответствующие углы равны и соответствующие стороны пропорциональны, то есть
и

Обозначение:

4) Признаки подобия двух треугольников

1-й признак: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.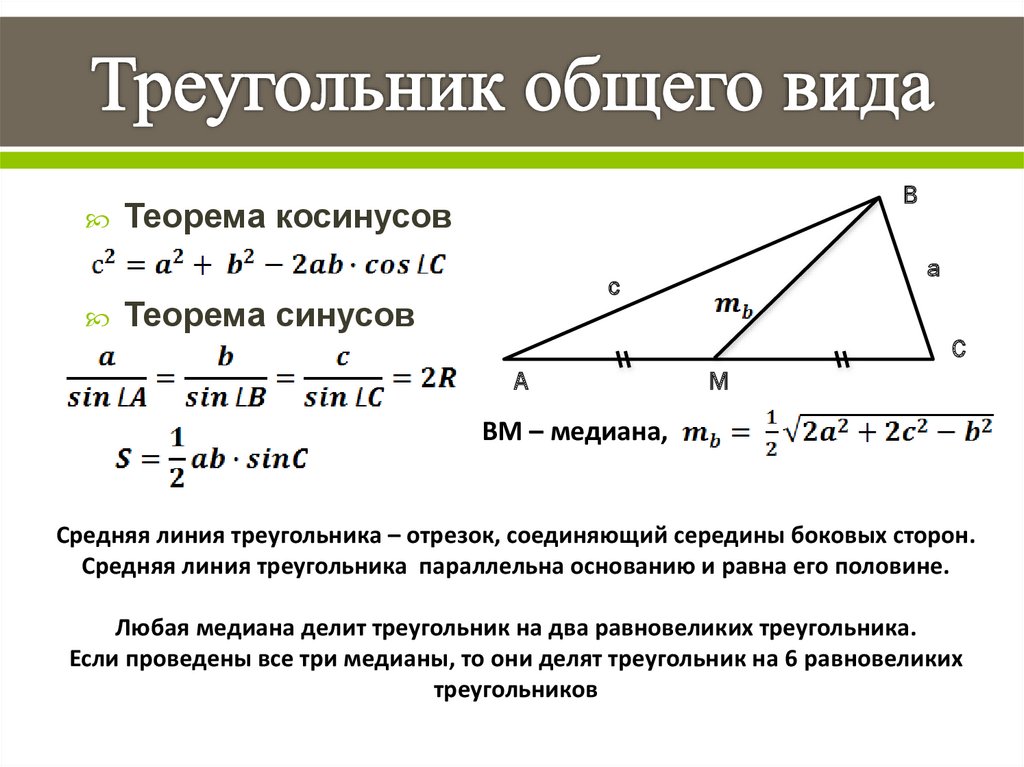

Коротко: если , то

2-й признак:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны

Коротко: если и , то

3-й признак:если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны, то есть

Коротко: если , то

5) Свойства подобных треугольников

если , то

, где

и — любые соответствующие медианы (проведенные к соответствующим сторонам)

и — любые соответствующие биссектрисы (проведенные к соответствующим сторонам)

и — любые соответствующие высоты (проведенные к соответствующим сторонам)

6) Подобие прямоугольных треугольников. Высота, проведенная из вершины прямого угла

Теорема: высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы:

7) Свойство медиан в треугольнике.

Теорема 1: Все медианы треугольника пересекаются в одной точке (центр тяжести треугольника) и делятся этой точкой в отношении 2:1, считая от вершин. То есть

Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),

То есть

Теорема 3: все три медианы делят треугольник на 6 равновеликих треугольников, то есть

8) Свойство биссектрис в треугольнике
Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.

То есть

Теорема 2: Все биссектрисы в треугольнике пересекаются в одной точке, которая является центром вписанной с треугольник окружности. В любой треугольник можно вписать окружность и только одну.

9) Свойство точки пересечения серединных перпендикуляров к сторонам треугольника:

Теорема: все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке и эта точка является центром описанной около треугольника окружности. Вокруг любого треугольника можно описать окружность и только одну.

10) Теорема о разделительном отрезке в треугольнике

Теорема: Отрезок, соединяющий вершину треугольника с противоположной стороной делит ее на отрезки, пропорциональные площадям образованных треугольников.

То есть

11) Средняя линия треугольника

Теорема: Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.

То есть и

12) Теорема синусов и теорема косинусов

Теорема синусов: Cтороны треугольника пропорциональны синусам противолежащих углов и каждое отношение стороны к синусу равно диаметру описанной около треугольника окружности.

То есть

Теорема косинусов: Квадрат стороны треугольника равне сумме квадратов двух других сторон минус удвоенное произведение этих сторон на синус угла между ними, то есть

13) Теорема Менелая

Теорема: Произведение отношений отрезков, на которые произвольная прямая делит стороны треугольника (или их продолжения) равно единице

То есть

Комментарий репетитора по математике: несправедливо выброшенная теорема из школьного курса геометрии. Рекомендую репетиторам включить ее в подготовку, по крайней мере к вузовским олимпиадам и вступительным экзаменам по математике в МГУ. В программу ЕГЭ теорема Менелая не входит, но несколько типов задач без нее решаются очень сложно.

14) Теорема Чевы

Теорема:если через вершины треугольника и произвольную внутреннюю точку провести отрезки к противоположным сторонам (чевианы), то их точки пересечения разделят стороны на отрезки, произведение отношений которых равно единице.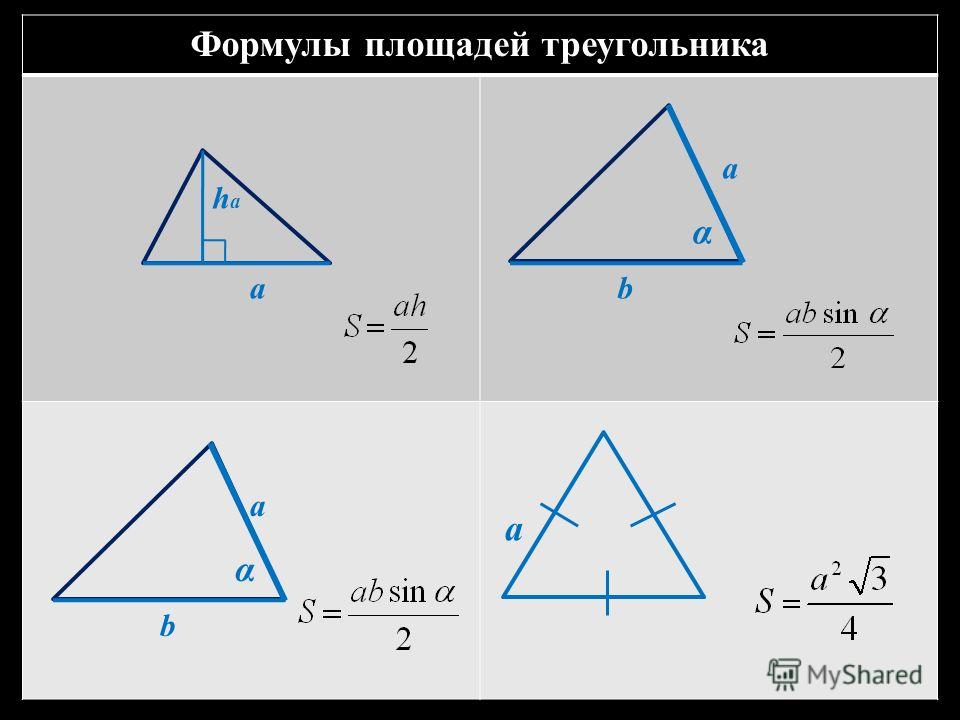

То есть

Колпаков А.Н. Репетитор по математике.

Метки: Геометрия, Справочник репетитора, Ученикам

Треугольник. Формулы определения и свойства треугольников.

В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.

Содержание:

Определение треугольника
Классификация треугольников
Свойства треугольников
Медианы треугольника
Биссектриссы треугольника
Высоты треугольника

Определение треугольника

Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр.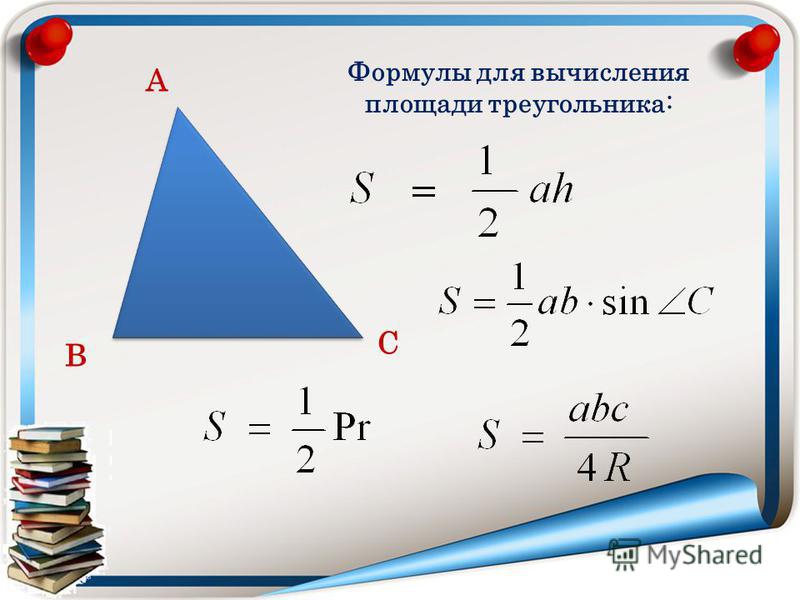 △ABC.

Треугольник ABC (△ABC)

Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.

Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:

угол α — ∠ВСА или ∠ACB;
угол β — ∠ВАC или ∠CAB;
угол γ — ∠АBC или ∠CBA;

Классификация треугольников

Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.

1.

Разносторонний – треугольник, у которого все стороны имеют разную длину.

a ≠ b ≠ c
∠ α ≠ ∠ β ≠ ∠ γ

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

a = b
∠ α=∠ β

3

.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

a = b = c
∠ α = ∠ β = ∠ γ = 60°

4.

Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

∠ α < 90°
∠ β < 90°
∠ γ < 90°

5.

Тупоугольный – треугольник, в котором один из углов больше 90°.

Два остальных угла – острые.

∠ α < 90°
∠ β < 90°
∠ γ > 90°

6.

Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

∠ α < 90°
∠ β < 90°
∠ γ = 90°

Свойства треугольника

1.Свойства углов и сторон треугольника.

Сумма всех углов треугольника равна 180°:

α + β + γ = 180°

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β, тогда a > b
если α = β, тогда a = b

2.

Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c
sin α		sin β		sin γ

3. Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a² = b² + c² — 2bc·cos α
b² = a² + c² — 2ac·cos β
c² = a² + b² — 2ab·cos γ

4. Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α

Медианы треугольника

Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

AO	=	BO	=	CO	=	2
OD		OE		OF		1

3. Медиана треугольника делит треугольник на две равновеликие по площади части

S_∆ABD = S_∆ACD
S_∆BEA = S_∆BEC
S_∆CBF = S_∆CAF

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

S_∆AOF = S_∆AOE = S_∆BOF =
= S_∆BOD = S_∆COD = S_∆COE

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны:

m_a = 12√2b²+2c²-a²
m_b = 12√2a²+2c²-b²
m_c = 12√2a²+2b²-c²

Формулы сторон через медианы

a =

√2(m_b²+m_c²)-m_a²

b =

√2(m_b²+m_c²)-m_b²

c =

√2(m_b²+m_c²)-m_c²

Биссектриссы треугольника

Биссектриса угла треугольника— луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника:

1. Биссектрисы треугольника пересекаются в одной точке О,которая называется ИНЦЕНТР. Инцентр равноудален от трех сторон треугольника, следовательно инцентр — центр вписанной окружности.

2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

AE	=	EC
AB	=	BC

3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Угол между La и La’ = 90°

4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

5. Если в треугольнике три биссектрисы равны, то треугольник — равносторонний.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

La =

√bcp(p-a)

b+c

Lb =

√bcp(p-b)

a+c

Lc =

√bcp(p-c)

a+b

p =

a + b + c

Формулы биссектрис треугольника через две стороны и угол:

La =

2bc·cos

a+b

Lb =

2ac·cos

a+c

Lc =

2ab·cos

b+c

Высоты треугольника

Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону.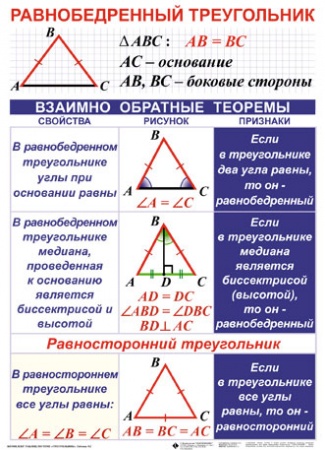

В зависимости от типа треугольника высота может содержаться

внутри треугольника — для остроугольного треугольника;
совпадать с его стороной — для катета прямоугольного треугольника;
проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

1. Высоты треугольника пересекаются в одной точке O, называемой ортоцентром треугольника.

2. Если в треугольнике две высоты равны, то треугольник — равнобедренный.

3. Если в треугольнике все высоты равны, то треугольник — равносторонний.

Формулы высот треугольника

h_a = b sin γ= c sin β
h_b= c sin α = a sin γ
h_c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь:

ha =

hb =

hc =

Прямоугольный треугольник, свойства, признаки и формулы

Прямоугольный треугольник, свойства, признаки и формулы.

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

Прямоугольный треугольник (понятие, определение)

Признаки равенства прямоугольных треугольников

Свойства прямоугольного треугольника

Формулы прямоугольного треугольника

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Прямоугольный треугольник (понятие, определение):

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

Сторона, противоположная прямому углу, называется гипотенузой. Гипотенуза (с греч. ὑποτείνουσα – «натянутая») – это самая длинная сторона прямоугольного треугольника, противоположная прямому углу.

Стороны, прилегающие к прямому углу, называются катетами. Катет (с греч. κάθετος – «перпендикуляр, опущенный, отвесный») – одна из двух сторон прямоугольного треугольника, образующих прямой угол.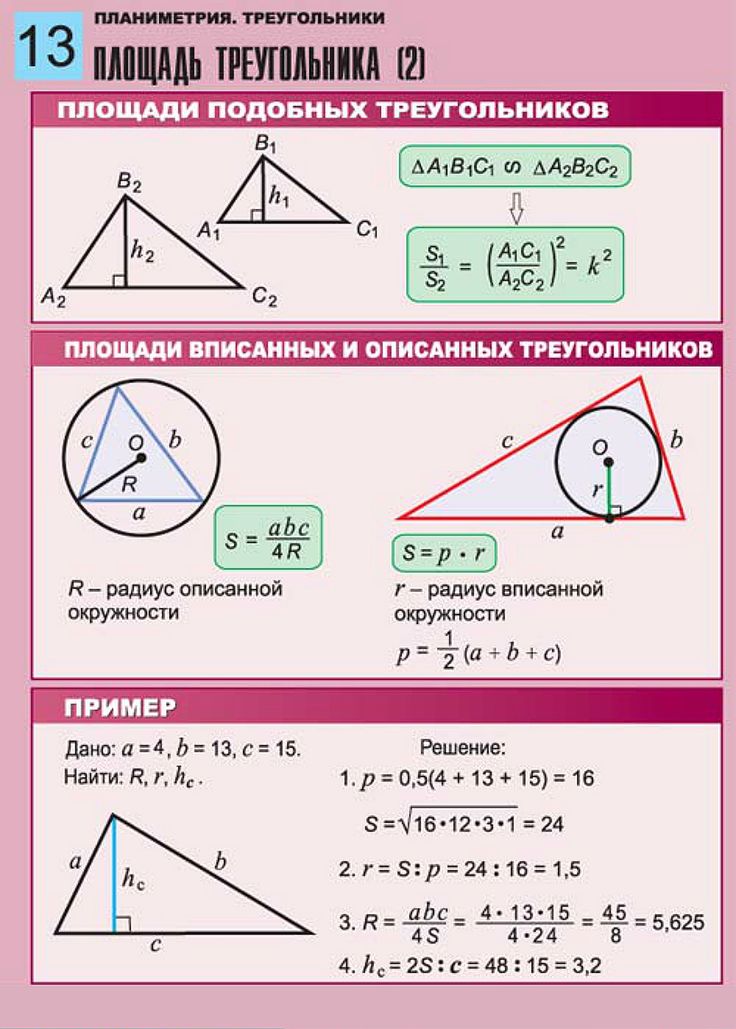

Для непрямоугольного треугольника гипотенуза и катеты не существуют.

Рис. 1. Прямоугольный треугольник

АВ, АС – катеты прямоугольного треугольника, ВС – гипотенуза прямоугольного треугольника, ∠ ВАС = 90°

Равнобедренный треугольник может быть прямоугольным (равнобедренным прямоугольным треугольником).

Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. В этом треугольнике каждый острый угол равен 45°.

Признаки равенства прямоугольных треугольников:

Признаки равенства прямоугольных треугольников основаны и вытекают из общих признаков равенства треугольников.

1. Равенство по двум катетам.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Рис. 2. Равенство прямоугольных треугольников по двум катетам

АВ = А₁В₁, АС = А₁С₁

2. Равенство по катету и прилежащему острому углу.

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 3. Равенство прямоугольных треугольников по катету и прилежащему углу

АВ = А₁В₁, ∠АВС = ∠А₁В₁С₁

3. Равенство по гипотенузе и острому углу.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 4. Равенство прямоугольных треугольников по гипотенузе и острому углу

ВС = В₁С₁, ∠АВС = ∠А₁В₁С₁

4. Равенство по гипотенузе и катету.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Рис. 5. Равенство прямоугольных треугольников по гипотенузе и катету

ВС = В₁С₁, АС = А₁С₁

5. Равенство по катету и противолежащему острому углу.

Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 6. Равенство прямоугольных треугольников по катету и противолежащему острому углу

АС = А₁С₁, ∠АВС = ∠А₁В₁С₁

Свойства прямоугольного треугольника:

1. В прямоугольном треугольнике сумма двух острых углов равна 90°.

2. В прямоугольном треугольнике катет, лежащий против угла в 30° , равен половине гипотенузы.

И наоборот, если в прямоугольном треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

Рис. 7. Прямоугольный треугольник с острым углом 30˚

b = c / 2

3. Теорема Пифагора:

Сумма квадратов катетов равна квадрату гипотенузы.

c² = a² + b² ,

где a, b – катеты, c – гипотенуза.

Рис. 8. Прямоугольный треугольник

4. В прямоугольном треугольнике центр описанной окружности – есть середина гипотенузы.

И соответственно радиус описанной окружности (R) равен половине гипотенузы.

где c – гипотенуза.

Рис. 9. Прямоугольный треугольник и описанная окружность

5. В прямоугольном треугольнике медиана, падающая на гипотенузу, равна половине гипотенузы.

Рис. 10. Прямоугольный треугольник и медиана, падающая на гипотенузу

АМ – медиана прямоугольного треугольника, падающая на гипотенузу, АМ = ВМ = МС, АМ = ВС/2

6. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника подобные исходному.

Рис. 11. Прямоугольный треугольник и высота, проведенная из вершины прямого угла

АВ/ВС = АН/АС = ВН/АВ

Формулы прямоугольного треугольника:

Пусть a и b – длины катетов прямоугольного треугольника, с – длина гипотенузы прямоугольного треугольника, h – высота прямоугольного треугольника, проведенная к гипотенузе (АН), R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 9, 11, 12).

Формулы сторон прямоугольного треугольника (a, b, c) по теореме Пифагора:

c² = a² + b² ,

a² = c² – b² ,

b² = c² – a² .

Формула радиуса вписанной окружности (r):

Рис. 12. Прямоугольный треугольник и вписанная окружность

Формула радиуса описанной окружности (R):

Формулы площади (S) прямоугольного треугольника:

Формулы высоты (h)прямоугольного треугольника:

Квадрат

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Коэффициент востребованности 24 063

Формула треугольника — Типы треугольников

Примечание: Оставшиеся два угла прямоугольного треугольника всегда острые. Важным свойством прямоугольных треугольников является Теорема Пифагора. Он утверждает, что в прямоугольном треугольнике, сумма квадратов основания и перпендикуляра равна квадрату гипотенузы треугольника.

На рисунке выше DABC — прямоугольный треугольник, поэтому (AB) ² + (АС) ² = (ВС) ² . Здесь AB = 6 и AC = 8, поэтому BC = 10, поскольку 6 ² + 8 ² = 36 + 64 = 100 = (BC) ² и BC = &redic;100.

Любой треугольник, в котором длины сторон относятся как 3:4, всегда является прямоугольным.

В общем случае, если x, by и z — длины сторон треугольника, в котором x ² + y ² = z ² , то такой треугольник называется прямоугольным.

Есть несколько пифагорейских троек, которые часто используются в вопросах. Лучше запомнить эти тройки.

3, 4 и 5
5, 12 и 13
7, 24 и 25
8, 15 и 17
9, 40 и 41
11, 60 и 61
12, 35 и 37
16, 63 и 65
20, 21 и 29
28, 45 и 53.

Любое кратное этих пифагорейских троек также будет пифагорейской тройкой, т. е. когда мы говорим, что это тройка 5, 12, 13, если мы умножим все эти числа на 3, это также будет тройкой, т. е. 15, 36, 39также будет пифагорейской тройкой.

(IV) 45 ° — 45 ° — 90 ° : Специальные треугольники: если три районы из треугольника 45 °. 90°, то перпендикулярная сторона этого прямоугольного треугольника в 1 / &редик; 2 раза больше гипотенузы треугольника. В треугольнике с углами 45°-45°-90° длины трех сторон этого треугольника относятся как 1:1: &redic;2.

Например, в ∆PQR, если PR = 2 см, то PQ = &redic;2 см и QR = &redic;2 см.

(v) 30 ° — 60 ° — 90 ° ТРИНГЛ. стороны этого треугольника находятся в отношении 1: &redic;3 : 2. Например, в ∆ABC, если AC = 3, то AB = 3&redic;3 и BC = 6. Подводя итог, приведенные ниже формулы могут быть применены к вычислить две другие стороны 30°-60°-9Треугольник 0°, когда дана одна из трех сторон.

Сторона, противоположная 30 ° = ½ гипотенузы.

Сторона, противоположная 60 ° = &redic;3/2 гипотенузы.

Некоторые важные свойства треугольников

(i) Сумма трех внутренних углов треугольника равна 180°.

In ∆ABC, ∠ABC + ∠BAC + ∠ACB = 180°

(ii) Сумма внутреннего угла и прилежащего к нему внешнего угла равна 180°.

На рисунке на предыдущей странице ∠ABC + ∠ABH = 180°

∠ABC + ∠CBI = 180°

(iii) Два внешних угла, имеющих одну и ту же вершину, конгруэнтны.

(iv) Мера внешнего угла равна сумме мер двух внутренних углов (называемых удаленными внутренними углами) треугольника, не смежного с ним.

(vi) Сумма любых двух сторон треугольника всегда больше третьей стороны.

В ∆ABC AB + BC > AC, а также AB + AC > BC и AC + BC > AB.

(vii) Разность любых двух сторон всегда меньше, чем разность третьей стороны.

Высота: Высота треугольника — это отрезок, проведенный из вершины перпендикулярно стороне, противоположной этой вершине. Относительно этой вершины и высоты противоположная сторона называется основанием.

Площадь треугольника равна: (длина высоты) × (длина основания) / 2,

BD = 5

В ∆ABC BD — высота до основания AC, а AE — высота до основания BC.

Формула треугольника : Площадь треугольника ∆ABC равна ½ × BD × AC = ½ × 5 × 8 = 20.

Площадь треугольника также равна (AE × BC) / 2. Если DABC вверху равнобедренный и AB = BC, то высота BD делит основание пополам; то есть AD = DC = 4. Точно так же любая высота равностороннего треугольника делит пополам сторону, к которой он обращен.

Конгруэнтность треугольников : Если стороны и углы одного треугольника равны соответствующим сторонам и углам другого треугольника, то говорят, что два треугольника равны.

Два треугольника конгруэнтны, если

Две стороны и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника (SAS).
2 угла и 1 сторона треугольника соответственно равны двум углам и соответствующей стороне другого треугольника (AAS).
Три стороны треугольника соответственно конгруэнтны трем сторонам другого треугольника (SSS).
1 сторона и гипотенуза прямоугольного треугольника соответственно конгруэнтны 1 стороне и гипотенузе другого прямоугольного треугольника. треугольник (правая сторона).

Подобие треугольников:

Говорят, что два треугольника подобны друг другу, если они похожи только по форме. Соответствующие углы этих треугольников равны, а соответствующие стороны только пропорциональны. Все конгруэнтные треугольники подобны, но не обязательно все подобные треугольники конгруэнтны.

Два треугольника подобны, если

Три стороны одного треугольника пропорциональны трем сторонам другого треугольника (SSS).
Два угла треугольника соответственно равны двум углам другого треугольника (AA).
Две стороны треугольника пропорциональны двум сторонам другого треугольника, а прилежащие к ним углы равны (SAS).

Рекомендуемое действие:

Начните подготовку с БЕСПЛАТНОГО доступа к 25+ макетам, 75+ видео и 100+ тестам по главам. Зарегистрируйтесь сейчас

Свойства треугольников :

Если два треугольника подобны, отношение сторон = отношение высот = отношение медиан = отношение биссектрис угла = отношение внутренних радиусов = отношение радиусов описанной окружности.
Соотношение областей = B ₁ H ₁ /B ₂ H ₂ = (S ₁) ² /(S ₂) ², где B ₁. ₁ — основание и высота первого треугольника, а b ₂ и h ₂ — основание и высота второго треугольника. s ₁ и s ₂ — соответствующие стороны первого и второго треугольника соответственно.
Два треугольника на каждой стороне перпендикуляра, проведенного из вершины прямого угла к наибольшей стороне, т. е. гипотенузе, подобны друг другу, а также подобны большему треугольнику.

∆ DBA аналогичен ∆ DCB, который аналогичен ∆ BCA.

Высота от вершины прямого угла до гипотенузы – это среднее геометрическое отрезков, на которые делится гипотенуза.

т. е. (DB) ² = AD * DC

Центр окружности : Центр окружности — это центр описанной окружности треугольника. Его можно найти пересечением серединных перпендикуляров.

Incenter : Incenter — это точка, представляющая центр вписанной окружности многоугольника. Соответствующий радиус вписанной окружности известен как внутренний радиус вписанной окружности.

Формулы треугольников | Суперпроф

Определение треугольника

Мы все сталкивались с треугольниками в своей жизни. От Великой пирамиды Гизы до веселых воскресных головоломок : мы все видели, как выглядят треугольники или пирамиды. Вопрос в том, как определить, что такое треугольник ?

Давайте взглянем на самое основное определение треугольника.

Tri- Префикс, означающий три
Угол Плодовое, которое образуется между двумя линиями
Треугольник Полигон с тремя сторонами, угла которых образуют три угла
. можно найти в самом слове. Независимо от того, с каким треугольником вы имеете дело, треугольник всегда будет иметь три стороны и три угла.
Лучшие репетиторы по математике
Поехали
Свойства треугольника
Теперь, когда мы знаем определение треугольника, давайте посмотрим на некоторые из свойств треугольников.
6
Собственность Наименование Описание
1 Угла Свои Свойство суммы длины Сумма двух сторон больше длины последней стороны
3 Свойство наибольшего угла Угол, противоположный наибольшей стороне, является наибольшим углом Угол, противоположный наибольшей стороне, является наибольшим углом
4 Свойство внешнего угла Внешний угол любого внутреннего угла треугольника равен сумме двух других внутренних углов
Как видите, эти свойства могут оказаться довольно сложными — что такое внешний угол и что такое «противоположная» сторона? Рассмотрим эти свойства более подробно.
Свойство суммы углов
Свойство суммы углов указывает, что все три внутренних угла треугольника должны составлять в сумме 180 градусов. Давайте посмотрим, что такое внутренние углы.
Определение
Внутренний угол Внутренний угол треугольника — это любой угол, образованный сторонами треугольника и находящийся внутри треугольника.

Можете ли вы сказать, какие из них являются внешними и внутренними треугольниками? Посмотрите на таблицу ниже и проверьте, правильно ли вы ответили.
Интерьер?
A No
B Yes
C Yes
D Yes
E №
Свойство суммы длины
Свойство суммы длины указывает, что длина двух сторон всегда больше последней стороны. Мы можем понять это свойство , выбрав наименьшую длину, которую вы можете придумать для всех сторон. Возьмем, к примеру, длину 1 см.
903
AB + BC 1 + 1 = 2
BC + CA 1 + 1
Как видите, сумма любой из сторон всегда больше последней стороны.
Свойство наибольшего угла
Свойство наибольшего угла утверждает, что наибольший угол лежит напротив наибольшей стороны треугольника. Доказательство для этого свойства довольно сложное, однако оно сводится к тому, что чем больше угол, тем длиннее линия, которую он проецирует. Угол0003 80 градусов проецирует более длинную линию
Угол 10 градусов проецирует меньшую линию
Свойство внешнего угла равен сумме двух других внутренних углов.
Давайте посмотрим на это на практике.

Внешний уголок 109 градусов
Угол A + Угол C 38 + 71 = 109
Увлажненный триангл
This Is Its Triangre. Начнем с рассмотрения равностороннего треугольника. Равносторонний треугольник можно определить по таблице ниже.

Равносторонний треугольник Определение
1 A Треугольник
2 Три равных сторона
3 Три равных углов
4 903 различать виды треугольников. Каждый треугольник имеет различных обозначений. Вы должны ознакомиться с этими обозначениями, чтобы понять, с каким типом треугольника вы имеете дело.

A Three same angles
B Three same sides

In order to find the perimeter or area of an equilateral triangle , просто следуйте приведенным ниже формулам.

Периметр P = 3*s
Площадь A =
Разносторонний треугольник
Из четырех треугольников давайте рассмотрим следующий тип треугольника: разносторонний треугольник. Разносторонний треугольник может быть определен таблицей ниже.

Scalene Triangle Definition
1 A triangle
2 Нет равных углов
3 Нет равных сторон
Как видите, разносторонний треугольник совершенно особенный. Это единственный тип треугольника, в котором по крайней мере две стороны или углы не равны. Помните, что когда две стороны имеют одинаковую длину, они автоматически образуют два угла одинаковой длины. Рассмотрим обозначения разносторонних треугольников.

404
Прямоугольный треугольник
Последний тип треугольника — прямоугольный. Этот тип треугольника представляет собой треугольник с наибольшим количеством специальных свойств. Давайте посмотрим на эти свойства.

A Укал нет той же длины, как и рынок по кривым
B Никакой стороны не имеют такой же длины. найти периметр или площадь разностороннего треугольника, просто следуя формулам ниже.

Периметр P = a+b+c
Площадь A = ½ *b*h
Равнобедренный треугольник
Третьим наиболее распространенным треугольником является равнобедренный треугольник . Рассмотрим свойства равнобедренного треугольника.
Isosceles Triangle Определение
1 A Triangle
2 09
3 Две стороны равны
Как упоминалось в предыдущем разделе, когда две стороны треугольника имеют одинаковую длину, они образуют два угла одинакового размера. Давайте посмотрим на обозначения для этого типа треугольника.
Периметр P = 2*S+C
Область A = ½*B*H
9 9037 9 9037 9 9037 9 9037 9 9037 9 9037 9 9037 9 9037 99
Property Description
1 Has one right angle (90 degrees)
2 The side opposite the right angle is the hypotenuse
3 Прямой угол — это наибольший угол прямоугольного треугольника

Прямоугольный треугольник обозначение можно увидеть ниже.

Теорема Пифагора
Теорема Пифагора применима только к прямоугольным треугольникам. В нем говорится, что если вы знаете, что длина гипотенузы в квадрате равна сумме квадратов двух других сторон. Давайте посмотрим, что это на самом деле означает.

Formula
c hypotenuse
a One side
b The other side

Калькулятор прямоугольного треугольника | Определение
Создано Альваро Диесом, Матеушем Мухой и Петром Малеком
Отзыв Джека Боуотера
Последнее обновление: 12 апреля 2022 г.
Содержание:
Что такое прямоугольный треугольник (или прямоугольный треугольник)?
Калькулятор гипотенузы
Как найти площадь прямоугольного треугольника
Другие соображения при работе с прямоугольным треугольником
Особые треугольники
Особые прямоугольные треугольники
Прямоугольные треугольники и параллелограммы
90 треугольники, встречающиеся по Пифагору
Тени и прямоугольные треугольники (радиус Земли)
FAQ
Калькулятор прямоугольного треугольника поможет вам найти длины сторон прямоугольного треугольника . Этот решатель треугольников также научит вас находить площадь прямоугольного треугольника, а также даст много информации о практическом использовании прямоугольного треугольника.
Что такое прямоугольный треугольник (или прямоугольный треугольник)?
Прежде всего, давайте объясним, что такое прямоугольный треугольник. Определение очень простое и может даже показаться очевидным для тех, кто его уже знает: прямоугольный треугольник — это треугольник, в котором один и только один из углов равен ровно 90° . Очевидно, что два других угла будут меньше прямого угла, потому что сумма всех углов треугольника всегда равна 180°.
В прямоугольном треугольнике стороны определяются особым образом. Сторона, противолежащая прямому углу, всегда является наибольшей в треугольнике и получает название «гипотенуза». Две другие стороны называются катетами. Связь между гипотенузой и каждым из катетов очень проста, как мы увидим 9.0003 когда мы будем говорить о теореме Пифагора .
Калькулятор гипотенузы
Если вы хотите вычислить только гипотенузу прямоугольного треугольника, эта страница и калькулятор прямоугольного треугольника отлично подойдут. Однако мы также рекомендуем использовать специальный инструмент, разработанный нами в Omni Calculators: калькулятор гипотенузы. Гипотенуза находится напротив прямого угла и может быть решена с помощью теоремы Пифагора. В прямоугольном треугольнике с катетом а и b и с гипотенузой c , теорема Пифагора утверждает, что: a² + b² = c² .
Чтобы найти c , извлеките квадратный корень из обеих частей, чтобы получить c = √(b²+a²) . Это расширение теоремы Пифагора можно рассматривать как «формулу гипотенузы». Калькулятор теоремы Пифагора также является отличным инструментом для вычисления гипотенузы.
Давайте теперь решим практический пример того, что потребуется, чтобы вычислить гипотенузу прямоугольного треугольника без использования каких-либо калькуляторов доступен в Omni:
Получите значения a и b ,
Квадрат a и b ,
Суммируйте оба значения: a² + b² ,
Извлеките квадратный корень из результата,
Квадратный корень даст положительный и отрицательный результат. Так как мы имеем дело с длиной, не обращайте внимания на отрицательный результат,
Полученное значение является значением гипотенузы c .
Теперь давайте посмотрим что будет происходить с помощью одного из калькуляторов Omni , например, калькулятор прямоугольного треугольника на этой веб-странице:
Вставьте значение a и b в калькулятор
Получить значение c немедленно
В качестве бонуса вы получите значение площади такого треугольника.
Как найти площадь прямоугольного треугольника
Мы уже видели, что расчет площади прямоугольного треугольника очень прост с калькулятором прямоугольного треугольника. В Omni Calculators у нас есть калькулятор, специально разработанный для этой цели: калькулятор площади прямоугольного треугольника. Среди вас есть даже один для авантюристов, которые хотели бы вычислить площадь любого треугольника: калькулятор площади треугольника. Давайте теперь более подробно рассмотрим, как вычислять площади прямоугольных треугольников.
Способ нахождения площади прямоугольного треугольника довольно прост. Все, что вам нужно, это длины основания и высоты . В прямоугольном треугольнике основание и высота – две стороны, образующие прямой угол. Поскольку умножение этих значений на значения вместе дает площадь соответствующего прямоугольника, а треугольник составляет половину этой площади, формула:
площадь = (1/2) основания * высота .
Если вы не знаете ни основания, ни высоты, вы можете найти их по теореме Пифагора. Используйте калькулятор прямоугольного треугольника, чтобы проверить свои расчеты или вычислить площадь треугольников со сторонами, имеющими большую или десятичную длину.
Другие соображения при работе с прямоугольным треугольником
Теперь мы увидим другие вещи, которые можно вычислить из прямоугольного треугольника с помощью некоторых инструментов, доступных в Omni. Стороны треугольника имеют определенный градиент или наклон. Мы можем использовать калькулятор уклона, чтобы определить наклон каждой стороны. Формула для наклона (в случае, если вы хотите рассчитать вручную):
наклон = (y₂ - y₁)/(x₂ - x₁)
Таким образом, если координаты (1,-6) и ( 4,8) , наклон сегмента равен (8 + 6)/(4 - 1) = 14/3 . Простой способ определить, является ли треугольник правильным, и вы просто знаете координаты, — посмотреть, умножаются ли наклоны любых двух линий на равные -1 .
Существует простой способ преобразования углов из радианов в градусы и градусы в радианы с помощью преобразования углов:
Если угол в радианах — умножить на 180/π ,
Если угол в градусах — умножить на π/180 .
Иногда вы можете столкнуться с проблемой отсутствия двух или даже трех длин сторон. В таких случаях калькулятор прямоугольного треугольника, калькулятор гипотенузы и метод, как найти площадь прямоугольного треугольника, не помогут. Вы должны использовать тригонометрические функции, чтобы найти недостающие части. Это можно сделать вручную или с помощью калькулятора треугольников.
Особые треугольники
Прямоугольный треугольник — это лишь один из множества существующих особых треугольников. Эти треугольники обладают одной или несколькими особыми характеристиками, которые делают их уникальными. Например, как мы видели, прямоугольный треугольник имеет прямой угол и, следовательно, гипотенузу, что делает его уникальным видом треугольника. Помимо прямоугольного треугольника, есть и другие особые треугольники с интересными свойствами.
Одним из самых известных специальных треугольников является равносторонний треугольник, у которого три равные стороны и все его углы равны 60°. Это значительно упрощает создание калькулятора решения треугольников, такого как калькулятор равностороннего треугольника, в котором можно вычислять различные параметры такого треугольника.
Другим особым треугольником является равнобедренный треугольник, у которого две стороны одинаковой длины , а значит, два угла одинаковой величины. В отличие от равностороннего треугольника, равнобедренные треугольники бывают разных форм, но все они имеют определенные свойства, которые используются калькулятором равнобедренных треугольников для получения всех параметров этих треугольников.
Есть много других особых треугольников. Однако сейчас мы рассмотрим несколько совершенно особых прямоугольных треугольников, которые помимо того, что они прямоугольные, обладают и другими особыми свойствами, которые делают их интересными.
Особые прямоугольные треугольники
Среди всех особых прямоугольных треугольников, пожалуй, самым особенным является так называемый треугольник «45 45 90». Это прямоугольный треугольник, который также является равнобедренным треугольником . Оба его катета имеют одинаковую длину (равнобедренные), а также он имеет ту особенность, что непрямые углы составляют ровно половину размера прямого угла, что и дало название прямоугольному треугольнику.
Этот прямоугольный треугольник можно получить, если разделить квадрат на его диагональ . Вот почему обе катеты (стороны квадрата) имеют одинаковую длину. Для тех, кто хочет узнать больше о самых особенных из особых прямоугольных треугольников, мы рекомендуем проверить калькулятор треугольника 45 45 90, созданный для этой цели.
Еще один очень интересный треугольник из группы особых прямоугольных треугольников это так называемый «30 60 90 «треугольник. Название происходит от наличия одного прямого угла (90 °), затем одного угла 30 ° и еще одного 60 °. Эти углы особенные из-за значений их тригонометрических функций (косинуса, синуса, тангенса и т. д. ).Последствия этого можно увидеть и понять с помощью калькулятора треугольника 30 60 90 , но для тех, кому лень переходить по ссылке, мы суммируем некоторые из них здесь . Предполагая, что более короткая сторона имеет длину a , далее следует треугольник:
вторая длина равна a√3 ,
гипотенуза равна 2a ,
площадь равна a²√(3/2) ,
периметр равен a(3 + √3) .
Прямоугольные треугольники и параллелограммы
На первый взгляд может показаться, что прямоугольный треугольник и параллелограмм не имеют ничего общего. Как решатель треугольников может помочь вам понять параллелограмм? Реальность такова, что любой параллелограмм можно разложить на 2 или более прямоугольных треугольника . Давайте возьмем пример прямоугольника, который проще всего увидеть.
Представьте себе прямоугольник, любой прямоугольник. Теперь нарисуйте след на одной из диагоналей этого прямоугольника (подробнее об этом вы можете узнать в калькуляторе диагоналей прямоугольника). Если разделить прямоугольник диагональю, то получится два прямоугольных треугольника . Глядя на треугольники, нет необходимости использовать калькулятор прямоугольного треугольника, чтобы убедиться, что оба треугольника равны, поэтому их площади будут одинаковыми. Это означает, что площадь прямоугольника вдвое больше площади каждого треугольника .
Если мы подумаем об уравнениях, это имеет смысл, поскольку площадь прямоугольника со сторонами a и b равна площади = a * b , а для прямоугольного треугольника равна площади = основание * высота / 2 , что в данном случае будет означать area = a * b /2 . Это именно то, что мы уже видели, просто разрезав прямоугольник по диагонали.
Это был простой пример прямоугольника, но то же самое относится и к площади квадрата. Для других параллелограммов процесс немного усложняется (он может включать до 4-х прямоугольных треугольников разных размеров), но при некоторой сноровке вы можете использовать ту же идею и вычислить площадь параллелограмма с помощью прямоугольного треугольника. угловые треугольники. Вы можете, конечно, быть еще более эффективным и просто использовать наш калькулятор.
Пифагорейские тройки, треугольники и математика
Геометрия и многоугольники, особенно треугольники, всегда идут рука об руку. Свойства некоторых треугольников, например прямоугольных, обычно интересны и шокируют даже нематематиков. Теперь мы рассмотрим интересный набор чисел очень тесно связан с прямоугольными треугольниками, которые любят математики, и, возможно, вы тоже.
Эти наборы чисел называются пифагорейскими тройками и представляют собой наборы из 3 целых чисел (назовем a , b и c ) и удовлетворяют теореме Пифагора: a² + b² = c² . То есть они могли бы образовать прямоугольный треугольник со сторонами длиной a , b и c . Количество чисел, удовлетворяющих этому соотношению, ограничено, но математики находят удовольствие в поиске новых.
Помимо любопытного фактора этой связи, она имеет некоторые интересные свойства, которые используются в криптографии . Учитывая приложения, которые можно найти для таких наборов чисел, математики исследовали даже больше, используя 4, 5. .. и больше наборов чисел, которые удовлетворяют аналогичному соотношению, в котором сумма квадратов всех чисел, кроме одного , дайте квадрат оставшегося числа.
С этими пифагорейскими тройками тесно связана также печально известная последняя теорема Ферма , в которой почти легендарный загадочный математик Пьер Ферма утверждал, что не может быть набора из трех целых чисел, удовлетворяющих соотношению: aⁿ + bⁿ = cⁿ для n больше 2. Эта гипотеза не была доказана математически и считается одной из самых важных математических проблем века.
Тени и прямоугольные треугольники (радиус Земли)
Мы много говорили о треугольниках, в частности о прямоугольных треугольниках и их приложениях в математике и геометрии. О чем мы еще не говорили, так это о полезности прямоугольных треугольников для расчетов в реальной жизни . Может показаться, что возможности применения вне геометрии ограничены, но давайте взглянем на тени.
Да, тени. Темный оттенок, отбрасываемый объектом при его освещении. Если бы вы посмотрели на форму, созданную тенью, объектом и землей, вы бы заметили, что это на самом деле прямоугольный треугольник! По крайней мере, когда объект совершенно вертикальный, а земля горизонтальная. В большинстве случаев это так или, по крайней мере, достаточно близко. Это означает, что мы можем использовать калькулятор прямоугольного треугольника, чтобы найти различную информацию об объектах под солнцем. Посмотрим, как.
Представьте, что у вас есть здание , высоту которого мы хотим узнать , но вы не можете измерить его напрямую, потому что оно слишком высокое, чтобы сбросить рулетку сверху. Что вы можете сделать, так это измерить длину тени на улице. Затем с помощью любого угломера и листа бумаги можно узнать угол между тенью и землей. Зная, что угол между зданием и землей равен 90°, вы можете ввести эти значения данных в калькулятор сторон и углов прямоугольного треугольника и получить значение высоты здания.
Используя эту технику, вы можете измерять высоту многих объектов при условии, что у вас есть яркий солнечный день или другие источники света для освещения объекта. На самом деле, это был очень распространенный метод измерения в старые времена. Вероятно, самое интересное и умопомрачительное использование прямоугольных треугольников принадлежит Эратосфену, которому удалось использовать прямоугольные треугольники и тени для измерения радиуса Земли , и теперь мы собираемся объяснить, как он это сделал.
Эратосфен заметил, что в день летнего солнцестояния было на Земле место, где колодцы не имели тени в полдень, т. е. солнце светило прямо на них. Заметив это, он поставил столб известной высоты на известном расстоянии от этого колодца и измерил величину тени в одно и то же время дня и в один и тот же день года в обоих местах. Затем, используя прямоугольные треугольники и тригонометрию, он смог измерить угол между двумя городами, а также радиус Земли , так как он знал расстояние между городами.
Это был поразительный подвиг, который теперь можно сделать гораздо проще, просто используя калькуляторы Omni, которые мы создали для вас .
Часто задаваемые вопросы
Длины каких сторон образуют прямоугольный треугольник?
Длины сторон a , b , c образуют прямоугольный треугольник тогда и только тогда, когда они удовлетворяют a² + b² = c² . Мы говорим, что эти числа образуют Тройка Пифагора .
2, 3 и 4 образуют прямоугольный треугольник?
У нас есть 4² = 16 и 2² + 3² = 4 + 9 = 13 , поэтому сумма квадратов двух меньших чисел НЕ равна квадрату наибольшего числа. То есть 2 3 и 4 не образуют пифагорову тройку, или, другими словами, не существует прямоугольного треугольника со сторонами 2, 3 и 4.
Как найти центр описанной окружности прямоугольного треугольника?
Для прямоугольного треугольника центр описанной окружности, т. е. центр описанной на треугольнике окружности, совпадает с серединой самой длинной стороны треугольника (ее гипотенуза ).
Как найти ортоцентр прямоугольного треугольника?
Ортоцентр прямоугольного треугольника, т. е. точка пересечения высот треугольника, совпадает с вершиной прямоугольного треугольника.
Альваро Диес, Матеуш Муха и Петр Малек
c (гипотенуза)
Посмотреть 18 подобных калькуляторов треугольников0011
Особые прямоугольные треугольники. Калькулятор | Формула
Автор: Hanna Pamuła, PhD прямоугольные треугольники
Специальные формулы для прямоугольных треугольников
Специальные правила для прямоугольных треугольников
Калькулятор специального прямоугольного треугольника — пример
FAQ
Этот специальный калькулятор прямоугольных треугольников поможет вам решить выбранный треугольник в мгновение ока. Выберите нужный вам треугольник и введите заданные значения — остальные параметры будут рассчитаны автоматически. Специальные прямоугольные треугольники — это прямоугольные треугольники, для которых существуют простые формулы. Это позволяет выполнять быстрые вычисления, поэтому вам не нужно использовать теорему Пифагора или какой-то продвинутый метод. Прокрутите вниз, чтобы узнать больше о специальных формулах и правилах для прямоугольных треугольников.
Специальные прямоугольные треугольники 30 60 90
Специальный прямоугольный треугольник 30° 60° 90° — один из самых популярных прямоугольных треугольников. Его свойства настолько особенные, потому что это половина равностороннего треугольника.
Если вы хотите узнать больше об этой особой форме, проверьте наш калькулятор, посвященный треугольнику 30° 60° 90°.
Специальные прямоугольные треугольники 45 45 90
Другой известный специальный прямоугольный треугольник — это треугольник 45° 45° 90°. Это единственный возможный прямоугольный треугольник, который также является равнобедренным. Кроме того, это форма, которая получается, когда мы разрезаем квадрат по диагонали:
Хотите знать свойства этого треугольника? Посмотрите на наш инструмент о треугольнике 45° 45° 90°.
Другие специальные прямоугольные треугольники
Существует много специальных прямоугольных треугольников, ниже вы найдете те, которые реализованы в нашем инструменте:
Специальные формулы прямоугольных треугольников
В правильном месте. Взгляните на эту аккуратную таблицу ниже, и все должно быть ясно! В этой таблице вы найдете формулы соотношения между углами специального прямоугольного треугольника, катетами, гипотенузой, площадью и периметром:
Special right triangle a (shorter leg) b (longer leg) c (hypotenuse) Area Perimeter Angle α Angle β
30° — 60° — 90° x x√3 2x x²√3/2 x(3+√3) 30° 60°
45° — 45° — 90° x x x√2 x²/2 x(2+√2) 45° 45°
x — 2x x 2x x√5 x² x(3+√5 ) ~26. 5° ~63.5°
x — 3x x 3x x√10 3x²/2 x(4+√10) ~18.5° ~71,5°
3x — 4x — 5x 3x 4x 5x 6x² 12x ~37° ~53°
Особые правила прямоугольного треугольника
Особые прямоугольные треугольники — это треугольники, которые имеют некоторые особенности, облегчающие вычисления. Конечно, самое важное специальное правило прямоугольного треугольника заключается в том, что у них должен быть один прямой угол плюс эта дополнительная функция. Как правило, специальные прямоугольные треугольники можно разделить на две группы:
Существует множество различных правил и вариантов, по которым мы можем выбрать треугольник и назвать его 9. 0007 специальный . В нашем специальном калькуляторе прямоугольных треугольников мы реализовали пять выбранных треугольников: два по углам и три по сторонам.
Специальный калькулятор прямоугольного треугольника — пример
Давайте рассмотрим пример: мы хотим найти длину гипотенузы прямоугольного треугольника, если длина одного катета 5 дюймов, а один угол равен 45°.
Выберите правильный тип специального прямоугольного треугольника . В нашем случае это треугольник 45°-45°-90°.
Введите заданное значение . Мы знаем, что сторона равна 5 дюймам, поэтому мы вводим это значение в поле a или b — неважно, где, потому что это равнобедренный треугольник.
Вау! Специальный калькулятор прямоугольного треугольника решил ваш треугольник! Теперь мы знаем, что:
Вторая ветвь b равна 5 в
Гипотенуза c равна 7,07 в
Периметр равен 17,07 в
Площадь нашего специального треугольника составляет 12,5 кв. дюймов.
Не ждите больше, попробуйте сами!
Часто задаваемые вопросы
Какие формулы для треугольника 45 45 90?
Треугольник 45° 45° 90° имеет следующие формулы, где x длина любой из равных сторон:
Гипотенуза = x√2 ;
Площадь = x²/2 ; и
Периметр = x(2+√2) ;
Как решить специальный прямоугольный треугольник 30 60 90?
Чтобы решить 30° 60° 90° специального прямоугольного треугольника, выполните следующие действия:
Найдите длину более короткой стороны. Мы назовем это x .
Более длинная сторона будет равна x√3 .
Его гипотенуза будет равна 2x .
Площадь равна A = x²√3/2 .
Наконец, периметр равен P = x(3+√3) .
Какие два особых треугольника в тригонометрии?
30° 60° 90° треугольники и 45° 45° 90° (или равнобедренный прямоугольный треугольник) — это два особых треугольника в тригонометрии . Хотя существует более двух различных специальных прямоугольных треугольников, они быстрее всего распознаются и с ними проще всего работать. Примером специальных прямоугольных треугольников, не основанных на углах, является прямоугольный треугольник, стороны которого образуют пифагорову тройку.
Является ли число 3, 4 и 5 пифагорейской тройкой?
Да . Целые числа a = 3 , b = 4 и c = 5 образуют пифагорову тройку, поскольку a² + b² = c² , а треугольник со сторонами abc является прямоугольным особым треугольником.
Ханна Памула, кандидат наук
Особый треугольник
Периметр
Посмотрите 18 подобных калькуляторов треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника и методы вычисления… Еще 151 здесь!
Площадь треугольника — это все пространство, занимаемое тремя сторонами данного треугольника. Площадь варьируется от одного типа данного треугольника к другому в зависимости от длины сторон и внутренних углов. Как правило, чтобы найти площадь, мы выполняем половину произведения основания и высоты.
В этой статье о площади треугольника , вы узнаете о формулах площади треугольника, о том, как найти площадь данного треугольника, как вычислить площадь треугольника с различными формами и многие другие понятия. относительно того же с решенными примерами.
Узнайте больше о геометрических фигурах здесь.
Какова площадь треугольника?
Треугольник — это замкнутая фигура с тремя углами, тремя сторонами и тремя вершинами. Рассмотрим треугольник с 3 вершинами, где X, Y и Z представлены как △XYZ (где △ представляет собой символ треугольника). Треугольник иногда также называют трехсторонним многоугольником/треугольником. 92\). Для расчета площади существуют предопределенные формулы для квадратов, треугольников, прямоугольников, кругов и т. д. В этой статье мы рассмотрим формулы площади треугольника, которые математически записываются как:
A = 1/2 × b × h .
Узнайте о центре треугольника здесь, в связанной статье
Формула площади треугольника
Существует три типа треугольников, основанных на сторонах; Равносторонний треугольник, равнобедренный треугольник и разносторонний треугольник. Кроме того, в зависимости от угла, они классифицируются как остроугольный треугольник, прямоугольный треугольник и тупоугольный треугольник. Общая формула площади треугольника эквивалентна половине высоты базового времени. то есть
Площадь треугольника (A)=\(\frac{1}{2}\times b\left(\text{base}\right)\times h\left(\text{height}\right)\)
Следовательно, чтобы вычислить площадь треугольника, мы должны иметь значения его основания (b) и высоты (h). Эта формула используется во всех типах треугольников, будь то разносторонний, равнобедренный или равносторонний. Различные формулы для вычисления площади перечислены ниже:
Технические характеристики Формула площади треугольника
Площадь, когда нам даны основание и высота треугольника. (A)=\(\frac{1}{2}\times b\left(\text{base}\right)\times h\left(\text{height}\right)\)
Площадь по формуле Герона. \(A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}\)
Здесь a, b и c — три стороны, а s — полупериметр треугольника и равен.
\(s=\frac{(a+b+c)}{2}\)
Площадь вычисляется с учетом двух сторон и прилежащего угла. 92}\)
Здесь b=основание и a=длина равной стороны.
Узнайте о центре тяжести треугольника здесь, в связанной статье
Как найти площадь треугольника?
Давайте обсудим различные типы треугольников, такие как площадь прямоугольного треугольника, равностороннего треугольника, равнобедренного треугольника, а также их формулы площади.
Узнайте больше о высоте и расстоянии здесь.
Площадь прямоугольного треугольника
В прямоугольном треугольнике или прямоугольном треугольнике один из углов равен 90°, а сумма двух других углов составляет 90°. Ниже показано изображение прямоугольного треугольника. Здесь в прямоугольном треугольнике три стороны известны как основание, высота и гипотенуза.
Гипотенуза – это наибольшая сторона треугольника, противоположная прямому углу. Площадь прямоугольного треугольника:
\(A=\frac{1}{2}\times \text{Основание}\times \text{Высота(Перпендикулярное расстояние)}\) 92}\)
Аналогичным образом можно вычислить и площадь разностороннего треугольника. Разносторонний треугольник — это треугольник, у которого все три стороны имеют разную длину, а все три угла имеют разную степень. Однако сумма трех внутренних углов любого треугольника всегда составляет 180 градусов, что соответствует свойствам суммы углов треугольника.
Узнайте о 3D измерениях здесь.
Периметр треугольника
Периметр треугольника представляет собой длину, пройденную вокруг треугольника, и определяется путем сложения всех трех сторон треугольника.
Периметр треугольника=\(\text{P(периметр)=(a+b+c) единиц}\)
, где a,b и c — стороны треугольника.
Площадь треугольника с тремя сторонами
Площадь треугольника с тремя сторонами разной длины можно рассчитать по формуле Герона. Формула Герона включает два основных шага.
Первый шаг заключается в определении полупериметра треугольника путем суммирования всех трех сторон треугольника и деления на два.
Следующим шагом является реализация значения полупериметра треугольника в основном уравнении под названием «Формула Герона» для расчета площади.
\(A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}\)
Где s — полупериметр треугольника.
\(s=\frac{(a+b+c)}{2}\)
Площадь с двумя сторонами и прилежащим к ней углом треугольника (SAS)
Рассмотрим приведенный ниже треугольник ABC, где вершина углы равны ∠A, ∠B и ∠C, а стороны равны a,b и c. Тогда формула для определения площади: 92\)).
У прямоугольного треугольника один из углов равен 90º. В прямоугольном треугольнике наибольшая сторона называется гипотенузой, которая всегда является стороной, противоположной прямому углу.
Вычисление длин сторон всегда будет удовлетворять теореме Пифагора в прямоугольном треугольнике.
Периметр прямоугольного треугольника равен сумме мер всех трех сторон = 3а, где а — сторона.
Поскольку длины сторон разностороннего треугольника неравны, а углы разной величины, разносторонний треугольник не проявляет симметрии.
Когда все стороны различны, можно вычислить площадь по формуле Герона.
Ознакомьтесь с другими темами по математике здесь.
Решенные примеры площади треугольника
Теперь давайте обсудим, как вычислить площадь треугольника, применяя различные формулы.
Решено Пример 1: Вычислите площадь треугольника, основание которого равно 12 см, а высота 5 см.
Площадь треугольника (A)=\(\frac{1}{2}\times b\left(\text{base}\right)\times h\left(\text{height}\right)\) 92\)
Решено Пример 6: Площадь прямоугольника в два раза больше площади треугольника. Периметр прямоугольника равен 58 см. Чему равна площадь треугольника?
Решение: Согласно вопросу, площадь прямоугольника = 2 × площадь треугольника И мы знаем, что площадь прямоугольника = длина × ширина
Периметр прямоугольника равен сумме его четырех сторон.
∴ Периметр прямоугольника = 2(длина + ширина)
И согласно вопросу Периметр прямоугольника равен 58. Итак, 2(длина + ширина) = 58 92\)
Так как сумма всех внутренних углов треугольника = 180º, то площадь кругов внутри треугольника имеет секторный угол в сумме 180º. Кроме того, угол сектора полного круга = 360º ⇒ Площадь кругов, которые также находятся в части треугольника (A) = πr2/2 ⇒ A = [3,14 × (22)]/2 = 6,28 см2 ∴ Требуемая площадь = 54 – 6,28 = 47,72 см2
Решено Пример 9: Диагональ квадрата равна стороне равностороннего треугольника. Если площадь квадрата 12 кв.см, то какова площадь равностороннего треугольника? 92 ⇒ a = 2 \sqrt{3} см \)
Диагональ квадрата d = a√2 ⇒ d = 2√3 × √2 ⇒ d = 2√6 Мы знаем, что площадь равностороннего треугольника A = √3/ 4 сторона ² Здесь диагональ квадрата равна стороне равностороннего треугольника сторона = d ⇒ A=3√4(26−−√)2⇒A=3√4(24)⇒A=34(26) 2⇒A=34(24) ⇒ A = 6√3 см²
Решено Пример 10: Рассмотрим прямоугольный треугольник. Площади трех квадратов, начерченных на каждой из его сторон, равны 25 кв.м., 16 кв.м. и 9 кв.м. соответственно. Чему равна площадь треугольника 9?0011
Решение: Площадь 1-го квадрата = 25 кв. м ⇒ Сторона = 5 м > Площадь 2-го квадрата = 16 кв. м ⇒ Сторона = 4 м > Площадь 3-го квадрата = 9 кв. м ⇒ Сторона = 3 м ∴ 3 стороны прямоугольного треугольника равны 5, 4 и 3. Здесь основание = 3, а высота = 4 (должна выполняться ∵ теорема Пифагора) >Площадь прямоугольного треугольника = (1/2) × основание × высота ⇒ Площадь = (1/2) × 3 × 4 = 6 кв. м
Узнайте о центре окружности треугольника здесь, в связанной статье
Мы надеемся, что приведенная выше статья о площади треугольника поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о площади треугольника
В. 1 Что такое треугольники?
Ответ 1 В геометрии треугольники — это многоугольники, имеющие три стороны и три вершины. Это 2D-фигуры с тремя прямыми сторонами. Сумма всех трех углов треугольника равна 180°.
»
В.2 Что такое треугольник?
Ответ 2 Типы треугольников по сторонам; Равносторонний треугольник, равнобедренный треугольник и разносторонний треугольник. Типы треугольников по углам; Остроугольный треугольник, прямоугольный треугольник и тупоугольный треугольник.
”
Q.3 Какова формула прямоугольного треугольника?
Ответ 3 Прямоугольный треугольник = половина (основание × перпендикуляр).
Q.4 Что такое равносторонний треугольник?
Ответ 4 Равносторонний треугольник – это треугольник, у которого все три стороны равны.
В.5 Как найти периметр и площадь прямоугольного треугольника?
Ответ 5 Площадь прямоугольного треугольника с основанием, равным «b», и высотой, равной «h», определяется по формуле 1/2 × b × h. Периметр получается сложением всех сторон.
Скачать публикацию в формате PDF
Подробнее на testbook.com
Среднее значение по математике: определение, статистика с типами, формулами и ключевыми терминами Факторы жизнеобеспечения, экологические циклы
Люди: демографическое давление, демографический дивиденд, человеческий капитал — оцепленная им область, в уплощенной плоскости. Как мы знаем, треугольник — это фигура с замком, имеющая три стороны и три вершины. Таким образом, формула площади треугольника — это все пространство, занимаемое внутри трех сторон треугольника. Общая процедура нахождения площади треугольника формула задается половиной произведения его основания и высоты.
В широком спектре термин «область» описывается как область, занимаемая внутри поля плоского объекта или фигуры. Измерение выполняется в квадратных единицах со средней единицей измерения в квадратных метрах (м ² ). Для расчета площади существуют предопределенные формулы для квадратов, прямоугольников, кругов, треугольников и т. д. В этом блоге мы будем изучать формулы площади треугольников для различных типов треугольников, а также некоторые проблемы с иллюстрациями.
Как определить площадь треугольника?
Площадь треугольника формулы может быть описана как общая область, ограниченная тремя сторонами любого конкретного треугольника.
Следовательно, чтобы найти площадь трехстороннего многоугольника, мы должны знать основание (b) и высоту (h). Это относится ко всем категориям треугольников, будь то разносторонний, равнобедренный или равносторонний. Обратите внимание на то, что основание и высота треугольника находятся под прямым углом друг к другу. Тогда единица площади рассчитывается в квадратных единицах (м ² , см ² ).
Иллюстрация: Можете ли вы найти площадь треугольника с основанием b = 3 см и высотой h = 4 см?
Используя формулу,
Площадь треугольника, A = 1/2 × b × h = 1/2 × 4 см × 3 см = 2 см × 3 см = 6 см²
Помимо формулы накладных расходов, мы есть метод Герона для вычисления площади треугольника, когда мы определяем длину его трех сторон. Точно так же тригонометрические функции используются для определения площади, когда мы знаем две стороны и угол между ними в треугольнике. Мы проанализируем область для всех приведенных здесь ситуаций.
Формула площади треугольника
Формула площади треугольника приведена ниже:
Формула площади треугольника = A = ½ (b × h) квадратных единиц
Где b и h — основание, а высота треугольника соответственно.
Теперь давайте разберемся, как вычислить площадь треугольника по данной формуле. Соответственно, как найти площадь треугольника с 3 сторонами по формуле Герона с примерами.
Площадь прямоугольного треугольника
Треугольник с углом в девяносто градусов, также называемый прямоугольным треугольником, имеет один угол, равный 90°, а сумма двух дополнительных острых углов составляет 90°. В результате высота треугольника будет равна длине перпендикулярной стороны.
Площадь прямоугольного треугольника = A = ½ × основание × высота (перпендикулярное пространство)
Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, в котором все стороны равны. Стойка-болт, проведенная от вершины треугольника к основанию, делит основание на две одинаковые части. Чтобы оценить площадь равностороннего треугольника, нужно знать размеры его сторон.
• Площадь равностороннего треугольника = A = (√3)/4 × сторона²
Площадь равнобедренного треугольника
У равнобедренного треугольника две равные стороны, а также углы, противоположные равным сторонам.
• Площадь равнобедренного треугольника = 1/4 b√(4a² – b²)
Периметр треугольника
Граница треугольника – это расстояние, заключенное вокруг треугольника, которое рассчитывается путем подсчета всех трех сторон. треугольника.
• Периметр треугольника = P = (a + b + c) единиц
Где a, b и c — поля треугольника.
Формула Герона – площадь треугольника с тремя сторонами
Часть треугольника с тремя сторонами измененных размеров можно найти по формуле Герона. Формула Герона состоит из двух важных шагов. Первым шагом является нахождение полупериметра треугольника путем суммирования всех трех сторон треугольника и деления его на 2. Следующим шагом является применение значения полупериметра треугольника в центральной формуле, называемой «Формула Герона». чтобы найти площадь треугольника.
Площадь треугольника по двум сторонам и углу между ними
В настоящее время возникает вопрос, когда мы знаем две стороны треугольника и угол между ними, то как найти его площадь.
Итак, если заданы любые два поля и угол между ними, то методы вычисления площади треугольника задаются следующим образом:
Площадь (∆ABC) = ½ bc sin A
Площадь (∆ABC) = ½ ab sin C
Площадь (∆ABC) = ½ ca sin B
Эти формулы очень легко вывести и проанализировать.
Например, если в ∆ABC A = 30° и b = 2, то c = 4 в единицах. Тогда площадь будет;
Площадь (∆ABC) = ½ bc sin A
= ½ (2) (4) sin 30
= 4 x ½ (поскольку sin 30 = ½)
= 2 кв. ед.
Площадь треугольника Решенные примеры
Иллюстрация 1:
Найдите площадь остроугольного треугольника с основанием 13 дюймов и высотой 5 дюймов.
Объяснение:
A = (½) × b × h кв. Единицы измерения
⇒ A = (½) × (13 дюймов) × (5 дюймов)
⇒ A = (½) × (65 дюймов²)
⇒ A = 32,5 дюйма²
Иллюстрация 2:
Найдите площадь треугольника с углом в девяносто градусов, основанием 7 см и высотой 8 см.
Объяснение:
A = (½) × b × h квадрат Единицы измерения
⇒ A = (½) × (7 см) × (8 см)
⇒ A = (½) × (56 см²)
⇒ A = 28 см²
Иллюстрация 3:
Найдите площадь тупоугольного треугольника с основанием 4 см и высотой 7 см.
Объяснение:
A = (½) × b × h квадратных единиц
⇒ A == (½) × (4 см) × (7 см)
⇒ A = (½) × (28 см²)
⇒ A = 14 см²
Часто задаваемые вопросы по формуле площади треугольника
Что вы понимаете под площадью треугольника?
Площадь треугольника — это площадь, ограниченная его границей или тремя сторонами треугольника.
Какой будет площадь, если известны две стороны треугольника и угол между ними?
Площадь будет эквивалентна половине произведения двух заданных сторон и синуса угла между ними.
Как узнать площадь треугольника, у которого известны три стороны?
Хотя значения трех сторон треугольника известны, мы сможем найти площадь этого треугольника, используя формулу Герона.
Как найти площадь треугольника с помощью векторов?
Предположим, векторы u и v образуют треугольник в пространстве. Теперь площадь этого треугольника эквивалентна половине произведения этих двух векторов, так что A = ½ |u × v|.
Как вычислить площадь треугольника по формуле?
Для предполагаемого треугольника, где основание треугольника равно b, а высота равна h, площадь треугольника может быть предварительно рассчитана по формуле, например; A = ½ (b × h) кв. Unit
Формулы площади треугольника
Вы можете узнать о формулах площади треугольника для различных типов треугольников, таких как равносторонний треугольник, прямоугольный треугольник и равнобедренный треугольник ниже.
• Площадь прямоугольного треугольника
Треугольник с углом в девяносто градусов, также называемый прямоугольным, имеет один угол, равный 90°, а сумма двух других острых углов составляет 90°. По этой причине высота треугольника равна длине стороны прямого угла.
Площадь прямоугольного треугольника = A = 1/2 × B × H
• Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, у которого все стороны равны. Перпендикуляр, проведенный из вершины треугольника к основанию, делит основание на две одинаковые части. Чтобы оценить площадь равностороннего треугольника, мы должны знать размеры его сторон.
Площадь равностороннего треугольника = A = (√3)/4 × сторона²
• Площадь равнобедренного треугольника
У равнобедренного треугольника двойные стороны равны, и углы, противоположные равным сторонам, также равны.
Площадь равнобедренного треугольника = A = 1/4 × b√4a ² −b ² 4a ² −b ²
Где «b» — основание, а «a» — степень единицы. одинаковых сторон.
Обратите внимание на приведенную ниже таблицу, в которой приведены все формулы площади треугольника.
Данные размеры Формула площади треугольника
Пока указаны основание и высота треугольника. A = 1/2 (основание × высота)
В то время как стороны треугольника указаны как a, b и c. (формула Герона)
Площадь разностороннего треугольника = √s(s−a)(s−b)(s−c)s(s−a)(s−b)(s−c)
, где a, b и c — стороны, а «s» — полупериметр; с = (а + b + с)/2
Пока указаны две стороны и прилежащий угол. A = 1/2 × плоскость 1 × плоскость 2 × sin(θ)
где θ — угол между данными двумя сторонами
Пока известны база и высота. Площадь прямоугольного треугольника = 1/2 × Основание × Высота
Пока это равносторонний треугольник и одна сторона указана. Площадь равностороннего треугольника = (√3)/4 × плоскость ²
Хотя это равнобедренный треугольник и известны эквивалентные сторона и основание. Площадь равнобедренного треугольника = 1/4 × b√4a ² −b ² 4a ² −b ²
равная сторона.
Площадь треугольника
Вы вычисляете площадь треугольника, применяя различные методы. Например, есть основная формула, согласно которой площадь треугольника равна произведению основания на высоту. Конечно, этот метод работает только тогда, когда вы определяете высоту треугольника.
Дополнительным является формула Герона, которая вычисляет площадь по трем сторонам треугольника в явном виде как квадратный корень из произведения s(s – a)(s – b)(s – c), где s – полу периметр треугольника, то есть s = (a + b + c)/2.
Теперь рассмотрим формулу площади треугольника, если вы определите две стороны и угол между ними. Предположим, мы знаем значения двух сторон треугольника a и b и прилежащего угла C.

г. Опустите под прямым углом AD из вершины А треугольника на сторону ВС и обозначьте эту высоту h. Тогда конкретный треугольник ACD является прямоугольным, поэтому sin C будет равен h/b. Следовательно, h = b sin C. Следовательно, площадь треугольника равна половине произведения основания на высоту h, следовательно, площадь также равна половине ab sin C. Несмотря на то, что фигура представляет собой остроугольный треугольник, вы можете понять из рассуждения в предыдущем разделе, что h = b sin C также выполняется, когда треугольник прямоугольный или тупоугольный. В результате получаем общую формулу
Как определить площадь поверхности треугольников
Треугольник — это многоугольник, три стороны которого могут быть одинаковыми или неравными. Площадь поверхности треугольника – это вся площадь поверхности внутри границ треугольника. Площадь поверхности указывается в квадратных единицах, таких как квадратные сантиметры или квадратные дюймы. Вычисление площади поверхности треугольника — обычная задача геометрии.
Измерьте три стороны треугольника. Самая длинная сторона является основанием треугольника. Если треугольник на бумаге, вы можете отмаркировать основание размером; или же, напишите свою базовую длину на блокноте.
Оцените высоту треугольника. Высота — это расстояние от основания до самого высокого угла треугольника. Линия высоты вертикальна к основанию и пересекает противоположный угол треугольника. Нарисуйте эту линию высоты на своем треугольнике, если это возможно, и отметьте измерение. Линия высоты будет проходить от конца до конца внутри треугольника.
Увеличьте базовую длину на высоту. Например, если ваш базовый размер равен 10 см, а высота равна 6 см, основание, увеличенное на высоту, составит 60 квадратных см.
Разделите результат умножения основания на высоту на два, чтобы определить площадь поверхности. На рисунке, когда вы делите 60 квадратных см на два, у вас есть итоговая площадь поверхности 30 квадратных см.
Чтобы найти площадь треугольника, умножьте основание на высоту, а затем разделите на 2. Деление на 2 происходит из-за того, что параллелограмм можно разделить на 2 треугольника.
Поскольку часть параллелограмма равна A = B * H, площадь треугольника должна составлять половину площади параллелограмма. В итоге формула площади треугольника:
A= 1/2.b.h Или A= b.h/2
Где b — основание, h — высота, а · означает умножение.
Основание и высота треугольника должны быть под прямым углом друг к другу. На каждой из приведенных ниже иллюстраций основание является стороной треугольника. Тем не менее, в зависимости от треугольника, высота может быть или не быть стороной треугольника. Например, в прямоугольном треугольнике на иллюстрации 2 высота является стороной треугольника, поскольку она перпендикулярна основанию. В треугольниках на рисунках 1 и 3 боковые стороны не расположены под прямым углом к основанию, поэтому для обозначения высоты нарисована пунктирная линия.
Иллюстрация 1: Найдите площадь остроугольного треугольника с основанием 15 дюймов и высотой 4 дюйма.
Ответ:
A= 1/2 .b.h
A= 1/2· (15 дюймов) · (4 дюйма)
A= 1/2· (60 дюймов²)
A= 30 дюймов²
_______________________________________________
Иллюстрация 2: Найдите площадь прямоугольного треугольника с основанием 6 см и высотой 9 см.
Ответ:
A= 1/2.b.h
A= 1/2 ·(6 см) · (9 см)
A= 1/2,(54 см²)
A= 27 см²
________________________________________
Рисунок 3: Найдите площадь тупоугольного треугольника с основание 5 дюймов и высота 8 дюймов.
a=1/2.b.h
Ответ:
A= 1/2 (5 дюймов) · (8 дюймов)
A= 1/2 (40 дюймов²)
A= 20 дюймов²
_______________________________________
Иллюстрация 4: Коврик в форме треугольника имеет площадь 18 квадратных футов и основание 3 фута. Найдите высоту.
Ответ:
На этом рисунке мы указали площадь треугольника и одно измерение, и нам предлагается работать в обратном направлении, чтобы найти другое измерение.
a= 1/2.b.h
18 футов² = 1/2\B7 (3 фута) · h
Умножая по отдельности две части уравнения на 2, мы получаем:
36 футов² = (3 фута) · h
Разделив две части уравнения по отдельности на 3 фута, мы получим:
12 футов = h
Вычислив это уравнение, мы получим:
h = 12 ft
__________________________________________
Краткий обзор: Укажите основание и высоту треугольника, мы можем узнать площадь. Зная площадь и основание или высоту треугольника, мы можем обнаружить другое измерение. Формула площади треугольника:
A=1/2bh или A=b.h/2, где b — основание, а h — высота.
Какова площадь треугольника по формуле?
Все мы знаем, что треугольник — это многоугольник, у которого три стороны. Площадь треугольника – это размер площади, покрытой треугольником. Получаем площадь треугольника в квадратных единицах. Площадь треугольника можно определить, используя следующие две формулы: основание увеличивается на высоту треугольника, деленную на 2, а вторая — методом Герона. Давайте обсудим формулу площади треугольника по существу.

Формула площади треугольника
Что такое площадь треугольника?
Площадь многоугольника — это количество квадратных единиц, покрываемых многоугольником. Площадь треугольника определяется путем умножения основания треугольника и высоты треугольника, а затем деления на 2. Деление на 2 подготовлено по той причине, что треугольник является частью параллелограмма, который можно разделить на 2 треугольника.
Площадь параллелограмма = Основание × Высота
Где,
В основание параллелограмма
Н высота параллелограмма
Точно так же треугольник является половиной параллелограмма, поэтому площадь треугольника равна:
A= 12×b×h
Где,
B основание треугольника
Н высота треугольника
Метод Герона для вычисления площади треугольника
Формула Герона — это метод вычисления площади треугольника, когда заданы длины всех трех сторон треугольника.
Пусть a, b и c — длины сторон треугольника.
Площадь треугольника равна:
Площадь=s(s−a)(s−b)(s−c)− √
Где s — половина периметра,
s= a+b+c2
Мы также можем определить площадь треугольника с помощью следующих процедур:
1. В этом методе две Стороны, одна из которых включает Угол, является точным
Площадь = 12×a×b×sinc
В приведенной выше формуле a, b, c должны рассматриваться как длины сторон треугольника
2. В этом методе мы находим площадь равностороннего треугольника
Площадь = 3√×a24
3. Таким образом, мы находим площадь треугольника на координатной плоскости с помощью Матрицы
12×⎡⎣⎢x1x2x3y1y2y3111⎤⎦⎥
Где, (x1, y1), (x2, y2), (x3, y3) — прямые трех вершин
4. В этом методе мы находим площадь треугольника, в котором два вектора из одной вершины находятся под рукой.
Площадь треугольника = 12(u→×v→)
Решенные иллюстрации
Q.1: Предположим, что стороны прямоугольного треугольника ABC имеют следующие размеры; 5 см, 12 см и 13 см.
No related posts.
Навигация по записям
Предыдущая статья6A3A ru: Диваны, кресла, пуфы
Следующая статьяНа одной координатной плоскости постройте графики функций и найдите приближенно координаты точек пересечения: 20 баллов ваши только помогите с этим… На одной координатной плоскости постройте графики
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта