Функции найти первую производную: Дифференцирование функции, заданной неявно

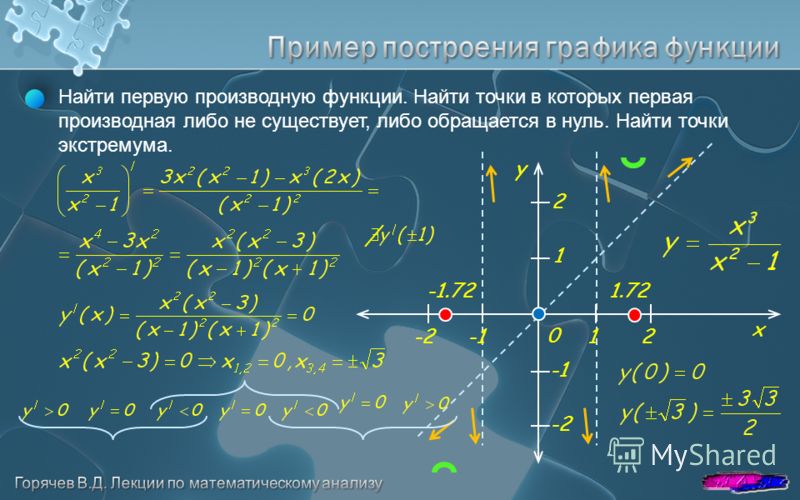
Найти первую и вторую производные функции с примером решения

Содержание:

1. Производная постоянной функции
2. Производная степенной функции
3. Производные тригонометрических функций
4. Производная логарифмической функции
5. Пример с решением

Производная постоянной функции

Производная функции —постоянное число, выражается формулой

Доказательство

Для любых имеем Отсюда при любом отношение и, следовательно,

 

Замечание. Постоянный множитель можно выносить за знак производной, т. е. . Действительно, если , то, по формуле 2 (см. теорему 5.3), что и требовалось показать.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Производная степенной функции

Производная функции , показатель которой является целым положительным числом, выражается формулой .

Доказательство. Используя формулу бинома Ньютона, можно записать

Таким образом, при имеем

Так как

Замечание. Случай степенной функции, показатель которой является любым вещественным числом.

Возможно вам будут полезны данные страницы:

Найти производную функции

Уравнения касательной и нормали

Найти предел используя правило лопиталя

Наибольшее и наименьшее значение функции

Производные тригонометрических функций

1) Производная функции выражается формулой

Доказательство. Имеем

Таким образом, при

Так как (первый замечательный предел), a в силу непрерывности

функции , то

 

2) Производная функции у — cos х выражается формулой

Доказательство. Имеем

Таким образом, при

Так как в силу непрерывности функции , то

 

3) Производная функции выражается формулой

Доказательство. Так как то по cos х теореме 5.3 получаем

следовательно,

 

4) Производная функция выражается формулой

Доказательство. Так как то, sinx аналогично предыдущему,

следовательно,

Производная логарифмической функции

Производная функции выражается формулой

Доказательство. Имеем

Таким образом, при

или

Положив имеем

(второй замечательный предел), а так как логарифмическая функция является непрерывной, то

Следствие. Если

Пример с решением

Используя правила и формулы дифференцирования, найти производную функции

Решение:

Имеем

Mathway | Популярные задачи

1	Trovare la Derivata — d/dx	натуральный логарифм x
2	Вычислим интеграл	интеграл натурального логарифма x по x
3	Trovare la Derivata — d/dx	e^x
4	Вычислим интеграл	интеграл e^(2x) по x
5	Trovare la Derivata — d/dx	1/x
6	Trovare la Derivata — d/dx	x^2
7	Trovare la Derivata — d/dx	1/(x^2)
8	Trovare la Derivata — d/dx	sin(x)^2
9	Trovare la Derivata — d/dx	sec(x)
10	Вычислим интеграл	интеграл e^x по x
11	Вычислим интеграл	интеграл x^2 по x
12	Вычислим интеграл	интеграл квадратного корня из x по x
13	Trovare la Derivata — d/dx	cos(x)^2
14	Вычислим интеграл	интеграл 1/x по x
15	Вычислим интеграл	интеграл sin(x)^2 по x
16	Trovare la Derivata — d/dx	x^3
17	Trovare la Derivata — d/dx	sec(x)^2
18	Вычислим интеграл	интеграл cos(x)^2 по x
19	Вычислим интеграл	интеграл sec(x)^2 по x
20	Trovare la Derivata — d/dx	e^(x^2)
21	Вычислим интеграл	интеграл в пределах от 0 до 1 кубический корень из 1+7x по x
22	Trovare la Derivata — d/dx	sin(2x)
23	Trovare la Derivata — d/dx	tan(x)^2
24	Вычислим интеграл	интеграл 1/(x^2) по x
25	Trovare la Derivata — d/dx	2^x
26	График	натуральный логарифм a
27	Trovare la Derivata — d/dx	cos(2x)
28	Trovare la Derivata — d/dx	xe^x
29	Вычислим интеграл	интеграл 2x по x
30	Trovare la Derivata — d/dx	( натуральный логарифм от x)^2
31	Trovare la Derivata — d/dx	натуральный логарифм (x)^2
32	Trovare la Derivata — d/dx	3x^2
33	Вычислим интеграл	интеграл xe^(2x) по x
34	Trovare la Derivata — d/dx	2e^x
35	Trovare la Derivata — d/dx	натуральный логарифм 2x
36	Trovare la Derivata — d/dx	-sin(x)
37	Trovare la Derivata — d/dx	4x^2-x+5
38	Trovare la Derivata — d/dx	y=16 корень четвертой степени из 4x^4+4
39	Trovare la Derivata — d/dx	2x^2
40	Вычислим интеграл	интеграл e^(3x) по x
41	Вычислим интеграл	интеграл cos(2x) по x
42	Trovare la Derivata — d/dx	1/( квадратный корень из x)
43	Вычислим интеграл	интеграл e^(x^2) по x
44	Вычислить	e^infinity
45	Trovare la Derivata — d/dx	x/2
46	Trovare la Derivata — d/dx	-cos(x)
47	Trovare la Derivata — d/dx	sin(3x)
48	Trovare la Derivata — d/dx	1/(x^3)
49	Вычислим интеграл	интеграл tan(x)^2 по x
50	Вычислим интеграл	интеграл 1 по x
51	Trovare la Derivata — d/dx	x^x
52	Trovare la Derivata — d/dx	x натуральный логарифм от x
53	Trovare la Derivata — d/dx	x^4
54	Оценить предел	предел (3x-5)/(x-3), если x стремится к 3
55	Вычислим интеграл	интеграл x^2 натуральный логарифм x по x
56	Trovare la Derivata — d/dx	f(x) = square root of x
57	Trovare la Derivata — d/dx	x^2sin(x)
58	Вычислим интеграл	интеграл sin(2x) по x
59	Trovare la Derivata — d/dx	3e^x
60	Вычислим интеграл	интеграл xe^x по x
61	Trovare la Derivata — d/dx	y=x^2
62	Trovare la Derivata — d/dx	квадратный корень из x^2+1
63	Trovare la Derivata — d/dx	sin(x^2)
64	Вычислим интеграл	интеграл e^(-2x) по x
65	Вычислим интеграл	интеграл натурального логарифма квадратного корня из x по x
66	Trovare la Derivata — d/dx	e^2
67	Trovare la Derivata — d/dx	x^2+1
68	Вычислим интеграл	интеграл sin(x) по x
69	Trovare la Derivata — d/dx	arcsin(x)
70	Оценить предел	предел (sin(x))/x, если x стремится к 0
71	Вычислим интеграл	интеграл e^(-x) по x
72	Trovare la Derivata — d/dx	x^5
73	Trovare la Derivata — d/dx	2/x
74	Trovare la Derivata — d/dx	натуральный логарифм 3x
75	Trovare la Derivata — d/dx	x^(1/2)
76	Trovare la Derivata — d/d@VAR	f(x) = square root of x
77	Trovare la Derivata — d/dx	cos(x^2)
78	Trovare la Derivata — d/dx	1/(x^5)
79	Trovare la Derivata — d/dx	кубический корень из x^2
80	Вычислим интеграл	интеграл cos(x) по x
81	Вычислим интеграл	интеграл e^(-x^2) по x
82	Trovare la Derivata — d/d@VAR	f(x)=x^3
83	Вычислим интеграл	интеграл 4x^2+7 в пределах от 0 до 10 по x
84	Вычислим интеграл	интеграл ( натуральный логарифм x)^2 по x
85	Trovare la Derivata — d/dx	логарифм x
86	Trovare la Derivata — d/dx	arctan(x)
87	Trovare la Derivata — d/dx	натуральный логарифм 5x
88	Trovare la Derivata — d/dx	5e^x
89	Trovare la Derivata — d/dx	cos(3x)
90	Вычислим интеграл	интеграл x^3 по x
91	Вычислим интеграл	интеграл x^2e^x по x
92	Trovare la Derivata — d/dx	16 корень четвертой степени из 4x^4+4
93	Trovare la Derivata — d/dx	x/(e^x)
94	Оценить предел	предел arctan(e^x), если x стремится к 3
95	Вычислим интеграл	интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x
96	Trovare la Derivata — d/dx	3^x
97	Вычислим интеграл	интеграл xe^(x^2) по x
98	Trovare la Derivata — d/dx	2sin(x)
99	Вычислить	sec(0)^2
100	Trovare la Derivata — d/dx	натуральный логарифм x^2

Найти первую производную функции

Все ресурсы для предварительного исчисления

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 Следующая →

Precalculus Help » Вводный расчет » Производные » Найдите первую производную функции

Рассмотрим функцию

Какова первая производная функции ?

Возможные ответы:

Правильный ответ:

Объяснение:

Обратите внимание, что  определено для всех 

Используя законы логарифмирования, мы можем записать как .

Использование цепного правила и правила произведения . У нас есть:

 .

Обратите внимание,

 .

 

Теперь замените , и мы получим окончательный ответ:

Сообщить об ошибке

Найдите производную от .

Возможные ответы:

Правильный ответ:

Объяснение:

Здесь используется простое экспоненциальное правило производных.

Умножьте значение показателя степени на функцию, затем вычтите 1 из старого показателя степени, чтобы получить новый показатель степени.

Формула выглядит следующим образом:

.

Используя нашу функцию,

 где и мы получаем следующую производную,

.

 

Сообщить об ошибке

Найдите производную от .

Возможные ответы:

Правильный ответ:

Объяснение:

Для этой задачи нам нужно использовать цепное правило.

Цепное правило гласит, что нужно работать снаружи внутрь. В этом случае внешняя функция  и внутренняя функция  . Затем производная становится внешней функцией, умноженной на производную внутренней функции.

Таким образом, мы используем следующую формулу

.

В нашем случае и .

Следовательно, результат

.

Сообщить об ошибке

Найдите первую производную следующей функции:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти первую производную полинома, все, что нам нужно знать, это как применить правило степени к простому члену с показателем степени:

Приведенная выше формула говорит нам, что для получения производной члена с коэффициентом и показателем степени , мы просто умножаем член на и вычитаем 1 из показателя степени. С учетом этого возьмем производную функции в задаче почленно:

Сообщить об ошибке

Найдите производную следующей функции:

Возможные ответы:

Правильный ответ:

Объяснение:

Мы видим, что наша функция включает ряд членов, возведенных в степень, поэтому нам нужно будет применить правило степени, а также правило цепочки, чтобы найти производную функции. Сначала мы применяем правило степени ко всем терминам в скобках, а затем применяем цепное правило, умножая весь результат на производную только от выражения в скобках:

Сообщить об ошибке

Какая первая производная от

по отношению к ?

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку мы берем производную по   , мы применяем степенное правило только к терминам, которые содержат . Поскольку все термины содержат , мы рассматриваем  как константу.

Производная константы всегда .

Итак, производная от

это ноль.

Сообщить об ошибке

Найти первую производную от

относительно

Возможные ответы:

Правильный ответ:

5

Объяснение:

Производная константы равна .

Сообщить об ошибке

Найдите первую производную от

относительно

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните правило степени, согласно которому нужно умножить на показатель степени перед константой, а затем вычесть показатель степени на 1.

Результат:

 

Возьмем производную от следующего члена:

Производную от :

Сила чего-то есть.

 

Наш результат:

 

Сообщить об ошибке

Найти первую производную функции

.

Возможные ответы:

Правильный ответ:

Объяснение:

Для функции

первая производная равна

Итак, для

первая производная равна

Сообщить об ошибке

Найти первую производную от

относительно .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти производную этого уравнения, вспомните правило степени, которое гласит: умножьте показатель степени перед константой, а затем вычтите единицу из показателя степени.

Возможна работа индивидуально с каждым термином:

Производное

IS,

Для Следующего семестра:

Производное:

Таким образом, Ответ:

. следующий термин:

Производная от :

Любая производная от константы .

 

Итак, первая производная от

равна

Сообщить об ошибке

← Предыдущая 1 2 3 4 5 Далее →

Уведомление об авторских правах

Все ресурсы Precalculus

12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Учитесь по понятиям

Что означает производная первого порядка? Ну, это говорит нам несколько вещей, где находится функция…

Краткий обзор

• Первая производная в первую очередь говорит нам о направлении, в котором движется функция. То есть он говорит нам, увеличивается функция или уменьшается.
• Первую производную можно интерпретировать как мгновенную скорость изменения.
• Первую производную также можно интерпретировать как наклон касательной.

Производная как наклон касательной

Напомним, что определение производной

$$ \displaystyle\lim_{h\to 0} \frac{f(x+h)-f(x)}{(x+h) — x}. $$

Без ограничения эта дробь вычисляет наклон линии, соединяющей две точки функции (см. левый график ниже).

Единственное, что делает предел, — это перемещает две точки ближе друг к другу, пока они не окажутся прямо друг над другом. Но фундаментальный расчет все же наклон. Таким образом, конечным результатом является наклон линии, касательной к кривой в точке $$(x, f(x))$$.

92 — 8 = 7 $$

Отвечать

Касательная в точке $$x = 1$$ имеет наклон $$m = 7$$.

Возрастание и убывание

Знак производной в конкретной точке скажет нам, возрастает или убывает функция вблизи этой точки. Это становится очевидным, когда мы думаем о производной как о наклоне касательной. Как показано на двух графиках ниже, когда наклон касательной положителен, функция в этой точке будет возрастать. Точно так же, когда наклон касательной отрицательный, функция будет уменьшаться. 92 + х — 12) = 6 (х + 4) (х — 3) $$

Шаг 2

Нарисуйте быстрый график производной.

Шаг 3

Интерпретируйте график.

Мы знаем, что когда производная положительна, функция возрастает. График выше показывает, что производная положительна (т. е. выше оси $$x$$), когда $$x 3$$.

Мы также можем видеть, что производная отрицательна (ниже оси $$x$$), когда $$-4

Отвечать

Функция возрастает на промежутках из $$(-\infty,-4)\cup(3,\infty)$$. Точно так же функция убывает на интервале $$(-4,3)$$.

График функции показан ниже для справки.

Производная как скорость изменения

Предположим, что $$D(t)$$ представляет расстояние бегуна от стартовой линии. Тогда производная от $$D(t)$$ определяется выражением

$$D'(t) = \lim_{h\to 0}\frac{D(t+h) — D(t)}{(t+h)-t}$$

Без ограничения дробь представляет

$$ \начать{выравнивать*} \frac{D(t+h) — D(t)}{(t+h)-t} & = \frac{\mbox{Расстояние, пройденное между двумя временами}}{\mbox{Прошедшее время}}\ \[6pt] & = \frac{\mbox{Изменение расстояния}}{\mbox{Изменение времени}}\\[6pt] & = \mbox{Средняя скорость изменения расстояния во времени}\\[6pt] & = \mbox{Средняя скорость} \конец{выравнивание*} $$

Когда мы применяем ограничение, истекшее время приближается к нулю. Таким образом, значение предела — это скорость в конкретный момент времени. Это по-прежнему скорость изменения, но теперь она мгновенная.

Пример 3

Предположим, что расстояние бегуна от стартовой линии может быть описано функцией $$D(t) = 10\sqrt{t} + 5$$ для всех значений $$t\in(0,16)$$, где $ $t$$ в секундах, а расстояние в метрах. Какова скорость бегуна при $$t = 9{-1/2} = \ frac 5 {\ sqrt t} $$

Шаг 2

Оцените $$D'(9)$$.

$$ D'(9) = \ гидроразрыв 5 {\ sqrt 9} = \ гидроразрыв 5 3 $$

Шаг 3

Интерпретируйте числовое значение.

Поскольку производная положительна, мы знаем, что функция возрастает. {th}$$ рабочего часа. Что означает уравнение $$B'(4) = 25$$ с точки зрения продаж и времени?

Шаг 1

Определите единицы производной.

$$ B'(t) = \frac{dB}{dt} = \frac{\mbox{Изменение количества книг}}{\mbox{Изменение во времени}} = \frac{\mbox{Количество книг}} {\mbox{часы}} $$

Единицами производной являются: книги, проданные в час.

Отвечать

$$B'(4)=25$$ означает, что в течение 4-го рабочего часа книги продавались со скоростью 25 книг в час.

Реклама

Практические задачи

Задача 1

Предположим, что $$f(x) = \sin x$$. Найдите наклон касательной в точке $$x = \frac \pi 3$$

Шаг 1

Найдите первую производную.

$$ f'(x) = \cos x $$

Шаг 2

Вычислить $$f’\left(\frac \pi 3\right)$$.

$$ f’\left(\frac \pi 3\right) = \cos \frac \pi 3 = \frac 1 2 $$

Отвечать

$$m = \frac 1 2$$

Проблема 2 92 — 6x + 3$$. Найдите интервалы, на которых $$f$$ возрастает, и интервалы, на которых она убывает.

Шаг 1

Найдите первую производную.

$$ f'(x) = \frac 1 2 x — 6 $$

Шаг 2

Определите, где $$f'(x) > 0$$.

$$ \начать{выравнивать*} f'(x) & > 0\\[6pt] \frac 1 2 x — 6 & > 0\\[6pt] \frac 1 2 x & > 6\\[6pt] х & > 12 \конец{выравнивание*} $$

Поскольку производная линейна и положительна, когда $$x>12$$, мы знаем, что производная будет отрицательной, когда $$x 92(4x-5) \конец{выравнивание*} $$

Шаг 3

Изучите график $$f'(x)$$.

На графике видно, что производная отрицательна (ниже оси $$x$$), когда $$x 2$$.

Отвечать 92$$ представляет собой высоту самолета (в тысячах футов) после $$t$$ часов полета. Найдите $$A'(3)$$ и интерпретируйте его в контексте.

Шаг 1

Найдите производную.

$$ А'(t) = 8 — 4t $$

Шаг 2

Оценка $$A'(3)$$.

$$ А'(3) = 8 -4(3) = 8 — 12 = -4 $$

Шаг 3

Определить единицы производной.

$$ \начать{выравнивать*} A'(t) & = \frac{dA}{dt}\\[6pt] & = \frac{\mbox{Изменение высоты}}{\mbox{Изменение во времени}}\\[6pt] & = \frac{\mbox{Изменение в тысячах футов}}{\mbox{Изменение в часах}}\\[6pt] & \Rightarrow \mbox{тысячи футов в час} \конец{выравнивание*} $$

Шаг 4

Интерпретируйте знак производной.

Поскольку производная отрицательна, мы знаем, что функция (высота) убывает. Значит, самолет должен снижаться.

Отвечать

Через 3 часа полета самолет снижается со скоростью 4000 футов в час. Это примерно 0,75 мили в час спуска. 92 + 13x — 12$$ представляет собой прибыль, полученную конкретной компанией (в тысячах долларов) от продажи $$x$$ тонн товаров. Найдите $$P'(15)$$ и интерпретируйте его в контексте.

Шаг 1

Найти $$P'(x)$$.

$$ Р'(х) = -2х + 13 $$

Шаг 2

Оценка $$P'(15)$$.

$$ P'(15) = -2(15) + 13 = 13 — 30 = -17 $$

Шаг 3

Определить единицы производной.

$$ \начать{выравнивать*} P'(x) & = \frac{dP}{dx}\\[6pt] & = \frac{\mbox{Изменение прибыли}}{\mbox{Изменение количества проданных товаров}}\\[6pt] & = \frac{\mbox{тысячи долларов}}{\mbox{тонны товаров}}\\[6pt] & = \mbox{тысяч долларов за тонну товара} \конец{выравнивание*} $$

Шаг 4

Интерпретируйте знак производной.

Поскольку производная отрицательна, функция (прибыль) убывает.

Отвечать

При продажах на уровне 15 тонн прибыль снижается в размере 17 тысяч долларов за тонну. То есть, если бы продажи выросли, прибыль, как ожидается, упадет с такой же скоростью.

Примечание. В бизнесе увеличение продаж не обязательно означает увеличение прибыли. Если затраты слишком высоки, производство большего количества товаров для продажи может стоить больше, чем деньги, полученные от продажи товаров.

Проблема 7

Предположим, что $$B(t)$$ представляет собой количество сахара в кровотоке человека (в миллиграммах сахара на децилитр крови) через $$t$$ минут после еды. Объясните, что контекстуально означает $$B'(30) = -8$$.

Шаг 1

Определить единицы производной.

$$ \начать{выравнивать*} B'(t) & = \frac{dB}{dt}\\[6pt] & = \frac{\mbox{Изменение уровня сахара в крови}}{\mbox{Изменение во времени}}\\[6pt] & = \frac{\mbox{Изменение в миллиграммах на децилитр}}{\mbox{Изменение в минутах}}\\[6pt] & = \mbox{миллиграмм на децилитр в минуту} \конец{выравнивание*} $$

Шаг 2

Интерпретируйте знак производной.

Поскольку производная отрицательна, функция (уровень сахара в крови) убывающая.

Отвечать

Через 30 минут уровень сахара в крови снижается со скоростью 8 миллиграммов на децилитр в минуту.

Проблема 8

Предположим, что $$L(t)$$ представляет собой длину ногтя (в мм) через $$t$$ дней после того, как он был подстрижен. Объясните, что контекстуально означает $$L'(6) > 0,08$$.

Шаг 1

Определите единицы производной.

$$ \начать{выравнивать*} L'(t) & = \frac{dL}{dt}\\[6pt] & = \frac{\mbox{Изменение длины}}{\mbox{Изменение во времени}}\\[6pt] & = \frac{\mbox{Изменение в мм}}{\mbox{Изменение в днях}}\\[6pt] & = \mbox{миллиметров в день} \конец{выравнивание*} $$

Шаг 2

Интерпретируйте знак производной.

Поскольку производная положительна, функция (длина) возрастает.

Отвечать

Через шесть дней после стрижки ноготь растет быстрее, чем на 0,08 миллиметра в день.

Проблема 9

Предположим, что $$D(t)$$ представляет собой расстояние от дома конкретного человека до $$t$$ минут после 8 утра. Напишите уравнение, имеющее значение «В 8:30 этот человек приближался к своему дому со скоростью 400 футов в минуту».

Шаг 1

Определите значение $$t$$ в измеряемой точке.

Поскольку $$t$$ измеряет время в минутах с 8 утра, интересующее нас время равно $$t = 30$$.

Шаг 2

Определите значение производной.

Поскольку расстояние человека изменяется со скоростью 400 футов в минуту, значение производной равно 400.

Шаг 3

Определить знак производной.

Поскольку расстояние от дома уменьшается, производная должна быть отрицательной.

Отвечать

$$ \displaystyle D'(30) = -400 $$

Проблема 10

Предположим, что $$V(t)$$ представляет собой напряжение в определенной электрической цепи через $$t$$ секунд после включения цепи. Напишите неравенство, означающее: «Через шесть секунд после включения цепи напряжение увеличивалось со скоростью 0,04 вольта в секунду».

No related posts.