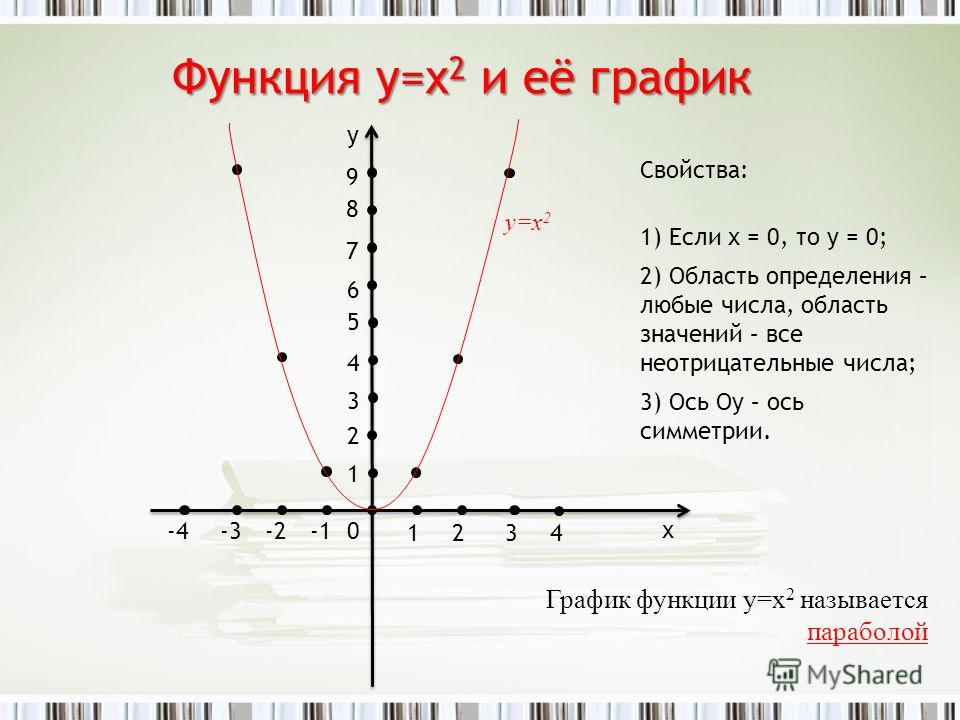
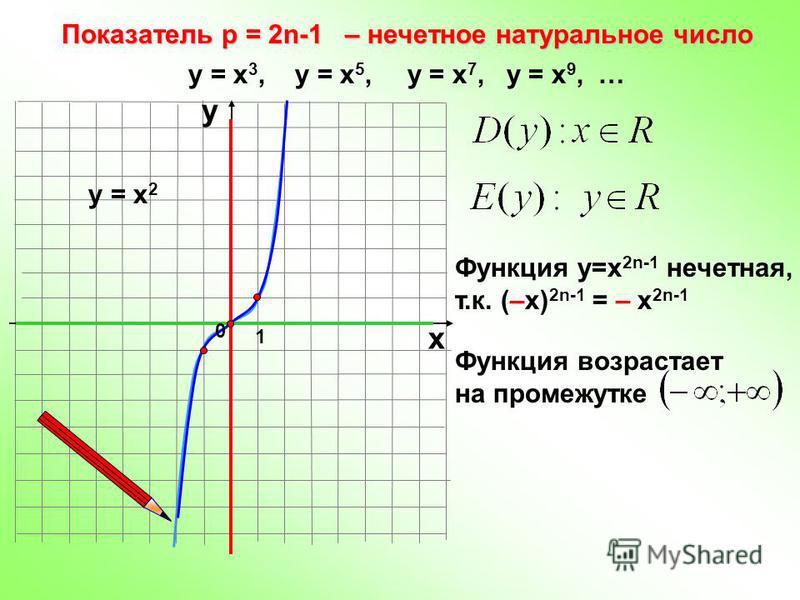
Графики функции у=2х — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1.
2.
3.
4.
У=2х
У= –2х-2
У= –2х
У=2х-2
0
Установите соответствие между
графиками функций и
формулами, задающими эти
функции
1
1.
2.
3.
4.
У= 2х
У= –2х-2
У= –2х
У= 2х-2
0
1
-2
Установите соответствие между
графиками функций и
формулами, задающими эти
функции

2.
3.
4.
У= 2х
У= –2х-2
У= –2х
У= 2х-2
0
Установите соответствие между
графиками функций и
формулами, задающими эти
функции
1
1.
2.
3.
4.
У= 2х
У= –2х+2
У= –2х
У= 2х-2
2
0
Установите соответствие между
графиками функций и
формулами, задающими эти
функции
1
5. Разбейте функции на 4 группы.
• у =х2 +2; у =х2 – 3; у =(х-2)2; у =х2 – 1;• у =х2 +4; у =(х+1)2; у =(х-1)2; у =(х+2)2?
у =х2 +2 у =х2 -1
у =х2+4 у =х2 -3
у =(х-2)2 у =(х+1)2
у =(х-1)2 у =(х+4)2
По какому принципу вы составили группы?
Постройте графики этих функций у себя в группах.
Запишите общий вид функций, графики которых вы
строили.
Сделайте вывод.
у =х2 +2 у =х2 -1
у =х2+4 у =х2 -3
1 группа
2 группа
у =(х-2)2 у =(х+1)2
у =(х-1)2 у =(х+2)2
3 группа
4 группа
1 группа:
1. у =х2 +2
Х
0
1
2. у =х2+4
2
-1
Х
-2
у
0
1
0
1
2
-1
-2
Х
0
1
-1
-2
0
1
2.
 у =(х -1)2
у =(х -1)22
3
Х
4
0
1
2
3
4
у
у
4 группа:
1. у =(х +1)2
у
2
у
3 группа:
1. у =(х -2)2
Х
-2
2. у =х2-3
у
Х
-1
у
2 группа:
1. у =х2 -1
Х
2
0
1
2. у =(х +2)2
2
-1
-2
-3
Х
у
0
1
-1
-2
-3
-4
у х 2
2
у х
2
у х 1
2
у=х²+а
Графики получились в результате
сдвига графика функции у=х²
вдоль оси у на а единиц вверх, если а>0
и на а единиц вниз, если а<0 .
у=х²+2
у=х²
у=х²-1
у ( х 2)
у х
2
2
у ( х 1)
2
у=(х+а)²
Графики получились в результате
сдвига графика функции у=х²
вдоль оси х на а единиц влево, если а>0
и на а единиц вправо, если а<0 .
у=(х+1)²
у=(х-2)²
Построение графиков
квадратичных функций с
помощью движения вдоль осей
координат
13. Построение графиков квадратичных функций с помощью движения вдоль осей координат
вд
о
л
ь
о
с
и
у
Построение графиков квадратичных
функций с помощью движения вдоль осей
координат
у=х2+а
↑на а
у=х2
↓на а
у=х2–а
где а > 0
у=(х+b)2
←
на b
у=х2
→
на b
в д о л ь оси х
где b > 0
у=(х-b)2
Укажите номер рисунка,
соответствующий графику функции:
у х 2,5
2
1.
Не верно
2.
Молодец!
3.
Подумай!
Укажите номер рисунка,
соответствующий графику функции:
у х 2,5
2
1.
Не верно
2.
Подумай!
3.
Молодец!
у ( х 2)
у х
2
2
у ( х 2) 1
2
(2;-1)
Координаты вершины параболы
Тест
у
у
у
Е
0
Н
х
● -4
у
-3
х
0
1
0
О
х
у
у
В
0
х
2
●
Р
0
-3
2
●
0
х
х
!
Определите, какая графическая модель соответствует каждой из данных функций.
Буквы, обозначающие графики, запишите под соответствующими формулами.
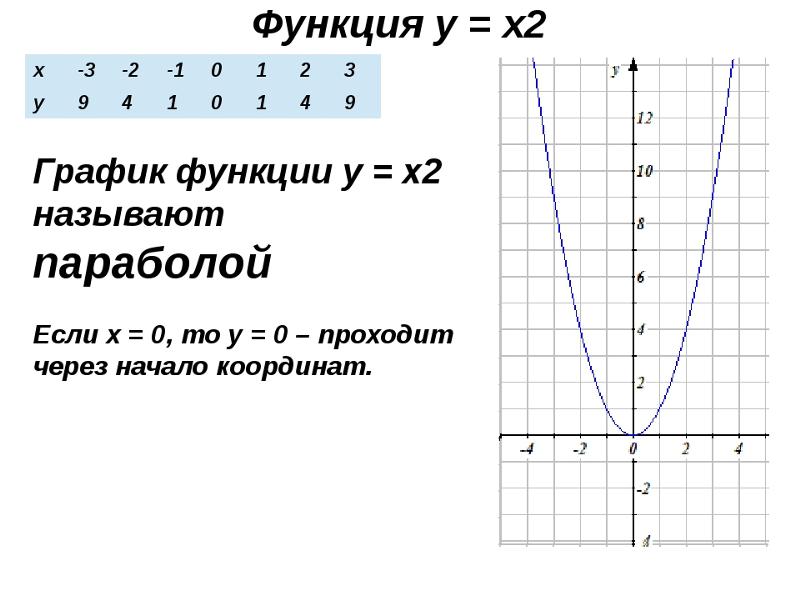
у=х2
у =х2-4
у=(х-2)2 у=(х+3)2
у=х2+1
у=( х-2)2-3
English Русский Правила
Характеристики экспоненциальных функций — Math 1 EOCT Review
Экспоненциальная функция является функцией формы F ( x ) = B X , где B > 0 и B ≠ 1.
Асимптота – это прямая линия, к которой кривая приближается сколь угодно близко, но никогда не достигает ее, так как уходит в бесконечность.
Асимптоты – это характеристика показательных функций.
Экспоненциальные функции, которые не были сдвинуты по вертикали, имеют асимптоту на y = 0, что соответствует оси x .
Показательные функции, сдвинутые по вертикали, имеют асимптоту, соответствующую своему сдвигу.
Пример 1:
Какова асимптота для каждой из следующих функций?
Решение:
Первая функция, f ( x ), вообще не была смещена; следовательно, асимптота для f ( x ) равно y = 0 , или x -ось .
Вторая функция, g ( x ), была сдвинута влево на две единицы. Горизонтальный сдвиг не влияет на асимптоту экспоненциальной функции.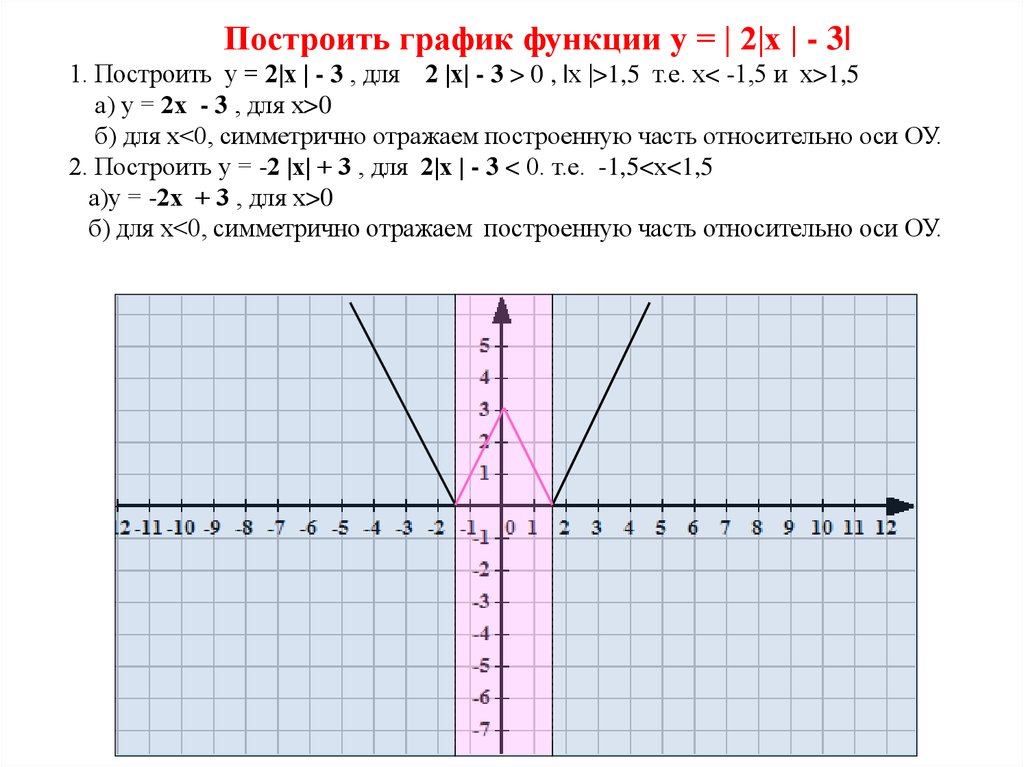 Таким образом, асимптота для г ( x ) равна y = 0 , или x -ось .
Таким образом, асимптота для г ( x ) равна y = 0 , или x -ось .
Вторая функция, h ( x ), сдвинута вправо на одну единицу. Горизонтальный сдвиг не влияет на асимптоту экспоненциальной функции. Итак, асимптота для h ( x ) равно y = 0 , или x -ось .
Пример 2:
Какова асимптота для каждой из следующих функций?
Решение:
Первая функция, f ( x ), была смещена на единицу вверх. Вертикальный сдвиг действительно влияет на асимптоту экспоненциальной функции. Итак, асимптота для f ( x ) равна y = 1 .
Вторая функция, г ( x ), был смещен на две единицы вверх. Вертикальный сдвиг действительно влияет на асимптоту экспоненциальной функции. Итак, асимптота для г ( x ) равна y = 2 .
Третья функция, h ( x ), была смещена на три единицы вниз. Вертикальный сдвиг действительно влияет на асимптоту экспоненциальной функции. Итак, асимптота для ч ( x ) равна y = -3 .
Домен функции — это набор всех возможных действительных входных значений, обычно представленных как x .Диапазон функции — это набор всех возможных реальных выходных значений, обычно представляемых как y .
Чтобы определить область определения и диапазон экспоненциальной функции, подумайте о графике экспоненциальной функции f ( x ) = e x .
Домен
График экспоненциальной функции существует для всех действительных значений x ; поэтому областью определения экспоненциальной функции является (-, ) или все действительные числа.
Примечание. Независимо от того, как график экспоненциальной функции смещается или отражается, домен останется прежним.
Независимо от того, как график экспоненциальной функции смещается или отражается, домен останется прежним.
Диапазон
График экспоненциальной функции существует для всех положительных действительных y -значений; поэтому диапазон экспоненциальной функции (0, ).
Примечание. Когда график экспоненциальной функции смещается или отражается по вертикали, диапазон изменяется.
- Если экспоненциальная функция положительна, выходное значение диапазона никогда не будет меньше или равно асимптоте функции.
- Если экспоненциальная функция отрицательна, выходное значение диапазона никогда не будет больше или равно асимптоте функции.
Пример 3:
Найдите область определения и диапазон функции, показанной ниже.
Решение:
График показательной функции существует для всех действительных значений x .
Следовательно, область определения функции (-, ) .
Поскольку экспоненциальная функция положительна, выходное значение диапазона никогда не будет меньше или равно асимптоте функции.
Так как функция на графике имеет горизонтальную асимптоту при y = -3, диапазон функции составляет (-3, ) .
Пример 4:
Найдите домен и диапазон функции ниже.
Решение:
Область определения экспоненциальной функции — все действительные числа.
Следовательно, область определения функции (-, ) .
Диапазон экспоненциальной функции формы f ( x ) = b x , где b , все > 0 действительные числа больше 1 и
7 b
6 . Таким образом, диапазон функции (2, ) .
конечное поведение функции описывает поведение функции при увеличении или уменьшении x значений. Для экспоненциальной функции вида y = b x , где b > 0 и b ≠ 1, применяется следующее.
- Если основание экспоненциальной функции больше единицы, график функции увеличивается до положительной бесконечности как x увеличивается.
- Если основание экспоненциальной функции находится в диапазоне от нуля до единицы, график функции уменьшается по мере приближения к горизонтальной асимптоте по мере увеличения значений x .
Пример 5:
Опишите конечное поведение следующей показательной функции.
Решение:
Основание показательной функции равно 8,7.
Поскольку основание больше единицы, график функции г ( x ), увеличивается.
Таким образом, по мере увеличения значений x функция увеличивается до положительной бесконечности .
Функция на увеличивается на интервале, если для любого x 1 и x 2 в интервале, где x 1 < x 1 1 < x 1 1 < x 1 1 < x 1 . ( x 1 ) < f ( x 2 ).
( x 1 ) < f ( x 2 ).
A function is decreasing on an interval if for any x 1 and x 2 in the interval, where x 1 < x 2 , then f ( x 1 ) > f ( x 2 ).
Пример 6:
График экспоненциальной функции f ( x ) приведен ниже. Является ли функция возрастающей, убывающей или постоянной на интервале [-2, 3]?
Решение:
Поскольку f (-2) < f (3), функция равна , увеличивая на интервале [-2, 3].
Средняя скорость изменения функции представляет собой отношение изменения значений функции или выходных значений к изменению x -значений или входных значений.
Средняя скорость изменения функции f ( x ) на интервале [a, b] определяется по следующей формуле.
Пример 7:
График экспоненциальной функции g ( x ) приведен ниже. Какова средняя скорость изменения на интервале [2, 3]?
Решение:
Используя график, определите значения г (2) и г (3).
Рассчитайте среднюю скорость изменения г ( x ) на интервале [2, 3], используя значения г (2), г (3) и формулу для среднего скорость изменения.
Итак, средняя скорость изменения г ( x ) на интервале [2, 3] составляет 2 .
Точка пересечения x графика экспоненциальной функции происходит, когда график пересекает ось x . Когда график пересекает ось x , f ( x ) = 0. Поскольку график экспоненциальной функции имеет горизонтальную асимптоту, экспоненциальная функция может не иметь x — точка пересечения. Расположение горизонтальной асимптоты на графике определяет, будет ли график иметь точку пересечения x .
Расположение горизонтальной асимптоты на графике определяет, будет ли график иметь точку пересечения x .
- Если горизонтальная асимптота лежит на оси x или выше нее, на графике не будет точки пересечения x .
- Если горизонтальная асимптота лежит ниже оси x , на графике будет точка пересечения x .
Пример 8:
Что такое x — перехват следующей экспоненциальной функции?
Решение:
Функция имеет горизонтальную асимптоту при y = 0.
Следовательно, функция никогда не пересекает ось x .
Итак, функция не имеет x -перехвата .
Пример 9:
Что такое x -пересечение следующей функции?
Решение:
Функция имеет горизонтальную асимптоту в точке г = -8.
Чтобы найти отрезок x , установите y = 0.
Следовательно, отрезок x равен 3 .
y -пересечение графика экспоненциальной функции происходит, когда график пересекает y -ось. Когда график касается или пересекает ось y , x = 0,
Пример 10:
Что такое y -пересечение следующей функции?
Решение:
Чтобы найти точку пересечения y , задайте x = 0,
.
График любой функции можно сдвинуть по горизонтали добавив сумму внутри функции или сдвинуть по вертикали добавив сумму вне функции.
В таблице ниже показано, как выполняются горизонтальные и вертикальные сдвиги.
Shifts of f ( x ) Horizontal Shift Vertical Shift f ( x ) → f ( x — h ) F ( x ) → F ( x )+ K Слева для H <0 . 0634 вниз для k < 0
0634 вниз для k < 0 вверх для k > 0
Для горизонтального сдвига сдвиг происходит в направлении, противоположном изменению, потому что в приведенной выше формуле 7 0 0 6 h 900 вычитается из 900 от x . Например, F ( x — (- H )) = F ( x + H ) указывает на сдвиг H Единицы слева, а F ( x — ч ) указывает на сдвиг ч единиц вправо.
Вертикальное смещение происходит в том же направлении, что и изменение. Например, f ( x ) + h указывает на сдвиг h единиц вверх, а f ( x ) — 7 h — h на сдвиг вниз.
Пример 11:
Если график f ( x ) = 2 x сдвинут на 5 единиц влево, каково уравнение нового графика?
Решение:
Горизонтальный сдвиг означает, что изменение происходит внутри функции.
Поскольку сдвиг составляет 5 единиц влево, из x вычитается -5, поэтому изменение положительное. Уравнение нового графика: -5)) = f ( x + 5) = 2 ( x + 5) .
Пример 12:
В каком направлении должен двигаться график f ( x ) = 2 x сдвиг для построения графика g ( x ) = 2 x — 3 ?
Решение:
Обратите внимание g ( x ) = f ( x ) — 3. В этом случае изменение — 3 находится за пределами функции, поэтому график сдвигается.
Поскольку 3 вычитается из f ( x ), график g ( x ) получается в результате сдвига f ( x ) вниз 3 шт.
Показательная функция имеет коэффициент , который определяет положение графика функции и равен y -перехвату.
для экспоненциальной функции формы y = A ⋅ B x , где B > 0, B ≠ 1 и A — это коэффициент, следующий .
- Если a > 0, график располагается над осью x .
- Если a < 0, график располагается ниже оси x .
Пример 13:
Определите, лежит ли график следующей экспоненциальной функции выше или ниже оси x . Также определите точку пересечения y графика.
Решение:
Определить расположение графа f ( x ) и пересечение y определяют коэффициент.
Коэффициент f ( x ) равен .
Видно, что коэффициент при f ( x ) положительный; следовательно, график f ( x ) лежит над осью x .
Отсечение y экспоненциальной функции равно коэффициенту. Итак, y -пересечение графика f ( x ) выглядит следующим образом.
Итак, y -пересечение графика f ( x ) выглядит следующим образом.
Чтобы построить график экспоненциальной функции, определите, является ли функция возрастающей или убывающей. Затем определите любые сдвиги. Наконец, создайте таблицу значений и график.
Пример 14:
Постройте график следующей экспоненциальной функции.
Решение:
Основание данной экспоненциальной функции равно 3. Поскольку 3 > 1, эта функция является возрастающей экспоненциальной функцией.
Также обратите внимание, что 1 вычитается из 3 х . Это означает, что график будет сдвинут вниз на единицу.
Создать таблицу значений.
График с использованием значений из таблицы выше.
Комментарий к уроку
Copyright © 2013 Study Island — Все права защищены.
1 2 лист родительских функций и преобразований с ответами0018
susanwalkerdavis. weebly.com › загрузки › 2 › translations_on_parent…
weebly.com › загрузки › 2 › translations_on_parent…
Для задачи 1-6 укажите имя родительской функции и опишите представленное преобразование. Вы можете использовать свой графический калькулятор для сравнения …
1–5 Родительские функции и преобразования — предварительное исчисление
precalculuscoach.com › 1–5-родительские функции-и-тр…
Вот ваши БЕСПЛАТНЫЕ ресурсы для вашего урока по родительским функциям и рабочему листу преобразований, заметкам с инструкциями в PowerPoint, викторине на выходе, работе с колокольчиками и многому другому!
[PDF] Назначение родительских функций и преобразований | Pre-Calculus
precalculuscoach.com › wp-content › uploads › 2017/08 › 1-5-Assig…
ОТВЕТЫ. Определите родительскую функцию, нарисуйте график и найдите домен и диапазон для каждой функции. 1. = . 2. = — .
[PDF] Название_____________________…
www.korpisworld.com › Математика › WS 02.4 Родительские функции и . ..
..
Рабочий лист 2.4 — Родительские функции и преобразования … 1,4 is. (А) 1/3 (Б) 1/2 (В) 0 (Г) 2/3 (Д) 3/2. _____7. График функции ( ) … II. Короткий ответ.
[PDF] Рабочий лист родительской функции 1 — SharpSchool
cdn5-ss13.sharpschool.com › Файл › Quadratics › transform_hmwk
Для задачи 1–6 укажите имя родительской функции и опишите представленное преобразование. Вы можете использовать свой графический калькулятор для сравнения …
[PDF] Algebra 2 1.2 worksheet
www.matsuk12.us › lib › Centricity › Domain › alg2 1_2 worksheet
График родительской функции (черный), преобразование (другой цвет), а также домен и диапазон преобразования. 1.) родительская функция: квадратичная.
[PDF] 1_График родительских функций и преобразований
lindblomeagles.org › ourpages › auto › ДЕНЬ 7 Граф родительских функций
30.09.2015 · Рабочий лист от Kuta Software LLC. -5-. Ответы на 1_Graphing: Родительские функции и преобразования. 1) х у. −8 −6 −4 −2. 2 4.
1) х у. −8 −6 −4 −2. 2 4.
[PDF] 10.3 Переводы пакета родительских функций KEY.pdf
www.htsdnj.org › cms › lib › NJ02211210 › Centricity › Domain › 1…
2. f(x) = |х—. 3. h(x) = √x+4. Ключ. Для задачи 1-6 укажите имя родительской функции и опишите представленное преобразование. Вы можете.
[PDF] Алгебра 2
www.cusd80.com › cms › lib › Centricity › Domain › 1.1 ws key.pdf
Постройте график родительской функции и заданной функции. Затем опишите преобразование, домен и диапазон. Имя. Период. 1) f(x)=√x+4 вверх по y.
[PDF] Родительские функции и преобразования — 1.1
ca01001129.schoolwires.net › CA01001129 › Centricity › Домен
y = 1/x. Х.-6. -4. Страница 2. 1.1. Своими словами напишите значение каждого словарного термина. родительская функция основное уравнение/график в семействе.
ähnliche sucalfragen
1.2 Рабочий лист родительских функций и преобразования с ответами
Родительские функции и преобразования рабочие лист PDF Ответы
2 7 Родительские функции и преобразования.
Для экспоненциальной функции вида y = b x , где b > 0 и b ≠ 1, применяется следующее.
- Если основание экспоненциальной функции больше единицы, график функции увеличивается до положительной бесконечности как x увеличивается.
- Если основание экспоненциальной функции находится в диапазоне от нуля до единицы, график функции уменьшается по мере приближения к горизонтальной асимптоте по мере увеличения значений x .
Функция на увеличивается на интервале, если для любого x 1 и x 2 в интервале, где x 1 < x 1 1 < x 1 1 < x 1 1 < x 1 .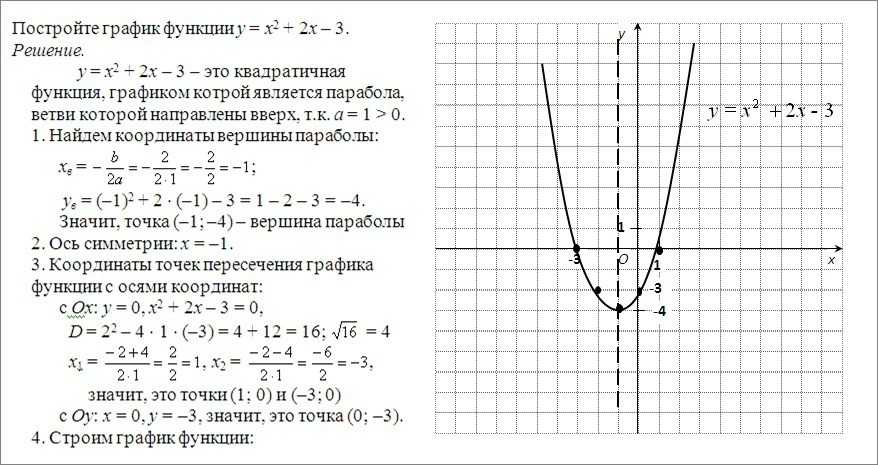 ( x 1 ) < f ( x 2 ).
( x 1 ) < f ( x 2 ).
A function is decreasing on an interval if for any x 1 and x 2 in the interval, where x 1 < x 2 , then f ( x 1 ) > f ( x 2 ).
Средняя скорость изменения функции представляет собой отношение изменения значений функции или выходных значений к изменению x -значений или входных значений.
Средняя скорость изменения функции f ( x ) на интервале [a, b] определяется по следующей формуле.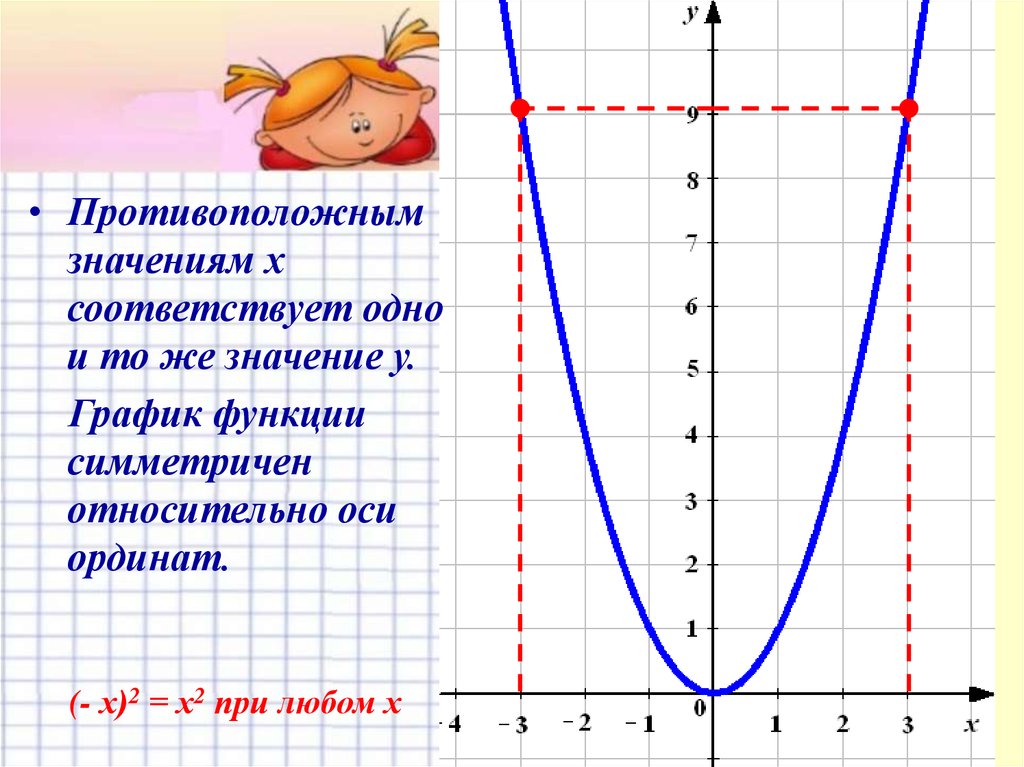
Поскольку график экспоненциальной функции имеет горизонтальную асимптоту, экспоненциальная функция может не иметь x — точка пересечения. Расположение горизонтальной асимптоты на графике определяет, будет ли график иметь точку пересечения x .
Расположение горизонтальной асимптоты на графике определяет, будет ли график иметь точку пересечения x .
- Если горизонтальная асимптота лежит на оси x или выше нее, на графике не будет точки пересечения x .
- Если горизонтальная асимптота лежит ниже оси x , на графике будет точка пересечения x .

 0634 вниз для k < 0
0634 вниз для k < 0
Показательная функция имеет коэффициент , который определяет положение графика функции и равен y -перехвату.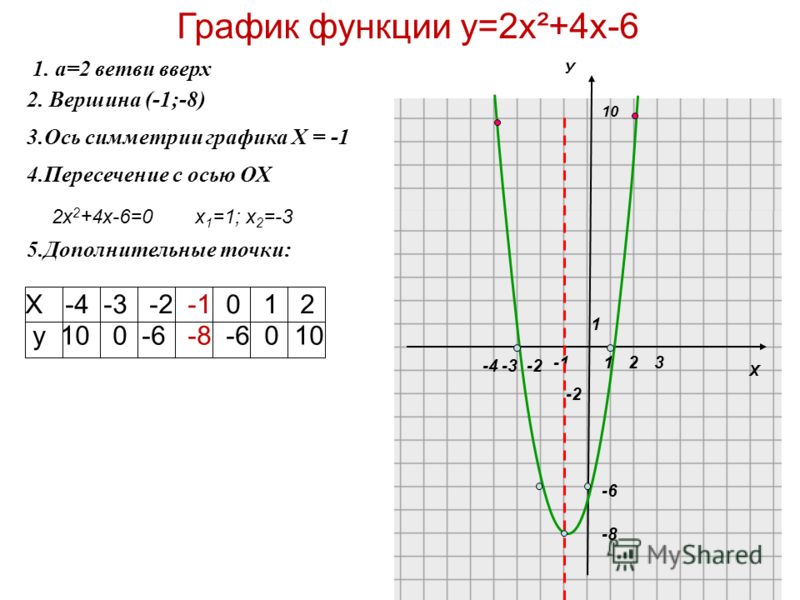
для экспоненциальной функции формы y = A ⋅ B x , где B > 0, B ≠ 1 и A — это коэффициент, следующий .
- Если a > 0, график располагается над осью x .
- Если a < 0, график располагается ниже оси x .
 Итак, y -пересечение графика f ( x ) выглядит следующим образом.
Итак, y -пересечение графика f ( x ) выглядит следующим образом.Чтобы построить график экспоненциальной функции, определите, является ли функция возрастающей или убывающей. Затем определите любые сдвиги. Наконец, создайте таблицу значений и график.
 weebly.com › загрузки › 2 › translations_on_parent…
weebly.com › загрузки › 2 › translations_on_parent… ..
.. 1) х у. −8 −6 −4 −2. 2 4.
1) х у. −8 −6 −4 −2. 2 4.