y корень x 2
Вы искали y корень x 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y корень из x 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «y корень x 2».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y корень x 2,y корень из x 2,корень из x 2 y 2,постройте график функции y 2 корень x,постройте график функции y корень x 2.
Где можно решить любую задачу по математике, а так же y корень x 2 Онлайн?
Решить задачу y корень x 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| 1 | Упростить | квадратный корень s квадратный корень s^7 | |
| 2 | Упростить | кубический корень 8x^7y^9z^3 | |
| 3 | Упростить | arccos(( квадратный корень 3)/2) | |
| 4 | Risolvere per ? | sin(x)=1/2 | |
| 5 | Упростить | квадратный корень s квадратный корень s^3 | |
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) 2+n-72)=1/(n+9) |
Функция КОРЕНЬ — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции КОРЕНЬ в Microsoft Excel.
Описание
Возвращает положительное значение квадратного корня.
Синтаксис
КОРЕНЬ(число)
Аргументы функции КОРЕНЬ описаны ниже.
Замечание
Если число отрицательное, то SQRT возвращает #NUM! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
-16 |
||
|
Формула |
Описание |
Результат |
|
=КОРЕНЬ(16) |
Квадратный корень числа 16. |
|
|
=КОРЕНЬ(A2) |
Квадратный корень -16. Так как число отрицательное, #NUM! возвращается сообщение об ошибке. |
#ЧИСЛО! |
|
=КОРЕНЬ(ABS(A2)) |
Старайтесь не #NUM! сообщение об ошибке: сначала с помощью функции ABS можно найти абсолютное значение -16, а затем найти квадратный корень. |
4 |
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
Определение 1- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.

При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю.
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Для нахождения области определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Пример 2Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1является постоянной функцией, f2является арктангенсом, f3– логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ
: область определения y=3·arctg x·ln x – множество всех действительных чисел.Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x)– произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x)является -∞, +∞D(f)=D(f).
Получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x — [0, +∞).
Области определения y=f(x) и y=−f(x)совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Пример 4Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Пример 5Найти область определения y=ln x2.
Решение
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.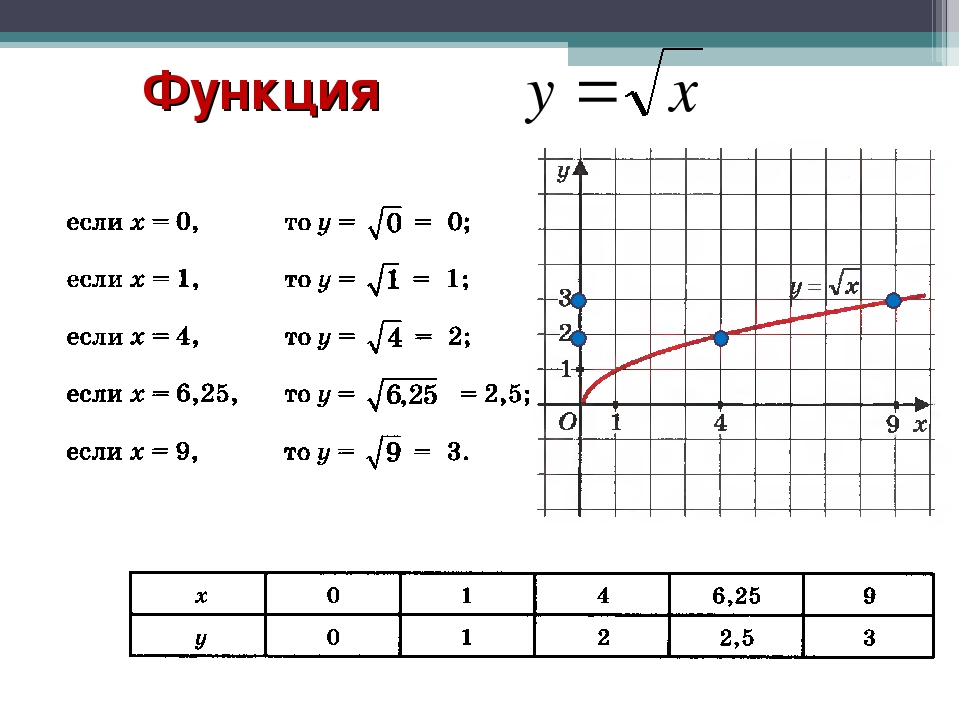
Ответ: (−∞, 0)∪(0, +∞).
Пример 6Найти область определения функции y=(arcsin x)-12.
Решение
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Пример 7Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3– логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 8Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3–это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4– это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Область определения логарифма с переменной в основании
Определение 3Определение логарифма существует для положительных оснований не равных 1.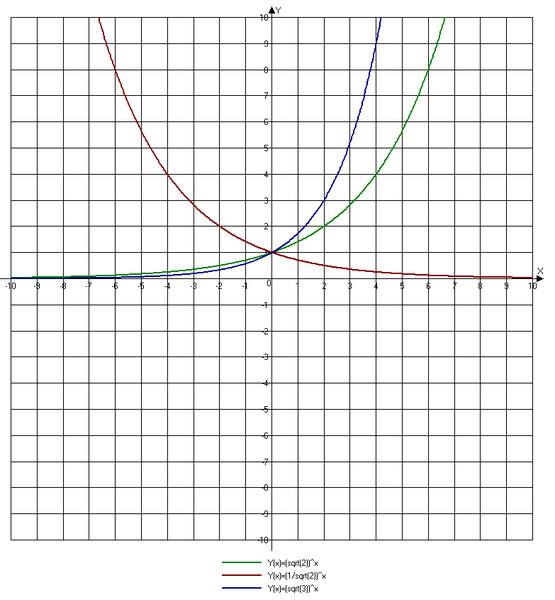 Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Пример 9Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞).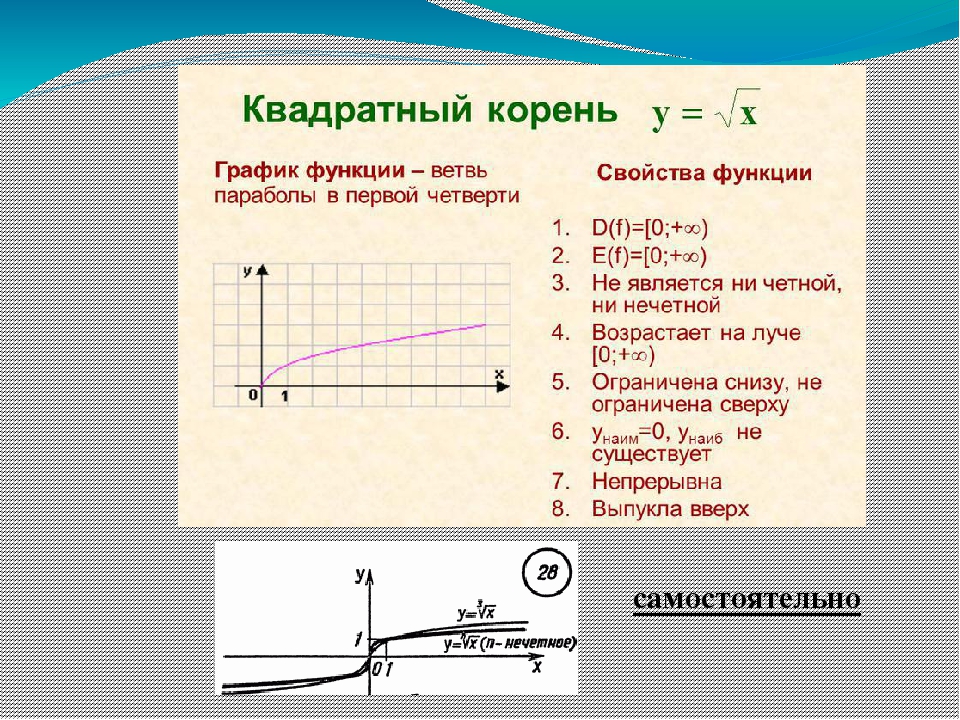 Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Пример 10Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения |
Сумма, разность, произведение функций f1, f2,…, fn | Пересечение множеств D(f1), D(f2), …, D(fn) |
Сложная функция y=f1(f2(f3(…fn(x))))
В частности, y=f1(f2(x)) | Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1)
x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y=k·x | R |
| Линейная y=k·x+b | R |
Обратная пропорциональность y=kx | -∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C — число | D(f) |
Дробная y=f1(x)f2(x)
В частности, если f1(x), f2(x) — многочлены | Множество всех x, которые одновременно удовлетворяют условиям
f2(x)≠0 |
| y=f(x)n, где n — четное | x∈D(f1), f(x)≥0 |
y=logf2(x)f1(x)
В частности, y=logaf1(x)
В частности, y=logf2(x)a | x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1
x∈D(f1), f1(x)>0
x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Как найти область определения функции
После этого экскурса в важную составную матанализа многие согласятся, что найти область определения функции не очень сложно. Ненамного сложнее, чем Московскую область на карте.
Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых, решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно.
Итак, чтобы находить области определения распространённых функций, порешаем
уравнения и неравенства с одной переменной. А в конце урока обобщим понятие на уровне теории. Пока же —
краткое определение. Область определения функции y=f(x)
— это множество значений X, для которых существуют значения Y.
А в конце урока обобщим понятие на уровне теории. Пока же —
краткое определение. Область определения функции y=f(x)
— это множество значений X, для которых существуют значения Y.
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Приступаем к практике. На рисунке изображён график функции . Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель нулю, получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции — это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения всех распространённых видов функций.
Пример 0. Как найти область
определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять)
()? Нужно всего лишь
решить неравенство
Как найти область
определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять)
()? Нужно всего лишь
решить неравенство
x — 5 ≥ 0,
так как для того, чтобы мы получили действительное значение игрека, подкоренное выражение должно быть больше или равно нулю. Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Постоянная (константа) определена при любых действительных
значениях x, следовательно, данная функция определена на всём
множестве R действительных чисел. Это можно записать и так:
областью определения данной функции является вся числовая прямая ]- ∞; + ∞[.
Это можно записать и так:
областью определения данной функции является вся числовая прямая ]- ∞; + ∞[.
Пример 1. Найти область определения функции y = 2.
Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x, следовательно, данная функция определена на всём множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.
В случае, когда функция задана формулой и n — натуральное число:
Пример 2. Найти область определения функции .
Решение. Как следует из
определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно, то есть,
если — 1 ≤ x ≤ 1.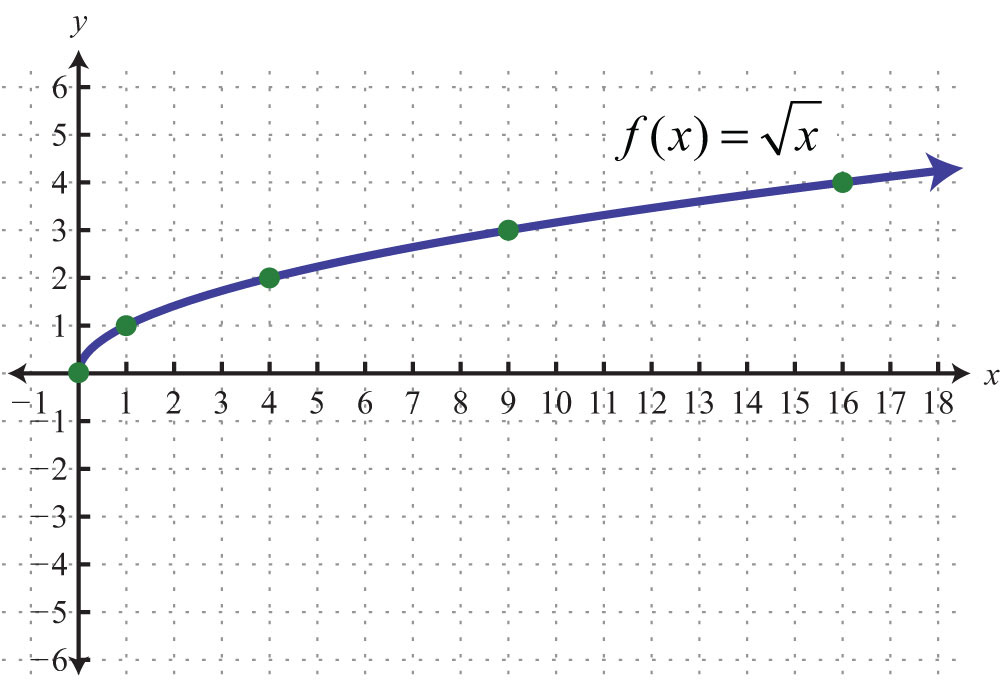 Следовательно, область определения данной функции — [- 1; 1].
Следовательно, область определения данной функции — [- 1; 1].
Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[;
если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[, то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).
Пример 3. Найти область определения функции
.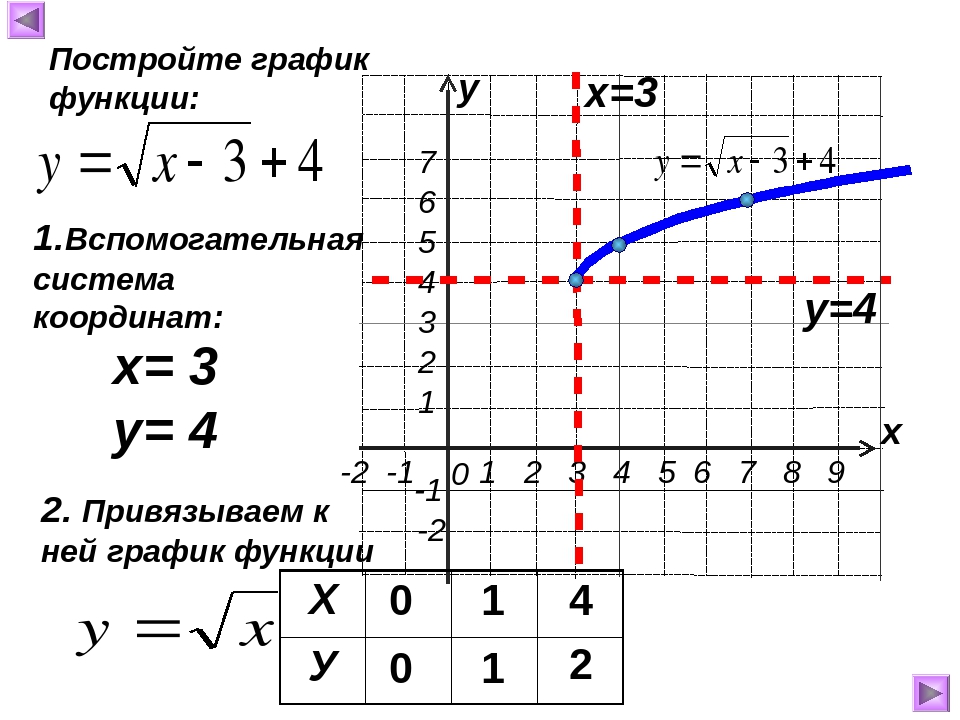
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой :
если — положительное, то областью определения функции является множество [0; + ∞[;
если — отрицательное, то областью определения функции является множество ]0; + ∞[.
Пример 4. Найти область определения функции .
Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[.
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше,
причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Пример 5. Найти область определения функции .
Решение. Дробный показатель степени данной степенной функции — отрицательный. Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля::
.
Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[.
Область определения показательной функции
В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[.
Область определения логарифмической функции
Логарифмическая функция
определена при условии, если её аргумент положителен, то есть, областью её определения является множество
]0; + ∞[.
Найти область определения функции самостоятельно, а затем посмотреть решение
Область определения функции y = cos(x) — так же множество R действительных чисел.
Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .
Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .
Пример 8. Найти область определения функции .
Решение. Внешняя функция — десятичный логарифм и на область её определения
распространяются условия области определения логарифмической функции вообще. То есть, её аргумент
должен быть положительным. Аргумент здесь — синус «икса». Поворачивая воображаемый циркуль по
окружности, видим, что условие sin x > 0
нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи»
и любого чётного или нечётного целого числа.
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) — множество [-1; 1].
Область определения функции y = arccos(x) — так же множество [-1; 1].
Область определения функции y = arctg(x) — множество R действительных чисел.
Область определения функции y = arcctg(x) — так же множество R действительных чисел.
Пример 9. Найти область определения функции .
Решение. Решим неравенство:
Таким образом, получаем область определения данной функции — отрезок
[- 4; 4].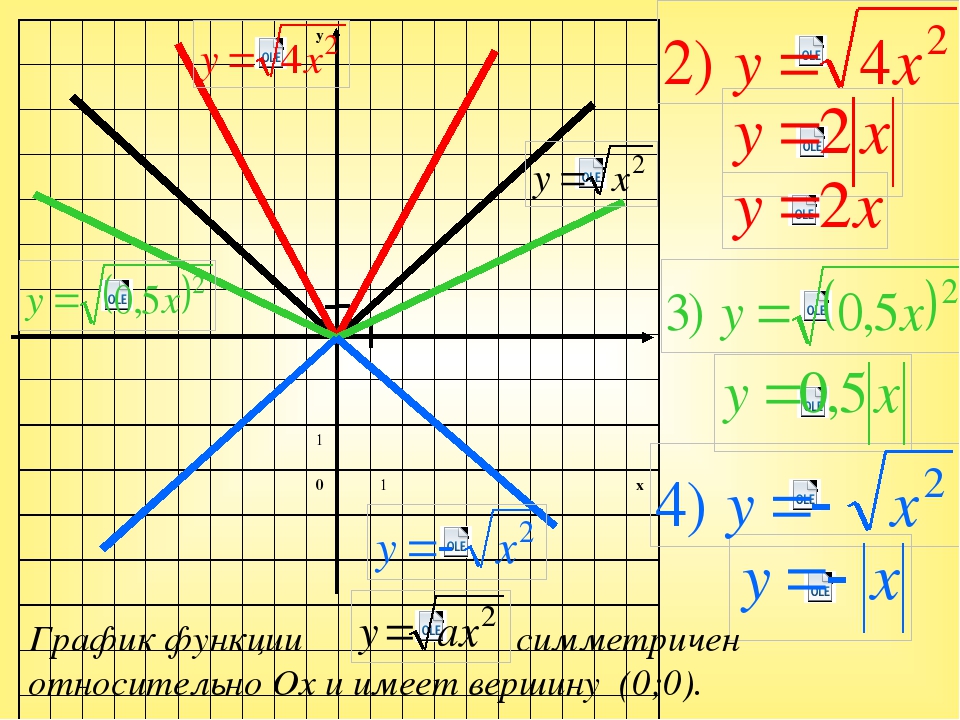
Пример 10. Найти область определения функции .
Решение. Решим два неравенства:
Решение первого неравенства:
Решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок [0; 1].
Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x, при которых знаменатель дроби обращается в нуль.
Пример 11. Найти область определения функции .
Решение. Решая равенство нулю знаменателя дроби, находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[.
Пример 12.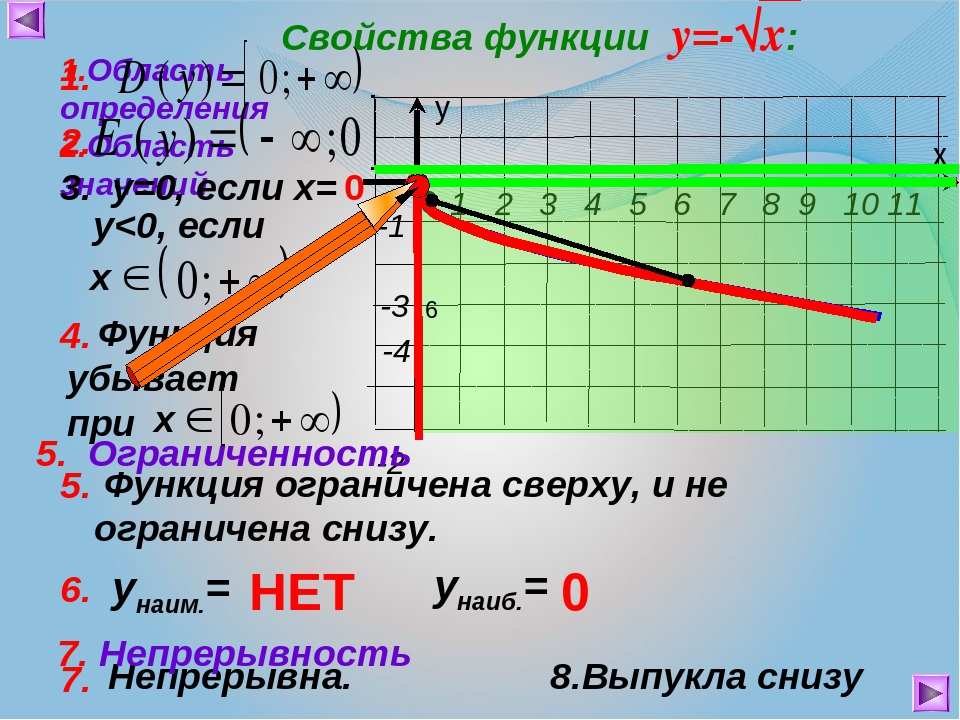 Найти область определения функции
.
Найти область определения функции
.
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[.
Пример 13. Найти область определения функции .
Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — все x, кроме -2 и 2.
Пример 14. Найти область определения функции .
Решение. Решим уравнение:
Уравнение не имеет действительных корней.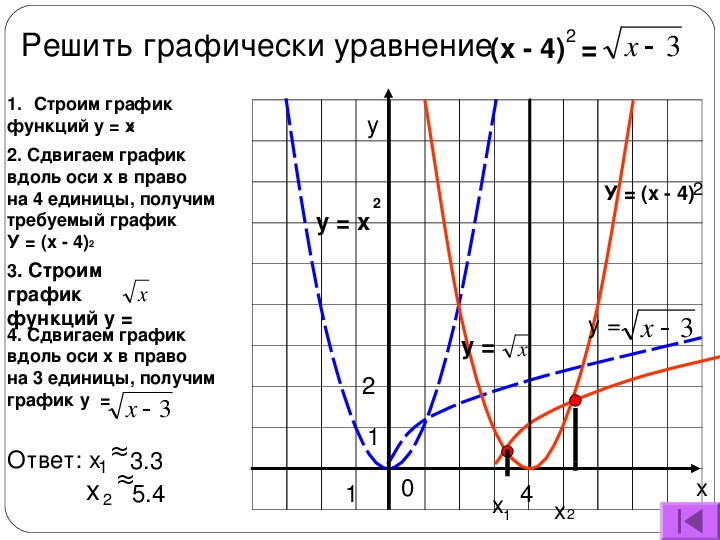 Но функция определена только на действительных
числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что
то же самое — множество R действительных чисел или,
что то же самое — ]- ∞; + ∞[.
Но функция определена только на действительных
числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что
то же самое — множество R действительных чисел или,
что то же самое — ]- ∞; + ∞[.
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.
Пример 15. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[.
Пример 16. Найти область определения функции .
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой
направлены вверх.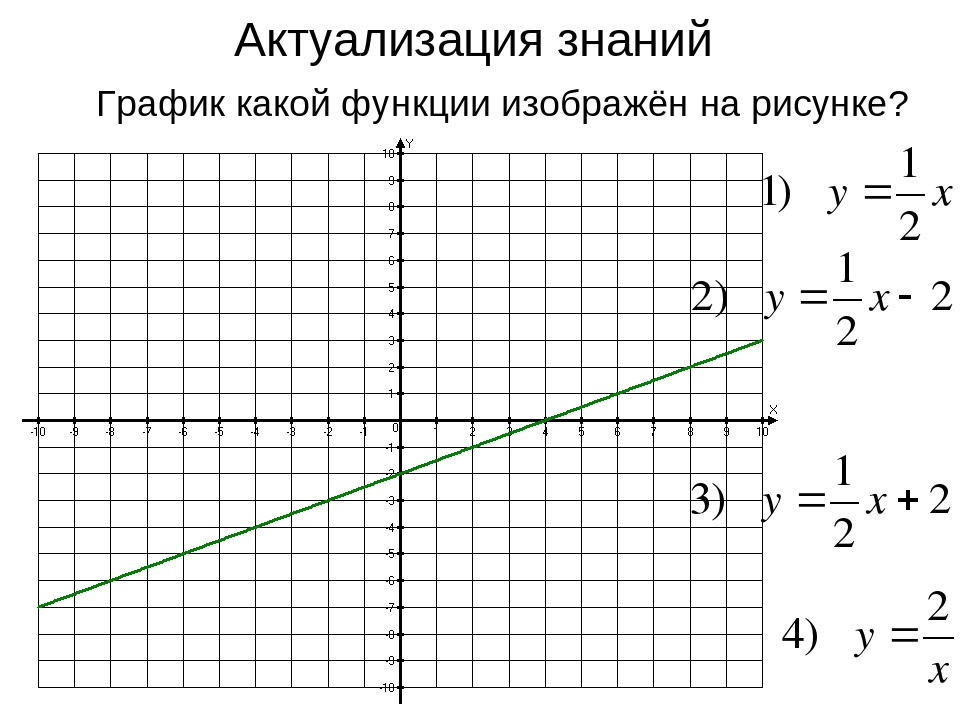 Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках
1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения
квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена
на отрезке [1; 2].
Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках
1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения
квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена
на отрезке [1; 2].
Найти область определения функции самостоятельно, а затем посмотреть решение
Если функция задана формулой вида y = kx + b, то область определения функции — множество R действительных чисел.
А теперь обобщим решения рассмотренных примеров. Каждой точке графика функции соответствуют:
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может
быть вычислен «игрек» — значение функции.
 Иначе говоря, множество значений аргумента, на котором
«функция работает».
Иначе говоря, множество значений аргумента, на котором
«функция работает».
Весь раздел «Исследование функций»
Урок 21. показательная функция — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №21. Показательная функция.
Перечень вопросов, рассматриваемых в теме:
— какая функция называется показательной;
— какие свойства имеет показательная функция в зависимости от ее основания;
— какой вид имеет график показательной функции в зависимости от ее основания;
— примеры реальных процессов, описываемых показательной функцией.
Глоссарий по теме
Функция вида , a>0, а≠1 называется показательной функцией с основанием а.
Функция называется монотонно возрастающей на промежутке <a; b>, если (чем больше аргумент, тем больше значение функции).
Функция называется монотонно убывающей на промежутке <a; b>, если (чем больше аргумент, тем меньше значение функции).
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.
Открытые электронные ресурсы:
http://fcior.edu.ru/ — Федеральный центр информационно-образовательных ресурсов
http://school-collection.edu.ru/ — Единая коллекция цифровых образовательных ресурсов
Теоретический материал для самостоятельного изучения
1. Определение, свойства и график показательной функции
Определение:
Функция вида y=ах, a>0, а≠1 называется показательной функцией с основанием а.
Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.
Основание а – заданное число.
Для положительного основания значение степени ах можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.
Сформулируем основные свойства показательной функции.
1. Область определения.
Как мы уже сказали, степень ах для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D(y)=R.
2. Множество значений.
Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.
Множество значений показательной функции Е(y)=R+, или Е(y)=(0; +∞).
3. Корни (нули) функции.
Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.
4. Монотонность.
При a>1 функция монотонно возрастает.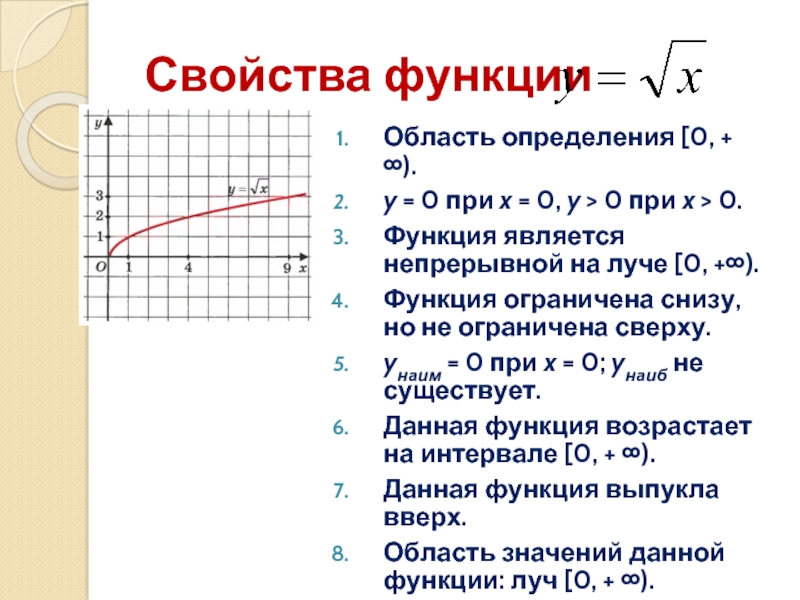
При 0<a<1 функция монотонно убывает.
5. При любом значении а значение функции y (0) = а0 =1.
6. График функции.
При a>1
Рисунок 1 – График показательной функции при a>1
При 0<a<1
Рисунок 2 – График показательной функции при 0<a<1
Независимо от значения основания а график функции имеет горизонтальную асимптоту y=0. Для 0<a<1 при х стремящемся к плюс бесконечности, для a>1 при х стремящемся к минус бесконечности.
2. Рассмотрим пример исследования функции y=–3х+1.
Решение:
1) Область определения функции – любое действительное число.
2) Найдем множество значений функции.
Так как 3х>0, то –3х<0, значит, –3х+1<1, то есть множество значений функции y=–3х+1 представляет собой промежуток (-∞; 1).
3) Так как функция y=3х монотонно возрастает, то функция y=–3х монотонно убывает. Значит, и функция y=–3х+1 также монотонно убывает.
4) Эта функция будет иметь корень: –3х+1=0, 3х=1, х=0.
5) График функции
Рисунок 3 – График функции y=–3х+1
6) Для этой функции горизонтальной асимптотой будет прямая y=1.
3. Примеры процессов, которые описываются показательной функцией.
1) Рост различных микроорганизмов, бактерий, дрожжей и ферментов описывает формула: N= N0·akt, N– число организмов в момент времени t, t – время размножения, a и k – некоторые постоянные, которые зависят от температуры размножения, видов бактерий. Вообще это закон размножения при благоприятных условиях (отсутствие врагов, наличие необходимого количества питательных веществ и т.п.). Очевидно, что в реальности такого не происходит.
2) Давление воздуха изменяется по закону: P=P0·a-kh, P– давление на высоте h, P0 – давление на уровне моря, h – высота над уровнем моря, a и k – некоторые постоянные.
3) Закон роста древесины: D=D0·akt, D– изменение количества древесины во времени, D0 – начальное количество древесины, t – время, a и k – некоторые постоянные.
4) Процесс изменения температуры чайника при кипении описывается формулой: T=T0+(100– T0)e-kt.
5) Закон поглощения света средой: I=I0·e-ks, s– толщина слоя, k – коэффициент, который характеризует степень замутнения среды.
6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.
Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т. д.
д.
Если предположить, что поток информации изменялся по тому же закону до того года, который принят за начальный, то будем двигаться по оси абсцисс влево от начала координат и над значениями аргумента -10, -20 и т.д. будем наносить на график значения функции уже в порядке убывания — уменьшая каждый раз вдвое.
Рисунок 4 – График функции y=2х – изменение количества информации
Закон изменения количества информации описывается показательной функцией y=2х.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Выберите показательные функции, которые являются монотонно убывающими.
- y=3x-1
- y=(0,4)x+1
- y=(0,7)-х
- y=
- y=3-2х
- y=102x +1
Решение:
Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.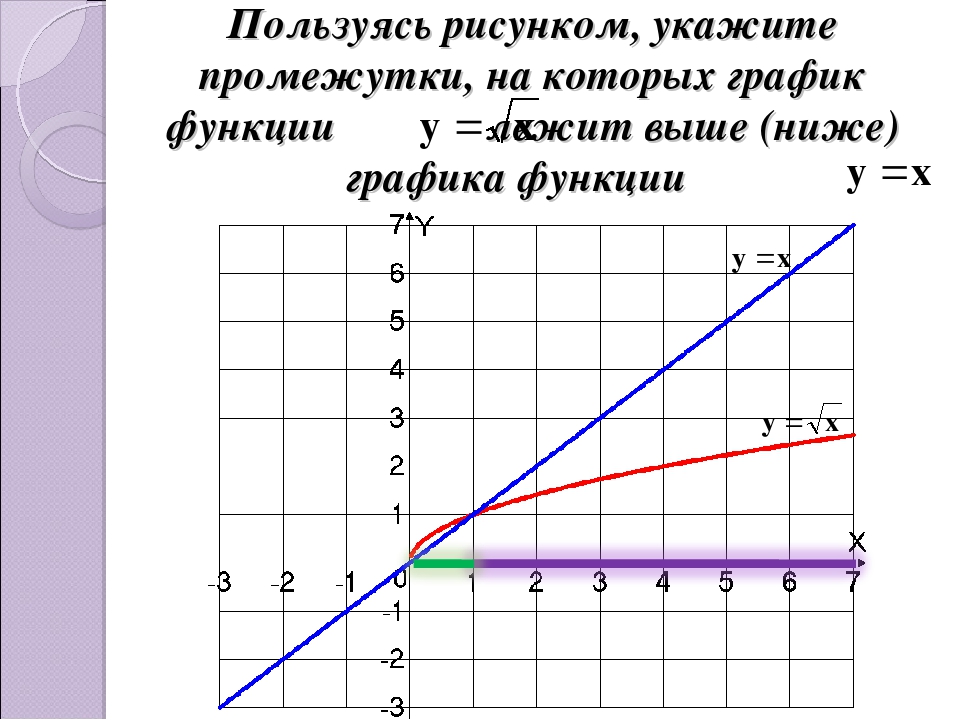
Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:
2) 4) 5)
Пример 2.
Найдите множество значений функции y=3x+1– 3.
Решение:
Рассмотрим функцию.
Так как 3x+1>0, то 3x+1– 3>–3, то есть множество значений:
(– 3; +∞).
Пример 3.
Найдите множество значений функции y=|2x– 2|
Рассмотрим функцию.
2x–2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2x– 2|0.
Урок алгебры по теме»Функция y=√x «
Донецкая общеобразовательная школа-интернат
І-ІІІ ступеней №3
Открытый урок по алгебре в 8 классе.
Тема:
«Функция у=, её свойства и график».
Разработала и провела
учитель I категории
Плахотник Н. С.
С.
Цель урока:
1. Обучающая
— познакомить учащихся с функцией квадратного корня и ее графиком, научить использовать график функции квадратного корня при решении иррациональных уравнений.
2. Развивающие
— развивать логическое мышление, внимание, математическую речь учащихся, самосознание, самооценку
3. Воспитательная
— воспитывать личностные качества: ответственность, добросовестность, самостоятельность, умение слушать друг друга
Ход урока.
Добрый день, ребята! Я рада вас видеть.
«День прожит не зря, если вы узнали что-то новое» — так сказал ученый Дэвид Эддингс.
Вот и сегодня на уроке вы познакомитесь с новой функцией, функцией у=√х; научитесь изображать график этой функции, изучите её свойства. В конце урока мы проверим ваши знания с помощью теста.
В конце урока мы проверим ваши знания с помощью теста.
Откройте тетради и запишите тему урока:
А сейчас повторим изученный вами ранее материал, который пригодиться вам при изучении новой темы
І. Актуализация опорных знаний.
Сформулируйте определение арифметического квадратного корня.
При каких значениях a выражение √a имеет смысл?
√100, √81, √0, √-25Имеет ли уравнение x2 = a корни при а > 0, a = 0, a < 0, и если имеет, то сколько?
Решите уравнения: x2 = 4, x2 =5, x2 =
= 4, = 5, =Сократите дробь: , , ,
Найдите площадь фигуры.
Задачи, приводящие к понятию функции y = √x.

а) сторона квадрата а = √S;
б) радиус круга r =
– Что особенного в этих заданиях? (Зависимость задана формулой y = с которой мы еще не встречались).
ІІ. Изложение новой темы.
Для построения графика функции у=√х, дадим как обычно, независимой переменной х несколько конкретных значений и вычислим соответствующие значения переменной у. Как вы думаете, могу ли я взять для вычислений, отрицательные значения х? (нет, так как квадратный корень из отрицательного числа не существует.)
Мы будем давать переменной х такие значения, для которых известно точное значение квадратного корня.
Итак: если х=0, то у= √0=0
Если х=1, то у= √1=1
Если х=4, то у= √4=2
Если х=6,25 то у= √6,25=2,5
Если х=9, то у= √9=3
Составим таблицу значений функций.
Запишите её.
Построим найденные точки на координатной плоскости. Они располагаются на некоторой линии, начертите её. Мы построили график функции у = √х.Работа по графику функции:
-найдите значение у, если х = 1,5; 5,5; 7,2; 15.
— найдите значение х, если у = 1,5; 1,8; 2,5.Принадлежат ли графику функции точки: А(64; 8), B(100; 10), С(-81; 9), D(25; -5).
С помощью графика сравнить числа: √0,5 и √0,8; √4,2 и √5,7; √7 и √8.
Свойства функции:
область определения: луч [0;+∞) или х≥0;
если х=0, то у=0;
у>0 при х>0;
f(х) возрастает при х принадлежащем [0;+∞);
у наим.=0 (при х=0), у наиб. не существует.
ІІІ. Первичное закрепление. А сейчас вы будете работать с тестом. Задания выполняйте по порядку, выписывая те буквы, под которыми находятся правильные ответы. Если задания будут выполнены верно, то вы получите фамилию математика. (ДЕКАРТ).
Если задания будут выполнены верно, то вы получите фамилию математика. (ДЕКАРТ).
Тест
1) Какой из графиков соответствует графику функции у=√х ? (чертежи подготовить учителю)
В) Г) Д) Б)
2) Какая из заданных точек принадлежит графику функции у=√х ?
К) (-1; 1) Л) (0; 5) М) (2; 4) Е) (4; 2).
3) Наименьшее значение функции у=√х равно :
А) 0,001 К) 0 В) 1 Г) не существует.
4) Область определения функции у= √х :
А) х ≥ 0 Н) х > 0 П) х < 0 О) х ≤ 0.
5) Корнем уравнения √х = 2-х является число, равное
П) 4; К) 0; С) 3; Р) 1.
6) Между какими целыми числами заключено число √27
В) 26 и 28; Т) 5 и 6; М) 13 и 14; К) 0 и 7
Что вы знаете об этом математике?
IV. Домашнее задание: §15 прочитать, выучить свойства функции,
Домашнее задание: §15 прочитать, выучить свойства функции,
решить № 355, 356, 363. Разгадать кроссворд.
V. Подведение итогов, выставление оценок.
VI. Рефлексия. Ребята, выберите смайлик, который больше всего подходит вашему настроению.
Функция, обратная квадратному корню
Чтобы найти обратную функцию квадратного корня, очень важно сначала набросать или изобразить данную проблему, чтобы четко определить, что такое область и диапазон. Я буду использовать домен и диапазон исходной функции, чтобы описать область и диапазон обратной функции, поменяв их местами. Если вам нужна дополнительная информация о том, что я имел в виду под «обменом домена и диапазона» между функцией и ее обратной, см. Мой предыдущий урок об этом.
Примеры того, как найти обратную функцию квадратного корня
Пример 1: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Укажите его домен и диапазон.
Каждый раз, когда я сталкиваюсь с функцией извлечения квадратного корня с линейным членом внутри радикального символа, я всегда думаю о ней как о «половине параболы», нарисованной сбоку. Поскольку это положительный случай функции квадратного корня, я уверен, что ее диапазон будет становиться все более положительным, проще говоря, стремительно увеличиваясь до положительной бесконечности.
Эта конкретная функция извлечения квадратного корня имеет этот график с определенными областью и диапазоном.
С этого момента мне придется решать обратную алгебру, следуя предложенным шагам. По сути, замените \ color {red} f \ left (x \ right) на \ color {red} y, поменяйте местами x и y в уравнении, решите для y, которое вскоре будет заменено соответствующей обратной записью, и, наконец, укажите домен и диапазон.
Не забудьте использовать методы решения радикальных уравнений для решения обратной задачи.Возведение квадратного корня в квадрат или во вторую степень должно устранить радикал. Однако вы должны сделать это с обеими сторонами уравнения, чтобы сохранить баланс.
Однако вы должны сделать это с обеими сторонами уравнения, чтобы сохранить баланс.
Убедитесь, что вы проверили домен и диапазон обратной функции из исходной функции. Они должны быть «противоположны друг другу».
Размещение графиков исходной функции и обратной к ней по одной координатной оси.
Вы видите их симметрию вдоль линии y = x? Посмотрите на зеленую пунктирную линию.2} = 1. Его домен и диапазон будут замененной «версией» исходной функции.
Пример 3: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Это график исходной функции, показывающий ее домен и диапазон.
Определение дальности обычно является сложной задачей. Лучший способ найти это — использовать график данной функции с ее областью определения. Проанализируйте, как функция ведет себя по оси Y, учитывая значения x из области.
Вот шаги, чтобы решить или найти обратное значение данной функции квадратного корня.
Как видите, все очень просто. Убедитесь, что вы делаете это осторожно, чтобы избежать ненужных алгебраических ошибок.
Пример 4: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Эта функция составляет 1/4 (четверть) окружности с радиусом 3, расположенной в Квадранте II. С другой стороны, это половина полукруга, расположенная над горизонтальной осью.
Я знаю, что он пройдет проверку горизонтальной линии, потому что ни одна горизонтальная линия не пересечет ее более одного раза. Это хороший кандидат на обратную функцию.
Опять же, я могу легко описать диапазон, потому что потратил время на его построение. Что ж, я надеюсь, что вы понимаете важность наличия наглядного пособия, которое поможет определить этот «неуловимый» диапазон.
Присутствие члена в квадрате внутри радикального символа говорит мне, что я буду применять операцию извлечения квадратного корня к обеим сторонам уравнения, чтобы найти обратное.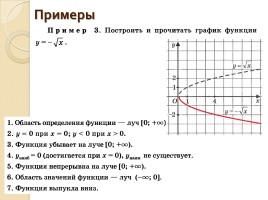 Поступая так, у меня будет плюс или минус. Это ситуация, когда я приму решение, какую из них выбрать в качестве правильной обратной функции. Помните, что обратная функция уникальна, поэтому я не могу позволить получить два ответа.
Поступая так, у меня будет плюс или минус. Это ситуация, когда я приму решение, какую из них выбрать в качестве правильной обратной функции. Помните, что обратная функция уникальна, поэтому я не могу позволить получить два ответа.
Как я решу, какой выбрать? Ключевым моментом является рассмотрение домена и диапазона исходной функции. Я поменяю их местами, чтобы получить домен и диапазон обратной функции. Используйте эту информацию, чтобы определить, какая из двух функций-кандидатов удовлетворяет требуемым условиям.
Хотя у них один и тот же домен, диапазон здесь — решающий фактор! Диапазон говорит нам, что обратная функция имеет минимальное значение y = -3 и максимальное значение y = 0.
Случай положительного квадратного корня не соответствует этому условию, так как он имеет минимум при y = 0 и максимум при y = 3. Отрицательный случай должен быть очевидным выбором, даже после дальнейшего анализа.
Пример 5: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Укажите его домен и диапазон.
Полезно увидеть график исходной функции, потому что мы можем легко определить ее домен и диапазон.
Отрицательный знак функции квадратного корня означает, что он находится ниже горизонтальной оси. Обратите внимание, что это похоже на Пример 4. Это также одна четверть круга, но с радиусом 5. Область вынуждает четверть круга оставаться в Квадранте IV.
Вот как мы алгебраически находим обратное.
Вы выбрали правильную обратную функцию из двух возможных? Ответ — случай с положительным знаком.
Практика с рабочими листами
Возможно, вас заинтересует:
Инверсия матрицы 2 × 2
Функция, обратная абсолютному значению
Функция, обратная постоянной
Обратная экспоненциальная функция
Функция, обратная линейной
Обратная логарифмическая функция
Обратная квадратичная функция
Обратная рациональная функция
9.
 1: Функция квадратного корня
1: Функция квадратного корняВ этом разделе мы обратим наше внимание на функцию квадратного корня, функцию, определяемую уравнением
\ [\ begin {массив} {c} {f (x) = \ sqrt {x}} \\ \ end {array} \]
Мы начинаем раздел с рисования графика функции, затем обращаемся к домену и диапазону.После этого мы исследуем ряд различных преобразований функции.
График функции квадратного корня
Давайте создадим таблицу точек, которая удовлетворяет уравнению функции, а затем нанесем точки из таблицы в декартовой системе координат на миллиметровую бумагу. Мы продолжим создавать и наносить точки, пока не убедимся в окончательной форме графика.
Мы знаем, что не можем извлечь квадратный корень из отрицательного числа. Поэтому мы не хотим помещать в нашу таблицу отрицательные значения x .Чтобы еще больше упростить наши вычисления, давайте использовать числа, квадратный корень которых легко вычисляется. Это напоминает идеальные квадраты, такие как 0, 1, 4, 9 и так далее.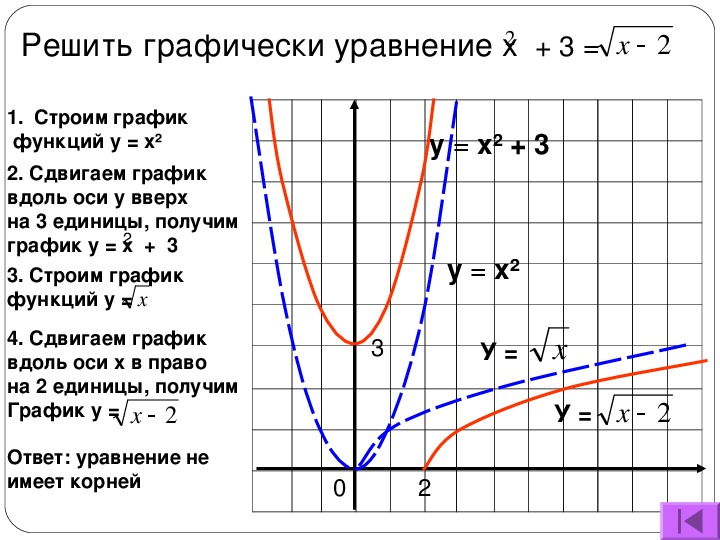 Мы поместили эти числа как значения x в таблицу на рис. , рис. 1, (b), а затем вычислили квадратный корень из каждого значения. На рис. 1 (a) каждая точка из таблицы изображена сплошной точкой. Если мы продолжим добавлять точки в таблицу, наносим их на график, график в конечном итоге заполнится и примет форму сплошной кривой, показанной на , рис. 1, (c).2 \), \ (x \ ge 0 \), что изображено на рис. 2 (c). Обратите внимание на точное совпадение с графиком функции квадратного корня в Рисунок 1 (c).
Мы поместили эти числа как значения x в таблицу на рис. , рис. 1, (b), а затем вычислили квадратный корень из каждого значения. На рис. 1 (a) каждая точка из таблицы изображена сплошной точкой. Если мы продолжим добавлять точки в таблицу, наносим их на график, график в конечном итоге заполнится и примет форму сплошной кривой, показанной на , рис. 1, (c).2 \), \ (x \ ge 0 \), что изображено на рис. 2 (c). Обратите внимание на точное совпадение с графиком функции квадратного корня в Рисунок 1 (c).
Последовательность графиков на рис. 2 также помогает нам определить область и диапазон функции квадратного корня.
- В рис. 2 (а) парабола открывается наружу неограниченно, как влево, так и вправо. Следовательно, доменом является \ (D_ {f} = (- \ infty, \ infty) \) или все действительные числа. Кроме того, граф имеет вершину в начале координат и неограниченно открывается вверх, поэтому диапазон равен \ (R_ {f} = [0, \ infty) \).
 {−1}} = [0, \ infty) \).
{−1}} = [0, \ infty) \).
Конечно, мы также можем определить область и диапазон функции квадратного корня, проецируя все точки на графике на оси x и y , как показано на рисунках 3 (a) и ( б) соответственно.
Рис. 3.} \ text {Спроецируйте на оси, чтобы найти домен и диапазон}} \\ \ nonumber \ end {array} \]Кто-то может возразить против диапазона, спросив: «Откуда мы знаем, что график изображение функции квадратного корня в Рисунок 3 (b) растет бесконечно? » Опять же, ответ кроется в последовательности графиков на рис. 2 .2 \), \ (x \ ge 0 \), открывается бесконечно вправо по мере того, как график уходит в бесконечность. Следовательно, после отражения этого графика по линии y = x результирующий график должен бесконечно подниматься вверх при движении вправо. Таким образом, диапазон функции квадратного корня равен \ ([0, \ infty) \).
Переводы
Если мы сдвинем график \ (y = \ sqrt {x} \) вправо и влево или вверх и вниз, это затронет домен и / или диапазон.
Пример \ (\ PageIndex {4} \)
Нарисуйте график \ (f (x) = \ sqrt {x − 2} \).Используйте свой график, чтобы определить домен и диапазон.
Мы знаем, что основное уравнение \ (y = \ sqrt {x} \) имеет график, показанный на Рисунках 1 (c). Если мы заменим x на x — 2, основное уравнение \ (y = \ sqrt {x} \) станет \ (f (x) = \ sqrt {x − 2} \). Из нашей предыдущей работы с геометрическими преобразованиями мы знаем, что это сдвинет график на две единицы вправо, как показано на Рисунках 4, (a) и (b).
Рисунок 4. Чтобы нарисовать график \ (f (x) = \ sqrt {x − 2} \), сдвиньте график \ (y = \ sqrt {x} \) на две единицы вправо.Чтобы найти область, мы проецируем каждую точку графика f на ось x, как показано на рис. 4 (a). Обратите внимание, что все точки справа от 2 или включая 2 заштрихованы на оси абсцисс. Следовательно, область определения f равна
Домен = \ ([2, \ infty) \) = {x: \ (x \ ge 0 \)}
Поскольку сдвига в вертикальном направлении не произошло, диапазон остается прежним. Чтобы найти диапазон, мы проецируем каждую точку графика на ось y, как показано на рис. , рис. , , 4, (b).Обратите внимание, что все точки, равные нулю и выше, заштрихованы на оси ординат. Таким образом, диапазон f равен
Чтобы найти диапазон, мы проецируем каждую точку графика на ось y, как показано на рис. , рис. , , 4, (b).Обратите внимание, что все точки, равные нулю и выше, заштрихованы на оси ординат. Таким образом, диапазон f равен
Диапазон = \ ([0, \ infty) \) = {y: \ (y \ ge 0 \)}.
Мы можем найти область определения этой функции алгебраически, исследуя ее определяющее уравнение \ (f (x) = \ sqrt {x − 2} \). Мы понимаем, что нельзя извлекать квадратный корень из отрицательного числа. Следовательно, выражение под радикалом должно быть неотрицательным (положительным или нулевым). То есть
\ (х — 2 \ ge 0 \).
Решение этого неравенства для x ,
\ (х \ ge 2 \).
Таким образом, область определения f — это Domain = \ ([2, \ infty) \), что соответствует графическому решению, приведенному выше.
Давайте посмотрим на другой пример.
Пример \ (\ PageIndex {5} \)
Нарисуйте график \ (f (x) = \ sqrt {x + 4} + 2 \). Используйте свой график, чтобы определить домен и диапазон f.
Используйте свой график, чтобы определить домен и диапазон f.
Опять же, мы знаем, что основное уравнение \ (y = \ sqrt {x} \) имеет график, показанный на рис. 1 (c). Если мы заменим x на x +4, основное уравнение \ (y = \ sqrt {x} \) станет \ (y = \ sqrt {x + 4} \).Из нашей предыдущей работы с геометрическими преобразованиями мы знаем, что это сдвинет график \ (y = \ sqrt {x} \) на четыре единицы влево, как показано на , рис. 5, (a).
Если мы знаем, что прибавляем 2 к уравнению \ (y = \ sqrt {x + 4} \), чтобы получить уравнение \ (y = \ sqrt {x + 4} + 2 \), это сдвинет график \ ( y = \ sqrt {x + 4} \) на две единицы вверх, как показано на рис. 5 (b).
Рис. 5. Перевод исходного уравнения \ (y = \ sqrt {x} \) для получения графика \ (y = \ sqrt {x + 4} + 2 \). Идентификация области \ (f (x ) = \ sqrt {x + 4} + 2 \), мы проецируем все точки на графике f на ось x, как показано на , рис.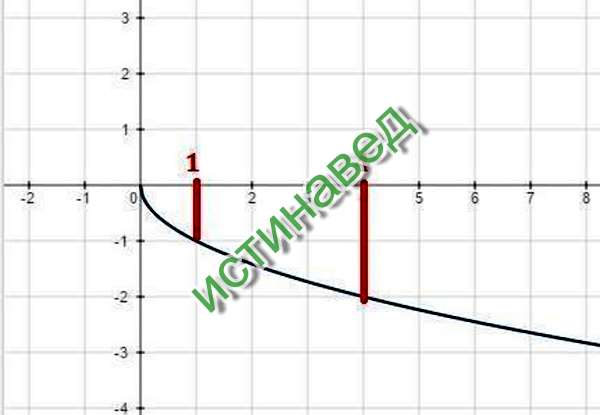 6, (a).Обратите внимание, что все точки справа от — 4 или включая его заштрихованы на оси x . Таким образом, область определения \ (f (x) = \ sqrt {x + 4} + 2 \) равна
6, (a).Обратите внимание, что все точки справа от — 4 или включая его заштрихованы на оси x . Таким образом, область определения \ (f (x) = \ sqrt {x + 4} + 2 \) равна
Домен = \ ([- 4, \ infty) \) = {x: \ (x \ ge −4 \)}
Рис. 6. Спроецируйте точки f на оси, чтобы определить область и диапазон. Аналогичным образом, чтобы найти диапазон f , спроецируйте все точки на графике f на ось y , как показано в . Рисунок 6 (б). Обратите внимание, что все точки на оси y больше или включают 2 затенены.Следовательно, диапазон f равен
Диапазон = \ ([2, \ infty) \) = {y: \ (y \ ge 2 \)}
Мы также можем найти область определения f алгебраически, исследуя уравнение \ (f (x) = \ sqrt {x + 4} + 2 \). Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под корнем должно быть неотрицательным (нулевым или положительным). Следовательно,
\ (х + 4 \ ge 0 \).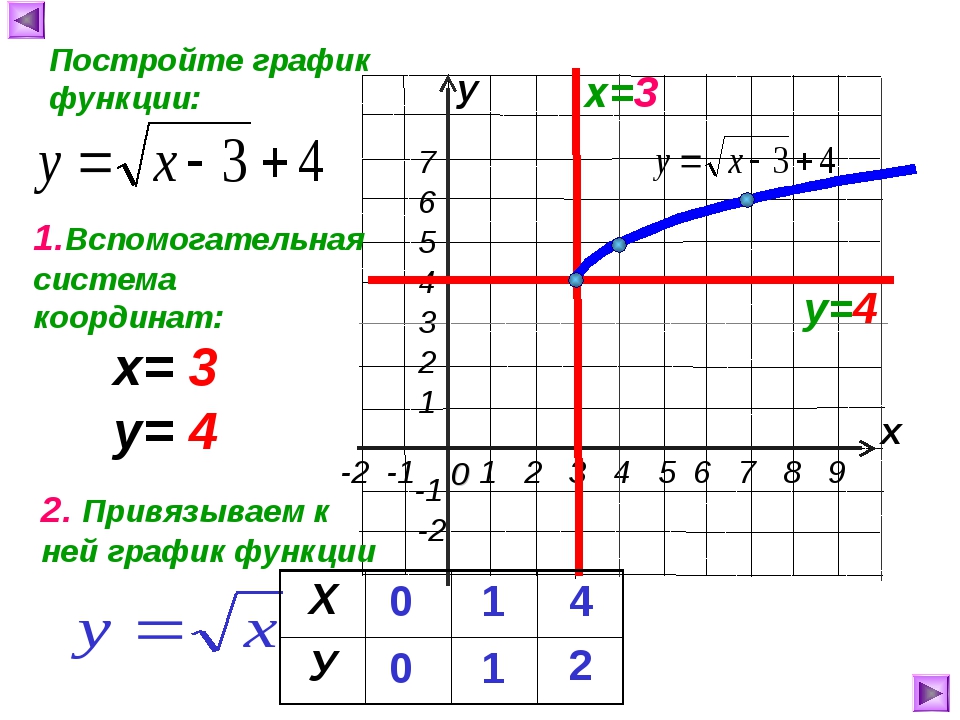
Решение этого неравенства для x ,
\ (х \ ge −4 \).
Таким образом, область определения f — это Domain = \ ([- 4, \ infty) \), что соответствует графическому решению, представленному выше.
Отражения
Если мы начнем с основного уравнения \ (y = \ sqrt {x} \), а затем заменим x на −x, тогда график полученного уравнения \ (y = \ sqrt {−x} \) будет захвачен путем отражения график \ (y = \ sqrt {x} \) (см. , рис. 1, (c)) по горизонтали поперек оси y. График \ (y = \ sqrt {−x} \) показан на Рисунке 7 (a).
Точно так же график \ (y = — \ sqrt {x} \) будет вертикальным отражением графика \ (y = \ sqrt {x} \) по оси x, как показано на , рис. (б).
Рис. 7. Отражение графика \ (y = \ sqrt {x} \) по осям x и y.Чаще всего вам будет предложено выполнить отражение и перевод.
Пример \ (\ PageIndex {6} \)
Нарисуйте график \ (f (x) = \ sqrt {4− x} \). Используйте полученный график, чтобы определить домен и диапазон f.
Используйте полученный график, чтобы определить домен и диапазон f.
Сначала перепишите уравнение \ (f (x) = \ sqrt {4− x} \) следующим образом:
\ (f (x) = \ sqrt {- (x − 4)} \)
Определение
Первые размышления .Обычно более интуитивно понятно выполнять размышления перед переводом.
Помня об этом, мы сначала нарисуем график \ (f (x) = \ sqrt {−x} \), который является отражением графика \ (f (x) = \ sqrt {x} \ ) по оси y . Это показано на рис. 8 (а).
Теперь в \ (f (x) = \ sqrt {−x} \) замените x на x — 4, чтобы получить \ (f (x) = \ sqrt {- (x − 4)} \). Это сдвигает график \ (f (x) = \ sqrt {−x} \) на четыре единицы вправо, как показано на , рис. 8, (b).
Рисунок 8. Отражение с последующим переводом. Чтобы найти область определения функции \ (f (x) = \ sqrt {- (x − 4)} \) или, что эквивалентно, \ (f (x) = \ sqrt {4 − x} \), спроецируйте каждый точка на графике f на оси x , как показано на рис. 9 (a). Обратите внимание, что все действительные числа, меньшие или равные 4, заштрихованы на оси x . Следовательно, домен f равен
9 (a). Обратите внимание, что все действительные числа, меньшие или равные 4, заштрихованы на оси x . Следовательно, домен f равен
Домен = \ ((- \ infty, 4] \) = {x: \ (x \ le 4 \)}.
Аналогичным образом, чтобы получить диапазон f, спроецируйте каждую точку на графике f на их ось, как показано на рис. 9 (b).Обратите внимание, что все действительные числа, большие или равные нулю, заштрихованы на оси ординат. Следовательно, диапазон f равен
.Диапазон = \ ([0, \ infty) \) = {x: \ (x \ ge 0 \)}.
Мы также можем найти область определения функции f , исследуя уравнение \ (f (x) = \ sqrt {4 − x} \). Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под корнем должно быть неотрицательным (нулевым или положительным). Следовательно,
\ (4 — х \ ge 0 \).
Рисунок 9. Определение области и диапазона \ (f (x) = \ sqrt {4 − x} \) Решите это последнее неравенство для x . Сначала вычтите 4 из обеих частей неравенства, затем умножьте обе части полученного неравенства на — 1. Конечно, умножение на отрицательное число меняет символ неравенства на противоположное.
Сначала вычтите 4 из обеих частей неравенства, затем умножьте обе части полученного неравенства на — 1. Конечно, умножение на отрицательное число меняет символ неравенства на противоположное.
\ (- х \ ge −4 \)
\ (х \ ле 4 \)
Таким образом, область определения f равна {x: \ (x \ le 4 \)}. В обозначении интервалов Domain = \ ((- \ infty, 4] \). Это хорошо согласуется с приведенным выше графическим результатом.
Чаще всего требуется сочетание вашего графического калькулятора и небольших алгебраических манипуляций, чтобы определить область определения функции квадратного корня.
Пример \ (\ PageIndex {7} \)
Нарисуйте график \ (f (x) = \ sqrt {5−2x} \) Используйте график и алгебраический метод, чтобы определить область определения функции.
Загрузите функцию в Y1 в меню Y = вашего калькулятора, как показано на рис. 10 (a). Выберите 6: ZStandard в меню ZOOM, чтобы построить график, показанный на рис. 10 (b).
10 (b).
Внимательно посмотрите на график , рис. 10, (b) и обратите внимание, что трудно сказать, идет ли график полностью вниз, чтобы «коснуться» оси x около \ (x \ приблизительно 2.5 \). Однако наш предыдущий опыт использования функции извлечения квадратного корня заставляет нас думать, что это всего лишь артефакт недостаточного разрешения калькулятора, который не позволяет графику «касаться» оси x в точке \ (x \ приблизительно 2,5 \).
Алгебраический подход разрешит проблему. Мы можем определить область определения f, исследуя уравнение \ (f (x) = \ sqrt {5 — 2x} \). Следовательно, Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под радикалом должно быть неотрицательным (нулевым или положительным).
\ (5 — 2x \ ge 0 \).
Решите это последнее неравенство для x . Сначала вычтем 5 из обеих частей неравенства.
\ (- 2x \ ge −5 \).
Затем разделите обе части этого последнего неравенства на −2. Помните, что мы должны обратить неравенство в тот момент, когда делим на отрицательное число.
\ (\ frac {−2x} {- 2} \ le \ frac {−5} {- 2} \).
\ (х \ le \ frac {5} {2} \).
Таким образом, область определения f равна {x: \ (x \ le \ frac {5} {2} \)}. В интервальной записи Домен = \ ((- \ infty, \ frac {5} {2}] \).Это хорошо согласуется с приведенным выше графическим результатом.
Дальнейшее самоанализ показывает, что этот аргумент также решает вопрос о том, «касается» ли граф оси x в точке \ (x = \ frac {5} {2} \). Если вас это не убедило, замените \ (x = \ frac {5} {2} \) на \ (f (x) = \ sqrt {5−2x} \) , чтобы увидеть
\ (f (\ frac {5} {2}) = \ sqrt {5-2 (\ frac {5} {2})} = \ sqrt {0} = 0 \).
Таким образом, график f «касается» оси x в точке \ ((\ frac {5} {2}, 0) \).
В упражнении Exercise 1-10 выполните все следующие задачи:
- Установите систему координат на миллиметровой бумаге.
 Обозначьте и масштабируйте каждую ось.
Обозначьте и масштабируйте каждую ось. - Заполните таблицу баллов по данной функции. Постройте каждую точку в своей системе координат, а затем используйте их, чтобы нарисовать график данной функции.
- Используйте карандаши разных цветов, чтобы спроецировать все точки на оси x и y , чтобы определить область и диапазон.Используйте интервальную нотацию для описания области данной функции.
Упражнение \ (\ PageIndex {1} \)
\ (f (x) = — \ sqrt {x} \)
- Ответ
х
0
1
4
9
ф (х)
0
– 1
– 2
– 3
Отметьте точки в таблице и используйте их для построения графика.

Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ((- \ infty, 0] \).
Упражнение \ (\ PageIndex {2} \)
\ (f (x) = \ sqrt {−x} \)
Упражнение \ (\ PageIndex {3} \)
\ (f (x) = \ sqrt {x + 2} \)
- Ответ
х
– 2
– 1
2
7
f ( x )
0
1
2
3
Отметьте точки в таблице и используйте их для построения графика.

Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([ — 2, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {4} \)
\ (f (x) = \ sqrt {5 − x} \)
Упражнение \ (\ PageIndex {5} \)
\ (f (x) = \ sqrt {x} +2 \)
- Ответ
Нанесите точки в таблицу и используйте их для построения графика f .
Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([2, \ infty) \).
Упражнение \ (\ PageIndex {6} \)
\ (f (x) = \ sqrt {x} −1 \)
Упражнение \ (\ PageIndex {7} \)
\ (f (x) = \ sqrt {x + 3} +2 \)
- Ответ
х
– 3
– 2
1
6
ф (х)
2
3
4
5
Постройте точки в таблице и используйте их для построения графика f .

- Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([ — 3, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([2, \ infty) \).
Упражнение \ (\ PageIndex {8} \)
\ (f (x) = \ sqrt {x − 1} +3 \)
Упражнение \ (\ PageIndex {9} \)
\ (f (x) = \ sqrt {3 − x} \)
- Ответ
х
– 6
– 1
2
3
f ( x )
3
2
1
0
Постройте точки в таблице и используйте их для построения графика f .

Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ (( — \ infty, 3] \). Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Диапазон = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {10} \)
\ (f (x) = — \ sqrt {x + 3} \)
В Exercises 11 — 20 выполните каждую из следующих задач.
- Установите систему координат на миллиметровой бумаге.Обозначьте и масштабируйте каждую ось. Не забудьте нарисовать все линии линейкой.
- Используйте геометрические преобразования, чтобы нарисовать график данной функции в вашей системе координат без использования графического калькулятора. Примечание. Вы можете проверить свое решение с помощью калькулятора, но вы сможете построить график без использования калькулятора.
- Используйте карандаши разных цветов, чтобы спроецировать точки графика функции на оси x и y .
 Используйте обозначение интервала для описания области и диапазона функции.
Используйте обозначение интервала для описания области и диапазона функции.
Упражнение \ (\ PageIndex {11} \)
\ (f (x) = \ sqrt {x} +3 \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a). Затем добавьте 3, чтобы получить уравнение \ (y = \ sqrt {x} + 3 \). Это сдвинет график \ (y = \ sqrt {x} \) вверх на 3 единицы, как показано в (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \).Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([3, \ infty) \).
Упражнение \ (\ PageIndex {12} \)
\ (f (x) = \ sqrt {x + 3} \)
Упражнение \ (\ PageIndex {13} \)
\ (f (x) = \ sqrt {x − 2} \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).
 Затем замените x на x — 2, чтобы получить уравнение \ (y = \ sqrt {x − 2} \). Это сдвинет график \ (y = \ sqrt {x} \) вправо на 2 единицы, как показано в (b).
Затем замените x на x — 2, чтобы получить уравнение \ (y = \ sqrt {x − 2} \). Это сдвинет график \ (y = \ sqrt {x} \) вправо на 2 единицы, как показано в (b).Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([2, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {14} \)
\ (f (x) = \ sqrt {x} −2 \)
Упражнение \ (\ PageIndex {15} \)
\ (f (x) = \ sqrt {x + 5} +1 \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем замените x на x + 5, чтобы получить уравнение \ (y = \ sqrt {x + 5} \). Затем добавьте 1, чтобы получить уравнение \ (f (x) = \ sqrt {x + 5} +1 \). Это сдвинет график \ (y = \ sqrt {x} \) влево на 5 единиц, а затем вверх на 1 единицу, как показано в (b).
Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([- 5, \ infty) \).
 Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([1, \ infty) \).
Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([1, \ infty) \).
Упражнение \ (\ PageIndex {16} \)
\ (f (x) = \ sqrt {x − 2} −1 \)
Упражнение \ (\ PageIndex {17} \)
\ (y = — \ sqrt {x + 4} \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, замените x на x + 4, чтобы получить уравнение \ (y = — \ sqrt {x + 4} \). Это сдвинет график \ (y = — \ sqrt {x} \) на четыре единицы влево, как показано в (c).
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([- 4, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ((- \ infty, 0] \).
Упражнение \ (\ PageIndex {18} \)
\ (f (x) = — \ sqrt {x} +4 \)
Упражнение \ (\ PageIndex {19} \)
\ (f (x) = — \ sqrt {x} +3 \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).
 Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \ (y = — \ sqrt {x} +3 \).Это сдвинет график \ (y = — \ sqrt {x} \) на три единицы вверх, как показано в (c).
Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \ (y = — \ sqrt {x} +3 \).Это сдвинет график \ (y = — \ sqrt {x} \) на три единицы вверх, как показано в (c).Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ((- \ infty, 3] \).
Упражнение \ (\ PageIndex {20} \)
\ (f (x) = — \ sqrt {x + 3} \)
Упражнение \ (\ PageIndex {21} \)
Чтобы построить график функции \ (f (x) = \ sqrt {3 − x} \), выполните последовательно каждый из следующих шагов без помощи калькулятора.
- Настройте систему координат и нарисуйте график \ (y = \ sqrt {x} \). Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \).
 Обозначьте график соответствующим уравнением.
Обозначьте график соответствующим уравнением. - Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x — 3)} \). Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {3 − x} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем замените x на — x , чтобы получить уравнение \ (y = \ sqrt {−x} \). Это будет отражать график \ (y = \ sqrt {x} \) по оси y , как показано на (b). Наконец, замените x на x — 3, чтобы получить уравнение \ ( y = \ sqrt { — ( x — 3)} \). Это сдвинет график \ (y = \ sqrt {−x} \) на три единицы вправо, как показано в (c).
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ((- \ infty, 3] \).
 Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {22} \)
Чтобы построить график функции \ (f (x) = \ sqrt {−x − 3} \), последовательно выполните каждый из следующих шагов.
- Настройте систему координат и нарисуйте график \ (y = \ sqrt {x} \). Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \).Обозначьте график соответствующим уравнением.
- Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x + 3)} \). Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {−x − 3} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
Упражнение \ (\ PageIndex {23} \)
Чтобы построить график функции \ (f (x) = \ sqrt {−x − 3} \), выполните последовательно каждый из следующих шагов без помощи калькулятора.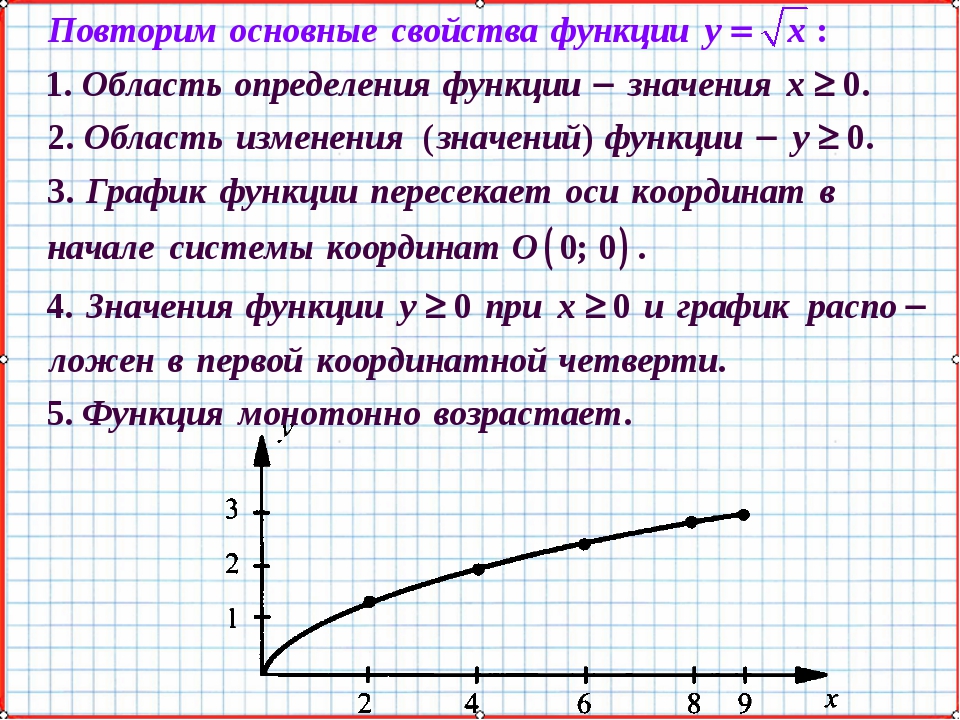
- Настройте систему координат и нарисуйте график \ (y = \ sqrt {x} \).Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \). Обозначьте график соответствующим уравнением.
- Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x + 1)} \). Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {−x − 1} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем замените x на −x, чтобы получить уравнение \ (y = \ sqrt {−x} \). Это будет отражать график \ (y = \ sqrt {x} \) по оси y, как показано в (b). Наконец, замените x на x + 1, чтобы получить уравнение \ (y = \ sqrt {- (x + 1)} \). Это сдвинет график \ (y = \ sqrt {−x} \) на одну единицу влево, как показано в (c).
Спроецируйте все точки на графике на ось x, чтобы определить область: Domain = \ ((- \ infty, −1] \).
 Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {24} \)
Чтобы построить график функции \ (f (x) = \ sqrt {1 − x} \), последовательно выполните каждый из следующих шагов.
- Настройте систему координат и нарисуйте график \ (y = \ sqrt {x} \). Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \). Обозначьте график соответствующим уравнением.
- Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x − 1)} \).Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {1 − x} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
В упражнениях 25 — 28 выполните каждую из следующих задач.
- Нарисуйте график данной функции с помощью графического калькулятора.
 Скопируйте изображение из окна просмотра на свою домашнюю работу. Обозначьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. Обозначьте свой график его уравнением.Используйте график, чтобы определить область определения функции и описать область с помощью интервальной записи.
Скопируйте изображение из окна просмотра на свою домашнюю работу. Обозначьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. Обозначьте свой график его уравнением.Используйте график, чтобы определить область определения функции и описать область с помощью интервальной записи. - Используйте чисто алгебраический подход, чтобы определить область определения данной функции. Для описания результата используйте обозначение интервалов. Согласен ли он с графическим результатом из части 1?
Упражнение \ (\ PageIndex {25} \)
\ (f (x) = \ sqrt {2x + 7} \)
- Ответ
Мы используем графический калькулятор, чтобы построить следующий график \ (f (x) = \ sqrt {2x + 7} \)
По нашим оценкам, домен будет состоять из всех действительных чисел справа от примерно — 3 . 5. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа.
 Следовательно, выражение под корнем в \ (f (x) = \ sqrt {2x + 7} \) должно быть больше или равно нулю.
Следовательно, выражение под корнем в \ (f (x) = \ sqrt {2x + 7} \) должно быть больше или равно нулю.\ (2x + 7 \ ge 0 \)
\ (2x \ ge −7 \)
\ (x \ ge — \ frac {7} {2} \)
Следовательно, домен равен \ ([- \ frac {7} {2}, \ infty) \).
Упражнение \ (\ PageIndex {26} \)
\ (f (x) = \ sqrt {7−2x} \)
Упражнение \ (\ PageIndex {27} \)
\ (f (x) = \ sqrt {12−4x} \)
- Ответ
Мы используем графический калькулятор, чтобы построить следующий график \ (f (x) = \ sqrt {12−4x} \).
По нашим оценкам, область будет состоять из всех действительных чисел справа от приблизительно 3. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа. Следовательно, выражение под корнем в \ (f (x) = \ sqrt {12−4x} \) должно быть больше или равно нулю.

\ (12−4x \ ge 0 \)
\ (- 4x \ ge −12 \)
\ (х \ ле 3 \)
Следовательно, домен равен \ ((- \ infty, 3] \).
Упражнение \ (\ PageIndex {28} \)
\ (f (x) = \ sqrt {12 + 2x} \)
В упражнениях 29 — 40 найдите область определения заданной функции алгебраически.
Упражнение \ (\ PageIndex {29} \)
\ (f (x) = \ sqrt {2x + 9} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. Таким образом, 2x + 9 должно быть больше или равно нулю. Поскольку \ (2x + 9 \ ge 0 \) означает, что \ (x \ ge — \ frac {9} {2} \), область представляет собой интервал \ ([- \ frac {9} {2}, \ infty ) \).
Упражнение \ (\ PageIndex {30} \)
\ (f (x) = \ sqrt {−3x + 3} \)
Упражнение \ (\ PageIndex {31} \)
\ (f (x) = \ sqrt {−8x − 3} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом.Таким образом, −8x − 3 должно быть больше или равно нулю. Поскольку \ (- 8x − 3 \ ge 0 \) означает, что \ (x \ le — \ frac {3} {8} \), область представляет собой интервал \ ((- \ infty, — \ frac {3} { 8}] \).
Упражнение \ (\ PageIndex {32} \)
\ (f (x) = \ sqrt {−3x + 6} \)
Упражнение \ (\ PageIndex {33} \)
\ (f (x) = \ sqrt {−6x − 8} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. Таким образом, −6x − 8 должно быть больше или равно нулю.Поскольку \ (- 6x − 8 \ ge 0 \) влечет, что \ (x \ le — \ frac {4} {3} \), область представляет собой интервал \ ((- \ infty, \ frac {4} {3 }] \).
Упражнение \ (\ PageIndex {34} \)
\ (f (x) = \ sqrt {8x − 6} \)
Упражнение \ (\ PageIndex {35} \)
\ (f (x) = \ sqrt {−7x + 2} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. Таким образом, −7x + 2 должно быть больше или равно нулю. Поскольку \ (- 7x + 2 \ ge 0 \) означает, что \ (x \ le \ frac {2} {7} \), область представляет собой интервал \ ((- \ infty, \ frac {2} {7} ] \).
Упражнение \ (\ PageIndex {36} \)
\ (f (x) = \ sqrt {8x − 3} \)
Упражнение \ (\ PageIndex {37} \)
\ (f (x) = \ sqrt {6x + 3} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. Таким образом, 6x + 3 должно быть больше или равно нулю. Поскольку \ (6x + 3 \ ge 0 \) означает, что \ (x \ ge — \ frac {1} {2} \), область представляет собой интервал \ ([- \ frac {1} {2}, \ infty ) \).
Упражнение \ (\ PageIndex {38} \)
\ (f (x) = \ sqrt {x − 5} \)
Упражнение \ (\ PageIndex {39} \)
\ (f (x) = \ sqrt {−7x − 8} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. 2} = \ pm xx2 = ± x
Почему некоторые люди говорят, что это правда: Это именно то, чему меня учили в школе: когда вы извлекаете квадратный корень, ответ всегда будет «плюс-минус» некоторого значения.
Почему некоторые люди говорят, что это ложь: Когда вы возводите в квадрат x, x, x, оно становится положительным, независимо от того, что было раньше; тогда, когда вы извлечете квадратный корень, он все равно будет положительным. Следовательно, ответ будет просто ∣x∣ | x | ∣x∣, а не ± x \ pm x ± x.
Выявите правильный ответ: \ color {# 20A900} {\ text {Выявите правильный ответ:}} Выявите правильный ответ:Утверждение ложно \ color {# D61F06} {\ textbf {false}} ложно.
Пояснение:
В своей стандартной области неотрицательных действительных чисел x \ sqrt {x} x определяется как «неотрицательное действительное число, которое в квадрате равно x.x.x. «Например, 25 = 5 \ sqrt {25} = 525 = 5 , а не ± 5 \ pm 5 ± 5. x \ sqrt {x} x определяется таким образом, поэтому это функция.
Функция — это отношение или карта между набором входных значений (домен) и набором выходных значений (диапазон), которая имеет свойство, что каждый принятый вход соответствует точно одному выходу. Это свойство широко известно как «прохождение теста вертикальной линии».
Чтобы x \ sqrt {x} x была функцией, ее оценка на любом входе должна быть единственным четко определенным выходом.Парабола 2×2 не пройдет проверку вертикальной линии и не будет функцией.
Расширение домена до всех действительных чисел и диапазона до комплексных чисел:
Поведение функции извлечения квадратного корня при расширении на область всех действительных чисел (положительные действительные числа, отрицательные действительные числа и 0) в точности отражает приведенный выше аргумент. Квадратный корень отрицательного числа — это комплексное число. Но даже с расширенной областью определения x \ sqrt {x} x аналогичным образом определяется, так что это все еще функция.2}} {| x |} + 1, ∣x∣x2 +1,
, где xxx — ненулевое действительное число.
См. Также
Функция квадратного корня Python — настоящий Python
Вы пытаетесь решить квадратное уравнение? Возможно, вам нужно рассчитать длину одной стороны прямоугольного треугольника. Для этих и других типов уравнений функция квадратного корня Python
sqrt ()может помочь вам быстро и точно вычислить решения.К концу этой статьи вы узнаете:
- Что такое квадратный корень
- Как использовать функцию квадратного корня Python,
sqrt () - Когда
sqrt ()может быть полезен в реальном мире
Погрузимся!
Python Pit Stop: Это руководство представляет собой quick и практический способ найти нужную информацию, так что вы вернетесь к своему проекту в кратчайшие сроки!
Квадратные корни в математике
В алгебре квадрат , x , является результатом умножения числа n на само себя: x = n²
Вы можете вычислить квадраты с помощью Python:
>>>>>> п = 5 >>> х = п ** 2 >>> х 25Оператор Python
**используется для вычисления степени числа.В этом случае 5 в квадрате или 5 в степени 2 дает 25.Таким образом, квадратный корень — это число n , которое при умножении само на себя дает квадрат x .
В этом примере n , квадратный корень, равен 5.
25 — это пример полного квадрата . Совершенные квадраты — это квадраты целых чисел:
>>>>>> 1 ** 2 1 >>> 2 ** 2 4 >>> 3 ** 2 9Возможно, вы запомнили некоторые из этих совершенных квадратов, когда выучили свои таблицы умножения на уроках элементарной алгебры.
Если вам дан маленький точный квадрат, может быть достаточно просто вычислить или запомнить его квадратный корень. Но для большинства других квадратов это вычисление может быть немного более утомительным. Часто оценки бывает достаточно, когда у вас нет калькулятора.
К счастью, у вас, как у разработчика Python, есть калькулятор, а именно интерпретатор Python!
Функция квадратного корня Python
МодульPython
mathв стандартной библиотеке может помочь вам работать с математическими задачами в коде.Он содержит множество полезных функций, таких какrestder ()иfactorial (). Он также включает функцию квадратного корня Pythonsqrt ().Вы начнете с импорта
math:Вот и все, что нужно! Теперь вы можете использовать
math.sqrt ()для вычисления квадратных корней.sqrt ()имеет простой интерфейс.Требуется один параметр,
x, который (как вы видели ранее) обозначает квадрат, для которого вы пытаетесь вычислить квадратный корень.В предыдущем примере это будет25.Возвращаемое значение
sqrt ()— это квадратный корень изxв виде числа с плавающей запятой. В примере это5,0.Давайте рассмотрим несколько примеров того, как (и как не использовать) использовать
sqrt ().Квадратный корень положительного числа
Один из типов аргументов, который вы можете передать функции
sqrt (), — это положительное число. Сюда входят типыintиfloat.Например, вы можете найти квадратный корень из
49, используяsqrt ():Возвращаемое значение —
7,0(квадратный корень из49) в виде числа с плавающей запятой.Наряду с целыми числами вы также можете передавать
>>>значения с плавающей запятой:>>> math.sqrt (70.5) 8,396427811873332Вы можете проверить точность этого квадратного корня, вычислив его обратную величину:
>>>>>> 8.396427811873332 ** 2 70,5Квадратный корень нуля
Даже
0— правильный квадрат для передачи функции квадратного корня Python:Хотя вам, вероятно, не придется часто вычислять квадратный корень из нуля, вы можете передать переменную в
sqrt (), значение которой вы на самом деле не знаете. Итак, хорошо знать, что в таких случаях он может обрабатывать ноль.Квадратный корень отрицательных чисел
Квадрат любого действительного числа не может быть отрицательным.Это потому, что отрицательный результат возможен только в том случае, если один фактор положительный, а другой отрицательный. Квадрат по определению является произведением числа и самого себя, поэтому получить отрицательный действительный квадрат невозможно:
>>>>>> math.sqrt (-25) Отслеживание (последний вызов последний): Файл "", строка 1, в ValueError: ошибка математического домена Если вы попытаетесь передать отрицательное число в
sqrt (), вы получитеValueError, потому что отрицательные числа не входят в область возможных действительных квадратов.Вместо этого квадратный корень отрицательного числа должен быть сложным, что выходит за рамки функции квадратного корня Python.Квадратных корней в реальном мире
Чтобы увидеть реальное применение функции квадратного корня Python, давайте обратимся к теннису.
Представьте, что Рафаэль Надаль, один из самых быстрых игроков в мире, только что ударил справа из заднего угла, где базовая линия пересекается с боковой линией теннисного корта:
Теперь предположим, что его противник нанес контратакующий удар (тот, который закроет мяч с небольшим ускорением вперед) в противоположный угол, где другая боковая линия встречается с сеткой:
Как далеко Надаль должен бежать, чтобы дотянуться до мяча?
Из нормативных размеров теннисного корта можно определить, что длина базовой линии составляет 27 футов, а длина боковой линии (на одной стороне сетки) — 39 футов.Итак, по сути, это сводится к решению гипотенузы прямоугольного треугольника:
Используя ценное геометрическое уравнение, теорему Пифагора, мы знаем, что a² + b² = c² , где a и b — катеты прямоугольного треугольника, а c — гипотенуза.
Таким образом, мы можем рассчитать расстояние, которое Надаль должен пробежать, переписав уравнение, чтобы найти c :
Вы можете решить это уравнение, используя функцию квадратного корня Python:
>>>>>> a = 27 >>> b = 39 >>> математика.sqrt (а ** 2 + b ** 2) 47.434164569Итак, Надаль должен пробежать около 47,4 фута (14,5 метра), чтобы дотянуться до мяча и сохранить точку.
Заключение
Поздравляем! Теперь вы знаете все о функции квадратного корня Python.
Вы покрыли:
- Краткое введение в квадратные корни
- Особенности функции квадратного корня Python,
sqrt () - Практическое применение
sqrt ()на реальном примере
Умение пользоваться
sqrt ()— это только половина дела.Другое дело — понять, когда его использовать. Теперь вы знаете и то, и другое, так что примените свое новое мастерство в использовании функции извлечения квадратного корня Python!Поиск производной квадратного корня от x — стенограмма видео и урока
Решение
Формула показывает, что производная квадратного корня из x равна (1/2) x -1/2. Это можно записать в нескольких разных формах:
Проверка вашей работы
Есть несколько различных способов, с помощью которых мы можем проверить нашу работу при работе с производными финансовыми инструментами.Первый касается определения производной с использованием лимитов.
Мы можем использовать это определение, чтобы проверить нашу работу. При этом мы должны получить тот же результат, что и при использовании формулы. Мы начинаем с того, что позволяем f ( x ) = sqrt ( x ) и подключаемся соответственно.
Теперь мы хотим найти предел, поскольку h приближается к 0.Один из способов оценки предела — подставить число, которое приближается к h , на h . Однако в этом случае мы бы вставили 0 для h . Вы понимаете, почему мы не можем этого сделать? Если вы думаете, что мы не можем подставить 0 вместо h , потому что это приведет к нулевому знаменателю, то вы правы! Следовательно, мы собираемся манипулировать лимитом, чтобы преобразовать его в форму, в которой мы можем вставить 0 для h без создания неопределенного выражения.Умножим все это на версию числа 1:
Помните, мы не меняли предел, поскольку в конечном итоге мы просто умножили его на единицу. Также обратите внимание, что теперь мы можем подставить ноль для h без создания нулевого знаменателя или неопределенного выражения. Давайте сделаем это, чтобы найти предел и, в процессе, найти производную квадратного корня из x . Как только мы подставим 0 для h , наше уравнение станет:
Видите ли, производная квадратного корня из x равна (1/2) x -1/2, и это именно то, что мы получили, когда использовали формулу.Уф! Это хорошие новости! Значит, мы сделали свою работу правильно.
Интегралы
Другой способ проверить нашу работу — использовать интегралы. Интегралы называются антипроизводными, и они в основном отменяют производные. То есть, если a является производной от b , то интеграл от a равен b + C , где C — константа.
Это говорит нам о том, что в нашем примере, поскольку производная sqrt ( x ) равна (1/2) x -1/2, интеграл от (1/2) x -1/2 — это sqrt ( x ) + C , где C — постоянная.Возможно, вы еще не знакомы с интегралами, но это нормально. Нам посчастливилось иметь два простых факта, которые позволят нам найти интеграл от (1/2) x -1/2.
1.) Интеграл от постоянной, умноженной на функцию, равен этой константе, умноженной на интеграл функции.
2.) Формула для интеграла x n равна:
Используя эти два правила, мы можем найти интеграл (1/2) x -1/2 и проверить, что это sqrt ( x ) + C , где C — это постоянный.Это позволит нам проверить, правильно ли мы сделали свою работу.
Как мы и надеялись, мы видим, что интеграл от (1/2) x -1/2 равен sqrt ( x ) + C , где C — константа. Большой! И снова наша работа проходит проверку.
При работе с производными функции производных с использованием пределов и интегралов чрезвычайно полезны для проверки правильности нашей работы.
Результаты обучения
Тщательно изучите урок и запомните достаточно информации, чтобы уверенно:
- Найдите производную квадратного корня x
- Использовать интегралы для проверки своей работы
Как нарисовать график функций квадратного корня, (f (x) = √ x)
В этой статье будет показано, как рисовать графики функции квадратного корня, используя только три различных значения для ‘x’, а затем находя точки через который строится график уравнений / функций, а также будет показано, как график перемещается по вертикали (перемещается вверх или вниз), перемещается по горизонтали (перемещается влево или вправо) и как график одновременно выполняет оба перевода.
Уравнение функции квадратного корня имеет вид … y = f (x) = A√x, где (A) не должно быть равно нулю (0). Если (A) больше нуля ( 0), то есть (A) является положительным числом, тогда форма графика функции квадратного корня аналогична верхней половине буквы «C». Если (A) меньше нуля (0), то есть (A) является отрицательным числом, форма графика аналогична форме нижней половины буквы «C». Пожалуйста, нажмите на изображение для лучшего просмотра.
Чтобы нарисовать график уравнения, … y = f (x) = A√x, мы выбираем три значения для ‘x’, x = (-1), x = (0) и x = (1 ). Мы подставляем каждое значение «x» в уравнение … y = f (x) = A√x и получаем соответствующее соответствующее значение для каждого «y».
Учитывая y = f (x) = A√x, где (A) — вещественное число и (A) не равно нулю (0), и подставив x = (-1) в уравнение, мы получаем y = f (-1) = A√ (-1) = i (мнимое число). Таким образом, первая точка не имеет реальных координат, следовательно, через эту точку нельзя построить никакой график.Теперь подставив x = (0), мы получаем y = f (0) = A√ (0) = A (0) = 0. Итак, вторая точка имеет координаты (0,0). Подставив x = (1), мы получим y = f (1) = A√ (1) = A (1) = A. Итак, третья точка имеет координаты (1, A). Поскольку первая точка имела координаты, которые не были реальными, теперь мы ищем четвертую точку и выбираем x = (2). Теперь подставим x = (2) в y = f (2) = A√ (2) = A (1.41) = 1.41A. Итак, четвертая точка имеет координаты (2,1.41A). Теперь мы нарисуем кривую через эти три точки. Пожалуйста, нажмите на изображение для лучшего просмотра.
Учитывая уравнение y = f (x) = A√x + B, где B — любое вещественное число, график этого уравнения будет преобразовывать единицы измерения по вертикали (B). Если (B) — положительное число, график будет двигаться вверх (B) единиц, а если (B) — отрицательное число, график будет двигаться вниз (B) единиц. Чтобы нарисовать графики этого уравнения, мы следуем инструкциям и используем те же значения «x» из шага №3. Пожалуйста, нажмите на изображение, чтобы лучше рассмотреть.
Дано уравнение y = f (x) = A√ (x — B), где A и B — любые действительные числа, и (A) не равно нулю (0), и x ≥ B.График этого уравнения будет преобразовывать единицы по горизонтали (B). Если (B) — положительное число, график переместится в правые (B) единицы, а если (B) — отрицательное число, график переместится в левые (B) единицы. Чтобы нарисовать графики этого уравнения, мы сначала устанавливаем выражение «x — B», которое находится под радикальным знаком Больше или равно нулю, и решаем относительно «x». То есть … x — B ≥ 0, тогда x ≥ B.
Теперь мы будем использовать следующие три значения для ‘x’, x = (B), x = (B + 1) и x = (B + 2).Мы подставляем каждое значение «x» в уравнение … y = f (x) = A√ (x — B) и получаем соответствующее соответствующее значение для каждого «y».
Дано y = f (x) = A√ (x — B), где A и B — действительные числа, и (A) не равно нулю (o), где x ≥ B. Подставляя x = (B) в Уравнение получаем y = f (B) = A√ (BB) = A√ (0) = A (0) = 0. Значит, первая точка имеет координаты (B, 0). Теперь подставив x = (B + 1), мы получим y = f (B + 1) = A√ (B + 1 — B) = A√1 = A (1) = A. Итак, вторая точка имеет координаты ( B + 1, A), и подставив x = (B + 2), мы получим y = f (B + 2) = A√ (B + 2-B) = A√ (2) = A (1.41) = 1,41 А. Итак, Третья Точка имеет координаты (B + 2,1,41A). Теперь мы нарисуем кривую через эти три точки. Пожалуйста, нажмите на изображение для лучшего просмотра.
Дано y = f (x) = A√ (x — B) + C, где A, B, C — действительные числа и (A) не равны нулю (0) и x ≥ B. Пронумеруйте, затем График в ШАГЕ №7 будет преобразовывать единицы измерения по вертикали (C). Если (C) — положительное число, график будет двигаться вверх (C) единиц, а если (C) — отрицательное число, график будет двигаться вниз (C) единиц.2 + x. Функция (f * g) (x) определена для x = все действительные числа, кроме интервала a, b 1. вычислить значение a и b 2. найти диапазон o
f (x) = √ (x — 2)
г (х) = х 2 + х
Область — это набор значений x, в которых определена функция.
Для f (x) у нас не может быть отрицательного числа под квадратным корнем. Таким образом, домен — это все действительные числа, большие или равные 2.
В интервальном обозначении: [2, ∞)
g (x) — парабола. Парабола содержит все действительные числа.
Поскольку f (x) имеет ограничение, (f * g) (x) определено для всех действительных чисел, кроме интервала -∞, 1,99.
а = -∞
b = 1,99 (цифра 9 повторяется)
Чтобы найти диапазон, мы оцениваем f (x), когда x приближается к бесконечности, начиная с x = 2.Диапазон — это предел f (x).
f (2) = √ (2 — 2)
= 0
f (20) = √ (20-2)
= √18
f (100) = √ (100-2)
= √98
f (500) = √ (500-2)
= √498
f (2000) = √ (2000 — 2)
= √1998
f (10000) = √ (10000 — 2)
= √9998
Как видите, когда x приближается к бесконечности, значение f (x) не достигает постоянного значения.Следовательно, предел не существует, и диапазон f (x) находится в интервале [0, ∞).
г (х) действительно имеет диапазон. Помещая g (x) в форме вершины, вершина даст нам диапазон. g (x) в вершинной форме —
г (x) = (x 2 + x + 1/4) — 1/4
г (x) = (x + 1/2) (x + 1/2) — 1/4
г (x) = (x + 1/2) 2 — 1/4
Вершина g (x) равна (-1/2, -1/4).Координата Y вершины сообщает нам диапазон. Поскольку парабола открывается вверх, диапазон значений g (x) находится в интервале (-1/4, ∞).
Следовательно, диапазон (f * g) (x) в обозначении интервала равен
[0, ∞)
.

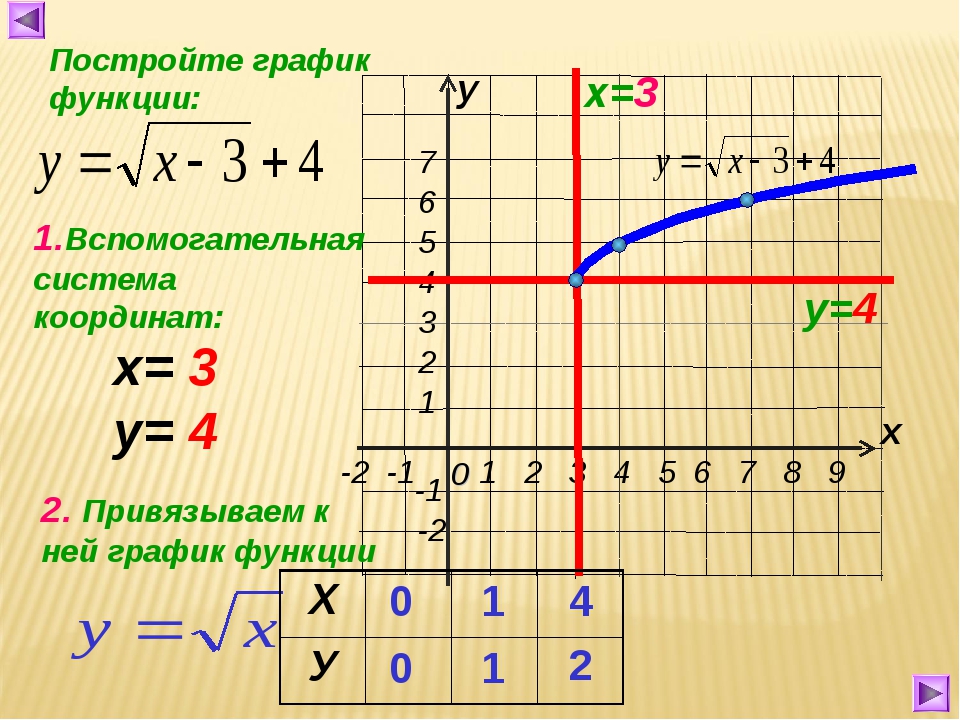
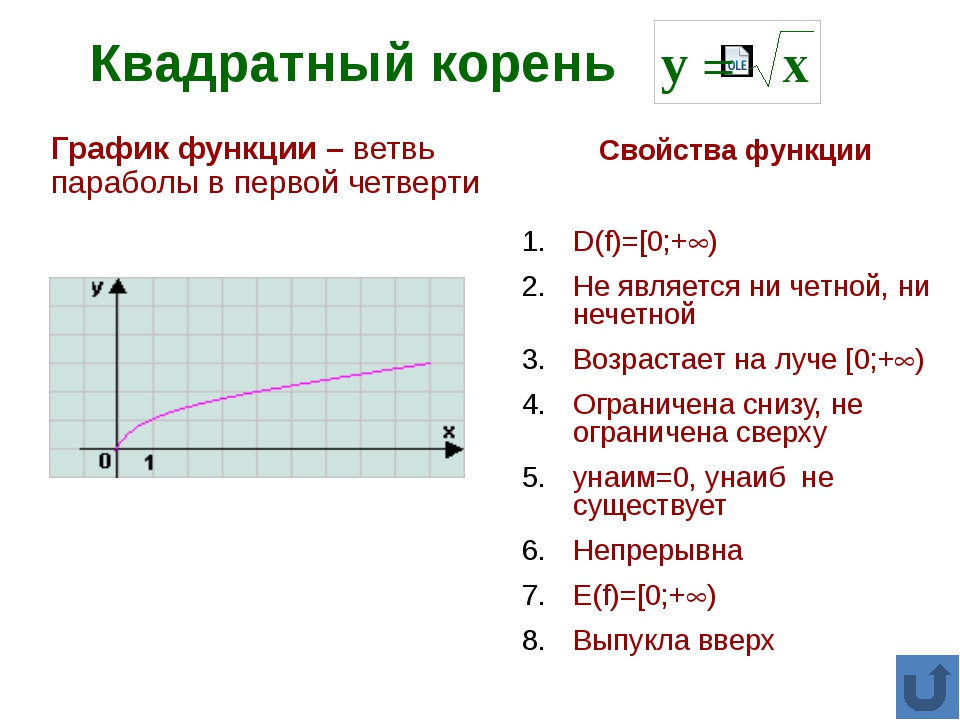
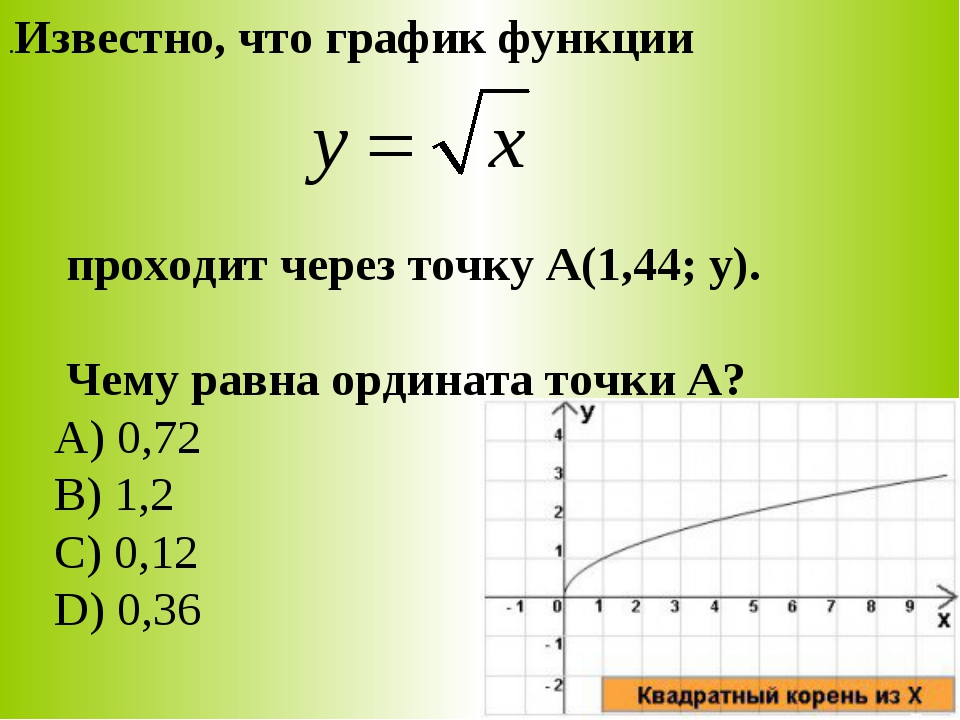 Иначе говоря, множество значений аргумента, на котором
«функция работает».
Иначе говоря, множество значений аргумента, на котором
«функция работает».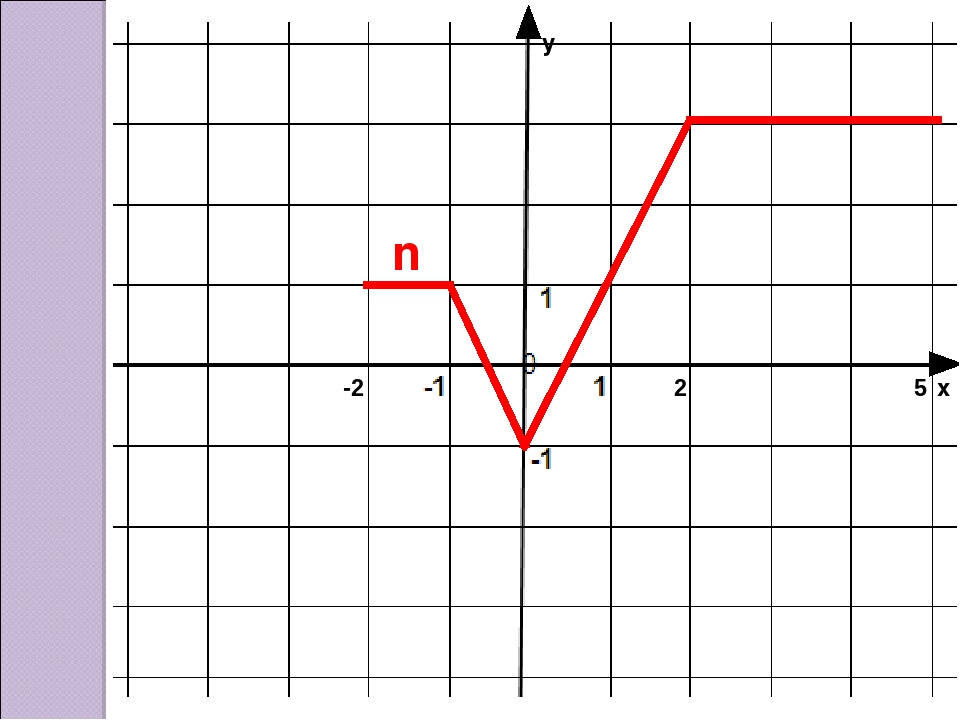
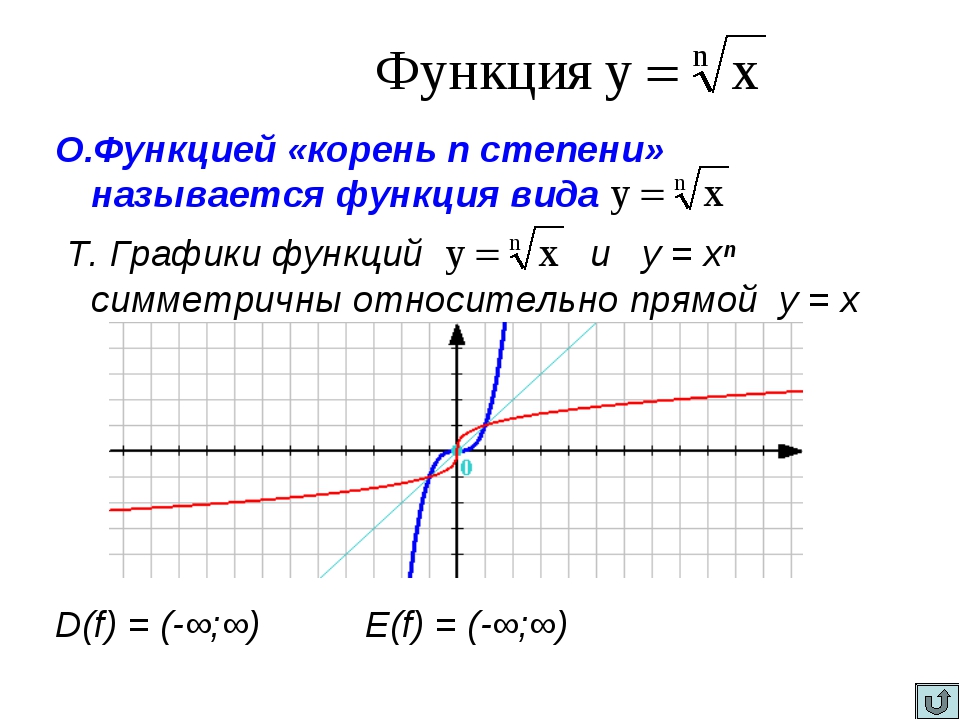 {−1}} = [0, \ infty) \).
{−1}} = [0, \ infty) \). Обозначьте и масштабируйте каждую ось.
Обозначьте и масштабируйте каждую ось.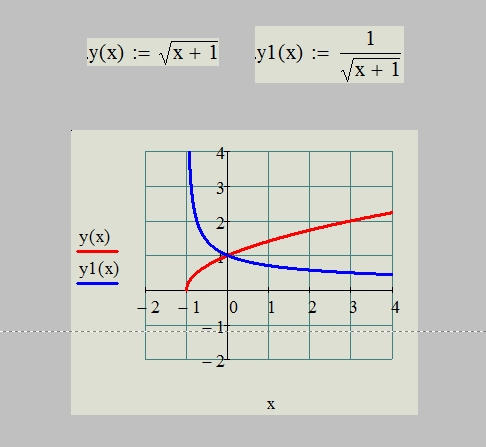


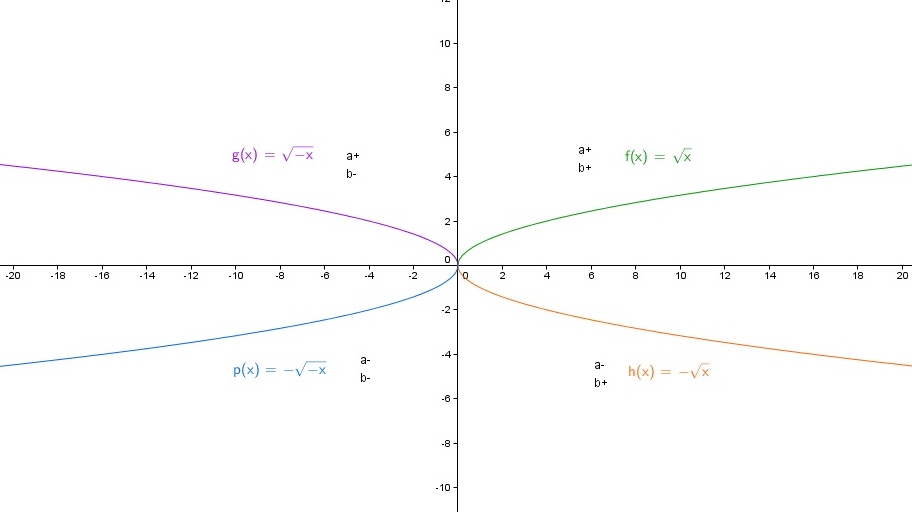
 Используйте обозначение интервала для описания области и диапазона функции.
Используйте обозначение интервала для описания области и диапазона функции.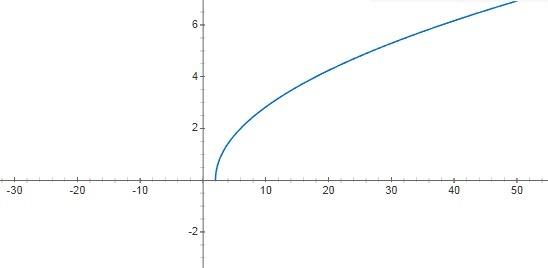 Затем замените x на x — 2, чтобы получить уравнение \ (y = \ sqrt {x − 2} \). Это сдвинет график \ (y = \ sqrt {x} \) вправо на 2 единицы, как показано в (b).
Затем замените x на x — 2, чтобы получить уравнение \ (y = \ sqrt {x − 2} \). Это сдвинет график \ (y = \ sqrt {x} \) вправо на 2 единицы, как показано в (b).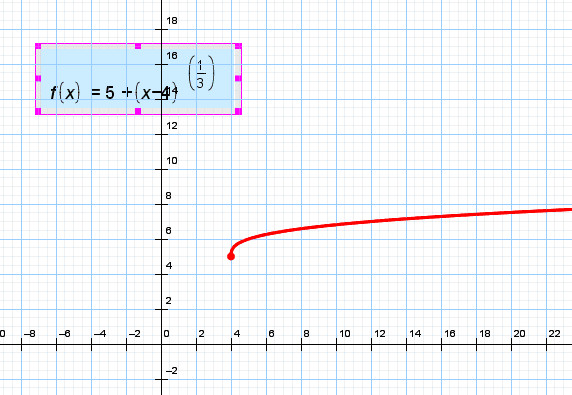 Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([1, \ infty) \).
Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([1, \ infty) \).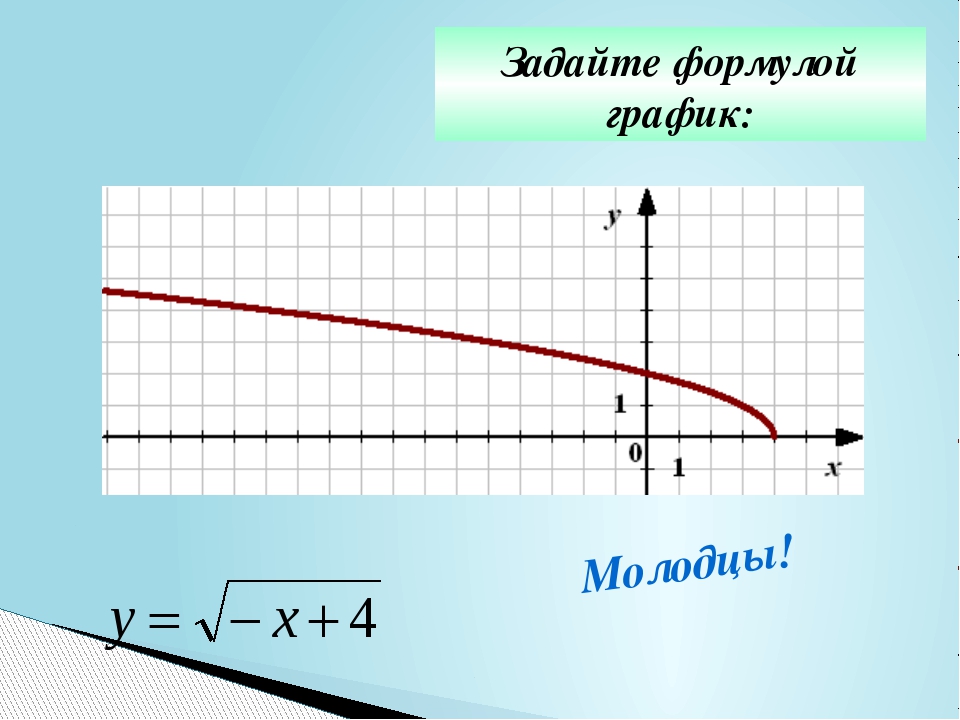 Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \ (y = — \ sqrt {x} +3 \).Это сдвинет график \ (y = — \ sqrt {x} \) на три единицы вверх, как показано в (c).
Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \ (y = — \ sqrt {x} +3 \).Это сдвинет график \ (y = — \ sqrt {x} \) на три единицы вверх, как показано в (c).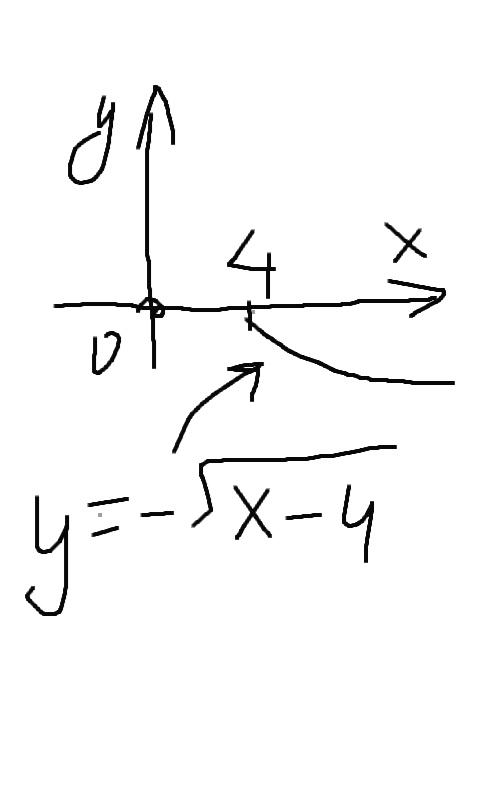 Обозначьте график соответствующим уравнением.
Обозначьте график соответствующим уравнением.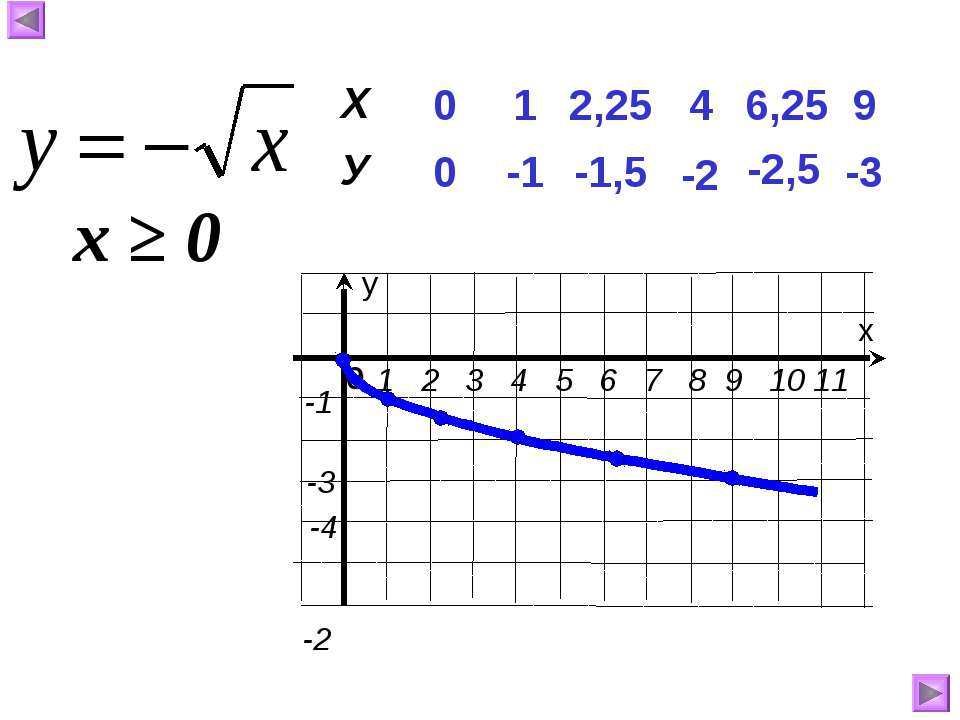 Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).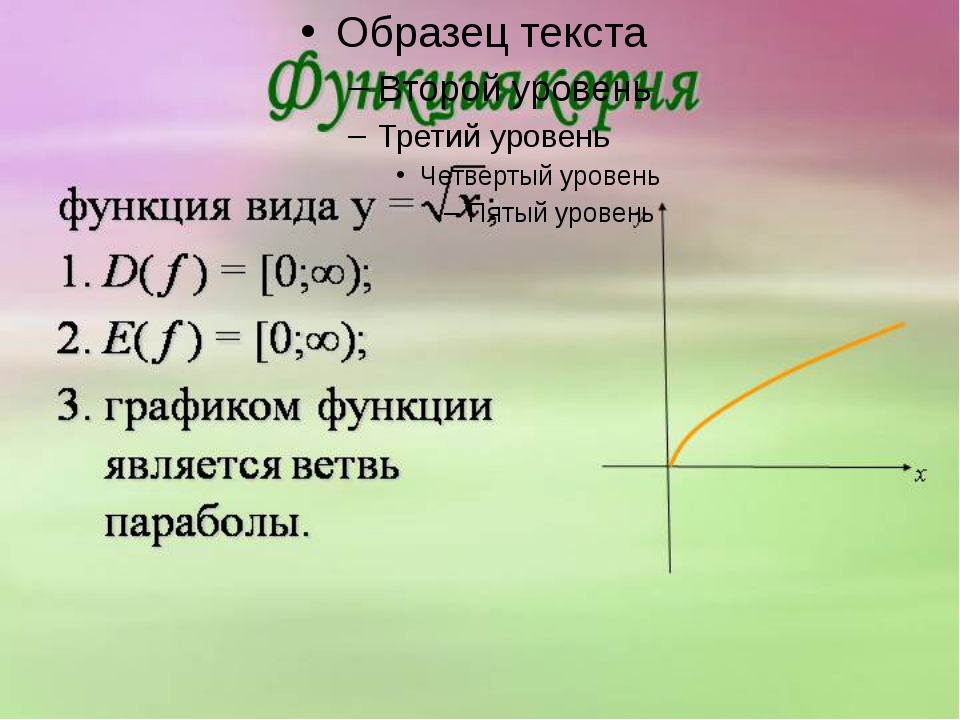 Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Range = \ ([0, \ infty) \). Скопируйте изображение из окна просмотра на свою домашнюю работу. Обозначьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. Обозначьте свой график его уравнением.Используйте график, чтобы определить область определения функции и описать область с помощью интервальной записи.
Скопируйте изображение из окна просмотра на свою домашнюю работу. Обозначьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. Обозначьте свой график его уравнением.Используйте график, чтобы определить область определения функции и описать область с помощью интервальной записи. Следовательно, выражение под корнем в \ (f (x) = \ sqrt {2x + 7} \) должно быть больше или равно нулю.
Следовательно, выражение под корнем в \ (f (x) = \ sqrt {2x + 7} \) должно быть больше или равно нулю.