Как определить четная или нечетная функция онлайн. Алгоритм исследования функции у = f(х) на четность
Определение 1. Функцияназываетсячетной (нечетной ),
если вместе с каждым значением переменной
значение –х также принадлежит
и выполняется равенство
Таким образом, функция может быть четной
или нечетной только тогда, когда ее
область определения симметрична
относительно начала координат на
числовой прямой (числа х и –х одновременно принадлежат
).
Например, функция
не является четной и нечетной, так как
ее область определения
не симметрична относительно начала
координат.
Функция
четная, так как
симметрична относительно начала
координат и.
Функция
нечетная, так как
и
.
Функция
не является четной и нечетной, так как
хотя
и симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,.
График четной функции симметричен
относительно оси Оу , так как если
точка
тоже принадлежит графику.
принадлежит графику, то и точка
тоже принадлежит графику.
При доказательстве четности или нечетности функции бывают полезны следующие утверждения.
Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).
б) Произведение двух четных (нечетных) функций есть функция четная.
в) Произведение четной и нечетной функций есть функция нечетная.
г) Если f – четная
функция на множествеХ , а функцияg определена на
множестве
,
то функция
–
четная.
д) Если f – нечетная
функция на множествеХ , а функцияg определена на
множестве
и четная (нечетная), то функция
–
четная (нечетная).
Доказательство . Докажем, например, б) и г).
б) Пусть
и
–
четные функции. Тогда,
поэтому.
Аналогично рассматривается случай
нечетных функций
и
.
г) Пусть f – четная
функция.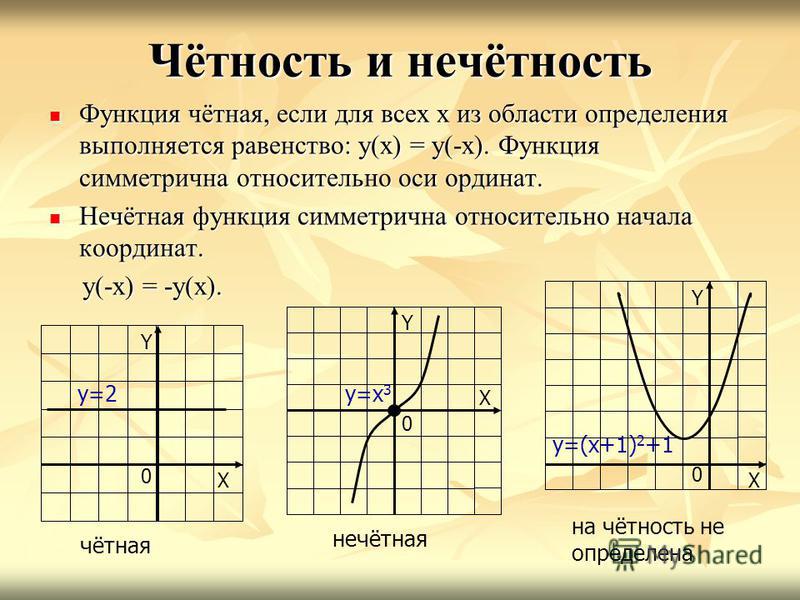 Тогда.
Тогда.
Остальные утверждения теоремы доказываются аналогично. Теорема доказана.
Теорема 2. Любую функцию
,
заданную на множествеХ , симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
Доказательство . Функцию
можно записать в виде
.
Функция
– четная, так как
,
а функция
– нечетная, поскольку.
Таким образом,
,
где
–
четная, а
–
нечетная функции. Теорема доказана.
Определение 2. Функция
называетсяпериодической , если
существует число
,
такое, что при любом
числа
и
также
принадлежат области определения
и выполняются равенства
Такое число T называетсяпериодом функции
.
Из определения 1 следует, что если Т – период функции
,
то и число –
(так как при заменеТ на –Т равенство сохраняется).
 С помощью метода
математической индукции можно показать,
что еслиТ – период функцииf ,
то и
С помощью метода
математической индукции можно показать,
что еслиТ – период функцииf ,
то и, тоже является периодом. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов.
Определение 3. Наименьший из положительных периодов функции называется ееосновным периодом.
Теорема 3. ЕслиТ – основной период функцииf , то остальные периоды кратны ему.
Доказательство . Предположим
противное, то есть что существует периодфункцииf (>0),
не кратныйТ . Тогда, разделивнаТ с остатком, получим
,
где
.
Поэтому
то есть
– период функцииf ,
причем
,
а это противоречит тому, чтоТ –
основной период функцииf
Хорошо известно, что тригонометрические
функции являются периодическими.
Основной период
и
равен
,
и
.
Найдем период функции
. Пусть
Пусть
— период этой функции. Тогда
(так как
.
илиилиили
.
Значение T , определяемое
из первого равенства, не может быть
периодом, так как зависит отх , т.е.
является функцией отх , а не постоянным
числом. Период определяется из второго
равенства:
.
Периодов бесконечно много, при
наименьший
положительный период получается при
:
.
Это – основной период функции
.
Примером более сложной периодической функции является функция Дирихле
Заметим, что если T –
рациональное число, то
и
являются рациональными числами при
рациональномх
при любом рациональном числе T .
Следовательно, любое рациональное числоT является периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное числоможно сделать выборомn сколь угодно близким к нулю).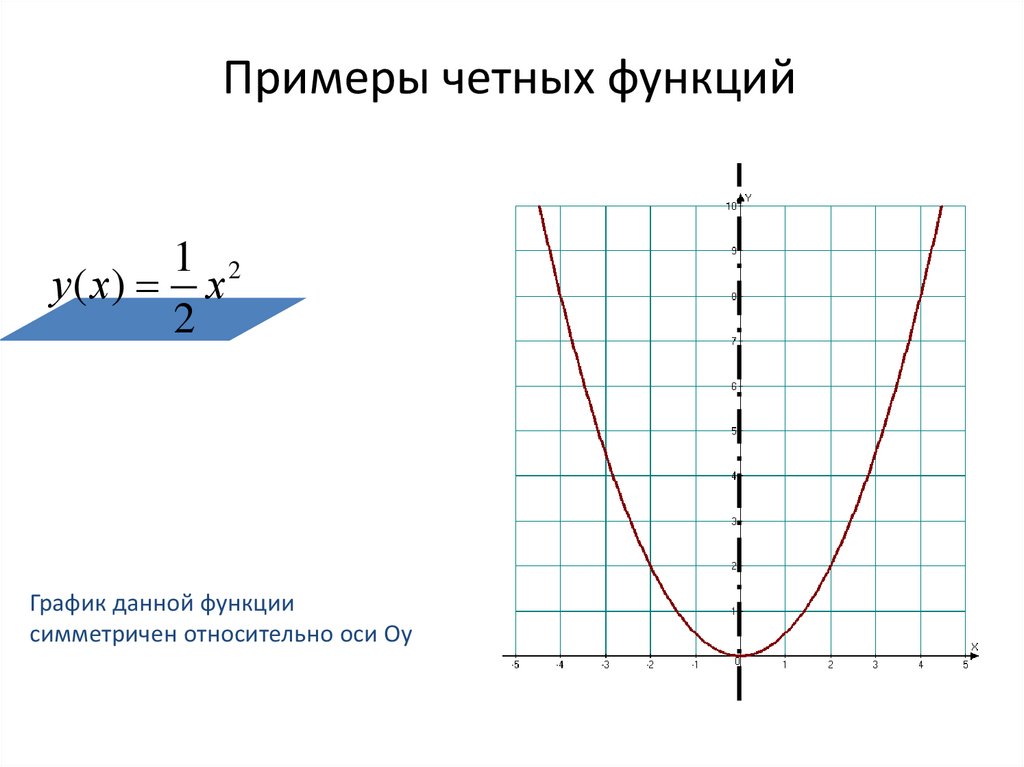
Теорема 4. Если функцияf задана на множествеХ и имеет
периодТ , а функцияg задана на множестве
,
то сложная функция
тоже имеет периодТ .
Доказательство . Имеем, поэтому
то есть утверждение теоремы доказано.
Например, так как cos x имеет период
,
то и функции
имеют период
.
Определение 4. Функции, не являющиеся периодическими, называются непериодическими .
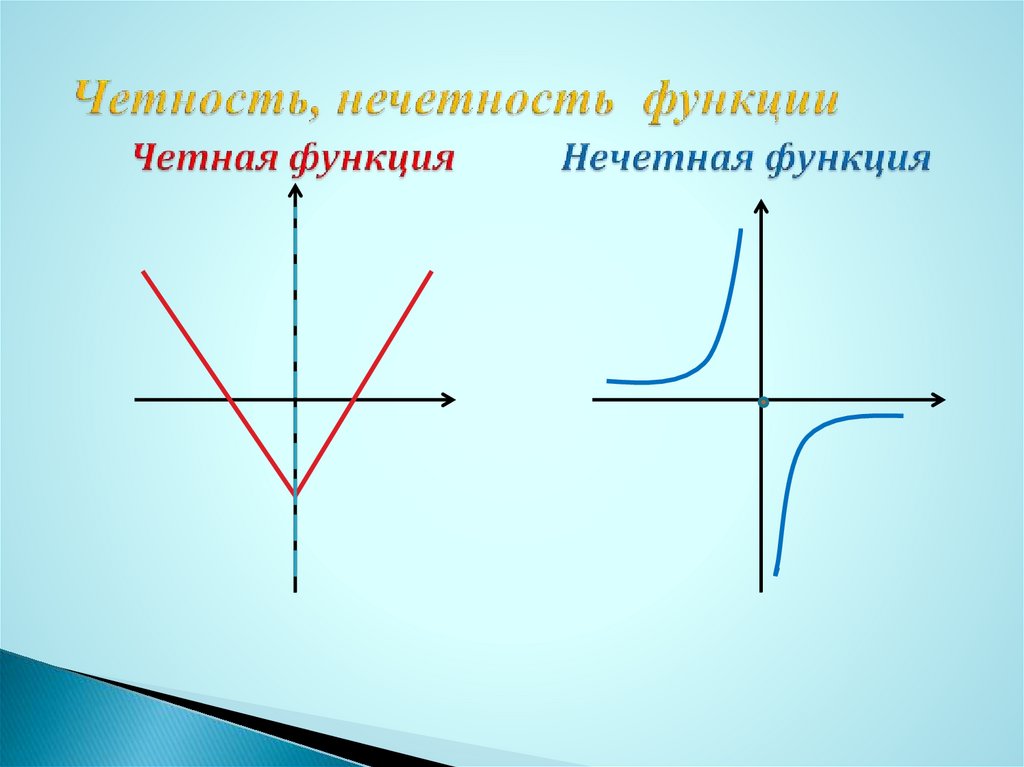
Графики четной и нечетной функции обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат.
Пример. Построить график функции \(y=\left|x \right|\).
Решение. Рассмотрим функцию: \(f\left(x \right)=\left|x \right|\) и подставим вместо \(x \) противоположное \(-x \).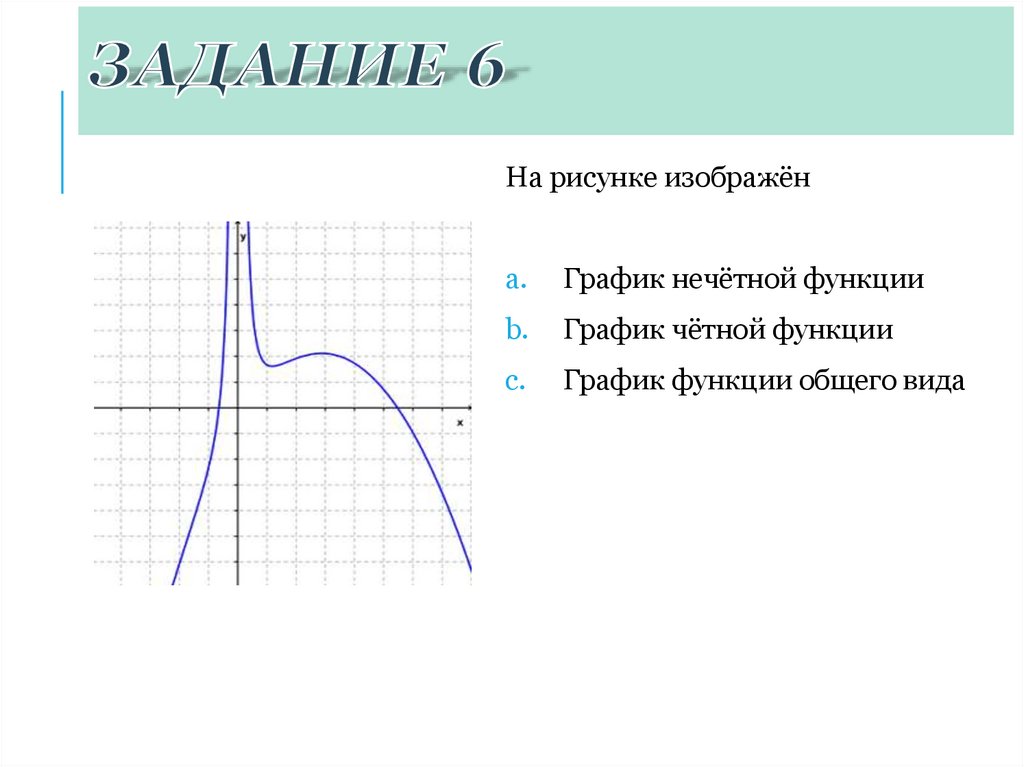 В результате не сложных преобразований получим:
$$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$
Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.
В результате не сложных преобразований получим:
$$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$
Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.
Значит эта функция — четная, а ее график будет симметричен относительно оси ординат (вертикальной оси). График этой функции приведен на рисунке слева. Это означает что при построении графика, можно строить только половину, а вторую часть (левее вертикальной оси рисовать уже симметрично правой части). Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.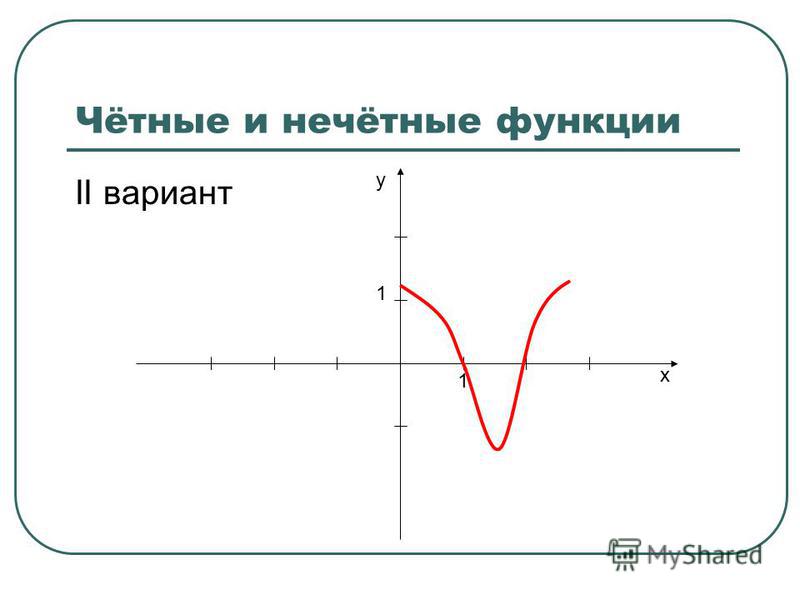
Вывод: функция не симметрична ни относительно начала координат ни относительно центра системы координат. Это произошло потому, что она представляет собой сумму двух функций: четной и не четной. Такая же ситуация будет если вычитать две разные функции. А вот умножение или деление приведет к другому результату. Например, произведение четной и нечетной функций дает нечетную. Или частное двух нечетных приводит к четной функции.
Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у . Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x ) образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x , а по оси ординат откладываются значения переменной y . Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции
.Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена.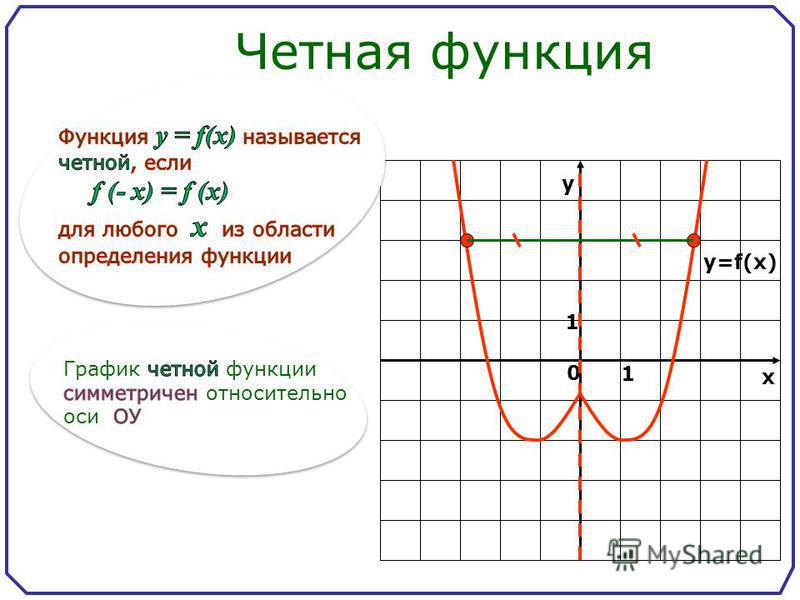
Область значений функции — это множество всех действительных значений y , которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции .
Значения х , при которых y=0 , называется нулями функции . Это абсциссы точек пересечения графика функции с осью Ох.
3) Промежутки знакопостоянства функции .
Промежутки знакопостоянства функции – такие промежутки значений x , на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
4) Монотонность функции
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции .
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = — f(x ). График нечетной функции симметричен относительно начала координат.
Четная функция
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x , принадлежащего области определения, выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
6) Ограниченная и неограниченная функции .
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7) Периодическость функции .
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Функция f называется периодической, если существует такое число, что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T) . T — это период функции.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.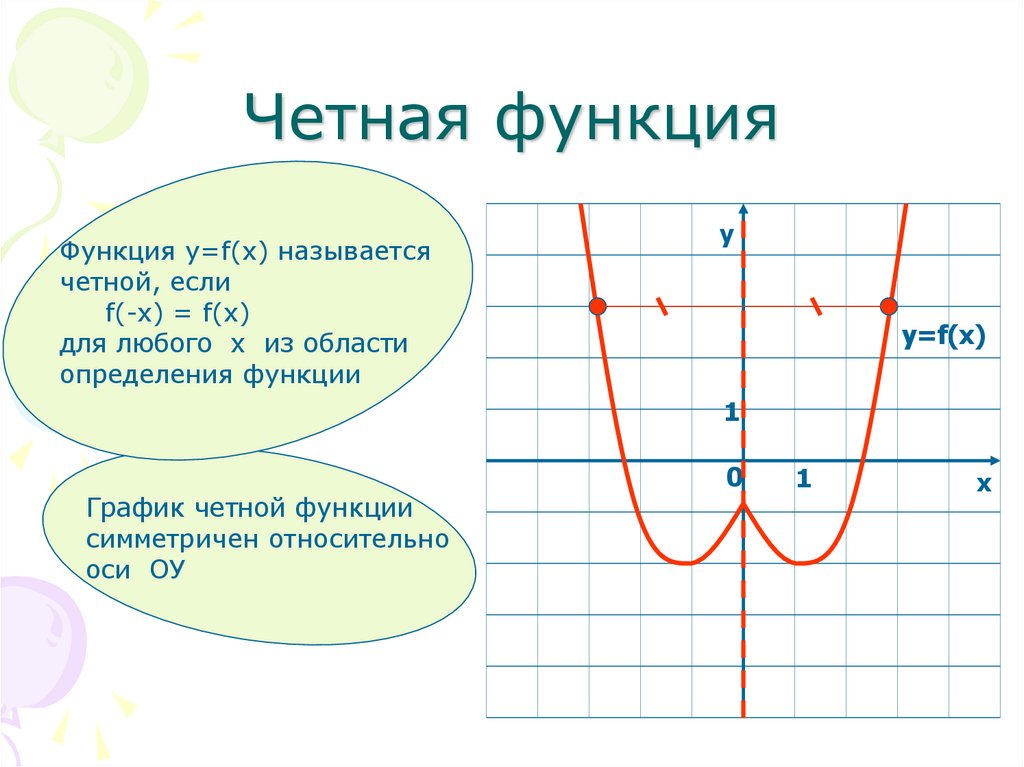
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:
- -x (противоположная точка) также лежит в данной области определения,
- f (-x) = f (x).
Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О, являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка — b тоже лежит в этой области.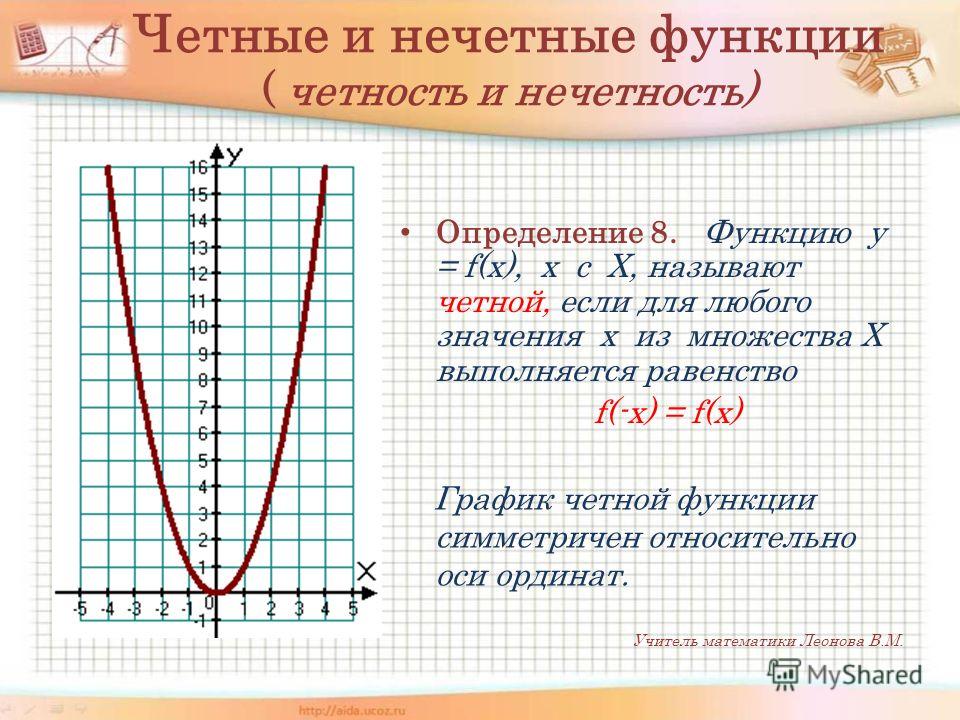 (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами. 2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых
производная равна нулю или не существует
называются критическими.
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.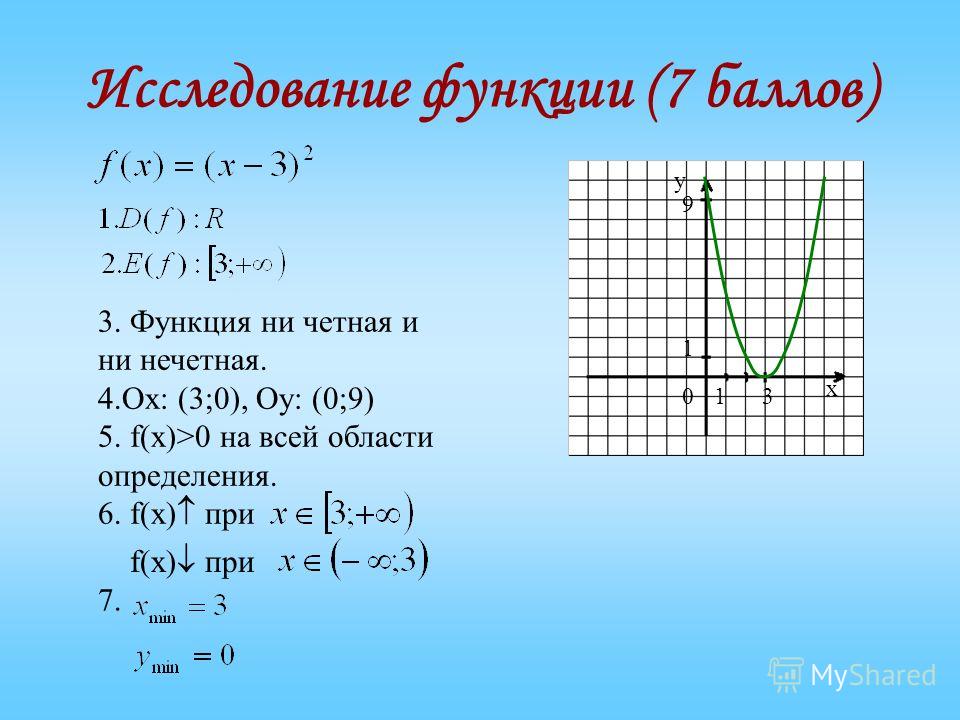
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.
В точках
функция имеет максимум.
Чётность функции. Определение чётной функции. Является ли чётной функция. Свойства функции.mp4
12+
3 месяца назад
Математика от Баканчиковой157 подписчиков
Алгебра 7-11 класс. Что такое чётная функция? Как доказать чётность функции? Сегодня, продолжая говорить о свойствах функции, мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме «Свойства функции», то обязательно посмотрите их, тогда это урок будет Вам очень понятен. А чтобы урок был Вам понятен, сначала мы напомним Вам, что такое функция, и как найти область определения функций, заданных целым и дробным выражениями. Затем объясним Вам определение двенадцатого свойства функции — чётности функции, которое дано в учебнике А.Г.Мордковича. Особо остановимся на том, как понимать y(-x) = y(x). Затем предложим Вашему вниманию определение чётной функции Любовь Николаевны, которое позволит Вам понять это свойство и легко решать упражнения на эту тему. На примере четырёх упражнений мы покажем Вам, как доказать, что функция является или не является чётной. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:30 Вспомним, что такое функция.
01:58 Перепишем определение чётной функции.
03:27 Как понимать y(-x) = y(x)?
05:07 Определение чётной функции Любовь Николаевны.
05:55 Пример чётной функции.
06:55 Упражнение 1.
10:11 Упражнение 2.
12:52 Упражнение 3.
15:06 Упражнение 4.
Если Вы впервые на нашем канале и у Вас остались вопросы или Вы хотите освежить в памяти некоторые термины и определения, рекомендуем Вам посмотреть следующие видео:
Что такое определение. Отличие определения от рассказа. https://rutube.ru/video/f187c6071dfe512aaa2204e3229097e1/
Что такое компоненты. Рассказ о Пете и Диме или зачем нужны компоненты. https://rutube.ru/video/2a05adba43e67d1ea1b5cab6d8e6d18a/
Функция. Определение. Пример, на котором функцию понимают ВСЕ. https://rutube.ru/video/e39b203540be6b34b1c6728b8a73a8c4/
Компоненты функции: аргумент, значение функции, область определения функции, область значений функции https://rutube.
На примере четырёх упражнений мы покажем Вам, как доказать, что функция является или не является чётной. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:30 Вспомним, что такое функция.
01:58 Перепишем определение чётной функции.
03:27 Как понимать y(-x) = y(x)?
05:07 Определение чётной функции Любовь Николаевны.
05:55 Пример чётной функции.
06:55 Упражнение 1.
10:11 Упражнение 2.
12:52 Упражнение 3.
15:06 Упражнение 4.
Если Вы впервые на нашем канале и у Вас остались вопросы или Вы хотите освежить в памяти некоторые термины и определения, рекомендуем Вам посмотреть следующие видео:
Что такое определение. Отличие определения от рассказа. https://rutube.ru/video/f187c6071dfe512aaa2204e3229097e1/
Что такое компоненты. Рассказ о Пете и Диме или зачем нужны компоненты. https://rutube.ru/video/2a05adba43e67d1ea1b5cab6d8e6d18a/
Функция. Определение. Пример, на котором функцию понимают ВСЕ. https://rutube.ru/video/e39b203540be6b34b1c6728b8a73a8c4/
Компоненты функции: аргумент, значение функции, область определения функции, область значений функции https://rutube. ru/video/b244f058080abfb736bb53076b8ad8cc/
Способы задания функции. Примеры. https://rutube.ru/video/be19beb2a973ffbad226194f7e36e0f8/
Координатная плоскость. Компоненты координатной плоскости. https://rutube.ru/video/37a4ebf9c234063e743767e8a50b45c0/
Графический способ задания функции. График функции. Определение. https://rutube.ru/video/f80ef74eb301c96a0159afedd02e6383/
Область определения функции. Как найти, если функция задана графиком, таблицей, рисунком, символом. https://rutube.ru/video/e3fda1d9390c06e95e6481060c7f7745/
Область определения функций, заданных формулой, целым выражением. Виды выражений в формулах функций. Область допустимых значений выражений. Алгебра 7-11 класс. https://rutube.ru/video/ad4dcae792272214637e31be0091ec7e/
Область определения функции, заданной формулой, дробным выражением. Алгебра 7-11 класс. https://rutube.ru/video/25a7399e239a12b0bd82b5e3f516ce8a/
Область определения функции, заданной формулой корня четной степени. Алгебра 7-11 класс. https://rutube.
ru/video/b244f058080abfb736bb53076b8ad8cc/
Способы задания функции. Примеры. https://rutube.ru/video/be19beb2a973ffbad226194f7e36e0f8/
Координатная плоскость. Компоненты координатной плоскости. https://rutube.ru/video/37a4ebf9c234063e743767e8a50b45c0/
Графический способ задания функции. График функции. Определение. https://rutube.ru/video/f80ef74eb301c96a0159afedd02e6383/
Область определения функции. Как найти, если функция задана графиком, таблицей, рисунком, символом. https://rutube.ru/video/e3fda1d9390c06e95e6481060c7f7745/
Область определения функций, заданных формулой, целым выражением. Виды выражений в формулах функций. Область допустимых значений выражений. Алгебра 7-11 класс. https://rutube.ru/video/ad4dcae792272214637e31be0091ec7e/
Область определения функции, заданной формулой, дробным выражением. Алгебра 7-11 класс. https://rutube.ru/video/25a7399e239a12b0bd82b5e3f516ce8a/
Область определения функции, заданной формулой корня четной степени. Алгебра 7-11 класс. https://rutube. ru/video/9ab883e3b9a1bf78e16f47d5722ee0a2/
Свойства функции. Нули функции. Алгебра 7-11 класс. https://rutube.ru/video/6e56bd59444a9af812beeed15d1d2993/
#СвойстваФункции #ЧётныеФункции #ЧётностьФункции #ЯвляетсяЛиЧётной #четнаялифункция #являетсяфункциячетнойилинечетной #определениечетнойфункции #выяснитьявляетсяфункциячетнойилинечетной #являетсяличетнойилинечетнойфункция #ничетнаянинечетнаяфункция #чётнаяфункция #найдитечетнуюфункцию #какаяфункцияявляетсячетной #областьопределениячетнойфункции #четнаяфункциясимметрична #четныефункциипримеры #докажитечтофункцияявляетсячетной #МатематикаОтБаканчиковой
чётность функции, четная ли функция, является функция четной или нечетной, определение четной функции, выяснить является функция четной или нечетной, является ли четной или нечетной функция , ни четная ни нечетная функция , чётная функция, найдите четную функцию, какая функция является четной, область определения четной функции, четная функция симметрична, четные функции примеры, докажите что функция является четной
ru/video/9ab883e3b9a1bf78e16f47d5722ee0a2/
Свойства функции. Нули функции. Алгебра 7-11 класс. https://rutube.ru/video/6e56bd59444a9af812beeed15d1d2993/
#СвойстваФункции #ЧётныеФункции #ЧётностьФункции #ЯвляетсяЛиЧётной #четнаялифункция #являетсяфункциячетнойилинечетной #определениечетнойфункции #выяснитьявляетсяфункциячетнойилинечетной #являетсяличетнойилинечетнойфункция #ничетнаянинечетнаяфункция #чётнаяфункция #найдитечетнуюфункцию #какаяфункцияявляетсячетной #областьопределениячетнойфункции #четнаяфункциясимметрична #четныефункциипримеры #докажитечтофункцияявляетсячетной #МатематикаОтБаканчиковой
чётность функции, четная ли функция, является функция четной или нечетной, определение четной функции, выяснить является функция четной или нечетной, является ли четной или нечетной функция , ни четная ни нечетная функция , чётная функция, найдите четную функцию, какая функция является четной, область определения четной функции, четная функция симметрична, четные функции примеры, докажите что функция является четной
Четные и нечетные числа.
 Игры для детей онлайн. Кроме того, это поможет вашим детям изучить понятия деления, простых чисел и квадратных корней. Это может показаться легкой темой для ума взрослого, но она может быть непонятна вашему ребенку. Ваши заботы скоро закончатся, поскольку SplashLearn предлагает вам индивидуальную платформу онлайн-обучения, дополненную играми, чтобы ваш ребенок был приклеен к образовательному форуму и удобно выбирал четные и нечетные числа. Введение
Игры для детей онлайн. Кроме того, это поможет вашим детям изучить понятия деления, простых чисел и квадратных корней. Это может показаться легкой темой для ума взрослого, но она может быть непонятна вашему ребенку. Ваши заботы скоро закончатся, поскольку SplashLearn предлагает вам индивидуальную платформу онлайн-обучения, дополненную играми, чтобы ваш ребенок был приклеен к образовательному форуму и удобно выбирал четные и нечетные числа. Введение Первым шагом является понимание разницы между нечетными и четными числами.
Любое число, деленное на два, дает ноль, так как остаток является четным числом. 2,4,8,56,100 и т. д. являются примерами четных чисел.
Напротив, любое число, деленное на два и дающее в остатке единицу, является нечетным числом. 3,5,9,57,101 и т. д. являются примерами нечетных чисел.
Как отличить четные числа от нечетных? Четность — это термин, используемый для различения целых чисел между четными и нечетными. Есть два пути:
Есть два пути:
- Анализируя место единиц: Рассмотрите число, проверьте место единиц, а затем классифицируйте его как четное и нечетное. Например, в 234 вместо единиц стоит 4, а значит, это четное число.
- По номерам группировки: Разделить весь набор на две группы. Если обе группы имеют одинаковые номера, это четное число. Если одна группа больше на 1 число, это нечетное число. Например, есть 53 стула. Может быть два одинаковых комплекта по 26 стульев и один дополнительный. Это нечетное число.
Дети обычно начинают изучать нечетные и четные числа во 2 классе. Они могут быстро научиться этому, играя в следующие четные и нечетные игры: Эта игра служит предшественником четных и нечетных чисел. Они практикуются в пропуске счета, чтобы выбрать правильную сумму. Реальные объекты, используемые в этой игре, помогают им определить понятия четных и нечетных чисел.
Отсутствие достаточной практики — первая причина, по которой дети не понимают четных и нечетных чисел. Четные и нечетные числа могут быть легкими, если дети знают, как поровну распределить числа по парам.
Как внести свой вклад в качестве родителя Как родитель, ваша главная задача должна заключаться в том, чтобы поощрять детей чаще практиковать четные и нечетные числа. Попробуйте взять их за руки и поощрять играть в эти развивающие игры. Заманите их забавными фактами об этих числах и объясните им применение четных и нечетных чисел в повседневной жизни.
SplashLearn — это платформа, которая сочетает онлайн-обучение с веселыми играми, чтобы поддерживать мотивацию вашего ребенка и в то же время впитывать глубокие знания о четных и нечетных числах. Напишите свой отзыв по адресу [email protected], если вы считаете эту статью заслуживающей внимания и хотите изучить продукты SplashLearn. Вы также можете зарегистрироваться бесплатно и сделать обучение математики увлекательным для вашего маленького ниндзя!
Часто задаваемые вопросы- Как детям учить четные и нечетные числа?
Интерактивные игры с четными и нечетными числами помогают детям с легкостью практиковать эту концепцию. Эти веселые четные и нечетные онлайн-игры укрепляют математические навыки детей и помогают им точно различать два типа чисел.
- Как научить детей понятиям четных и нечетных чисел?
Вы можете научить детей понятиям четных и нечетных чисел, объяснив им, что нечетные числа — это числа, которые нельзя разделить на равные части, такие как 1, 3, 5, 7 и т.
 д. Тогда как четные числа — это числа, которые можно разделить на равные части, такие как 2, 4, 6, 8 и т. д. Четные и нечетные онлайн-игры также можно использовать для обучения детей этому понятию.
д. Тогда как четные числа — это числа, которые можно разделить на равные части, такие как 2, 4, 6, 8 и т. д. Четные и нечетные онлайн-игры также можно использовать для обучения детей этому понятию. - Как помочь ребенку понять четные и нечетные числа?
Вы можете помочь своему ребенку понять четные и нечетные числа, играя в интерактивные онлайн-игры. Эти нечетные и четные математические игры помогают детям использовать свои моторные и математические навыки, чтобы с легкостью решать забавные математические задачи. Дети умеют правильно считать заданные предметы парами, определять правильные четные или нечетные числа и выбирать правильный вариант, чтобы узнать ответы.
- Как дети могут играть в игры на четные и нечетные числа?
Дети могут играть в нечетные и четные математические игры онлайн на нескольких устройствах, таких как iPad, ноутбук и т. д., через различные приложения и веб-сайты.

- Какие самые интересные занятия на четные и нечетные числа для детей?
Одними из лучших забавных занятий для детей, посвященных четным и нечетным числам, являются: маркировка любого предмета, например набора цветных карандашей, числами и сортировка четных и нечетных чисел, бросание игральных костей и определение четных и нечетных чисел и т. д.
Попробуйте SplashLearn бесплатно
Формулы для четных и нечетных строк в Excel
Советы и учебные пособия по Excel
Редактировать
Добавить в избранное Избранное
Автор: Дон | Правки: дон
Курс Excel Macro & VBA (от новичка до эксперта) (скидка 80 %)
Формулы для определения четности или нечетности текущей ячейки; это позволяет выполнять определенные вычисления, увеличивать значение, закрашивать строки с использованием условного форматирования и т.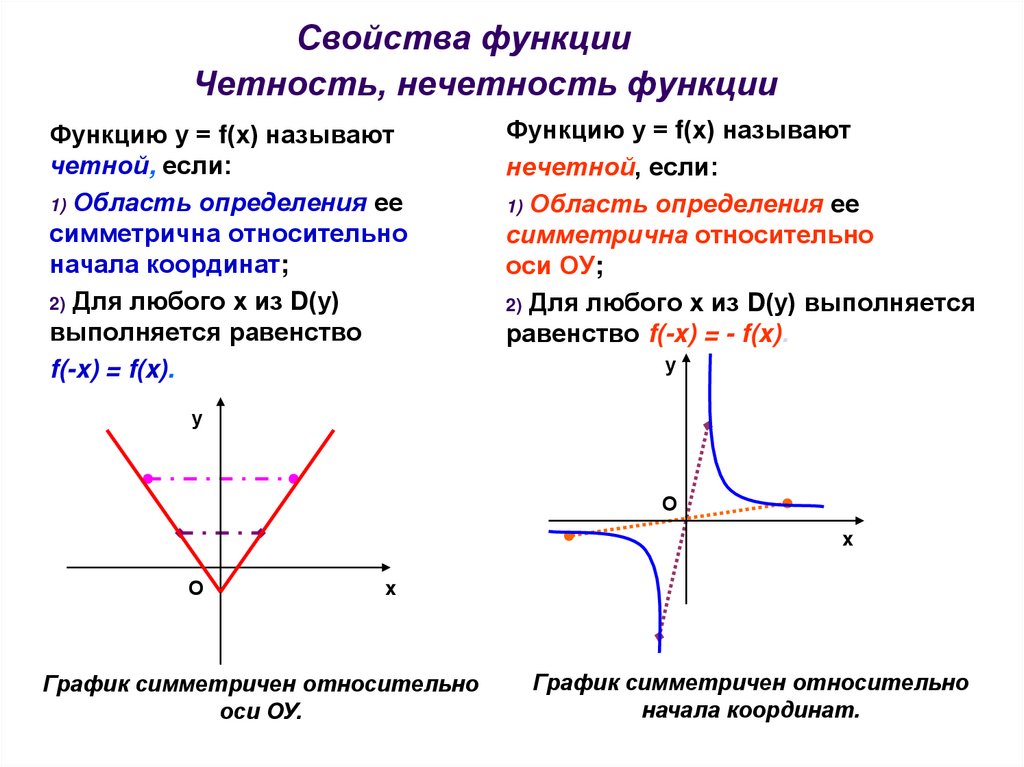 д.
д.
Разделы:
Формула для четных и нечетных строк (более новые версии Excel)
Формула для четных и нечетных строк (Excel 2002 и более ранние версии)
Дополнительные примеры
Примечания
Формула для четных и нечетных строк (более новые версии Excel
) Проверить, является ли текущая строка нечетной:
=ISODD(ROW())
ISODD — это функция, которая проверяет, является ли число четным или нечетным. Возвращает TRUE для нечетных строк и FALSE для четных.
ROW возвращает номер строки ячейки. Если вы оставите функцию ROW пустой, без аргумента, как в этом примере, она будет ссылаться на строку, в которую вы поместили функцию; однако вы также можете включить в функцию ссылку на диапазон, и тогда она вернет номер строки для этой ссылки на диапазон.
Проверить, является ли текущая строка четной:=ЕСЧЕТ(СТРОКА())
ЕСЧЕТ это функция, которая проверяет, является ли число четным или нечетным. Возвращает FALSE для нечетных строк и TRUE для четных строк.
Возвращает FALSE для нечетных строк и TRUE для четных строк.
ROW возвращает номер строки ячейки. Если вы оставите функцию ROW пустой, без аргумента, как в этом примере, она будет ссылаться на строку, в которую вы поместили функцию; однако вы также можете включить в функцию ссылку на диапазон, и тогда она вернет номер строки для этой ссылки на диапазон.
Одна формула для проверки четных/нечетных строк
Неважно, какую из приведенных выше формул вы используете, обе они будут возвращать чередующиеся значения ИСТИНА/ЛОЖЬ для диапазона.
Если вы введете их в Excel и скопируете, это будет выглядеть так:
Добавить немного логики
Если вы хотите сделать что-то конкретное с нечетными/четными строками, вы можете обернуть вышеуказанные функции внутри Оператор ЕСЛИ выглядит следующим образом:
=ЕСЛИ(ЕСЧЕТ(СТРОКА()),"Чет","Нечет")
В этом примере выводится Четный для четных строк и Нечетный для нечетных строк, но вы можете сделать так, как хотите.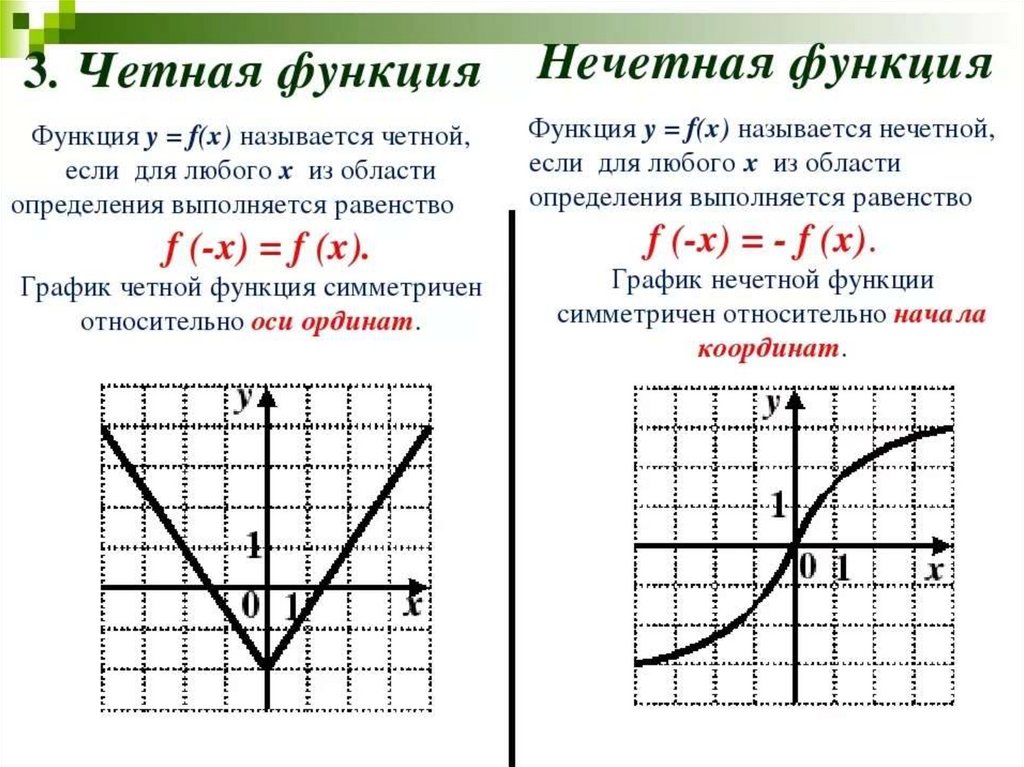
Формула нечетных и четных строк (Excel 2002 и более ранние версии)
В более ранних версиях Excel у вас не было функций ISODD и ISEVEN, и вам приходилось использовать функцию MOD() вместе с небольшой логикой типа программирования .
=ЕСЛИ(MOD(СТРОКА(),2)=0,"Чет","Нечет")
СТРОКА функция возвращает строку ячейки. Если вы оставите функцию ROW пустой, без аргумента, она будет ссылаться на строку, в которую вы поместили функцию; однако вы также можете включить в функцию ссылку на диапазон, и тогда она вернет номер строки для этой ссылки на диапазон.
MOD — это функция, которая действительно творит чудеса, и, хотя она выглядит пугающе, она довольно проста. Функция ОСТАТ возвращает остаток после деления числа на другое число. В этом случае он разделит текущий номер строки на 2; если оно может разделить число на 2 без остатка, то вы знаете, что это четное число и, в данном случае, четная строка.
Логика формулы знает, что строка четная, потому что она берет результат функции ОСТАТ, остаток после деления, а затем проверяет, равен ли он 0 или нет. Если остатка нет, то это то же самое, что 0, который проверяется в =0 часть формулы, и Excel выведет аргумент ИСТИНА из оператора ЕСЛИ.
Если остатка нет, то это то же самое, что 0, который проверяется в =0 часть формулы, и Excel выведет аргумент ИСТИНА из оператора ЕСЛИ.
Вывод True/False Простая формула
Вам не нужно использовать оператор IF, если вы просто хотите получить значения TRUE и FALSE в Excel.
=MOD(ROW(),2)=0
Измените 0 на 1, если вы хотите, чтобы он возвращал false для четных строк.
Дополнительные примеры
Увеличение значения через каждые X строк в Excel
Быстрое затенение каждой второй строки в Excel
Суммарные значения из каждого X количества строк в Excel
Примечания
Это простые примеры, которые позволят вам в дальнейшем создавать формулы, которые могут выполнять мощные функции в Excel, такие как увеличение чисел на основе строки, затенение строк использование условного форматирования и многое другое.
Загрузите прилагаемую книгу, чтобы получить эти примеры в Excel.
Функция Excel: ЕСЛИ(), ISEVEN(), ISODD(), MOD(), СТРОКА()
Версия Excel: Эксель 2003, Эксель 2007, Эксель 2010, Эксель 2013, Эксель 2016
Курс Excel VBA — от новичка до эксперта
200+ видеоуроков 50+ часов обучения Более 200 руководств Excel
Станьте мастером VBA и макросов в Excel и узнайте, как автоматизировать все свои задачи в Excel с помощью этого онлайн-курса.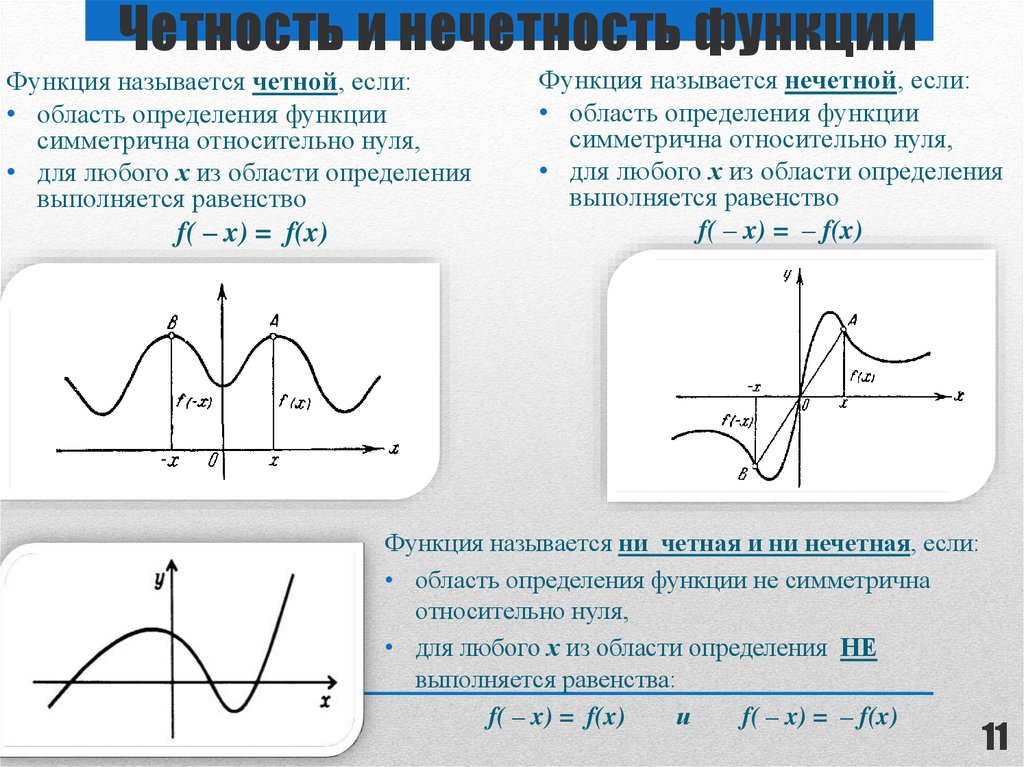

 д. Тогда как четные числа — это числа, которые можно разделить на равные части, такие как 2, 4, 6, 8 и т. д. Четные и нечетные онлайн-игры также можно использовать для обучения детей этому понятию.
д. Тогда как четные числа — это числа, которые можно разделить на равные части, такие как 2, 4, 6, 8 и т. д. Четные и нечетные онлайн-игры также можно использовать для обучения детей этому понятию.