Функция х у в квадрате: Функция игрек равен икс в квадрате. График функции y=x^2. Свойства функции игрек равен икс в квадрате. График функции игрек равно икс в квадрате

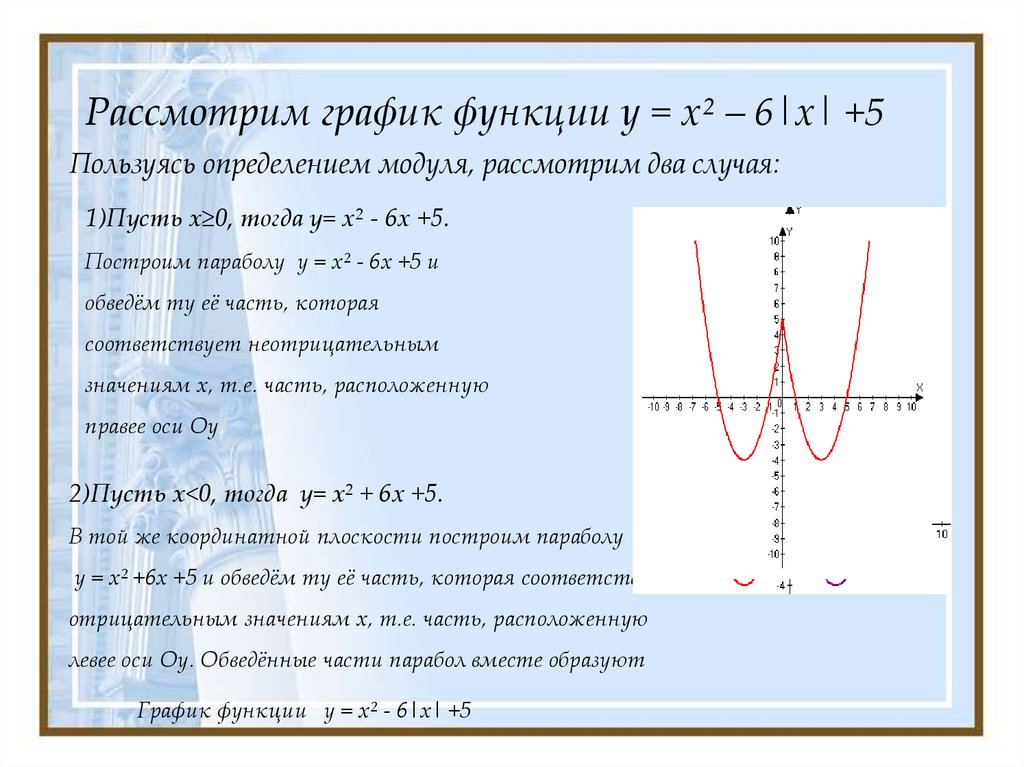
Функция у = х в квадрате и её график

Похожие презентации:

Функция у=х2 и её график

Функция y = x2 и её график

Применение производной к исследованию функции и построению графика функции

Линейная функция и её график. (7 класс)

Функция у=√х, её свойства и график

Функция у х, её свойства и график

Линейная функция и её график

Функция y = x2 и её график

Функция корень из х. Ее свойства и график

Квадратичная функция, её свойства и график. 8 класс

№ 37.1(б,г) Найдите значение функции y = x2, соответствующее заданному значению аргумента:
б) 3;
х=3
у = х2
у = 32 = 9
г) 0.
х=0
у = х2
у = 02 = 0
№ 37.2(б,г) Найдите значение функции y = x2, соответствующее заданному значению аргумента:
1
б) 2 ;
3
7
х =
3
у = х2
2
7
49
у = =
9
3
г) 1,6.
х = 1,6
у = х2
у = 1,62 = 2,56
№ 37.3(б,г) Найдите значения аргумента, которым соответствует заданное значение функции y = x2:

б) 6,25;
у = 6,25
х2 = 6,25
х1 = 2,5
г) 2,25;
х2 = – 2,5
у = 2,25
х2 = 2,25
х1 = 1,5
х2 = – 1,5
№ 37. 4(б,г) Найдите значение функции y = – x2, соответствующее заданному значению аргумента:
б) 0;
х=0
у = – х2
у = – 1 · 02 = 0
г) 4;
х=4
у = – х2
у = – 1 · 42 = – 16
№ 37.5(б,г) Найдите значение функции y = – x2, соответствующее заданному значению аргумента:
1
б) 3 ;
4
13
х=
4
у = – х2
2
169
13
у = 1 =
16
4
г) 2,5.
х = 2,5
у = – х2
у = – 1 · 2,52 = – 6,25
№ 37.6(б,г) Найдите значения аргумента, которым соответствует заданное значение функции y = – x2:
1
б) ;
4
1
у=
4
1
х =
4
2
1
х =
4
2
1
х1 =
2
1
х2 =
2
№ 37.6(б,г) Найдите значения аргумента, которым соответствует заданное значение функции y = – x2:
г) – 1;
у=–1
– х2 = – 1
х2 = 1
х1 = 1
х2 = – 1
№ 37.7(б,г) Не выполняя построения, ответьте на вопрос,
принадлежит ли графику функции y = x2 заданная
точка:
х
у
у = х2
6 = 32 неверно
Ответ: не принадлежит
х
у
у = х2
9 = (– 3)2
Ответ: принадлежит
верно
№ 37. 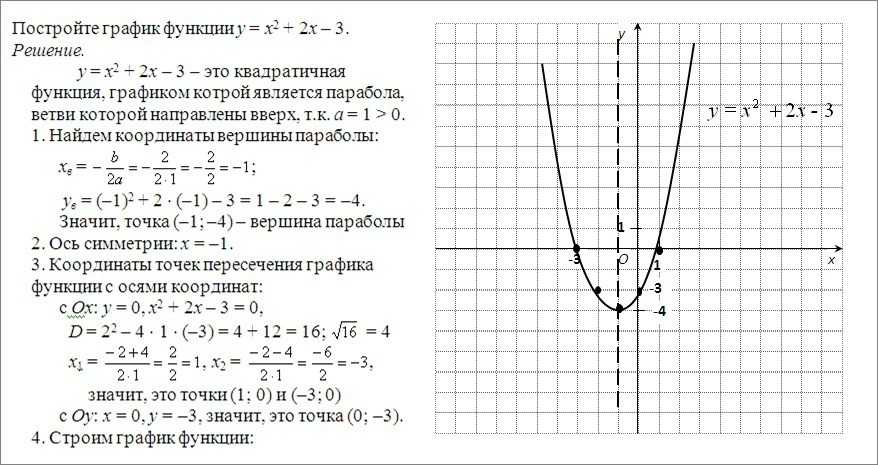8(б,г) Не выполняя построения, ответьте на вопрос,
принадлежит ли графику функции y = x2 заданная
точка:
х
у
у = х2
2,4 = 1,22
неверно
Ответ: не принадлежит
х
у
у = х2
6,25 = (– 2,25)2
Ответ: принадлежит
верно
№ 37.9(б,г) Не выполняя построения, ответьте на вопрос,
принадлежит ли графику функции y = x2 заданная
точка:
х
у
у = х2
2
4 2
= верно
9 3
Ответ: принадлежит
М – точка IV четверти, а
все точки параболы лежат
в I и II четвертях.
Ответ: не принадлежит
№ 37.10(б,г) Не выполняя построения, ответьте на вопрос,
принадлежит ли графику функции y = – x2
заданная точка:
х
у
у = – х2
4 = – 1 · (– 2)2
4 = – 4 неверно
Ответ: не принадлежит
№ 37.10(б,г) Не выполняя построения, ответьте на вопрос,
принадлежит ли графику функции y = – x2
заданная точка:
х
у
у = – х2
– 6 = – 1 · (– 3)2
–6=–9
неверно
Ответ: не принадлежит
№ 37. 12
а) x = — 2
у
y=4
x=2
y=4
б) y = 4
x1 = 2
x2 = — 2
в) y < 4
y>4
0
1
х
г) 0 < x < 2
x ϵ (- 2; 2)
x ϵ (- ∞; 2),
(2; + ∞)
у ϵ (0; 4)
10.08.2020
Классная
р а б о т а.
Функция у = х2 и её график
РТ № 37.10
–9
–4
–1
0
у
0
1
–1
1
х
у = – х2
–4
–9
РТ № 37.11
парабола
РТ № 37.12
у
0
1
1
х
оси у
ветви
(0; 0)
РТ № 37.13
у
0
0
1
1
х
нет
(– ∞; 0), (0; +∞)
нет
=0
(0; +∞)
(– ∞; 0)
РТ № 37.16
9
9
1
3
=1
=1
=9
=3
–3
–1
=1
=–1
=9
=–3
4
4
2
–2
нет
нет
=4
=–2
=4
=2
У: стр. 143 § 37
З: § 37 № 13 – 15.

English     Русский Правила

Учебная презентация к уроку алгебры в 7 классе «Функция х в квадрате и её график» | Методическая разработка по алгебре (7 класс) на тему:

Слайд 1

Функция y = x 2 и её график Алгебра 7 класс Яковлева Любовь Викторовна МБОУ «Самосдельская СОШ им. Шитова В.А.»

Слайд 2

Цели урока: рассмотреть свойства и график функции у = х 2 ; научиться строить и «читать» график данной функции; научиться решать уравнения графическим способом.

Слайд 3

Назовите координаты точек, симметричных данным точкам относительно оси y : (- 2; 6) (- 1; 4) (0; 0) (- 3; — 5) ( 2; 6) (1; 4) (0; 0) (3; — 5) y х

Слайд 4

Найдите значение функции y = 5x + 4, если: х = — 1 х = — 2 х = 3 х = 5 y = — 1 y = — 19 y = — 6 y = — 29

Слайд 5

Укажите область определения функции: y = 16 – 5 x х ≠ 0 х ≠ 7 х – любое число

Слайд 6

Зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной. Расшифруйте термины Функция Независимая переменная, значения которой выбирают произвольно. Аргумент Все значения, которые принимает независимая переменная. Область определения Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.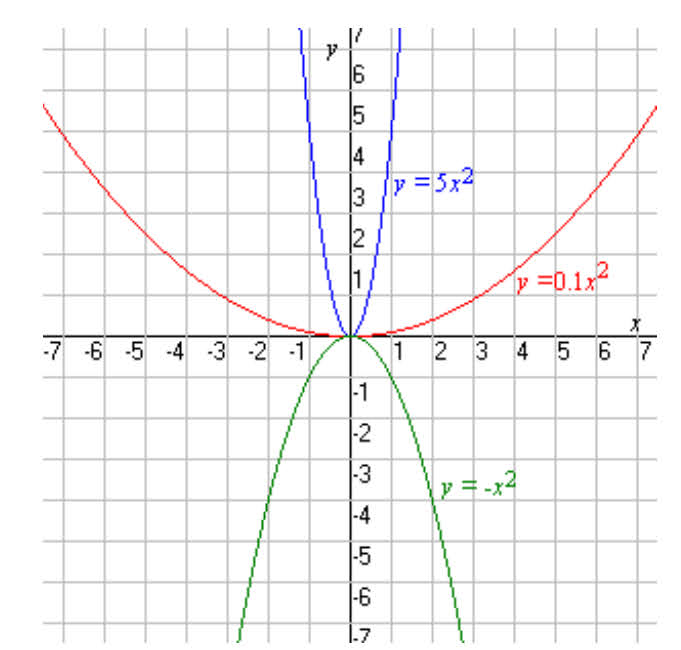 Линейная функция График функции Функция, заданная формулой вида y = kx + b , где х – переменная, k и b некоторые числа, её графиком является прямая.

Слайд 7

Зависимость площади квадрата от длины его стороны квадратичная функция Зависимая переменная Независимая переменная y = x 2 y x

Слайд 8

Функция y = x 2 Математическое исследование

Слайд 9

х — 3 — 2 , 5 — 2 — 1,5 — 1 — 0,5 0 y Заполните таблицу значений функции y = x 2 : х 0 0, 5 1 1,5 2 2,5 3 y — 9 — 6,25 — 4 — 2,25 — 1 — 0,25 0 0 2,5 1 2,5 4 6,25 9

Слайд 10

Постройте график функции y = x 2 парабола

Слайд 11

Свойства функции y = x 2

Слайд 12

Область определения функции D(f): х – любое число. Область значений функции E(f): все значения у ≥ 0.

Слайд 13

Если х = 0, то у = 0. График функции проходит через начало координат .

Слайд 14

Если х ≠ 0, то у > 0. Все точки графика функции, кроме точки (0; 0), расположены выше оси х . I II

Слайд 15

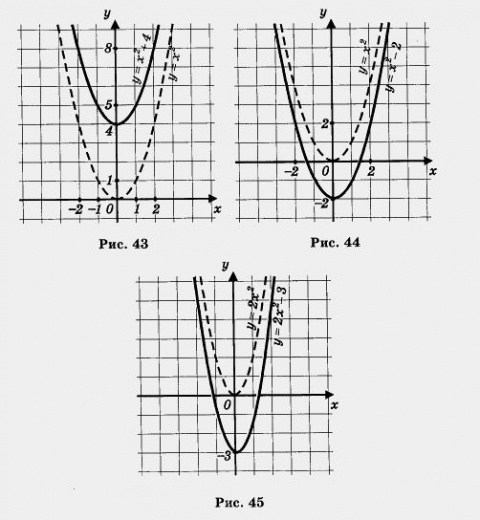Противоположным значениям х соответствует одно и то же значение у. График функции симметричен относительно оси ординат. Функция чётная. (- х) 2 = х 2 при любом х

Слайд 16

Геометрические свойства параболы Обладает симметрией Ось разрезает параболу на две части: ветви параболы Точка (0; 0) – вершина параболы Парабола касается оси абсцисс Ось симметрии

Слайд 17

«Знание – орудие, а не цель» Л. Н. Толстой Найдите у, если: х ≈ -2,5 х = — 2 у ≈ 1,9 у ≈ 6,7 у ≈ 9,6 х = 1,4 х = — 2,6 х = 3,1 у = 6 у = 4 Найдите х, если: — 1,4 — 3 , 1 х ≈ 2,5 х = 2

Слайд 18

Найдите несколько значений х, при которых значения функции : меньше 4 больше 4

Слайд 19

При каких значениях а точка Р(а; 64) принадлежит графику функции у = х 2 . Принадлежит ли графику функции у = х 2 точка : Не выполняя вычислений, определите, какие из точек не принадлежат графику функции у = х 2 : P(-18; 324) R(-99; -9081) S(17; 279) (-1; 1) (0; 8) (-2; 4) (3; -9) (1,8; 3,24) (16; 0) а = 8; а = — 8 принадлежит не принадлежит не принадлежит

Слайд 20

Решите графически уравнение: х 2 = 5 х 2 = — 1 x 2 = х +1 y = — 1 y = x + 1 y = х 2 y = 5 нет решений х ≈ — 2,2; х ≈ 2,2 х ≈ — 0,6; х ≈ 1,6

Слайд 21

Домашнее задание Изучить п. 23. Выполнить упр. № 484, № 486, № 487, № 494(а).

Слайд 22

Удачи вам!

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92. #

# «Нас просят решить, определяет ли он функцию.» #

# «Если независимо от того, какое значение первой переменной, «\x,» есть» #
# «ровно одно значение второй переменной,» \y, «подключено» #
# к ней внутри отношение — тогда это будет функция. Если это» #
# «не удается хотя бы для одного значения первой переменной, то она не сможет» #
# «быть функцией. То есть, если для некоторого значение первой переменной «#

#», есть два или более значений (или нет значений) переменной»#
# «вторая переменная связана с ней внутри отношения, то она» #
# «не будет функцией.» #

# «Примечание — вообще говоря, не существует процедуры, позволяющей решить, является ли» #
# «произвольно заданное отношение функциональным [ — является функцией или нет].» #
# «Правда в том, что таких процедур вообще нет. Наш «#
#» случай, к счастью, оказывается достаточно простым, чтобы принять» #
# «решение, скажем так, руководствуясь здравым чутьем! !» #

# «У нас есть:» \qquad \qquad x \ =\ y^2.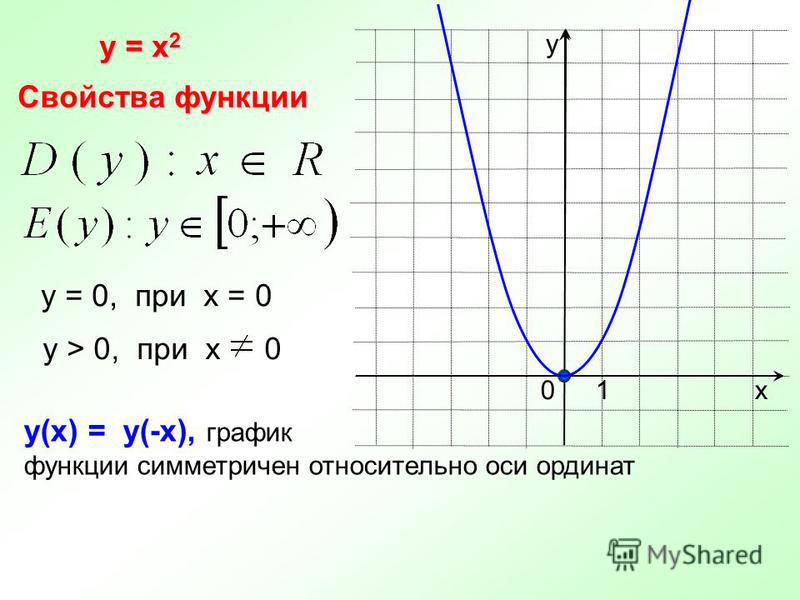 № 92 \ = \ 1. #

# \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad y \ = \ \pm sqrt{1}. #

# \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad y \ = \ -1, 1. #

# «Итак, для «\\x\\» value» \ 1, «имеются два значения для» \\y\\#
# «, связанные с ним в заданном отношении:»\-1, 1 . \\»Итак, больше, чем» #
# «одно значение для» \\y, \»для этого значения»\\x. \\»На этом решение заканчивается» #
# «прямо здесь». № 92 \ = \ 0. #

# \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad y \ = \ 0, \quad «только». #

# «И мы бы пришли к выводу, что для «\\x\\» взятия значения»\0, #
# «имеется ровно одно значение» \\y\\» связанное с ним в заданном» #
# «отношение:» \\0. \\»Ровно одно значение для» \\y, \»связано с этим» #
# «значение» \\x. #

# «Что это говорит нам о том, является ли данное отношение» #
# «функцией? НИЧЕГО !!» №

# «Поскольку существует ровно одно значение «\\y\\» для этого значения» \\x, #
# «мы не можем исключить отношение как функцию, как мы сделали» #
# «выше используя значение «\\1\\» для «\\x. #

# «Из этого мы также не можем сказать, что отношение является функцией», #
# «либо. Почему ? Работа здесь рассказала нам, что произошло со значениями » #
# » для «\\y\\» связано со значением «\\0\\»для»\\x\\»— ровно одно»#
#»значение для»\\y. \\»Но это ничего не сказало нам о значениях для «\\y\\» #
# «связан с любым другим значением для «\\x. \\»Другие значения для» #
#\\x\\»могут иметь ровно одно значение для»\\y\\»связанного с ним,» #
#»могут иметь более одного значения для»\\y\ \»подключен к нему или» #
# «может не иметь значений для»\\y\\»подключен к нему. Мы не можем знать» #
# «если не вернемся назад и не проверим значения для» \\x, » кроме «\\0.» #

# «Какие другие значения для «\\x,» мы должны проверить — кроме «\\0 \\»?» #

# «Правда, вообще никак не определить какие» #
#»другие значения для «\\x\\» (если они есть) надо проверить. Нам «#
#» повезло мы выбрали значение «\\1\\»для»\\x\\»выше — которое «#
#»позволило нам принять решение об этом отношении.