Задача 7: Задачи 7 ЕГЭ профильная математика, сортировка по темам

Задачи 7 ЕГЭ профильная математика, сортировка по темам

MATHM >> ЕГЭ >> ЕГЭ профиль >>

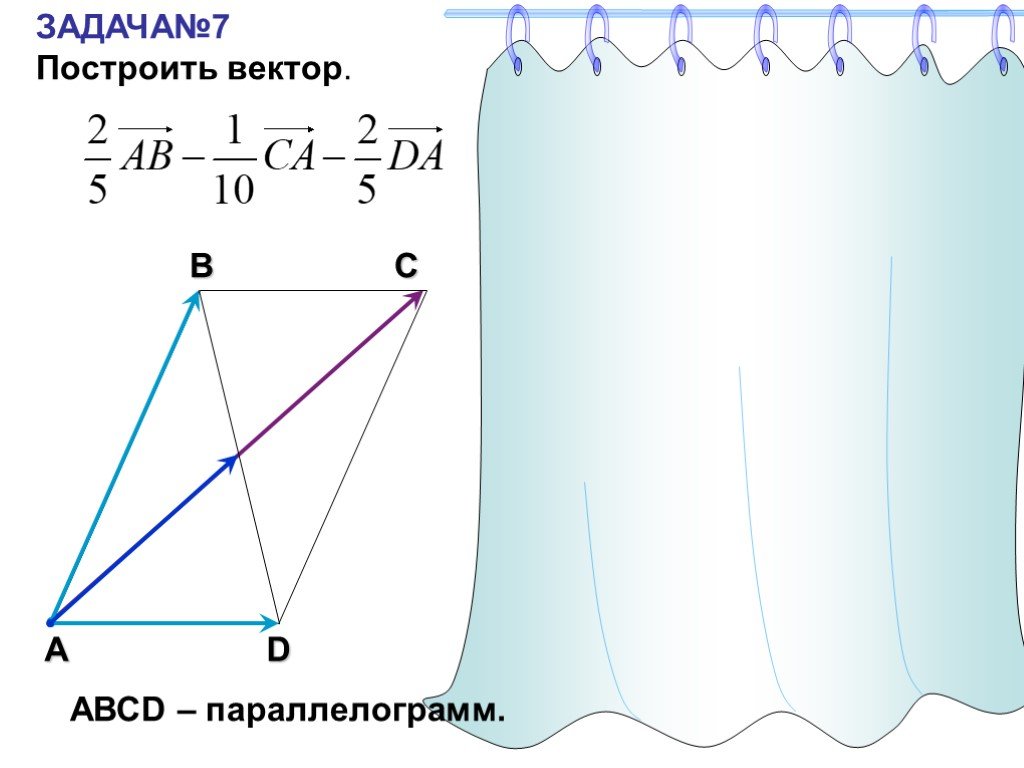
Задача 7

ЗАДАЧА 7
сортировка
по сложности

ЗАДАЧА 7
сортировка
по темам

СПИСОК ТЕМ

Тема 1: Применение производной к исследованию функций
Тема 2: Геометрический смысл производной, касательные
Тема 3: Физический смысл производной
Тема 4: Первообразные и интегралы

Задачи разделены на темы. Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи мы постарались расположить по возрастанию сложности.

Тема 1: Применение производной к исследованию функций, точки экстремума

1. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;6). Найдите точку экстремума функции f (x), принадлежащую отрезку (−3;5).
   

посмотреть ответ

2. На рисунке изображен график функции y = f (x) и двенадцать точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂. В скольких из этих точек производная функции f (x) отрицательна?
   

посмотреть ответ

3. На рисунке изображен график функции y = f (x) и восемь точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈.
   В скольких из этих точек производная функции f (x) положительна?
   

посмотреть ответ

4. На рисунке изображен график y = f ′(x) — производной функции y = f (x). На оси абсцисс отмечены восемь точек x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. Сколько из этих точек лежит на промежутках возрастания функции f (x)?
   

посмотреть ответ

5. На рисунке изображен график функции y = f (x), определенной на интервале
   (−9;10). Определите количество целых точек, в которых производная функции отрицательна.
   

посмотреть ответ

6. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;11). В какой точке отрезка [−4;10] функция f (x) принимает наименьшее значение?
   

посмотреть ответ

7. На рисунке изображен график функции y = f (x). Определите количество целых точек на интервале (−8;10), в которых производная функции положительна.
   

посмотреть ответ

8. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;11). В какой точке отрезка [−4;10] функция f (x) принимает наибольшее значение?
   

посмотреть ответ

9. На рисунке изображен график функции y = f (x). Определите количество точек экстремума на интервале (−1;10).
   

посмотреть ответ

10. На рисунке изображен график функции y = f (x), определенной на интервале
    (−6;7). Определите количество целых точек, в которых производная функции отрицательна.
    

посмотреть ответ

11. На рисунке изображен график функции y = f (x). Определите количество целых точек, в которых производная функции положительна.
    

посмотреть ответ

12. На рисунке изображен график функции y = f (x), определенной на интервале
    (−6;5). Определите количество точек минимума на интервале (−1;4).
    

посмотреть ответ

13. На рисунке изображен график функции y = f (x), определенной на интервале
    (−3;5). Определите количество точек экстремума на интервале (−3;5).
    

посмотреть ответ

14. На рисунке изображен график функции y = f (x), определенной на интервале
    (−6;5). Определите количество точек минимума на интервале (−6;5).
    

посмотреть ответ

15. На рисунке изображен график функции y = f (x), определенной на интервале
    (−6;7). Определите количество точек максимума на интервале (−6;7).
    

посмотреть ответ

16. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−7;8). Найдите точку максимума функции f (x) на отрезке [−3;5].
    

посмотреть ответ

17. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−7;8). Найдите точку минимума функции f (x) на отрезке [−3;5].
    

посмотреть ответ

18. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). Найдите количество точек максимума функции f (x) на интервале (−5;6).
    

посмотреть ответ

19. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;5). Найдите количество точек экстремума функции f (x) на интервале (−4;5).
    

посмотреть ответ

20. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;6). Найдите промежутки убывания функции f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.
    

посмотреть ответ

21. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;6). Найдите промежутки возрастания функции f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.
    

посмотреть ответ

22. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите промежутки убывания функции f (x).
    В ответе укажите длину наибольшего из них.
    

посмотреть ответ

23. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). Найдите количество точек экстремума функции f (x) на интервале (−5;6).
    

посмотреть ответ

24. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). Найдите промежутки убывания функции f (x). В ответе укажите длину наибольшего из них.
    

посмотреть ответ

25. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). Найдите промежутки возрастания функции f (x). В ответе укажите длину наибольшего из них.
    

посмотреть ответ

26. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). Найдите промежутки возрастания функции f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.
    

посмотреть ответ

27. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). Найдите количество точек, в которых производная функции f (x) равна 0.
    

посмотреть ответ

28. На рисунке изображен график функции y = f (x). На оси абсцисс отмечены точки −5,2; −3,8; −2,8; 1,4; 4,6. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
    

посмотреть ответ

29. На рисунке изображен график функции f (x), определенной на интервале (−9;10). Определите количество точек, в которых касательная к графику функции параллельна прямой y = −5 или совпадает с ней.
    

посмотреть ответ

30. На рисунке изображен график функции y = f (x), определенной на интервале (−5;6). Найдите сумму точек экстремума функции f (x).
    

посмотреть ответ

31. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;6). Найдите количество точек экстремума функции f (x) на интервале (−4;6).
    

посмотреть ответ

32. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;6). Найдите количество точек максимума функции f (x) на интервале (−4;6).
    

посмотреть ответ

33. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;6). Найдите количество целых точек на интервале (−4;6), в которых функция f (x) возрастает.
    

посмотреть ответ

34. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−2;8). Найдите количество целых точек на интервале (−2;8), в которых функция f (x) убывает.
    

посмотреть ответ

35. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−2;7). Найдите промежутки убывания функции f (x). В ответе укажите длину наибольшего из них.
    

посмотреть ответ

36. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите промежутки возрастания функции f (x). В ответе укажите длину наибольшего из них.
    

посмотреть ответ

37. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите количество точек экстремума функции f (x) на интервале (−3;7).
    

посмотреть ответ

38. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите количество точек минимума функции f (x) на интервале (−3;7).
    

посмотреть ответ

39. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите количество целых точек на интервале (−3;7), в которых функция f (x) возрастает.
    

посмотреть ответ

40. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите количество целых точек на интервале (−3;7), в которых функция f (x) убывает.
    

посмотреть ответ

41. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите промежутки возрастания функции f (x). В ответе укажите длину наибольшего из них.
    

посмотреть ответ

42. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−3;7). Найдите промежутки возрастания функции f (x). В ответе укажите их количество.
    

посмотреть ответ

43. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). В какой точке отрезка [−4;5] функция f (x) принимает наибольшее значение?
    

посмотреть ответ

44. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;5). В какой точке отрезка [1;5] функция f (x) достигает своего наибольшего значения?
    

посмотреть ответ

Тема 2: Геометрический смысл производной, касательные

1. На рисунке изображены график функции y = f (x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f (x) в точке x₀.
   

посмотреть ответ

2. На рисунке изображены график функции y = f (x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f (x) в точке x₀.
   

посмотреть ответ

3. На рисунке изображены график функции y = f (x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f (x) в точке x₀.
   

посмотреть ответ

4. На рисунке изображен график функции y = f (x), определенной на интервале
   (−6;7). Определите количество точек, в которых касательная к графику функции параллельна прямой y = 3 или совпадает с ней.
   

посмотреть ответ

5. На рисунке изображены график функции y = f (x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f (x) в точке x₀.
   

посмотреть ответ

6. На рисунке изображены график функции y = f (x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f (x) в точке x₀.
   

посмотреть ответ

7. Прямая y = 5 − 2x является касательной к графику функции y = ln(2 − 2x) − 4. Найдите абсциссу точки касания.

посмотреть ответ

8. Прямая y = 2x − 1 параллельна касательной к графику функции y = − x² − 2x + 2. Найдите абсциссу точки касания.

посмотреть ответ

9. Прямая y = 2x − 1 параллельна касательной к графику функции y = 2x² − 2x − 4. Найдите абсциссу точки касания.

посмотреть ответ

10. Прямая y = 2x − 1 параллельна касательной к графику функции y = ln(2x + 3) − 3. Найдите абсциссу точки касания.

посмотреть ответ

11. Прямая y = 2x − 8 является касательной к графику функции y = x³ − 3x² + 2x − 4. Найдите абсциссу точки касания.

посмотреть ответ

12. Прямая y = − 24x + 35 является касательной к графику функции y = 3 − 2x³. Найдите абсциссу точки касания.

посмотреть ответ

13. Прямая y = 6x + 10 является касательной к графику функции y = ( x + 1)(x² − 2). Найдите абсциссу точки касания.

посмотреть ответ

14. Прямая y = −3x + 4 является касательной к графику функции y = x ⁻¹ − 2x + 2. Найдите абсциссу точки касания.

посмотреть ответ

15. На рисунке изображены график функции y = f (x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 4. Найдите f ′(4).
    

посмотреть ответ

16. На рисунке изображены график функции y = f (x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой −4. Найдите f ′(−4).
    

посмотреть ответ

17. На рисунке изображены график функции y = f (x). Прямая, проходящая через точку (1;1), касается графика этой функции в точке с абсциссой 5. Найдите f ′(5).
    

посмотреть ответ

18. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−5;6). Найдите количество точек, в которых касательная к графику функции f (x) параллельна прямой y = − x + 3 или совпадает с ней.
    

посмотреть ответ

19. На рисунке изображен график y = f ′(x) — производной функции y = f (x), определенной на интервале (−4;5). Найдите количество точек, в которых касательная к графику функции f (x) параллельна прямой y = x + 14 или совпадает с ней.
    

посмотреть ответ

20. Прямая y = 2x − 1 является касательной к графику функции y = ax² + 4x − 3. Найдите a.

посмотреть ответ

21. Прямая y = 2 − x является касательной к графику функции y = x² + 3bx + 6. Найдите b, если абсцисса точки касания отрицательна.

посмотреть ответ

22. Прямая y = 4 − 2x является касательной к графику функции y = −2x² + 4bx + 2. Найдите b, если абсцисса точки касания отрицательна.

посмотреть ответ

23. Прямая y = 2 + x является касательной к графику функции y = 2cx² − x + 1. Найдите c, если абсцисса точки касания отрицательна.

посмотреть ответ

Тема 3: Физический смысл производной

1. Материальная точка движется прямолинейно по закону x(t) = 1,5t³ − 2t² − t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 4с.

посмотреть ответ

2. Материальная точка движется прямолинейно по закону x(t) = 0,75t³ − 2t² + 2, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 8 с.

посмотреть ответ

3. Материальная точка движется прямолинейно по закону x(t) = t² − 2t − 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?

посмотреть ответ

4. Материальная точка движется прямолинейно по закону x(t) = 0,5t² + 2t + 1, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 5 м/с?

посмотреть ответ

5. Материальная точка движется прямолинейно по закону x(t) = 0,25t² + t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 10 м/с?

посмотреть ответ

Тема 4: Первообразные и интегралы

1. На рисунке изображен график некоторой функции y = f (x). Функция — одна из первообразных функции f (x). Найдите площадь закрашенной фигуры. В ответе запишите площадь, умноженную на 3.
   

посмотреть ответ

2. На рисунке изображен график некоторой функции y = f (x). Функция — одна из первообразных функции f (x). Найдите площадь закрашенной фигуры. В ответе запишите площадь, умноженную на 3.
   

посмотреть ответ

3. На рисунке изображен график функции f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F (5) − F (−1), где F (x) — одна из первообразных функции f (x).
   

посмотреть ответ

4. На рисунке изображен график функции f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F (7) − F (0), где F (x) — одна из первообразных функции f (x).
   

посмотреть ответ

5. На рисунке изображен график функции f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F (8) − F (1), где F (x) — одна из первообразных функции f (x).
   

посмотреть ответ

6. На рисунке изображен график функции f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F (5) − F (−1), где F (x) — одна из первообразных функции f (x).
   

посмотреть ответ

7. На рисунке изображен график функции y = F (x) — одной из первообразных функции f (x), определенной на интервале (−12;11). Найдите количество решений уравнения f (x) = 0 на отрезке [−10;10].
   

посмотреть ответ

8. На рисунке изображен график функции y = F (x) — одной из первообразных функции f (x), определенной на интервале (−6;5). Найдите количество решений уравнения f (x) = 0 на интервале (−6;5).
   

посмотреть ответ

9. На рисунке изображен график функции y = F (x) — одной из первообразных функции f (x) касательная к нему в точке с абсциссой x₀. Найдите значение функции функции f (x) в точке x₀.
   

посмотреть ответ

10. На рисунке изображен график функции y = F (x) — одной из первообразных функции f (x) касательная к нему в точке с абсциссой x₀. Найдите значение функции функции f (x) в точке x₀.
    

посмотреть ответ

Задача 7 ОГЭ математика



Задача 7 ОГЭ математика

MATHM >> ОГЭ >>

Задача 7

Задачи разделены на уровни сложности.

Задачи из любого уровня вполне реально встретить на настоящем экзамене ОГЭ, более сложные встретятся если «не повезло».

Сложность 1 (легкие задачи)

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

Сложность 2 (немного более сложные задачи)

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

посмотреть ответ

TASK™ 7 Информация о продукте | Smooth-On, Inc.

Инструкции

Материалы следует хранить и использовать в теплой среде (73° F / 23° C). Этот продукт имеет ограниченный срок годности и должен быть использован как можно скорее. Все жидкие уретаны чувствительны к влаге и поглощают атмосферную влагу. Инструменты и емкости для смешивания должны быть чистыми и изготовлены из металла, стекла или пластика. Смешивание должно производиться в хорошо проветриваемом помещении. Носите защитные очки, одежду с длинными рукавами и резиновые перчатки, чтобы свести к минимуму риск загрязнения.

Поскольку нет двух одинаковых приложений, рекомендуется небольшое тестовое приложение для определения пригодности для вашего проекта, если производительность этого материала вызывает сомнения.

Нанесение разделительного состава — Разделительное средство необходимо для облегчения извлечения из формы при заливке на большинство поверхностей или поверх них. Используйте разделительный состав, специально предназначенный для изготовления пресс-форм ( Universal™ Mold Release или Mann’s Ease Release™ 200 , который можно приобрести у Smooth-On или у вашего дистрибьютора Smooth-On). На все поверхности, которые будут соприкасаться с пластиком, следует нанести обильный слой разделительной смазки.0005

ВАЖНО: Чтобы обеспечить полное покрытие, нанесите разделительное средство и нанесите на все поверхности мягкой кистью. Затем нанесите легкий туман и дайте разделительному составу высохнуть в течение 30 минут.

Силиконовые каучуковые формы Smooth-On обычно не требуют смазки при заливке уретановой смолы в форму. Применение разделительного состава продлит срок службы формы.

---

Предварительно смешайте часть А и часть В перед дозированием.

Измерение — Надлежащее соотношение смешивания Flame Out™ составляет 1 часть А на 1 часть В по объему. Вылейте равные количества в емкость для смешивания.

При тонировании или пигментировании Flame Out™, добавьте краситель в часть B и тщательно перемешайте перед добавлением части. A.

Перемешивание — Преднамеренно перемешайте, несколько раз очищая стенки и дно емкости для смешивания. Будьте осторожны, чтобы не выплеснуть материал с низкой вязкостью из контейнера.

---

ВАЖНО: Срок годности продукта уменьшается после вскрытия. Оставшийся продукт следует использовать как можно скорее. Немедленная замена крышек на обоих контейнерах после выдачи продукта поможет продлить срок годности неиспользованного продукта. XTEND-IT™ Dry Gas Blanket (доступен в Smooth-On) значительно продлит срок годности неиспользованных жидких уретановых продуктов.

---

Заливка — При заливке Flame Out™ в резиновую форму, вылейте смесь в одну точку в самой нижней точке формы. Если инкапсулируете объект, не выливайте смесь непосредственно на объект.

Пусть смесь ищет свой уровень. Равномерный поток поможет свести к минимуму захваченный воздух.

Для достижения наилучших результатов. . . Наилучшие результаты достигаются при использовании метода литья под давлением. После заливки смешанного состава весь литейный узел (форма, конструкция плотины и т. д.) помещается в камеру высокого давления и подвергается воздействию давления воздуха 60 фунтов на квадратный дюйм (4,2 кг/см2) в течение 1 часа.

Отверждение — Важно: Используйте этот продукт с вентиляцией, по крайней мере, размером с комнату или вблизи принудительной вентиляции и не вдыхайте пары. Испарения, которые могут быть видны при значительной массовой концентрации, быстро рассеиваются при соответствующей вентиляции. Отливки значительной массы могут быть горячими на ощупь и вызывать раздражение кожи сразу после отверждения. Дайте отливке остыть до комнатной температуры, прежде чем обращаться с ней.

Время извлечения готовой отливки из формы зависит от массы и конфигурации формы. Отливки с малой массой или тонкостенные отверждения требуют больше времени для отверждения, чем отливки с более высокой массовой концентрацией.

При изготовлении вращающихся или полых отливок заполнение жесткой пеной ( Foam-iT! 5 или другой) обеспечит легкое армирование. Обратная засыпка пеной рекомендуется, если отливки будут подвергаться воздействию температуры выше 85°F / 30°C.

Пост-отверждение — Пост-отверждение рекомендуется, если отливки тонкие или с низкой массовой концентрацией. Отливки должны подвергаться пост-отверждению в форме или опорной конструкции. Дайте материалу высохнуть в течение 1 часа при комнатной температуре, а затем в течение 2 часов при 150–160°F (65–72°C). Перед обработкой отливке или детали необходимо дать остыть до комнатной температуры.

Характеристики — Отвержденные отливки из Flame Out™ отличаются жесткостью и долговечностью. Они устойчивы к влаге, умеренному нагреву, растворителям, разбавленным кислотам и могут подвергаться механической обработке, грунтовке/окраске или приклеиваться к другим поверхностям (необходимо удалить любой разделительный состав). Отливки можно выставлять на улицу после грунтовки и покраски.

---

Описание задачи

Устранение неоднозначности смысла слова (WSD), задача определения значения слова в контексте, уже давно признана важной задачей компьютерной лингвистики. Традиционные подходы к WSD основаны на предположении, что в основе каждого слова в документе лежит одно однозначное коммуникативное намерение. Однако существует класс языковых конструкций, известный как 99011 каламбуры , в которых лексико-семантическая двусмысленность является преднамеренным следствием коммуникативного акта. То есть говорящий или пишущий намеревается интерпретировать определенное слово или другую лексическую единицу как имеющую одновременно два или более отдельных значения. Хотя каламбуры являются повторяющейся и ожидаемой чертой многих типов дискурса, они привлекли относительно мало внимания в области компьютерной лингвистики и обработки естественного языка в целом или WSD в частности.

Фон

Каламбур — это форма игры слов, в которой одно означающее ( например, слово или фраза) предполагает два или более значений, используя полисемию или фонологическое сходство с другим означающим для предполагаемого юмористического или риторического эффекта. Например, первая из следующих двух каламбурных шуток использует противоположные значения слова «интерес», а вторая использует звуковое сходство между поверхностной формой «пропан» и скрытой целью «профан»:

Раньше я был банкиром, но потерял интерес.

Когда церковь покупала газ для своего ежегодного барбекю, выручка шла от священного газа к пропану.

Каламбуры, в которых два значения имеют одинаковое произношение, известны как гомофонный или совершенный , а те, которые основаны на сходных, но не идентичных по звучанию знаках, известны как гетерофонный или несовершенный . Там, где знаки рассматриваются как письменные, а не устные последовательности, аналогичное различие можно провести между гомографические и гетерографические каламбуры.

Сознательное или неявное лингвистическое знание, особенно лексической семантики и фонологии, является важной предпосылкой для производства и интерпретации каламбуров. Это уже давно сделало их привлекательным предметом изучения в теоретической лингвистике и привело к небольшому, но растущему объему исследований каламбуров в компьютерной лингвистике. Однако на сегодняшний день большинство вычислительных методов обработки каламбуров сосредоточено на алгоритмах генерации или моделировании их фонологических свойств.

Сводка задач

Участникам предоставляется два набора данных:

Набор данных 1: омографические каламбуры.

Первый набор данных будет содержать несколько сотен коротких контекстов (шутки, слоганы, афоризмы, и т.д. ). В некоторых из этих контекстов одно слово будет использоваться как омографический каламбур; в остальном не будет каламбура.

Набор данных 2: Гетерографические каламбуры.

Второй набор данных будет аналогичен первому, за исключением того, что каламбуры будут гетерографическими, а не гомографическими.

Для одного или обоих наборов данных участвующие системы соревнуются в любой или во всех трех подзадачах, оцениваемых на последовательных этапах:

Подзадача 1: Обнаружение каламбура.

No related posts.