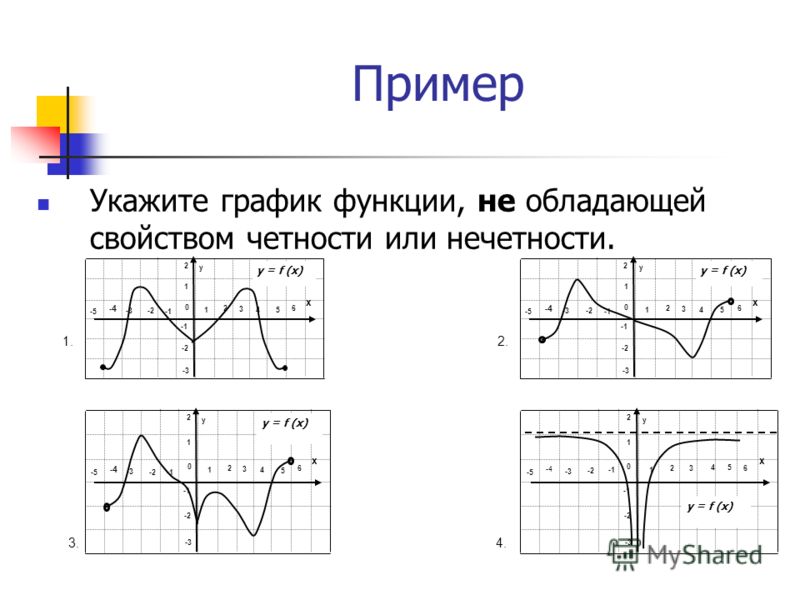
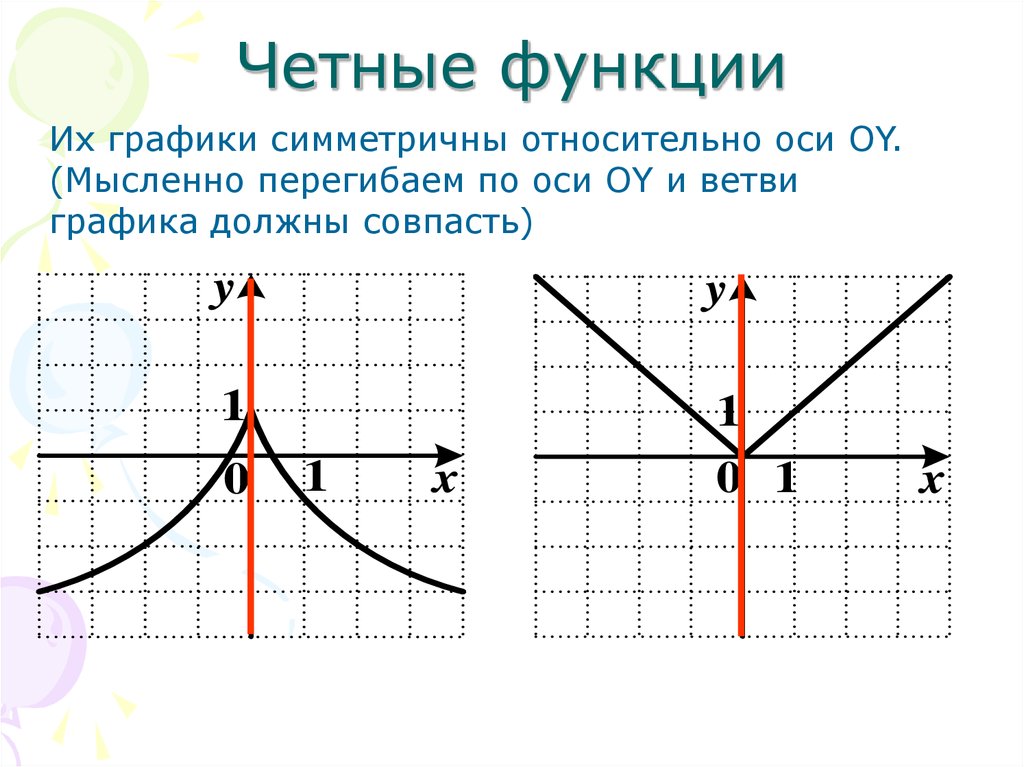
Если функция нечетная и не нечетная. Четные и нечетные функции. Периодические функции. Примеры нечетной функции
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:
- -x (противоположная точка) также лежит в данной области определения,
- f (-x) = f (x).
Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О, являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка — b тоже лежит в этой области.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами.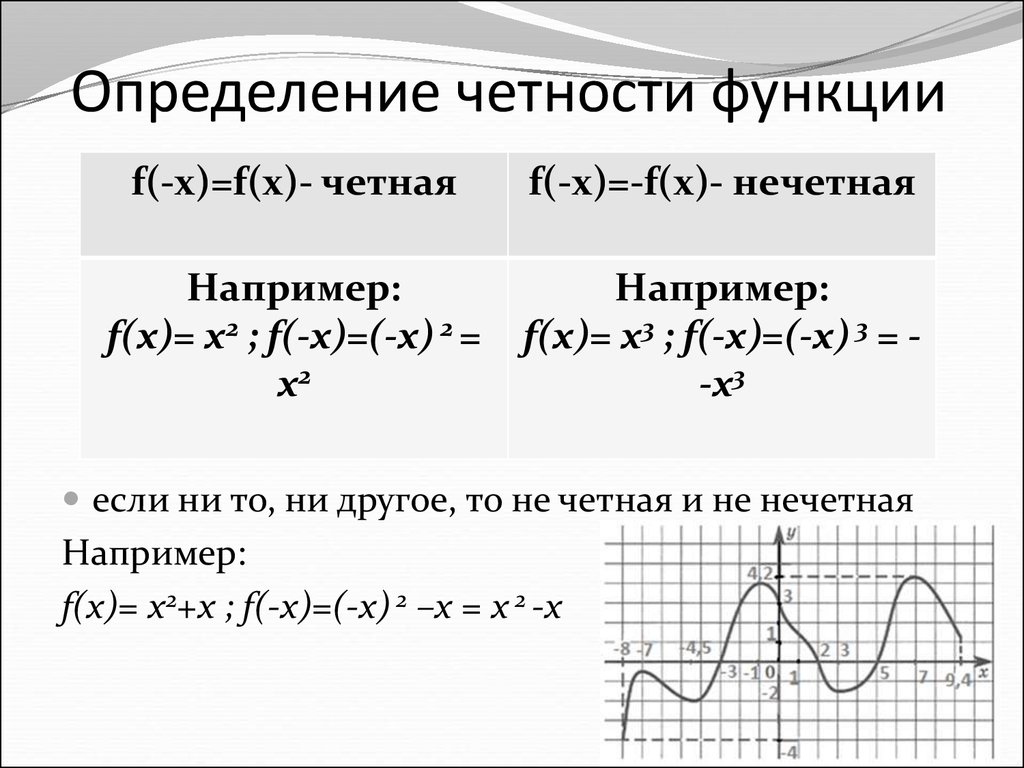
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
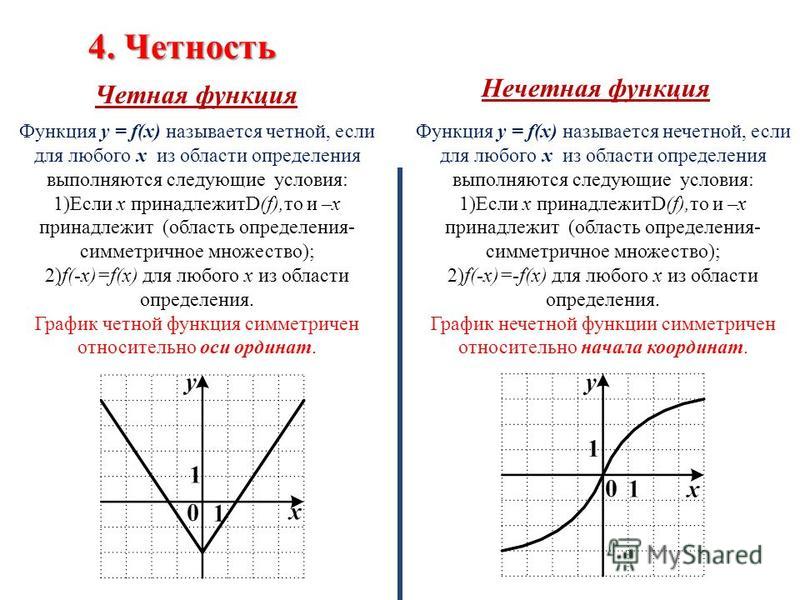
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
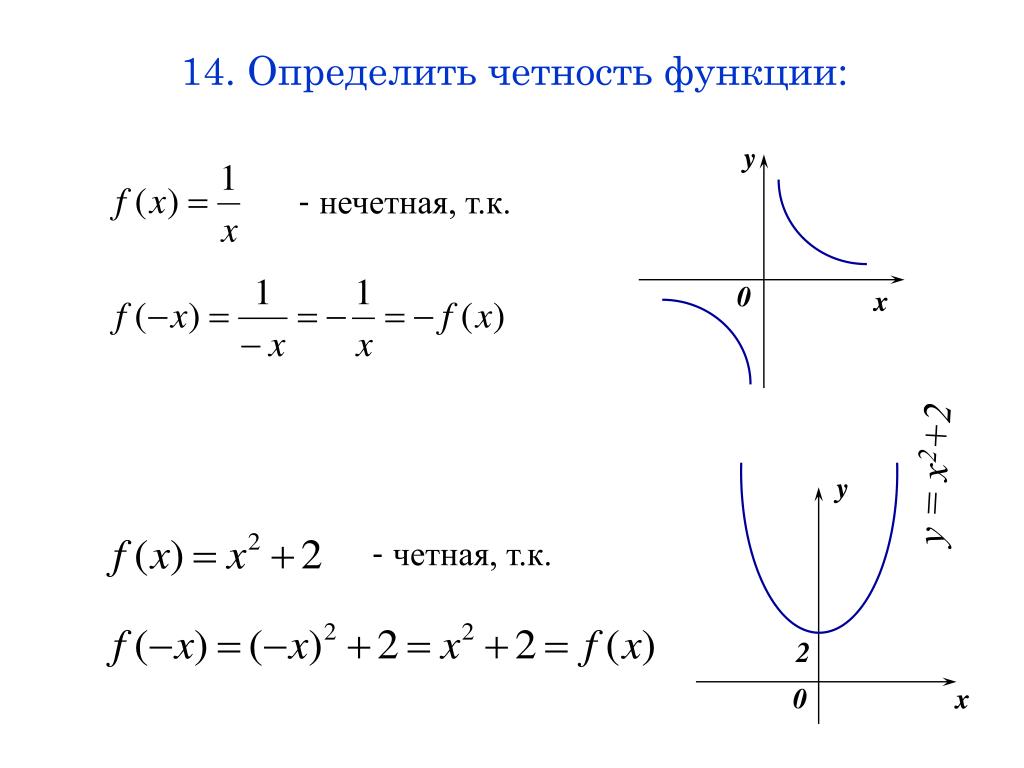
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.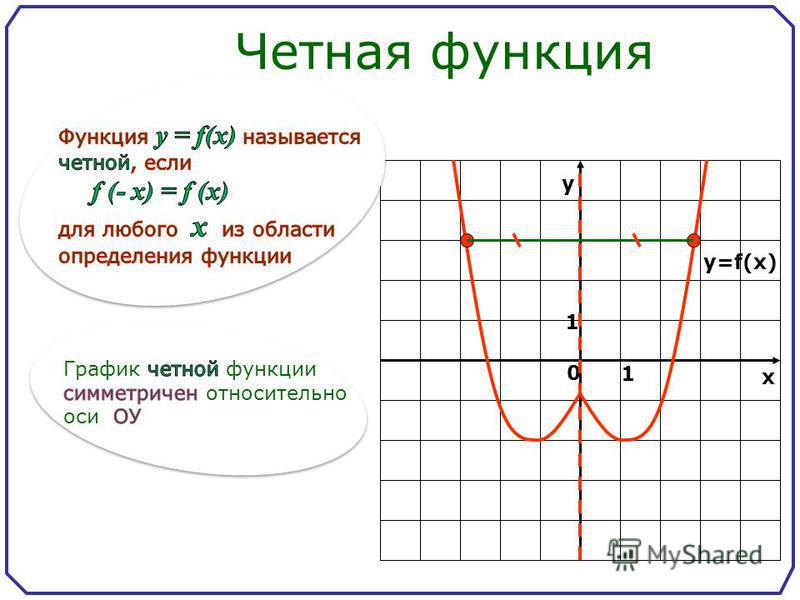 е. функция является четной.
е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
Какая функция называется четной и нечетной. Исследование функции
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:
- -x (противоположная точка) также лежит в данной области определения,
- f (-x) = f (x).
Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О, являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка — b тоже лежит в этой области. Из вышесказанного, таким образом, вытекает вывод: четная функция имеет симметричный по отношению к оси ординат (Oy) вид.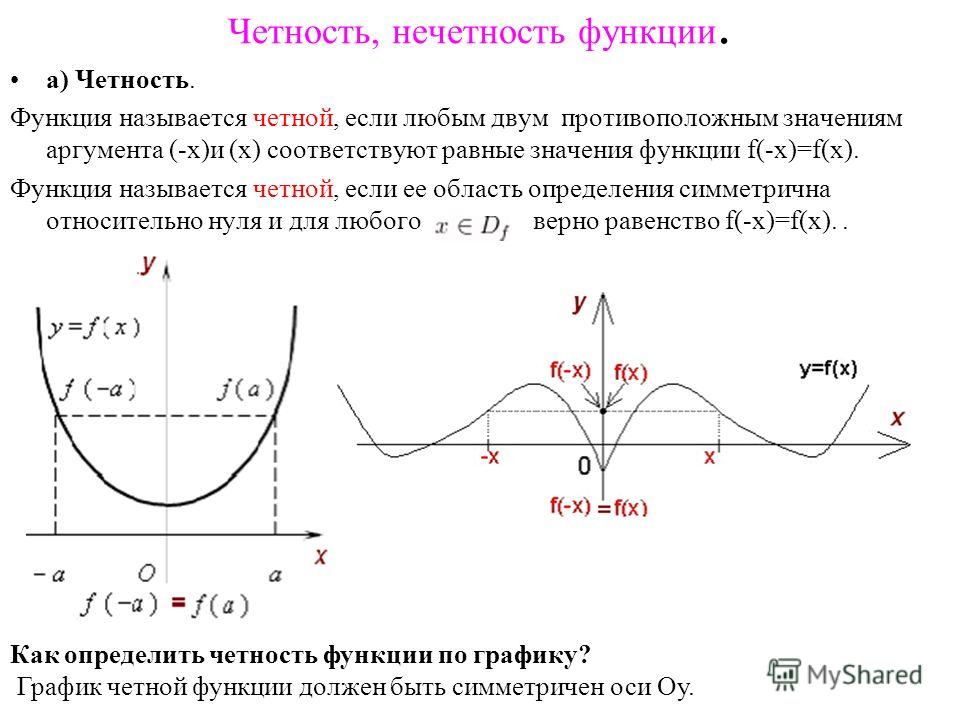 (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами.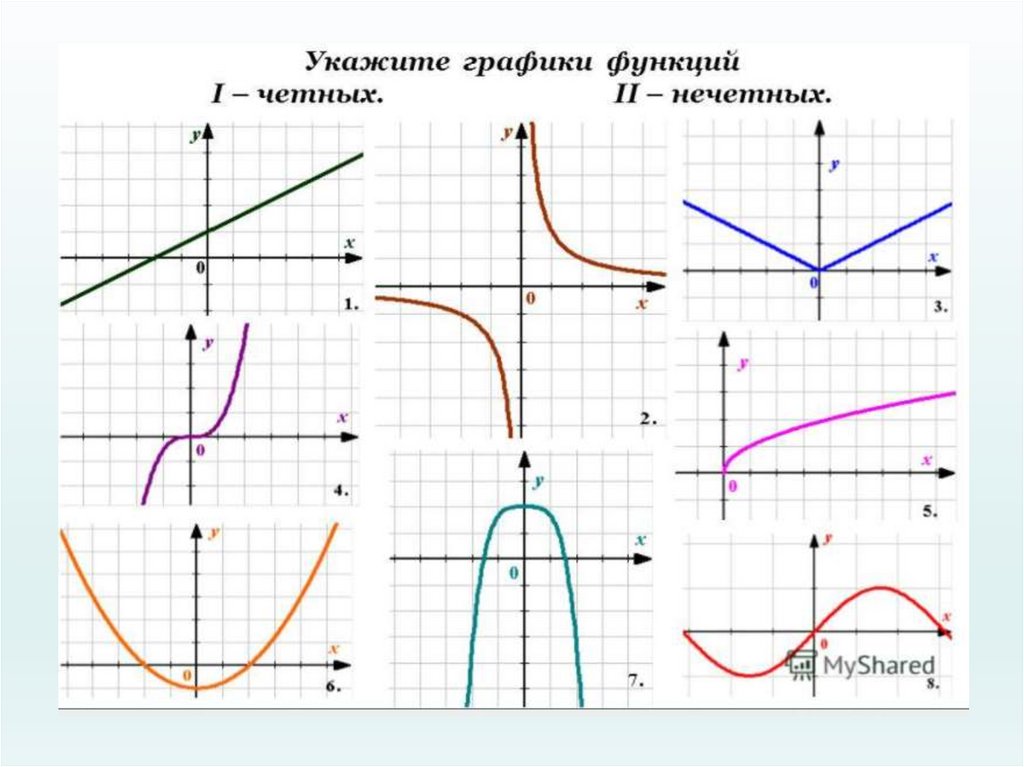
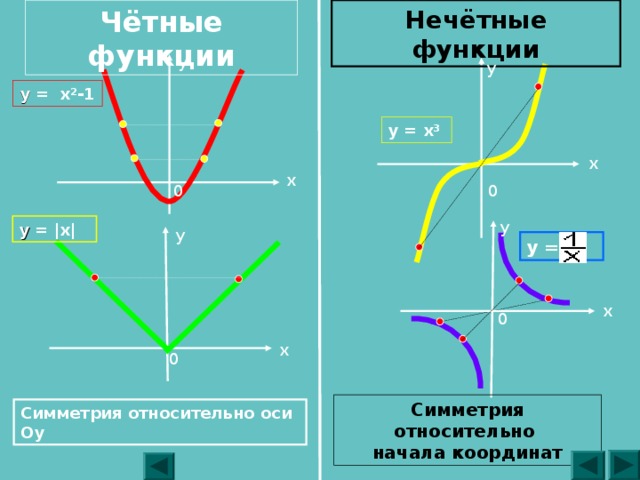
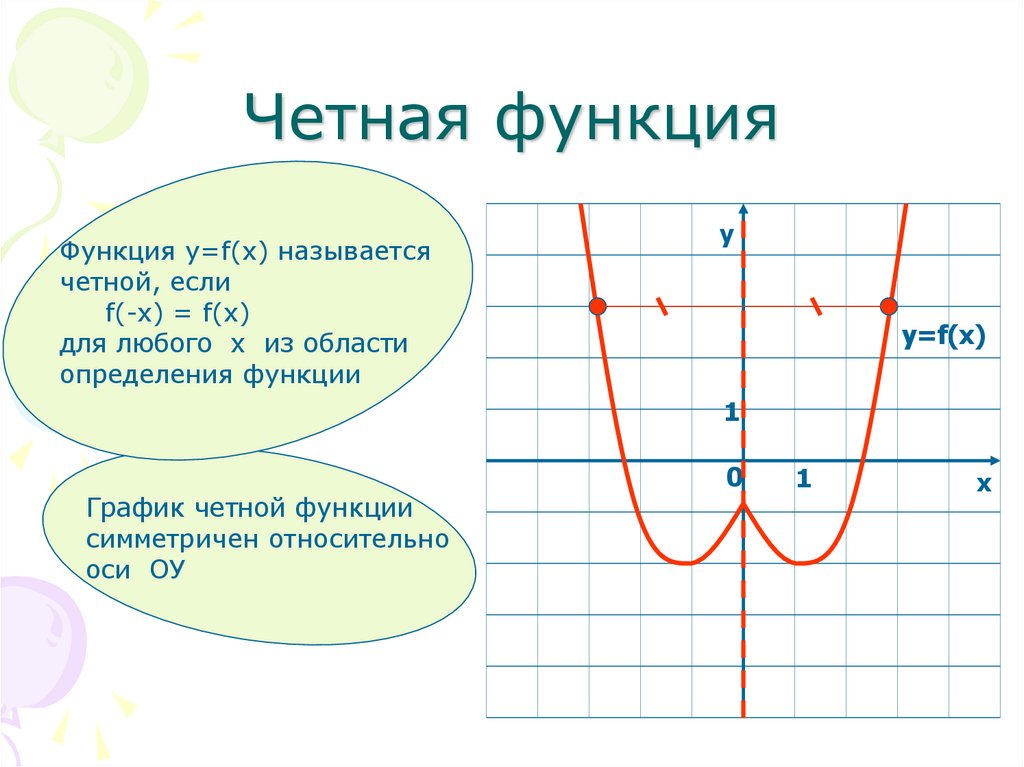
Четная функция.
Четной называется функция, знак которой не меняется при изменении знака x .
x выполняется равенство f (–x ) = f (x ). Знак x не влияет на знак y .
График четной функции симметричен относительно оси координат (рис.1).
Примеры четной функции:
y = cos x
y = x 2
y = –x 2
y = x 4
y = x 6
y = x 2 + x
Пояснение:

При любом значении x функция положительная. Знак x не влияет на знак y . График симметричен относительно оси координат. Это четная функция.
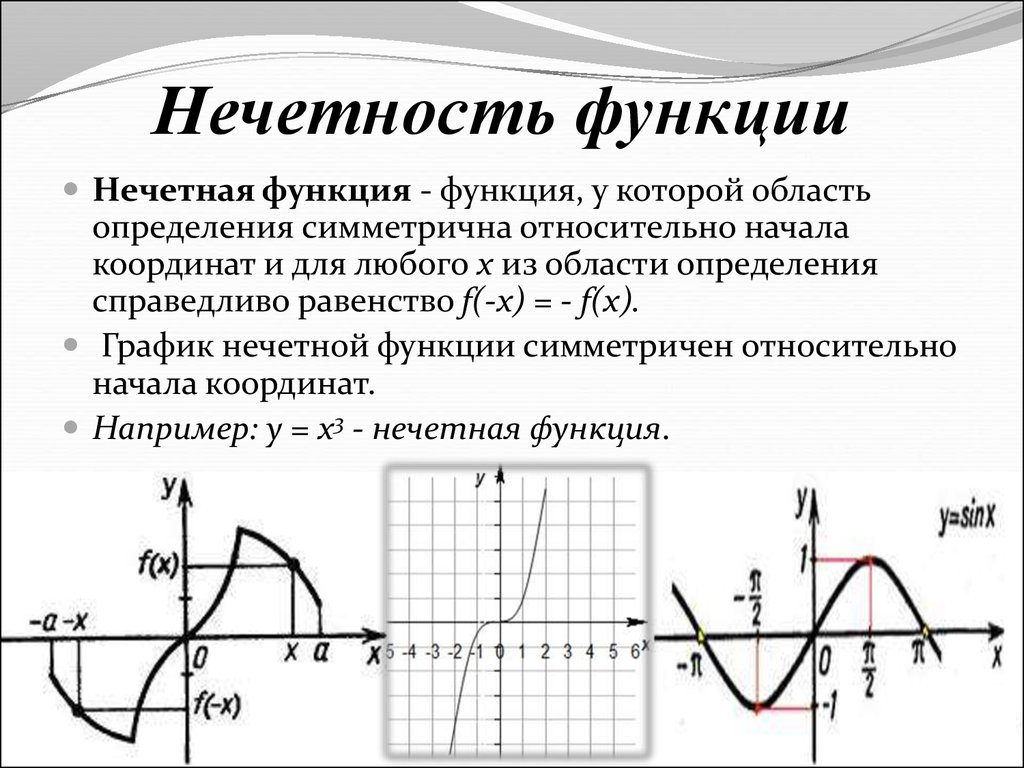
Нечетная функция.
Нечетной называется функция, знак которой меняется при изменении знака x .
Говоря иначе, для любого значения x выполняется равенство f (–x ) = –f (x ).
График нечетной функции симметричен относительно начала координат (рис.2).
Примеры нечетной функции:
y = sin x
y = x 3
y = –x 3
Пояснение:
Возьмем функцию y = –x 3 .
Все значения у в ней будут со знаком минус. То есть знак x влияет на знак y . Если независимая переменная – положительное число, то и функция положительная, если независимая переменная – отрицательное число, то и функция отрицательная: f (–x ) = –f (x ).
График функции симметричен относительно начала координат. Это нечетная функция.
Свойства четной и нечетной функций:
ПРИМЕЧАНИЕ:
Не все функции являются четными или нечетными. Есть функции, которые не подчиняются такой градации. К примеру, функция корня у = √х не относится ни к четным, ни к нечетным функциям (рис.3). При перечислении свойств подобных функций следует давать соответствующее описание: ни четна, ни нечетна.
Периодические функции.
Как вы знаете, периодичность – это повторяемость определенных процессов с определенным интервалом. Функции, описывающие эти процессы, называют периодическими функциями
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной
функции симметричен относительно начала
координат.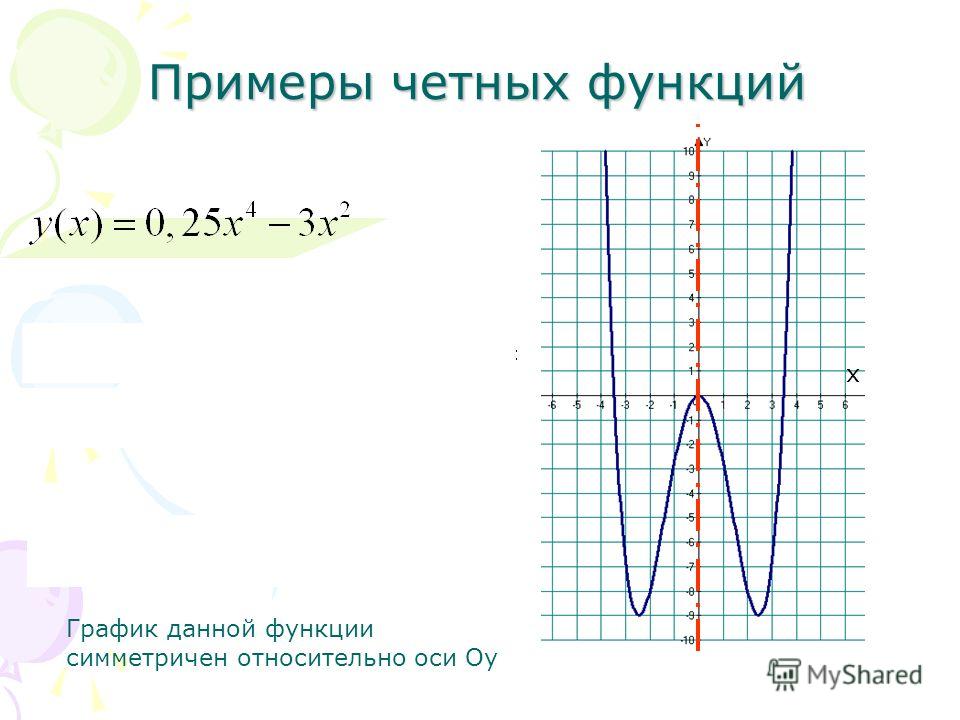
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых производная равна нулю или не существует называются критическими.
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т.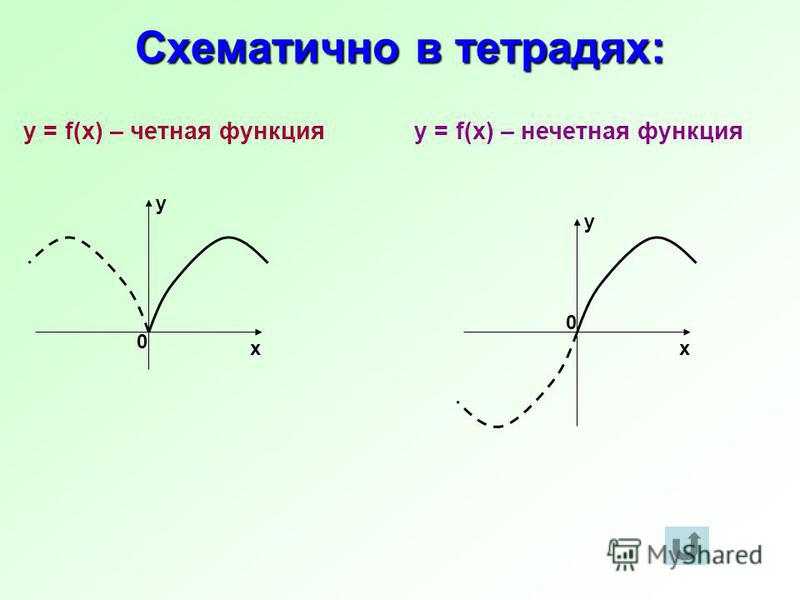 экстремума.
Итак, исследуем критические точки
экстремума.
Итак, исследуем критические точки
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.
В точках
функция имеет максимум.
Графики четной и нечетной функции обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат.
Пример. Построить график функции \(y=\left|x \right|\).
Решение. Рассмотрим функцию: \(f\left(x \right)=\left|x \right|\) и подставим вместо \(x \) противоположное \(-x \). В результате не сложных преобразований получим:
$$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$
Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.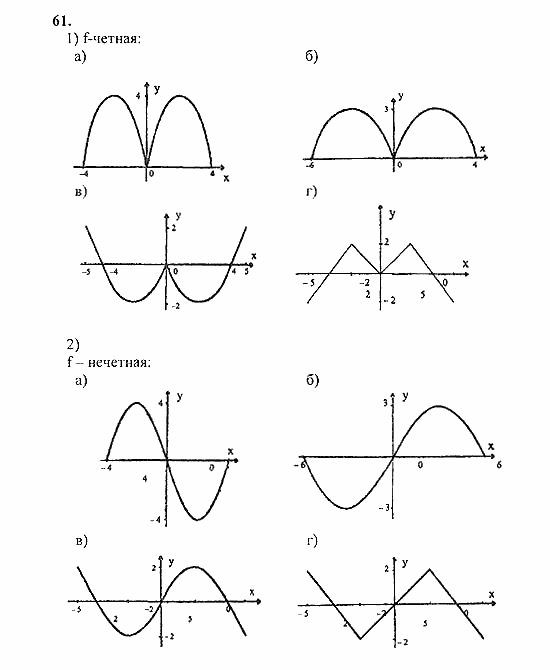
Значит эта функция — четная, а ее график будет симметричен относительно оси ординат (вертикальной оси). График этой функции приведен на рисунке слева. Это означает что при построении графика, можно строить только половину, а вторую часть (левее вертикальной оси рисовать уже симметрично правой части). Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Пример. Построить график функции \(y=x\left|x \right|\).
Решение. Выполним проверку так же как в предыдущем примере:
$$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right)$$
Это означает, что исходная функция является нечетной (знак функции поменялся на противоположный).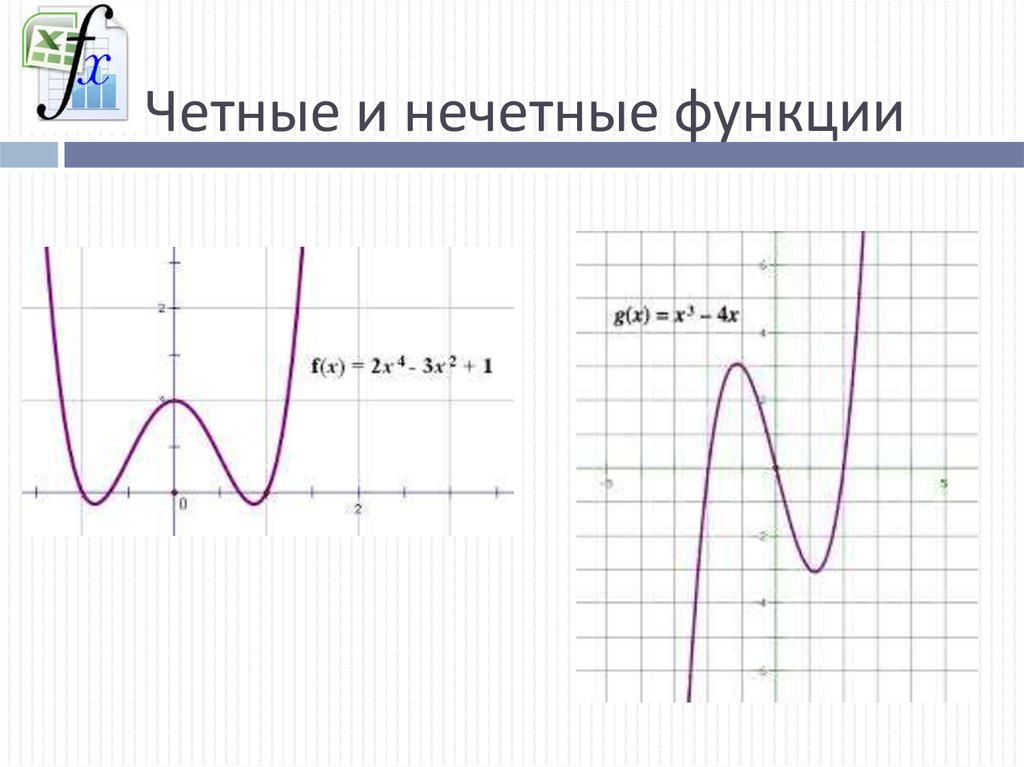 {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).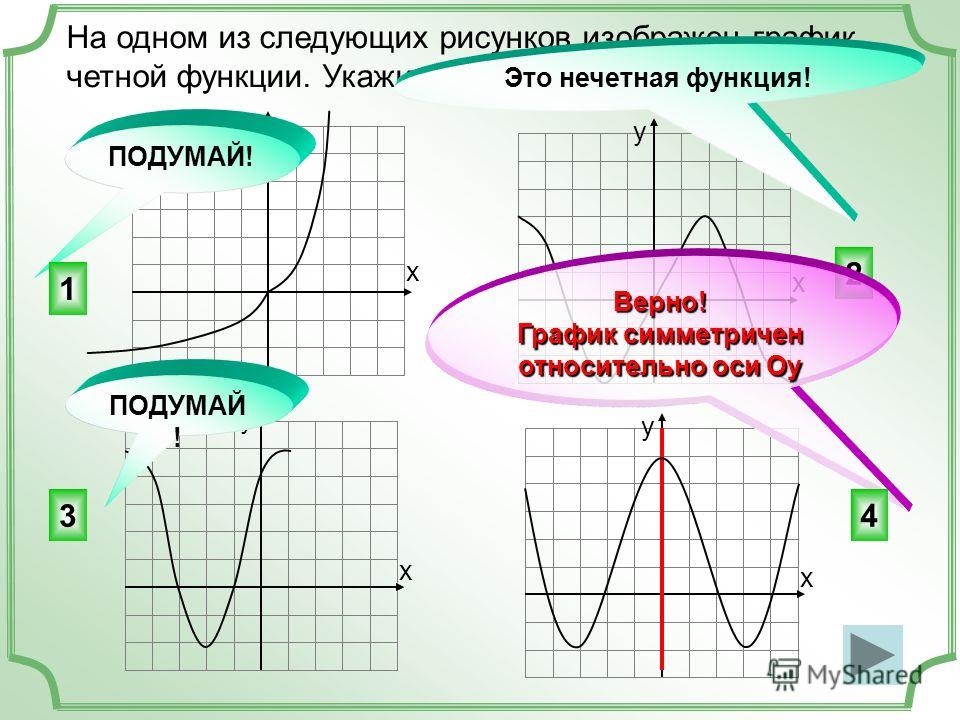
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.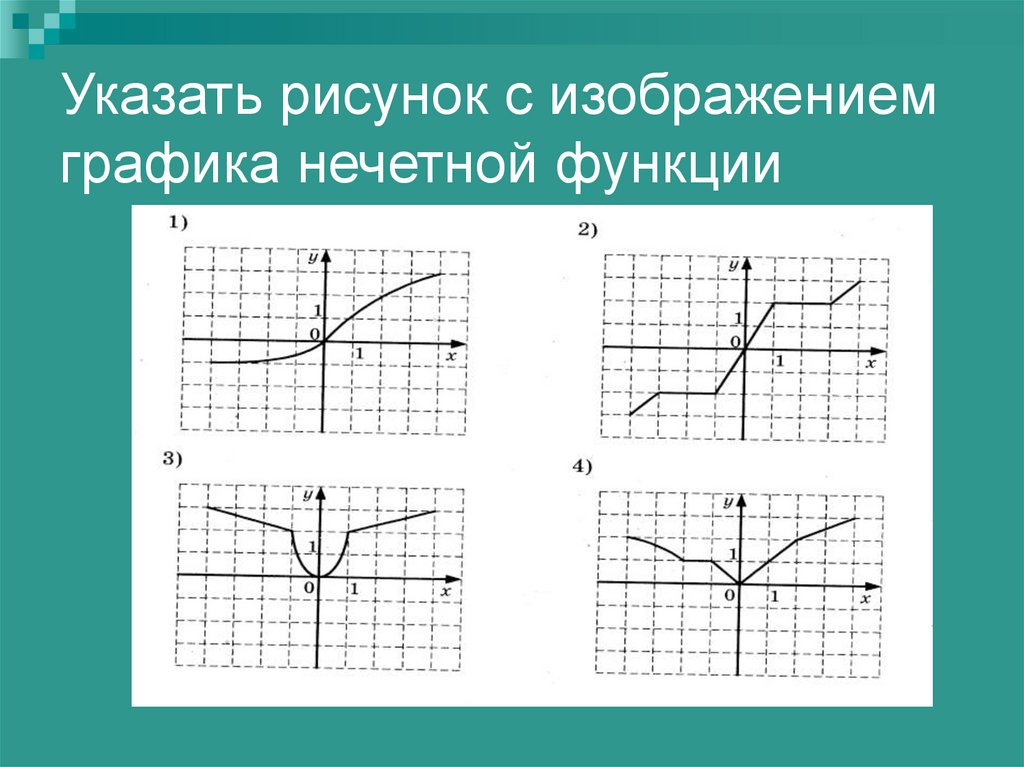
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Чётность функции — Вики
Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.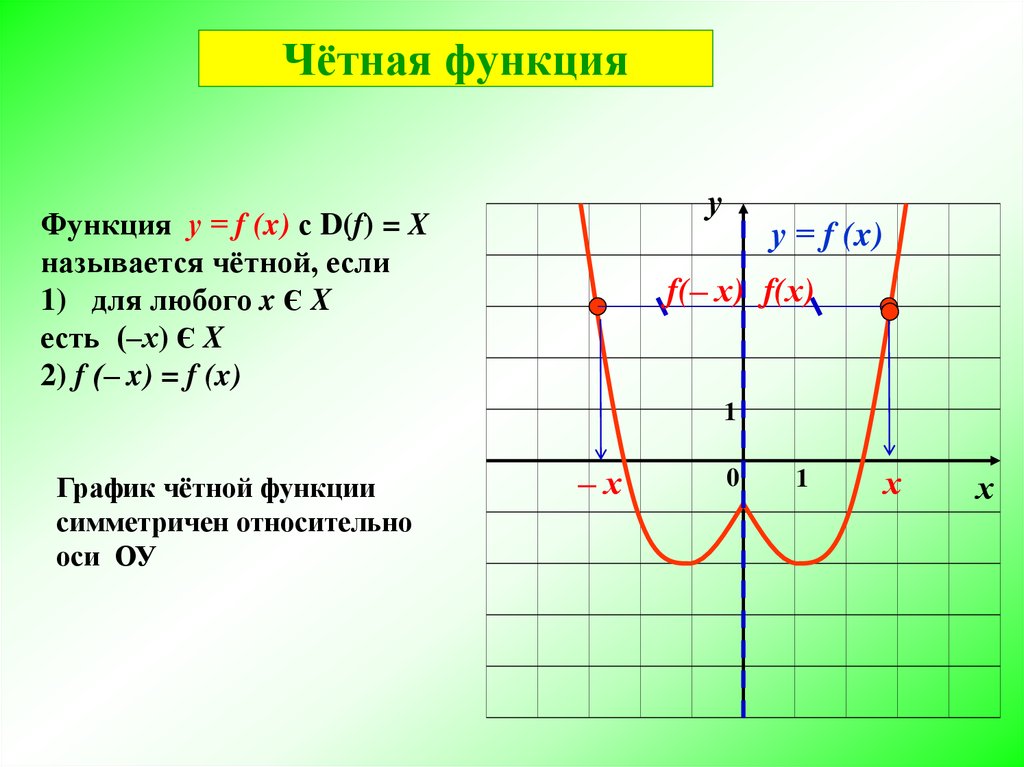 {3}+1} ни чётная, ни нечётная
{3}+1} ни чётная, ни нечётная
- Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат).
- Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
- Ни чётная, ни нечётная функция (или функция общего вида). В эту категорию относят функции, не попадающие в предыдущие 2 категории.
Содержание
- 1 Строгое определение
- 2 Свойства
- 3 Примеры
- 3.1 Нечётные функции
- 3.2 Чётные функции
- 4 Литература
Строгое определение
Определения вводятся для любой симметричной относительно нуля области определения X⊂R{\displaystyle X\subset \mathbb {R} }, например, отрезка или интервала.
- Функция f:X→R{\displaystyle f:X\to \mathbb {R} } называется чётной, если справедливо равенство
- f(−x)=f(x),∀x∈X.
 {\displaystyle f(-x)=f(x),\quad \forall x\in X.}
{\displaystyle f(-x)=f(x),\quad \forall x\in X.}
- Функция называется нечётной, если справедливо равенство
- f(−x)=−f(x),∀x∈X.{\displaystyle f(-x)=-f(x),\quad \forall x\in X.}
- Функции, не принадлежащие ни одной из категорий выше, называются ни чётными, ни нечётными (или функциями общего вида).
Функции, принимающие нулевое значение на всей своей области определения, причём эта область определения симметрична относительно нуля, являются одновременно чётными и нечётными; например, функции f(x) = 0 и f(x) = 0/х. Любая функция, являющаяся одновременно чётной и нечётной, тождественно равна нулю на всей своей области определения.
Свойства
- График нечётной функции симметричен относительно начала координат O{\displaystyle O}.
- График чётной функции симметричен относительно оси ординат Oy{\displaystyle Oy}.
- Произвольная функция f:[−X,X]⊂R→R{\displaystyle f:[-X,X]\subset \mathbb {R} \to \mathbb {R} } может быть единственным образом представлена в виде суммы нечётной и чётной функций:
- f(x)=g(x)+h(x),{\displaystyle f(x)=g(x)+h(x),}
- где
- g(x)=f(x)−f(−x)2,h(x)=f(x)+f(−x)2.
 {2k+1},} где k∈Z{\displaystyle k\in \mathbb {Z} } — произвольное целое число.
{2k+1},} где k∈Z{\displaystyle k\in \mathbb {Z} } — произвольное целое число.- Сигнум: f(x)={ 1,x>0 0,x=0−1,x<0{\displaystyle f(x)={\begin{cases}\ \ 1,&x>0\\\ \ 0,&x=0\\-1,&x<0\end{cases}}}
- Кубический корень y=x3{\displaystyle y={\sqrt[{3}]{x}}} и вообще корень любой положительной нечётной степени y=x2k+1,k∈N.{\displaystyle y={\sqrt[{2k+1}]{x}},\quad k\in \mathbb {N} .}
- Тригонометрические функции: синус f(x)=sinx,{\displaystyle f(x)=\sin x,}тангенс f(x)=tgx,{\displaystyle f(x)=\operatorname {tg} x,}котангенс f(x)=ctgx,{\displaystyle f(x)=\operatorname {ctg} x,}косеканс f(x)=cosecx.{\displaystyle f(x)=\operatorname {cosec} x.}
- Обратные тригонометрические функции: арксинус f(x)=arcsinx,{\displaystyle f(x)=\arcsin x,}арктангенс f(x)=arctgx,{\displaystyle f(x)=\operatorname {arctg} x,}арккотангенс f(x)=arcctgx,{\displaystyle f(x)=\operatorname {arcctg} x,}арккосеканс f(x)=arccosecx.{\displaystyle f(x)=\operatorname {arccosec} x.
 {2}}}\right)} при b=0.
{2}}}\right)} при b=0.- Функция Дирихле.
- Кардинальный синус sinc x (как нормированный, так и ненормированный).
- Функции Матьё cei(x).
Литература
- И. М. Гельфанд, Е. Г. Глаголева, Э. Э. Шноль. Функции и графики. Основные приемы. — М.: Наука, 1968. — (Библиотечка физико-математической школы, выпуск 2). (Перевод на англ.: Functions and Graphs. The MIT Press, 1969, Birkhäuser: Boston, 1990 и 1998)
Что такое нечетная функция? (Ответы на 5 часто задаваемых вопросов) – JDM Educational
Функции полезны во многих областях математики, а нечетные функции обладают интересным свойством, которое стоит изучить.
Итак, что такое нечетная функция? Алгебраически нечетная функция f(x) — это функция, в которой f(-x) = –f(x) для всех значений x в области определения функции. Визуально нечетная функция f(x) обладает вращательной симметрией относительно начала координат, то есть график выглядит как зеркальное отражение при повороте на 180 градусов вокруг начала координат (0,0).

Конечно, есть много способов идентифицировать нечетные функции и использовать их свойства.
В этой статье мы поговорим о том, что такое нечетные функции и как определить, что функция нечетная. Мы также ответим на некоторые распространенные вопросы о нечетных функциях.
Начнем.
Что такое нечетная функция?
Нечетная функция — это функция, удовлетворяющая уравнению f(-x) = –f(x) для каждого значения x в области определения функции. Это означает, что он может иметь повторяющиеся значения y.
Но как выглядит нечетная функция? Что ж, с визуальной точки зрения нечетная функция обладает вращательной симметрией относительно начала координат.
Если вы повернете график на 180 градусов вокруг точки (0, 0), вы снова получите тот же график. Если вы повернете «верхнюю» половину графика (часть над осью x) на 180 градусов вокруг начала координат, вы получите нижнюю половину графика (часть под осью x) и наоборот.
См. пример ниже, который представляет собой график кубической функции f(x) = x 3 :
Кубическая функция f(x) = x 3 симметрична относительно начала координат (нечетная функция).
Вот некоторые типы нечетных функций:
- Линии, проходящие через начало координат – любая линия с нулевой точкой пересечения по оси y (b = 0) и ненулевым наклоном (m не равно нулю) будет иметь уравнение f(x) = мкс.
- Кубическая функция – любая кубическая функция вида f(x) = ax 3 (для не нуля).
- Синусоидальная функция без смещения по вертикали или горизонтали – эти функции имеют вид f(x) = Asin(x), где A — действительное число (A не равно нулю).
Полиномиальные функции только с нечетными показателями также являются нечетными функциями. Например, f(x) = x + x 3 + x 5 .
Давайте рассмотрим некоторые конкретные примеры нечетных функций, а также некоторые нечетные функции.
Пример 1: Нечетная функция (линейная)
Возьмем функцию f(x) = 5x. Эта функция проходит через начало координат, и мы можем легко показать, что f(-x) = -f(x) для каждого значения x в области:
- f(-x) = 5(-x) [подставьте –x в функцию 5x]
- f(-x) = -5x
- f(-x) = -f( x) [определение f(x) = 5x]
Вы можете увидеть вращательную симметрию относительно точки (0, 0) (симметрию относительно начала координат) на графике ниже.
Прямая f(x) = 5x проходит через начало координат. Это нечетная функция, поскольку она имеет вращательную симметрию относительно начала координат.
Пример 2: Нечетная функция (кубическая)
Возьмем кубическую функцию f(x) = 2x 3 . Эта функция проходит через начало координат, и мы можем легко показать, что f(-x) = -f(x) для каждого значения x в области:
- f(-x) = 2(-x) 3 [подставьте –x в функцию 5x]
- f(-x) = -2x 3 [минус, возведенный в нечетную степень, является отрицательным]
- f(-x) = -f(x ) [определение f(x) = 2x 3 ]
Вы можете увидеть вращательную симметрию относительно точки (0, 0) (симметрия относительно начала координат) на графике ниже.
График кубической функции f(x) = 2x 3 . Это нечетная функция, поскольку она имеет вращательную симметрию относительно начала координат.Пример 3: нечетная (квадратичная) функция
Напомним, что квадратичная функция имеет вид f(x) = ax 2 + bx + c, где a не равно нулю.

Возьмем функцию f(x) = 3x 2 + 5, которая имеет a = 3, b = 0 и c = 5. Мы можем доказать, что f(x) не является нечетным, следующим образом:
- f(-x) = 3(-x) 2 + 5 [подставить –x в функцию]
- f(-x) = 3x 2 + 5 [(-x) 2 = (-x)(-x) = +x 2 , так как произведение двух отрицательных чисел положительно]
- f(-x) = f(x) [поскольку f(x) = 3x 2 + 5]
Таким образом, эта функция не нечетна, так как f(-x) не равно f(x) для всех значений x. Например, f(1) = 8, а f(-1) = 8.
Вы можете увидеть отсутствие симметрии относительно начала координат на графике ниже.
График квадратичной функции f(x) = 3x 2 + 5, которая не является нечетной функцией.Пример 4. Нечетная функция (линейная)
Напомним, что линейная функция имеет форму f(x) = ax + b, где a не равно нулю. Если b не равно нулю, то эта функция нечетна.

Возьмем функцию f(x) = 2x – 7, которая имеет a = 2 и b = -7. Мы можем доказать, что f(-x) не равно -f(x) для каждого x на одном примере: x = -1 и x = 1.
- Для x = 1: f(1) = 2(1 ) – 7 = -5
- Для x = -1: f(-1) = 2(-1) – 7 = -9
Поскольку -9 не равно –(-5), то f(-1) не равно равно -f(1), а f(-x) не равно -f(x) для каждого x в области.
Таким образом, эта строка не является нечетной функцией.
Вы можете увидеть отсутствие симметрии относительно начала координат на графике ниже.
График линейной функции f(x) = 2x – 7, которая не является нечетной функцией.Как определить, является ли функция нечетной
Есть несколько способов определить, является ли функция нечетной:
- Алгебраически — для этого нужно сделать доказательство, показав, что f(-x) такое же, как -f(x).
- Графически — для этого необходимо построить график функции и посмотреть, симметричен ли график относительно начала координат, то есть имеет ли он вращательную симметрию на 180 градусов относительно точки (0, 0).

- Из таблицы — для этого необходимо проверить каждую пару противоположных значений x и убедиться, что значения y являются противоположными.
Как определить, является ли функция нечетной алгебраически
Чтобы сказать, что функция является нечетной алгебраически, нам нужно провести доказательство, используя данную функцию и определение нечетной функции.
Допустим, у нас есть функция f(x) = 2x 3 – 5x.
Чтобы доказать, что эта функция нечетна алгебраически, нам нужно доказать, что f(-x) = -f(x), так как это определение нечетной функции. Итак:
- f(-x) = 2(-x) 3 – 5(-x) [используя определение f(x) и подставив –x]
- f(-x) = – 2x 3 + 5x [поскольку отрицательное возведение в четную степень положительно]
- f(-x) = -( 2x 3 – 5x) [вычесть -1]
- f(-x) = -f(x) [по определению, f(x) = 2x 3 – 5x]
Как узнать, является ли функция нечетной на графике если мы получим вращательную симметрию относительно начала координат.

Например, рассмотрим кубическую функцию f(x) = 2x 3 – 5x снова (на фото ниже)
График кубической функции f(x) = 2x 3 – 5x, которая является нечетной функцией .Глядя на график, мы видим, что если мы повернем «верхнюю половину» (часть над осью x) на 180 градусов вокруг начала координат, мы получим «нижнюю половину» (часть под осью x). ).
Таким образом, функция нечетная (или симметричная относительно начала координат).
Как узнать, является ли функция нечетной из таблицы
Мы также можем посмотреть на таблицу, чтобы определить, является ли функция нечетной. Нам нужно будет увидеть, являются ли значения y противоположными для противоположных значений x.
. 2
3 -1 1 0 0 1 -1 2 -3 3 -6 4 -10 The y values are opposite for opposite x значений, так как:
- f(-4) = -f(4) = 10
- f(-3) = -f(3) = 6
- f(-2) = -f (2) = 3
- f(-1) = -f(1) = 1
Поскольку f(-x) = -f(x) для каждой пары значений x в таблице, мы можем сделать вывод, что график имеет нечетную функцию.

Может ли нечетная функция быть отрицательной?
Нечетная функция может быть отрицательной в некоторых точках (фактически нечетная функция должна иметь некоторые отрицательные значения y). Однако по определению оно не может быть отрицательным во всех точках (если только мы не ограничим каким-либо образом область определения).
Подумайте об этом так: если f(x) нечетно, а f(1) отрицательно (f(1) < 0), то f(-1) = -f(1), что положительно. Таким образом, нечетная функция может иметь некоторые отрицательные результаты, но не все.
Возможно, самым простым примером является линейная функция f(x) = x.
Эта функция нечетная и имеет несколько отрицательных выходов (на самом деле, каждый отрицательный вход дает отрицательный результат). Вы можете увидеть его график ниже.
График f(x) = x, который является нечетной линейной функцией. Обратите внимание, что он имеет как положительные, так и отрицательные значения y.Может ли нечетная функция быть однозначной?
Нечетная функция может быть однозначной.
 Однако не всякая нечетная функция является взаимно однозначной.
Однако не всякая нечетная функция является взаимно однозначной.Например, f(x) = x — нечетная функция, и она является однозначной (проходит тест горизонтальной линии).
Однако f(x) = sin(x) также является нечетной функцией, но она не является взаимно однозначной (она не проходит тест горизонтальной линии, если только мы не ограничим ее область определения одним периодом или меньше).
Это синусоидальная функция, которая является нечетной, но не однозначной.Может ли нечетная функция иметь обратную?
Нечетная функция может иметь обратную, если она взаимно однозначна.
Всегда ли сумма двух нечетных функций является нечетной функцией?
Сумма двух нечетных функций всегда является нечетной функцией. Мы можем доказать это в общем случае.
Допустим, у нас есть две нечетные функции, f(x) и g(x).
По определению нечетной функции:
- f(-x) = -f(x)
- g(-x) = -g(x)
Пусть их сумма есть функция h (х) = f(х) + g(х).
 Чтобы доказать, что h(x) нечетно, нам нужно показать, что h(-x) = -h(x):
Чтобы доказать, что h(x) нечетно, нам нужно показать, что h(-x) = -h(x):- h(-x) = f(-x) + g(-x) [определение из h(x) с подставленным –x]
- h(-x) = -f(x) + g(-x) [поскольку f(-x) = -f(x)]
- h(-x) = -f(x) – g(x) [поскольку g(-x) = -g(x)]
- h(-x) = -(f( x) + g(x)) [вынести a -1]
- h(-x) = -h(x) [поскольку h(x) = f(x) + g(x)]
Таким образом, сумма двух нечетных функций также является нечетной функцией.
Вы можете сложить 3, 4 или столько нечетных функций, сколько захотите, и результирующая функция будет нечетной.
Может ли нечетная функция иметь точку перегиба?
Нечетная функция может иметь точку перегиба. Однако не все нечетные функции имеют точку перегиба.
Рассмотрим нечетную функцию f(x) = x 3 .
Первая производная равна f’(x) = 3x 2 .

Вторая производная равна f’’(x) = 6x.
Вторая производная равна нулю, когда f»(x) = 0, или:
- 6x = 0
- x = 0
Для x > 0, f»(x) положительно (например, f»(1) = 6 > 0).
При x < 0 значение f’’(x) отрицательное (например, f’’(-1) = -6 < 0).
Итак, знак f’’(x) меняется с отрицательного на положительный при x = 0,
Так как вторая производная f(x) меняет знак при x = 0, то x = 0 является точкой перегиба на графике этой функции.
Кубическая функция f(x) = x 3 имеет точку перегиба при x = 0, где ее вторая производная (равная 6x) меняет знак.С другой стороны, функция f(x) = x не имеет точки перегиба, так как вторая производная всегда равна нулю (f’(x) = 1 и f”(x) = 0).
Проходят ли нечетные функции через источник?
Некоторые нечетные функции проходят через начало координат (например, нечетные полиномиальные функции, которые всегда имеют нулевой постоянный член).
 Однако не все нечетные функции проходят через начало координат.
Однако не все нечетные функции проходят через начало координат.Например, рассмотрим функцию y = 1/x. Это нечетно, так как f(-x) = 1/-x = -(1/x) = -f(x) для каждого x в области (x = 0 исключается, так как у нас не может быть нулевых знаменателей).
Однако эта функция не проходит через источник.
Обратная функция y = 1/x нечетна, но не проходит через начало координат (ее область определения — ненулевые действительные числа).Если нечетная функция имеет в своей области определения ноль, то она должна пройти через начало координат. Причина в том, что по определению нечетной функции f(-x) = -f(x) для всех x в области.
Так как x = 0 находится в домене, мы имеем f(-0) = -f(0), что означает f(0) = -f(0), или 2f(0) = 0, и, таким образом, f( 0) = 0 (это представляет начало координат).
Заключение
Теперь вы знаете, что такое странные функции и как они выглядят. Вы также знаете ответы на некоторые распространенные вопросы о нечетных функциях.
Вы также можете прочитать мою статью о четных функциях.

Все о суммах и произведениях четных и нечетных функций вы можете узнать из моей статьи здесь.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
~Джонатон
Определение, примеры, различия и список
Если бы кто-то указал и закричал: «Эй, смотрите, странная функция!» вы, вероятно, подумали бы, что они видели график странной формы. На самом деле нечетные функции имеют симметричные графики, и слово «нечетный» используется в его математическом контексте, а не для обозначения «чего-то странного».
Можно было бы также предположить, что нечетные функции являются полной противоположностью четных функций, и положить этому конец. Это предположение было бы ужасно неверным. Разницу между нечетными и четными функциями нельзя просто классифицировать, думая, что если нечетная, то она должна быть нечетной.

По мере углубления в тему нечетных функций мы увидим, какую формулу используют нечетные функции, а также как это связано с симметрией таких функций.
Что такое нечетные функции? 9{\circ}\) вокруг начала координат, \((0,0)\), на наборе осей результирующий график выглядит идентично исходному.
Формальное определение нечетной функции выглядит следующим образом:
нечетная функция — это функция, для которой \(f(-x)=-f(x)\) для всех значений домен \(f\).
Это означает, что для каждого значения \(x\) в области определения нечетной функции \(f(x)\) значение функции \(f(-x)\) совпадает со значением \( -f(x)\).
Это также может быть показано графически и обсуждается более подробно в следующих разделах. 9{\circ}\) относительно начала координат, результат будет выглядеть так же, как исходный график. Таким образом, мы можем видеть, что эта функция симметрична относительно начала координат.
Разница между четными и нечетными функциями
Прежде чем приступить к изучению этого раздела, рекомендуется сначала изучить тему «Четные функции»!
Основное различие между четными и нечетными функциями заключается в их осях симметрии.
 Нечетные функции, как известно, симметричны относительно начала координат . Четные функции, с другой стороны, 9{2}\) — StudySmarter Originals
Нечетные функции, как известно, симметричны относительно начала координат . Четные функции, с другой стороны, 9{2}\) — StudySmarter OriginalsВ следующей таблице приведены два основных различия между нечетными и четными функциями. = -f(x)\) для всех значений \(x\) в области определения \(f(x)\)
\(f(-x) = f(x)\) для всех значений \ (x\) в области \(f(x)\) График нечетной функции симметричен относительно начала координат График четной функции симметричен относительно оси Y Как определить, является ли функция нечетной
Мы можем использовать различия, упомянутые в предыдущем разделе, чтобы определить графически или алгебраически, является ли функция нечетной .
Алгебраическое определение четности или нечетности функции
Чтобы определить четность функции с помощью алгебраических методов, достаточно применить формулу \(f(-x) = -f(x)\) и посмотреть, является ли она Справедливо.
 9{3} — 12x\end{split}\end{equation}\]
9{3} — 12x\end{split}\end{equation}\]\(f(-x) = -f(x)\) для всех значений \(x\) в области определения \(f (x)\), поэтому мы можем заключить, что \(f(x)\) — нечетная функция.
Графическое определение нечетности функции
Самый простой способ определить нечетность функции — использовать ее график. Графики предоставляют нам лучший способ визуализации функций, а также полезны для их интерпретации.
В следующем примере показано, как графически определить, является ли функция нечетной: 9{-3},\) и т. д. — все нечетные функции. Для этих функций \(f(-x) = -f(x)\) для всех значений \(x\). То есть, если вы подставите \(-x\) в каждую из этих функций и упростите, то результирующий ответ будет таким же, как умножение каждой из этих функций на \(-1\).
Другая группа функций, которые часто дают нечетные функции, — это тригонометрические функции. Например, рассмотрим \(y = sin(x)\).
Имеем \(f(-x) = sin(-x)\) и \(-f(x) = -sin(x)\). Мы знаем из тригонометрии, что \(sin(-x)\) то же самое, что сказать \(-sin(x)\) и поэтому \(f(-x)\) равно \(-f(x)\) для всех значений \(х\) в области определения функции.
 Таким образом, \(y = sin(x)\) — нечетная функция.
Таким образом, \(y = sin(x)\) — нечетная функция.Если мы посмотрим на график для \(y=sin(x)\), мы также увидим, насколько он симметричен относительно начала координат:
График \(y = sin(x)\) — StudySmarter Originals
К другим нечетным тригонометрическим функциям относятся \(tan(x), cot(x)\) и \(cosec(x)\). Все они удовлетворяют определению нечетной функции.
Нечетные функции также могут быть дробями. Рассмотрим следующий пример:
Вам задана функция \(g(x) = \frac{cos(x)}{x}\). Определите, является ли функция нечетной функцией, используя алгебраические методы.
Решение
Шаг 1: Определить \(g(-x)\).
\[\begin{equation}\begin{split}g(-x) & = \frac{cos(-x)}{-x} \\& = \frac{cos(x)}{-x} \\& = — \frac{cos(x)}{x}\end{split}\end{equation}\]
Шаг 2: Определить \(-g(x)\).
\[-g(x) = — \frac{cos(x)}{x}\]
Шаг 3: Является ли \(g(x)\) нечетной функцией?
Да.
 \(g(-x) = -g(x)\) для всех значений \(x\) в области определения функции, поэтому \(g(x)\) является нечетной функцией. 9{\circ}\) вокруг исходной точки, результирующий график будет выглядеть так же, как и исходный.
\(g(-x) = -g(x)\) для всех значений \(x\) в области определения функции, поэтому \(g(x)\) является нечетной функцией. 9{\circ}\) вокруг исходной точки, результирующий график будет выглядеть так же, как и исходный.- Можно определить, является ли функция нечетной, используя алгебраические или графические методы.
- Функция может быть ни четной, ни нечетной.
- Тригонометрические функции также могут быть нечетными функциями.
Четные и нечетные функции — Википедия, бесплатная энциклопедия
Из Википедии, бесплатная энциклопедия
Перейти к: навигация, поиск
По математике, четные функции и нечетные функции являются функциями, которые удовлетворяют определенным соотношениям симметрии относительно аддитивных инверсий. Они важны во многих областях математического анализа, особенно в теории степенных рядов и рядов Фурье.
Содержимое
- 1 Функции четности
- 2 Нечетные функции
- 3 Некоторые факты
- 3.
 1 Основные свойства
1 Основные свойства - 3.2 Серия
- 3.3 Алгебраическая структура
- 3.4 Гармоники
- 3.
- 4 Каталожные номера
- 5 См. также
[править]
Чётные функции
f(x) = x 2 , пример четной функции
Пусть f ( x ) будет вещественной функцией действительной переменной. Тогда f равно даже , если для всех действительных 9 выполняется следующее уравнение0719 x :
- f ( − x ) = f ( x )
Общая функция для получения четной составляющей функции:
Геометрически четная функция симметрична относительно оси y , а это означает, что ее график остается неизменным после отражения относительно оси y .
Примеры четных функций: | х |, х 2 , x 4 , cos( x ) и cosh( x ).

Даже функции не могут быть взаимно однозначными картами.
[править]
Дополнительные функции
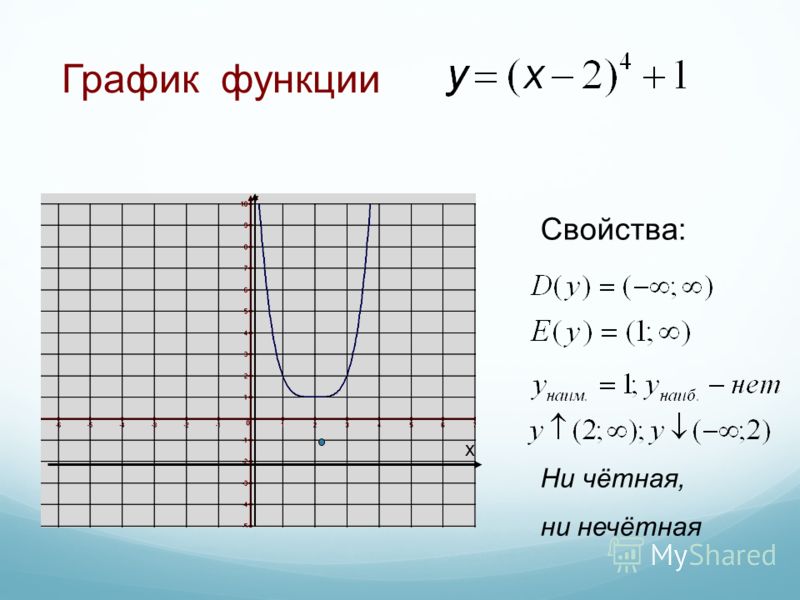
f(x) = x, пример нечетной функции
Опять же, пусть f ( x ) будет вещественной функцией вещественной переменной. Тогда f равно нечетному , если для всех действительных x выполняется следующее уравнение:
- f ( − х ) = — f ( х )
Общая функция для получения нечетного компонента функции:
Геометрически нечетная функция симметрична относительно начала координат, что означает, что ее график остается неизменным после поворота на 180 градусов вокруг начала координат.
Примеры нечетных функций: x , x 3 , sin( x ) и sin( x ).
[править]
Некоторые факты
Примечание: нечетность или четность функции не означает ни дифференцируемость, ни даже непрерывность.
 Свойства, включающие ряды Фурье, ряды Тейлора, производные и т. д., могут использоваться только тогда, когда можно предположить, что они существуют. Основные свойствах ).
Свойства, включающие ряды Фурье, ряды Тейлора, производные и т. д., могут использоваться только тогда, когда можно предположить, что они существуют. Основные свойствах ).- В общем случае сумма четной и нечетной функций не является ни четной, ни нечетной; например х + х 2 .
- Сумма двух четных функций четна, и любая константа, кратная четной функции, четна.
- Сумма двух нечетных функций нечетна, и любое постоянное кратное нечетной функции является нечетным.
- Произведение двух четных функций является четной функцией.
- Произведение двух нечетных функций снова является четной функцией.
- Произведение четной функции на нечетную является нечетной функцией.
- Частное двух четных функций является четной функцией.
- Частное двух нечетных функций является четной функцией.
- Частное четной функции и нечетной функции является нечетной функцией.
- Производная четной функции нечетна.

- Производная нечетной функции четна.
[править]
Серия
- Ряд Тейлора четной функции включает только четные степени.
- Ряд Тейлора нечетной функции включает только нечетные степени.
- Ряд Фурье периодической четной функции включает только косинусоидальные члены.
- Ряд Фурье периодической нечетной функции включает только члены по синусоиде.
[править]
Алгебраическая структура
- Любая линейная комбинация четных функций четна, а четные функции образуют векторное пространство над вещественными числами. Точно так же любая линейная комбинация нечетных функций является нечетной, и нечетные функции также образуют векторное пространство над действительными числами. Фактически, векторное пространство всех вещественных функций есть прямая сумма подпространств четных и нечетных функций. Другими словами, каждую функцию можно однозначно записать как сумму четной и нечетной функций:
- Четные функции образуют коммутативную алгебру над вещественными числами.


 {\displaystyle f(-x)=f(x),\quad \forall x\in X.}
{\displaystyle f(-x)=f(x),\quad \forall x\in X.} {2k+1},} где k∈Z{\displaystyle k\in \mathbb {Z} } — произвольное целое число.
{2k+1},} где k∈Z{\displaystyle k\in \mathbb {Z} } — произвольное целое число.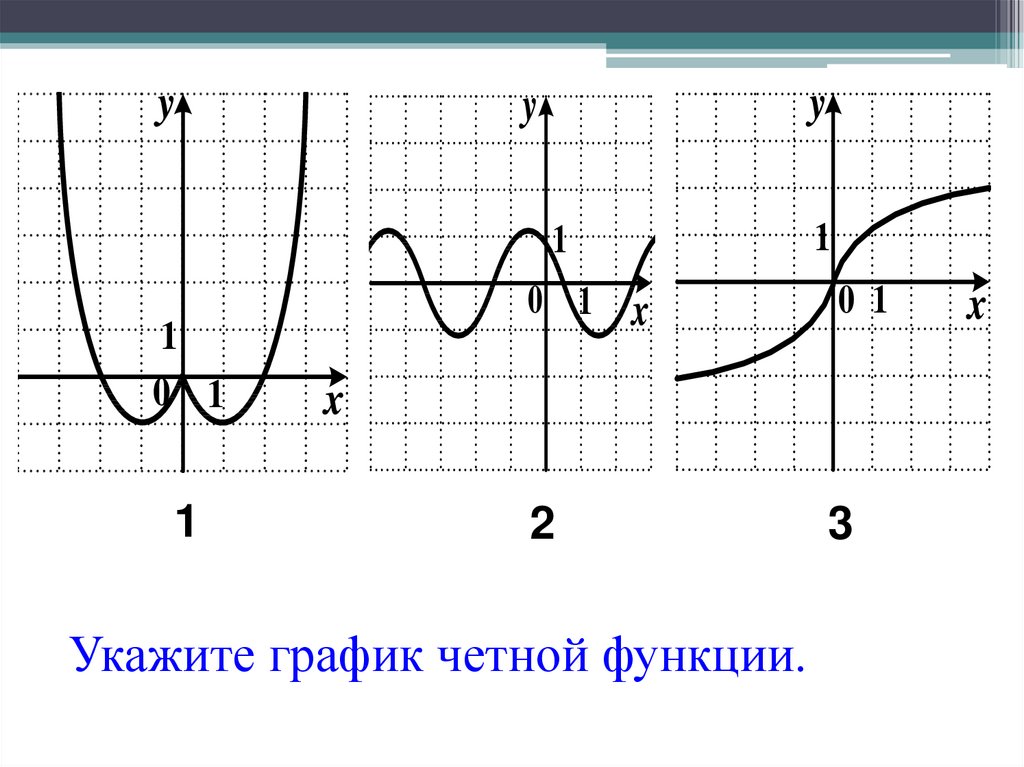 {2}}}\right)} при b=0.
{2}}}\right)} при b=0.




 Однако не всякая нечетная функция является взаимно однозначной.
Однако не всякая нечетная функция является взаимно однозначной.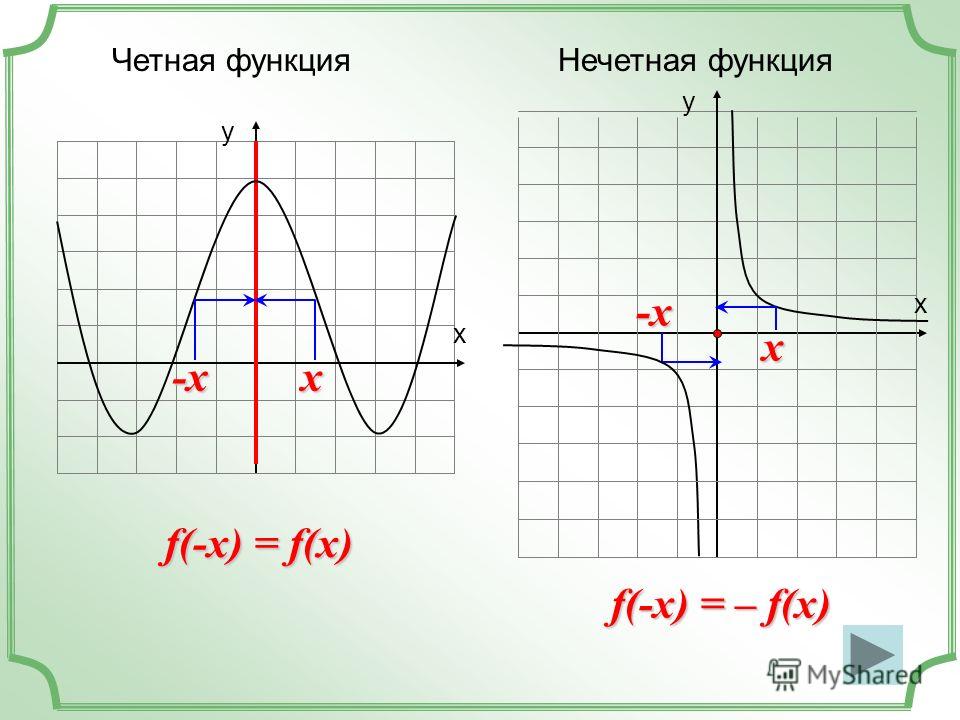 Чтобы доказать, что h(x) нечетно, нам нужно показать, что h(-x) = -h(x):
Чтобы доказать, что h(x) нечетно, нам нужно показать, что h(-x) = -h(x):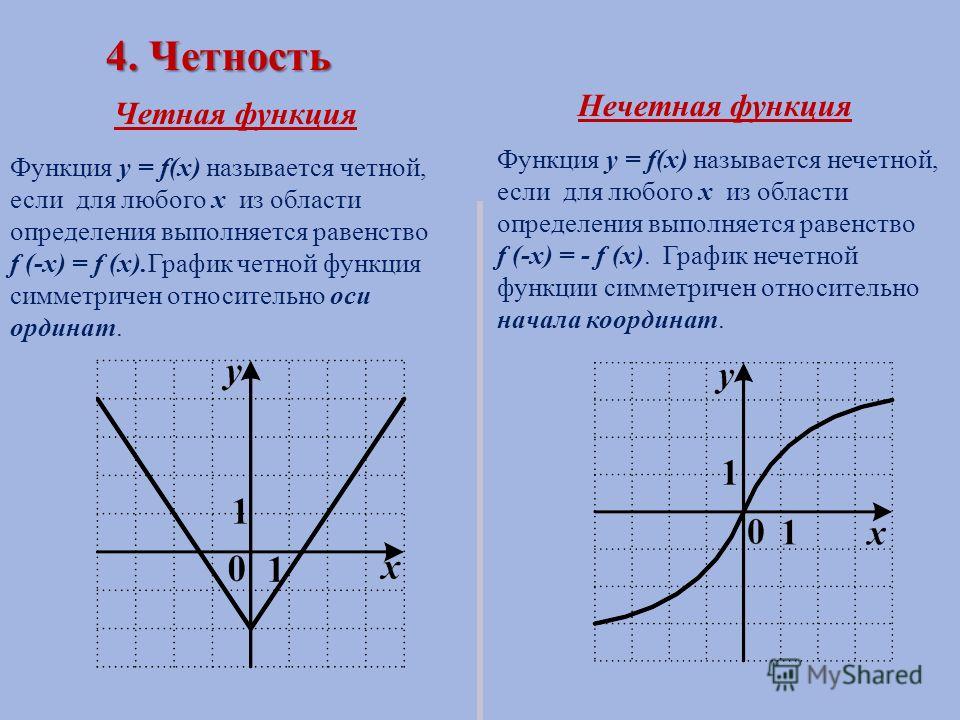
 Однако не все нечетные функции проходят через начало координат.
Однако не все нечетные функции проходят через начало координат.

 Нечетные функции, как известно, симметричны относительно начала координат . Четные функции, с другой стороны, 9{2}\) — StudySmarter Originals
Нечетные функции, как известно, симметричны относительно начала координат . Четные функции, с другой стороны, 9{2}\) — StudySmarter Originals 9{3} — 12x\end{split}\end{equation}\]
9{3} — 12x\end{split}\end{equation}\]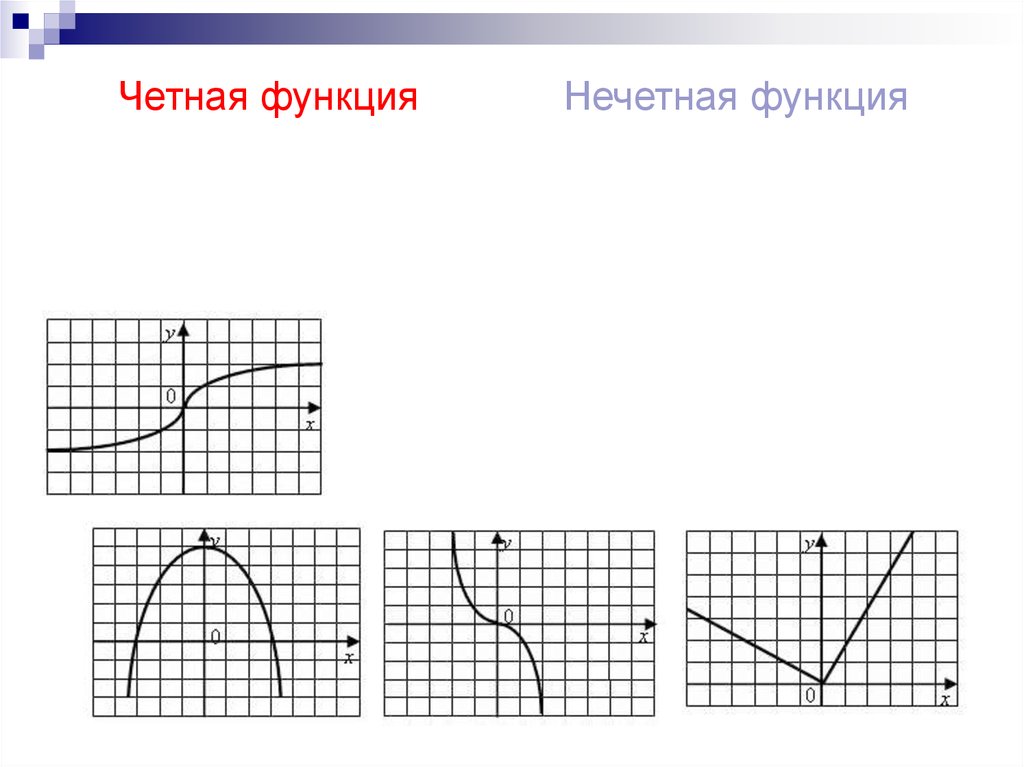 Таким образом, \(y = sin(x)\) — нечетная функция.
Таким образом, \(y = sin(x)\) — нечетная функция.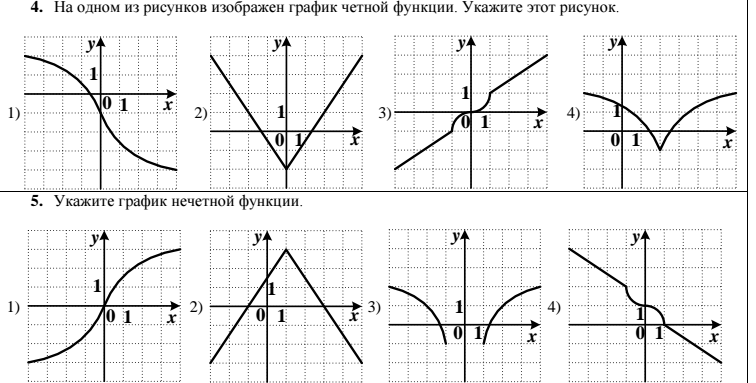 \(g(-x) = -g(x)\) для всех значений \(x\) в области определения функции, поэтому \(g(x)\) является нечетной функцией. 9{\circ}\) вокруг исходной точки, результирующий график будет выглядеть так же, как и исходный.
\(g(-x) = -g(x)\) для всех значений \(x\) в области определения функции, поэтому \(g(x)\) является нечетной функцией. 9{\circ}\) вокруг исходной точки, результирующий график будет выглядеть так же, как и исходный. 1 Основные свойства
1 Основные свойства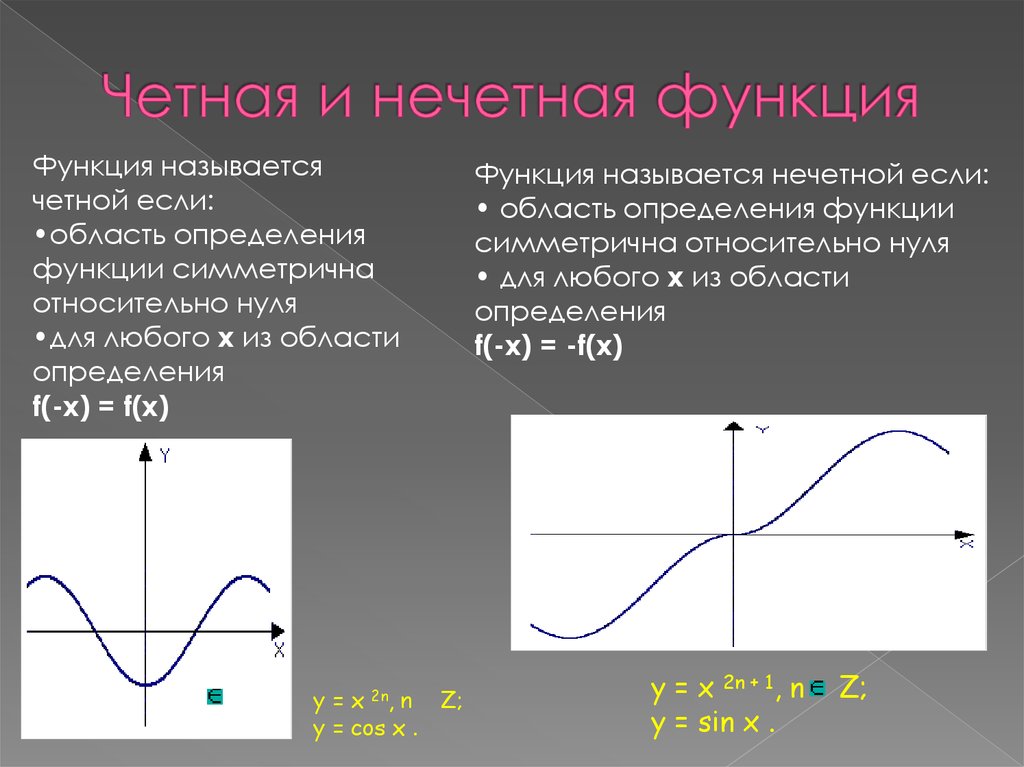
 Свойства, включающие ряды Фурье, ряды Тейлора, производные и т. д., могут использоваться только тогда, когда можно предположить, что они существуют. Основные свойствах ).
Свойства, включающие ряды Фурье, ряды Тейлора, производные и т. д., могут использоваться только тогда, когда можно предположить, что они существуют. Основные свойствах ).