Коллинеарность векторов. Онлайн калькулятор.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор проверит являются два вектора коллинеарными (параллельными) и даст подробное решение.
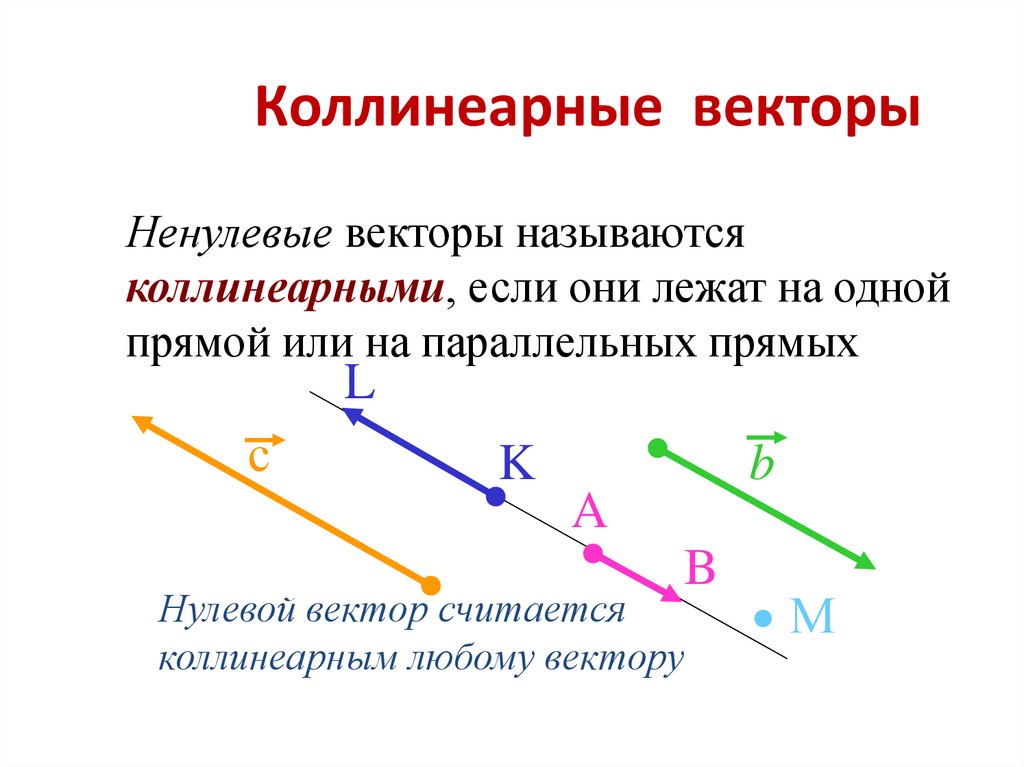
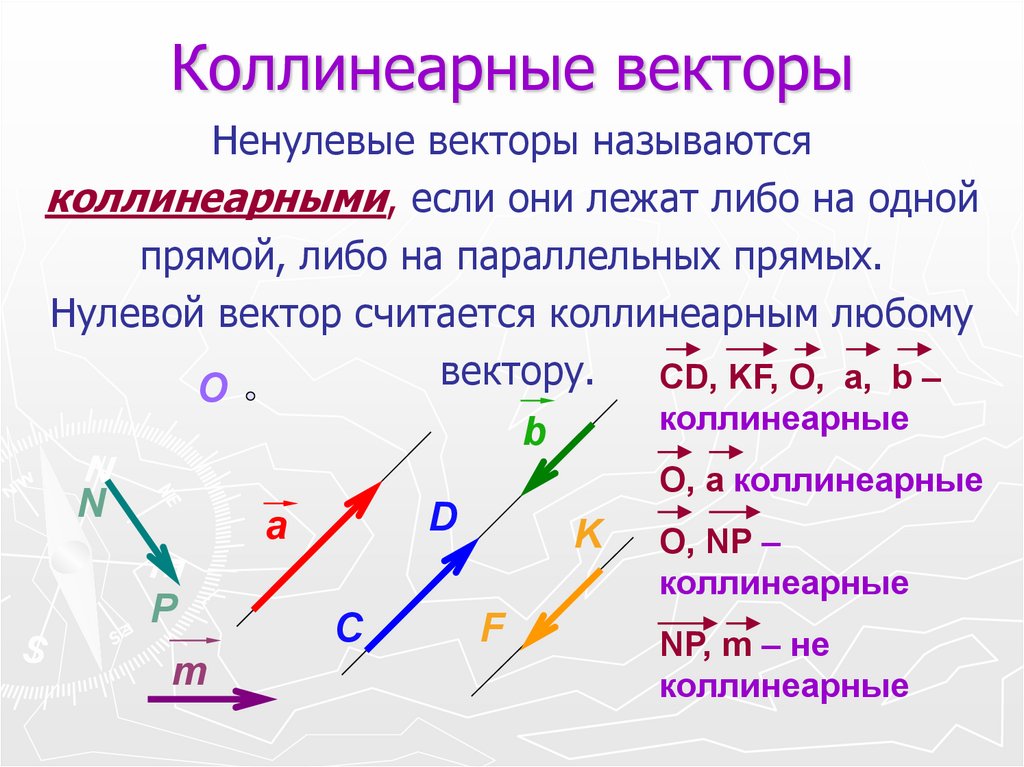
Коллинеарность векторов — это отношение параллельности векторов, так два ненулевых вектора являются коллинеарными (параллельными), если они лежат на параллельных прямых или на одной прямой.
Укажите размерность пространства 23
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора
Задайте координаты первого вектора
a̅ =
{
;
}
Задайте координаты второго вектора
b̅ =
{
;
}
Как проверить являются ли два вектора коллинеарными (параллельными)
Если два ненулевых вектора a и b лежат на одной прямой или на параллельных прямых, то такие векторы называются – коллинеарными.
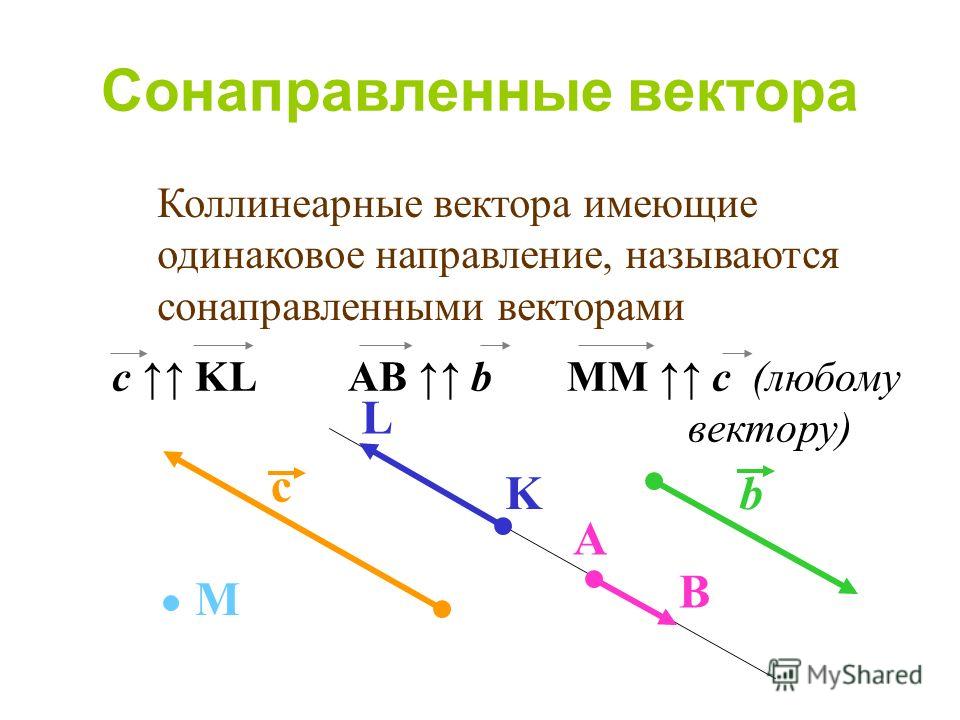
Сонаправленные векторы – одинаково направленные коллинеарные векторы.
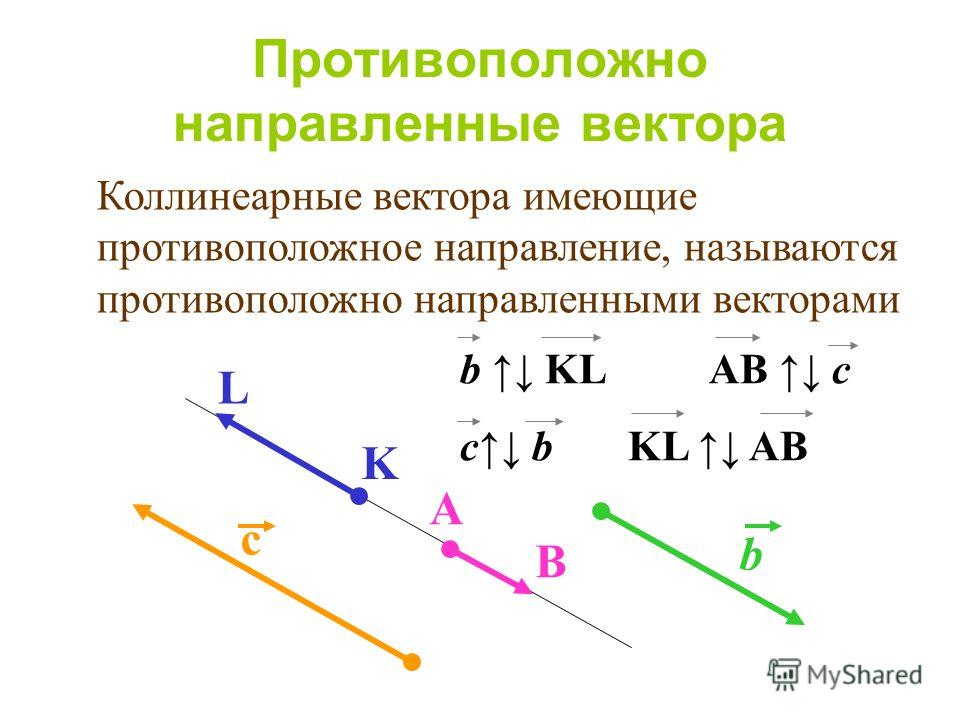
Антиколлинеарные векторы – противоположено направленные коллинеарные векторы.
Коллинеарные векторы обозначаются как: a||b.
Определить что векторы a = {ax; ay; az} и b = {bx; by; bz} являются коллинеарными можно если вычислить их векторное произведение. Если векторное произведение векторов равно нулю, то векторы коллинеарны.
Например, найдем векторное произведение векторов a и b
a = {2; 2; 10} b = {1; 1; 5}
Решение
N̅ = [a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axby — k̅ aybx = ax ay bx by
i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (ax
ax = 2
ay = 2
az = 10
bx = 1
by = 1
bz = 5
N̅ = [a × b] = i̅ (2 ⋅ 5 — 1 ⋅ 10) — j̅ (2 ⋅ 5 — 1 ⋅ 10) + k̅ (2 ⋅ 1 — 1 ⋅ 2) = i̅ (10 — 10) — j̅ (10 — 10) + k̅ (2 — 2) = 0i̅ +0j̅ +0k̅
N̅ = [a × b] = 0i̅ +0j̅ +0k̅
N̅ = {0 ; 0 ; 0}
Векторное произведение векторов равно нулю, следовательно, векторы a и b коллинеарны.
Так как векторное произведение векторов находится при помощи определителя квадратной матрицы, то для векторов a = {ax; ay} и b = {bx; by} определить являются ли векторы коллинеарными можно если координаты векторов связаны отношением:
a = {ax; ay}
b = {bx; by}
q – коэффициент пропорциональности Условие коллинеарности векторов
a = {ax; ay; az}
b = {bx; by; bz}
q – коэффициент пропорциональности
Если коэффициент пропорциональности q > 0, то векторы a и b сонаправленны.
Если коэффициент пропорциональности q a и b антиколлинеарные, т. е. противоположно направлены.
е. противоположно направлены.
Чтобы проверить выполняется ли равенство необходимо составить систему уравнений и вычислить коэффициент пропорциональности q в каждом уравнении:
a = {ax; ay;}b = {bx; by;}
q – коэффициент пропорциональности
Если в первом и во втором уравнении коэффициенты пропорциональности q равны, то координаты векторов пропорциональны и векторы коллинеарны.
a = {ax; ay; az}b = {bx; by; bz}
q – коэффициент пропорциональности
Если в первом, втором и в третьем уравнении коэффициенты пропорциональности q равны, то координаты векторов пропорциональны и векторы коллинеарны.
Пример 1. Определим, являются ли два вектора плоскости коллинеарными (параллельными). Координаты обоих векторов заданны точками.
Определим, являются ли два вектора плоскости коллинеарными (параллельными). Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay} = {-2 — 5 ; 11 — 9} = {-7 ; 2}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy} = {-3 — 0 ; 1 — 12} = {-3 ; -11}
Проверим, есть ли для векторов AB и CD коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ABx = q ⋅ CDx
AB y = q ⋅ CDy
| -7 = q ⋅ (-3) тогда, q = — | 7 |
| -3 |
| 2 = q ⋅ (-11) тогда, q = | 2 |
| -11 |
| = — | 2 |
| 11 |
| ≠ — | 2 |
| 11 |
| В первом уравнении коэффициент пропорциональности равен | 7 |
| 3 |
| , во втором — | 2 |
| 11 |
Следовательно, система несовместима и не имеет решений. Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD |
Пример 2. Определим, являются ли два вектора плоскости коллинеарными (параллельными).
Координаты вектора a: (2 ; 6)
Координаты вектора b: (7 ; 21)
Проверим, есть ли для векторов a и b коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ax = q ⋅ bx
ay = q ⋅ by
| 2 = q ⋅ 7 тогда, q = | 2 |
| 7 |
| 6 = q ⋅ 21 тогда, q = | 6 |
| 21 |
| В первом уравнении коэффициент пропорциональности равен | 2 |
| 7 |
| , во втором | 2 |
| 7 |
Коэффициент пропорциональности в каждом уравнении имеет одно и тоже значение, следовательно координаты векторов a и b пропорциональны и следовательно векторы коллинеарны. Значение коэффициента пропорциональности больше нуля, значит векторы a и b сонаправлены. Значение коэффициента пропорциональности больше нуля, значит векторы a и b сонаправлены. |
Пример 3. Определим, являются ли два вектора пространства коллинеарными (параллельными). Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay; Bz — Az} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; 1/5 ; -275/4}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy; Dz — Cz} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}
Проверим, есть ли для векторов AB и CD коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ABx = q ⋅ CDx
ABy = q ⋅ CDy
ABz = q ⋅ CDz
| -8 = q ⋅ 7 тогда, q = — | 8 |
| 7 |
| 1/5 = q ⋅ 6 тогда, q = | 1/5 |
| 6 |
| -275/4 = q ⋅ 7 тогда, q = — | 275/4 |
| 7 |
| = — | 275 |
| 28 |
| ≠ — | 275 |
| 28 |
| В первом уравнении коэффициент пропорциональности равен — | 8 |
| 7 |
| , во втором | 1 |
| 30 |
| и в третьем — | 275 |
| 28 |
Следовательно, система несовместима и не имеет решений. Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD не коллинеарны. Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD не коллинеарны. |
Пример 4. Определим, являются ли два вектора пространства коллинеарными (параллельными).
Координаты вектора a: (0 ; 1 ; 7)
Координаты вектора b: (2 ; 0 ; 6)
Проверим, есть ли для векторов a и b коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ax = q ⋅ bx
ay = q ⋅ by
az = q ⋅ bz
| 0 = q ⋅ 2 тогда, q = | 0 |
| 2 |
| 1 = q ⋅ 0 | |
| 7 = q ⋅ 0 | |
| Сделаем проверку, подставим значение коэффициента в уравнения | ||
Следовательно, система несовместима и не имеет решений. Координаты векторов a и b не пропорциональны, значит векторы a и b не коллинеарны. Координаты векторов a и b не пропорциональны, значит векторы a и b не коллинеарны. |
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Условие коллинеарности векторов — онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Коллинеарность ненулевых векторов выполняется, если они лежат на одной прямой или параллельны одной прямой. Нулевой вектор коллинеарен любому другому.
Нулевой вектор коллинеарен любому другому.
Наш сервис используют студенты и школьники для решения задач по алгебре, геометрии. С помощью онлайн-калькулятора можно быстро узнать, коллинеарны ли векторы, свериться с собственными вычислениями или изучить предложенный алгоритм. Вы получаете ответ бесплатно, без отвлечения на регистрацию. Количество проверок не ограничено.
Вариант 1 с представление векторов координатами
- Обозначьте размерность векторов. Меняйте число кнопками «+», «-»
- Выберите форму представления векторов. Далее рассмотрим пример для варианта с координатами.
- Введите значение вектора в соответствующие поля и нажмите кнопку «Рассчитать».
- Получаем решение и ответ
Вариант 2 с представлением векторов точками.
- После выбора размерности как в варианте 1 меняем форму представления векторов с координат на точки
- Получаем
- Вводим данные в соответствующие поля
- Отправляем задание на вычисления кнопкой «Рассчитать»
- Получаем подробное решение и ответ
Материалы, которые помогут вам лучше разобраться в теме:
- Векторы на плоскости и в пространстве — основные определения
- Координаты вектора в декартовой системе координат (ДСК)
- Нахождение длины вектора, примеры и решения
- Нахождение координат вектора через координаты точек
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Длина вектора. Модуль вектора
- Векторное произведение векторов
- Умножение вектора на число
- Угол между векторами
- Смешанное произведение векторов
- Сложение и вычитание двух векторов
- Скалярное произведение векторов
- Определение вектора по двум точкам
- Разложение вектора по базису
- Проверить являются ли вектора базисом
- Ортогональность векторов
- Компланарность векторов
- Проекция вектора на вектор
- Площадь треугольника, построенного на векторах
- Площадь параллелограмма, построенного на векторах
Проверка условий коллинеарности векторов
Выполнение любого из условий свидетельствует о коллинеарности двух векторов:
- Существует число n, при подстановке которого равенство α⇀=n·b⇀верно.

- Равны отношения координат векторов. При этом компоненты векторов отличны от нуля
- Признаком коллинеарности векторов для трехмерных задач является совпадение векторного произведения с нулевым вектором
Калькулятор разработан на основе формул, которые поочередно проверяют соответствие данных перечисленным критериям. Автоматический подсчет исключает ошибки, которые могут появиться при самостоятельном анализе задачи.
Чтобы определить коллинеарность векторов онлайн, достаточно ввести одну из форм представления векторов – координатами или точками – и дождаться решения. Пошаговые вычисления помогут разобраться в теме на примере реального задания. Так легко выполнять подготовку к занятиям, осваивать непонятный материал.
Часто в процессе обучения встречаются объемные примеры, которые требуют применения нескольких теорем. В разделе с векторами вы найдете другие калькуляторы. Их последовательное использование поможет получить верный ответ.
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Процент
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
Коллинеарность векторов, условия коллинеарности векторов.
Навигация по странице:
- Определение коллинеарности векторов
- Условия коллинеарности векторов
- Примеры задач на коллинеарность векторов
- плоские задачи
- пространственные задачи
Смотрите также онлайн калькулятор для проверки коллинеарности векторов.
Онлайн упражнения на тему коллинеарность векторов на плоскости.
Онлайн упражнения на тему коллинеарность векторов в пространстве.
Определение.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Найдем их векторное произведение
| a × b = | i | j | k | = i (aybz — azby) — j (axbz — azbx) + k (axby — aybx) = |
| ax | ay | az | ||
| bx | by | bz |
= i (aynaz — aznay) — j (axnaz — aznax) + k (axnay — aynax) = 0i + 0j + 0k = 0
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}
Так как b = na, то вектора a и b коллинеарны.
Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | .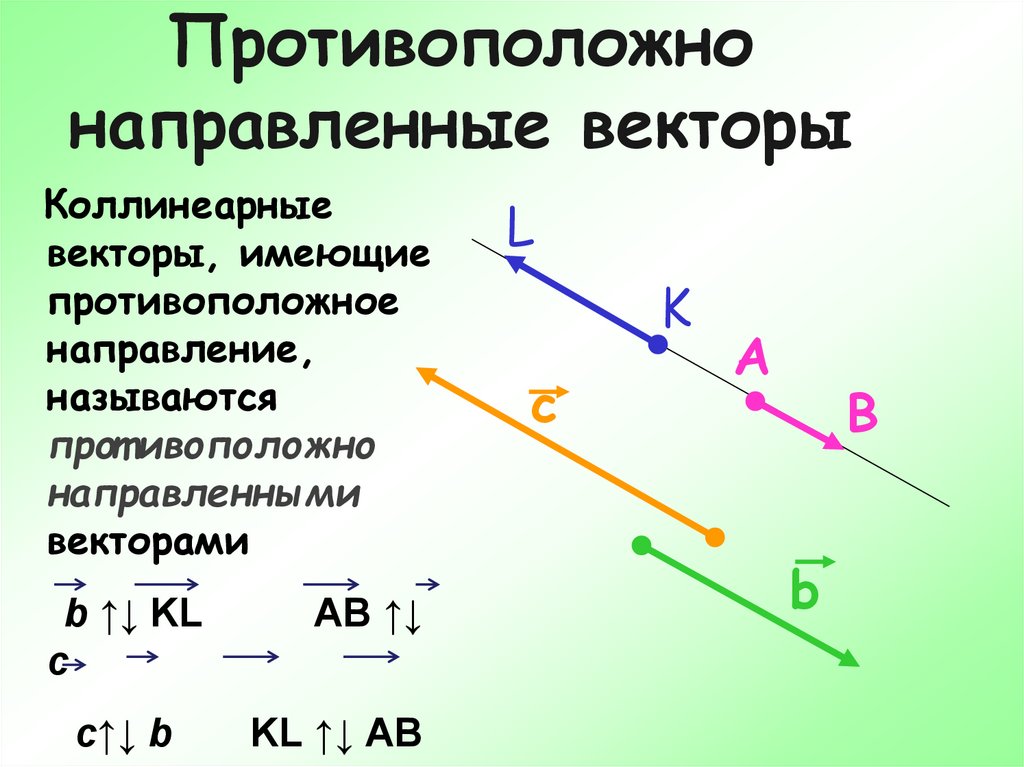 |
| bx | by |
Значит:
| 3 | = | 2 | . |
| 9 | n |
Решим это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
Вектора a и b коллинеарны т. к. к. | 1 | = | 2 | = | 3 | . |
| 4 | 8 | 12 |
| Вектора a и с не коллинеарны т.к. | 1 | = | 2 | ≠ | 3 | . |
| 5 | 10 | 12 |
| Вектора с и b не коллинеарны т.к. | 5 | = | 10 | ≠ | 12 | . |
| 4 | 8 | 12 |
Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Так как b = na, то вектора a и b коллинеарны.
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Калькулятор проверки векторной коллинеарности
| 0 | ||||
| АС | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Коллинеарность векторов — это отношение параллелизма векторов, поэтому два ненулевых вектора коллинеарны (параллельны), если они лежат на параллельных прямых или на одной прямой.
Размер помещения 23
Укажите форму первого вектора Координаты начальной и конечной точек первого вектораКоординаты первого вектора
Укажите форму второго вектора Координаты начальной и конечной точек второго вектораКоординаты второго вектора
Введите координаты первого вектора
а̅ =
{
;
}
Введите координаты второго вектора
б̅ =
{
;
}
Как проверить, являются ли два вектора коллинеарными (параллельными)
Пример #1
Определить, являются ли два вектора, расположенные в двумерном пространстве, коллинеарными (параллельными). Координаты обоих векторов заданы точками.
Координаты точки А вектора АВ: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)
Пошаговое решение:
Вычислить координаты первого вектора из двух точек A и B:
AB = {x B — x A ; y B — y A } = {-2 — 5; 11 — 9} = {-7; 2}
Рассчитать координаты второго вектора по двум точкам C и D:
CD = {x D — х С ; y D — y C } = {-3 — 0; 1-12} = {-3; -11}
Проверим, являются ли векторы AB и CD
иметь коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений системы), для этого составим систему уравнений и проверим, выполняется ли равенство у = q ⋅ CD у
| -7 = q ⋅ (-3) тогда, q = — | 7 |
| -3 |
| 2 = q ⋅ (-11) then, q = | 2 |
| -11 |
| = — | 2 |
| 11 |
| ≠ — | 2 |
| 11 |
| В первом уравнении коэффициент пропорциональности равен | 7 |
| 3 |
| , во втором — | 2 |
| 11 |
Следовательно, система несовместна и не имеет решений. Координаты векторов AB и CD
непропорциональны, а это означает, что векторы AB и CD
не коллинеарны. Координаты векторов AB и CD
непропорциональны, а это означает, что векторы AB и CD
не коллинеарны. |
Пример #2
Определить, являются ли два вектора, расположенные в двумерном пространстве, коллинеарными (параллельными).
Координаты вектора a: (2; 6)
Координаты вектора b: (7 ; 21)
Пошаговое решение:
Проверим, имеют ли векторы a и b коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений системы), для этого составим систему уравнений и проверим, выполняется ли равенство
a x = q ⋅ b x
a y = q ⋅ b y
| 2 = q ⋅ 7 then, q = | 2 |
| 7 |
| 6 = q ⋅ 21 then, q = | 6 |
| 21 |
| В первом уравнении коэффициент пропорциональности составляет | 2 |
| 7 |
| , во втором | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. 0007 0007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коэффициент пропорциональности в каждом уравнении имеет одинаковое значение, поэтому координаты векторов a и b пропорциональны, поэтому векторы коллинеарны. Значение коэффициента пропорциональности больше нуля, значит, векторы a и b являются соруководителями. |
Пример №3
Определить, являются ли два вектора в трехмерном пространстве коллинеарными (параллельными). Координаты обоих векторов заданы точками.
Координаты точки А вектора АВ: (7; 0,2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
Пошаговое решение:
Вычислить координаты первого вектора из двух точек A и B:
AB = {x B — х А ; у Б — у А ; z B — z А } = {-1 — 7; 0-0,2; 2/8 — 69} = {-8; 1/5 ; -275/4}
Вычислить координаты второго вектора по двум точкам C и D:
CD = {x D — x C ; у Д — у С ; z D — z C } = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7; 6; 7}
Проверим, имеют ли векторы AB и CD коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений системы), для этого составим систему уравнений и проверим, выполняется ли равенство
AB x = Q ⋅ CD x
AB y = Q ⋅ CD y
AB Z = Q вно then, q = —
| 1/5 = q ⋅ 6 then, q = | 1/5 |
| 6 |
| -275/4 = q ⋅ 7 тогда q = — | 275/4 |
| 7 |
| = — | 275 |
| 28 |
| ≠ — | 275 |
| 28 |
| В первом уравнении коэффициент пропорциональности равен — | 8 |
| 7 |
| , во втором | 1 |
| 30 |
| и в третьем — | 275 |
| 28 |
| . |
Пример №4
Определить, являются ли два вектора векторов, расположенных в трехмерном пространстве, коллинеарными (параллельными).
Координаты вектора a: (0; 1; 7)
Координаты вектора b: (2 ; 0 ; 6)
Пошаговое решение:
Проверим, имеют ли векторы a и b коэффициент пропорциональности q (одинаковый для всех уравнений системы), для этого составим систему уравнений и проверим, выполняется ли равенство
| 0 = q ⋅ 2 then, q = | 0 |
| 2 |
| 1 = q ⋅ 0 | |
| 7 = q ⋅ 0 | |
| Проверим, подставим значение коэффициента в уравнения | ||
Следовательно, система несовместима и не имеет решений. Координаты векторов а и b не пропорциональны, значит, векторы а и b не лежат на одной прямой. Координаты векторов а и b не пропорциональны, значит, векторы а и b не лежат на одной прямой. |
| Следующие калькуляторы также могут оказаться полезными0004 | Калькулятор умножения матриц |
| Калькулятор транспонирования матриц | |
| Калькулятор детерминанта матрицы | |
| Калькулятор обратной матрицы | Длина сегмента линии a|
| Калькулятор векторных координат по двум точкам | |
| Калькулятор векторного модуля (длины) | |
| Калькулятор векторного сложения и вычитания | |
| Калькулятор векторного скалярного произведения. Используя длину векторов и косинус угла между векторами. | |
| Калькулятор векторного скалярного произведения. Используя векторные координаты. | |
| Калькулятор векторного произведения. Используя векторные координаты. | |
| Калькулятор векторного тройного произведения | |
| Калькулятор векторного умножения на число | |
| Калькулятор угла между векторами | |
| Vector Collinearity Check Calctulator | |
| Вектор калькулятор копланарности | |
| Combinatorics Calculators | |
| Перчатки N -Elements Calculator | 9|
Комбинации NELEMS на M. Calculator Calculator | |
| Комбинации NELEMS на M. Calculator | |
| Комбинации NELENTIONS | |
| . Калькулятор | |
| Калькулятор систем счисления | |
| Калькулятор римских чисел | |
| Римские цифры от 1 до 3999 | |
| Калькулятор систем счисления | |
| Двоичный калькулятор. Сложение, вычитание, умножение и деление двоичных чисел. | |
| Фракционные калькуляторы | |
| Упрощающий калькулятор фракций | |
| Неправильный с калькулятором смешанной фракции | |
| Смешанный фракция с неправомерным калькулятором | |
| FRUCTION FRUCHT0006 | |
| Возведение дроби в степень. Онлайн калькулятор. | |
| Десятичный калькулятор до фракции | |
| Фракция до десятичного калькулятора | |
| Сравнение фракций калькулятор | |
| Common Denminator Calculator | |
| Trigomometers Calculators | |
| Тригонометрические калькуляторы | |
| Trigomonters Calculators | |
111. | |
| Калькулятор тангенса | |
| Cotangent Calculator | |
| Secant Calculator | |
| Cosecant Calculator | |
| Arcsine Calculator | |
| Arccosine Calculator | |
| Arctangent Calculator | |
| Arccotangent Calculator | |
| Калькулятор арксеканса | |
| Калькулятор арккосеканса | |
| Калькуляторы (Теория чисел) | |
| Кальцентатор математических выражений | |
| Кальцентационные скобки | |
| Prime Factorization Calculator | |
| GCD и LCM Calculator с шагами | GCD и LCM Calculator с шагом |
| GCD и LCM -калькулятор LCM -Calculator. | Калькулятор Gcd и Lcm для любого количества чисел |
| Разбить число на его разрядное значение | |
Разделить число на отношение. Онлайн калькулятор с шагами Онлайн калькулятор с шагами | |
| Процентный калькулятор с шагами | |
| Научная нотация для десятичного преобразования калькулятор | |
| Научный преобразователь нотации | |
| Калькулятор по факту | |
| . С шагами | |
| Калькулятор остатка | |
| Корневой калькулятор | |
| Десятичный калькулятор периода | |
| Калькулятор большого числа | |
| Калькулятор закругления | . |
| Калькулятор площади квадрата | |
| Калькулятор площади прямоугольника | |
| Тренеры по математике | |
| Дополнение математического тренера | |
| Вычитание математического тренера | |
| Умножение математического тренера | |
| Дивизион Математика | |
| Онлайн-тренажер внимательности для дошкольников | |
Онлайн-тренажер по математике сложения, вычитания, умножения. Найдите правильный ответ. Найдите правильный ответ. | |
| Online Numeric Expression Trainer | |
| Converters | |
| Length Converter | |
| Speed Converter | |
| Acceleration Converter | |
| Physics Calculators | |
Mechanics | |
| Speed Time Калькулятор расстояния | |
| Калькулятор расстояния скорости ускорения | |
| Калькулятор времени перемещения | |
| Time Calculator | |
| Newton’s Second Law Calculator | |
| Gravitational Force Calculator | |
| Momentum Calculator | |
| Impulse Calculator | |
| Object Weight Calculator | |
Optics | |
| Калькулятор отражения и преломления света | |
Электричество и магнетизм | |
| Ом калькулятор закона ом | |
| Coulom’s Law Calculator | |
| Калькулятор поля электрического поля | |
| Point Electric Calculator Q | |
| Ука в калькуляторе | |
. Защита. Каллятор Защита. Каллятор | |
| . | |
| Калькулятор потенциальной энергии заряда | |
| Калькулятор потенциала электрического поля | |
| Калькулятор емкости проводника и сферы | |
Конденсаторы | |
| Калькулятор емкости плоскопараллельных, цилиндрических и сферических конденсаторов | |
| Калькулятор напряженности электрического поля в плоскопараллельных, цилиндрических и сферических конденсаторах | |
| Напряжение (разность потенциалов) плоскопараллельных, цилиндрических и сферических конденсаторов Калькулятор | |
| Калькулятор расстояния между пластинами в параллельном пластинчатом конденсаторе | |
| Калькулятор площади пластин в параллельном пластинчатом конденсаторе | |
| Калькулятор запасенной энергии в заряженном конденсаторе | |
| Калькулятор объемной плотности энергии параллельных пластинчатых, цилиндрических и сферических конденсаторов | |
| Астрономические калькуляторы | |
| Вес объекта на других планетах | |
| Гравитационное ускорение на планетах Солнечной системы и их спутниках | |
| Генераторы | |
| Генератор случайных чисел | |
| Генератор паролей |
Научиться считать с вектором 002
Подборка бесплатных математических ресурсов (калькуляторы, упражнения, игры, викторины, напоминания о курсах), обучающих методам векторного исчисления.
Векторы : Напоминание
Координаты вектора из двух точек
Пусть (O, `vec (i)`, `vec (j)`) система, A и B две точки, которые являются соответствующими координатами (`x_a`,`y_(a)`) и (`x_(b)` ,`y_(b)`) в
система (O,`vec(i)`,`vec(j)`) .
Координаты вектора `vec(AB)` равны (`x_(b)`-`x_(a)`,`y_(b)`-`y_(a)`) в системе (O,`vec (i)`,`vec(j)`).
калькулятор векторных координат
позволяет вам сделать этот тип расчета.
Направляющий вектор прямой
Если в системе линия D имеет уравнение `y=m*x+p`, то вектор `vecu(1;m)` является направляющим вектором D.
Координаты середины отрезка
Середина [AB] имеет координаты `((x_(a)+x_(b))/2;(y_(a)+y_(b))/2)` в система (O,`vec(i)`,`vec(j)`).
Расстояние между двумя точками
На плоскости задана ортонормированная система (O,`vec(i)`,`vec(j)`) .
Если A и B две точки с координатами (`x_(a)`,`y_(a)`) и (`x_(b)`,`y_(b)`) в (O,`vec(i) `,`vec(j)`) система,
затем 92)`, расстояние AB также является нормой вектора `vec(AB)`, который можно вычислить с помощью
калькулятор векторной нормы
.
Точечный продукт
В плане в ортонормированной системе `(O,vec(i),vec(j))` ,
`vec(u)` представляет собой вектор координат (x,y), а `vec(v)` представляет собой вектор координат (x’,y’), скалярное произведение определяется формулой
хх’+уу’.
калькулятор скалярного произведения
позволяет этот тип расчета для n-мерных векторов.
9vec(v)` и вектор `vec(w)`.
Его можно рассчитать с помощью
скалярный калькулятор тройного произведения.
Определитель двух векторов (2×2)
В ортонормированной системе координат (O,`vec(i)`,`vec(j)`) вектор `vec(u)` имеет координаты (x,y) (`vec(i)`,`vec(j)`), вектор `vec(v)` имеет координаты (x’,y’). Определитель для vec(u) и vec(v) задается формулой формула xx’-yy’ .
Этот
Пример показывает вычисление определителя векторов [[3;12];[45;2]], выполненное с помощью калькулятора определителя 2×2.
Примечание. Когда определитель двух векторов равен нулю, эти два вектора коллинеарны.
Определитель трех векторов (3×3)
В ортонормированной системе координат (O,`vec(i)`,`vec(j)`,`vec(k)`) вектор `vec(u)` имеет координаты (х, у, z) , вектор `vec(v)` имеет координаты (x’,y’,z’), вектор `vec(k)` имеет координаты (x»,y»,z»). Определитель `vec(u)`, `vec(v)`, `vec(k)` задается формулой xy’z»+x’y»z+x»yz’- xy»z’-x’yz»-x»y’z .
Это пример, сделанный с калькулятором определителя 3×3, подробно описывает вычисление определителя векторов [[3;1;0];[3;2;1];[4;0;7]] .
Векторы: калькуляторы
- cross_product : калькулятор перекрестного произведения. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- определитель : калькулятор определителя.
 Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
Функция определителя вычисляет онлайн определитель векторов или определитель матрицы. - dot_product : Калькулятор скалярного произведения. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.
- product_vector_number : произведение вектора на число. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
- scalar_triple_product : вычисление скалярного тройного произведения. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- vector_calculator : векторный калькулятор. Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.

- vector_coordinates : вычисление координат вектора по двум точкам. Векторный калькулятор позволяет вычислять координаты вектора по координатам двух точек онлайн.
- vector_difference : вычисление разницы двух векторов. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- vector_norm : вычисление нормы вектора. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- vector_sum : вычисление суммы двух векторов. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Векторы: игры и викторины
- Викторина по векторам (векторам): Эта викторина позволяет попрактиковаться в векторном исчислении: вычисление координат, нормы, середины отрезка, скалярного произведения.

Векторы : упражнения
- Упражнение 1524, ордината вектора направления прямой — векторы — уравнения — уравнения прямых и линейных систем : Цель этого упражнения состоит в том, чтобы определить ординату вектора направления из уравнения прямой.
- Упражнение 3441, координаты вектора по координатам двух точек — векторы : Цель этого исправленного упражнения состоит в том, чтобы вычислить координаты вектора по координатам двух точек.
- Упражнение 3442, вычисление расстояния между двумя точками — векторами. Целью этого исправленного упражнения является вычисление расстояния между двумя точками по их координатам.
- Упражнение 3443, вычисление координат середины отрезка — векторы. Целью этого упражнения с исправленной аналитической геометрией является вычисление координат середины отрезка по координатам.

Алгебраический расчет | Уравнения | Финансы | Реальные функции | Тригонометрические функции | Фракции | Геометрия | Матрицы | Числа | Комплексные числа | Статистика | Числовые последовательности | Время | Векторы
9 лучших бесплатных онлайн-сайтов с калькулятором точечного произведения
Вот список из лучших бесплатных онлайн-сайтов с калькулятором точечного произведения . Скалярное произведение или Скалярное произведение — это тип операции, которая суммирует произведение двух или более равных векторных значений. Эта операция используется для проверки того, являются ли два входных вектора ортогональными или нет. Чтобы выполнить расчет скалярного произведения, пользователи могут попробовать эти онлайн-калькуляторы скалярного произведения.
С помощью этих калькуляторов пользователи могут легко вычислить скалярное произведение, используя значения входного вектора. Некоторые из этих веб-сайтов также позволяют пользователям вводить более двух векторных значений: два (x1, x2) и три (x1, x2, x3) и четыре (x1,x2,x3,x4) и другие измерения. . Помимо векторных значений, некоторые калькуляторы также могут использовать Величина и Расчет угла . Процесс вычисления скалярного произведения на всех этих веб-сайтах довольно прост. Тем не менее, чтобы помочь новым пользователям, я включил необходимые шаги расчета в описание каждого веб-сайта.
Некоторые из этих веб-сайтов также позволяют пользователям вводить более двух векторных значений: два (x1, x2) и три (x1, x2, x3) и четыре (x1,x2,x3,x4) и другие измерения. . Помимо векторных значений, некоторые калькуляторы также могут использовать Величина и Расчет угла . Процесс вычисления скалярного произведения на всех этих веб-сайтах довольно прост. Тем не менее, чтобы помочь новым пользователям, я включил необходимые шаги расчета в описание каждого веб-сайта.
Эти веб-сайты также являются дополнительными онлайн-инструментами, которые могут пригодиться. Используя дополнительные инструменты, пользователи могут выполнять научные расчеты , бизнес-расчеты, дополнительные вектора, скалярное умножение, и многое другое. Просмотрите список, чтобы узнать больше об этих веб-сайтах.
Мой любимый онлайн-калькулятор скалярного произведения Веб-сайт:
onlinemschool. com — мой любимый веб-сайт, поскольку он может использовать входные векторы до 6 измерений для решения скалярного произведения. Кроме того, он довольно прост в использовании.
com — мой любимый веб-сайт, поскольку он может использовать входные векторы до 6 измерений для решения скалярного произведения. Кроме того, он довольно прост в использовании.
Вы также можете ознакомиться со списками лучших бесплатных веб-сайтов с онлайн-калькулятором шага точек, онлайн-калькулятором уклона и онлайн-калькулятором мощности.
onlinemschool.com
onlinemschool.com — это бесплатный онлайн-калькулятор скалярного произведения . Это способный веб-сайт для решения задач векторного скалярного произведения . Кроме того, он позволяет пользователям решать векторы до 6 измерений . Преимущество этого калькулятора в том, что он поддерживает векторных значений 9.0095 в обоих координатах и точках . Теперь выполните следующие шаги.
Как рассчитать скалярное произведение онлайн с помощью onlinemschool.com:
- Запустите этот веб-сайт и откройте калькулятор скалярного произведения .

- После этого укажите размерность векторного значения.
- Теперь укажите векторное представление (точки или координаты).
- Затем введите все значения координат или точек.
- Наконец, нажмите на равно , чтобы просмотреть окончательный ответ вместе с шагами расчета.
Дополнительные функции:
- На этом веб-сайте пользователи могут найти множество онлайн-калькуляторов с такими векторами, как Векторный калькулятор величины, умножение скалярного вектора, векторная проекция, коллинеарные векторы, ортогональные векторы, и другие.
Заключительные мысли:
Это один из лучших бесплатных онлайн-калькуляторов скалярных произведений, который каждый может использовать для выполнения вычислений скалярных произведений.
Домашняя страница
calculatesoup.com
calculatesoup.com — бесплатный онлайн-калькулятор скалярных произведений. Используя этот веб-сайт, пользователи могут вычислить скалярное произведение двух или более векторов, несущих три значения координат. Перед началом расчета пользователи также могут указать значение Значимая цифра между 3 и 8 . Он также показывает несколько примеров точечных продуктов, чтобы помочь пользователям. Теперь выполните следующие шаги, чтобы рассчитать скалярный продукт онлайн с помощью этого веб-сайта.
Используя этот веб-сайт, пользователи могут вычислить скалярное произведение двух или более векторов, несущих три значения координат. Перед началом расчета пользователи также могут указать значение Значимая цифра между 3 и 8 . Он также показывает несколько примеров точечных продуктов, чтобы помочь пользователям. Теперь выполните следующие шаги, чтобы рассчитать скалярный продукт онлайн с помощью этого веб-сайта.
Как рассчитать скалярный продукт онлайн с помощью calculatesoup.com:
- Посетите этот веб-сайт, используя предоставленную ссылку.
- После этого введите от двух до более шагов значения вектора.
- Далее укажите значащее Значение фигуры .
- В конце нажмите кнопку Вычислить , чтобы начать процесс вычисления.
Дополнительные функции:
- Этот веб-сайт также предлагает онлайн-калькуляторы по математике, финансам, времени и дате, научным, бизнес-калькуляторам и статистическим калькуляторам.

Заключительные мысли:
Это хороший онлайн-калькулятор скалярного произведения, который предлагает все инструменты для выполнения вычислений скалярного произведения.
Домашняя страница
symbolab.com
symbolab.com — еще один бесплатный онлайн-калькулятор скалярных произведений. Этот веб-сайт может не только решать скалярный продукт, но также может показывать пользователям этапы расчета. В отличие от других подобных веб-сайтов, он требует, чтобы пользователи вручную вводили точечный продукт с закрывающими скобками. Он также предоставляет хороший набор примеров скалярного произведения. Теперь выполните следующие шаги.
Как рассчитать скалярное произведение онлайн с помощью symbolab.com:
- Посетите этот веб-сайт и откройте раздел Скалярное произведение .
- Теперь вручную напишите выражение скалярного произведения.
- Затем нажмите кнопку Перейти , чтобы начать процесс расчета.

- В конце просмотрите рассчитанный ответ вместе с некоторыми этапами расчета.
Дополнительные функции:
- Этот веб-сайт также предлагает дополнительные векторные калькуляторы, такие как Добавить векторы, Вычесть векторы, Скалярное умножение, Перекрестное произведение, и многое другое.
Заключительные мысли:
Это еще один хороший онлайн-калькулятор скалярного произведения, который может решать различные типы векторных задач.
Домашняя страница
emathhelp.net
emathhelp.net — еще один бесплатный онлайн-калькулятор скалярного произведения. Используя этот веб-сайт, пользователи могут решать задачи скалярного произведения до 3 измерений . Это также не позволяет пользователям решать скалярные произведения более 2 вектора . После выполнения расчета он показывает формулу, которую он использует для выполнения расчета, а также шаги расчета. Теперь выполните следующие шаги.
Теперь выполните следующие шаги.
Как рассчитать скалярный продукт онлайн с помощью emathhelp.net:
- Запустите этот веб-сайт, используя предоставленную ссылку.
- После этого введите векторные координаты обоих входных векторов.
- Затем нажмите кнопку Calculate , чтобы начать процесс расчета.
- Наконец, просмотрите решение вместе с шагами расчета.
Дополнительные функции:
- Этот веб-сайт содержит расширенные калькуляторы, с помощью которых пользователи могут решать задачи по исчислению, дискретной математике, линейной алгебре, геометрии, и по базовой математике .
Заключительные мысли:
Это еще один хороший онлайн-калькулятор скалярных произведений, который позволяет пользователям вычислять скалярные произведения двух векторов, содержащих до 3 значений координат.
Домашняя страница
omnicalculator.com
omnicalculator. com — еще один хороший онлайн-калькулятор точечных произведений. На этом веб-сайте пользователи могут найти скалярное произведение двух векторов, несущих трех значений координат . Помимо вычисления скалярного произведения, он также может вычислять угол между векторами, используя тот же набор входных значений, что и для вычисления скалярного произведения.
com — еще один хороший онлайн-калькулятор точечных произведений. На этом веб-сайте пользователи могут найти скалярное произведение двух векторов, несущих трех значений координат . Помимо вычисления скалярного произведения, он также может вычислять угол между векторами, используя тот же набор входных значений, что и для вычисления скалярного произведения.
Этот веб-сайт также предоставляет теоретическое объяснение скалярных произведений. Кроме того, он также предоставляет несколько примеров, подчеркивающих расчет скалярного произведения. Теперь проверьте следующие шаги.
Как рассчитать скалярный продукт онлайн с помощью omnicalculator.com:
- Посетите этот веб-сайт, используя предоставленную ссылку.
- После этого введите значения координат обоих входных векторов.
- Затем позвольте этому веб-сайту выполнить расчет и просмотреть рассчитанное значение скалярного произведения вместе со значением угла между векторами.

Дополнительные функции:
- Этот веб-сайт также предлагает дополнительные бесплатные онлайн-калькуляторы, такие как калькулятор остатка , калькулятор корня, калькулятор научных понятий, стандартный форумный калькулятор, калькулятор суммы цифр, и более.
Заключительные мысли:
Это еще один способный онлайн-калькулятор скалярного произведения, который любой может использовать для выполнения вычислений скалярного произведения.
Домашняя страница
byjus.com
byjus.com — следующий бесплатный онлайн-калькулятор скалярных произведений. Этот веб-сайт предлагает онлайн-учебные материалы, а также калькуляторы для студентов. Одним из калькуляторов, которые он предлагает, является калькулятор скалярного произведения . Этот калькулятор позволяет пользователям вычислять два вектора до 3 размера . Кроме того, он также предоставляет инструкции по использованию этого калькулятора. Теперь выполните следующие шаги.
Теперь выполните следующие шаги.
Как рассчитать скалярный продукт онлайн с помощью byjus.com:
- Посетите этот веб-сайт, используя предоставленную ссылку.
- После этого введите значения обоих векторов x и y .
- Теперь нажмите кнопку Calculate Dot Product , чтобы начать процесс вычисления.
- В конце просмотрите конечное значение скалярного произведения, которое вы также можете скопировать.
Дополнительные функции:
- Дополнительные калькуляторы : На этом веб-сайте пользователи могут найти множество калькуляторов для физики, математики, химии .
- Учебные материалы : Он также предоставляет большое количество учебных материалов для студентов различных учебных заведений.
Заключительные мысли:
Это еще один способный онлайн-калькулятор скалярного произведения онлайн-сайт, который может вычислить скалярное произведение двух векторов до трех измерений.
Домашняя страница
Learningaboutelectronics.com
Learningaboutelectronics.com — еще один бесплатный онлайн-калькулятор точечного произведения. С помощью этого веб-сайта пользователи могут быстро вычислить скалярное произведение, используя два вектора, несущие одну пару из трех значений координат. Помимо этого, он также может вычислить произведение Dot , используя значение Magnitude и Cosine Angle . Теперь выполните следующие шаги.
Как рассчитать скалярное произведение онлайн с помощью Learningaboutelectronics.com:
- Посетите этот веб-сайт, используя предоставленную ссылку.
- После этого введите значения обоих значений вектора.
- Теперь нажмите кнопку Calculate для просмотра скалярного произведения.
Дополнительные функции:
- Этот веб-сайт также предлагает различные учебные пособия по языкам программирования, основанные на HTML, CSS, PHP, Linux, и других.

Заключительные мысли:
Это еще один способный онлайн-калькулятор точечного произведения, который любой может использовать без особых хлопот.
Домашняя страница
inchcalculator.com
inchcalculator.com — еще один бесплатный онлайн-калькулятор точечного произведения. Этот веб-сайт может выполнять вычисления как 2-мерного , так и 3-мерного скалярного произведения . Кроме того, он также показывает формулу расчета скалярного произведения, которую он использует для выполнения расчета. Теперь выполните следующие шаги.
Как рассчитать скалярный продукт онлайн с помощью inchcalculator.com:
- Посетите этот веб-сайт и откройте Калькулятор скалярного произведения .
- После этого выберите вариант 2D или 3D.
- Теперь введите значения вектора.
- Наконец, нажмите кнопку Calculate , чтобы начать процесс расчета.

Дополнительные функции:
- На этом веб-сайте также есть полезные векторные калькуляторы, такие как калькулятор векторного вычитания , калькулятор сложения векторов, калькулятор векторной нормы, и другие.
Последние мысли:
Это еще один хороший онлайн-калькулятор скалярного произведения, с помощью которого пользователи могут выполнять вычисления как в 2D, так и в 3D.
Домашняя страница
amesweb.info
amesweb.info — последний бесплатный онлайн-калькулятор точечного произведения. Этот калькулятор может использовать компоненты вектора , а также компоненты Magnitude и Angle , чтобы узнать скалярное произведение. В дополнение к этому, он также показывает формулу расчета скалярного произведения вместе с диаграммами компонентов скалярного произведения. Теперь проверьте следующие шаги.
Как рассчитать скалярный продукт онлайн с помощью amesweb.


 Координаты векторов AB и CD непропорциональны, значит, векторы AB и CD не лежат на одной прямой.
Координаты векторов AB и CD непропорциональны, значит, векторы AB и CD не лежат на одной прямой. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.