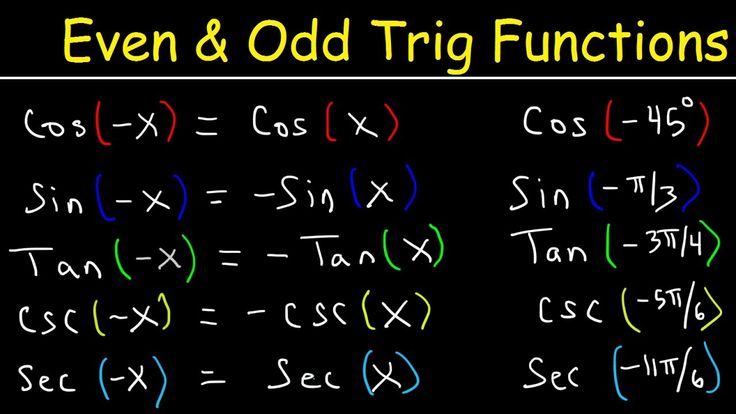Функция ODD в Excel — voxt.ru
Функция Excel ODD
Функция ODD является встроенной функцией в excel, так как название предполагает, что она округляет любое заданное число до его нечетного значения, число может быть как отрицательным, так и положительным, поэтому, например, если данный вход = ODD (-1,5), округленный результат будет -3 , и если заданный вход = ODD (1.5), то результат равен 3.
Синтаксис
Формула ODD имеет только один обязательный параметр, т.е. количество.
Обязательный параметр:
- количество: Числовое значение, которое будет округлено до ближайшего нечетного целого числа.
Вы можете скачать этот шаблон Excel с функцией ODD здесь — Шаблон Excel с функцией ODD
Пример # 1
В этом примере давайте рассмотрим набор положительных целых чисел 40, 18, 10, 26, 19, 20, 14, 17, 30 и 27, чтобы понять работу с ODD. Теперь примените формулу ODD в ячейке, как показано в таблице ниже. Эта функция округляет все значения до ближайших нечетных чисел, например 41, 19, 11, 27, 19, 21, 15, 17, 31 и 27.
Теперь примените формулу ODD в ячейке, как показано в таблице ниже. Эта функция округляет все значения до ближайших нечетных чисел, например 41, 19, 11, 27, 19, 21, 15, 17, 31 и 27.
Пример # 2
В этом примере мы берем образец отрицательных целых чисел и затем применяем к ним формулу ODD.
Давайте рассмотрим набор положительных целых чисел -40, -18, -10, -26, -19, -20, -14, -17, -30 и -27, чтобы понять работу с ODD. Теперь примените формулу ODD в ячейке, как показано в таблице ниже. Эта функция округляет все значения до ближайших нечетных чисел как -41, -19, -11, -27, -19, -21, -15, -17, -31 и -27.
Пример # 3
В этом примере возьмем положительные значения точки для ODD.
Здесь значение точки сначала округляется до почти целого значения, чем работает нечетное. Для значения 27,9 нечетное возвращает 29 в качестве выходных данных, поскольку 27,9 сначала рассматривается как> 27 ~ 28, а затем нечетное округляется до ближайшего целого значения.
Для значений в таблице ниже 40.18, 18.1, 10.26, 26.19, 19.19, 19.14, 14.17, 17.3, 30.27 и 27.9 вывод будет 41, 19, 11, 27, 19, 21, 15, 17, 31 и 29.
Пример # 4
В этой функции ODD, например, возьмем отрицательные значения точки для ODD.
Давайте рассмотрим набор значений отрицательных точек -40,18, -18,1, -10,26, -26,19, -19,19, -19,14, -14,17, -17,3, -30,27 и -27,9, чтобы понять работу с ODD. Теперь примените формулу ODD в ячейке, как показано в таблице ниже. Эта функция округляет все значения до ближайших нечетных чисел как -41, -19, -11, -27, -21, -21, -15, -19, -31 и -29.
ODD можно использовать как функцию VBA.
Dim ODDnumber As Long
ODDnumber = Application.worksheetfunction.odd («14»)
Msgbox (ODDnumber) // Вернуть ближайшее нечетное значение в окне сообщения.
На выходе будет «15», и оно будет напечатано в окне сообщения.
То, что нужно запомнить
- Если предоставленное число не является числовым значением, то ODD вернет #VALUE! Ошибка.

- Независимо от значения (+ ve и –ve) числа, значение округляется в большую сторону и отключается от нуля.
- Если число является нечетным целым числом, округление не производится.
УЗНАТЬ БОЛЬШЕ >>
Post Views: 271
Похожие записи
Прокрутить вверх|
Новости
Программы Turbo Pascal Игры Документация «Странности» FAQ Ссылки Благодарности Об авторе
|
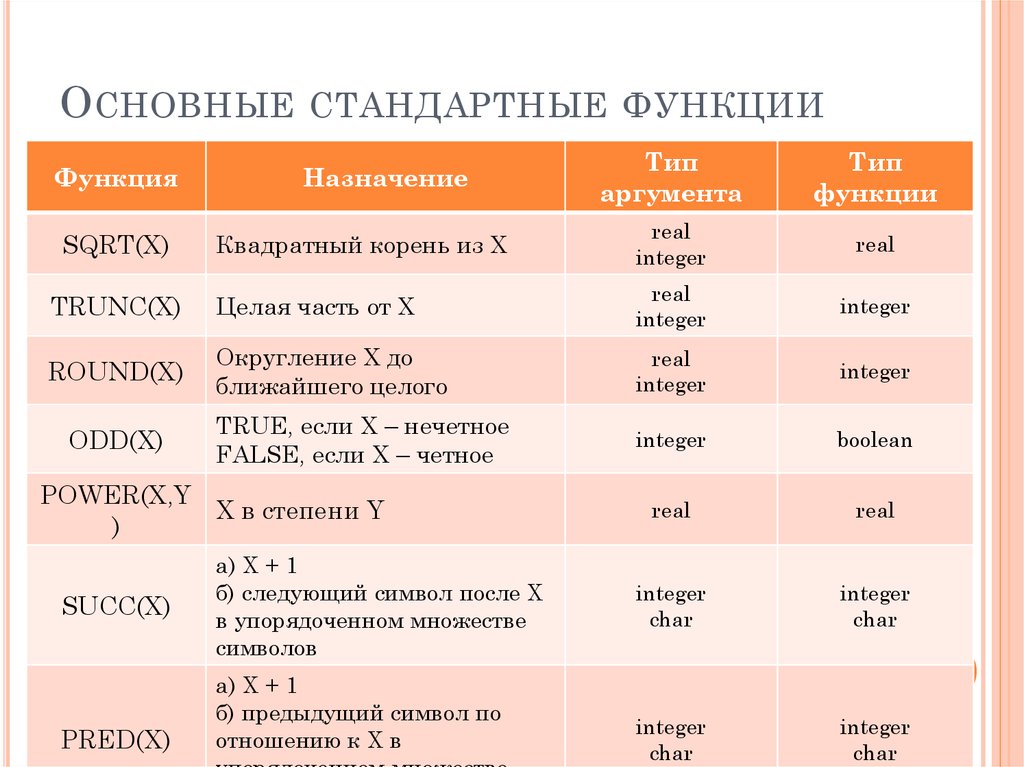
5. СТАНДАРТНЫЕ ТИПЫ К стандартным относятся целые, действительные, логические, ЦЕЛЫЕ типы определяют константы, переменные и функции, значения 
Над целыми операндами можно выполнять следующие арифметические + — * div mod Результат арифметической операции над целыми операндами есть вели- 17 div 2 = 8, 3 div 5 = 0. Операции отношения, примененные к целым операндам, дают результат Abs(X), Sqr(X), Succ(X), Pred(X), и которые определяют соответственно абсолютное значение Х, Х в квад- Sin(X), Cos(X), ArcTan(X), Ln(X), Exp(X), Sqrt(X). Эти функции вычисляют синус, косинус и арктангенс угла, заданного X=5 Odd(X)=TRUE , X=4 Odd(X)=FALSE. Для быстрой работы с целыми числами определены процедуры: Inc(X) X:=X+1 Dec(X) X:=X-1 Dec(X,N) X:=X-N ДЕЙСТВИТЕЛЬНЫЕ типы определяет те данные, которые реализуются 1.Тип Диапазон 2. Количество цифр 3. Требуемая 1
2
3 4 Тип Real определен в стандартном ПАСКАЛЕ и математическим сопро- сложение + , вычитание — , умножение * , деление / . К величинам действительного типа применимы все операции отношения, Abs(X), Sqr(X), Sin(X), Cos(X), ArcTan(X), Ln(X), Exp(X), Функция Frac(X) возвращает дробную часть X, функция Int(X) — целую Trunc(X) и Round(X), дающие целый результат. Первая из них выделяет целую часть действи- ЛОГИЧЕСКИЙ тип (Boolean) определяет те данные, которые могут при- not and or xor. Логический тип определен таким образом, что FALSE < TRUE. Это поз- СИМВОЛЬНЫЙ тип (Char) определяет упорядоченную совокупность симво- ‘A’ ‘a’ ‘Ю’ ‘ю’; -с помощью конструкции вида #K, где K — код соответствущего симво- Ord(C) Chr(K). Первая функция определяет порядковый номер символа С в наборе сим- Pred(C) Succ(C). Pred(‘F’) = ‘E’ ; Succ(‘Y’) = ‘Z’ . При отсутствии предыдущего или последующего символов значение со- Для литер из интервала ‘a’..’z’ применима функция UpCase(C), кото- рая переводит эти литеры в верхний регистр ‘A’.  .’Z’. .’Z’.АДРЕСНЫЙ тип (Pointer) определяет переменные, которые могут содер- |
Нечетная функция — определение, свойства, график, примеры
LearnPracticeDownload
Нечетные функции — это функции, которые возвращают обратное отрицательное значение при замене x на –x. Это означает, что f(x) — нечетная функция, когда f(-x) = -f(x). Некоторыми примерами нечетных функций являются тригонометрическая функция синуса, функция тангенса, функция косеканса и т. Д. Давайте подробно разберемся с нечетными функциями и их свойствами в следующем разделе.
1. | Что такое нечетная функция? |
| 2. | Общая формула функции ODD |
| 3. | Графическое представление нечетной функции |
| 4. | Свойства нечетных функций |
| 5. | Часто задаваемые вопросы о нечетных функциях |
Что такое нечетная функция?
Функция нечетная, если −f(x) = f(−x) для всех x. График нечетной функции будет симметричен относительно начала координат. Например, f(x) = x 3 нечетно. То есть функция на одной стороне оси абсцисс инвертирована по знаку по отношению к другой стороне или графически симметрична относительно начала координат.
Пример нечетной функции
Посмотрите на пример нечетной функции, график f(x) = x 5
Посмотрите на график в 1 st и 3 квадранта и . График выглядит симметричным относительно начала координат. Обратите внимание, что все функции, имеющие нечетную мощность, являются нечетными функциями.
Обратите внимание, что все функции, имеющие нечетную мощность, являются нечетными функциями.
f(x) = x 7 — нечетная функция, но f(x) = x 3 + 2 нечетная функция. Можете ли вы проверить с помощью правила нечетной функции?
Общая формула нечетной функции
Алгебраически, не глядя на график, мы можем определить, является ли функция четной или нечетной, найдя формулу для отражений.
f(−x) = −f(x) для всех x
Пример:
Определите характер функции f(x) = 1/x
Функция является нечетной, если f(−x ) = −f(x) и даже если f(x) = f(−x),
Найдем f(−x), чтобы определить характер функции.
f(−x) = 1/-x = −1/x
= −f(x) (∵ f(x) = 1/x)
Поскольку f(−x) = −f(x), функция нечетная.
Графическое представление нечетной функции
Нечетные Функции симметричны относительно начала координат. Функция на одной стороне оси абсцисс инвертирована по знаку относительно другой стороны или графически симметрична относительно начала координат. Вот несколько примеров нечетных функций, обратите внимание на симметрию относительно начала координат.
Вот несколько примеров нечетных функций, обратите внимание на симметрию относительно начала координат.
y = x 3
f(x) = −x нечетно
f(x) = 6sin(x)
Свойства нечетных функций
Как и другие функции в математике, нечетные функции имеют свои собственные свойства, которые можно использовать для легкого определения нечетной функции. Давайте посмотрим на несколько свойств.
- Сумма двух нечетных функций нечетна.
- Разница между двумя нечетными функциями нечетна.
- Произведение двух нечетных функций четно.
- Частное от деления двух нечетных функций четно.
- Композиция двух нечетных функций нечетна.
- Композиция четной функции и нечетной функции четна.
☛Статьи о нечетной функции
Ниже приведен список тем, тесно связанных с нечетной функцией. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
- Экспоненциальная функция
- Полиномиальные функции
- Квадратичные функции
- Линейные функции
- Постоянные функции
Примеры нечетных функций
Пример 1. Алгебраически определите, является ли заданная функция f(x) = −3x 3 + 2x четной, нечетной или ни одной из них.
Решение:
Подставим −x в функцию f(x) = 3x 3 + 2x, а затем упростить.
Функция является нечетной, если −f(x) = f(−x)
Найдем f(-x)
f(x) = −3x 3 + 2x
f(−x) = -3(−x) 3 + 2(−x)
= −3(−1) 3 (x) 3 + 2(−x)
= 3x 3 − 2x −−−(1)
−f(x) = −(−3x 3 + 2x)
= 3x 3 − 2x −−−(2)
из (1) и (2) можно сказать, что f(−x) = −f(x)
и данная функция является нечетной функцией.f(x) = −3x 3 + 2x — нечетная функция.

Пример 2: Определите характер функции f(x) = x 3 + 2x.
Решение: Функция равна
- , даже если f(x) = f(−x)
- нечетно, если f(−x) = −f(x)
Найдем f(−x), чтобы определить характер функции
f(−x) = (−x) 3 + 2(−x)
= −x 3 − 2x
= -(х 3 + 2х)
= −f(x)f(−x) = −f(x) это нечетная функция.
Пример 3: Нарисуйте график нечетной функции для примера 2, т. е. f(x) = x 3 + 2x, и объясните, почему это нечетная функция.
Решение: Построим график данной функции
- Обратите внимание, что график симметричен относительно начала координат.
- Для каждой точки (x,y) на графике соответствующая точка (−x,−y) также находится на графике
- Например, (1,3) находится на графике f(x), и соответствующая точка отражения (−1,−3) также находится на графике.

Следовательно, данная функция f(x) нечетна.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по нечетной функции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о нечетной функции
Что такое нечетные функции в исчислении?
В исчислении нечетная функция определяется как −f(x) = f(−x) для всех x. График нечетной функции будет симметричен относительно начала координат. Например, f(x) = x 3 нечетно.
Что такое уравнение нечетной функции?
Уравнение нечетной функции, математически выраженное как −f(x) = f(−x) для всех x.
Как определить, является ли функция нечетной функцией или нет?
Если функция удовлетворяет следующим условиям, она является нечетной функцией:
- Если значение f(−x) совпадает со значением f(x) для каждого значения x, функция четная.

- Если значение f(−x) НЕ совпадает со значением f(x) для любого значения x, функция не является четной.
- Если функция имеет четную степень, функция не обязательно должна быть четной.
Является ли Cos x нечетной функцией?
Уравнение нечетной функции, математически выраженное как −f(x) = f(−x) для всех x. При подстановке значения имеем cos(−x) = cos x. Следовательно, cosx НЕ нечетная функция, а четная.
Как узнать, предназначен ли график для нечетной функции, четной или ни для одной?
Существуют определенные правила, позволяющие определить, является ли построенный график нечетной функцией или нет. Правила перечислены ниже.
- НЕЧЕТНЫЙ, если он симметричен относительно начала координат,
- ДАЖЕ, если он симметричен относительно оси Y
- НИ ОДНА, если не указано иное.
Каковы три основных свойства нечетной функции?
Существуют различные свойства, определяющие четную функцию. Два основных свойства:
Два основных свойства:
- Когда мы вычитаем две нечетные функции, результирующая разность будет нечетной.
- Когда мы умножаем две нечетные функции, получается четное произведение.
- Когда мы складываем две нечетные функции, получается нечетная сумма.
Есть ли функция, которая не является ни нечетной, ни четной?
Функция не может быть ни четной, ни нечетной. Пример: x 3 — x + 1
Почему синус является нечетной функцией?
Мы знаем, что sin (-x) = -sin (x). График sin(x) симметричен относительно начала координат. Итак, нечетная функция.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по нечетной функции
Рабочие листы по математике и
наглядный учебный план
Нечетная функция
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Дополнительно. .. Меньше
.. Меньше
В этой статье описаны синтаксис формулы и использование функции ODD в Microsoft Excel.
Описание
Возвращает число, округленное до ближайшего нечетного целого числа.
Синтаксис
НЕЧЕТНЫЙ (число)
Синтаксис функции ODD имеет следующие аргументы:
Замечания
Если число не является числом, НЕЧЕТНОЕ возвращает ошибку #ЗНАЧ! значение ошибки.
Независимо от знака числа, значение округляется в большую сторону при отклонении от нуля. Если число является нечетным целым числом, округления не происходит.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Формула | Описание | Результат |
|---|---|---|
=НЕЧЕТНОЕ(1,5) | Округляет 1,5 до ближайшего нечетного целого числа. | 3 |
=НЕЧЕТНЫЙ(3) | Округляет 3 до ближайшего нечетного целого числа. |

 Результат выполнения операции получения
Результат выполнения операции получения
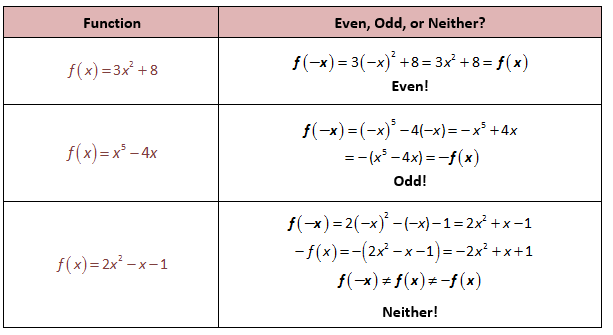 9e-39 .. 1.7e+38
11 6
9e-39 .. 1.7e+38
11 6

 C, где C — код соответствущего управ-
C, где C — код соответствущего управ-