Функция параболы и ее график: Квадратичная функция и её график — урок. Алгебра, 7 класс.

Содержание

Квадратичная функция, ее график и свойства

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Квадратичная функция. Её свойства и график.

Определение квадратичной
функции
Квадратичной функцией называется
функция , которую можно задать формулой
вида:
y=
2
ax +bx
+c
где: a, b, c –
числа
Х – независимая переменная
а 0
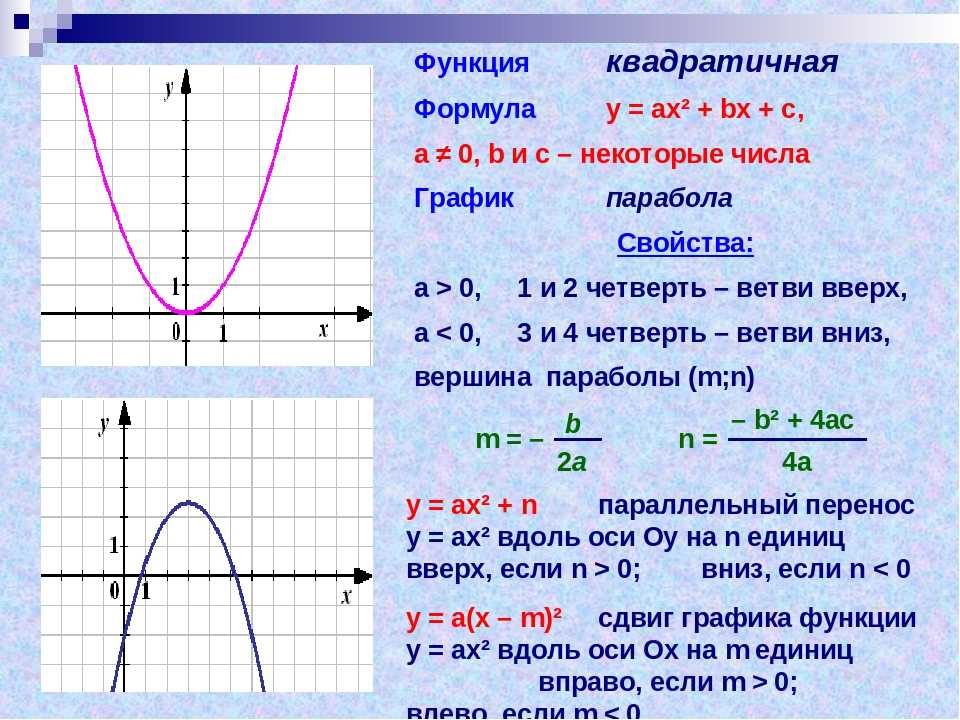
График квадратичной функции – парабола.

3.

Алгоритм построения параболы у = ах2 + bх + с :1. Найти координаты вершины параболы, построить
на координатной плоскости соответствующую точку,
провести ось симметрии.
2.
Определить направление ветвей параболы.
3. Найти координаты еще нескольких точек,
принадлежащих искомому графику ( в частности,
координаты точки пересечения параболы с осью у и
нули функции, если они существуют).
4. Отметить на координатной плоскости
найденные точки и соединить их плавной линией.
—
.
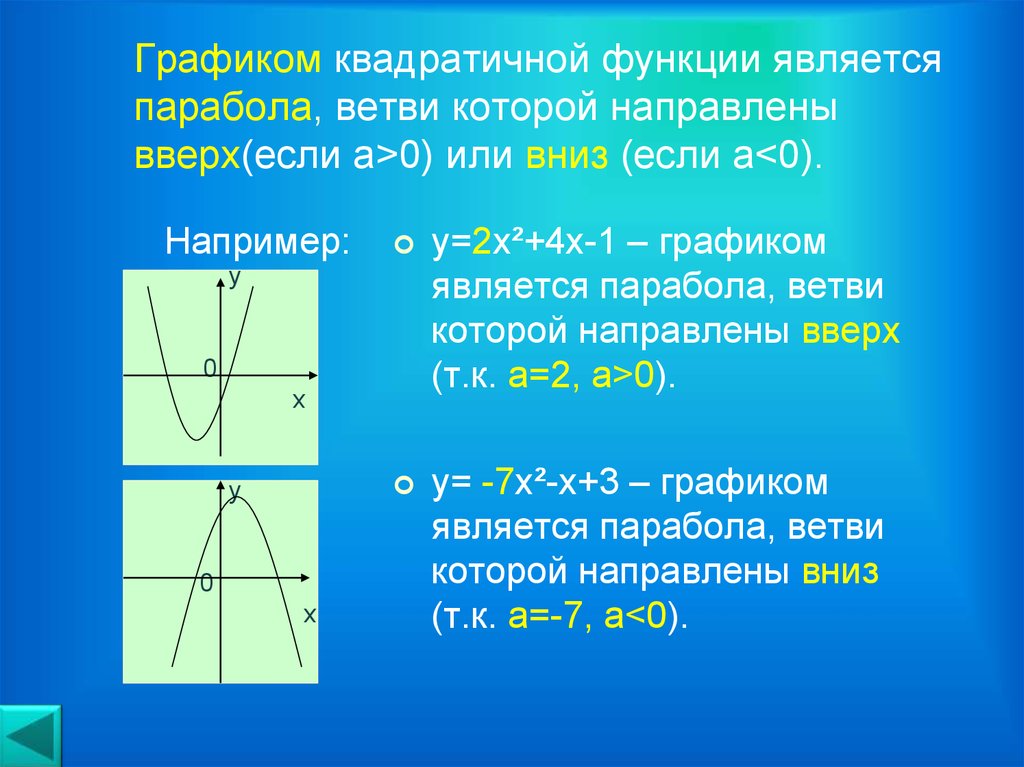
Графиком квадратичной функции
у = ах2 + bх + с является парабола, которая получается из
параболы
у = ах2 параллельным переносом.
Вершина параболы — ( х0; уо) ,
b
где : хо = 2a
у0 =
4ac b 2
4a
Осью параболы будет прямая
b
х=2a

5. Свойства квадратичной функции

Функция непрерывна
Множество значений при a>0 —
Множество значений при a<0 10
8
6
4
2
0
-3
-2
-1
0
-2
1
2
3
4
5
Многие свойства
квадратичной функции
зависят от значения
дискриминанта.

Дискриминантом квадратного уравнения
ах2 + bх + с = 0 называется выражение
D =b2 – 4ac
Возможны три случая:
D 0
D 0
D 0
если дискриминант больше нуля, то парабола
пересекает ось абсцисс в двух точках,
если дискриминант равен нулю, то парабола
касается оси абсцисс,
если дискриминант меньше нуля, то парабола не
пересекает ось абсцисс,
абсцисса вершины параболы равна
—
ветви параболы
направлены вверх,
При
у
b
2a
При
ветви параболы
направлены
вниз
у
f(x0)
х
х
b
2a

9. Область значений функции – Е (f) = [ -1 ; + )

Функция возрастает в
промежутке [ +3; +
)
Функция убывает в
промежутке ( ;+3]
Наименьшее значение
функции равно -1
Наибольшего значения
функции не существует
f(x) > 0 при х < 2, или
х>4
f(x) < 0 при 2 < х < 4
Ось симметрии
Область значений функции –

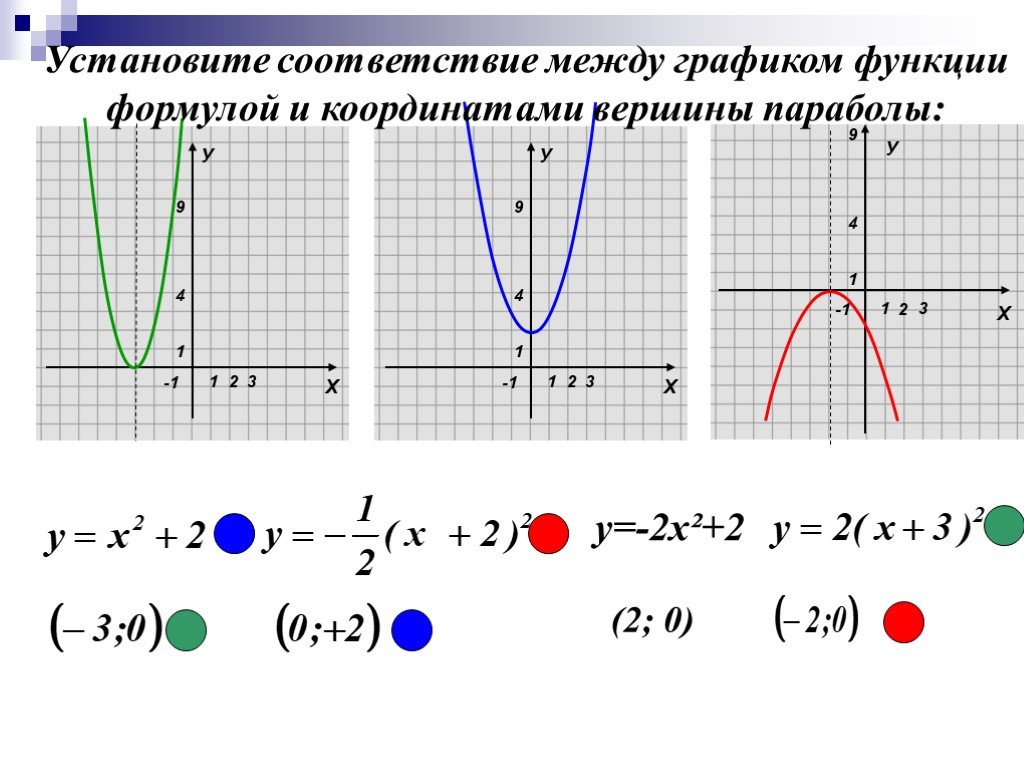
10. Постройте график функции у=2х²+4х-6, опишите его свойства

Проверь себя:
1.

D(y)=
;
У
2. у=0, при х=1; -3
3. у>0, при х ; 3 1;
у<0, при х 3;1
4. у↓, если х ; 1
у↑, если х 1;
5. унаим= -8, если х= -1
унаиб – не существует.
6. Е(y): 8 ;
1
-1
-2
1 2 3
Х
Задание
1. Построить график функции и
описать ее свойства у=2х²+4х-1
2. Построить график функции и
описать ее свойства у= -7х²-х+3

English Русский Правила

Как описать свойства графика функции парабола. Квадратичная функция и ее график

На уроках математики в школе Вы уже познакомились с простейшими свойствами и графиком функции y = x 2 . Давайте расширим знания по квадратичной функции .

Задание 1.

Построить график функции y = x 2 . Масштаб: 1 = 2 см. Отметьте на оси Oy точку F (0; 1/4). Циркулем или полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1) . Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?

Результат: какую бы точку на параболе y = x 2 вы не взяли, расстояние от этой точки до точки F(0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.

Можно сказать иначе: расстояние от любой точки параболы до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = -1/4. Эта замечательная точка F(0; 1/4) называется фокусом параболы y = x 2 , а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.

Интересные свойства параболы:

1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.

2. Если вращать параболу вокруг оси симметрии (например, параболу y = x 2 вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.

Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.

3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе (рис. 2).

4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола (рис. 3) .

5. В парках развлечений иногда устраивают забавный аттракцион «Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.

6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.

7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.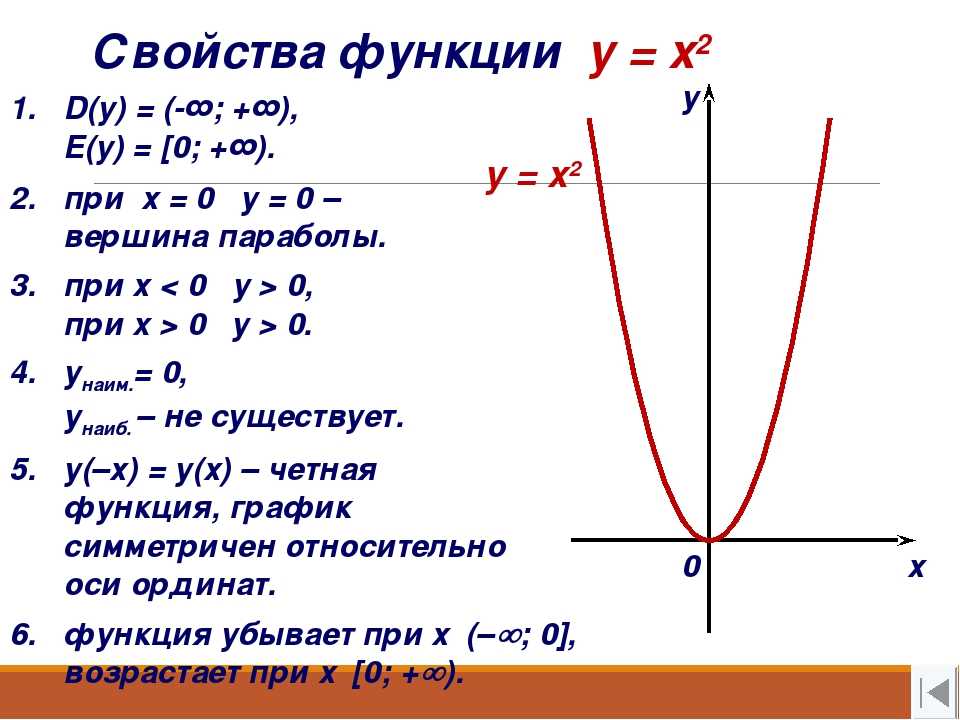

Построение графика квадратичной функции

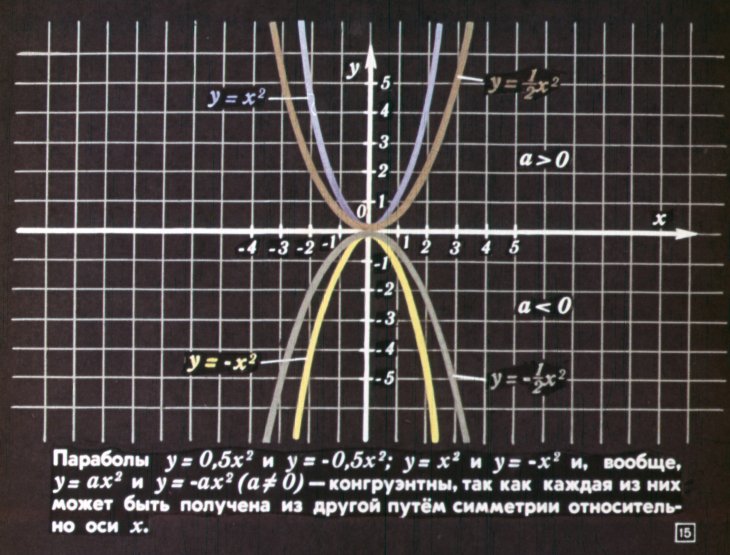
На уроках математики вы изучали получение из графика функции y = x 2 графиков функций вида:

1) y = ax 2 – растяжение графика y = x 2 вдоль оси Oy в |a| раз (при |a| рис. 4 ).

2) y = x 2 + n – сдвиг графика на n единиц вдоль оси Oy, причем, если n > 0, то сдвиг вверх, а если n

3) y = (x + m) 2 – сдвиг графика на m единиц вдоль оси Ox: если m 0, то влево, (рис. 5) .

4) y = -x 2 – симметричное отображение относительно оси Ox графика y = x 2 .

Подробнее остановимся на построении графика функции y = a(x – m) 2 + n .

Квадратичную функцию вида y = ax 2 + bx + c всегда можно привести к виду

y = a(x – m) 2 + n, где m = -b/(2a), n = -(b 2 – 4ac)/(4a).

Докажем это.

Действительно,

y = ax 2 + bx + c = a(x 2 + (b/a) x + c/a) =

A(x 2 + 2x · (b/a) + b 2 /(4a 2) – b 2 /(4a 2) + c/a) =

A((x + b/2a) 2 – (b 2 – 4ac)/(4a 2)) = a(x + b/2a) 2 – (b 2 – 4ac)/(4a).

Введем новые обозначения.

Пусть m = -b/(2a) , а n = -(b 2 – 4ac)/(4a) ,

тогда получим y = a(x – m) 2 + n или y – n = a(x – m) 2 .

Сделаем еще замены: пусть y – n = Y, x – m = X (*).

Тогда получим функцию Y = aX 2 , графиком которой является парабола.

Вершина параболы находится в начале координат. X = 0; Y = 0.

Подставив координаты вершины в (*), получаем координаты вершины графика y = a(x – m) 2 + n: x = m, y = n.

Таким образом, для того, чтобы построить график квадратичной функции, представленной в виде

y = a(x – m) 2 + n

путем преобразований, можно действовать следующим образом:

a) построить график функции y = x 2 ;

б) путем параллельного переноса вдоль оси Ox на m единиц и вдоль оси Oy на n единиц – вершину параболы из начала координат перевести в точку с координатами (m; n) (рис. 6) .

Запись преобразований:

y = x 2 → y = (x – m) 2 → y = a(x – m) 2 → y = a(x – m) 2 + n.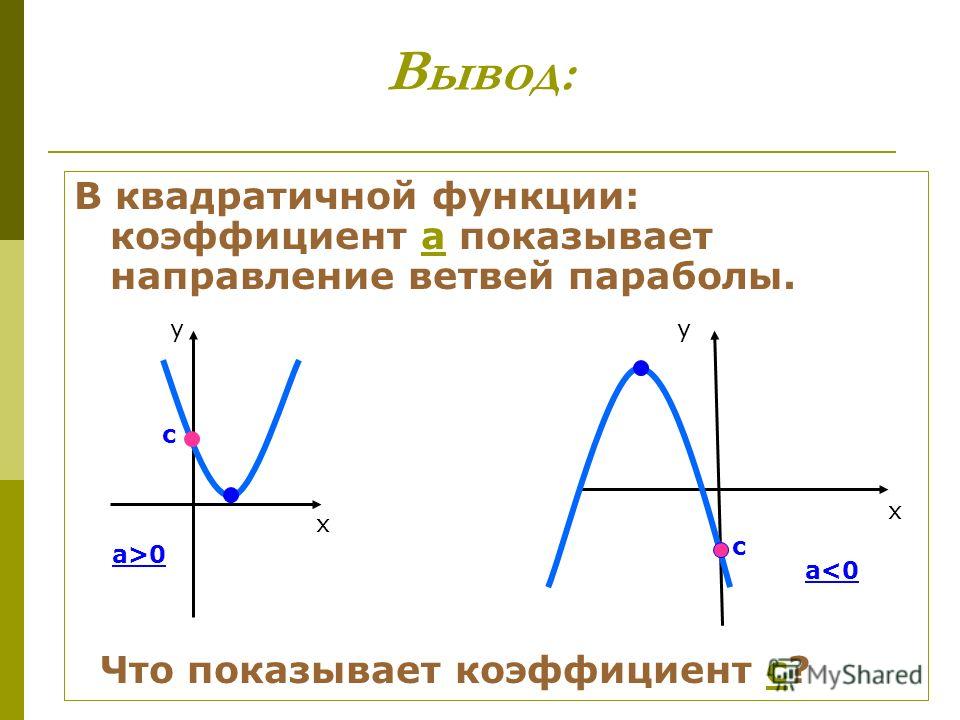

Пример.

С помощью преобразований построить в декартовой системе координат график функции y = 2(x – 3) 2 – 2.

Решение.

Цепочка преобразований:

y = x 2 (1) → y = (x – 3) 2 (2) → y = 2(x – 3) 2 (3) → y = 2(x – 3) 2 – 2 (4) .

Построение графика изображено на рис. 7 .

Вы можете практиковаться в построении графиков квадратичной функции самостоятельно. Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3) 2 + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести

бесплатное 25-минутное занятие с онлайн репетитором после . Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам

Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.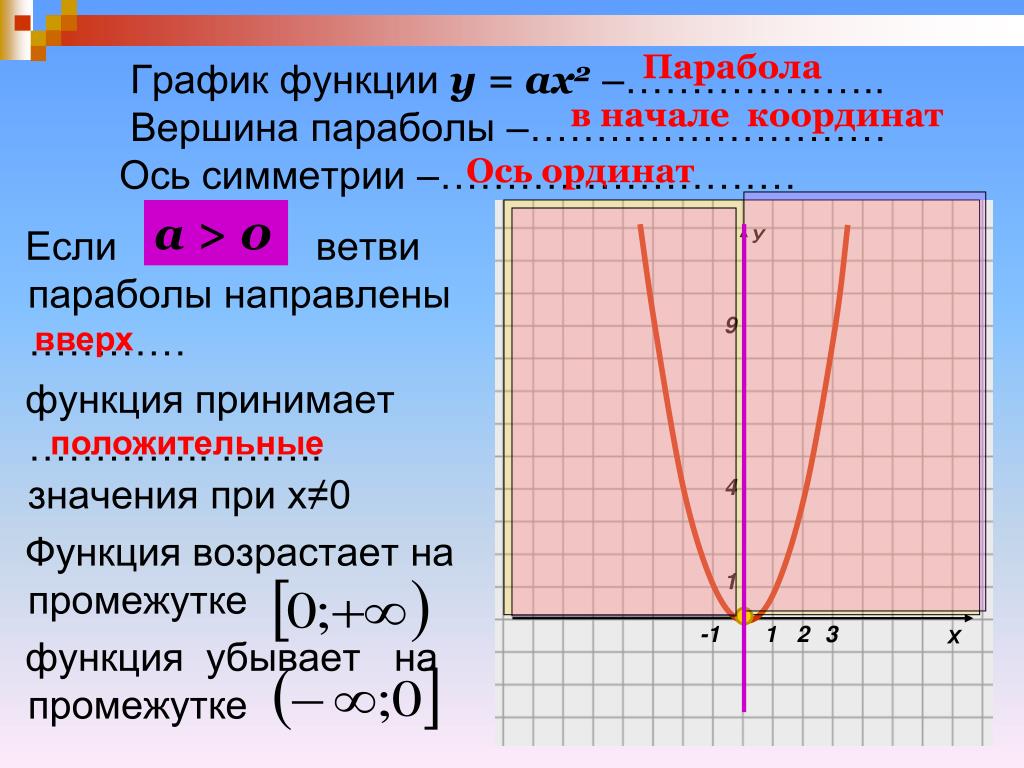 сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Квадратичные функции и их графики

Цели обучения

Квадратичные функции
- Корни или нули квадратичной функции
- Характеристики параболы
  - вершина
  - ось симметрии
  - x/y — пересечения
Классификация решений квадратных уравнений
- Дискриминант

Изогнутые антенны, подобные показанным на фото, обычно используются для фокусировки микроволн и радиоволн для передачи телевизионных и телефонных сигналов, а также спутниковой и космической связи. Поперечное сечение антенны имеет форму параболы, которую можно описать квадратичной функцией.

Набор спутниковых антенн. (кредит: Мэтью Колвин де Валле, Flickr)

Характеристики парабол

График квадратичной функции представляет собой U-образную кривую, называемую параболой . Одной из важных особенностей графа является то, что он имеет крайнюю точку, называемую вершиной . Если парабола раскрывается, вершина представляет собой самую низкую точку на графике или минимальное значение квадратичной функции. Если парабола направлена вниз, вершина представляет собой самую высокую точку на графике или максимальное значение . В любом случае вершина является поворотной точкой на графе. График также симметричен, вертикальная линия проходит через вершину, называемую осью симметрии .

Точка пересечения y — это точка, в которой парабола пересекает ось y . Точки пересечения x — это точки, в которых парабола пересекает ось x . Если они существуют, x -перехватов представляют собой нулей или корни квадратичной функции, значения x при которых y = 0.

Пример: определение характеристик параболы

Определить вершину, ось симметрии, нули и y — точка пересечения параболы, показанной ниже.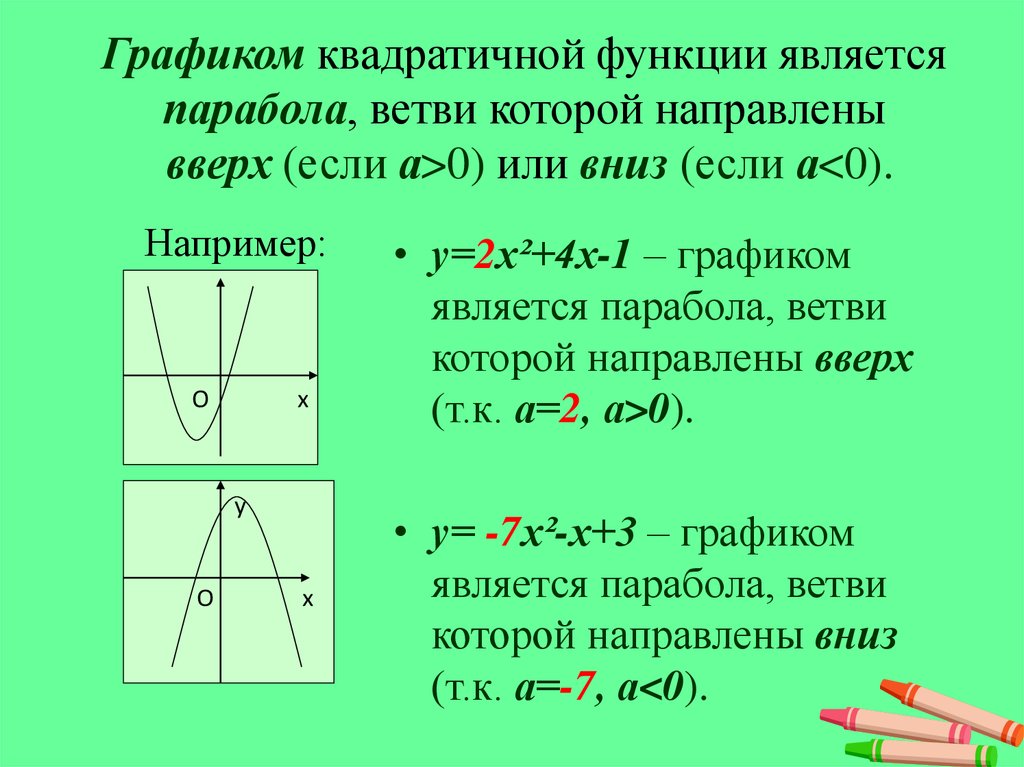

Решение

Попробуйте

Общие и стандартные формы квадратичных функций

Общая форма квадратичной функции представляет функцию в виде 9{2}+4x+3[/латекс]. В этой форме [латекс]а=1,\текст{ }b=4[/латекс] и [латекс]с=3[/латекс]. Поскольку [latex]a>0[/latex], парабола открывается вверх. Ось симметрии: [латекс]x=-\frac{4}{2\left(1\right)}=-2[/latex]. Это также имеет смысл, поскольку на графике видно, что вертикальная линия [latex]x=-2[/latex] делит график пополам. Вершина всегда находится вдоль оси симметрии. Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. 9{2}+k[/latex]

, где [latex]\left(h,\text{ }k\right)[/latex] — это вершина. Поскольку вершина появляется в стандартной форме квадратичной функции, эта форма также известна как вершинная форма квадратичной функции .

Для заданной квадратичной функции в общем виде найдите вершину параболы.

Одна из причин, по которой мы можем захотеть идентифицировать вершину параболы, заключается в том, что эта точка сообщит нам, где происходит максимальное или минимальное значение выходного сигнала ( 92+bx+c[/latex]

Мы можем определить вершину [latex](h,k)[/latex], выполнив следующие действия:

Идентифицировать a , b и c .
Найдите h , координату x вершины, подставив a и b в [latex]h=-\frac{b}{2a}[/latex].
Найдите k , y -координату вершины, оценивая [latex]k=f\left(h\right)=f\left(-\frac{b}{2a}\right)[/ латекс] 9{2}-6x[/latex], напишите уравнение в общем виде, а затем в стандартном виде.
Решение
В этом разделе мы продолжим изучение квадратичных функций, в том числе решим задачи, связанные с площадью и движением снаряда. Работа с квадратичными функциями может быть менее сложной, чем работа с полиномиальными функциями более высокой степени, поэтому они предоставляют хорошую возможность для детального изучения поведения функции.

Классификация решений квадратных уравнений
Как и в предыдущих прикладных задачах, нам также необходимо найти точки пересечения квадратных уравнений для графического построения парабол. Напомним, что мы находим y — пересечение квадратичного уравнения путем оценки функции на входе, равном нулю, и мы находим x — пересечений в местах, где выход равен нулю. Обратите внимание, что количество перехватов размером x может варьироваться в зависимости от расположения графика.
Количество пересечений параболы по оси x
Математики также определяют x пересечений как корни квадратичной функции.
Как: Имея квадратичную функцию [латекс]f\влево(х\вправо)[/латекс], найдите 9{2}+5x — 2[/латекс].
Решение
В Примере: Нахождение y – и x – точек пересечения параболы, квадратичное уравнение было легко решено путем разложения на множители. Однако есть много квадратичных уравнений, которые нельзя разложить на множители. {2}+4x — 4[/latex ]. 9{2}-4ac<0[/latex], то число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений нет. Однако вы можете использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания.

Важные термины

ось симметрии: вертикальная линия, проведенная через вершину параболы, относительно которой парабола симметрична; он определяется как [latex]x=-\frac{b}{2a}[/latex]. 92-4ac[/latex], который говорит, имеет ли квадратное число действительные или комплексные корни
вершина: точка, в которой парабола меняет направление, соответствующее минимальному или максимальному значению квадратичной функции

нули

в заданной функции значения x , при которых y = 0, также называемые корнями

Обратная квадратичная функция — ChiliMath

Поиск

Здесь нам нужно найти обратную функцию , из чего следует, что обратная ДОЛЖНА сама быть функцией.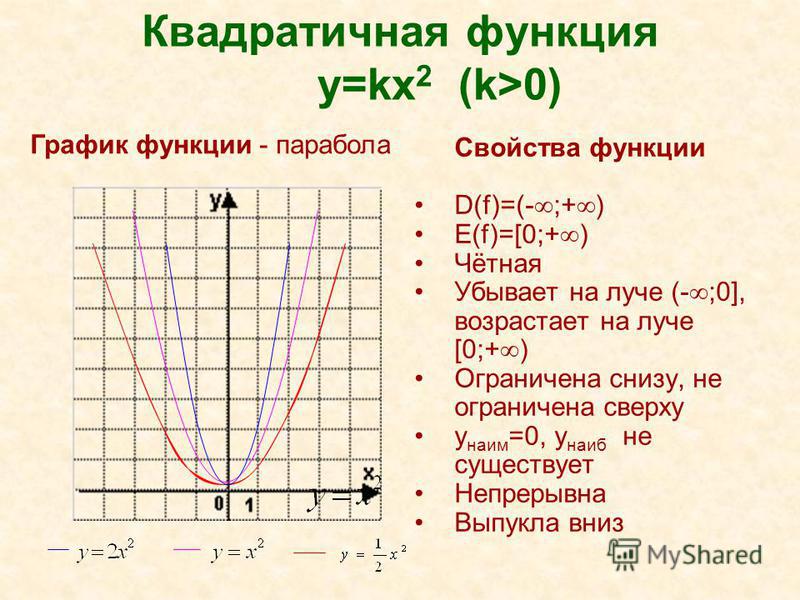 В противном случае мы получили обратную функцию, не являющуюся функцией.

Не всем функциям естественно «повезло» иметь обратные функции. Это происходит в случае с квадратичными уравнениями, потому что все они не проходят тест горизонтальной линии. Однако, если я ограничу их домен тем, где значения x создают график, который прошел бы тест горизонтальной линии, тогда у меня будет обратная функция. 9{ — 1}}\left( x \right), если ни одна горизонтальная линия не пересекает его график более одного раза.

Пример графика с обратной функцией

Пример графика без обратной функции

Ниже приведены основные стратегии алгебраического решения обратной функции.

Основные этапы поиска функции, обратной квадратичной функции

Замените f(x) на y.
Поменяйте местами \color{red}x и \color{blue}y. Другими словами, 92} + 2, если он существует. Укажите его домен и диапазон.
Первое, что я понял, это то, что эта квадратичная функция не имеет ограничения на область определения. Я уверен, что когда я нарисую это, я смогу нарисовать горизонтальную линию, которая будет пересекать его более одного раза. Следовательно, обратная функция не является. Я даже не буду применять ключевые шаги, описанные выше, чтобы найти его обратное.
Диаграмма показывает, что она не прошла тест горизонтальной линии, поэтому обратная функция не является функцией. Я остановлюсь здесь. 92} + 2,\,\,x \ge 0, если он существует. Укажите его домен и диапазон.
Та же самая квадратичная функция, как показано в примере 1, имеет ограничение на область определения, которая равна x \ ge 0. После построения функции по оси xy я вижу, что график представляет собой параболу, разрезанную пополам для всех x значения равны или больше нуля. Это должно пройти тест горизонтальной линии, который говорит мне, что я действительно могу найти его обратную функцию, выполнив предложенные шаги.
На приведенном ниже графике я четко определил домен и диапазон, потому что мне понадобится эта информация, чтобы помочь мне определить правильную обратную функцию в конце.
Помните, что область определения и область значений обратной функции исходят из области значений и области значений исходной функции соответственно. Это называется подменой домена и диапазона .
Даже без решения обратной функции, я могу легко определить ее домен и диапазон, используя информацию из графика исходной функции: домен равен x ≥ 2 , а диапазон равен y ≥ 0 .
Видите, как я меняю домен и диапазон исходной функции, чтобы получить домен и диапазон обратного? 92} — 1,\,\,x \le 0 , если он существует. Укажите его домен и диапазон.
Эта проблема очень похожа на пример 2. Диапазон начинается с \color{red}y=-1 и может опускаться как можно ниже.
Теперь, это шаги по решению для обратного.
Применение операции извлечения квадратного корня приводит к получению двух уравнений из-за положительного и отрицательного случаев. Чтобы выбрать правильную обратную функцию из двух, я предлагаю вам найти домен и диапазон каждого возможного ответа. Теперь правильная обратная функция должна иметь домен из диапазона исходной функции; и диапазон, исходящий из домена той же функции.
Ниже приведены графики исходной и обратной функции на одной оси координат.
Пример 4: Найдите обратную функцию ниже, если она существует. Укажите его домен и диапазон.
Я бы сначала построил график этой функции и четко определил домен и диапазон. Обратите внимание, что ограничение в области делит параболу на две равные половины. Я буду иметь дело с левой половиной этой параболы. Ясно, что это имеет обратную функцию, потому что проходит тест горизонтальной линии. 92} — 4ac} } \over {2a}}}}
, где a, b и c могут содержать переменные.
Это ожидаемо, так как мы ищем функцию, а не точные значения.
Ключевым шагом здесь является выбор подходящей обратной функции в конце, потому что у нас будут плюс (+) и минус (-) случаи. Мы можем сделать это, найдя домен и диапазон каждой функции и сравнив их с доменом и диапазоном исходной функции.
No related posts.