Квадратичная функция с параметрами в природе, физике, экономике.
Группа «физики»: «Квадратичная функция с параметрами в физике»
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных книг говорится: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические уравнения».
Изучение многих физических процессов и закономерностей приводит к решению задач с параметрами. Рассматривая траекторию полета камня, брошенного над горизонтом, линии струй фонтана, полет космической ракеты мы видим их разнообразие и явное сходство.
Параболы используются в радиолокации при создании узконаправленных антенн, в астрономии –радиотелескопы, ярким примером является Зеленчугская обсерватория. Для уменьшения размеров телескопов используются параболические зеркала. А также применение парабол мы наблюдаем в самолетостроении, в баллистике и автомобильной промышленности (для уменьшения сопротивления воздуха-обтекаемости).
В спортивных состязаниях в таких видах, как метание копья и молота, толкание ядра и других видах легкой атлетики присутствует движение по параболе. Зададим вопрос, отчего зависит многообразие линий параболы и можем сказать: «От разных значений коэффициентов квадратичной функции, то есть параметров».
1.Зависимость перемещения тела от времени при равноускоренном движении прямо пропорционально квадрату времени движения S=at2/2.
2. При стрельбе на горизонтальной поверхности под различными углами к горизонту зависимость дальности полета снаряда от угла вылета выражается формулой:
Из этой формулы следует, что при изменении угла вылета снаряда от 90° до 0° дальность его падения сначала увеличится от нуля до некоторого максимального значения, а затем снова уменьшится до нуля. Из этой формулы следует, что максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе) под углом 450;
3. Примерами зависимостей квадратичной функции являются зависимости мощности электрического тока P=I2R при постоянном сопротивлении, угол поворота при равнопеременном движении ϕ=ω0t+εt2/2, кинетической энергии E=mv2/2 и другие формулы, связывающие различные физические величины.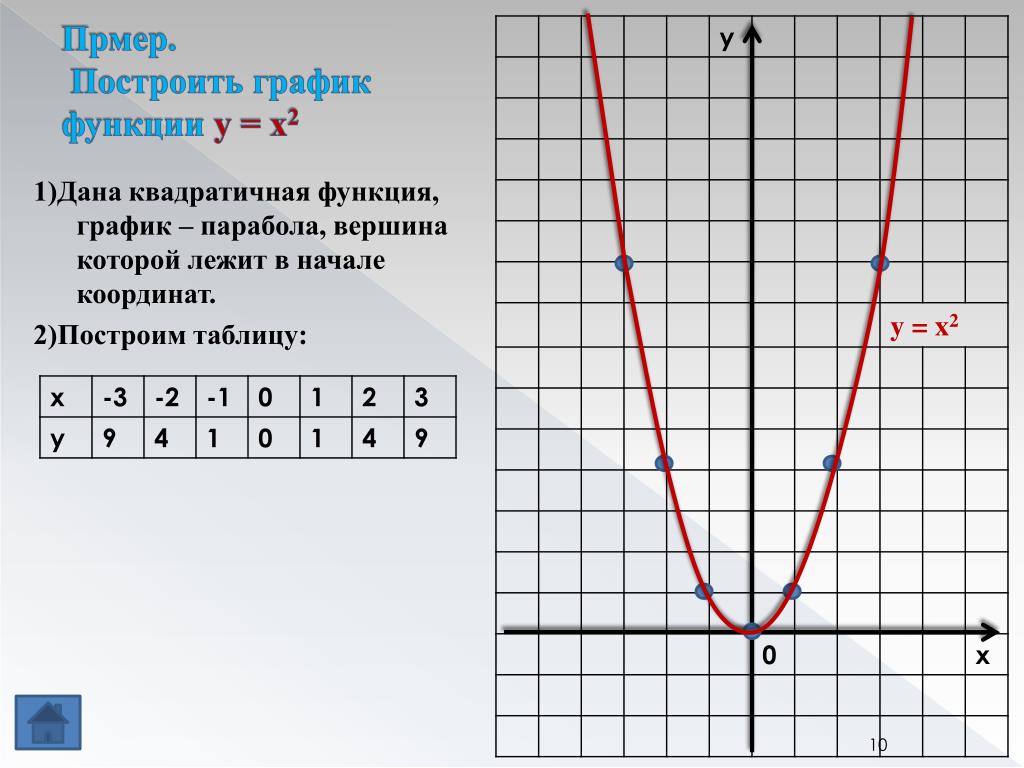
4. Иллюстрацией вида графика квадратичной функции (параболы) является траектория движения тела, брошенного под углом к горизонту
5.Основное уравнение МКТ идеального газа (различные формы записи)Р=1/3 рv2, где Р-давление, р-плотность, v-средняя квадратичная скорость.
6. При протекании электротока I(Ампер) через проводник, на концах его наводится разница потенциалов – электронапряжение U(Вольт), значит проводник имеет некоторое электрическое сопротивление R(Ом):
R=U/I =t*U/Q =U2/P, где Р-мощность преобразования энергии.
7. Квадратичная зависимость скорости света подтверждается астрономическими наблюдениями. Количественный преобразовательный коэффициент равен:
СZ = S*w2 = r2*w2 = (r*w)2, (метр2)
и есть полная площадь сечения материи, описывает количество материи для электрической индуктивности и выражено в квадратичной зависимости от величины «длинна» и величины «число витков».
Хорошо известно, что траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха).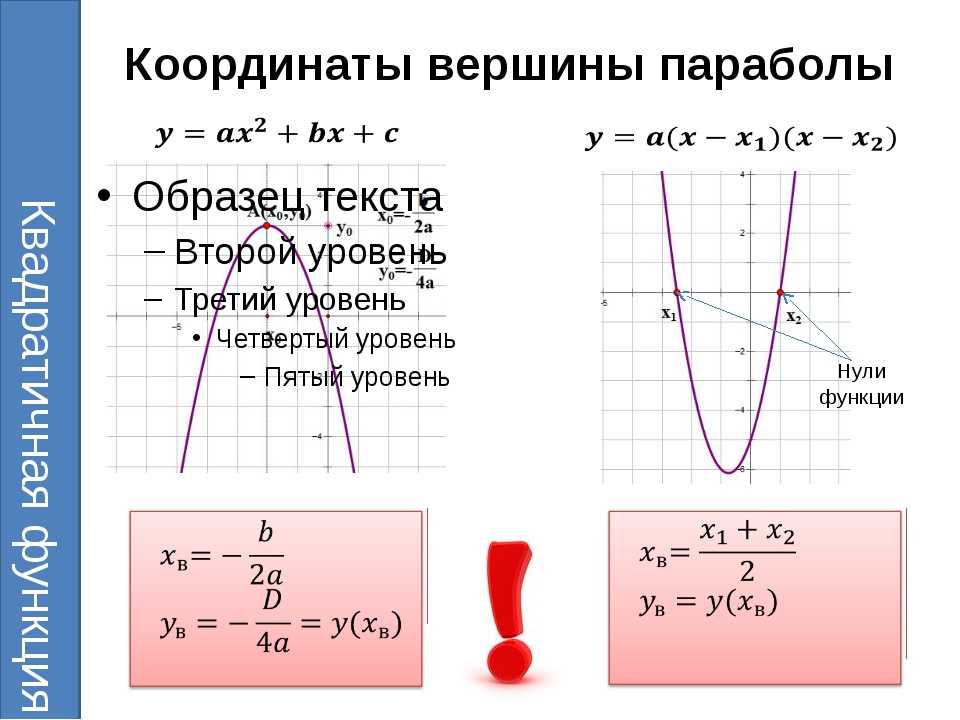
Однако мало кто знает, что зона достижимости для пущенных нами камней вновь будет параболой. В данном случае мы говорим об огибающей кривой траекторий камней, выпущенных из данной точки (рис. 1) под разными углами, но с одной и той же начальной скоростью. Если рассматривать такую огибающую в пространстве, то возникнет поверхность, образованная вращением этой параболы вокруг ее оси. Такая поверхность носит название параболоида вращения.
Рис. 1
Как и другие конические сечения, парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно ее оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (рис. 2).
Рис. 2
Очевидно, что пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в ее фокусе. На этом основана идея телескопов-рефлекторов, зеркала которых выполнены в виде параболоидов вращения.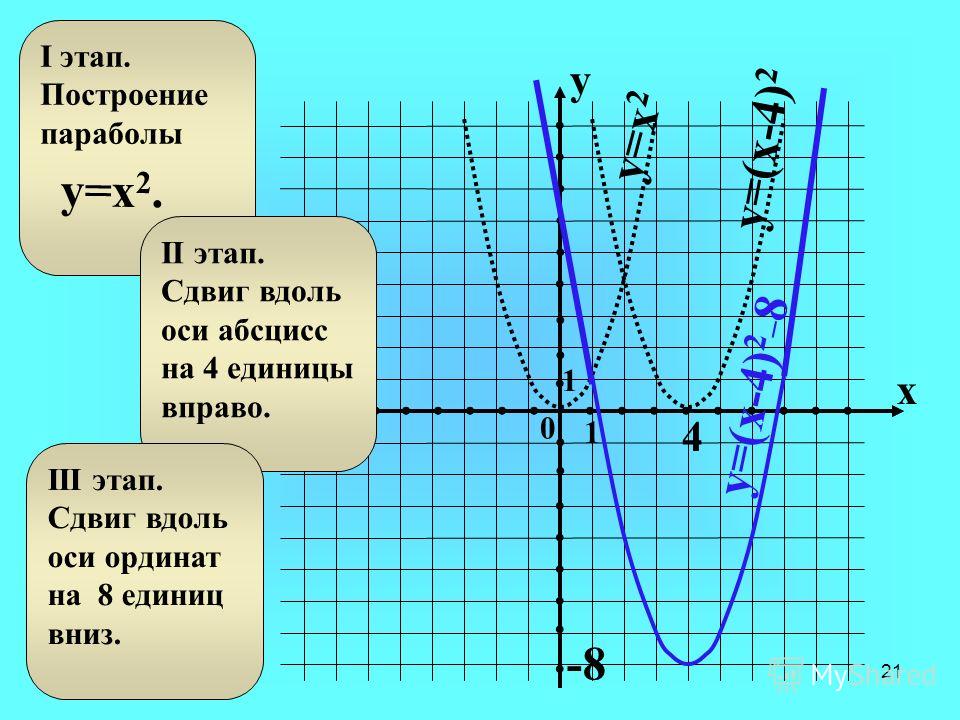
Любопытно, что параболоид вращения образует поверхность жидкости в цилиндрическом сосуде, если его вращать относительно своей оси.
Если параболоид вращения равномерно сжать к одной из плоскостей, проходящих через его ось, то получается поверхность, которая называется эллиптическим параболоидом. Это название объясняется тем, что любое плоское сечение этой поверхности — либо эллипс, либо парабола (рис. 3). Уравнение эллиптического параболоида имеет вид
.
Рис. 3
Если , то такой эллиптический параболоид будет параболоидом вращения.
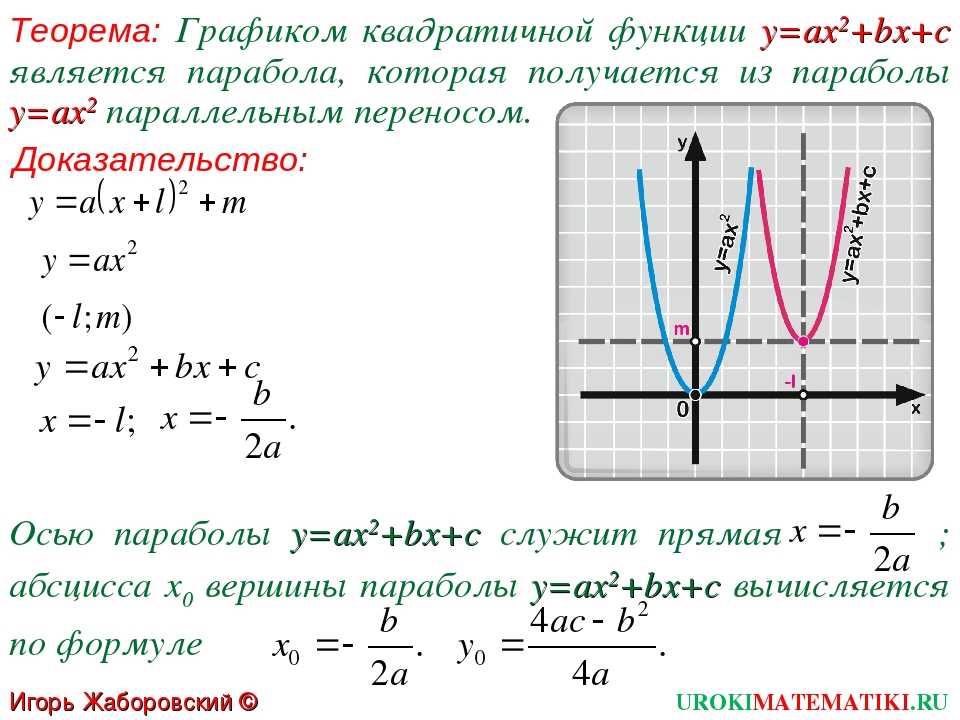
Определение и символическое представление Квадратичные функции могут быть представлены символически уравнением, у ( х ) = ах 2 + бх + с , , где a , b и c — константы, а a ≠ 0. Графическое представление Квадратичные функции — это нелинейные функции, графически представленные параболами. Параболы имеют характерную ∪-форму и открываются либо вверх, либо вниз, как показано ниже, На эти графики следует обратить внимание:
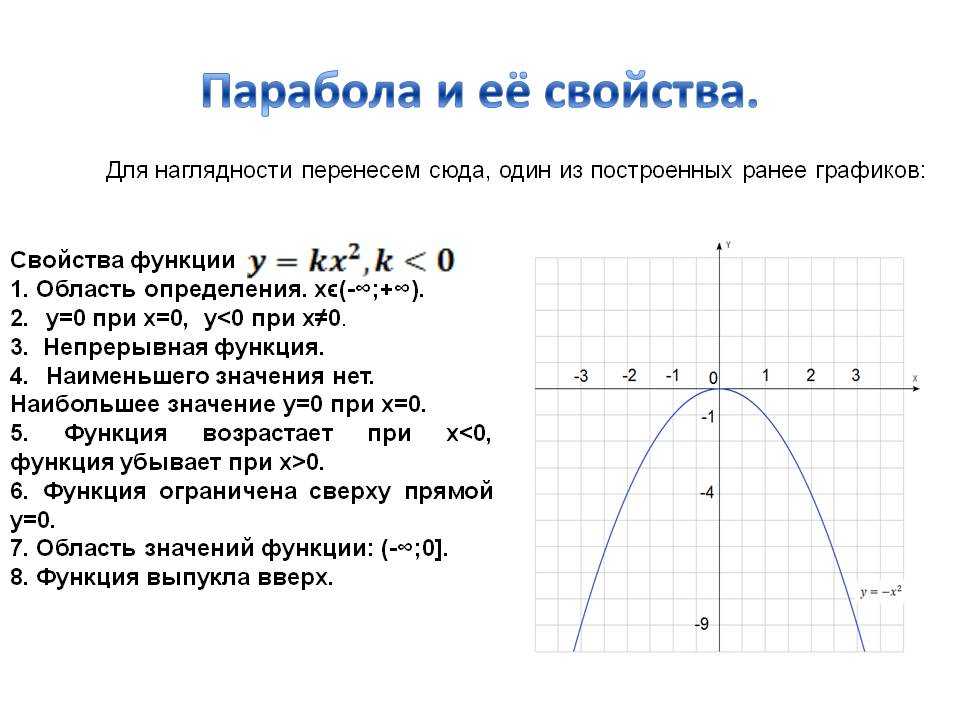
Стандартная форма дает представление о том, как будет выглядеть график квадратичной функции. Анализируя квадратное уравнение в стандартной форме, у ( х ) = ах 2 + бх + с , вы можете получить представление о том, как будет выглядеть график. Старший коэффициент говорит вам, в каком направлении открывается парабола, а именно .
Кроме того, константа c является точкой пересечения y квадратичной функции. y (0) = a · 0 2 + b · 0 + c y (0) = c . Обратите внимание, что квадратичная функция всегда будет пересекать ось y , но может не пересекать ось x (мы обсудим эту тему более подробно позже). Наконец, изучив стандартную форму квадратного уравнения, вы увидите, что областью определения квадратных функций являются все действительные числа (т. е. нет значения x , которое нельзя было бы подставить в уравнение y ( x ) = ах 2 + bx + c ). Однако диапазон квадратичных функций составляет , а не всех действительных чисел, а скорее варьируется в зависимости от формы кривой.
Пример Простейшая квадратичная функция задается как y = x 2 . Чтобы построить график этой функции вручную, вы можете использовать следующую таблицу значений: Изучив эту таблицу значений, вы увидите, что функциональные значения симметричны относительно вертикальной линии x = 0. Вы можете нанести эти точки на плоскость xy- и провести через них плавную кривую, чтобы сформировать параболу, как показано ниже,
***** В следующем разделе мы рассмотрим, как найти вершину параболы. Вершина квадратичной функции |
Эта форма называется стандартной. Коэффициент a в этой форме называется старшим коэффициентом, потому что он связан с наибольшей степенью x (т. е. квадратом члена).
Этот факт можно вывести математически, установив x = 0 (помните, что точки, лежащие на оси Y, должны иметь координату x 
Квадратичные функции и производная | |
| Квадратичная функция — это полиномиальная функция степени 2. Нас интересует изучение производной простых функций с помощью интуитивного и визуального подхода. Для изучения производной квадратичной функции мы собираемся следовать тому же подходу, который мы использовали в случай линейной функции. ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ Производную функции в точке можно определить как мгновенную скорость изменения или как наклон касательной к точке. график функции в этой точке. Мы можем сказать, что этот наклон тангенса функции в точке есть наклон функция. Наклон функции, вообще говоря, будет зависеть от x. Тогда, начиная с функции, мы можем получить новую функцию, производную от исходной функции. Процесс нахождения производной функции называется дифференцированием. Значение производной функции для любого значения x представляет собой наклон исходной функции в точке x. Затем начинаем проводить касательную к параболе в точке. Но как мы можем провести касательную? Мы можем использовать увеличительное стекло!. Затем проводим параллельную прямую касательной, проходящей через значение x-1, и получаем прямоугольный треугольник. Длина вертикальной стороны — наклон касательной. Производная функция квадратичной функции является линейной функцией. Производная квадратичной функции: Как уже знал Ферма, в локальном максимуме или минимуме касательная горизонтальна, производная равна 0. Мы можем видеть что в вершине параболы касательная горизонтальна и что производная функции пересекает ось x в точке это значение. Когда а является отрицательным числом, парабола открывается вниз, а ее производная является линейной функцией с отрицательным наклоном. В этом случае вершина является максимальной и, как и прежде, касательная в этой точке горизонтальна. Одна простая и интересная идея заключается в том, что когда мы переводим вверх и вниз график функции (мы добавляем или вычитаем число из исходной функции),
производная не меняется. |
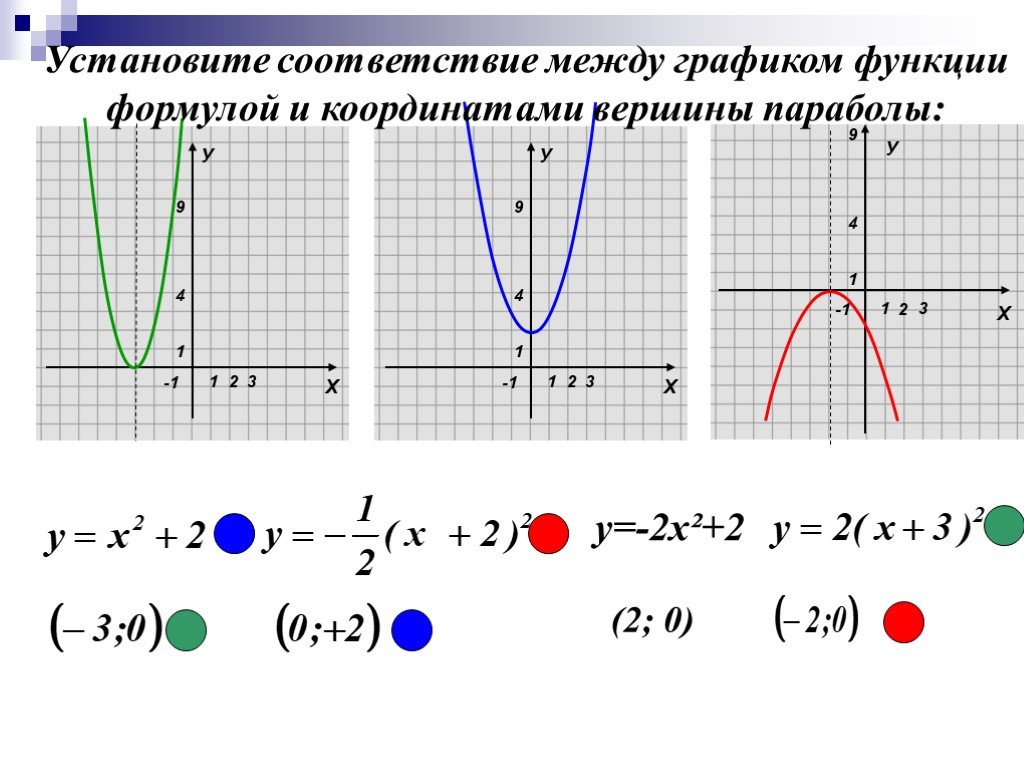
Если мы посмотрим очень близко к точке параболы, мы увидим, как парабола напоминает касательную. Эта касательная линия
является наилучшей линейной аппроксимацией параболы в этой точке: