Visual basic практическая работа «Решение квадратного уравнения»
Лабораторная работа №1. Решение квадратного уравнения.
Задача. Составить программу решения квадратного уравнения ax2+bx+c=0.
1. Вывод результата с помощью оператора Print
Решение. Рассмотрим блок-схему решения данной задачи:
Введем вспомогательные переменные d, x1, x2.
Программа написана справа от блок-схемы.
Private Sub Command1_Click()
a = InputBox(«Введите а»)
b = InputBox(“Введите b”)
c = InputBox(«Введите c»)
d = b * b — 4 * a * c
If d
Print «Нет решения»
Else
X1 = (-b + Sqr(d)) / (2 * a)
X2 = (-b — Sqr(d)) / (2 * a)
Print “x1=”; X1
Print “x2=”; X2
End If
End Sub
Для выполнения программы нажимает клавишу F5.
Вводим значения коэффициентов a, b, c. Результат работы программы читаем в форме.
Контрольные примеры:
a=1, b = 2, c = 1, ответ: x1 = -1, x2 = -1
a=5, b = 6, c = 7, ответ: Нет решения
a=1567, b = -110, c = -15, ответ: x1=0,13904296372987 x2=-6,88451334809872E-02
a=1.5, b = 1, c = -4, сообщение об ошибке. Следует нажать кнопку End.
При вводе десятичных дробей через окно InputBox следует применять запятую.
a=1,5, b = 1, c = -4, ответ: x1 = 1,3333333, x2 = -2
Если запустить программу и ничего не вводить (a=0, b = 0, c = 0), а нажимать ОK (Enter), то появится сообщение об ошибке.
Следует нажать кнопку End.
2) Добавление новых элементов в форму
Главным объектом среды программирования Visual Basic является форма. До сих пор на форме мы располагали только одну кнопку, результат читали также на поверхности формы.
Инструментальное меню Visual Basic содержит много элементов, которые также можно разместить на форме. Познакомимся поближе со второй строкой этой панели.
Буква А означает надпись. При наведении на неё курсора появляется слово Label (читается лэйбл, переводится этикетка, надпись). На форме надпись будет растягиваться аналогично командной кнопке — в виде прямоугольника. В неё мы будем печатать поясняющие надписи.
Справа от неё находится кнопка текстовое окно TextBox (читается ТекстБокс, текстовая панель). В текстовое окно можно вводить и выводить информацию (числа, слова).
Создадим форму для задачи «Нахождение корней квадратного уравнения», используя вышеперечисленные элементы инструментального меню.
Прежде всего создадим в тетради эскиз формы. Он может выглядеть так:
Создадим на форме места под будущие надписи и окна. Методом растягивания, перетаскивания и изменения размеров создайте форму с кнопкой, четырьмя лейблами, и четырьмя текстовыми окнами.
Изменение свойств формы
Щелкнем на свободном месте формы. Она будет ограничена квадратными маркерами по восьми направлениям изменения размеров формы.
Справа активизировалась панель свойств этой формы – Properties – Form1 (читается пропетиз фом ван, переводится свойства формы один). В этом окне слева расположены названия свойств, а справа их значения. Значения мы можем менять по своему усмотрению. Названия свойств являются ключевыми словами языка VB, их постепенно надо запоминать. Нам надо изменить текст в заголовке формы. Изменение текста заголовка формы выполняется в строке Caption (произносится — кэпшн, переводится заголовок). Щелкаем мышкой по этому свойству, печатаем – Решение квадратного уравнения, нажимаем Enter.
Текст появляется в заголовке формы.
Изменим цвет формы. Для этого в свойствах находим строку BackColor (бэк колор, задний цвет). На вкладке Palette (палетте, палитра) выбираем нужный нам цвет для формы, щелкнув по нему указателем мыши.
Выделяем командную кнопку и в разделе свойств Caption печатаем Вычислить.
Выделяет объект Label1. В разделе свойств Caption печатаем а =. Переходим к свойству Alignment (читается — элайнмент, переводится выравнивание). Раскрываем список этой строки и выбираем выравнивание по правому краю 1. Right Justify (Райт джустифай, правое, если много текста, то левая и правая границы выровнены). Можно было нажать клавишу с цифрой 1.
Свойство Font (фонт, вид шрифта) позволит нам настроить вид символов. В диалоговом окне можно выбрать тип шрифта, начертание (обычный, курсив, полужирный) и размер 14. Сделайте так, чтобы текст а = выглядел как а =. “это достигается применением шрифта Times New Roman (Таймс Нью Роман)
Аналогично меняем содержимое объектов Label2, Label3.
В свойстве Caption объекта Label4 записываем Ответ:
В свойствах текстового окна Text1 находим строку Text. Стираем существующую надпись, можно пробелом, и подтверждаем изменение клавишей Enter или щелчком мыши на другом объекте.
Аналогично поступаем с остальными текстовыми окнами. Форма готова.
Точечная запись — в качестве переменной
Объектно-ориентированные языки программирования работают с объектами. В качестве объекта может быть форма, командная кнопка, надпись, текстовое окно и др. Каждый из этих объектов имеет свойства. Эти свойства можно менять по нашему усмотрению либо на Панели свойств (Properties), либо из программы. Для того, чтобы изменить свойства из программы, точнее, иметь доступ к свойствам объекта их командной строки, нужно указать название объекта и через точку свойство. Например, чтобы иметь доступ к содержимому первого текстового окна нашего проекта по свойству Text, надо сделать запись: Text1.
Text. –(в программном коде)
Такая запись может использоваться в качестве переменной. Свойство может содержать какое-либо значение. Это значение мы можем записать при запуске программы, или программист, при составлении программы, поместит в него какое-нибудь значение.
Сравните две строки:
Text1.Text = “5” — эта строка помещает значение 5 в текстовое окно Text1.
a= Text1.Text — эта строка присваивает переменной a содержимое текстовой строки. Если в текстовом окне ничего нет, то Visual Basic помещает в него специальное значение Null. Это ни нуль, не пробел, а пустое место.
для этой формы будет выглядеть так:
Private Sub Command1_Click()
a = Text1.Text
b = Text2.Text
c = Text3.Text
d = b * b — 4 * a * c
If d
Text4.Text = “Нет решения”
Else
X1 = (-b + Sqr(d)) / (2 * a)
X2 = (-b — Sqr(d)) / (2 * a)
Text4.
Text = “x1=” & X1 & “ x2=” & X2
End If
End Sub
Программу следует проверить на контрольных примерах. Перемещение по окнам сверху вниз — клавишей Tab. . Перемещение по окнам снизу вверх клавишным аккордом — Shift +Tab. Программа будет работать правильно для корректных данных, иначе будет появляться сообщение об ошибке.
Не понимаю, что случается, если b и c равны нулю — d будет тоже ноль, а корень из нуля нормально себе вычисляется. Отдельной обработки для этого не нужно! Разве что проверка d >= 0 у вас запоздала — надо бы это делать до попытки вычисления корня из d. Ещё совет: объявляйте d там, где присваиваете ему значение в первый раз — здесь это всегда происходит в одном и том же месте всего один раз, так что альтернатива — объявлять где-то наверху — не востребована. Ну и раз вы выбрали метод Parse, кидающий исключение при некорректном параметре, вы тогда и обрабатывайте исключение, иначе программа свалится с непонятным для пользователя сообщением. Лучше, как Progger посоветовал, всё же взять TryParse. Напоследок, C# — не какой-то редкий язык и форумная подсветка синтаксиса его знает, так что код на C# вкладывайте лучше в [syntax lang=»csharp»][/syntax] (можно просто выбрать этот язык из списка «Подсветка синтаксиса» над полем ответа, и всё само вставится). Получится удобочитаемее! — Вт сен 09, 2014 22:49:49 — Дальше. Косметическая деталь: если операторы внутри вашего if писать на отдельной строке, это сделает удобным добавление новых операторов, если это в будущем пригодится (раз скобка, два скобка, и никаких лишних движений. А некоторые даже однооператорные тела сразу в скобки берут, но последнее уже больше дело вкуса, чем первое). Косметическая деталь №2: я бы поставил пробелы после двоеточия внутри строк — «Введите значение a: «, например. (Понятно, для чего? Текст в консоли будет выглядеть не так: Кстати, про объявление d я написал, а про строки забыл. С ними аналогично. (Да и рефакторингу повторных кусков в цикл это поможет — опять же меньше переделывать.) Вы неплохо выбрали задачу: улучшать её можно достаточно долго, пока вы будете изучать всё новые вещи! — Вт сен 09, 2014 22:54:01 — Посыпьте мне голову: там же WriteLine! Совет с пробелами бессмыслен. — Вт сен 09, 2014 23:09:49 — (Хотя, по мне, при вводе однострочных вещей лучше вводить на той же строке, что и prompt.) |
Так при чтении сразу видно тип, и не надо держать в голове d, пока чтение не дошло до неё.
Кроме того, можно будет заставлять его делать это до тех пор, пока не введёт число. Тут тоже цикл, только другой.
Как решать квадратные уравнения – mathsathome.com
Решение квадратных уравнений: видео-урок коэффициент 𝑥
2 .Введите значения ‘a’, ‘b’ и ‘c’ в решатель квадратного уравнения ниже, чтобы вычислить значения 𝑥, которые удовлетворяют уравнению.
Например, квадратное уравнение имеет ‘a’=2, ‘b’=1 и ‘c’=-3.
Как решать квадратные уравнения
Чтобы решить квадратное уравнение, первым делом нужно приравнять одну часть уравнения к нулю. 3 способа решения квадратных уравнений: разложение на множители, завершение квадрата или использование квадратной формулы. Если квадратное уравнение нельзя разложить на множители, необходимо использовать формулу квадрата или квадрата.
Если квадратное выражение имеет коэффициент 𝑥 2 , равный 1, то его можно решить, разложив на множители следующим образом: можно использовать квадратную формулу:
Вот список методов, которые можно использовать для решения квадратных уравнений:
- Если 𝑥 2 равно числу, извлеките квадратный корень из обеих частей уравнения, чтобы решить его.
- Если квадратное число содержит только члены 𝑥 2 и 𝑥, разложите 𝑥 на множители и решите.
- Попробуйте разложить на множители, найдя два числа, которые складываются, чтобы получить коэффициент 𝑥, и умножаются, чтобы получить постоянный член. Решите, установив каждый фактор равным нулю.
- Если квадратное число содержит коэффициент 𝑥 2 больше 1, попробуйте разделить член 𝑥 и разложить на множители путем группировки.
- Если квадратное число нельзя разложить на множители, дополните квадрат и решите.
- Если квадратное число нельзя разложить на множители, используйте квадратичную формулу.
Все квадратные уравнения можно решить с помощью квадратной формулы, поэтому этот метод всегда будет работать для решения квадратных уравнений.
Как решать квадратные уравнения с использованием квадратных корней
Если квадратное уравнение имеет форму 𝑥 2 =k, квадратный корень с обеих сторон. Решения 𝑥 = ± √ k. Например, если 𝑥 2 = 4 затем 𝑥 = ± 2.
. .
В следующем примере 𝑥 2 равно неквадратному числу. Мы по-прежнему извлекаем корень из обеих частей уравнения, чтобы получить решение.
Например, решить 𝑥 2 -5=0.
Первый шаг — добавить 5 к обеим частям уравнения, чтобы 𝑥 2 =5.
Следующим шагом будет извлечение квадратного корня из обеих частей уравнения так, чтобы 𝑥=±√5.
Оценка ±√5 на калькуляторе, 𝑥≈-2,24 или 𝑥≈2,24.
Как решать квадратные уравнения с помощью факторинга
Чтобы решить квадратное уравнение ‘𝑥 2 + b 𝑥+c=0’ с помощью факторинга:
Решение квадратных уравнений с помощью факторинга: Пример 1
Например, решите квадратное уравнение с помощью факторинга.
Здесь и .
Шаг 1. Задумайте два числа, которые в сумме дают b и умножаются на c
Числа 1 и 3 сложить, чтобы получить 4, и умножить, чтобы получить 3.
Шаг 2. Разложите квадратное выражение как (𝑥+ m )(𝑥+ n 1)=900 m и n — это два числа из шага 1
В шаге 1 два числа, которые складываются, чтобы получить 4, и умножаются, чтобы получить 3, были 1 и 3 .
Следовательно, квадратное уравнение можно разложить на множители до .
Шаг 3. Решите квадратное уравнение, приравняв каждую скобку к нулю
Либо либо .
Находим значения 𝑥, при которых каждая скобка равна нулю.
Для , решение .
Для решения .
Следовательно, решения этого квадратного уравнения равны 𝑥=-3 и 𝑥=-1.
Решение квадратных уравнений с помощью факторизации: примеры с отрицательными числами
Чтобы решить квадратное уравнение с помощью факторизации, подумайте о двух числах, которые в сумме образуют коэффициент 𝑥, и умножьте их, чтобы получить постоянный член.
Для квадратного числа используйте следующие правила, чтобы найти два числа:
- Если b и c оба положительны, оба числа будут положительными
- Если c положительно, а b отрицательно, оба числа будут отрицательными 9 Если отрицательно, одно число будет положительным, а одно число отрицательным
Легче разложить на множители квадратичные числа, если вы знаете, какие знаки следует ожидать в скобках.
Вот несколько примеров решения квадратных уравнений методом факторизации.
- В примере 1, .
Поскольку b и c положительны, квадратичный фактор будет равен .
Два числа, которые складываются, чтобы получить 6, и умножаются, чтобы получить 8, это 4 и 2.
Таким образом, факторизованный квадратичный равен и так, и .
- В примере 2 .
Здесь c является положительным, а b отрицательным, поэтому квадратичный фактор будет равен .
Два числа, которые складываются, чтобы получить -5, и умножаются, чтобы получить 6, -3 и -2.
Следовательно, факторизованный квадратичный равен и так, и .
- В примере 3 .
Здесь c отрицательно, поэтому квадратичный фактор будет равен .
Два числа, которые складываются, чтобы получить 2, и умножаются, чтобы получить -3, это 3 и -1.
Следовательно, факторизованный квадратичный равен и так, или .
- В примере 4, .
Здесь c отрицательно, поэтому квадратичный фактор будет равен .
Два числа, которые складываются, чтобы получить -3, и умножаются, чтобы получить -10, это 2 и -5.
Следовательно, факторизованный квадратичный равен и так, и .
Как решать квадратные уравнения с разностью двух квадратов
Любое квадратное уравнение вида 𝑥 2 -a 2 =0 можно разложить на множители как (𝑥+a)(𝑥-a)=0 с помощью разность двух квадратов. Следовательно, решения равны 𝑥=a и 𝑥=-a. Например, 𝑥 2 -25=0 делит на (𝑥+5)(𝑥-5)=0 и имеет решения 𝑥=5 и 𝑥=-5.
Квадратные уравнения вида можно решить методом разности двух квадратов.
Чтобы определить разность двух квадратов, квадратное число должно состоять из двух членов, разделенных знаком минус.
Для квадратичного , это то же самое, что и .
Следовательно, это может быть учтено как и установка каждой скобки равной нулю для решения, и .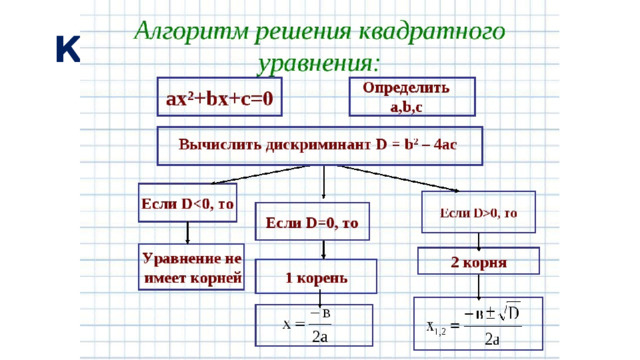
Разность двух квадратов также может быть использована для решения квадратичных уравнений вида . Эти квадратичные уравнения будут учитывать форму, которую можно решить, установив каждую скобку равной нулю.
Например, решить, используя разность двух квадратов.
Можно разложить на множители как .
Таким образом, решения и .
Как решать квадратные уравнения с коэффициентом 𝑥
2 Больше 1Чтобы решить квадратное уравнение со старшим коэффициентом больше 1, используйте квадратную формулу или разложите на множители и решите.
Разложить квадратичное число a 𝑥 2 + b 𝑥+c, когда a больше 1:
- Разделите средний член на два члена, которые умножаются, чтобы получить значение а × в .
- Умножьте первые два члена и два последних члена отдельно.
- Фактор всего выражения путем группировки.
Например, разложить на множители и решить квадратное число .
В этом квадратном , и
Шаг 1. Разделите средний член на два члена, которые умножаются, чтобы получить значение a × c
Средний член равен . Это будет разделено на два члена, которые при умножении равны значению 2 × 6.
разбивается на потому, что 4×3=12, то есть 2×6.
Шаг 2. Разложите на множители первые два члена и два последних члена отдельно
Квадратичный в настоящее время записывается как .
Первые два члена можно разложить как , а последние два члена можно разложить как .
Поэтому можно записать как .
Шаг 3. Разложите все выражение на множители путем группировки
В уравнении есть общий множитель, который равен .
можно сгруппировать, чтобы получить .
Шаг 4. Решите квадратное уравнение, приравняв каждую скобку к нулю
В настоящее время квадратное уравнение записывается как .
Следовательно, или или .
Решение этих уравнений или .
Примеры решения квадратных уравнений с a>1 методом факторизации
Вот несколько примеров решения квадратных уравнений со старшим коэффициентом больше 1 с использованием факторизации методом группировки.
| Equation | Split the middle term | Factor | Group | Solutions |
| , | ||||
| , | ||||
| , | ||||
| , |
How to Solve Quadratic Equations by Completing the Square
Все квадратные уравнения можно решить, составив квадрат, а затем переставив уравнение для 𝑥. Например, уравнение 𝑥 2 +4𝑥+1=0 можно записать как (𝑥+2) 2 -3=0.
Прибавляя 3 к обеим частям уравнения, (𝑥+2) 2 =3. Извлекая квадратный корень, 𝑥+2=±√3 и, следовательно, 𝑥=-2±√3.
Чтобы решить уравнение, заполнив квадрат, выполните следующие действия:
- Заполните квадрат, написав 𝑥 2 +b𝑥+c=0 в форме
- Переместите постоянный член на другую сторону знака равенства
- Квадратный корень с обеих сторон
- Найдите 𝑥
Например, завершите квадрат и решите, .
Шаг 1. Заполните квадрат
Чтобы заполнить квадрат, напишите в форме .
В и .
Таким образом, завершение квадрата по приведенной выше формуле становится .
Это упрощается до .
Заполнение квадрата завершено, и теперь мы решаем уравнение, переставляя 𝑥.
Шаг 2. Перенесите постоянную часть на другую сторону от знака равенства
Добавим 3 к обеим частям уравнения, чтобы получилось
Шаг 3.
Квадратный корень с обеих сторон
Извлечение квадратного корня с обеих сторон, становится .
Помните, что при извлечении квадратного корня есть два решения. Положительное и отрицательное решение.
Шаг 4. Найдите 𝑥
Просто вычтите два с обеих сторон, чтобы получилось .
Два решения: и .
Пример решения квадратного уравнения со старшим коэффициентом больше 1 с использованием функции «Завершение квадрата»
Если квадратное уравнение имеет старший коэффициент больше 1, сначала вынесите этот коэффициент перед завершением квадрата.
Например, решить, заполнив квадрат.
Так как старший коэффициент равен 2, вычтите его, чтобы получить .
Теперь мы можем разделить обе части на 2, чтобы получить .
Теперь, заполнив квадрат, мы получим .
Решая 𝑥, получаем .
Examples of Solving Quadratic Equations by Completing the Square
Here are some examples of solving quadratic equations by completing the square
| Quadratic Equation | Complete the Square | Solutions |
, используйте квадратичную формулу 𝑥=[-b±√(b 2 -4ac)]/2a. Квадратная формула является наиболее надежным методом решения квадратного уравнения. Его всегда можно использовать для получения решений.
Формула квадрата
Чтобы использовать формулу квадрата, сначала найдите значения -b, b 2 -4ac и 2a, чтобы эти три значения можно было ввести непосредственно в формулу.
Например, решить квадратное уравнение.
Здесь , и .
Поэтому и .
Ввод этих значений в квадратичную формулу, .
Поэтому и .
и .
Решение квадратных уравнений с помощью квадратичной формулы Примеры
Here are some examples of using the quadratic formula to solve quadratic equations:
| Equation | a | b | c | Quadratic Formula | Solutions |
| 3 | 5 | 1 | , | ||
| 2 | 3 | -5 | , | ||
| 2 | -5 | 1 | , | ||
| 1 | 3 | -1 | , | ||
| -1 | 4 | 2 | , |
Решение квадратных уравнений, записанных не в стандартной форме
Чтобы решить квадратное уравнение, записанное не в стандартной форме, сначала перестройте его так, чтобы оно имело вид a𝑥 2 +b𝑥+c=0 .
Затем его можно разложить на множители или использовать для решения квадратичную формулу.
Решение квадратного уравнения, записанного не в стандартной форме: Пример 1
Например, решить квадратное уравнение .
Первый шаг — умножить обе части уравнения на знаменатель .
Уравнение становится .
Раскрытие скобок, .
Вычитание 4 с обеих сторон, .
можно разложить на множители, чтобы получить .
Поэтому или .
Решение квадратного уравнения, записанного не в стандартной форме: Пример 2
Решите квадратное уравнение, .
Раскрытие скобок, .
Вычитание с обеих сторон, .
Мы можем решить эту проблему, найдя квадратный корень из обеих сторон, чтобы .
Решение квадратного уравнения при заданном «y»
При заданном y в квадратном уравнении соответствующие значения x можно найти, переставив уравнение, равное нулю, и найдя x.
Например, в уравнении найдите значения, для которых .
Подставляя в уравнение .
Добавление 3 к обеим сторонам, .
Факторинг, .
Следовательно, и .
Как решать квадратные уравнения с помощью графика
Для квадратного уравнения, которое установлено равным нулю, решения представляют собой точки пересечения оси x его графика. Построение квадратичного уравнения — один из способов найти точки пересечения. Их можно увидеть на графике как решения квадратного уравнения.
Например, график показан ниже.
График имеет точки пересечения x и .
Это решения .
Решение квадратных уравнений с комплексными решениями
Для квадратного уравнения вида a 𝑥 2 +bx+c=0, комплексные решения будут существовать, если b 2 -4ac<9001. Это связано с тем, что невозможно получить реальные ответы при нахождении квадратного корня из отрицательного числа в квадратной формуле. Вместо этого решения будут содержать мнимые компоненты.
Например, найдите решения для .
а=1, б=2 и с=5.
Следовательно, .
Следовательно, квадратичная формула становится .
С , .
Поэтому упрощает до и так, .
Решение квадратных уравнений
|
Квадратное уравнение с одной переменной: ax 2 + bx + c = 0, где a, b и c — действительные числа с a
≠ 0. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
