Функция x это: Функции y=|x|, y=[x],y={x}, y=sign(x) и их графики. Функция f(x)=|x|

Функции y=|x|, y=[x],y={x}, y=sign(x) и их графики. Функция f(x)=|x|

Функция $f(x)=|x|$

$|x|$ — модуль. Он определяется следующим образом: Если действительное число будет неотрицательным, то значение модуля совпадает с самим числом. Если же отрицательно, то значение модуля совпадает с абсолютным значением данного числа.

Математически это можно записать следующим образом:

Пример 1

Исследуем и построим её график.

1. $D\left(f\right)=R$.
2. По определению модуля действительного числа, получим, что$E\left(f\right)=[0,\infty )$
3. $f\left(-x\right)=|-x|=|x|=f(x)$. Значит, функция четна.
4. При $x=0,\ y=0$. Точка $\left(0,0\right)$ — единственное пересечение с координатными осями.
5. \[f’\left(x\right)=\left\{ \begin{array}{c} {1,x >0,} \\ {-1,xФункция будет возрастать на промежутке $x\in (0,+\infty )$

   Функция будет убывать на промежутке $x\in (-\infty ,0)$

6. Значения на концах области определения.

   \[{\mathop{\lim }_{x\to -\infty } y\ }=+\infty \] \[{\mathop{\lim }_{x\to +\infty } y\ }=+\infty \]
   

   Рисунок 1.

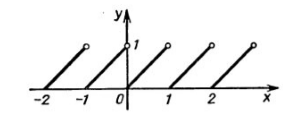
Функция $f(x)=[x]$

Функция $f\left(x\right)=[x]$ — функция целой части числа. Она находится округлением числа (если оно само не целое) «в меньшую сторону».

Готовые работы на аналогичную тему

Пример: $[2,6]=2.$

Пример 2

Исследуем и построим её график.

1. $D\left(f\right)=R$.
2. Очевидно, что эта функция принимает только целые значения, то есть $\ E\left(f\right)=Z$
3. $f\left(-x\right)=[-x]$. Следовательно, эта функция будет общего вида.
4. $(0,0)$ — единственная точка пересечения с осями координат.
5. $f’\left(x\right)=0$
6. Функция имеет точки разрыва (скачка функции) при всех $x\in Z$.

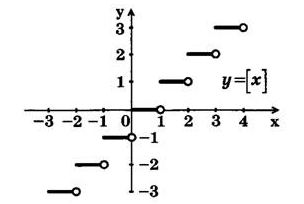
Рисунок 2.

Функция $f\left(x\right)=\{x\}$

Функция $f\left(x\right)=\{x\}$ — функция дробной части числа. Она находится «отбрасыванием» целой части этого числа.

$\{2,6\}=0,6$

Пример 3

Исследуем и построим график функции

1. $D\left(f\right)=R$.

2. Очевидно, что эта функция никогда не будет отрицательной и никогда не будет больше единицы, то есть $\ E\left(f\right)=[0,1)$

3. $f\left(-x\right)=\{-x\}$. Следовательно, данная функция будет общего вида.

   Пересечение с осью $Ox$: $\left(z,0\right),\ z\in Z$

   Пересечение с осью $Oy$: $\left(0,0\right)$

4. $f’\left(x\right)=0$

5. Функция имеет точки разрыва (скачка функции) при всех $x\in Z$

   

   Рисунок 3.

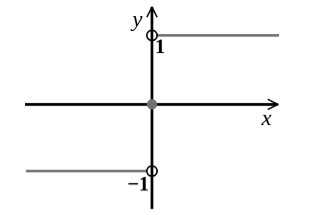
Функция $f(x)=sign(x)$

Функция $f\left(x\right)=sign(x)$ — сигнум-функция. Эта функция показывает, какой знак имеет действительное число. Если число отрицательно, то функция имеет значение $-1$. Если число положительно, то функция равняется единице. При нулевом значении числа, значение функции также будет принимать нулевое значение.

Математически это можно записать следующим образом:

Пример 4

Исследуем и построим график функции

1. $D\left(f\right)=R$.
2. Непосредственно из определения, получим
3. \[\ E\left(f\right)=\left\{-1\right\}\cup \left\{0\right\}\cup \{1\}\]

4. $f\left(-x\right)=sign\left(-x\right)=-sign(x)$. Следовательно, данная функция будет нечетной.

   Пересечение с осью $Ox$: $\left(0,0\right)$

   Пересечение с осью $Oy$: $\left(0,0\right)$

5. $f’\left(x\right)=0$

6. Функция имеет точку разрыва (скачка функции) в начале координат.

   

   Рисунок 4.

Функции и графики — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Координаты и базовые понятия о функциях

К оглавлению…

Длина отрезка на координатной оси находится по формуле:

Длина отрезка на координатной плоскости ищется по формуле:

Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:

Функция – это соответствие вида

y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.

Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.

Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).

Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.

Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.

Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.

Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.

Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.

Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.

Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.

 

График линейной функции

К оглавлению…

Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):

 

График квадратичной функции (Парабола)

К оглавлению…

График параболы задается квадратичной функцией:

Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x₁; 0) и (x₂; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x₀; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):

При этом:

• если коэффициент a > 0, в функции y = ax² + bx + c, то ветви параболы направлены вверх;
• если же a < 0, то ветви параболы направлены вниз.

Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:

 

Графики других функций

К оглавлению…

Степенной функцией называют функцию, заданную формулой:

Приведем несколько примеров графиков степенных функций:

Обратно пропорциональной зависимостью называют функцию, заданную формулой:

В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:

Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.

Показательной функцией с основанием а называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):

Логарифмической функцией называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:

График функции y = |x| выглядит следующим образом:

 

Графики периодических (тригонометрических) функций

К оглавлению…

Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:

где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T₁, который определяется формулой:

Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:

График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:

График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Что такое функция — материалы для подготовки к ЕГЭ по Математике

 

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула – это зависимость давления жидкости от глубины .

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

Знакомое вам обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины по определенному закону, или правилу, обозначаемому .

Другими словами: меняем (независимую переменную, или аргумент) – и по определенному правилу меняется .

Совсем необязательно обозначать переменные и . Например, – зависимость длины от температуры , то есть закон теплового расширения. Сама запись означает, что величина зависит от .

2. Можно дать и другое определение.

Функция – это определенное действие над переменной.

Это означает, что мы берем величину , делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину .

В технической литературе встречается определение функции как устройства, на вход которого подается – а на выходе получается .

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Например, функция каждому действительному числу ставит в соответствие число в два раза большее, чем .

 

Повторим еще раз: каждому элементу множества по определенному правилу мы ставим в соответствие элемент множества . Множество называется областью определения функции. Множество – областью значений.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция . Каждому значению соответствует одно и только одно значение . И наоборот – зная , можно однозначно найти .

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.

Пример такого соответствия в математике – функция . Один и тот же элемент второго множества соответствует двум разным элементам первого множества: и .

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению соответствует не одно, а целых три значения .

Ты нашел то, что искал? Поделись с друзьями!

Перечислим способы задания функции.

1. С помощью формулы. Это удобный и привычный для нас способ. Например:

,

,

,

.

Это примеры функций, заданных формулами.

2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

3. С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» — строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция задается описанием:

Читайте также: Чтение графика функции

Функция

	Главная > Учебные материалы > Математика:  Функция
	1.Понятие функции. 2.Свойства функций. 3.Основные элементарные функции.
	1 2 3 4 5 6 7 8 9
	1. Понятие функции    Понятие «функция» является одним из основных понятий в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией.    Переменая х называется независимой переменной или аргументом, y — зависимой переменной от x, буква f обозначает закон соответствия. Множество X называется областью определения функции, а множество Y, соответственно, областью значений функции.
	2. Cвойства функций    1.Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если  ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида.    2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1< (>) x2, f(x1) < (>) f(x2).    3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом  Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической.    4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | < M. В противном случае функция называется неограниченной.
	3. Основные элементарные функции Степенная функция    у = х  область определения (-∞,∞) область значений (-∞,∞) нечетная возрастает на (-∞,∞) непериодическая
	у = х²  область определения (-∞,∞) область значений (0,∞) четная возрастает на (0,∞) убывает на (-∞,0) непериодическая
	у = х³   область определения (-∞,∞) область значений (-∞,∞) нечетная возрастает на (-∞,∞) непериодическая
	у = 1/х область определения (-∞,0)U(0,∞) область значений (-∞,0)U(0,∞) нечетная убывает на (-∞;0) и на ( 0;∞) непериодическая
	у = 1/х²   область определения (-∞,0)U(0,∞) область значений (0,∞) четная возрастает на (-∞,0) и убывает на (0,∞) непериодическая
	область определения [0,∞) область значений [0,∞) общего вида, возрастает на [0; ∞) непериодическая
	область определения (-∞,∞) область значений (-∞,∞) нечетная возрастает на (-∞,∞) непериодическая
	Показательная функция    у = а ͯ      (a>0  a≠1) область определения (-∞,∞) область значений (0; ∞)  общего вида возрастает на (-∞,∞), если a>1; убывает на (-∞,∞), если 0<a<1 непериодическая
	Логарифмическая функция    у = log ₐ x    (a>0  a≠1) область определения (0,∞) область значений (-∞; ∞)  общего вида возрастает на (0,∞), если a>1; убывает на (0,∞), 0<a<1 непериодическая
	Тригонометрические функции    y = sin x область определения (-∞; ∞)  область значений [-1; 1]  нечетная возрастает на [-π/2 + 2πn, π/2 + 2πn]; убывает на [π/2 + 2πn, 3π/2 + 2πn], nϵZ; период  Т=2π
	y = cos x область определения (-∞; ∞)  область значений [-1; 1]  четная возрастает на [-π + 2πn, 2πn]; убывает на [2πn, π + 2πn], nϵZ; период  Т=2π
	y = tg x область определения (-π/2 + πn, π/2 + πn) nϵZ; область значений (-∞; ∞)  нечетная возрастает на (-π/2 + πn, π/2 + πn) nϵZ; период  Т=π
	y = ctg x область определения (πn, π + πn) nϵZ; область значений (-∞; ∞)  нечетная убывает на (πn, π + πn) nϵZ; период  Т=π
	y = arcsin x область определения [-1; 1] область значений [-π/2; π/2]  нечетная возрастает на [-1; 1]
	y = arccos x область определения [-1; 1] область значений [0; π]  функция центрально-симметрична относительно точки (0; π/2) убывает на [-1; 1]
	y = arctg x область определения (-∞; ∞) область значений [-π/2; π/2]  нечетная возрастает на (-∞; ∞)
	y = arcctg x область определения (-∞; ∞) область значений [0; π]  ни четная, ни нечетная убывает на (-∞; ∞)
	Пример 1. Найти область определения функции.
	Пример 2 Выяснить четность или нечетность функции.		График функции y=x³+2sin x
	Пример 3
	1 2 3 4 5 6 7 8 9

Функция sign(x) — это… Что такое Функция sign(x)?

функция mod_osso — Новое функциональное средство, введенное в Oracle9iAS Release 2. Оно является расширением Oracle HTTP Server, которое позволяет HTTP серверу стать партнерским приложением (см. Partner Applications) для SSO (см. Single Sign On, SSO). Приложения,… …   Справочник технического переводчика

Функция ошибок — График функции ошибок В математике функция ошибок (функция Лапласа)  это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных ур …   Википедия

Функция Лапласа — График функции ошибок В математике функция ошибок  это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как . Дополнительная функция ошибок,… …   Википедия

Функция Ляпунова — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. В теории обыкновенных дифференциальных уравнений, функция Ляпунова является скалярной функцией, которая… …   Википедия

Функция sgn(x) — График функции y = sgn x Функция (другое обозначение: ), читается «сигнум» (от лат. signum  знак)  кусочно постоянная функция, определённа …   Википедия

Sign функция — График функции y = sgn(x) Функция (другое обозначение: , читается: «сигнум», от лат. signum знак) определяется следующим образом …   Википедия

Функция Радемахера — Графики функций Радемахера с Функция Радемахера  кусочно постоянная периодическая функция, принимающая только два значения 1 и −1 на всей обл …   Википедия

Функция знака — График функции y = sgn(x) Функция (другое обозначение: , читается: «сигнум», от лат. signum знак) определяется следующим образом …   Википедия

R-функция — (функция В. Л. Рвачёва)  числовая функция действительных переменных, знак которой вполне определяется знаками ее аргументов при соответствующем разбиении числовой оси на интервалы и . Впервые R функции были введены в работах… …   Википедия

Однородная функция — степени   числовая функция такая, что для любого и выполняется равенство: причём называют порядком однородности. Различают также положительно однородные функции, для которых равенство …   Википедия

Функция sgn(x) — это… Что такое Функция sgn(x)?

График функции y = sgn x

Функция (другое обозначение: ), читается «сигнум» (от лат. signum — знак) — кусочно-постоянная функция, определённая следующим образом:

Функция не является элементарной.

Часто используется представление

При этом производная модуля в нуле, которая, строго говоря, не определена, доопределяется средним арифметическим соответствующих производных слева и справа.

Функция применяется в теории обработки сигналов, в математической статистике и других разделах математики, где требуется компактная запись для индикации знака числа.

История

Функцию sgn(x) ввёл Леопольд Кронекер в 1878 г., сначала он обозначал её иначе: [x]. В 1884 г. Кронекеру понадобилось в одной статье использовать, наряду с sgn, функцию «целая часть», которая также обозначалась квадратными скобками. Во избежание путаницы Кронекер ввёл обозначение , которое (за вычетом точки перед аргументом) и закрепилось в науке.

Свойства функции

См. также

Источники

• Бронштейн И. Н., Семендяев К. А. Справочник по математике. — М.: Наука, 1964. — 608 с.
• Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Основные математические формулы. Справочник. — Минск: Вышэйшая школа, 1988. — 269 с.

Функции — Алгебра — Математика A-Level Revision

В этом разделе рассматриваются функции в рамках более широкой темы алгебры.

Функцию можно рассматривать как правило, которое берет каждый элемент x набора и присваивает ему одно и то же значение y , известное на его изображении.

x → Функция → y

Буква, например f, g или h , часто используется для обозначения функции. Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x ² + 5 .Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.

Пример

f (4) = 4 ² + 5 = 21, f (-10) = (-10) ² +5 = 105 или, альтернативно, f : x → x ² + 5 .

Фраза «y является функцией x» означает, что значение y зависит от значения x, поэтому:

• y можно записать через x (например, y = 3x).
• Если f (x) = 3x и y является функцией x (т.е. y = f (x)), тогда значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4» s.

Пример

Если f (x) = 3x + 4, найти f (5) и f (x + 1).

f (5) = 3 (5) + 4 = 19
f (x + 1) = 3 (x + 1) + 4 = 3x + 7

Домен и диапазон

Область функции — это набор значений, которые вам разрешено вводить в функцию (то есть все значения, которые может принимать x).Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x ² , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку, если y = x ² , y не может быть отрицательным.

Индивидуальные переговоры

Мы говорим, что функция — это взаимно однозначно , если для каждой точки y в диапазоне функции существует только одно значение x такое, что y = f (x).f (x) = x ² не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2). На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.

Функции составления

fg означает выполнение функции g, затем функции f. Иногда fg записывается как fog

Пример

Если f (x) = x ² и g (x) = x — 1, то
gf (x) = g (x ² ) = x ² — 1
fg (x) = f (x — 1) = (х — 1) ²

Как видите, fg не обязательно равно gf

Обратная функция

Обратной функцией функции является функция, которая обращает эффект исходной функции.Например, y = 2x, обратное y = ½ x.
Чтобы найти обратную функцию, поменяйте местами x «s и y» s и сделайте y предметом формулы.

Пример

Найдите обратное к f (x) = 2x + 1
Пусть y = f (x), поэтому y = 2x + 1
поменяет местами x «s и y» s:
x = 2y + 1
Сделайте y объектом формулы:
2y = x — 1, поэтому y = ½ (x — 1)
Следовательно, f ^-1 (x) = ½ (x — 1)

f ^-1 (x) — это стандартное обозначение, обратное f (x).Говорят, что обратное существует тогда и только тогда, когда существует функция f ^-1 с ff ^-1 (x) = f ^-1 f (x) = x

.

Обратите внимание, что график f ^-1 будет отражением f в линии y = x.

Это видео объясняет больше об обратном функции

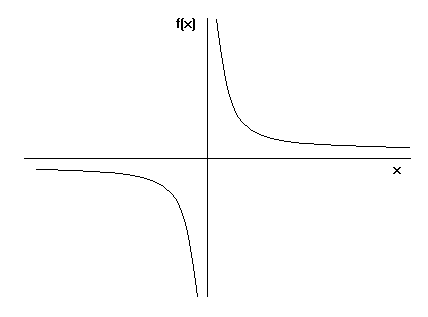
Графики

Функции можно изобразить. Функция непрерывная , если на ее графике нет разрывов. Пример прерывистого графа y = 1 / x, поскольку граф нельзя нарисовать, не отрывая карандаш от бумаги:

Функция периодическая , если ее график повторяется через равные промежутки времени, этот интервал известен как период.

Функция равна даже , если она не меняется при замене x на -x. График такой функции будет симметричным по оси ординат. Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Функция нечетная , если знак функции изменяется при замене x на -x. График функции будет иметь симметрию вращения относительно начала координат (например, y = x³).

Функция модуля

Модуль числа — это величина этого числа.Например, модуль -1 (| -1 |) равен 1. Модуль x, | x |, равен x для значений x, которые положительны, и -x для значений x, которые отрицательны. Итак, график y = | x | y = x для всех положительных значений x и y = -x для всех отрицательных значений x:

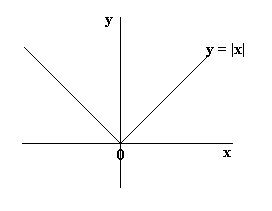
Преобразование графиков

Если y = f (x), график y = f (x) + c (где c — константа) будет графиком y = f (x), сдвинутым на c единиц вверх (в направлении y- ось).
Если y = f (x), график y = f (x + c) будет графиком y = f (x), сдвинутым на c единиц влево.
Если y = f (x), график y = f (x — c) будет графиком y = f (x), сдвинутым на c единиц вправо.
Если y = f (x), график y = af (x) представляет собой отрезок графика y = f (x), масштабный коэффициент (1 / a), параллельный оси x. [Масштабный коэффициент 1 / a означает, что «растяжение» фактически приводит к сжатию графика, если a — число больше 1]

Пример

График y = | x — 1 | будет таким же, как на приведенном выше графике, но со смещением на одну единицу вправо (так, чтобы точка V попала в ось x на 1, а не на 0).

,

Линейные уравнения

Линейное уравнение — это уравнение для прямой линии

Это все линейные уравнения:

		y = 2x + 1
		5x = 6 + 3 года
		y / 2 = 3 — x

Рассмотрим более подробно один пример:

Пример: y = 2x + 1 — линейное уравнение:

График y = 2x + 1 представляет собой прямую линию

• Когда x увеличивается, y увеличивается на вдвое быстрее , поэтому нам нужно 2x
• Когда x равен 0, y уже равен 1.Так что +1 тоже нужен
• Итак: y = 2x + 1

Вот несколько примеров значений:

х	г = 2х + 1
-1	y = 2 × (-1) + 1 = -1
0	y = 2 × 0 + 1 = 1
1	y = 2 × 1 + 1 = 3
2	y = 2 × 2 + 1 = 5

Убедитесь сами, что эти точки являются частью строки выше!

Различные формы

Существует много способов написания линейных уравнений, но они обычно имеют констант (например, «2» или «c») и должны иметь простых переменных (например, «x» или «y»).

Примеры: Это линейные уравнения:

Но переменные (например, «x» или «y») в линейных уравнениях имеют НЕ :

Примеры: Это НЕ линейных уравнений:

		y 2 — 2 = 0
		3√x — y = 6
		x 3 /2 = 16

Форма пересечения откоса

Наиболее распространенной формой является уравнение угла наклона прямой:

Пример: y = 2x + 1

• Уклон: м = 2
• Перехват: b = 1

Форма остроконечного откоса

Еще одна распространенная форма — это форма «точка-уклон» уравнения прямой линии:

y — y 1 = m (x — x 1 )

Пример: y — 3 = (¼) (x — 2)

Он имеет вид y — y ₁ = m (x — x ₁ ) где:

Общая форма

А есть еще Общая форма уравнения прямой:

Ax + By + C = 0

(A и B не могут быть одновременно 0)

Пример: 3x + 2y — 4 = 0

Он имеет вид Ax + By + C = 0 , где:

Есть и другие, менее распространенные формы.

Как функция

Иногда линейное уравнение записывается как функция с f (x) вместо y:

г = 2х — 3

f (x) = 2x — 3

Это такие же!

И функции не всегда записываются с использованием f (x):

г = 2х — 3

w (u) = 2u — 3

ч (г) = 2z — 3

Это тоже такие же!

Функция идентичности

Существует специальная линейная функция, которая называется «Функция идентификации»:

f (x) = x

А вот его график:

Делает 45 ° (уклон 1)

Это называется «Идентификацией», потому что получается , идентичное тому, что входит:

В	Из
0	0
5	5
-2	-2
…etc	… и т. Д.

Постоянные функции

Другой особый тип линейной функции — Постоянная функция … это горизонтальная линия:

f (x) = С

Независимо от того, какое значение «x», f (x) всегда равно некоторому постоянному значению.

Использование линейных уравнений

Вы можете прочитать о том, что можно делать с помощью строк:

,

Состав функций

«Композиция функций» применяет одну функцию к результатам другой:

Результат f () отправляется через g ()

Записано: (g º f) (x)

Что означает: g (f (x))

Пример: f (x) = 2x + 3 и g (x) = x ²

«x» — это просто заполнитель . Во избежание путаницы назовем его просто «ввод»:

f (ввод) = 2 (ввод) +3

г (ввод) = (ввод) ²

Начнем:

(g º f) (x) = g (f (x))

Сначала мы применяем f, затем применяем g к этому результату:

(g º f) (x) = (2x + 3) ²

Что если мы поменяем местами порядок f и g?

(f º g) (x) = f (g (x))

Сначала мы применяем g, затем применяем f к этому результату:

(f º g) (x) = 2x ² +3

Получаем другой результат!

Когда мы меняем порядок, результат редко бывает одинаковым.

Так что будьте осторожны, какая функция стоит первой.

Символ

Символ композиции — маленький кружок:

(g º f) (x)

Это , а не , а заполненная точка: (g · f) (x), поскольку это означает, что умножить на .

Самостоятельная композиция

Мы даже можем составить функцию сама с собой!

Пример: f (x) = 2x + 3

(f º f) (x) = f (f (x))

Сначала мы применяем f, затем применяем f к этому результату:

(f º f) (x) = 2 (2x + 3) +3 = 4x + 9

Мы могли бы обойтись без красивой диаграммы:

(f º f) (x) = f (f (x))

= е (2x + 3)

= 2 (2x + 3) +3

= 4x + 9

Домены

До сих пор это было легко, но теперь мы должны рассмотреть Домены функций.

Домен — это набор всех значений , которые входят в функцию.

Функция должна работать для всех значений, которые мы ей даем, поэтому зависит от нас, , чтобы убедиться, что мы получили правильный домен!

Пример: домен для √x (квадратный корень из x)

У нас не может быть квадратного корня из отрицательного числа (если мы не используем мнимые числа, но это не так), поэтому мы должны исключить отрицательных чисел:

Область √x — все неотрицательные действительные числа

На числовой прямой это выглядит так:

В нотации конструктора множеств записано:

{x | x ≥ 0}

Или, используя интервальную запись, это:

[0, + ∞)

Важно правильно оформить домен, иначе мы получим плохие результаты!

Область составной функции

Мы должны получить для обоих Доменов правильно (составная функция и — первая использованная функция).

При выполнении, например, (g º f) (x) = g (f (x)):

• Убедитесь, что мы получили домен для f (x) правильно,
• Затем также убедитесь, что g (x) получает правильный домен

Пример: f (x) = √x и g (x) = x ²

Область f (x) = √x — все неотрицательные действительные числа

Область g (x) = x ² — это все действительные числа

Составная функция:

(g º f) (x) = g (f (x))

= (√x) ²

= х

Итак, «x» обычно имеет Домен всех действительных чисел…

… но поскольку это составная функция , мы должны также учитывать f (x) ,

Таким образом, домен состоит из неотрицательных вещественных чисел

Почему оба домена?

Ну, представьте себе, что функции — это машины … первый плавит отверстие пламенем (только для металла), второй просверливает отверстие немного больше (работает с деревом или металлом):

То, что мы видим в конце, — это просверленное отверстие, и мы можем подумать, что «это должно работать для дерева или металла ». Но если мы поместим дрова в g º f, то первая функция f разожжет огонь и все сожжет!

Так что то, что происходит «внутри машины», важно.

Функция разложения

Мы можем пойти другим путем и разбить функцию на набор других функций.

Пример: (x + 1 / x) ²

Эта функция может быть выполнена из этих двух функций:

f (х) = х + 1 / х

г (х) = х ²

И получаем:

(g º f) (x) = g (f (x))

= г (х + 1 / х)

= (х + 1 / х) ²

Это может быть полезно, если исходная функция слишком сложна для работы.

Сводка

• «Функциональная композиция» применяет одну функцию к результатам другой.
• (g º f) (x) = g (f (x)) , сначала примените f (), затем примените g ()
• Мы также должны учитывать область определения первой функции
• Некоторые функции можно разделить на две (или более) более простые функции.

,

Выражения и операторы — веб-технологии для разработчиков

Дополнение ( + )	Chrome Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
Сложение ( x + = y )	Хром Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
Назначение ( x = y )	Хром Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
асинхронная функция выражение	Chrome Полная поддержка 55	Край Полная поддержка 15	Firefox Полная поддержка 52	IE Нет поддержки №	Опера Полная поддержка 42	Safari Полная поддержка 10.1	WebView Android Полная поддержка 55	Chrome Android Полная поддержка 55	Firefox Android Полная поддержка 52	Опера Android Полная поддержка 42	Safari iOS Полная поддержка 10.3	Samsung Интернет Android Полная поддержка 6.0	nodejs Полная поддержка 7.6.0 Полная поддержка 7.6.0 Полная поддержка 7.0.0 Отключено Начиная с версии 7.0.0: эта функция находится за флагом времени выполнения --harmony .
ожидание	Хром Полная поддержка 55	Край Полная поддержка 14	Firefox Полная поддержка 52	IE Нет поддержки №	Опера Полная поддержка 42	Safari Полная поддержка 10.1	WebView Android Полная поддержка 55	Chrome Android Полная поддержка 55	Firefox Android Полная поддержка 52	Опера Android Полная поддержка 42	Safari iOS Полная поддержка 10.3	Samsung Интернет Android Полная поддержка 6.0	nodejs Полная поддержка 7.6.0 Полная поддержка 7.6.0 Полная поддержка 7.0.0 Отключено Начиная с версии 7.0.0: эта функция находится за флагом времени выполнения --harmony .
Побитовое И ( a & b )	Хром Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
Поразрядное присвоение И ( x & = y )	Chrome Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
Побитовое НЕ ( ~ )	Хром Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
Побитовое ИЛИ ( a | b )	Chrome Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
Назначение побитового ИЛИ ( x | = y )	Chrome Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.b )	Хром Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.= y )	Хром Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
класс	Хром Полная поддержка 42	Край Полная поддержка 13	Firefox Полная поддержка 45	IE Нет поддержки №	Опера Полная поддержка 29	Safari Полная поддержка 7	WebView Android Полная поддержка 42	Chrome Android Полная поддержка 42	Firefox Android Полная поддержка 45	Опера Android Полная поддержка 29	Safari iOS Полная поддержка 7	Samsung Интернет Android Полная поддержка 4.0	nodejs Полная поддержка 6.0.0 Полная поддержка 6.0.0 Полная поддержка 5.0.0 Отключено Начиная с версии 5.0.0: эта функция находится за флагом времени выполнения --harmony .
Оператор запятой	Хром Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 4	Safari Полная поддержка 1	WebView Android Полная поддержка 1	Chrome Android Полная поддержка 18	Firefox Android Полная поддержка 4	Опера Android Полная поддержка 10.1	Safari iOS Полная поддержка 1	Samsung Интернет Android Полная поддержка 1.0	nodejs Полная поддержка 0.1.100
Условный оператор ( c? T: f )	Chrome Полная поддержка 1	Край Полная поддержка 12	Firefox Полная поддержка 1	IE Полная поддержка 3	Опера Полная поддержка 3	Safari Полная поддержка 1	WebView Android

.