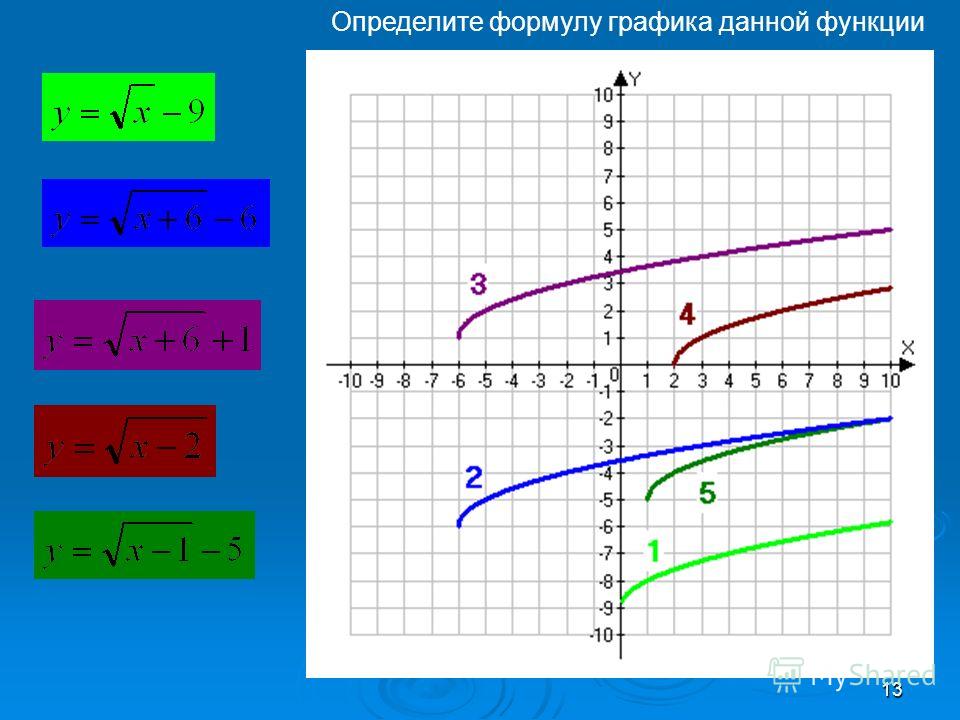
Решите уравнения:
(х+2)(х-2)= 4(х-1)(х+1)
4(х+2)(х-3)=(х-2)(х+2)…
Найдите значение выражения:
1/ 1/35 — 1/50
…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Выражение корень из 27 минус корень из 3 плюс 1 минус корень из 12
Ответы
Дашуточка2005
03. 2 при а =2 при b =5 ответ должен получиться 5000…
2 при а =2 при b =5 ответ должен получиться 5000…
andrmarka321 13.12.2020 15:22
очень надо 1 и 2…
sssfgdgd 27.06.2019 09:30
Доказать тождество tg a(1+cos2a)=sin2a…
ttleuberlin 28.04.2020 09:40
МНЕ ОЧЕНЬ НУЖНО…
кпрооо 28.04.2020 09:40
Найдите значение выражения.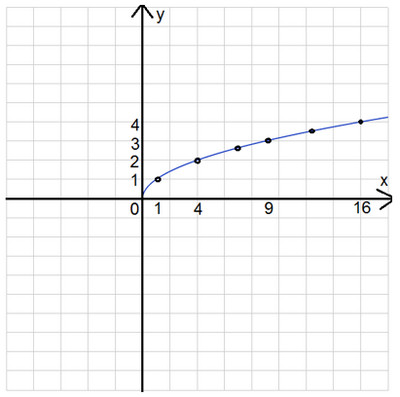 2. ответ: ….
2. ответ: ….
Родительские функции — типы, свойства и примеры
При работе с функциями и их графиками вы заметите, что графики большинства функций выглядят одинаково и следуют схожим шаблонам. Это потому, что функции, имеющие одинаковую степень, будут следовать схожей кривой и иметь одни и те же родительские функции.
Родительская функция представляет семейство функций в простейшей форме.
Это определение прекрасно описывает родительские функции. Мы используем родительские функции, чтобы направлять нас в графике функций, которые находятся в том же семействе. В этой статье мы:
- Просмотрите все уникальные родительские функции (возможно, вы уже встречались с некоторыми ранее).
- Узнайте, как определить родительскую функцию, которой принадлежит функция.
Способность идентифицировать и отображать функции с помощью их родительских функций может помочь нам лучше понять функции, так чего же мы ждем?
Что такое родительская функция?
Теперь, когда мы понимаем, насколько важно для нас освоить различные типы родительских функций, давайте сначала начнем понимать, что такое родительские функции и как на их семейства функций влияют их свойства.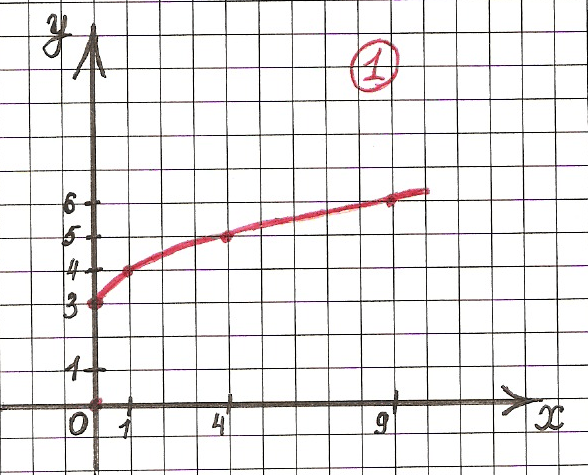
Определение родительской функции
Родительские функции являются простейшей формой данного семейства функций . Семейство функций — это группа функций, имеющих одну и ту же высшую степень и, следовательно, одинаковую форму графиков .
На приведенном выше графике показаны четыре графика, изображающие U-образный график, который мы называем параболой. Поскольку все они имеют одну и ту же высшую степень двойки и одинаковую форму, мы можем сгруппировать их в одно семейство функций. Сможете ли вы угадать, к какому семейству они принадлежат?
Все эти четыре функции являются квадратичными, и их простейшая форма будет y = x 2 . Следовательно, родительская функция для этого семейства y = x 2 .
Поскольку родительские функции являются простейшей формой данной группы функций, они могут сразу же дать вам представление о том, как будет выглядеть данная функция из того же семейства.
Какие существуют типы родительских функций?
Пришло время освежить наши знания о функциях, а также узнать о новых функциях. Как мы уже упоминали, знакомство с известными родительскими функциями поможет нам лучше и быстрее понять и построить графики функций.
Как мы уже упоминали, знакомство с известными родительскими функциями поможет нам лучше и быстрее понять и построить графики функций.
Почему бы нам не начать с того, что мы могли уже выучить в прошлом?
Первые четыре родительские функции включают многочлены с возрастающими степенями. Давайте посмотрим, как ведут себя их графики, и отметим домен и диапазон соответствующих родительских функций.
Функции-константыФункции-константы — это функции, которые определяются своей соответствующей константой, c. Все постоянные функции будут иметь горизонтальную линию в качестве графика и содержать только константу в качестве члена.
Все постоянные функции будут иметь все действительные числа в качестве области определения и y = c в качестве диапазона. У каждого из них также есть точка пересечения с осью y в точке (0, c).
Движение объекта в состоянии покоя — хороший пример постоянной функции.
Линейные функции Линейные функции имеют x в качестве термина с наивысшей степенью и общую форму y = a + bx. Все линейные функции имеют прямую линию в виде графика .
Все линейные функции имеют прямую линию в виде графика .
Родительская функция линейных функций y = x, и проходит через источник. Область определения и диапазон всех линейных функций равны , все действительные числа .
Эти функции представляют отношения между двумя объектами, которые линейно пропорциональны друг другу.
Квадратичные функцииКвадратичные функции — это функции с 2 в высшей степени . Все квадратичные функции возвращают параболу в виде графика . Как обсуждалось в предыдущем разделе, квадратичные функции имеют y = x 2 в качестве родительской функции .
Вершина родительской функции y = x 2 лежит в начале координат. Он также имеет домен всех действительных чисел и диапазон [0, ∞) . Обратите внимание, что эта функция увеличивается, когда x является положительным , и уменьшается, когда x является отрицательным .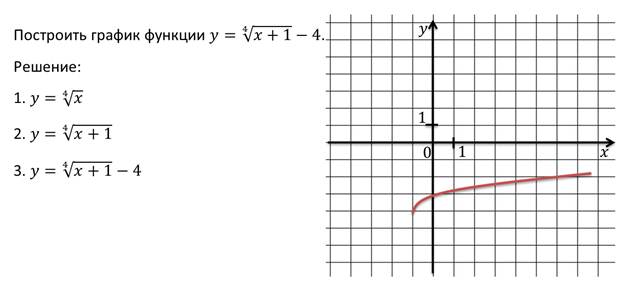
Хорошим применением квадратичных функций является движение снаряда. Мы можем наблюдать за движением снаряда объекта, рисуя график квадратичной функции, которая его представляет.
Кубические функцииПерейдем к родительской функции многочленов с 3 в качестве высшей степени . Кубические функции имеют общую родительскую функцию y = x 3 . Эта функция возрастает по всей области определения .
Как и в случае с двумя предыдущими родительскими функциями, график y = x 3 также проходит через начало координат. Его домен и диапазон равны (-∞, ∞) или также всем действительным числам.
Функции абсолютного значенияРодительская функция функций абсолютного значения: y = |x| . Как видно из графика родительской функции, ожидается, что функции абсолютного значения вернут V-образные графики .
Вершина y = |x| также находится в истоке.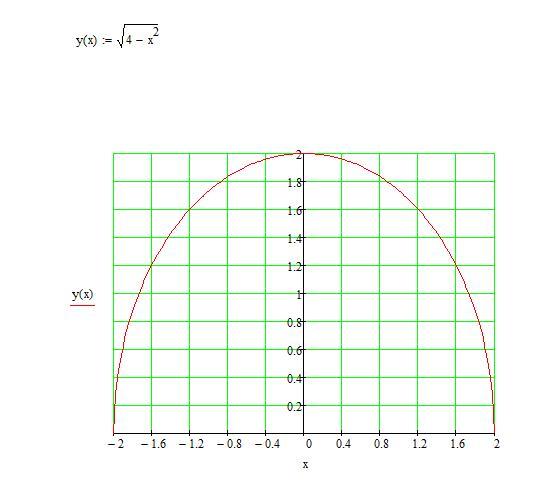 Поскольку он простирается на оба конца оси x, y= |x| имеет область определения в точке (-∞, ∞). Абсолютные значения никогда не могут быть отрицательными, поэтому родительская функция имеет диапазон [0, ∞) .
Поскольку он простирается на оба конца оси x, y= |x| имеет область определения в точке (-∞, ∞). Абсолютные значения никогда не могут быть отрицательными, поэтому родительская функция имеет диапазон [0, ∞) .
Мы используем функции абсолютного значения, чтобы подчеркнуть, что значение функции всегда должно быть положительным.
Радикальные функцииДвумя наиболее часто используемыми радикальными функциями являются функции квадратного и кубического корня .
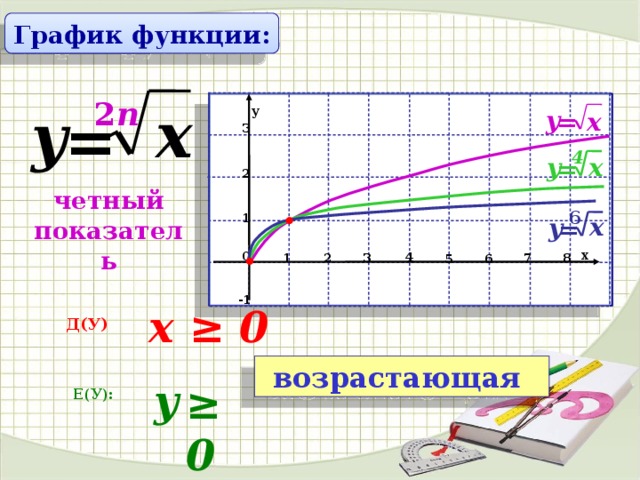
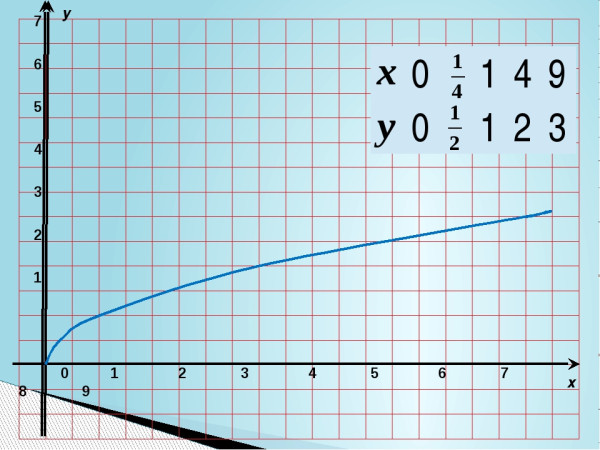
Родительская функция функции извлечения квадратного корня: y = √x . Его график показывает, что его значения x и y никогда не могут быть отрицательными.
Это означает, что область и диапазон значений y = √x равны [0, ∞ ) . Начальная точка или вершина родительской функции также находится в начале координат . Родительская функция y = √x также возрастает по всей области определения .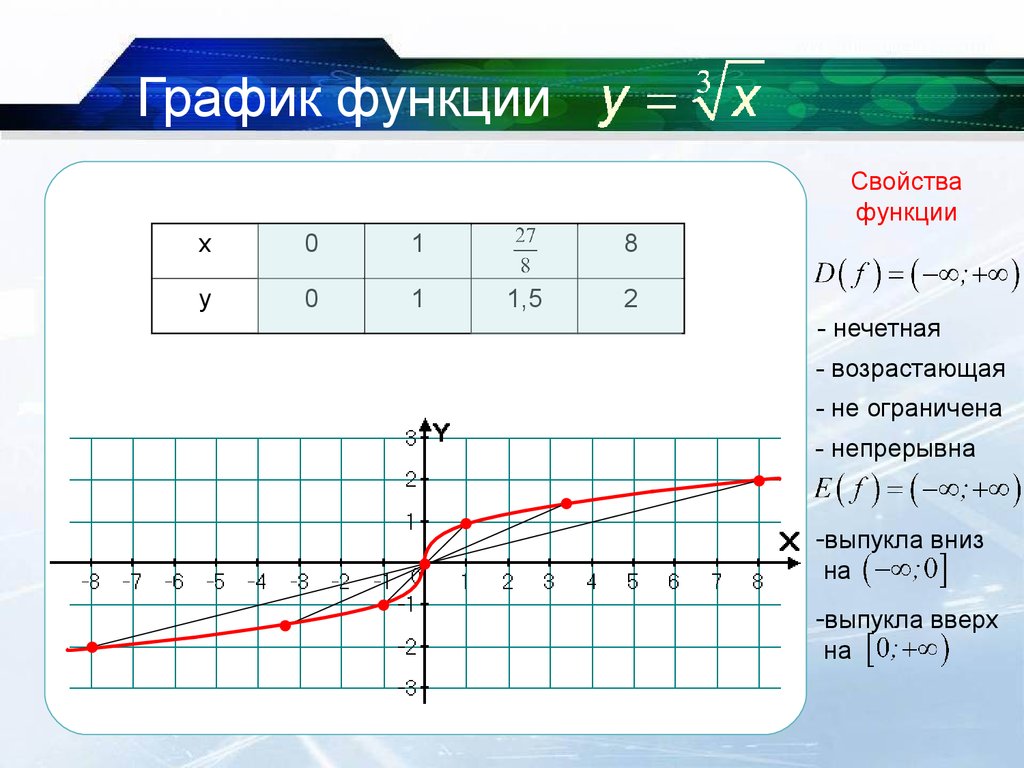
Давайте теперь изучим родительскую функцию функций кубического корня. Подобно функции квадратного корня, ее родительская функция выражается как y = ∛ x .
График показывает, что родительская функция имеет домен и диапазон (-∞, ∞) . Мы также можем видеть, что y = ∛x равно увеличивается по всему домену .
Экспоненциальные функцииЭкспоненциальные функции — это функции, которые имеют алгебраические выражения в их показателе. Их родительская функция может быть выражена как y = b x , где b может быть любой ненулевой константой. График родительской функции y = e x , показан ниже, и из него видно, что никогда не будет равно 0 .
И когда x = 0, y проходит через ось y при y = 1. Мы также можем видеть, что родительская функция никогда не находится ниже оси y, поэтому его диапазон (0, ∞ ). Его домен , однако могут быть все действительные числа . Мы также можем видеть, что эта функция возрастает на по всей области определения.
Его домен , однако могут быть все действительные числа . Мы также можем видеть, что эта функция возрастает на по всей области определения.
Одним из наиболее распространенных применений экспоненциальных функций является моделирование роста населения и сложных процентов.
Логарифмические функцииЛогарифмические функции являются обратными функциями экспоненциальных функций. Его родительская функция может быть выражена как y = log b x , где b — ненулевая положительная константа. Посмотрим на график, когда b = 2 .
Как и в случае с экспоненциальной функцией, мы видим, что x никогда не может быть меньше или равно нулю при y = log 2 x. Следовательно, его домен равен (0,∞) . Однако его диапазон содержит все действительные числа . Мы также можем видеть, что эта функция возрастает на по всей области определения.
Мы используем логарифмические функции для моделирования природных явлений, таких как сила землетрясения. Мы также применяем его при расчете скорости распада периода полураспада в физике и химии.
Взаимные функцииВзаимные функции — это функции, которые содержат постоянный числитель и x в качестве знаменателя. Его родительская функция y = 1/x .
Как видно из его графика, x и y никогда не могут быть равны нулю. Это означает, что его домен и диапазон равны (-∞, 0) U (0, ∞) . Мы также можем видеть, что функция убывает на по всей области определения .
В нашем путешествии с функциями и графиками есть много других родительских функций, но эти восемь родительских функций относятся к наиболее часто используемые и обсуждаемые функции .
Вы даже можете обобщить то, что вы уже узнали, создав таблицу, показывающую все свойства родительских функций.
Как найти родительскую функцию? Что, если нам дана функция или ее график, и нам нужно определить ее родительскую функцию? Мы можем сделать это, запомнив важные свойства каждой функции и определив, какой из родительских графов, которые мы обсуждали, соответствует данному.
Вот несколько наводящих вопросов, которые могут нам помочь:
- Какова высшая степень функции?
- Содержит ли он квадратный или кубический корень?
- Находится ли функция в показателе степени или знаменателе?
- График функции убывающий или растущий?
- Что такое домен или диапазон функции?
Если мы сможем ответить на некоторые из этих вопросов путем проверки, мы сможем вывести наши варианты и в конечном итоге определить родительскую функцию.
Попробуем f(x) = 5(x – 1) 2 . Мы можем видеть, что самая высокая степень f(x) равна 2 , поэтому мы знаем, что эта функция является квадратичной функцией. Следовательно, его родительская функция y = x 2 .
Почему бы нам не построить график f(x) и не подтвердить наш ответ?
Из графика видно, что он образует параболу, подтверждая, что его родительская функция y = x 2 .
Просмотрите несколько первых разделов этой статьи и свои собственные заметки, а затем давайте попробуем ответить на несколько вопросов, чтобы проверить наши знания о родительских функциях.
Пример 1
Графики пяти функций показаны ниже. Какие из следующих функций не принадлежат данному семейству функций?
Решение
Функции, представленные на графиках A, B, C и E, имеют одинаковую форму, но смещаются либо вверх, либо вниз. Фактически эти функции представляют семейство экспоненциальных функций . Это означает, что все они также имеют общую родительскую функцию: y=b х .
С другой стороны, график D представляет собой логарифмическую функцию, поэтому D не принадлежит к группе экспоненциальных функций.
Пример 2
Какие из следующих функций не принадлежат данному семейству функций?
- y = 5x 2
- y = -2x 2 + 3x -1
- y = x (3x 2 )
- y = (x -1) (x + 1)
2
2
Функция y = 5x 2 имеет наивысшую степень двойки, поэтому она является квадратичной функцией.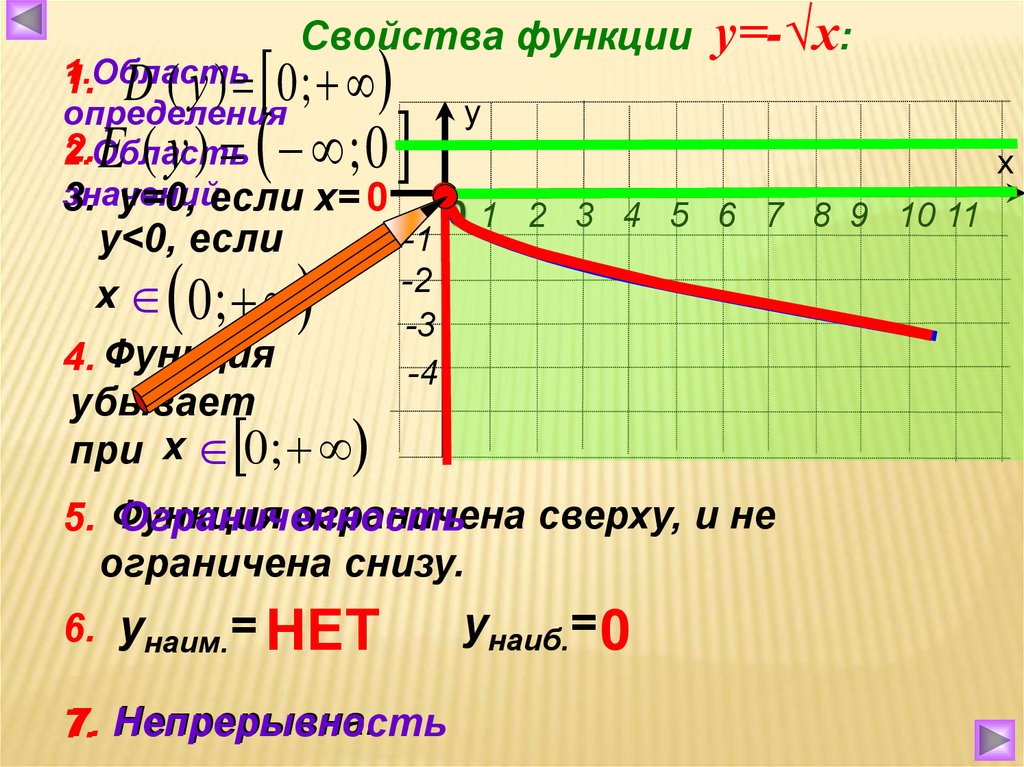 Это означает, что его родительская функция y = x 2 . То же самое касается y = -2x 2 + 3x – 1. Отсюда мы можем подтвердить, что рассматриваем семейство квадратичных функций.
Это означает, что его родительская функция y = x 2 . То же самое касается y = -2x 2 + 3x – 1. Отсюда мы можем подтвердить, что рассматриваем семейство квадратичных функций.
Применяя разность совершенных квадратов к четвертому варианту, имеем y = x 2 – 1. Это тоже квадратичная функция. Это оставляет нам третий вариант.
При расширении y = x(3x 2 ) становится y = 3x 3, , и это показывает, что его высшая степень равна 3. Следовательно, она не может быть частью данного семейства функций.
Пример 3
Определите родительскую функцию следующих функций на основе их графиков. Также определите домен и диапазон каждой функции.
Решение
Начнем с f(x). Мы видим, что его график имеет параболу, поэтому мы можем сказать, что f(x) является квадратичной функцией .
- Это означает, что f(x) имеет родительскую функцию y = x 2 .

- Граф простирается по обе стороны от x, поэтому он имеет доменов (-∞, ∞) .
- Парабола никогда не опускается ниже оси x, поэтому ее диапазон составляет [0,∞) .
Из графика видно, что значения x и y функции g(x) никогда не будут отрицательными. Они также показывают возрастающую кривую, которая напоминает график функции извлечения квадратного корня .
- Следовательно, родительская функция g(x) равна y = √x .
- Граф простирается до правой части x и никогда не меньше 2, поэтому его домен равен [2, ∞) .
- Парабола никогда не опускается ниже оси x, поэтому ее диапазон составляет [0,∞) .
График h(x) показывает, что их значения x и y никогда не будут равны 0. Симметричные кривые также выглядят как график обратных функций.
- Это означает, что h(x) имеет родительскую функцию y = 1/x.

- Пока x и y никогда не равны нулю, h(x) по-прежнему действует, поэтому он имеет как домен , так и диапазон (-∞, ∞) .
Прямые линии, изображающие i(x), говорят о том, что это линейная функция.
- Имеет родительскую функцию y = x.
- Граф простирается по обе стороны от x и y, поэтому он имеет домен и диапазон (-∞, ∞) .
Пример 4
Определите родительскую функцию следующих функций.
- f(x) = x 3 – 2x + 1
- g(x) = 3√x + 1
- h(x) = 4/ x
- i(x) = e x + 1
Решение
- Наивысшая степень f(x) равна 3, так что это кубическая функция. Это означает, что он имеет родительскую функцию y = x 3 .
- Функция g(x) имеет радикальное выражение 3√x. Поскольку в ней есть член с квадратным корнем, функция является функцией квадратного корня и имеет родительскую функцию y = √x.

- Мы видим, что x находится в знаменателе для h(x), так что оно обратное. Следовательно, его родительская функция равна y = 1/x .
- Показатели функции содержат x, поэтому уже одно это говорит нам о том, что i(x) является экспоненциальной функцией. Следовательно, его родительская функция может быть выражена как y = b x , где b — константа. Для случая i(x) у нас есть y = e x в качестве родительской функции.
Математическая функция Python | sqrt()
Улучшить статью
Сохранить статью
- Уровень сложности: Базовый
- Последнее обновление: 08 июл, 2022
Улучшить статью
Сохранить статью
кв() 9Функция 0008 — это встроенная функция языка программирования Python, которая возвращает квадратный корень из любого числа.
Синтаксис: мат.кв.(х) Параметр: x - любое число такое, что x>=0 Возвращает: Возвращает квадратный корень числа передается в параметре.
(math.sqrt( 3.5 )) |
Вывод:
0,0 2.0 1.8708286933869707
Ошибка: Когда x<0, он не выполняется из-за ошибки времени выполнения.
|
Выход:
Traceback (последний последний вызов):
Файл "/home/67438f8df14f0e41df1b55c6c21499ef.py", строка 8, в
печать (математика.кв.(-1))
ValueError: ошибка математического домена
Практическое применение: По заданному числу проверьте, является ли оно простым или нет.
Подход: Запустите цикл от 2 до sqrt(n) и проверьте, делится ли любое число в диапазоне (2-sqrt(n)) на n.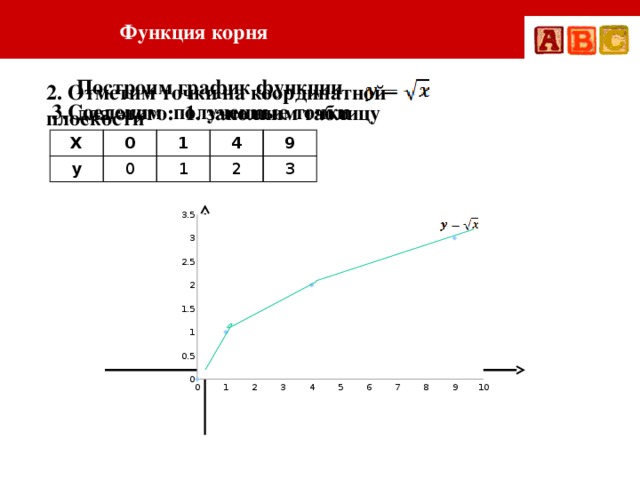
|


 0
1.8708286933869707
0
1.8708286933869707