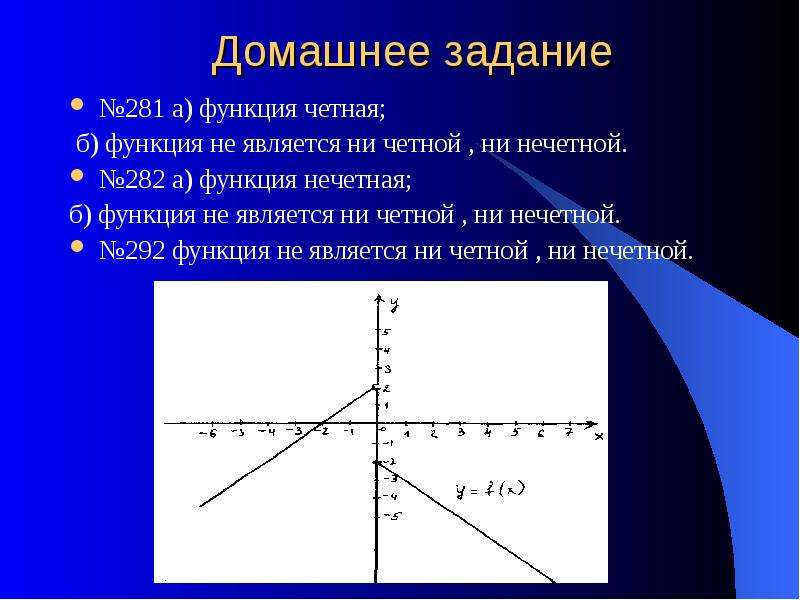
это что? Четная и нечетная функция, корни функции.
Что такое функция? Представим себе машину, которая двигается по дороге из одного города в другой. Мы можем в каждый момент времени определить положение машины. То есть у нас есть множество различных моментов времени и множество точек, определяющих положение машины на дороге. При этом положение машины на дороге зависит от того, в какой момент времени мы определяем это положение. То есть одно множестве переменных величин зависит от другого множества, каждая отдельная переменная из одного множества зависит от переменной из другого множества. Зависимость одной переменной от другой называется функциональной зависимостью.
Функция – это чтоВ этой статье мы рассмотрим что такое функция, дадим определения области определения функции и области ее значений, понятие графика функции.
Содержание
Область определения и область значений функции
– значение функции в точке .
Если область определения функции и область ее значений определены в множестве рациональных чисел, то функцию называют числовой.
Элементы множества еще называют значениями аргумента, а соответствующие им элементы – значениями функции.
Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
Например, область определения функции, заданной формулой , состоит из всех чисел, кроме нуля.
Как найти область определения функции
Для того, чтобы найти область определения функции, мы должны определить – где функция будет существовать, при каких значениях аргумента. Приведем примеры:
Пример 1
Найти область определения функции
Зададимся вопросом – при каких значениях функция будет существовать? Очевидно, что функция существует, если знаменатель дроби не равен нулю. То есть .
Для определения этого значения решим уравнение:
.
Находим, .
То есть функция не будет существовать при значении . Тогда областью определения функции (где она существует) – будут все значения кроме 5.
Через интервалы можно записать так:
.
Пример 2
Найти область определения функции .
Здесь функция определена при любых значениях аргумента. То есть D(f) – все числа.
Пример 3
Определить область определения функции
.
Выражение, стоящее под знаком квадратного корня, должно быть больше или равно нулю. Таким образом, мы можем записать:
Решим данное неравенство и получим: .
Тогда область определения функции будет интервал значений аргумента .
График функции
Графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. То есть график функции – это изображение на координатной плоскости множества пар , связанных зависимостью , где .
Способы задания функции
Функция может быть задана аналитически в виде формулы , где переменная – элемент множества значений аргумента, а переменная – соответствующее значение функции.
Например, формула определяет некоторую функцию, где каждому значению переменной , взятому из области определения функции, соответствует единственное значение переменной .
Функция полностью определяется заданием множества пар , где принимает все значения из , а – соответствующие значения функции.
Однако не всякое множество точек координатной плоскости является графиком некоторой функции. Например, если мы рассмотрим следующий график, то увидим, что значению соответствуют три значения , и, следовательно, такое соответствие не является функцией.
График не является графиком функцииДля того, чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси , пересекалась с указанным графиком не более чем в одной точке.
Монотонность функции
Функция называется возрастающей на данном числовом промежутке , если большему значению аргумента соответствует большее значение функции . Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .
Функция называется убывающей на данном числовом промежутке , если большему значению аргумента соответствует меньшее значение функции .
Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .
Функция только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
О монотонности функции можно судить по ее графику. Например, функция, график которой изображен ниже является монотонно возрастающей на всей числовой оси.
Монотонно возрастающая функцияА вот эта функция является монотонно убывающей.
Монотонно убывающая функция – график функции.А теперь рассмотрим вот такой график функции – на ней функция убывает на промежутке и возрастает на промежутке .
График функции которая монотонно убывает и монотонно возрастает на определенных интервалах области определения функции.Пример
Докажите, что функция, заданная формулой , где , возрастающая.
Решение: Пусть , где и . Тогда .
Поскольку , то и , а, значит, . То есть большему значению аргумента соответствует большее значение функции, таким образом, функция возрастающая на промежутке .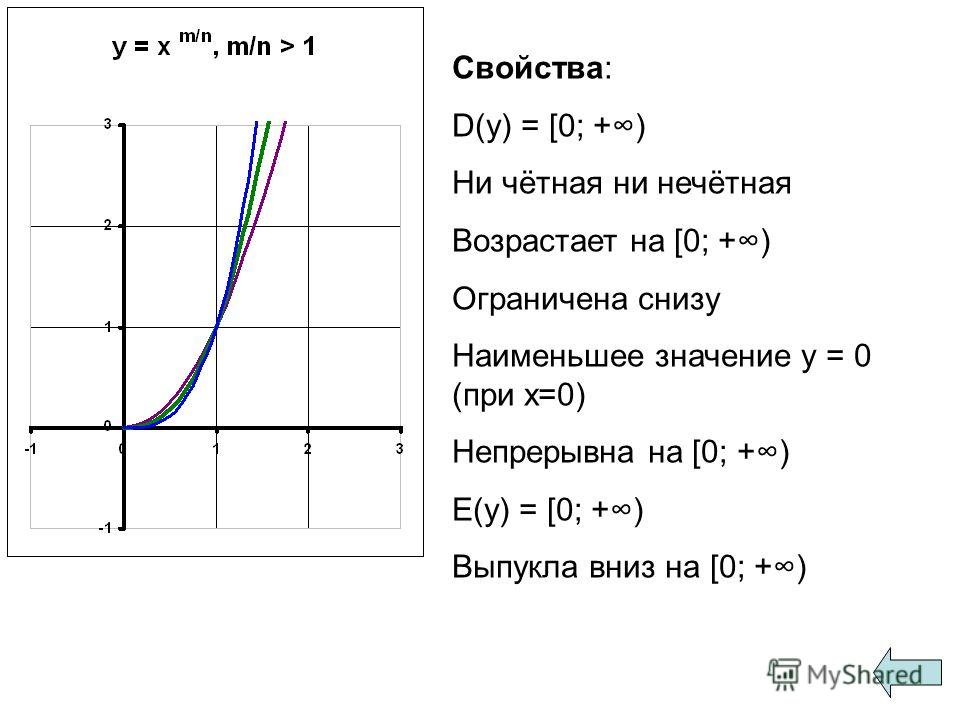
Четные и нечетные функции
Пример 1
Доказать, что функция не является ни четной, ни нечетной.
Доказательство.
Областью определения данной функции является вся числовая прямая, то есть условие 1 выполнено. Проверяем условие 2.
Чтобы доказать, что функция не является четной, нам нужно доказать, что условие 2 для четной функции не выполняется, то есть что .
Пусть , тогда . Проверяем: , а , таким образом . Функция не является четной. Одновременно, не выполняется и второе условие для нечетной функции, мы получили, что: . То есть функция не является нечетной.
Пример 2
Определите четность или нечетность функции:
Решение: область определения данной функции – вся числовая ось, кроме точки (на ноль делить нельзя). Найдем .
Получим: . Вынесем минус за скобки:
.
Отсюда выходит, что , то есть выполняется условие для нечетной функции. А, значит, функция – нечетная функция.
Пример 3
Определить четность или нечетность функции:
.
Решение: Первое условие о симметричности области определения функции выполняется, так как область определения функции . Переменим знак аргумента функции и упростим:
.
Получается, что . То есть функция – четная.
Периодические функции
Если – период функции, то , где , , также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривается наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это обстоятельство используется при построении графиков.
Промежутки знакопостоянства и корни функции
Числовые промежутки, на которых функция сохраняет свой знак (то есть остается положительной или отрицательной), называются промежутками знакопостоянства функции.
О промежутках знакопостоянства функции можно сделать вывод, посмотрев на график функции.
x\) находится под прямой \(y=-2x+1\). Это – отрезок от -1 до 0. Точки -1 и 0 включаем.
Ответ: \(x=\left[-1;0\right]\)
Рейтинг пользователей
за неделю
- за неделю
- один месяц
- три месяца
Помогай другим
Отвечай на вопросы и получай ценные призы каждую неделю
См. подробности
Объяснение урока: Четные и нечетные функции
В этом объяснении мы узнаем, как определить, является ли функция четной, нечетной, или ни по графику функции, ни по ее правилу.
Четность функции описывает, является ли функция четной или нечетной.
Определение: четные и нечетные функции 𝑓( 𝑥),
для каждого 𝑥 в области определения функции.
Обратите внимание, что единственная функция, определенная на множестве действительных чисел,
и четное, и нечетное равно 𝑓(𝑥)=0; таким образом, как только мы определили четность функции, нам не нужно проверять ее снова.
Графики четных и нечетных функций также обладают некоторыми ключевыми свойствами, которые могут чтобы их было легко идентифицировать. Рассмотрим графики функции 𝑓(𝑥)=𝑥+4 и 𝑔(𝑥)=𝑥.
Мы можем проверить четность 𝑓(𝑥) вычислением 𝑓(−𝑥): 𝑓(−𝑥)=(−𝑥)+4=𝑥+4=𝑓(𝑥).
𝑓(𝑥) является четной функцией. Обратите внимание, как график 𝑓(𝑥)=𝑥+4 имеет симметрия отражения относительно к оси 𝑦 или прямой 𝑥=0. Это связано с тем, что вывод функции будет таким же, если мы введем 𝑥 или −𝑥. Например, точки (2,8) и (−2,8) лежат на кривой 𝑦=𝑓(𝑥).
Фактически, 𝑓(−𝑥)=𝑓(𝑥) подразумевает, что график функции будет иметь отражательную симметрию относительно 𝑦-ось для каждого значения 𝑥 в области определения функции. Эти функции называются даже функциями, поскольку функция 𝑓(𝑥)=𝑥 будет обладать этим свойством, если 𝑛 — любое четное целое число.
Теперь рассмотрим функцию 𝑔(𝑥)=𝑥. Чтобы проверить четность этой функции, мы оценим 𝑔(−𝑥):
𝑔(−𝑥)=(−𝑥)=−𝑥=−𝑔(𝑥).
𝑔(𝑥) — нечетная функция. На этот раз граф 𝑔(𝑥) имеет вращательную симметрию порядка 2 относительно начала координат, что означает, что его график остается неизменным после поворот на 180∘ о (0,0). Это потому, что если точка с координатами (𝑥,𝑦) лежит на кривой, то поскольку 𝑔(−𝑥)=−𝑔(𝑥), соответствующая точка с координатами (−𝑥,−𝑦) также должна лежать на кривой. Например, с момента с координатами (2,8) лежит на кривой 𝑦=𝑔(𝑥), тогда точка с координатами (−2,−8) также должна лежать на кривой.
𝑔(−𝑥)=−𝑔(𝑥) означает, что график функция будет иметь порядок вращательной симметрии 2 относительно начала координат для каждого значения 𝑥 в области определения функции. Эти функции называются нечетными функциями, поскольку функция 𝑔(𝑥)=𝑥 будет обладать этим свойством, если 𝑛 — любое нечетное целое число.
Если нечетная функция определена в нуле, то ее график должен проходить через начало координат. Мы можем продемонстрировать это, положив 𝑥=0 в определении нечетной функции,
𝑔(𝑥)=−𝑔(𝑥).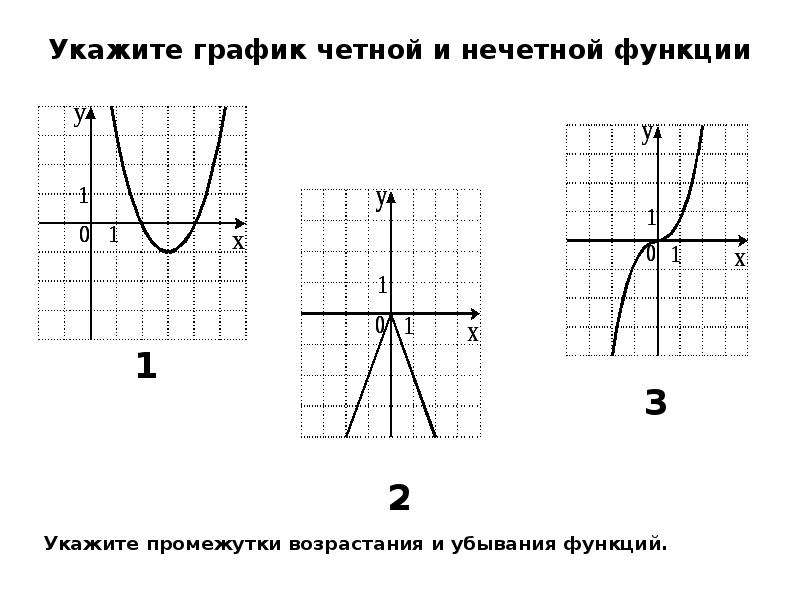
Поскольку для нечетной функции 𝑔(−𝑥)=−𝑔(𝑥), мы можем сделать вывод, что абсолютное значение на самом деле эта функция должна быть четной; для любой нечетной функции 𝑔(𝑥), если ℎ(𝑥)=|𝑔(𝑥)|, то ℎ четно.
Определение: графики четных и нечетных функций
График любой четной функции имеет отражательную симметрию относительно оси 𝑦.
График любой нечетной функции имеет вращательную симметрию порядка 2 относительно начала координат.
Мы можем использовать как определение функции, так и ее график, чтобы определить четность функции. В нашем первом примере мы покажем, как использовать определение функции, чтобы определить, является ли функция четной, нечетной или ни той, ни другой.
Пример 1. Определение четности линейной функции
Является ли функция 𝑓(𝑥)=4𝑥−3 четной, нечетной или ни одной?
Ответ
Напомним, что функция 𝑓(𝑥) является
- четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
- нечетной функцией, если 𝑓(−𝑥)=−𝑓( 𝑥) ,
для каждого 𝑥 в области определения функции.
Поскольку 𝑓(𝑥) — линейная функция, ее область определения равна ℝ. Это симметрично относительно 0, поэтому мы знаем, что симметрично применяются свойства четных и нечетных функций. Чтобы проверить четность 𝑓(𝑥), мы оценим 𝑓(−𝑥): 𝑓(−𝑥)=4(−𝑥)−3=−4𝑥−3.
Заметим, что 𝑓(−𝑥)≠𝑓(𝑥), и равно как и 𝑓(−𝑥)=−𝑓(𝑥).
Функция не является ни четной, ни нечетной.
В наших следующих двух примерах мы рассмотрим, как определение четных и нечетных функций (относительно симметрии их графиков) может помочь нам определить четность функции.
Пример 2. Определение того, является ли построенная на графике функция четной, нечетной или ни одной из них
Определите, является ли функция, представленная на следующем рисунке, четной, нечетной или ни одной из них.
Ответ
Напомним, что график четной функции имеет отражательную симметрию с
относительно оси 𝑦, а график нечетной функции имеет вращательную симметрию порядка 2 о происхождении.
Важно понимать, что это должно выполняться
верно для каждое значение 𝑥 в области определения функции, и поэтому мы должны
убедитесь, что область определения функции симметрична относительно 0.
Область определения функции — это множество возможных 𝑥-значений, которые можно заменить в функцию; это можно вывести из графика функции, посмотрев на разброс 𝑥-значений слева направо.
Областью определения этой функции являются значения 𝑥 в интервале [−8,8], не считая 𝑥=0. Используя обозначение набора, домен задается [−8,8]−{0}.
Так как эта область симметрична относительно 0, мы можем теперь проверить, является ли функция четное, нечетное или ни то, ни другое.
Мы наблюдаем, что график имеет отражательную симметрию относительно оси 𝑦, или линия 𝑥=0. Это означает, что для любого значения 𝑥 в области определения функция, 𝑓(−𝑥)=𝑓(𝑥).
Функция четная.
В нашем предыдущем примере мы продемонстрировали, как определить четность функции, заданной в ограниченной области, по ее графику. В примере 3 мы увидим, как этот процесс можно применить к функциям, определенным в неограниченной области.
Пример 3. Определение четности построенной на графике рациональной функции
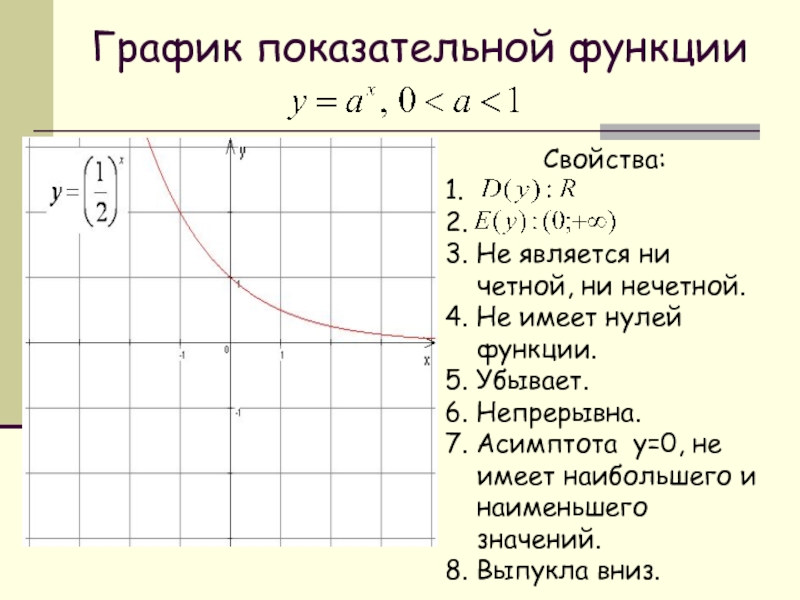
Является ли функция, представленная цифрой, четной, нечетной или ни одной?
Ответ
Напомним, что график нечетной функции имеет вращательная симметрия порядка 2 относительно начала координат, а график четной функции имеет отражательную симметрию относительно начала координат. 𝑦-ось. Важно понимать, что это должно быть верным для каждых значений 𝑥 в домен функции, и поэтому мы должны убедиться, что домен функции симметрична относительно 0.
График функции имеет вертикальную асимптоту, заданную при 𝑥=0. Это единственное значение 𝑥, где функция не определена;
следовательно, его область определения определяется выражением
ℝ−{0}.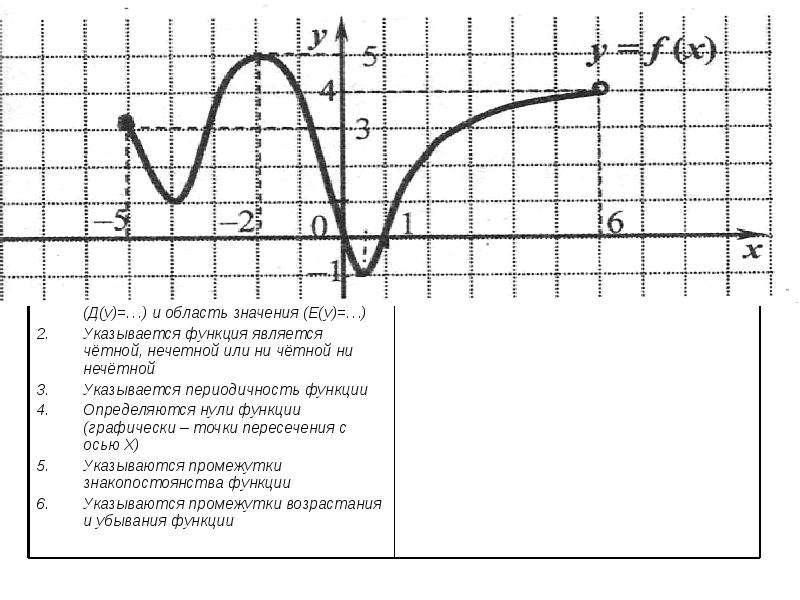
Так как эта область симметрична относительно 0, мы можем теперь проверить, является ли функция является четным, нечетным или ни тем, ни другим.
Мы видим, что граф не имеет отражательных симметрия задается осью 𝑦, поэтому эта функция не может быть четной.
Однако график остается неизменным после поворота на 180° вокруг начала координат.
Следовательно, функция нечетная.
В наших предыдущих двух примерах мы начали с проверки того, что домен функции был симметричен относительно 0. Поскольку четность функции зависит от ее симметричные свойства относительно оси 𝑦 или начала координат, следует, что функция, область определения которой не симметрична относительно 0, будет ни четным, ни нечетным.
В следующем примере мы увидим, как подтверждение этого элемента определение может сэкономить нам время при определении, является ли функция четной, странно, или ни то, ни другое.
Пример 4.
Определение того, является ли изображенная на графике функция четной, нечетной или ни той, ни другойЯвляется ли функция, представленная цифрой, четной, нечетной или ни той, ни другой?
Ответ
График четной функции имеет отражательную симметрию относительно 𝑦-ось, а график нечетной функции имеет вращательная симметрия из порядок 2 о происхождении. Важно понимать, что это должно выполняться верно для
Область определения функции — это набор возможных входных данных или 𝑥-значений, что мы можем подставить в эту функцию.
Областью определения этой функции является интервал 2≤𝑥≤6. Этот домен не симметричный около 0,
Поскольку область определения этой функции не симметрична относительно 0, мы можем вывести
что функция не четная и не нечетная.
В нашем следующем примере мы рассмотрим, как определить четность тригонометрической функции из ее уравнения, используя следующие определения.
Определение: четность тригонометрических функций
𝑓(𝑥)=𝑥cos и 𝑓(𝑥)=𝑥sec являются четными функциями.
𝑓(𝑥)=𝑥sin, 𝑓(𝑥)=𝑥csc, 𝑓(𝑥)=𝑥tan и 𝑓(𝑥)=𝑥cot — нечетные функции.
Пример 5. Определение четности функции
Является ли функция 𝑓(𝑥)=𝑥6𝑥tan четной, странно или нет?
Ответ
Функция 𝑦=𝑓(𝑥) является
- четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
- нечетной функцией, если 𝑓(−𝑥)=− 𝑓(𝑥),
для каждого 𝑥 в области определения функции.
Начнем с определения области определения функции. Нам нужно убедиться, что это симметричный относительно 0; в противном случае симметричные свойства четных и нечетных функций не будет применяться.
𝑥6𝑥tan является произведением двух функций,
поэтому его домен будет пересечением доменов каждой функции.
Поскольку 𝑥 — многочлен, мы знаем, что его областью определения является множество действительных чисел.
Область определения функции тангенса представляет собой множество действительных чисел, кроме тех, где cos(𝑥)=0. Это означает, что область определения функции tan6𝑥 равна множество действительных чисел, за исключением тех, что делают cos6𝑥=0. Значения 𝑥, которые make cos6𝑥=0 𝑥=𝜋12,3𝜋12,−𝜋12,−3𝜋12 и так далее. Эти значения симметричны относительно оси 𝑦, что означает, что домен tan6𝑥 должен быть симметричным. около 0,
Таким образом, пересечение двух доменов также симметрично относительно 0, поэтому теперь мы можем проверить четность, оценив 𝑓(−𝑥): 𝑓(−𝑥)=(−𝑥)(−6𝑥).tan
И мы перепишем (−𝑥) как (−𝑥)=(−1×𝑥)=(−1)×𝑥=−𝑥.
Чтобы вычислить тангенс(−6𝑥), мы можем рассмотреть график
функции tan6𝑥; это горизонтальный участок
график 𝑦=(𝑥)tan с масштабным коэффициентом 16.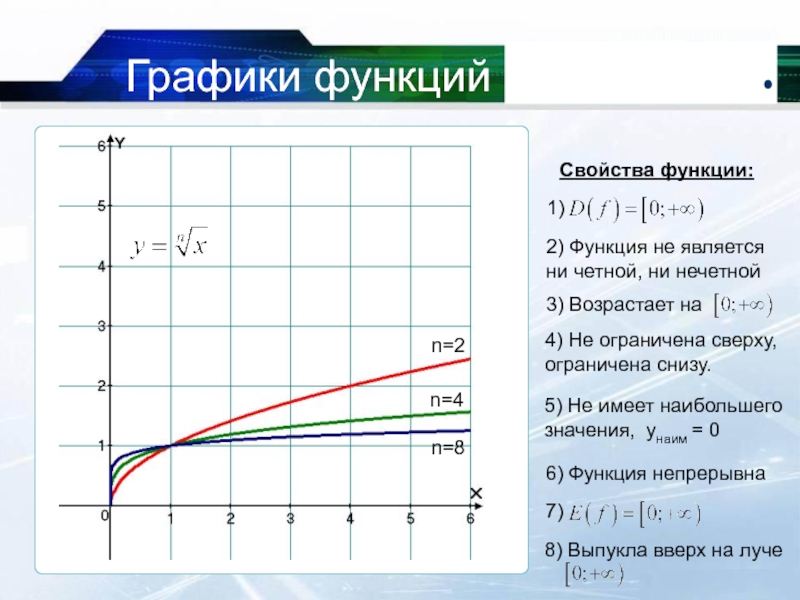
Мы видим, что tan6𝑥 нечетно, так как график нечетного функция имеет вращательная симметрия порядка 2 относительно начала координат.
Следовательно, тантан(−6𝑥)=−(6𝑥) и мы можем написать 𝑓(−𝑥) как 𝑓(−𝑥)=(−𝑥)×(−6𝑥)=−𝑥×6𝑥=−𝑥6𝑥=−𝑓(𝑥).тантантан
Теперь мы можем видеть, для каждого 𝑥 в домене из 𝑓, 𝑓(−𝑥)=−𝑓(𝑥).
Следовательно, функция 𝑓(𝑥)=𝑥6𝑥tan нечетна.
В примере 5 мы умножили нечетную функцию 𝑥 на четную функцию tan(6𝑥), что привело к нечетной функции. Фактически, произведение четной и нечетной функций всегда будет нечетным. Мы можем обобщить этот результат наряду с некоторыми другими свойствами комбинирования функций.
Определение: Комбинация четных и нечетных функций
Пусть 𝑓 и 𝑓 — четные функции а 𝑔 и 𝑔 — нечетные функции:
- 𝑓±𝑓 четная, а 𝑔±𝑔 нечетная,
- 𝑓±𝑔 не четная и не нечетная, 900 11 𝑓⋅𝑓,𝑓𝑓, 𝑔⋅𝑔 и 𝑔𝑔 четные,
- 𝑓⋅𝑔 и 𝑓𝑔 нечетные.
Теперь мы узнаем, как применять эту концепцию для определения четности кусочно определенной функции.
Пример 6. Определение четности кусочно-определенной функции
Определить, является ли функция 𝑓 четной, нечетной или ни одной, учитывая, что 𝑓(𝑥)=−9𝑥−8𝑥0,9𝑥−8𝑥≥0.ifif
Ответ
Функция 𝑓(𝑥) является четной функцией, если 𝑓(−𝑥)= 𝑓(𝑥),
для каждого 𝑥 в области определения функции.
Нам нужно убедиться, что область определения функции симметрична относительно 0; в противном случае симметричные свойства четных и нечетных функций не будут применяться.
Область определения кусочно определенной функции есть объединение подобластей различных
подфункции. В этом вопросе у нас есть подфункция,
−9𝑥–8, определенный на интервале
]−∞,0[ и другое,
9𝑥–8, определенные на интервале
[0,∞[. Обе подфункции линейны, поэтому они определены на всем своем протяжении.
поддомен. Следовательно, объединение этих интервалов есть множество действительных чисел. Домен 𝑓(𝑥) можно записать как ℝ.
Это симметрично относительно 0, поэтому теперь мы можем проверить четность функции, оценив 𝑓(−𝑥). Нам нужно будет сделать это для отрицательных и положительных входных данных отдельно, чтобы определить отображает ли функция отражательную симметрию относительно оси 𝑦.
Для 𝑥0, −𝑥 будет положительным: 𝑓(−𝑥)=9×(−𝑥)−8=−9𝑥−8.
Это равно другой части кусочной функции, подфункции, используемой для отрицательных значений 𝑥.
Тогда для 𝑥>0 −𝑥 будет отрицательным: 𝑓(−𝑥)=−9×(−𝑥)−8=9𝑥−8.
Опять же, это равно другой части кусочной функции, подфункция, используемая для положительных значений 𝑥.
Мы можем подтвердить наши выводы и проверить, что происходит при 𝑥=0, рисуя эскиз графика.
График имеет отражательную симметрию относительно оси 𝑦.
Поскольку 𝑓(−𝑥)=−𝑓(𝑥) для всех 𝑥 в области
𝑓, функция четная.
Теперь мы исследуем, как на четность функции может влиять ее область определения.
Пример 7. Определение четности функций
Определите, является ли функция 𝑓(𝑥)=9𝑥 четный, нечетный или ни один из них 𝑓∶]−7,7]→ℝ.
Ответ
Функция 𝑓(𝑥) является
- четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
- нечетной функцией, если 𝑓(−𝑥)=−𝑓( 𝑥),
для каждого 𝑥 в области определения функции.
Нам нужно убедиться, что область определения функции симметрична относительно 0; в противном случае симметричные свойства четных и нечетных функций не будут применяться.
Нам дано, что 𝑓∶]−7,7]→ℝ. Мы можем прочитать это как «функция 𝑓 отображает числа слева, справа и слева». замкнутый интервал от −7 до 7 на множество действительных чисел». Область определения — это интервал ]−7,7], а область значений — множество действительных чисел.
Может показаться, что этот домен симметричен относительно 0;
однако нам говорят, что 𝑥 может быть равно 7, но не может
быть равным −7.
Это означает, что он не симметричен относительно 0,
Поскольку область определения 𝑓(𝑥) не симметрична относительно 0, функция не четная и не нечетная.
В нашем последнем примере мы покажем, как знание четности функции может помочь нам получить информацию о ее переменных.
Пример 8. Нахождение неизвестного в рациональной функции по заданной четности
Найдите значение 𝑎, если 𝑓 является четным функция, где 𝑓(𝑥)=68𝑥+𝑎𝑥−3 и 𝑥≠0.
Ответ
Мы знаем, что если 𝑓 и 𝑓 четные функции, их частное 𝑓𝑓 тоже четный. Точно так же говорят, что функция 𝑓(𝑥) быть четным, если 𝑓(−𝑥)=𝑓(𝑥) для каждого 𝑥 в области определения функции.
Поскольку функция числителя не зависит от 𝑥, это даже. Это означает, что функция в знаменателе также должна быть четной. Пусть функция 𝑓(𝑥)=8𝑥+𝑎𝑥−3 так, что 𝑓(−𝑥)=8(−𝑥)+𝑎(−𝑥)−3=8𝑥−𝑎𝑥−3.
Чтобы функция была четной, 𝑓(−𝑥)=𝑓(𝑥) для каждого значения
𝑥 в домене 𝑓:
8𝑥−𝑎𝑥−3=8𝑥+𝑎𝑥−3.
Вычитая 8𝑥 и добавляя 3 к обеим частям, это уравнение упрощается до −𝑎𝑥=𝑎𝑥.
Поскольку 𝑥≠0, мы можем разделить на 𝑥: −𝑎=𝑎.
Это уравнение может быть истинным только в том случае, если 𝑎=0.
Чтобы 𝑓 была четной функцией, 𝑎=0.
Теперь мы повторим ключевые моменты этого объяснения. Ключевые моменты 𝑥), для каждого 𝑥 в области определения функции.
Суммы и произведения четных и нечетных функций (3 ключевые идеи) – JDM Educational
Графики четных и нечетных функций имеют симметрию (относительно оси Y или начала координат). Однако мы также можем сказать, какой тип функции мы получим, сложив или умножив две или более из них вместе.
Итак, что вам нужно знать о суммах и произведениях четных и нечетных функций? Сумма или произведение двух четных функций четно. Произведение двух нечетных функций также четно. Сумма двух нечетных функций нечетна. Произведение четной и нечетной функции также нечетно. Сумма четной функции и нечетной функции не является ни четной, ни нечетной, если только одна или обе не равны нулю.
Конечно, мы можем добавить столько четных функций, сколько захотим, и все равно получить четную функцию. Точно так же мы можем добавить столько нечетных функций, сколько захотим, и все равно получить нечетную функцию.
В этой статье мы более подробно рассмотрим суммы и произведения как четных, так и нечетных функций.
Мы также рассмотрим несколько примеров, чтобы прояснить концепцию.
Начнем.
Суммы и произведения четных и нечетных функций
Помните, что четные и нечетные функции имеют следующие ключевые характеристики:
- Для четной функции f(x): f(-x) = f(x) для всех x в домене.
- Для нечетной функции f(x): f(-x) = -f(x) для всех x в области.
В таблице ниже показано, чего следует ожидать при сложении или умножении четных и нечетных функций.
| f(x) | g(x) | Сумма (f+g) | Произведение (f*g) |
|---|---|---|---|
| Четный | Четный | Четный | Четный |
| Четный | Нечетный | Ни один | Нечетный |
| Нечетный | Нечетный | Нечетный | 9 0377 Четный
четных и нечетных функций.
Начнем с суммы двух четных функций.
Каждое событие не является транзакцией, но…
Пожалуйста, включите JavaScript
Каждое событие не является транзакцией, но каждая транзакция является событием.
Сумма двух четных функций
Сумма двух четных функций всегда будет четной. Чтобы доказать это, предположим, что f(x) и g(x) — четные функции.
Тогда f(-x) = f(x) и g(-x) = g(x). Глядя на их сумму:
- (f + g)(-x)
- =f(-x) + g(-x) [по определению суммы функций]
- =f( x) + g(x) [поскольку f(x) и g(x) являются четными функциями]
- = (f + g)(x) [по определению суммы функций]
Итак (f + g)(-x) = (f + g)(x), что означает, что сумма f(x) и g(x) четна.
Обратите внимание, что разность двух четных функций также является четной, поскольку на самом деле это сумма двух четных функций (изменение знака четной функции означает, что она все еще четная).
Обратите внимание, что мы можем добавить любое количество четных функций, и сумма будет четной (мы можем доказать это, взглянув на группу из 2 функций одновременно).
Пример: сумма двух четных функций
Пусть f(x) = x 2 + 1 и g(x) = x 4 + 3.
Обе функции f(x) и g(x) четны функции, так как они являются полиномами, члены которых имеют четные степени x.
График четной функции f(x) = x 2 + 1. График четной функции g(x) = x 4 + 3.Их сумма:
- f(x) + g(x)
- =(x 2 + 1) + (x 4 + 3) [определение f(x) и g(x)]
- =x 4 + x 2 + 4 [переставить и объединить одинаковые члены]
Это также четная функция, поскольку это многочлен, члены которого имеют четные степени x.
Четная функцияСумма двух нечетных функций
Сумма двух нечетных функций всегда будет нечетной.
Чтобы доказать это, предположим, что f(x) и g(x) — нечетные функции.
Тогда f(-x) = -f(x) и g(-x) = -g(x). Глядя на их сумму:
- (f + g)(-x)
- =f(-x) + g(-x) [по определению суммы функций]
- =-f (x) + -g(x) [поскольку f(x) и g(x) являются нечетными функциями]
- =-(f + g)(x) [по определению суммы функций]
Итак, (f + g)(-x) = -(f + g)(x), что означает, что сумма f(x) и g(x) нечетна.
Обратите внимание, что разность двух нечетных функций также является нечетной, поскольку на самом деле она является суммой двух нечетных функций (изменение знака нечетной функции означает, что она все еще нечетная).
Обратите внимание, что мы можем добавить любое количество нечетных функций, и сумма будет нечетной (мы можем доказать это, взглянув на группу из 2 функций одновременно).
Пример: сумма двух нечетных функций
Пусть f(x) = x 3 + 2x и g(x) = x 7 + 4x 5 .
И f(x), и g(x) являются нечетными функциями, поскольку они являются полиномами, члены которых имеют нечетные степени x.
График нечетной функции f(x) = x 3 + 2x. График нечетной функции g(x) = x 7 + 4x 5 .Их сумма равна:
- f(x) + g(x)
- =(x 3 + 2x) + (x 7 + 4x 5 904 52 ) [определение f(x ) и g(x)]
- =x 7 + 4x 5 + x 3 + 2x [переставить члены]
номинал, члены которого имеют нечетные степени х.
График нечетной функцииСумма четной и нечетной функций нечетная функция не является ни четной ни нечетным, если только одна или обе функции не равны нулю (ноль бывает и четным, и нечетным).
Чтобы доказать это, предположим, что f(x) — четная функция, а g(x) — нечетная функция.
Тогда f(-x) = f(x) и g(-x) = -g(x). Глядя на их сумму:
- (f + g)(-x)
- =f(-x) + g(-x) [по определению суммы функций]
- =f(x) + -g(x) [поскольку f(x) — четная функция, а g(x) — нечетная функция]
- =f(x) – g(x)
Теперь рассмотрим (f + g)(x) :
- (f + g)(x)
- =f(x) + g(x) [по определению суммы функций]
Это не то же самое, что (f + g )(-x), если только g(x) = 0. Итак, (f + g)(x) нечетно.
Глядя на –(f + g)(x):
- -(f + g)(x)
- =-f(x) – g(x) [по определению суммы функции]
Это не то же самое, что (f + g)(-x), если только f(x) = 0. Таким образом, (f + g)(x) не нечетно.
Таким образом, (f + g)(x) не является ни четным, ни нечетным, если только:
- Если f(x) = 0, то (f + g)(x) нечетно.
- Если g(x) = 0, то (f + g)(x) четно.
- Если f(x) = 0 и g(x) = 0, то (f + g)(x) одновременно четно и нечетно (поскольку сумма равна нулю).
Пример: Сумма четной и нечетной функций
Пусть f(x) = x 2 + 3 и g(x) = x 3 – 4x.
Тогда f(x) — четная функция (многочлен с четными показателями), а g(x) — нечетная функция (многочлен с нечетными показателями).
График четной функции f(x) = x 2 + 3. График нечетной функции g(x) = x 3 – 4x.Их сумма равна:
- f(x) + g(x)
- =(x 2 + 3) + (x 3 – 4x) [определение f(x) и g(x)]
- =x 3 9045 2 + х 2 – 4x + 3 [переставить члены]
Эта функция не является ни четной, ни нечетной, так как это полином с четными и нечетными показателями.
График функцииПроизведение двух четных функций
Произведение двух четных функций всегда будет четным.
Чтобы доказать это, предположим, что f(x) и g(x) — четные функции.
Тогда f(-x) = f(x) и g(-x) = g(x). Глядя на их произведение:
- (f*g)(-x)
- =f(-x)*g(-x) [по определению произведения функций]
- =f( x)*g(x) [поскольку f(x) и g(x) являются четными функциями]
- =(f*g)(x) [по определению суммы функций]
Итак (f*g)(-x) = (f*g)(x), что означает, что произведение f(x) и g(x) четно.
Обратите внимание, что частное двух четных функций также является четным, поскольку на самом деле оно является произведением двух четных функций (взятие обратной величины четной функции все равно дает нам четную функцию). Единственное, на что нужно обратить внимание, это нулевые знаменатели!
Обратите внимание, что мы можем умножать любое количество четных функций, и произведение будет четным (мы можем доказать это, взглянув на группу из 2 функций одновременно).
Пример: Произведение двух четных функций
Пусть f(x) = 3x 2 + 5 и g(x) = x 4 – 2.
И f(x), и g(x) четные функции, так как они являются полиномами, члены которых имеют четные степени x.
График четной функции f(x) = 3x 2 + 5. График четной функции g(x) = x 4 – 2.Произведение:
- f(x)*g(x)
- =(3x 2 + 5)*(x 4 9045 2 – 2) [определение f(x) и g(x)]
- =3x 6 – 6x 2 + 5x 4 – 10 [ФОЛЬГА]
- =3x 904 51 6 + 5x 4 – 6x 2 – 10 [переставить члены]
Это также четная функция, поскольку это многочлен, члены которого имеют четные степени x.
График четной функцииПроизведение двух нечетных функций две нечетные функции всегда будут четными.
Чтобы доказать это, предположим, что f(x) и g(x) — нечетные функции.Тогда f(-x) = -f(x) и g(-x) = -g(x). Глядя на их произведение:
- (f*g)(-x)
- =f(-x)*g(-x) [по определению произведения функций]
- =-f(x)*-g(x) [поскольку f(x) и g(x) являются нечетными функциями]
- =f(x)*g(x) [произведение двух отрицательных чисел равно положительный]
- = (f*g)(x) [по определению суммы функций]
Итак, (f*g)(-x) = (f*g)(x), что означает, что произведение f(x) и g(x) четно.
Обратите внимание, что частное двух нечетных функций также является нечетным, поскольку на самом деле оно является произведением двух нечетных функций (взятие обратной величины нечетной функции означает, что оно все еще нечетное).
Обратите внимание, что если мы умножаем более 2 нечетных функций, необходимо рассмотреть 2 случая:
- Произведение четного числа нечетных функций четно.
- Произведение нечетного числа нечетных функций нечетно.
Пример: Произведение двух нечетных функций
Пусть f(x) = 4x 5 – 8x и g(x) = 5x 3 + x.
И f(x), и g(x) являются нечетными функциями, поскольку они являются полиномами, члены которых имеют нечетные степени x.
График нечетной функции f(x) = 4x 5 – 8x. График нечетной функции g(x) = 5x 3 + x.Произведение:
- f(x)*g(x)
- =(4x 5 – 8x) + (5x 3 + x) [определение отношение f(x) и g (x)]
- =20x 8 + 4x 6 – 40x 4 – 8x 2 [ФОЛЬГА]
Произведение Чета и Ана Нечетная функция
Произведение четной и нечетной функций является нечетной функцией, если ни одна из функций не равна нулю, и в этом случае произведение равно нулю (что является одновременно четным и нечетным).
Чтобы доказать это, предположим, что f(x) — четная функция, а g(x) — нечетная функция.
Тогда f(-x) = f(x) и g(-x) = -g(x). Глядя на их продукт:
- (f*g)(-x)
- =f(-x)*g(-x) [по определению произведения функций]
- =f(x)*-g (x) [поскольку f(x) — четная функция, а g(x) — нечетная функция]
- =-f(x)*g(x)
- =-(f*g)( x)
Поскольку (f*g)(-x) = -(f*g)(x), мы знаем, что (f*g)(x) — нечетная функция.
Пример: Произведение четной и нечетной функций
Пусть f(x) = x 4 – 5 и g(x) = x 5 + 2 шт.
Тогда f(x) — четная функция (многочлен с четными показателями), а g(x) — нечетная функция (многочлен с нечетными показателями).
График четной функции f(x) = x 4 – 5. График нечетной функции g(x) = x 5 + 2x.Их продукт:
- f(x)*g(x)
- =(x 4 – 5)*(x 5 + 2x) [определение f(x) и g (х)]
- =х 9 + 2x 5 – 5x 5 – 10x [ФОЛЬГА]
- = x 9 – 3x 5 – 10x [объединить похожие термины]
Эта функция нечетная, поскольку многочлен с нечетными показателями.