правило, примеры. Перевод десятичных чисел в дробь и наоборот — онлайн калькулятор Перевод десятичной дроби в смешанное число
Словари. Энциклопедии. История. Литература. Русский язык » История » Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры. Перевод десятичных чисел в дробь и наоборот — онлайн калькулятор Перевод десятичной дроби в смешанное число
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:
Примеры перехода от десятичной записи дробей к обычнойОсобое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае?
Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.
Более быстрый способ
В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
- Посчитать, сколько цифр стоит после запятой.
 {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.Наконец, последний пример:
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
\[\frac{22}{25}\to 1\frac{22}{25}\]
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз.
 Ещё парочка примеров:
Ещё парочка примеров:\[\begin{align}& 2,15\to 0,15=\frac{15}{100}=\frac{3}{20}\to 2\frac{3}{20}; \\& 13,8\to 0,8=\frac{8}{10}=\frac{4}{5}\to 13\frac{4}{5}. \\\end{align}\]
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
Попробуйте потренироваться сами — это очень просто.
 Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтомуА какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 10 3 , а 10 = 2 ∙ 5, поэтому
\[\begin{align}& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end{align}\]
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.
На этом урок окончен. Переходим к более сложной обратной операции — см. «
Алгебра и математика – сложные науки, которые легко не даются даже тем, кто уделяет им достаточно много времени. Проблемы могут возникнуть с любыми задачами. Например, не каждый знает, как десятичную дробь перевести в обыкновенную дробь.
Особенности дроби
Чтобы легко переводить один вид дроби в другой, лучше всего понимать, что это такое.
 Их можно назвать нецелым числом. Оно состоит из одной или же нескольких частей единицы.
Их можно назвать нецелым числом. Оно состоит из одной или же нескольких частей единицы.В первую очередь, выделяют обыкновенные или так называемые простые дроби. В отношении любого вида действует правило, что знаменатель не может равняться нулю . Если это так, то это значит, что значение целое, то есть оно не может быть дробью.
Существует несколько видов написания такого числа. Используется горизонтальная линия или наклонная черта, причем второй вариант может выглядеть в печатном виде тремя разными способами. В школьных тетрадях же, как правило, обыкновенные дроби записывают с классической горизонтальной линией.
Помимо простых, выделяют смешанные и составные дроби. Первые отличаются тем, что имеют ещё и целое число, записываемое в начале. У составных числитель и знаменатель как будто тоже является ещё одной дробью.
Как десятичную дробь перевести в обыкновенную дробь?
Десятичную дробь перевести в обычную дробь не так трудно, так как, несмотря на внешние изменения, суть числа останется одинаковой.

Десятичная дробь формируется из двух составляющих. Первая располагается до знака и обозначает целое число. Вторая, та, что находится после него, это десятые, сотые и другие числа. Их название зависит от того, насколько они отдалены от запятой.
Иногда превратить одну дробь в другую очень просто, особенно если нецелая часть – это десятые, а не сотые или тысячные. Классический пример –0,5. В первую очередь, его стоит правильно прочитать, то тогда получится ноль целых, пять десятых. Ноль целых никак записать не получится, а вот пять десятых легко превращаются в 5/10. Всё, что остается – провести сокращение путем деления на пять. Результат – ½.
Дробь с целым числом
Необходимо рассмотреть и другие примеры, с повышенной сложностью. Стоит взять 2,25. Как и до этого, для начала, лучше всего правильно обозначить название дроби.
В этот раз имеется две целых, двадцать пять сотых. В связи с тем, что после знака находится две цифры, то они являются сотыми.
Как десятичную дробь перевести в обыкновенную дробь:
- Нецелая часть записывается в виде 25/100.
- Осталось дописать две целых. Они ставятся в начало, и таким образом получается смешанная дробь.
- 25/100 можно сократить. Для простоты, реально начинать с деления на 5, но неплохо сразу воспользоваться числом 25. В результате сокращения получается ¼.
- Остается лишь подписать две целые к ¼. Результат – 2 ¼.
Наконец, стоит рассмотреть и процесс работы с тысячными. Для разбора возьмем 4,112. Вновь работу нужно начать с верного прочтения. Получится четыре целых, сто двенадцать тысячных. Без труда удастся выделить первую цифру, 4, а затем подставить к ней сто двенадцать тысячных. Они выглядят так – 112/100.
Остается лишь сократить, чтобы придать лучший вид. В этом конкретном примере общим делителем является шесть.
 Результат – простая дробь 4 14/125.
Результат – простая дробь 4 14/125.Перевод дробей в проценты
Практически любую дробь реально без особого труда перевести в проценты. Чтобы это сделать, нужно понимать, что процент – это одна сотая . Другими словами, 1% сразу возможно легко записать в дробном виде – 1/100 или 0,01.
В случае же с другими вариантами, придется обратиться к десятичным дробям, то есть тем, что пишутся через запятую. С ними задача решается очень просто. Достаточно умножить десятичную дробь на 100, и получится искомый процент.
- 0,27 * 100% = 27%
Если же необходимо осуществить перевод обыкновенной дроби, то сначала её придется превратить в десятичную.
- Например, 2/5 равняются 0,4.
- 0,4 * 100% = 40%.
Если процесс перевода в проценты всё равно вызывает трудности, то, при желании, можно воспользоваться различными автоматическими сервисами, которых достаточно много в интернете. Вписав в соответствующие поля числитель и знаменатель, удастся легко узнать, какой из этого получится процент.

В целом же, перевод дробей в проценты всегда завязан на умножении на 100. Для того, чтобы легко с этим справляться, необходимо понимать, как перевести обыкновенную дробь в десятичную, но, для начала, стоит разобраться и в обратном процессе.
Видео инструкция
В самом начале нужно все-таки узнать, что такое дробь и каких видов она бывает. А бывает она трех видов. И первый из них это обыкновенная дробь, например ½, 3/7,3/432 и т. д. Эти числа также можно записывать при помощи горизонтальной черточки. И первое, и второе будет одинаково верно. Цифра сверху называется числительным, а снизу знаменателем. Есть даже поговорка, для тех людей, кто постоянно путает эти два названия. Она звучит так: «Зззззапомни! Зззззнаменатель — внизззззу! ». Это поможет не запутаться. Обыкновенная дробь это всего лишь два числа, которые делятся друг на друга. Черточка в них и обозначает знак деления. Ее можно заменить знаком двоеточие. Если стоит вопрос «как дробь перевести в число», то это очень просто.

Второй вид дробей называется десятичным. Это ряд цифр с запятой. К примеру, 0,5, 3,5 и т. д. Назвали их десятичными, только потому, что после запетой первая цифра обозначает «десятки», вторая в десять раз больше «сотни» и так далее. А первые цифра до запятой, называются целыми. Например, число 2,4 звучит так, двенадцать целых и двести тридцать четыре тысячных. Такие дроби появляются в основном из-за того, что поделив два числа без остатка не получается. И большинство обыкновенных дробей, во время того как их будут переводить в числа, в конечном итоге имеют вид десятичной дроби. Например, одна вторая ровняется ноль целым пяти десятым.
И заключительный третий вид. Это смешанные числа. Пример этого можно привести такой, как 2½. Звучит так, две целых и одна вторая. В старших классов такой вид дробей уже не используются. Их наверняка необходимо будет приводить или в обыкновенный вид дроби, или в десятичный.
 Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.Если на нем получается не целые числа и после запятой идет очень много цифр, то тогда данное значение можно округлить. Округляется все очень просто. Сначала следует определиться, к какой цифре нужно округлить. Следует рассмотреть пример. Человеку нужно округлить число ноль целых, девять тысяч семьсот пятьдесят шесть десятитысячных или в цифровом значении 0,6. Округление необходимо сделать до сотых. Это означает, что в данный момент до семи сотых. После цифры семь в дроби идет пять. Теперь нужно использовать правила для округления.
 Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.Также возникают ситуации, когда человеку необходимо быстро перевести обыкновенную дробь в число, а калькулятора рядом нет. Для этого стоит применить деление столбиком. Первым делом следует на листке написать рядом друг с другом числитель и знаменатель. Между ними ставится уголок деления, он похож на букву «Т», только лежащую на боку. Для примера можно взять дробь десять шестых. И так, десять следует поделить на шесть. Сколько шестерок может вместиться в десятке, только одна. Единица записывается под уголком. Десять отнять шесть получится четыре. Сколько шестерок будет в четверке, несколько. Значит, в ответе после единицы ставится запятая, а четверка умножается на десять. В сорока шесть шестерок. В ответе дописывается шестерка, а от сорока отнимается тридцать шесть.
 Получается опять четыре.
Получается опять четыре.В данном примере произошло зацикливание, если продолжить делать все точно также получится ответ 1,6(6) Цифру шесть продолжается для бесконечности, но применив правило округления, можно привести получение число к 1,7. Что намного удобней. Из этого можно сделать вывод, что не все обыкновенные дроби можно перевести в десятичные. В некоторых происходит зацикливание. Но зато любую десятичную дробь можно перевести в простую. Здесь поможет элементарное правило, как слышится, так и пишется. Например, число 1,5, слышится, как одна целых двадцать пять сотых. Так и нужно записать, одна целая, двадцать пять поделить на сто. Одна целая это сто, а значит, простая дробь будет сто двадцать пять на сто (125/100) . Все также просто и понятно.
Вот и было разобраны самые основные правила и преобразования, которые связанны с дробями. Все они несложные, но знать их следует. В повседневную жизнь уже давно вошли дроби, особенно десятичные. Это хорошо видно на ценниках в магазинах.
 Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.Простые дроби не всегда удобны в обращении. В отчет или в ведомость их не вставишь, да и современные компьютерные программы не всегда дружат с такими числами. Перевести простую дробь в (или в десятичную дробь) не составит труда.
Вам понадобится
- листок бумаги, ручка, калькулятор
Инструкция
Перевести дробь в число — значит разделить числитель на знаменатель. Числитель — это верхняя часть дроби, знаменатель — нижняя. Если под рукой есть калькулятор, то нажмите на кнопки, и задача выполнена.
 В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).
В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).Если калькулятора под рукой не оказалось, но придется делить в столбик. Напишите числитель дроби рядом со знаменателем, между ними уголочек, означающий деление. К примеру, переведите в число дробь 10/6. Для начала 10 разделите на 6. Получится 1. Запишите результат по уголком. Перемножьте 1 на 6, получится 6. Вычтите 6 из 10. Получится остаток 4. Остаток нужно снова разделить на 6. Допишите к 4 цифру 0, и разделите 40 на 6. Получится 6. Запишите 6 в результат, после запятой. Перемножьте 6 на 6. Получится 36. Вычтите 36 из 40. Получится вновь остаток 4. Далее можно не продолжать, поскольку становится очевидным, что результатом будет число 1,66(6). Округлите данную дробь до того разряда, который вам необходим.
 Например, 1,67. Это и есть окончательный результат.
Например, 1,67. Это и есть окончательный результат.Как считать дроби на калькуляторе / 5-Minute Crafts
Большинство калькуляторов по умолчанию работают с десятичными дробями. Например, калькулятор работает с «0,5» вместо «1/2». Тем не менее, есть несколько способов посчитать дроби на обычном калькуляторе, а затем преобразовать их из десятичной формы в обыкновенную. Также есть специальные калькуляторы, которые могут выполнять действия с простыми дробями, но это непросто даже с их помощью.
5-минутные ремесла хочет показать вам, как складывать, вычитать, умножать и делить дроби на разных калькуляторах.
Как считать дроби на научном калькуляторе
Такой калькулятор предназначен для решения задач в технике и науке, поэтому его возможности шире, чем у обычного. Такой калькулятор может иметь 2 поля: одно отражает введенные значения, а другое – результат.
В калькуляторе такого типа есть кнопка, позволяющая ввести число в виде обыкновенной дроби.

Хотите знать, как вы это делаете? Допустим, вам нужно ввести число 3/4.
- Включите калькулятор. Затем нажмите цифру 3, которая должна быть числителем.
- Нажмите кнопку, которая изменяет формат числа, позволяя вам вводить обыкновенную дробь. Он расположен в верхнем левом углу и обозначается a b / c или 2 прямоугольниками, один из которых закрашен, а другой нет. В строке ввода появится символ, похожий на ˩.
- Нажмите цифру 4, которая должна быть знаменателем.
- Таким образом, число 3/4 вводится в калькулятор в виде обыкновенной дроби для дальнейших расчетов.
Допустим, мы хотим узнать результат простого действия сложения 1 3 / 4 и 3 / 8 . Начнем с ввода смешанной дроби, затем перейдем к сложению.
Шаг 1. Нажмите цифру 1 на калькуляторе.
Шаг 2. Затем нажмите кнопку, позволяющую изменить формат числа, и введите число в виде обыкновенной дроби.
 На этот раз это нужно сделать на данном этапе, чтобы калькулятор распознал это число как смешанную дробь.
На этот раз это нужно сделать на данном этапе, чтобы калькулятор распознал это число как смешанную дробь.Шаг 3. Нажмите цифру 3.
Шаг 4. Нажмите кнопку, позволяющую ввести число в виде обыкновенной дроби. Затем нажмите цифру 4. Теперь смешанная дробь введена!
Шаг 5. Теперь нажмите кнопку добавления и добавьте вторую дробь, введя ее таким же образом.
Шаг 6. Наконец, нажмите кнопку равенства, чтобы получить результат. Калькулятор покажет результат в виде смешанной дроби. Точно так же вы можете выполнять и другие действия с дробями.
Обратите внимание, что формат числа в результате такой же, как и слагаемые.
Эти калькуляторы имеют свои особенности:
- Если при вычислениях смешать обыкновенные и десятичные дроби, то результат будет отображаться в виде десятичной дроби, что вы можете видеть на картинке выше.
- Дроби в результатах вычислений всегда отображаются после приведения их к несократимым дробям.

Как считать дроби на обычном калькуляторе
В обычном калькуляторе нет кнопки для ввода дроби, но есть другие функции, которые могут облегчить вашу работу.
Допустим, вы получили результат, работая с десятичными дробями, но теперь вам нужно записать это число в виде обыкновенной дроби. Как преобразовать десятичную дробь в обыкновенную?
- Введите десятичную дробь на калькуляторе. В нашем примере мы использовали 0,7143. Нажмите кнопку умножения.
- Чтобы преобразовать десятичную дробь в обыкновенную, выберите число, которое будет стоять в знаменателе получившейся обыкновенной дроби. Допустим, это 7. Умножьте на него десятичную дробь.
- Полученное число округлить до ближайшего целого числа и записать в числитель. В данном случае это 5. И цифра 7, соответственно, написана в знаменателе.
Таким образом, получается, что число 0,7143 можно представить в виде обыкновенной дроби 5/7.
Этот метод имеет недостаток : он может привести к ошибке в расчете, поэтому конечный результат необходимо проверить.
 Просто разделите числитель на знаменатель: чем меньше погрешность, тем ближе будет результат к исходной десятичной дроби, а значит, полученную ранее обыкновенную дробь можно использовать для дальнейших расчетов.
Просто разделите числитель на знаменатель: чем меньше погрешность, тем ближе будет результат к исходной десятичной дроби, а значит, полученную ранее обыкновенную дробь можно использовать для дальнейших расчетов.Но что, если у вас есть обыкновенные дроби и вы хотите преобразовать их в десятичные дроби, чтобы работать с ними с помощью обычного калькулятора? Как преобразовать обыкновенную дробь в десятичную? Возьмем дробь 7/4 и преобразуем ее в десятичную дробь.
- Введите на калькуляторе число 7, которое является числителем. Нажмите кнопку деления.
- Введите 4 (знаменатель дроби) в качестве делителя.
- Нажмите кнопку равенства. В результате вы получите десятичную дробь. Итак, вы преобразовали 7/4 в десятичную дробь 1,75.
Важно: Обыкновенная дробь после преобразования в десятичную дробь может стать бесконечным десятичным расширением. Если это так, его можно округлить.
Как работать с дробями с помощью кнопок памяти (MR, M-, M+) на калькуляторе
Некоторые модели калькуляторов имеют кнопки памяти, которые позволяют сохранить определенное число в памяти устройства и выполнять над ним операции сложения или вычитания.
 Эти функции можно использовать при работе с дробями. Например, давайте посмотрим, как их можно использовать при добавлении чисел 1 / 4 и 3 / 8 .
Эти функции можно использовать при работе с дробями. Например, давайте посмотрим, как их можно использовать при добавлении чисел 1 / 4 и 3 / 8 .Шаг 1. Сначала введите дробь 1/4. Нажмите цифру 1 на калькуляторе, затем нажмите кнопку деления.
Шаг 2 . Введите число 4 и нажмите кнопку M+. Если результат деления не отображается после нажатия кнопки M+, начните заново и перед нажатием кнопки M+ здесь и на шаге 5 нажмите кнопку =.
Шаг 3. Результат деления этих чисел выводится на экран калькулятора, а также сохраняется в памяти калькулятора.
Шаг 4. Теперь таким же образом введите вторую дробь. Сначала нажмите цифру 3 на калькуляторе, затем нажмите кнопку деления.
Шаг 5. Затем введите число 8 и нажмите кнопку M+.
Шаг 6. На экране калькулятора отображается результат деления этих чисел, который также сохраняется в памяти калькулятора.


 {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ. Ещё парочка примеров:
Ещё парочка примеров: Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому Их можно назвать нецелым числом. Оно состоит из одной или же нескольких частей единицы.
Их можно назвать нецелым числом. Оно состоит из одной или же нескольких частей единицы.

 Результат – простая дробь 4 14/125.
Результат – простая дробь 4 14/125.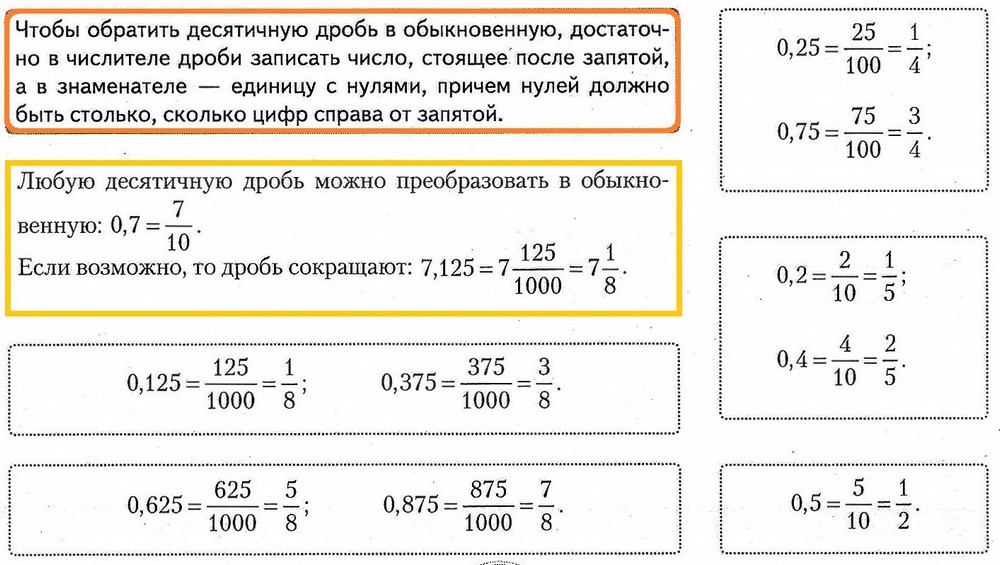

 Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором. Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8. Получается опять четыре.
Получается опять четыре. Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений. В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).
В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону). Например, 1,67. Это и есть окончательный результат.
Например, 1,67. Это и есть окончательный результат.
 На этот раз это нужно сделать на данном этапе, чтобы калькулятор распознал это число как смешанную дробь.
На этот раз это нужно сделать на данном этапе, чтобы калькулятор распознал это число как смешанную дробь.
 Просто разделите числитель на знаменатель: чем меньше погрешность, тем ближе будет результат к исходной десятичной дроби, а значит, полученную ранее обыкновенную дробь можно использовать для дальнейших расчетов.
Просто разделите числитель на знаменатель: чем меньше погрешность, тем ближе будет результат к исходной десятичной дроби, а значит, полученную ранее обыкновенную дробь можно использовать для дальнейших расчетов. Эти функции можно использовать при работе с дробями. Например, давайте посмотрим, как их можно использовать при добавлении чисел 1 / 4 и 3 / 8 .
Эти функции можно использовать при работе с дробями. Например, давайте посмотрим, как их можно использовать при добавлении чисел 1 / 4 и 3 / 8 .