Геометрическая и арифметическая прогрессия: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен (9 класс), Математика.

Задачи по теме «Арифметическая и геометрическая прогрессии» 9 класс онлайн-подготовка на Ростелеком Лицей

Тема 11: Прогрессии. Профильный уровень

• Видео
• Тренажер
• Теория

Заметили ошибку?

1. Тема урока, повторение теории

 

Здесь мы рассмотрим задачи на арифметическую и геометрическую прогрессии, начнем с краткого повторения теории.

 

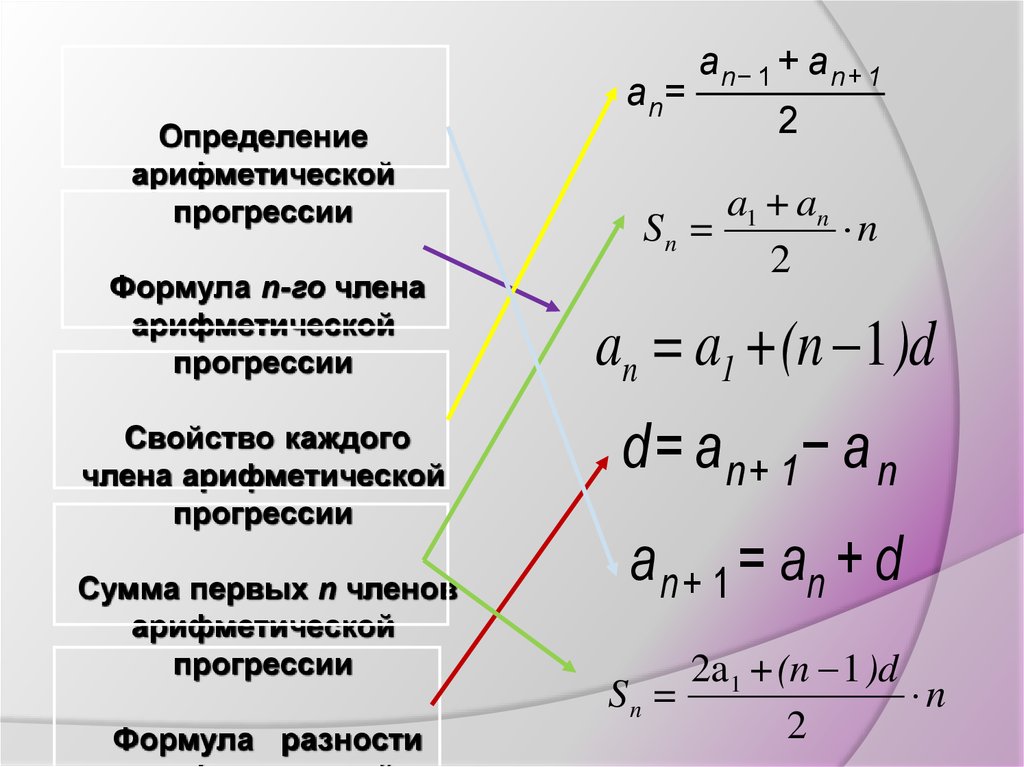
 арифметическая прогрессия, если = = … =  где  – разность прогрессии.  – формула го члена;  – сумма n членов;   , ,… — характеристическое свойство арифметической прогрессии; , если

 

 – геометрическая прогрессия, если , где – знаменатель прогрессии,  – формула n-го члена;  – сумма n первых членов, ,  — характеристическое свойство; , если

 

2. Решение задач

 

 

Рассмотрим задачи

 

1.      Три числа составляют конечную геометрическую прогрессию. Если из последнего числа вычесть 16, то получится конечная арифметическая прогрессия. Найдите два последних числа, если первое равно 9. Обозначим искомые числа y и z. Дано:  – геометрическая прогрессия,  – арифметическая прогрессия. Найти: . Решение: Воспользуемся характеристическим свойством геометрической и арифметической прогрессий и составим систему:        или        Ответ:

2.      Сумма трех чисел, составляющих конечную арифметическую прогрессию, равна 24. Если второе число увеличить на 1, а последнее на 14, то получится конечная геометрическая прогрессия. Найдите эти числа. Обозначим числа . Дано:  – арифметическая прогрессия,  – геометрическая прогрессия, Найти:   Решение: Воспользуемся характеристическим свойством геометрической и арифметической прогрессий и составим систему:           Ответ:

3.      Сумма третьего и седьмого членов арифметической прогрессии равна 100. Найдите сумму первых девяти членов прогрессии. Дано: арифметическая прогрессия, Найти: . Решение:      Ответ:450.

4.      Сумма трех чисел, образующих арифметическую прогрессию, равна 111. Второе число больше первого в 5 раз. Найдите эти числа. Дано:  – арифметическая прогрессия,   Найти: Решение:  – характеристическое свойство, подставляем: 2Ответ: 7,4; 37; 66,6.

5.      В возрастающей геометрической прогрессии Найти  и .Дано: Найти: . Решение: =72, т.к.   – мы видим, что это корни квадратного уравнения  Ответ: 3; 24.

6.      Докажите тождество: . Доказательство: – геометрическая прогрессия, т.к. ;     Тождество верно при . При  подставляем и получаем 0=0 – верно. Вывод: Тождество верно при всех

 

3. Подведение итогов

 

 

Мы рассмотрели смешанные задачи на арифметическую и геометрическую прогрессию.

 

 

Список литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл. : Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

 

Домашнее задание

Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.

№№ 527 — 530.

 

Дополнительные WEB-ресурсы

1. РЕШУ ЕГЭ (Источник). 
2. Задачи (Источник). 
3. Задачи (Источник).

 

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Видеоурок: Задачи по теме «Арифметическая и геометрическая прогрессии» по предмету Алгебра за 9 класс.

Некоторые свойства арифметико-геометрической прогрессии | Статья в журнале «Юный ученый»

 

В школьном курсе математики в полной мере изучаются два специальных вида последовательностей — арифметическая и геометрическая прогрессии, однако последовательности, обобщающие их, т. е. сочетающие их свойства и признаки, в явном виде не рассматриваются.

Известно, что ряд различных типов последовательностей по природе своей являются рекуррентными, или возвратными, в том смысле, что каждый следующий член последовательности по определенному правилу выражается через некоторое фиксированное число предыдущих.

К таким последовательностям относятся арифметическая и геометрическая прогрессии, последовательность Фибоначчи и др. [1]

В данной статье представлены итоги исследования рекуррентной последовательности , заданной по правилу , где числа и называем соответственно знаменателем и разностью этой последовательности, а саму последовательность — арифметико-геометрической прогрессией.

Актуальность исследования обусловлена тем, что в настоящее время эта проблема стала особенно значима для науки и практики. Этим вопросом занимаются многие теоретики и исследователи. Изучению прогрессий посвящены статьи в периодических изданиях и монографии многих ученых. Как правило, информация, посвященная данной проблеме, изложенная в учебной литературе, имеет общий характер, а в современных монографиях по этой теме анализируются более узкие вопросы проблемы.

Высокая значимость и недостаточная теоретическая разработанность проблемы изучения арифметико-геометрической прогрессии определяют несомненную новизну данного исследования.

Определение 1. [2] Арифметико-геометрическая прогрессия задается следующим рекуррентным соотношением:

, (1)

где и  — постоянные, называемые соответственно знаменателем и разностью арифметико-геометрической прогрессии.

Замечание 1. При q=1 и d=0 получим стационарную последовательность .

В случае и в (1), получим арифметическую прогрессию , а при и , — геометрическую прогрессию: .

Вышеуказанное замечание отражается в названии рассматриваемой последовательности: арифметико-геометрическая прогрессия.

Рассмотрим примеры арифметико-геометрических прогрессий.

1) ;

2) .

Указание явных формул для нахождения общего члена последовательности, а также для суммы ее первых n членов являются основными задачами о последовательностях.

Арифметико-геометрическая прогрессия является обобщением арифметической и геометрической прогрессий. А значит, по аналогии можно вывести формулы для нахождения общего члена арифметико-геометрической прогрессии, а также для суммы ее первых n членов, и установить характеристическое свойство данного типа последовательности, а также ряд других важных свойств.

В ходе исследования были получены конкретные результаты:

1. Выведена формула n-го члена последовательности: .

Пусть в соотношении (1) . Прибавив к обеим частям равенства выражение , получим

.

Последнее соотношение является рекуррентным, поэтому можно записать аналогичные равенства для :

, ,…, .

Перемножив выписанные равенства, имеем:

Разделив обе части последнего равенства на произведение , получим , откуда .

Таким образом, получили формулу общего члена арифметико-геометрической прогрессии

. (2)

2. Доказано, что арифметико-геометрическая прогрессия сходится и ограничена только в случае, когда ;

Из формулы общего члена арифметико-геометрической прогрессии следует, что

а) при арифметико-геометрическая прогрессия сходится к числу

, а значит, при эта последовательность ограничена.

б) при арифметико-геометрическая прогрессия расходится и не ограничена.

3. Выведена формула суммы первых n членов арифметико-геометрической прогрессии: . Также установлено, что сумма бесконечного числа членов последовательности не существует.

Рассмотрим n-ую частичную сумму арифметико-геометрической прогрессии .

Согласно соотношению (1), имеем:

Тогда

. (3)

Умножив последнее равенство на знаменатель , получим

или (4)

Из равенства (3) вычтем равенство (4) и выполним преобразования.

Преобразуя последнее равенство, получим формулу суммы первых n членов арифметико-геометрической прогрессии: .              (5)

4. Доказано, что арифметико-геометрическая прогрессия является возвратной последовательностью второго порядка и задается возвратным уравнением ; как следствия были получены характеристические свойства арифметической и геометрической прогрессий.

Действительно, будем утверждать, что при k=1 и при любом справедливо равенство . Осталось определить значения .

В силу соотношения (1) , тогда

.

Из равенства следует, что

,

,

, откуда уравняв коэффициенты, получим систему линейных уравнений с двумя переменными , решением которой является .

Итак, верно равенство . Что и требовалось доказать.

5. Выведены формулы для нахождения разности и знаменателя арифметико-геометрической прогрессии: и .

6. Доказано характеристическое свойство арифметико-геометрической прогрессии : последовательность , где , является геометрической прогрессией с тем же знаменателем , то есть .              (6)

Доказательство. Согласно формуле (2)

.

Упростив правую часть равенства (6), получим:

.

Тогда .

Таким образом, доказано равенство (6), которое и является характеристическим свойством арифметико-геометрической прогрессии.

Все полученные результаты являются новыми. Данные результаты имеют научную и практическую ценность, в частности, они могут быть использованы при решении геометрических задач. [2]

В доступной нам литературе подобные исследования ранее не встречались, лишь некоторые свойства арифметико-геометрической прогрессии встречаются без доказательства.

 

Литература:

 

1.      Маркушевич А. И. Возвратные последовательности — М.: Наука, 1975. — 47 с.
2.      Суконник Я. Н. Арифметико-геометрическая прогрессия. Научно-популярный физико-математический журнал «Квант», № 1 1975г. — с.80
3.      Вавилов В. В., Красников П. М. Математические коллоквиумы. — М.: Школа им. А. Н. Колмогорова СУНЦ МГУ, 2006. — с. 60

Арифметическая, геометрическая и гармоническая прогрессия

Прежде чем углубляться в значение таких терминов, как арифметика, геометрическая прогрессия и гармоническая прогрессия, мы должны сначала понять, что такое пассаж. В математике, как и в реальной жизни, человек сталкивается с несколькими примерами прогрессии. Прогрессия — это не что иное, как последовательность, демонстрирующая определенный паттерн. В случае системы счисления проход представляет собой ряд или последовательность чисел, которые либо имеют общую разность, либо стандартное соотношение, либо чьи общие значения демонстрируют некоторую закономерность.

Арифметические прогрессии — это ряды чисел, в которых разница между первым и вторым членами, вторым и третьим членами и т. д. одинакова. Разница между двумя последовательными членами ряда называется «общей разностью». Геометрическая прогрессия немного отличается от арифметической прогрессии. Здесь значения в прогрессии умножаются на один и тот же коэффициент, который называется общей разностью. Гармоническая прогрессия — это прогрессия, в которой обратные члены членов, составляющих последовательность, находятся в AP. Читайте дальше, чтобы узнать больше о формулах AP, GP и HP, примерах и их различиях.

Что такое арифметическая прогрессия?

Как обсуждалось выше,  арифметическая прогрессия – это любой ряд чисел, дробей или значений, в котором два последовательных термина имеют одинаковую разницу. Разница между любыми двумя соседними терминами называется общей разностью, которая обычно обозначается буквой d. Если у нас есть первый член ряда, общая разность и количество членов в этой конкретной последовательности, мы можем узнать значения других членов.

Формулы, относящиеся к арифметической прогрессии

Пусть ₁ , ₂ , ₃ , ₄ ,…. Будь арифметической прогрессией.

Первый член ряда равен a₁, а общая разность представлена ​​буквой d.

Таким образом, общая разность d = a ₂ — a ₁  

Если в ряду n членов, то n ^-й -й член будет иметь вид $a_{n}=a_{1}+ (n-1) d$

Сумма всех членов арифметического ряда с n членами определяется выражением $S=\dfrac{n}{2}\left(a_{1}+a_{n}\right )$. Более общая формула для нахождения значения любого количества терминов, скажем, через термины m (любой термин до n ^-й -й член) до n равен $S=\dfrac{n-m+1}{2}\left(a_{m}+a_{n}\right)$.

Примеры арифметической прогрессии   

5,10,15,20,25,30.

В вышеприведенном ряду первый член a₁ = 5, общая разность d = ( 10-5)=5. Общее количество членов, n = 6

Следовательно, сумма членов $S=\dfrac{n}{2}\left(a_{1}+a_{n}\right)=\dfrac{6}{ 2}(5+30)=105$

Что такое геометрическая прогрессия?

Подобно тому, как члены арифметической прогрессии связаны общей разностью, последовательность, в которой любые два соседних члена связаны общим отношением, условно обозначается r. Разделив любой член на следующий за ним член, мы можем получить обыкновенное отношение.

Формулы, относящиеся к геометрической прогрессии

Пусть a ₁ , a ₂ , a ₃ , a ₄ ,…. {n}-1}{r-1}\right)$ 9{4}\right)}{1-\dfrac{1}{2}}=\dfrac{15}{8}$

Что такое гармоническая прогрессия?

Гармоническая последовательность, пожалуй, самая запутанная из трех. На первый взгляд ряд может показаться набором произвольных чисел без четкой закономерности. Однако это определенно не так. В случае гармонической прогрессии обратные величины всех членов ряда находятся в арифметической прогрессии.

Формула гармонического прогресса

$H . P .=\dfrac{1}{a+(r-1) d}$

 

Здесь

«a» — первый член A.P.

«d» — общая разность

«n» — количество членов в A.P. 20-й член HP равен 20 и 40, рассчитайте 100-й член HP.

Решение: Ниже приведено соответствие AP заданному HP,

20-й член HP=$ a+19d= \dfrac{1}{40}$…(1)

10-й член AP= $a+ 9d= \dfrac{1}{20}$…(2)

Для уравнений (1) и (2)

После вычисления

$a=\dfrac{ 29}{400}$, $d=\dfrac{-1}{400}$

Мы должны написать выражение в виде, чтобы найти 100-й член,

$a+99d= \dfrac{29}{400}+99\left(\dfrac{-1}{400}\right)$

$\begin {align} &\Стрелка вправо a+99 d=\dfrac{29}{400}-\dfrac{99}{400} \\ &\Стрелка вправо a+99 d=\dfrac{29-99}{400} \\ &\Rightarrow a+99 d=\dfrac{-70}{400} \end{align}$

11-й член H. {\text {th}} \text {term AP }}$

11-й член HP = $\dfrac{400}{-70}=\dfrac{-40}{7}$

100-й член HP равен $\dfrac{-40}{7}$.

Разница между арифметической прогрессией и геометрической прогрессией

Два основных арифметических действия включают сложение и умножение. Умножение есть не что иное, как многократное сложение. Геометрическая прогрессия включает в себя термины, являющиеся произведением терминов, стоящих перед ними, и знаменателя. Арифметическая прогрессия включает члены, где один член есть не что иное, как сумма членов, стоящих перед ним, и общая разность. Поэтому может показаться веским аргументом, что геометрическая прогрессия на самом деле является арифметической прогрессией за вычетом определенных членов, или, скорее, арифметическая прогрессия является геометрической прогрессией, в которой отсутствуют определенные члены.

Однако между арифметической прогрессией и геометрической прогрессией есть некоторые ключевые различия.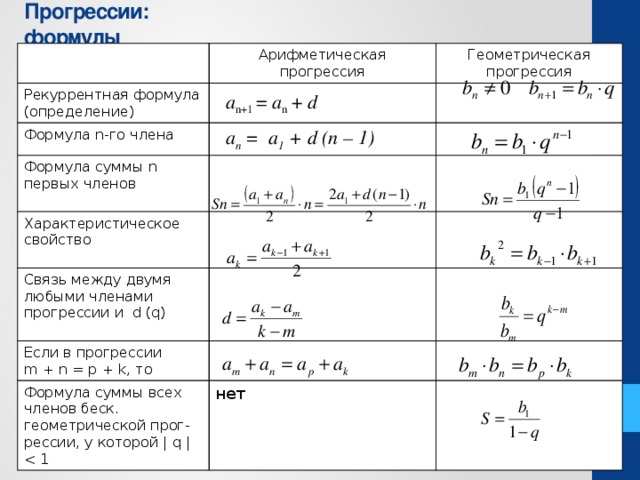 The following table gives us the main points of difference between the two:

Sr. No.	Basis of Comparison	AP	GP
1.	Идентификация	Общее отличие	Common ratio
2.	Variations in terms	Linear	Exponential
3.	Advanced by	Addition /вычитание	Умножение/деление
4.	Бесконечная последовательность	2 Расходящаяся0003	Расходящиеся или сходящиеся

Заключение

Прогрессия в математике — это последовательность чисел, которая демонстрирует определенный образец. Арифметическая прогрессия – это ряд, в котором разница между любыми двумя соседними членами равна одной и той же. Точно так же геометрическая прогрессия — это прогрессия, в которой любые два последовательных члена связаны знаменателем. Гармоническая прогрессия — это такая последовательность, в которой обратные величины всех членов прогрессии находятся в арифметической прогрессии. Текущая тема, единица прогресса на экзамене за доской, имеет промежуточные уровни. Теоретические и числовые аспекты этого материала имеют решающее значение с точки зрения экзамена, поскольку тест на доске является субъективным. Раздел преимущества в счете также предоставляет некоторую числовую информацию. Единица прогрессии имеет умеренный вес, потому что она содержит лишь небольшое количество математики.

Арифметические прогрессии и геометрические прогрессии

Все предметы

• Предварительные
  • Умножение и деление с использованием нуля
  • Общие математические символы
  • Викторина: способы показать умножение и деление, умножение и деление на ноль и общие математические символы
  • Свойства основных математических операций
  • Тест: свойства основных математических операций
  • Группировка символов и порядок операций
  • Группы чисел
  • Викторина: Группы чисел
  • Способы показать умножение и деление
  • Порядок операций
  • Викторина: группировка символов и порядок действий
• Целые числа
  • Оценка сумм, разностей, произведений и частных
  • Викторина: оценка сумм, разностей, произведений и частных
  • Правила делимости
  • Викторина: правила делимости
  • Факторы, простые числа, композиты и деревья факторов
  • Место Значение
  • Викторина: Факторы, простые числа, композиты и факторные деревья
  • Викторина: Значение места
• Десятичные
  • Использование таблицы стоимости места
  • Викторина: использование таблицы значений мест
  • Десятичные вычисления
  • Викторина: Десятичные вычисления
  • Оценка сумм, разностей, произведений и частных
  • Викторина: оценка сумм, разностей, произведений и частных
  • Что такое десятичные дроби?
  • Повторяющиеся десятичные дроби
• Фракции
  • Правильные и неправильные дроби
  • Смешанные номера
  • Переименование дробей
  • Викторина: правильные и неправильные дроби, смешанные числа и переименование дробей
  • Факторы
  • Мультипликаторы
  • Что такое дроби?
  • Викторина: Факторы и множители
  • Сложение и вычитание дробей
  • Сложение и вычитание смешанных чисел
  • Тест: сложение и вычитание дробей и смешанных чисел
  • Умножение дробей и смешанных чисел
  • Деление дробей и смешанных чисел
  • Тест: умножение и деление дробей и смешанных чисел
  • Упрощение дробей и сложных дробей
  • Викторина: Упрощение дробей и сложных дробей
  • Преобразование дробей в десятичные
  • Преобразование десятичных дробей в дроби
  • Преобразование бесконечных повторяющихся десятичных дробей в дроби
  • Викторина: Преобразование дробей в десятичные дроби, Преобразование завершающих десятичных дробей в дроби и Преобразование бесконечных повторяющихся десятичных дробей в дроби
• Проценты
  • Применение процентов
  • Викторина: Применение процентов
  • Изменение процентов, десятичных знаков и дробей
  • Важные эквиваленты
  • Викторина: изменение процентов, десятичных знаков и дробей, а также важные эквиваленты
• Целые числа и рациональные числа
  • Викторина: Рациональные числа (числа со знаком, включая дроби)
  • Целые числа
  • Викторина: Целые числа
  • Рациональные числа (числа со знаком, включая дроби)
• Экспоненты и корни в степенях
  • Викторина: Квадратные корни и кубические корни
  • Полномочия и показатели
  • Викторина: Полномочия и показатели
  • Квадратные корни и кубические корни
• Степени десяти и научная нотация
  • Викторина: Научная нотация
  • Силы десяти
  • Викторина: Силы десяти
  • Научная нотация
• Измерения
  • Метрическая система
  • Преобразование единиц измерения
  • Викторина: обычная система США, метрическая система и перевод единиц измерения
  • Точность
  • Значащие цифры
  • Викторина: точность и значащие цифры
  • Традиционная система США
  • Расчет измерений базовых фигур
  • Викторина: Расчет размеров базовых фигур
• Графики
  • Гистограммы
  • Викторина: гистограммы
  • Линейные графики
  • Викторина: линейные графики
  • Круговые диаграммы или круговые диаграммы
  • Введение в графики
  • Викторина: круговые диаграммы или круговые диаграммы
  • Графики координат
  • Викторина: Графики координат
• Вероятности и статистика
  • Викторина: Статистика
  • Вероятность
  • Викторина: Вероятность
  • Статистика
• Серия номеров
  • Арифметические прогрессии
  • Геометрические прогрессии
  • Викторина: арифметические прогрессии и геометрические прогрессии
• Переменные Алгебраические выражения и простые уравнения
  • Викторина: переменные и алгебраические выражения
  • Решение простых уравнений
  • Викторина: Решение простых уравнений
  • Переменные и алгебраические выражения
• Текстовые задачи
  • Ключевые слова
  • Викторина: Процесс решения и ключевые слова
  • Процесс решения
• Базовые тесты по математике

Вернуться к началу

Адам Беде

был добавлен в ваш список для чтения

!

OkUndo
   Управление списком чтения×

Adam Bede

добавлен в ваш список чтения

!

Хорошо    Управление моим списком для чтения×

Удаление #книги# из вашего списка для чтения также удалит все закладки страниц, связанных с этим заголовком.