Срединный отрезок в треугольнике: Замечательные линии треугольника

Какой треугольник считается остроугольным. Виды треугольников, углы и стороны

Треугольники

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Виды треугольников

Треугольник называется равнобедренным, если у него две сторны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Треугольник, у которого все сторны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.

Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.

Треугольник называется

тупоугольным, если один из его углов — тупой, то есть больше 90°.

Основные линии треугольника

Медиана

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Медиана разбивает треугольник на два треугольника одинаковой площади.

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.

Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Высота

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.

В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Срединный перпендикуляр

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника .

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Формулы и соотношения

Признаки равенства треугольников

Два треугольника равны, если у них соответственно равны:

две стороны и угол между ними;

два угла и прилежащая к ним сторона;

три стороны.

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны, если у них соответственно равны:

гипотенуза и острый угол;

катет и противолежащий угол;

катет и прилежащий угол;

два катета ;

гипотенуза и катет .

Подобие треугольников

Два треугольника подобны, если выполняется одно из следующих условий, называемых признаками подобия:

два угла одного треугольника равны двум углам другого треугольника;

две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны;

три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.

В подобных треугольниках соответствующие линии (высоты , медианы , биссектрисы и т. п.) пропорциональны.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности :

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

a 2 = b 2 + c 2 — 2bc cos

Формулы площади треугольника

Произвольный треугольник

a, b, c — стороны; — угол между сторонамиa и b ;- полупериметр;R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; h a — высота, проведенная к стороне a .

Деление треугольников на остроугольные, прямоугольные и тупоугольные. Классификация по соотношению сторон делит треугольники на разносторонние, равносторонние и равнобедренные. Причем каждый треугольник одновременно принадлежит к двум . Например, он может быть прямоугольным и разносторонним одновременно.

Определяя вид по типу углов, очень внимательны. Тупоугольным будет называться такой треугольник, у которого один из углов является , то есть составляет боле 90 градусов. Прямоугольный треугольник может быть вычислен по наличию одного прямого (равного 90 градусам) угла. Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла острыми.

Определяя вид треугольника по соотношению сторон, для начала вам придется узнать длины всех трех сторон. Однако если по условию длины сторон вам не даны, помочь вам смогут углы. Разносторонним будет являться треугольник, все три стороны которого имеют разную длину. Если длины сторон неизвестны, то треугольник может быть классифицирован как разносторонний в случае, если все три его угла являются разными.

Разносторонний треугольник может быть тупоугольным, прямоугольным и остроугольным.

Равнобедренным будет являться треугольник, две из трех сторон которого равны между собой. Если длины сторон вам не даны, ориентируйтесь по двум равным между собой углам. Равнобедренный треугольник, как и разносторонний, может быть и тупоугольным, и прямоугольным и остроугольным.

Равносторонним может быть только такой треугольник, все три стороны которого имеют одинаковую длину. Все его углы также равны между собой, и каждый из них равен 60-ти градусам. Отсюда ясно, что равносторонние треугольники всегда являются остроугольными.

Простейший из многоугольников – это треугольник. Он образуется при помощи трех точек, лежащих в одной плоскости, но не лежащих на одной прямой, попарно соединенных отрезками. Тем не менее, треугольники бывают разных типов, а значит, обладают разными свойствами.

Инструкция

Принято выделять три типа : тупоугольные, остроугольные и прямоугольные. Это по типу углов.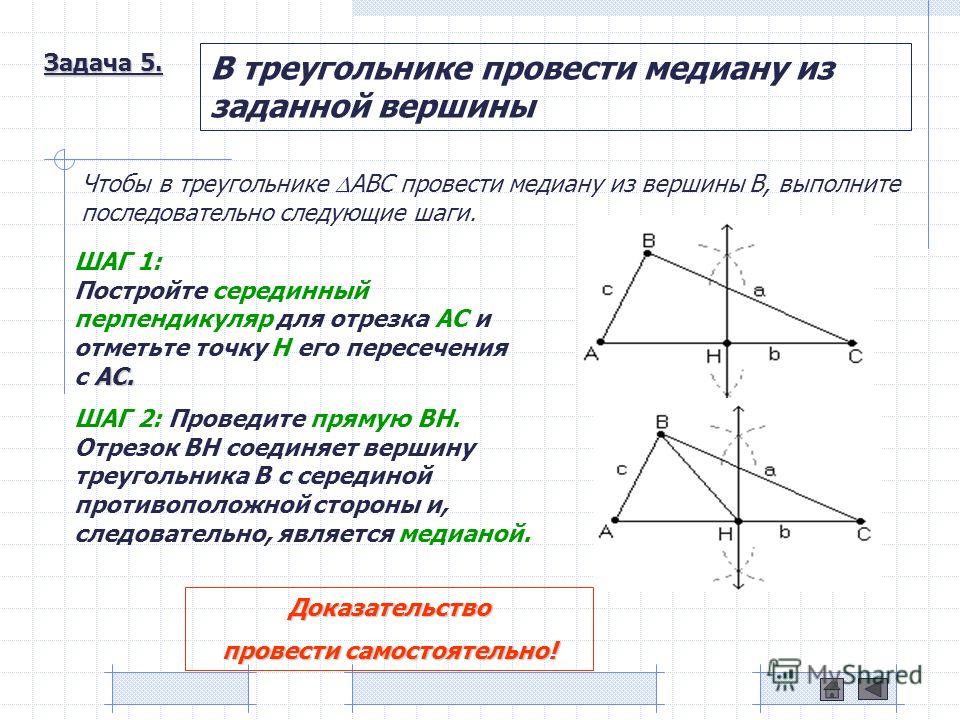 Тупоугольным называется треугольник, у которого один из углов является тупым. Тупым называется угол, имеющий величину больше девяноста градусов, но меньше ста восьмидесяти. Например, в треугольнике ABC угол ABC равен 65°, угол BCA равен 95°, угол CAB равен 20°. Углы ABC и CAB меньше 90°, но угол BCA больше, значит, треугольник тупоугольный.

Остроугольным называется треугольник, у которого все углы являются острыми. Острым называется угол, имеющий величину меньше девяноста и больше нуля градусов. Например, в треугольнике ABC угол ABC равен 60°, угол BCA равен 70°, угол CAB равен 50°. Все три угла меньше 90°, значит треугольник . Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.

Если в треугольнике один из углов равен девяноста градусам, это значит, что он не относится ни широкоугольному типу, ни к остроугольному. Это прямоугольный треугольник.

Если вид треугольника определять по соотношению сторон, они будут равносторонние, разносторонние и равнобедренные. В равностороннем треугольнике все стороны равны, а это, как вы выяснили, говорит о том, что треугольник остроугольный. Если у треугольника равны только две стороны или стороны не равны между собой, он может быть и тупоугольным, и прямоугольным, и остроугольным. Значит, в этих случаях необходимо вычислить или измерить углы и делать умозаключения, согласно пунктам 1, 2 или 3.

Видео по теме

Источники:

• тупоугольный треугольник

Равенство двух или более треугольников соответствует случаю, когда все стороны и углы данных треугольников равны. Однако существует ряд более простых критериев для доказательства данного равенства.

Вам понадобится

• Учебник по геометрии, лист бумаги, простой карандаш, транспортир, линейка.

Инструкция

Откройте учебник по геометрии седьмого класса на параграфе о признаках равенства треугольников. Вы увидите, что существует ряд основных признаков, доказывающих равенство двух треугольников. Если два треугольника, равенство которых проверяется, являются произвольными, то для них существует три основных признака равенства. Если же известна какая-то дополнительная информация о треугольниках, то основные три признака дополняются еще несколькими. Это относится, например, к случаю равенства прямоугольных треугольников.

Прочитайте первое правило о равенстве треугольников. Как известно, оно позволяет считать треугольники равными, если можно доказать, что какой-либо один угол и две прилегающие к нему стороны двух треугольников равны. Для того чтобы понять, данный закон, начертите на листе бумаги с помощью транспортира два одинаковых определенных угла, образованных двумя лучами, исходящими из одной точки. Отмерьте линейкой одинаковые стороны от вершины нарисованного угла в обоих случаях. Используя транспортир, измерьте величины полученных углов двух образованных треугольников, убедитесь, что они равны.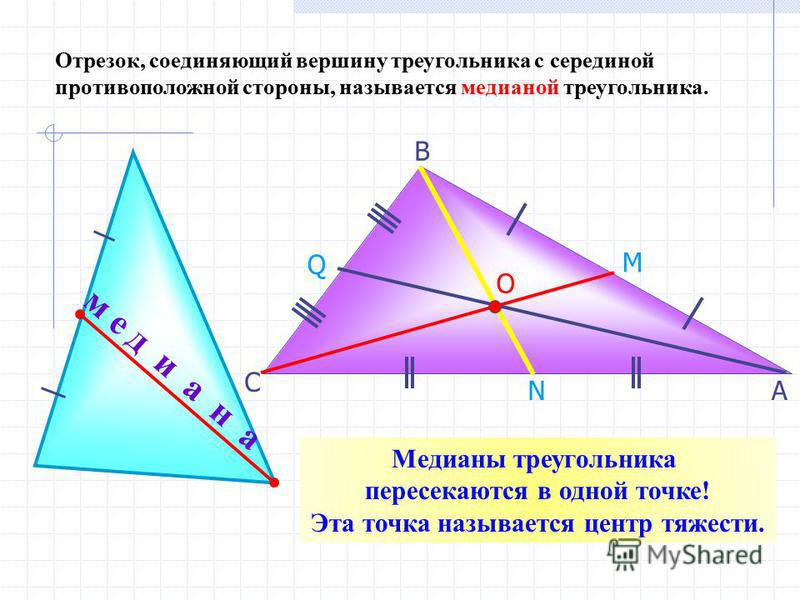

Для того чтобы не прибегать к таким практическим мерам для понимания признака равенства треугольников, прочитайте доказательство первого признака равенства. Дело в том, что каждое правило о равенстве треугольников имеет строгое теоретическое доказательство, просто его не удобно использовать в целях запоминания правил.

Прочитайте второй признак равенства треугольников. Он гласит, что два треугольника будут равны в том случае, если какая-либо одна сторона и два прилегающие к ней угла двух таких треугольников равны. Для того чтобы запомнить данное правило, представьте нарисованную сторону треугольника и два прилежащих к ней угла. Представьте, что длины сторон углов постепенно увеличиваются. В конце концов, они пересекутся, образуя третий угол. В данной мысленной задаче важным является то, что точка пересечения сторон, которые мысленно увеличиваются, а также полученный угол однозначно определяются третьей стороной и двумя прилегающими к ней углами.

Если вам не дана никакая информация об углах исследуемых треугольников, то используйте третий признак равенства треугольников. По данному правилу, два треугольника считаются равными, если все три стороны одно из них равны соответствующим трем сторонам другого. Таким образом, данное правило говорит о том, что длины сторон треугольника однозначно определяют все углы треугольника, а значит, они однозначно определяют и сам треугольник.

Видео по теме

Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.

Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).

Рис. 1. Иллюстрация к примеру

Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).

Рис. 2. Четырехугольники

Значит, «лишней» фигурой является треугольник (рис. 3).

Рис. 3. Иллюстрация к примеру

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.

Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.

Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).

Рис. 4. Остроугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).

Рис. 5. Прямоугольный треугольник

Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).

Рис. 6. Тупоугольный треугольник

По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.

Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).

Рис. 7. Равнобедренный треугольник

Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.

Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).

Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники

Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).

Рис. 9. Равносторонний треугольник

В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.

Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).

Рис. 10. Разносторонний треугольник

Выполните задание. Распределите данные треугольники на три группы (рис. 11).

Рис. 11. Иллюстрация к заданию

Сначала распределим по величине углов.

Остроугольные треугольники: № 1, № 3.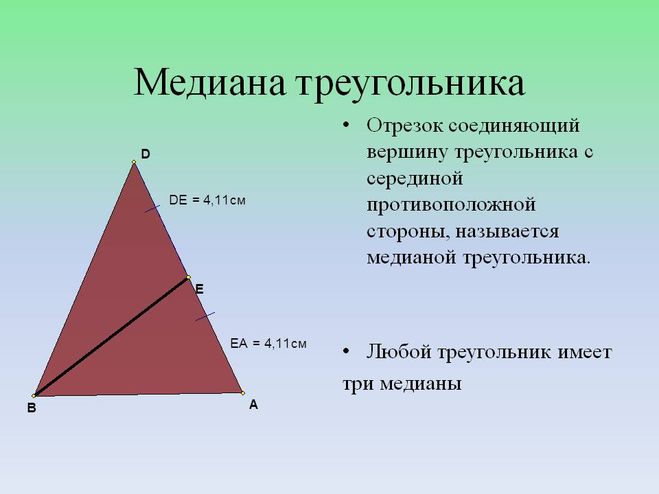

Прямоугольные треугольники: № 2, № 6.

Тупоугольные треугольники: № 4, № 5.

Эти же треугольники распределим на группы по числу равных сторон.

Разносторонние треугольники: № 4, № 6.

Равнобедренные треугольники: № 2, № 3, № 5.

Равносторонний треугольник: № 1.

Рассмотрите рисунки.

Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).

Рис. 12. Иллюстрация к заданию

Можно рассуждать так.

Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.

Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.

Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.

Сегодня на уроке мы познакомились с различными видами треугольников.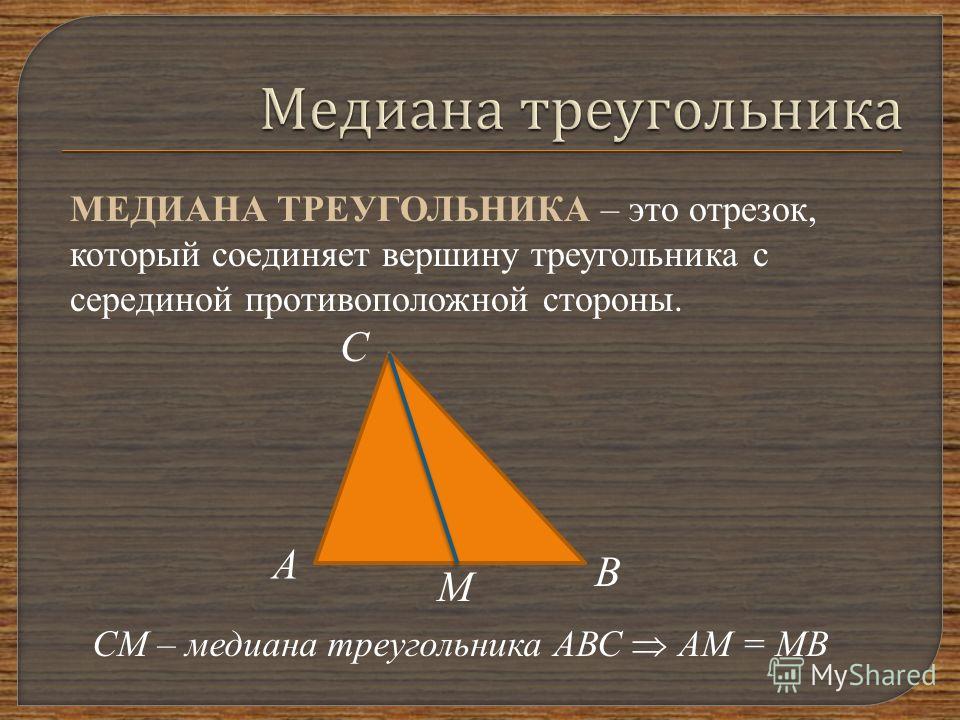

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Домашнее задание

1. Закончите фразы.

а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.

б) Точки называются … , отрезки — его … .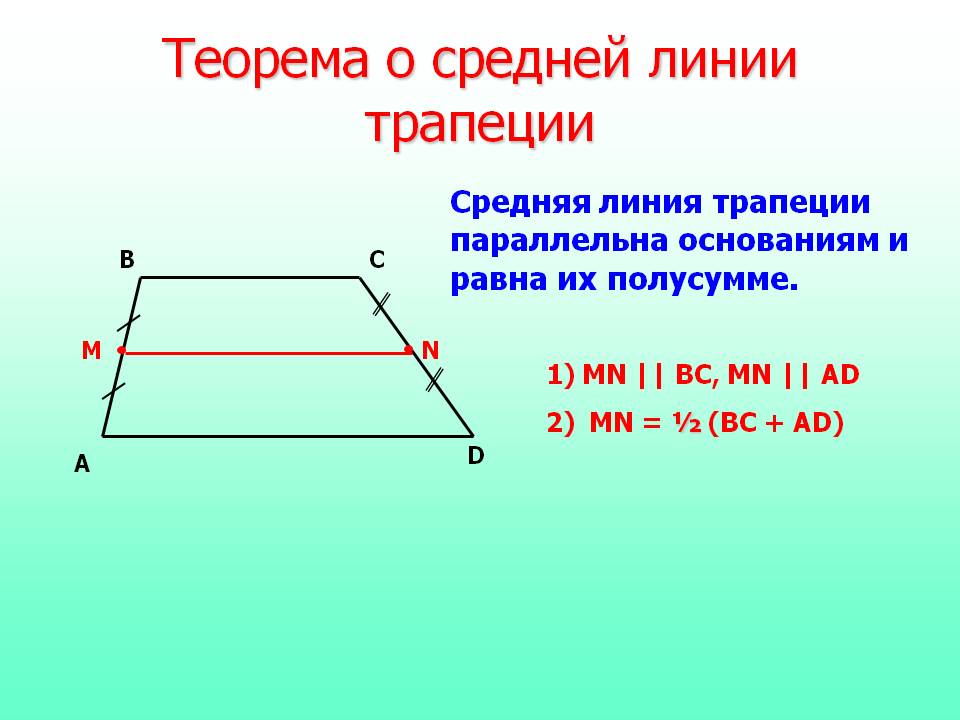 Стороны треугольника образуют в вершинах треугольника ….

в) По величине угла треугольники бывают … , … , … .

г) По числу равных сторон треугольники бывают … , … , … .

2. Начертите

а) прямоугольный треугольник;

б) остроугольный треугольник;

в) тупоугольный треугольник;

г) равносторонний треугольник;

д) разносторонний треугольник;

е) равнобедренный треугольник.

3. Составьте задание по теме урока для своих товарищей.

Треугольник — это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами (а, b, c), которые соответствуют заглавным буквам, обозначающим противоположные вершины (A, B, C).

Если в треугольнике все три угла острые, то это остроугольный треугольник .

Если в треугольнике один из углов прямой, то это прямоугольный треугольник . Стороны, образующие прямой угол, называются катетами . Сторона, противоположная прямому углу, называется гипотенузой .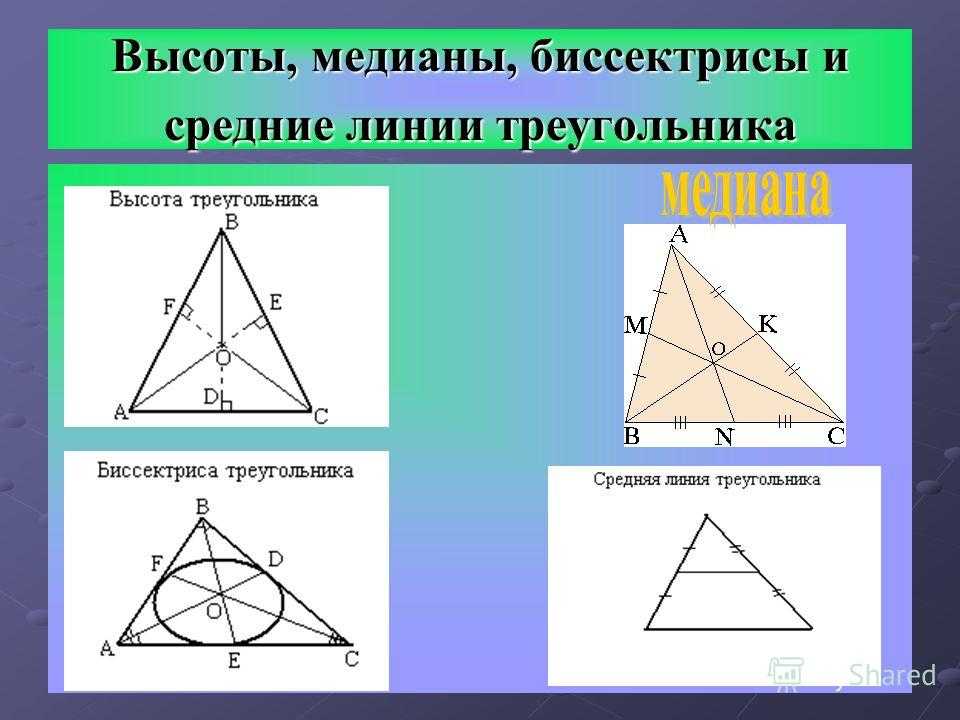

Если в треугольнике один из углов тупой, то это тупоугольный треугольник.

Треугольник равнобедренный , если две его стороны равны; эти равные стороны называются боковыми, а третья сторона называется основанием треугольника.

Треугольник равносторонний , если все его стороны равны.

Основные свойства треугольников

В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.
В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180º .
Из двух последних свойств следует, что каждый угол в равностороннем
треугольнике равен 60º.

4. Продолжая одну из сторон треугольника, получаем внешний
угол. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним.

5. Любая сторона треугольника меньше суммы двух других сторон и больше
их разности.

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

A) две стороны и угол между ними;
b) два угла и прилегающая к ним сторона;
c) три стороны.

Признаки равенства прямоугольных треугольников.

Два прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;
2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;
3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;
4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;
5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или её продолжение). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника . Ортоцентр остроугольного треугольника расположен внутри треугольника, а ортоцентр тупоугольного треугольника — снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Медиана — это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся его центром тяжести . Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Свойство медианы равнобедренного треугольника. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.

Биссектриса — это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся центром вписанной окружности . Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.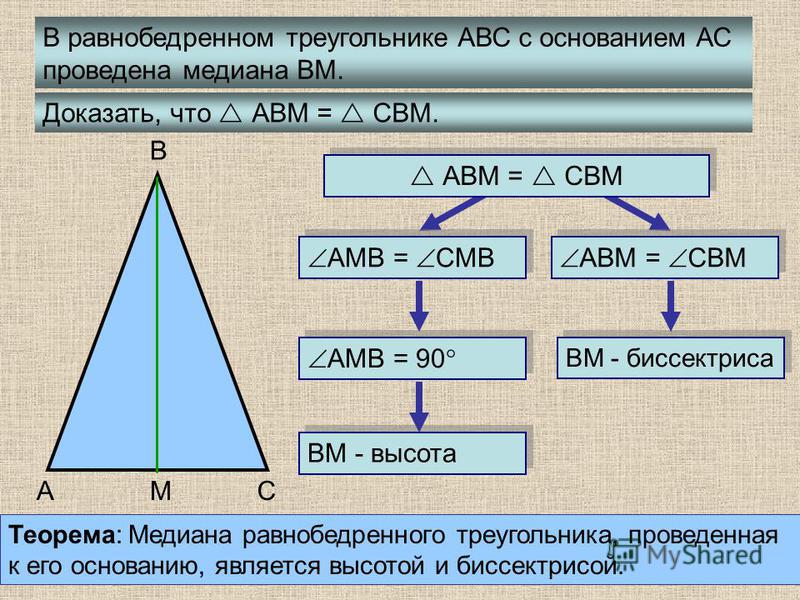

Срединный перпендикуляр — это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанной окружности. В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном — снаружи; в прямоугольном — в середине гипотенузы. Ортоцентр, центр тяжести, центр описанной и центр вписанной окружности совпадают только в равностороннем треугольнике.

Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. c 2 = a 2 + b 2 .

Доказательства теоремы Пифагора можно посмотреть здесь.

Теорема синусов . Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Доказательства теоремы синусов и теоремы косинусов можно посмотреть здесь .

Теорема о сумме углов в треугольнике. Сумма внутренних углов треугольника равна 180°.

Теорема о внешнем угле треугольника . Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Сметанный крем с желатином для торта – рецепт

Окунь морской красный рецепты приготовления

№ 404 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Помогите мне с треугольниками. – Рамблер/класс

№ 404 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Помогите мне с треугольниками. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

1) Прочитай определение и назови определяемое понятие.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Найди на чертеже отрезки, которые являются средними линиями треугольников:
 
3)   Сколько средних линий можно провести в треугольнике?
 
4)   Построй треугольник АВС и проведи его среднюю линию, соединяющую середины сторон AВ и ВС. Найди отношение длины стороны АС к длине средней линии. Повтори эксперимент еще 2 раза. Сформулируй гипотезу.
 
5)   Рассмотри расположение средней линии треугольника и стороны АС на чертежах к предыдущему заданию. Сформулируй гипотезу.
 
6)   Построй треугольник АВС и проведи все его средние линии. Измерь углы треугольника АВС и углы треугольника, образованного средними линиями. Сформулируй гипотезу.
 

ответы

1) Определяемое понятие — отрезок, соединяющий середины сторон треугольника.
2) ML, NV.
3) В треугольнике можно провести 3 средние линии.
4) MN — средняя линия;
AC = 2MN;     АС/MN = 2

Гипотеза: средняя линия, соединяющая середины двух сторон треугольника равна половине третьей стороны.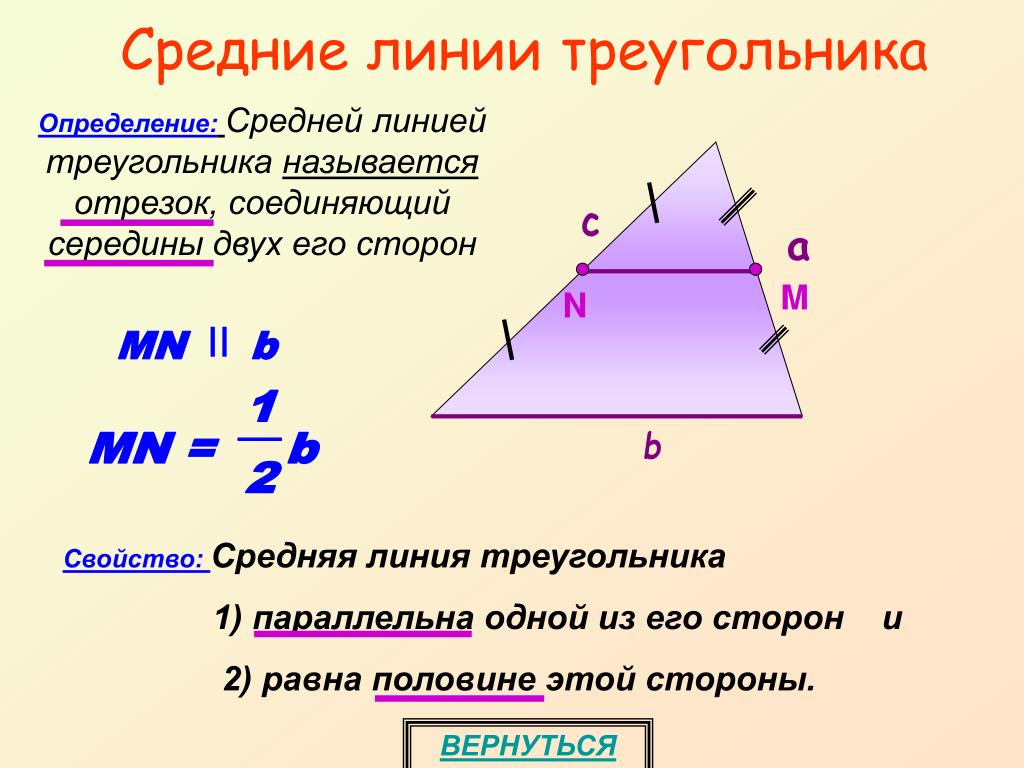
5) Средняя линия MN параллельна АС.
6)

Гипотеза: углы треугольника АВС равны соответствующим углам треугольника, образованного его средними линиями.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Психология

3 класс

5 класс

Репетитор

похожие вопросы 5

Приветик! Кто решил? № 411 Математика 6 класс Виленкин.

Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)

ГДЗМатематика6 классВиленкин Н.Я.

Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.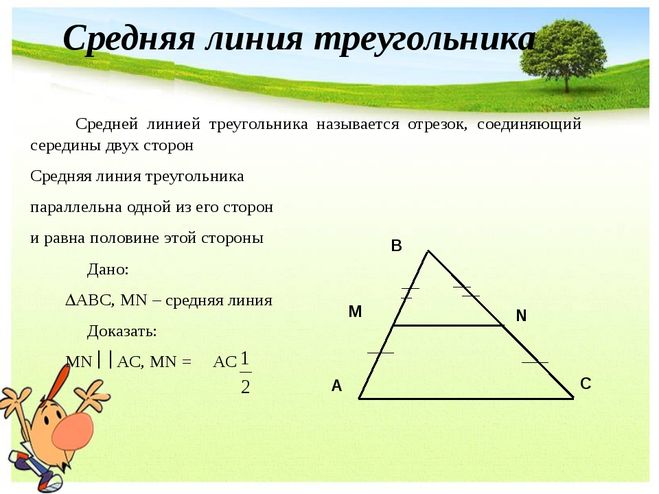 В.

   Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.

   Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.

Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?

ГДЗМатематика6 классДорофеев Г. В.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос.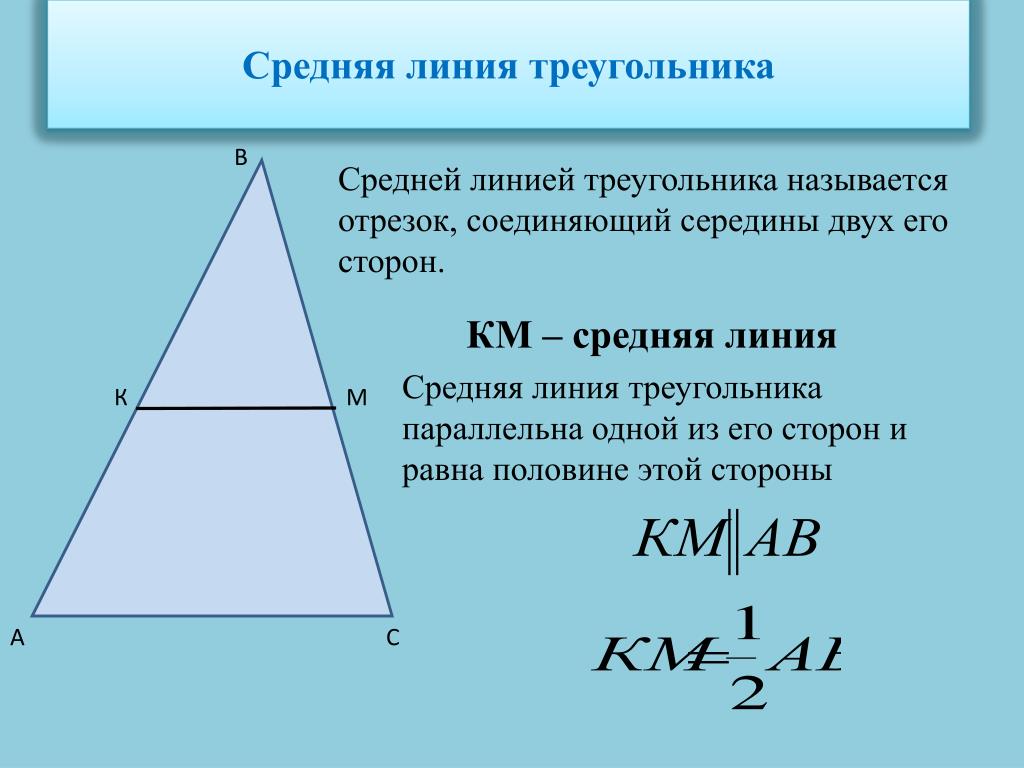 , шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

геометрия — Соединение середины сторон треугольника

спросил 9 лет, 9 месяцев назад

Изменено 9 лет, 9 месяцев назад

Просмотрено 18 тысяч раз

$\begingroup$

В треугольнике $\треугольник ABC$ $AB=8$, $BC=14$ и $CA=10$. Точки $M$, $N$ и $P$ являются серединами сторон $AB$, $BC$ и $CA$ соответственно. Если $M$, $N$ и $P$ соединены в треугольник, то каков периметр треугольника $\triangle MNP$?

• геометрия
• треугольники

$\endgroup$

2

$\begingroup$

$\displaystyle \frac{8}{14}=\frac{4}{MP}\Rightarrow MP=7$

$\displaystyle \frac{14}{8}=\frac{7}{ NP}\Rightarrow NP=4$

$\displaystyle\frac{14}{10}=\frac{7}{MN}\Rightarrow MN=5$

Периметр$=MP+NP+MN=7+4 +5=16$

$\endgroup$

2

$\begingroup$

Хорошо известно, что $NPM$ подобен $ABC$ с коэффициентом масштабирования $\frac{1}{2}$ (от $ABC$ до $NPM$). Таким образом, перимитер $NPM$ равен $\frac{8+14+10}{2}=16$.

$\endgroup$

$\begingroup$

Я думаю, вам нужны только основные свойства средних сегментов (или средних линий):

Определение: Отрезок линии, соединяющий середины двух сторон треугольника, называется средним отрезком.

Лемма: Средний сегмент треугольника параллелен третьей стороне, и его длина равна половине длины третьей стороны.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Объяснение урока: Теоремы о средней линии треугольника

В этом объяснении мы узнаем, как использовать теорему о средней линии треугольника, чтобы доказать параллельность прямых в треугольнике или найти недостающую длину стороны.

Давайте начнем с понимания того, что такое теорема о середине треугольника. состояния.

Теорема: теорема о середине треугольника (часть 1)

Отрезок, проходящий через середину одной стороны треугольника, также параллельна другой стороне треугольника и делит третью сторону пополам. треугольник.

Мы можем доказать это, рассмотрев треугольник 𝐴𝐶𝐷 с прямой отрезок 𝐸𝐵, проходящий через середину, 𝐸, из 𝐴𝐷 и это параллельно 𝐷𝐶.

Мы можем построить прямую ⃖⃗𝐴𝑌 так, что ⃖⃗𝐴𝑌⫽𝐸𝐵⫽𝐷𝐶.

Отрезки 𝐴𝐷 и 𝐴𝐶 являются секущими этих трех параллельных линии. Напомним, что если набор параллельных прямых делит секущую на отрезки одинаковой длины, то это множество делит любую другую секущую на отрезки одинаковой длины.

Учитывая, что 𝐴𝐷 было разделено на два конгруэнтных отрезки параллельными прямыми, ⃖⃗𝐴𝑌, 𝐸𝐵, и 𝐷𝐶, затем другая поперечная, 𝐴𝐶, также должны быть разделены на два конгруэнтных сегменты.

Следовательно, 𝐴𝐵=𝐵𝐶.

Таким образом, мы доказали, что третья сторона треугольника был разделен пополам.

Верно и обратное утверждение этой теоремы, то есть если у нас есть треугольник где две стороны разделены отрезком пополам, то этот отрезок равен параллельно третьей стороне. Это определено ниже.

Теорема: обращение середины треугольника Теорема (часть 1)

Отрезок, соединяющий середины двух сторон треугольника, параллелен в третью сторону.

Мы также можем увидеть еще одну теорему о середине треугольника.

Теорема: Теорема о середине треугольника (Часть 2)

Длина отрезка, соединяющего середины двух сторон треугольника треугольника равна половине длины третьей стороны.

Давайте посмотрим, как мы можем доказать эту теорему. Рассмотреть возможность △𝐴𝐶𝐷, где 𝐸 и 𝐵 — это середины 𝐴𝐷 и 𝐴𝐶 соответственно такие, что 𝐴𝐸=𝐸𝐷 и 𝐴𝐵=𝐵𝐶. Мы можем построить луч 𝐸𝐹 такой, что 𝐸𝐹⫽𝐴𝐶 и 𝐸𝐹 пересекается 𝐷𝐶 в 𝐹.

Затем мы можем применить теорему о середине треугольника, которая утверждает, что линия отрезок, соединяющий середины двух сторон треугольника, параллелен третья сторона. Это означает, что 𝐸𝐵⫽𝐷𝐶.

Поскольку мы построили 𝐸𝐹⫽𝐴𝐶, то по теореме о середине треугольника в котором говорится, что отрезок, проходящий через середину одной стороны треугольник, который также параллелен другой стороне треугольника, делит третью сторону пополам сторона треугольника, мы имеем, что 𝐷𝐶 делится пополам. Следовательно, 𝐷𝐹=𝐹𝐶, а 𝐹 есть середина 𝐷𝐶. Более того, 𝐹𝐶=12𝐷𝐶.

Тогда мы можем рассмотреть четырехугольник 𝐸𝐵𝐶𝐹.

𝐸𝐵𝐶𝐹 — четырехугольник с двумя парами противоположных стороны параллельны, что по определению является параллелограммом. В параллелограмме, противоположные стороны равны. Следовательно, 𝐸𝐵=𝐹𝐶=12𝐷𝐶.

Таким образом, мы доказали теорему: отрезок, соединяющий середины двух сторон треугольника равна половине длины третьей стороны.

Стоит отметить, что теоремы 1 и 2 здесь часто упоминаются в совокупности как теорема о середине треугольника, формулируемая следующим образом: линия отрезок, соединяющий середины двух сторон треугольника, параллелен третью сторону и составляет половину его длины.

В следующих вопросах мы увидим, как можно применить треугольник теорема о срединном отрезке и ее обращение для нахождения неизвестных длин сторон, начиная с вопроса, где нам нужно найти периметр фигуры.

Пример 1. Нахождение периметра четырехугольника с помощью треугольника Теорема о средней линии

Учитывая, что 𝐷 и 𝐸 являются серединами из 𝐴𝐵 и 𝐴𝐶 соответственно, 𝐴𝐷=32см, 𝐴𝐸=19см, и 𝐷𝐸=39см, определить периметр 𝐷𝐵𝐶𝐸.

Ответ

Мы можем начать с заполнения заданной длины на рисунке, что это 𝐴𝐷=32см, 𝐴𝐸=19см, и 𝐷𝐸=39см.

Так как 𝐷 и 𝐸 являются серединами 𝐴𝐵 и 𝐴𝐶, мы знаем, что 𝐸𝐶=𝐴𝐸=19см а также 𝐷𝐵=𝐴𝐷=32.cm

Теорема о середине треугольника утверждает, что отрезок, соединяющий середины двух сторон треугольника параллельны третьей стороне и равны половину своей длины.

Таким образом, мы можем сказать, что 𝐶𝐵⫽𝐷𝐸 и 𝐶𝐵=2×(𝐷𝐸).

Учитывая, что 𝐷𝐸=39 см, у нас есть 𝐶𝐵=2×39=78.cm

Наконец, нам нужно вычислить периметр 𝐷𝐵𝐶𝐸. Это расстояние вокруг внешней стороны 𝐷𝐵𝐶𝐸, трапеция в нижней части фигуры. С использованием 𝐷𝐸=39см, 𝐸𝐶=19см, 𝐶𝐵=78см, и 𝐷𝐵=32см, у нас есть периметрсм𝐷𝐵𝐶𝐸=𝐷𝐸+𝐸𝐶+𝐶𝐵+𝐷𝐵=39+19+78+32=168.

Таким образом, мы имеем ответ, что периметр 𝐷𝐵𝐶𝐸 это 168 см.

В следующем примере мы применим теорему о средней линии треугольника. раз в разных треугольниках на одной и той же фигуре. При работе над проблемой например, может быть полезно обрисовать или выделить определенные треугольники, чтобы что мы можем правильно определить ключевые сегменты, с которыми мы работаем.

Пример 2. Применение теоремы о средней линии треугольника для решения задачи

На приведенном рисунке 𝐸, 𝐹, и 𝐷 — середины 𝐵𝐶, 𝐴𝐵, и 𝐴𝐶 соответственно. Найди периметр △𝐸𝐹𝐷.

Ответ

Нам сообщают, что 𝐸, 𝐹, и 𝐷 — середины 𝐵𝐶, 𝐴𝐵, и 𝐴𝐶 соответственно. Чтобы рассчитать периметр △𝐸𝐹𝐷, нам нужно будет определить длины 𝐹𝐷, 𝐷𝐸, и 𝐸𝐹.

Для этого можно вспомнить, что длина отрезка, соединяющего середины двух сторон треугольника равны половине длины третья сторона.

Рассмотрим 𝐹𝐷.

𝐹𝐷 — отрезок, соединяющий середины двух сторон треугольника. Таким образом, 𝐹𝐷 составляет половину длины 𝐵𝐶 (4,6 см). Таким образом, у нас есть 𝐹𝐷=12×4,6=2,3 см

Таким же образом можно рассмотреть 𝐷𝐸.

Снова применяя теорему о средней линии треугольника, мы получаем, что 𝐷𝐸 должен быть вдвое короче 𝐴𝐵 (5,5 см). Таким образом, у нас есть 𝐷𝐸=12×5,5=2,75 см

Наконец, мы можем вычислить длину 𝐸𝐹 таким же образом.

𝐸𝐹 должен быть вдвое короче 𝐴𝐶 (6,2 см). Таким образом, у нас есть 𝐸𝐹=12×6,2=3,1 см

Отсюда, поскольку 𝐹𝐷=2,3 см, 𝐷𝐸=2,75см, и 𝐸𝐹=3,1 см, мы можем вычислить периметр △𝐸𝐹𝐷 как периметрсм△𝐸𝐹𝐷=𝐹𝐷+𝐷𝐸+𝐸𝐹=2,3+2,75+3,1=8,15.

Мы можем дать ответ, что периметр △𝐸𝐹𝐷 это 8,15 см.

В следующем примере мы увидим, как мы можем применить наши знания о треугольнике теорема о середине отрезка, чтобы помочь нам доказать геометрические свойства внутри заданная фигура.

Пример 3.

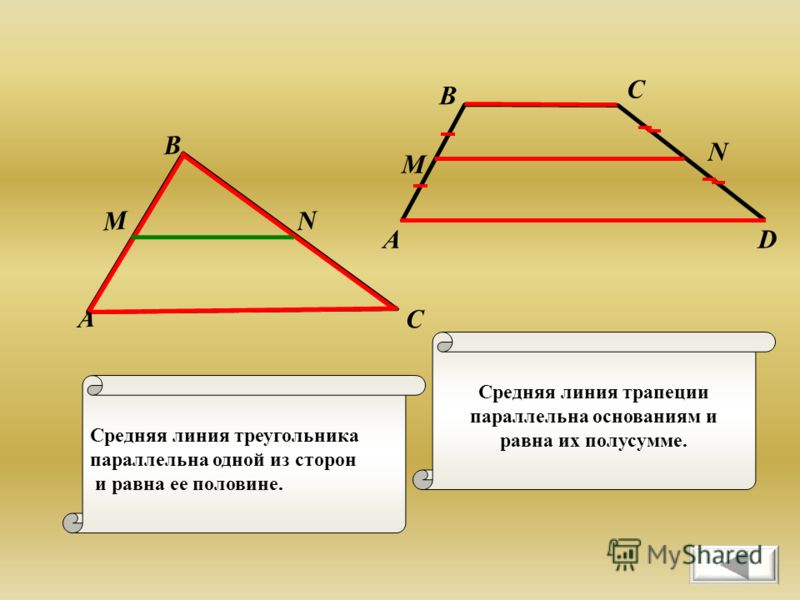Завершение доказательства с использованием теоремы о середине треугольника

На данном рисунке 𝐸 и 𝐹 равны середины 𝐴𝐵 и 𝐴𝐶 соответственно, 𝐵𝐷=12𝐵𝐶, а 𝐵 лжет на 𝐷𝐶. Какова форма 𝐸𝐹𝐵𝐷?

Ответ

Нам дано, что 𝐸 и 𝐹 являются середины 𝐴𝐵 и 𝐴𝐶 соответственно. Использование треугольника середине отрезка, мы знаем, что отрезок, соединяющий середины Две стороны треугольника параллельны третьей стороне и составляют ее половину длина.

Следовательно, 𝐸𝐹⫽𝐵𝐶 и 𝐸𝐹=12𝐵𝐶.

Нас просят определить форму 𝐸𝐹𝐵𝐷.

𝐸𝐹𝐵𝐷 кажется параллелограммом; однако мы должны доказать, что это так. Параллелограмм определяется как четырехугольник две пары противоположных сторон параллельны. Мы продемонстрировали, теорема о середине треугольника, что 𝐸𝐹⫽𝐵𝐶, и поскольку нам дано что 𝐵 лежит на 𝐷𝐶, затем 𝐸𝐹⫽𝐵𝐷.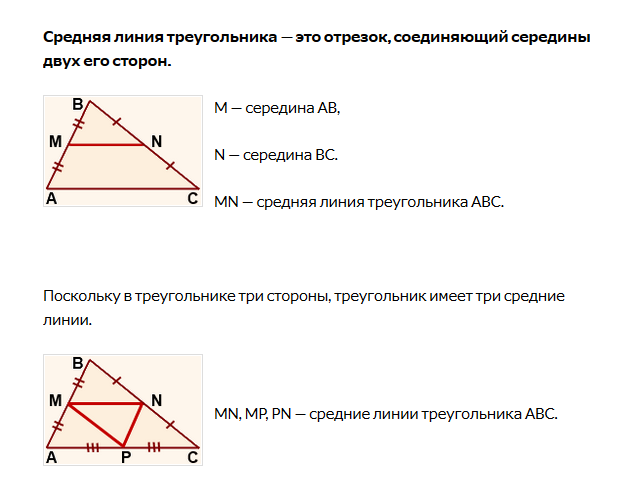

В вопросе нам дали, что 𝐵𝐷=12𝐵𝐶, и мы доказали, что 𝐸𝐹=12𝐵𝐶. Следовательно, 𝐸𝐹 соответствует 𝐵𝐷.

Теперь мы продемонстрировали, что у 𝐸𝐹𝐵𝐷 есть пара противоположные стороны, 𝐸𝐹 и 𝐵𝐷, которые параллельны и конгруэнтны. Следовательно, 𝐸𝐹𝐵𝐷 должен быть параллелограммом.

Теперь мы увидим пример того, как мы можем применить обратную сторону треугольника теорема о середине отрезка для определения неизвестной длины.

Пример 4. Применение теоремы о средней линии треугольника для решения задач с учетом Периметр

Периметр квадрата 𝐴𝐵𝐶𝐷 равен 352. Найдите 𝐴𝐹.

Ответ

В этом вопросе нам не дают никакой информации о длинах любых сегменты линии. Однако нам дана информация о том, что периметр этот квадрат составляет 352 единицы длины. Учитывая, что периметр — это расстояние вокруг внешнего края и что у квадрата 4 конгруэнтные стороны, мы можем вычислить длину одной стороны как длина одной стороны квадрата единиц длины=352÷4=88.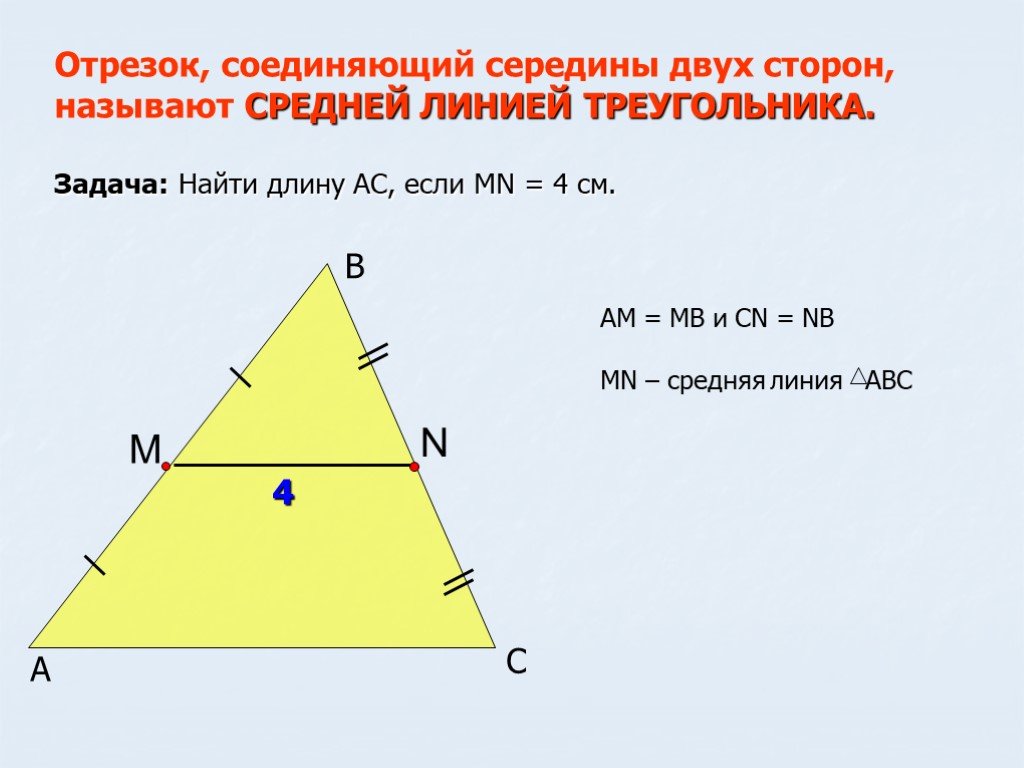

В этот момент мы можем попытаться угадать длину 𝐴𝐹; однако в подобных вопросах мы должны применить наши знания геометрии, чтобы продемонстрировать и доказать , что наша расчетная длина верна.

Мы можем вспомнить, что диагонали квадрата делят друг друга пополам, поэтому диагонали 𝐴𝐶 и 𝐷𝐵 делятся пополам в 𝑀. Следовательно, мы имеем, что 𝑀 является серединой 𝐴𝐶.

Затем мы можем применить обратную теорему о средней линии треугольника, которая утверждает, что отрезок, проходящий через середину одной стороны треугольник, который также параллелен другой стороне треугольника, делит пополам третья сторона треугольника.

Следовательно, 𝐴𝐵 делится пополам 𝑀𝐹, и 𝐴𝐹=𝐹𝐵.

Ранее мы подсчитали, что длина одной стороны составляет 88 единиц длины, поэтому 𝐴𝐵=88 единиц длины. С 𝐴𝐹=𝐹𝐵, то 𝐹 — середина из 𝐴𝐵 и 𝐴𝐹=12𝐴𝐵.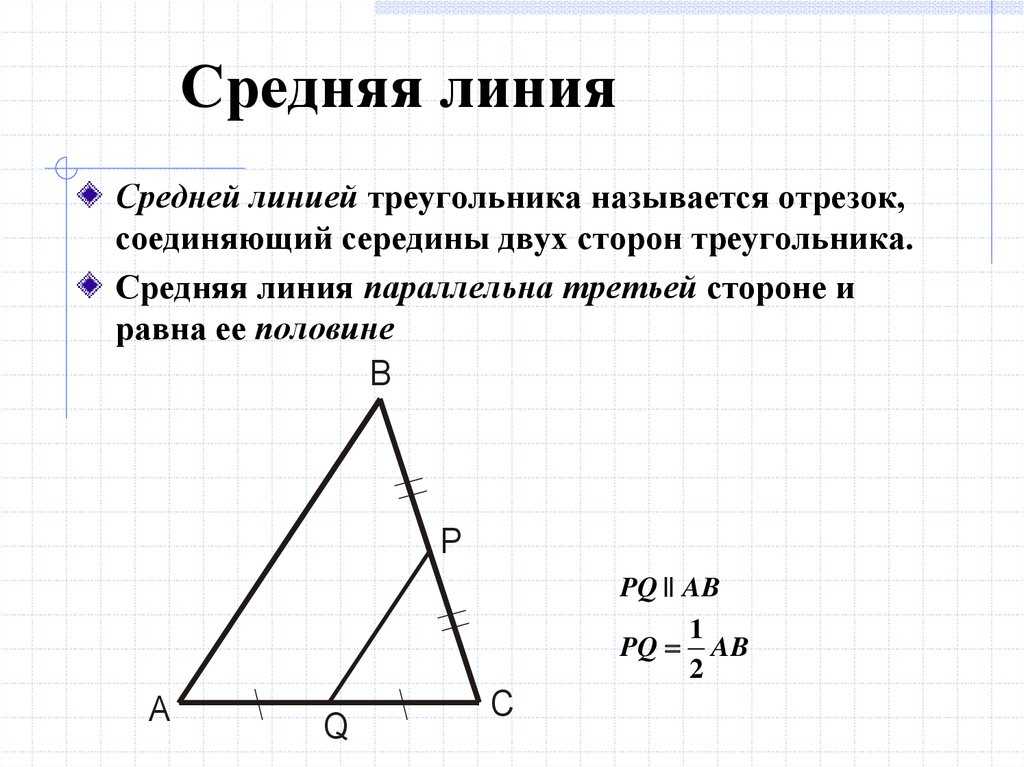 Мы можем определить длину 𝐴𝐹 как 𝐴𝐹=12𝐴𝐵=12×88=44.lengthunits

Следовательно, мы можем дать ответ, что 𝐴𝐹 равно 44 единицы длины.

В последнем примере мы увидим, как мы можем использовать обратную сторону треугольника теорема о середине отрезка для доказательства геометрического свойства данной фигуры.

Пример 5. Завершение доказательства с использованием теоремы о середине треугольника

Что из следующего на данном рисунке верно?

1. 𝐸 — середина 𝐹𝐺.
2. 𝐹 — середина 𝐴𝐷.
3. 𝐹𝐺=12𝐴𝐵
4. 𝐶𝐷=12𝐴𝐵

Ответ

На рисунке видно, что у нас есть две пары конгруэнтных сторон длины: 𝐴𝐸 и 𝐸𝐶 и 𝐵𝐺 и 𝐺𝐶. Поэтому мы можем констатировать что 𝐸 и 𝐺 являются серединами 𝐴𝐶 и 𝐵𝐶 соответственно. Мы можем вспомнить, что по теорема о середине треугольника, отрезок, соединяющий середины треугольников Две стороны треугольника параллельны третьей стороне и составляют половину его длина.

Таким образом, на рисунке имеем, что 𝐸𝐺⫽𝐴𝐵⫽𝐶𝐷.

Теперь мы рассмотрим варианты, которые нам представлены, и определим какой из них верный.

В выборе A мы обращаемся к утверждению, что 𝐸 является середина 𝐹𝐺. На самом деле у нас есть уже доказано, что 𝐸 является серединой 𝐴𝐶. Мы должны быть осторожны, чтобы не спутать два отрезка линии. Здесь мы не можем доказать, что 𝐸 является середина 𝐹𝐺.

Далее давайте посмотрим на выбранное утверждение 𝐵: 𝐹 — середина 𝐴𝐷. Мы можем рассмотреть треугольник 𝐴𝐶𝐷.

Учитывая, что 𝐹𝐸 проходит через середина 𝐴𝐶 и параллельна 𝐶𝐷, то по обратному теорема о середине треугольника, третья сторона должна делить пополам, 𝐴𝐷. Следовательно, 𝐴𝐹=𝐹𝐷, и 𝐹 является серединой 𝐴𝐷. Утверждение, данное в варианте B, истинный.

При выборе C нам нужно определить, является ли утверждение, что 𝐹𝐺=12𝐴𝐵 верно. Давайте рассмотрим △𝐴𝐵𝐶. Применение треугольника теорема о средней линии позволила бы нам доказать, что 𝐸𝐺=12𝐴𝐵.

Так как 𝐹 можно наблюдать не лежать на точке 𝐸 и 𝐹∈𝐺𝐸, то 𝐹𝐺 тоже не может быть одинаковым длина как 𝐸𝐺. Таким образом, это утверждение не правда.

Наконец, рассмотрим вариант D: 𝐶𝐷=12𝐴𝐵. Мы не можем применить теорему о середине треугольника или ее обратную теорему, чтобы продемонстрировать что это утверждение верно. Как и в случае выбора C, отрезок, который может быть продемонстрировал, что он вдвое короче 𝐴𝐵 это 𝐸𝐺, не 𝐶𝐷.

Таким образом, верное утверждение дано в варианте B: 𝐹 — середина 𝐴𝐷.

Мы видели, как можно применить теорему о средней линии треугольника и ее обратную теорему. Теперь мы можем обобщить основные моменты.

Ключевые точки

• Отрезок, проходящий через середину одной стороны треугольника, также параллельна другой стороне треугольника и делит третью сторону пополам.

  No related posts.