1.1.4 Геометрическое изображение комплексных чисел. Комплексная плоскость.
Если для изображения действительных чисел используются точки числовой прямой, то изображениями комплексных чисел служат точки координатной плоскости.
Введем на плоскости прямоугольную декартову систему координат с осями х иу. Тогда каждому комплексному числубудет отвечать точка с координатами. Эту точку чаще всего обозначают той же буквой, что и само число.
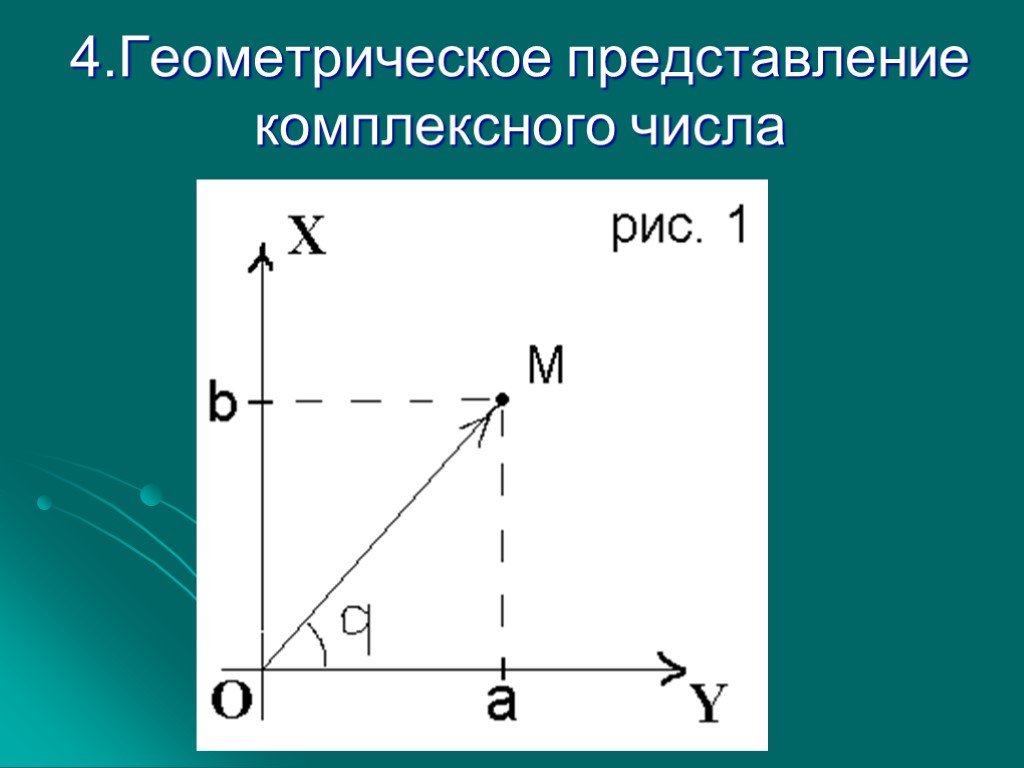
При таком способе изображения комплексных чисел любому действительному числу, т.е. числу вида , отвечает точка, лежащая на осих. Таким образом, приходим к уже известному способу изображения действительных чисел точками числовой прямойх. В связи с этим осьхназываютдействительной осью. Комплексным же числам видаотвечают точкиосиу; по этой причине осьуназываютмнимой осью. На рис. 1 указаны изображения некоторых комплексных чисел.
Наряду
с изображением комплексных чисел точками
плоскости применяется и другой способ
изображения – с помощью векторов
плоскости.
Изображение комплексных чисел с помощью векторов имеет то преимущество, что оно хорошо «увязано» с операцией сложения комплексных чисел. Пусть числам ,соответствуют векторы,. Тогда числусоответствует вектор с координатами, т.е. вектор. Таким образом,сложение комплексных чисел геометрически сводится к сложению соответствующих векторов. Напомним, что сложение векторов осуществляется по правилу параллелограмма (рис. 3).
у
х
Рис. 3 Рис. 4
Поскольку
сложение комплексных чисел сводится к
сложению векторов, это же должно быть
верно и по отношению к вычитанию. Если
вектор
изображает комплексное число,
а вектор- число,
то векторявляется изображением числа.
1.2 Тригонометрическая форма комплексного числа и
ее применение.
1.2.1. Модуль и аргумент комплексного числа.
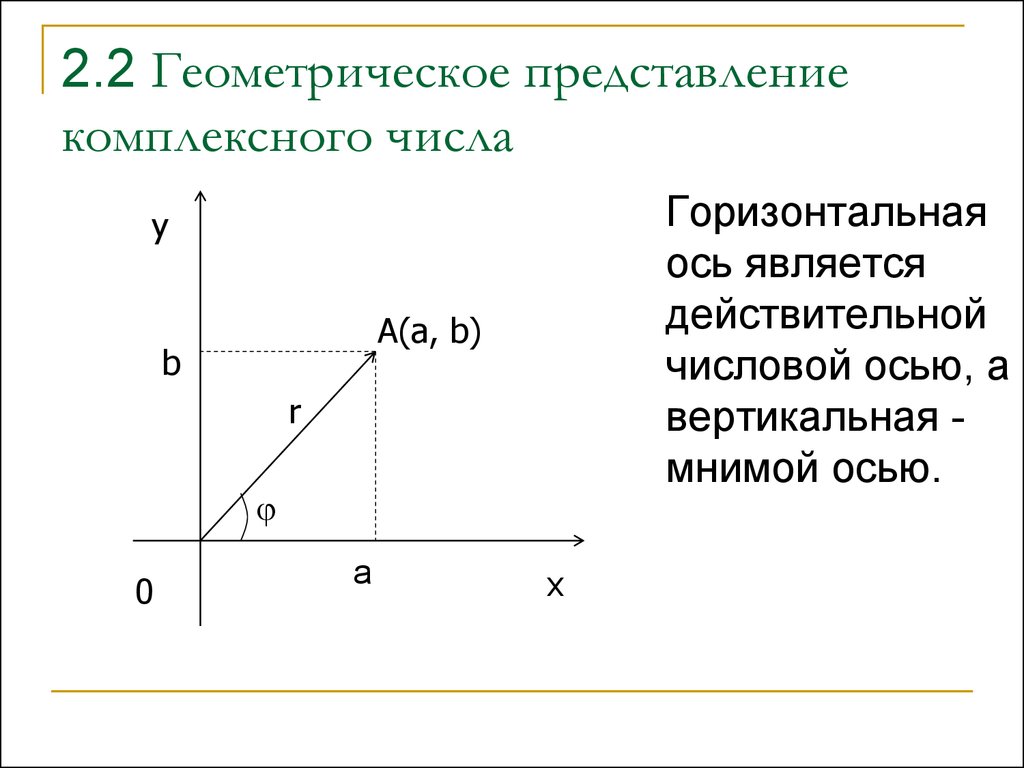
Комплексное число в прямоугольной декартовой системе координатхОуизображается либо точкойАс абсциссойаи ординатойb, либо радиус-вектором этой точки. Длина вектораназываетсямодулем комплексного числаи обозначается символом:
(1)
Угол , образованный векторомс положительным направлением осиОх, называетсяаргументомчислаи обозначается. Связь между аргументом комплексного числа и его действительной и мнимой частями выражается формулами
(2)
или . (3)
Формулы
(2) и (3) позволяют для заданного комплексного
числа
находить модуль и аргумент.
Обратно,
если заданы модульи аргументкомплексного числа,
то числонаходится с помощью равенств:
. (4)
Аргумент комплексного числа определяется неоднозначно: если - аргумент числа, то, где, — также аргумент этого числа. Для однозначности определения аргумента его выбирают в промежуткеи называютглавным значением аргумента.Главное значение аргумента обозначают .
Так как , то аргументможно представить в виде
.
Пример 1.Найти модуль и аргумент комплексного числа.
Используя формулу (1), находим модуль данного числа:
.
Далее, согласно формуле (2), получим
Так как точка, изображающая данное число, лежит во IIчетверти, тои, следовательно,.
Для главного значения аргумента справедливы соотношения:
В самом деле, так как главное значение лежит междуи, то:
если точкалежит вIилиIVчетверти, то и;
если точкалежит вIIчетверти, то и;
3) если точкалежит вIIIчетверти, то и;
Пример
2.
Найти модуль и аргумент комплексного
числа.
Решение.Вычислим модуль:.
Следовательно, , где.
1. История возникновения комплексных чисел
жүктеу/скачать 259 Kb.
|
1 2 3 4 5 6 7 8 9 … 12
Байланысты:
комплекс числа
1589902813
- Бұл бет үшін навигация:
- 1. История возникновения комплексных чисел……………………………..5
Государственное бюджетное образовательное учреждение
Работу выполнила Калистратова Ксения Владимировна, студентка группы ИС-113 Руководитель Мудренко Галина Александровна г.  Навашино
2013 г. Содержание
Введение……………………………………………………………………….3 1. История возникновения комплексных чисел……………………………..51.1 Развитие понятия о числе…………………………………………………51.2 На пути к комплексным числам………………………………………….6 1.3 Утверждение комплексных чисел в математике………………………..8 2. Комплексные числа и их свойства………………………………………..11 2.1 О комплексных числах…………………………………………………..11 2.2 Геометрическое изображение комплексных чисел……………………..12 2.3 Тригонометрическая и показательная формы комплексного числа……14 3. Действия с комплексными числами………………………………………17 3.1 Сложение комплексных чисел……………………………………………17 3.2 Вычитание комплексных чисел…………………………………………..17 3.3 Произведение комплексных чисел……………………………………….18 3.5 Геометрический смысл алгебраических операций………………………19 4. 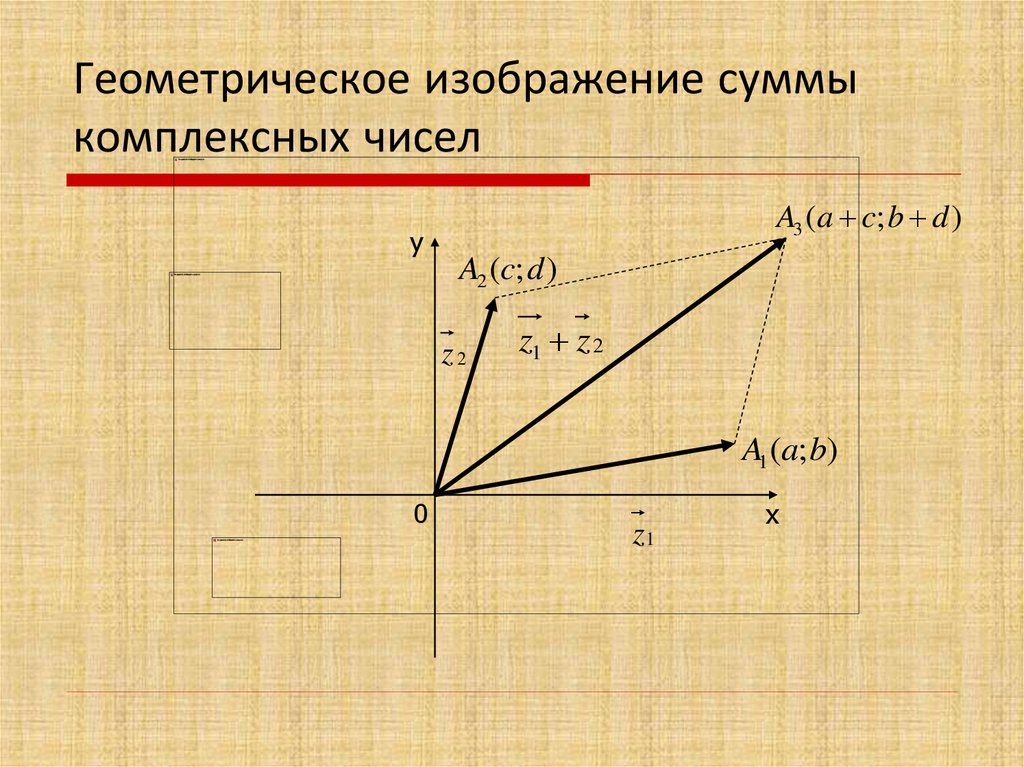 Применение комплексных чисел к решению алгебраических уравнений
3-ей и 4-ой степеней………………………………………………………… 22 4.1 Формула Кардано………………………………………………………….22 4.2 Метод Феррари для уравнения 4-ой степени…………………………….23 Заключение……………………………………………………………………..25 Литература……………………………………………………………………..26 Приложение : Приложение 1-6 :Страницы биографии ученых математиков Приложение: Презентация Введение В программе математики школьного курса теория чисел вводится на примерах множеств натуральных чисел, целых, рациональных, иррациональных, т.е. на множестве действительных чисел, изображения которых заполняют всю числовую ось. Но уже в 8 классе запаса действительных чисел не хватает, решая квадратные уравнения при отрицательном дискриминанте. Поэтому было необходимо пополнить запас действительных чисел при помощи комплексных чисел, для которых квадратный корень из отрицательного числа имеет смысл. Рассмотрев тему «Комплексные числа» на занятиях высшей математики мы заинтересовались данной темой и решили углубить свои познания в этой области.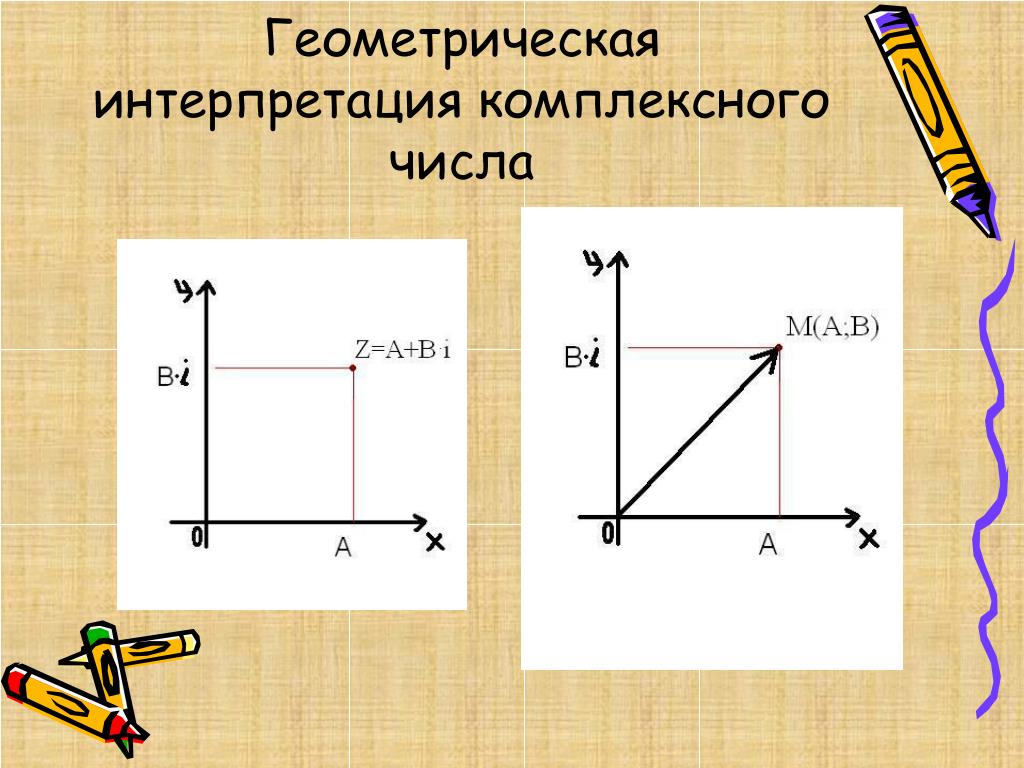 
Выбор темы «Комплексные числа», их прошлое и настоящее» заключается в том, что понятие комплексного числа расширяет знания о числовых системах, о решении широкого класса задач как алгебраического, так и геометрического содержания, о решении алгебраических уравнений любой степени и о решение задач с параметрами. Большое значение комплексных чисел в математике и её приложениях широко известно. Их изучение имеет самостоятельный интерес. Алгебру комплексных чисел можно успешно использовать в элементарной геометрии, тригонометрии, теории геометрических преобразований, а также в электротехнике и различных задачах с механическим и физическим содержанием.  Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники (слайд 2).
Цель настоящего реферата знакомство с историей появления комплексных чисел, их свойствами, действиями над ними, а также с решением уравнений с комплексным переменным. В рамках достижения поставленной цели были поставлены и решены следующие задачи: — ввести понятие комплексных чисел и изучить историю их открытия; — рассмотреть различные свойства и формы комплексных чисел, математические операции с ними; — использовать изученный материал для решения практических задач в течение учебного года; — оценить значение и роль комплексных чисел в математике, в повышении интереса в изучении комплексных чисел студентами в развитии их творческих и исследовательских способностей. 
жүктеу/скачать 259 Kb. Достарыңызбен бөлісу: |
1 2 3 4 5 6 7 8 9 … 12
©melimde.com 2023
әкімшілігінің қараңыз
Геометрическое представление комплексных чисел
- Автор Гнанамбигай GS
- Последнее изменение 27-01-2023
Геометрическое представление комплексных чисел: В сочетании с действительными числами мнимые числа также называются комплексными числами, которые имеют несколько применений в реальной жизни. Помимо математики, они широко используются в физике, технике, астрофизике и многих других областях. Комплексные числа широко используются в квантовой физике для изучения периодических движений, таких как световые волны и переменные токи. Следовательно, жизненно важно хорошо разбираться в основах комплексных чисел для будущих приложений.
В этой статье давайте рассмотрим комплексные числа с геометрической точки зрения и узнаем, как геометрически представлять комплексные числа.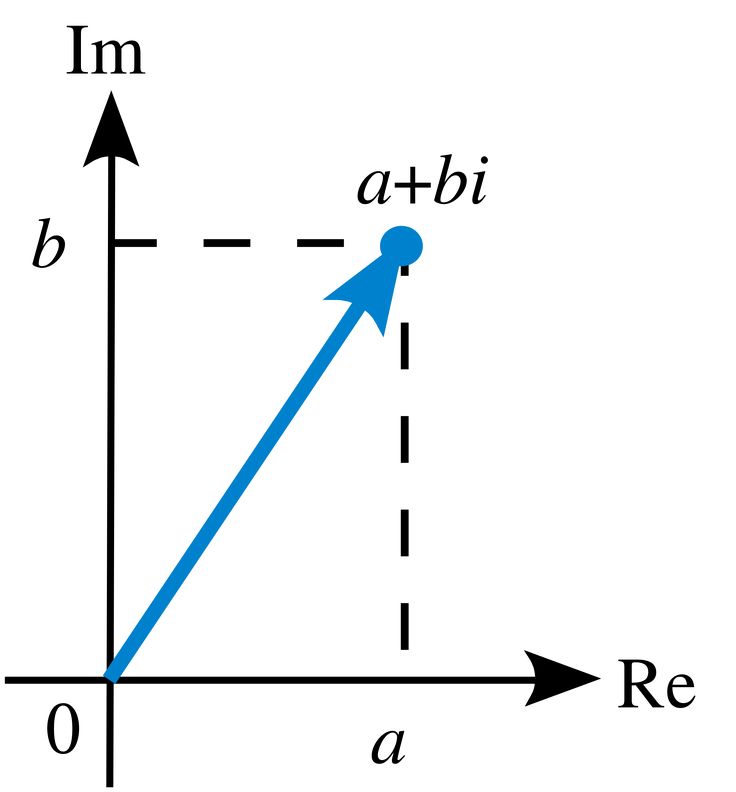
2} = \, – 1.\)
Геометрическое представление комплексных чисел
Как и любая пара чисел, комплексное число \(a + ib,\) также может быть представлено в виде точки на координатной плоскости путем нанесения \(a\) на \(x \) -оси и \(b\) на \(y\) -оси. Плоскость, которая используется для интерпретации комплексных чисел, называется комплексной плоскостью. Обозначается буквой \(C.\)
Комплексные числа на плоскости Гаусса (плоскость Аргана)
Комплексную плоскость также называют плоскостью Гаусса или плоскостью Аргана. Это похоже на декартову систему координат, где:
- 1. Ось \(х\) называется действительной осью – образована действительными числами
- 2. Ось \(у\) называется мнимой осью – образована мнимыми числами
При построении графика комплексное число \(a + ib,\) соответствует упорядоченной паре \(\left( {a,\,b} \right)\), как показано ниже.
Как нанести комплексные числа на комплексную плоскость?
Шаг 1: Определите действительную и мнимую части комплексного числа.
Шаг 2: Переместите вдоль реальной оси столько же, сколько и действительную часть.
Шаг 3: Переместите параллельно мнимой оси столько, сколько мнимая часть.
Шаг 4: Точка, к которой вы пришли, является требуемым представлением комплексных чисел на плоскости Гаусса.
Обратите внимание, как комплексное число \( – 2 + 3i\) нанесено на комплексную плоскость.
Модуль комплексных чисел
Когда комплексное число \(a + ib\) наносится на плоскость Аргана, расстояние точки от начала координат \(\left( {0,\,0} \right)\ ) называется модулем этого комплексного числа. Его также называют величиной или абсолютным значением комплексного числа. 9{ – 1}}\left( {\frac{y}{x}} \right)\)
Полярная форма комплексного числа записывается с использованием модуля и аргумента этого комплексного числа. Сначала нанесите комплексное число на плоскость Аргана, как показано на рисунке.
- Из рисунка можно написать:
- \(\sin\,\theta = \frac{x}{r} \Rightarrow x = r\,\sin\,\theta\)
- \(\ cos \,\theta = \frac{y}{r} \Rightarrow y = r\,\cos \,\theta \)
- \(\следовательно, x + iy = r\left( {\cos \,\theta + i\,\sin\,\theta } \right)\)
- Следовательно, полярная форма комплексного числа записывается как \(r\left( {\cos \,\theta + i\,\sin \,\theta} \right).
\)
\)Сопряженное комплексное число Числа
Каждое комплексное число имеет комплексно-сопряженное число. Сопряженным комплексным числом является его зеркальное отражение поперек оси \(x\) или действительной оси. Сопряженное комплексное число \(z,\) представлено как \(\overline z .\)
Из рисунка видно, что комплексно-сопряженное число \(x + iy\) равно \(x – iy. \) Комплексно-сопряженное число идентифицируется координатой \(\left( {x,\, – y} \right).\) Кроме того, аргумент комплексного числа и сопряженного числа одинаков \(\theta ,\) но в противоположных направлениях.
Алгебраически комплексное сопряжение комплексного числа получается изменением знака мнимой части комплексного числа.
| Complex Number | Complex Conjugate |
| \(a + ib\) | \(a – ib\) |
| \( – p – iq\) | \ ( – p + iq\) |
| \(x – iy\) | \(x + iy\) |
Аргумент и модуль комплексного сопряжения
Если аргумент комплексного числа равен \(\theta ,\), то аргумент его комплексно-сопряженного числа равен \( – \theta .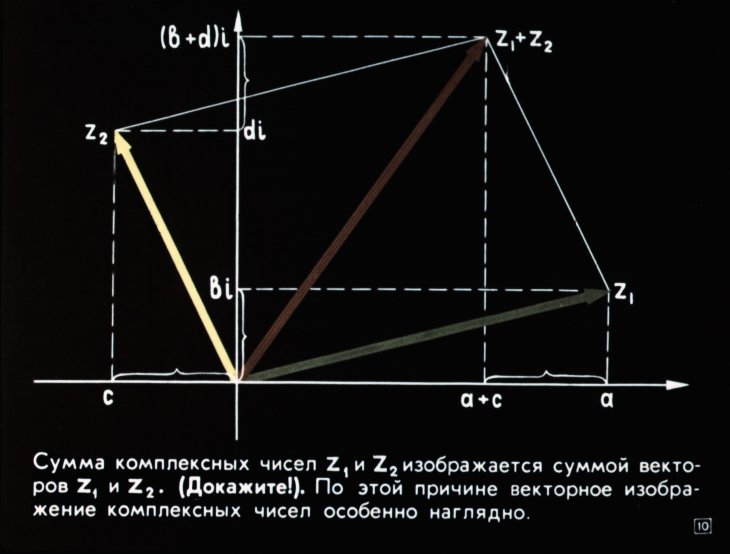
{\rm{o}}}\) поворотом комплексного числа на комплексной плоскости. Например, отрицание \(a + bi\) равно \( – a – bi.\) Вычитание комплексных чисел также использует правило параллелограмма. Вычитаемое сначала инвертируется, а затем прибавляется к уменьшаемому, чтобы получить разницу между двумя комплексными числами.
Графическое умножение комплексных чисел
Для двух комплексных чисел, скажем \({z_1}\) и \({z_2},\), величина и аргумент их произведения определяются как:
\(\left| { {z_1}{z_2}} \right| = \left| {{z_1}} \right|\left| {{z_2}} \right|\)
\(\arg \left( {{z_1}{z_2 }} \right) = \arg \left( {{z_1}} \right) + \arg \left( {{z_2}} \right)\)
Произведение \(wz\) графически представлено, как показано здесь .
Графическое разделение комплексных чисел
Для двух комплексных чисел, скажем, \({z_1}\) и \({z_1},\), величина и аргумент их отношения определяются как:
\(\left| {\ frac {{{z_1} }}{{{z_2}}}} \right| = \left| {\ frac {{{z_1}}}{{{z_2}}}} \right|\)
\(\arg \left( { \frac{{{z_1}}}{{{z_2}}}} \right) = \arg \left( {{z_1}} \right) – \arg \left( {{z_2}} \right)\)
Отношение \({\frac{{{z_1}}}{{{z_2}}}}\) графически выглядит так:
Решенные примеры геометрического представления комплексных чисел
Q.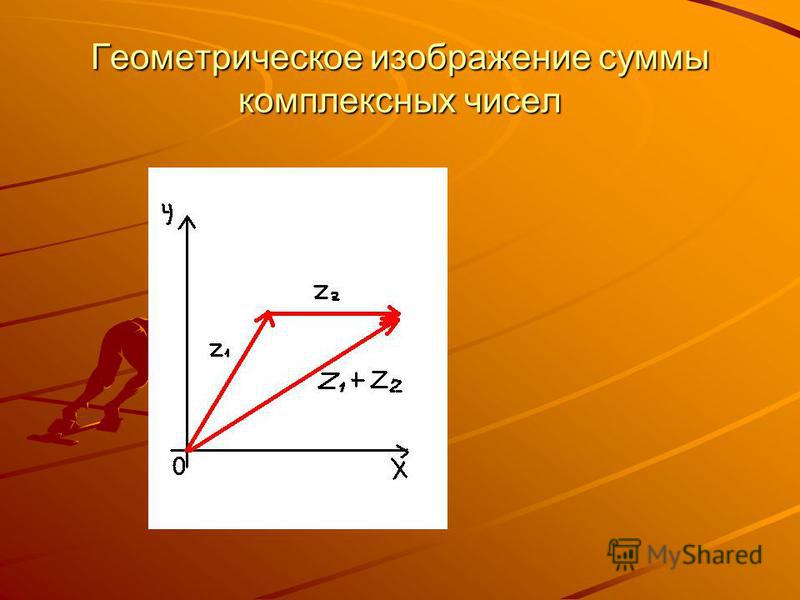
1. Что такое \ (\ arg \, z + \ arg \, {\ overline z } \)?
Ответ:
Давайте сначала нанесем \(z\) и \({\overline z } \) на комплексную плоскость. Поскольку это комплексно-сопряженные числа, их аргументы равны в \ ( {\ overline z } , \) в противоположных направлениях.
\(\ arg \, z + \ arg \, {\ overline z } = \ theta + \ theta = 2 \ theta \)
Q.2. В каком квадранте комплексной плоскости лежит \(1 – 4i\)?
Ответ:
Комплексное число \(1 – 4i\) может быть представлено координатой \(\left( {1,\, – 4} \right)\) на комплексной плоскости.
Комплексное число \(1 – 4i\) лежит в четвертом квадранте.
Q.3. Нанесите на график комплексное число, его отрицание и сопряженное число.
Ans:
| Type | Rectangular Form | Coordinates |
| Complex Number \(\left( z \right)\) | \(x + iy\) | \(\left( {x,\,y} \right)\) |
| Отрицание \(\left( { – z} \right)\) | \( – x – iy\) | \(\left( { – x,\, – y} \right)\) |
| Комплексное сопряжение \(\left( {\overline z } \right) \) | \(x – iy\) | \(\left( {x,\, – y} \right)\) |
| Комплексно-сопряженное (отрицательное) \(\left( {\overline { – z} } \right)\) | \( – x + iy\) | \(\left( { – x,\,y} \right)\) |
Q.
4. Найдите аргумент и модуль \(1 + i\sqrt 3 .\)
Ответ: 9{\rm{o}}}\)
Резюме
Статья начинается с определения комплексных чисел как состоящих из двух частей – действительной и мнимой. Затем он объясняет геометрическое представление комплексного числа. Далее в ней подробно рассматриваются геометрические представления различных операций, таких как сложение, вычитание, умножение и деление двух комплексных чисел. Это также объясняет, как модуль и аргумент связаны с комплексным числом. В статье также объясняются модуль и аргумент комплексных чисел, их произведения и отношения. Решенные примеры помогают нам понять концепции и вычисления, связанные с операциями с комплексными числами.
Часто задаваемые вопросы о геометрическом представлении комплексных чисел
Q.1. Каково геометрическое представление комплексного числа?
Ответ: Геометрическое представление комплексного числа нанесено на комплексную плоскость. Комплексная плоскость похожа на координатную плоскость, за исключением того, что горизонтальная ось имеет действительные числа, а вертикальная ось — мнимые числа.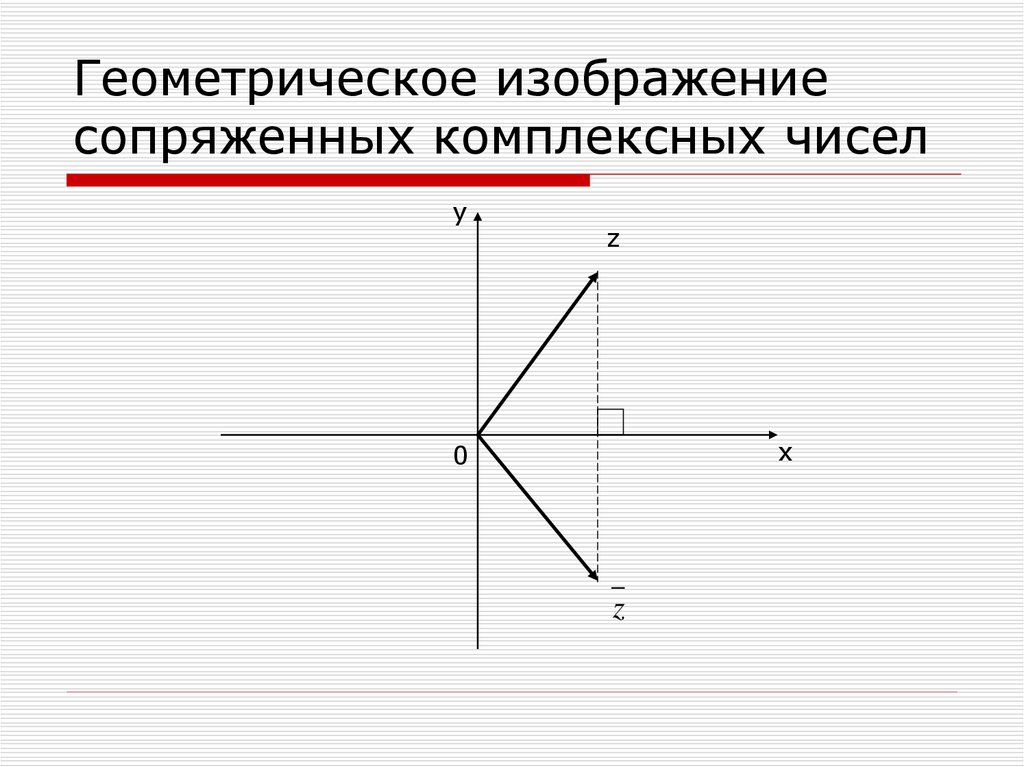
Комплексное число \( – 2 – 3i\) нанесено на комплексную плоскость координатой \(\left( { – 2,\, – 3} \right).\)
Q.2. Как геометрически разделить комплексное число?
Ответ: Для двух комплексных чисел, скажем, \(w\) и \(z,\), величина и аргумент их отношения определяются как:
\(\left| {\ frac {w} {z}} \right| = \frac{{\left|w \right|}}{{\left|z \right|}}\)
\(\arg \left( {\frac{w}{z}} \right ) = \arg \left( w \right) – \arg \left( z \right)\)
Отношение \(\frac{w}{z}\) графически представлено, как показано здесь.
Q.3. Чему равен квадрат комплексного числа? 92}} \right) + i\left( {2b} \right)\)
Q.4. Как складывать комплексные числа?
Ответ: Геометрическое сложение двух комплексных чисел следует правилу параллелограмма. Шаги для сложения двух комплексных чисел \({z_1},\) и \({z_2}\) геометрически:
Шаг 1: Постройте \({z_1}\) и \({z_2}\) на комплексной плоскости .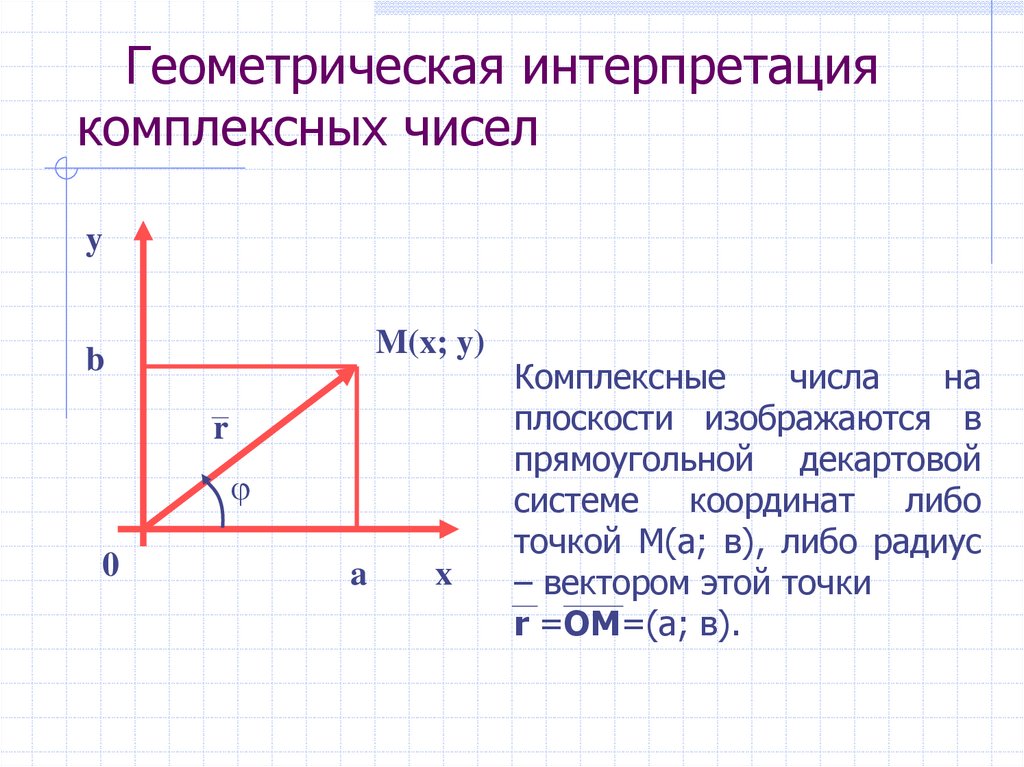
Шаг 2: Постройте параллелограмм с координатами \({z_1}\) и \({z_2}\) в качестве противоположных вершин.
Шаг 3: Проведите диагональ от начала координат как результирующий вектор.
Шаг 4: Сумма двух комплексных чисел является четвертой вершиной параллелограмма.
Q.5. Чему равно произведение двух комплексных чисел?
Ответ: Для двух комплексных чисел, скажем, \(w\) и \(z,\), величина и аргумент их произведения определяются как:
\(\left| {wz} \right| = \left| w \right|\left| z \right|\)
\(\arg \left( {wz} \right) = \arg \left( w \right) + \arg \left( z \right)\)
Продукт \(wz\) графически представлен так, как показано здесь.
Мы надеемся, что эта статья о геометрическом представлении комплексных чисел окажется вам полезной. Если у вас есть какие-либо вопросы, связанные с этой страницей или в целом о геометрическом представлении комплексных чисел, свяжитесь с нами через поле для комментариев ниже, и мы свяжемся с вами как можно скорее.
Комплексный анализ
←Комплексный анализ→
Сложение и вычитание
Геометрически сложение двух комплексных чисел $Z_1$ и $Z_2$ можно представить как сложение векторов с помощью закон параллелограмма . Векторная сумма $Z_1+Z_2$ представляет собой диагональ параллелограмма, образованного двумя оригинальные векторы.
Самый простой способ представить разницу $Z_1-Z_2$ — это представить ее в терминах добавление отрицательного вектора $Z_1 + \left(-Z_2\right)$. Отрицательный вектор — это тот же вектор как его положительный аналог, только указывающий в противоположном направлении.
Используйте следующий апплет, чтобы изучить эту геометрическую интерпретацию. Активируйте поля ниже, чтобы показать сложение или вычитание. Вы также можете перетаскивать точки $Z_1$ и $Z_2$.
Упражнение 1: Можете ли вы придумать геометрическую интерпретацию сложения из трех комплексных чисел? Вообще, какой была бы геометрическая интерпретация сложения $n$ комплексных чисел?
Умножение
В предыдущем разделе мы определили умножение двух комплексных чисел $Z_1$ и $Z_2$ как
\begin{выравнивание*}
Z_1 Z_2 &=& \влево( x_1 + i y_1 \вправо) \влево( x_2 + i y_2 \вправо)\\
&=& (x_1x_2-y_1y_2) + i(x_1y_2+x_2y_1).
\end{выравнивание*}
В этом случае, чтобы оценить, что происходит геометрически, нам нужно рассмотреть полярную форму
$Z_1$ и $Z_2$. То есть
\begin{выравнивание*}
Z_1 &=& r_1 \left( \cos \phi_1 + i \sin \phi_1 \right) \\
Z_2 &=& r_2 \left( \cos \phi_2 + i \sin \phi_2 \right)
\end{выравнивание*} Тогда произведение можно записать в виде
\begin{выравнивание*}
Z_1 Z_2 &=& r_1 r_2 \big[ \left(\cos \phi_1 \cos\phi_2 — \sin \phi_1 \sin \phi_2\right) \big.\\
&+& \большой. i\left(\sin \phi_1 \cos\phi_2 + \cos \phi_1 \sin \phi_2\right)\big].
\end{выравнивание*}
Теперь с помощью теорем сложения синуса и косинуса это выражение можно упростить до
\begin{выравнивание*}
Z_1 Z_2 &=& r_1 r_2 \big[ \cos \left( \phi_1 +\phi_2 \right) + i \sin \left( \phi_1 +\phi_2 \right)\big].
\end{выравнивание*}
Таким образом, произведение $Z_1Z_2$ имеет модуль $r_1r_2$ и аргумент $\phi_1+\phi_2$.
В следующем апплете вы можете оценить, что происходит с аргументом произведения.
Перетаскивайте точки $Z_1$ и $Z_2$ и наблюдайте за поведением углов.
Затем перетащите ползунок ниже.
На следующей анимации вы можете оценить, что происходит с аргументом произведения.
Упражнение 2: Рассмотрим сейчас \begin{выравнивание*} Z_1 &=& r_1 \left( \cos \phi_1 + i \sin \phi_1 \right) \\ Z_2 &=& r_2 \left( \cos \phi_2 + i \sin \phi_2 \right) \end{выравнивание*} такой, что $Z_2\neq 0$. Найдите полярное представление $Z_1/Z_2$. Какова геометрическая интерпретация этого выражения?
Умножение комплексных чисел как растяжение (сжатие) и вращение
В приведенном ниже апплете набор точек определяется случайным образом на комплексной плоскости. Затем каждая точка умножается на заданное комплексное число $z$. На правом экране перетащите точку $z$ и проанализируйте поведение баллов (⭕), умноженных на $z$, и попробуйте ответить на вопрос следующие вопросы:
- Что происходит, когда $z$ находится внутри или снаружи единичного круга?
- Что произойдет, если $z$ будет двигаться только по единичному кругу?
Примечание: Вы также можете изучить поведение точек (⚫), умноженных на $1/z$, активировав
поле Умножить на 1/z .