Параметрические функции: Дифференциальное и интегральное исчисления для втузов, т.1

Дифференциальное и интегральное исчисления для втузов, т.1

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т.1: Учебное пособие для втузов.— 13-е изд.— М.: Наука. Главная редакция физико-математической литературы, 1985. — 432 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Первый том включает разделы: введение в анализ, дифференциальное исчисление (функций одной и нескольких переменных), неопределенный и определенный интегралы. Настоящее издание не отличается от предыдущего (1978 г.). Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ § 1. Действительные числа. § 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11. n при n целом и положительном § 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23. x, sin x, cos x Упражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента § 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2. Геометрическое изображение функции двух переменных § 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов § 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6. Интегрирование по частям § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9. Формула Чебышева § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII

18.11. Параметрическое задание функции и ее дифференцирование.

Пусть даны две функции x = (t), y = (t) одной независимой переменной t, определенные и непрерывные в некотором интервале (, ).

Если функция x = (t) строго монотонна, то она имеет обратную функцию t = (x), непрерывную и монотонную в некотором интервале (a, b). Поэтому y является сложной функцией, зависящей от переменной x посредством переменной t, называемой параметром:

y = f(x) = ((x)), x  (a, b).

Эта функция непрерывна по теореме о непрерывности сложной функции. Итак, система функций (18.26) определяет функцию y = f(x) переменной x, а сами уравнения (18.26) называются параметрическими уравнениями функции y = f(x) (см. рис. 18.13). Такой способ задания функции называется параметрическим. Пример 18.18. Рассмотрим функцию y = f(x), заданную параметрически системой уравнений (

а > 0)

t [ 0,] (18.27)

Так как функция убывает на отрезке [ 0,] (см. рис. 18.14), то существует обратная функция t = (x) = arccos , x[—a,a]. Если подставим ее во второе уравнение вместо t, то получим искомую функцию в явном виде: y = a sin(arccos ) = =a. Знак плюс перед корнем выбираем в силу того, что функция y = a sin t неотрицательна при t [ 0,]. Таким образом, уравнения (18.27) есть параметрические уравнения функции y = , x [—a,a], графиком которой является верхняя полуокружность (см. рис. 18.15). Взяв   t  2, получим, что система (18.27) есть параметрические уравнения функции y = f(x) = –, графиком которой является нижняя полуокружность (см. рис. 18.15).

Пусть функции x = (t) и y = (t) дифференцируемы в области определения (, ) и (t)  0. Тогда обратная функция t = (x) дифференцируема и . По теореме о производной сложной функции получим

. Следовательно,

или, короче, . (18.28)

Таким образом, производная функции, заданной параметрически, сама является функцией, заданной параметрически:

если t (, ), то зt (, ).

Найдем вторую производную функции, заданной параметрически уравнениями (18.26). Так как вторая производная есть производная от первой производной, то, согласно формуле (18.28), получим

. (18.29)

Аналогично можно получить производную от у по х любого порядка.

Пусть задано уравнение, связывающее переменные х и у, вида

F (x,y) = 0. (18.30)

Мы уже сталкивались с подобным уравнением, рассматривая уравнение линии на плоскости в п. 7.1.

Пусть существует такой интервал (a, b), что для каждого x₀  (a, b) существует по крайней мере одно число у, удовлетворяющее уравнению F (x,y) = 0.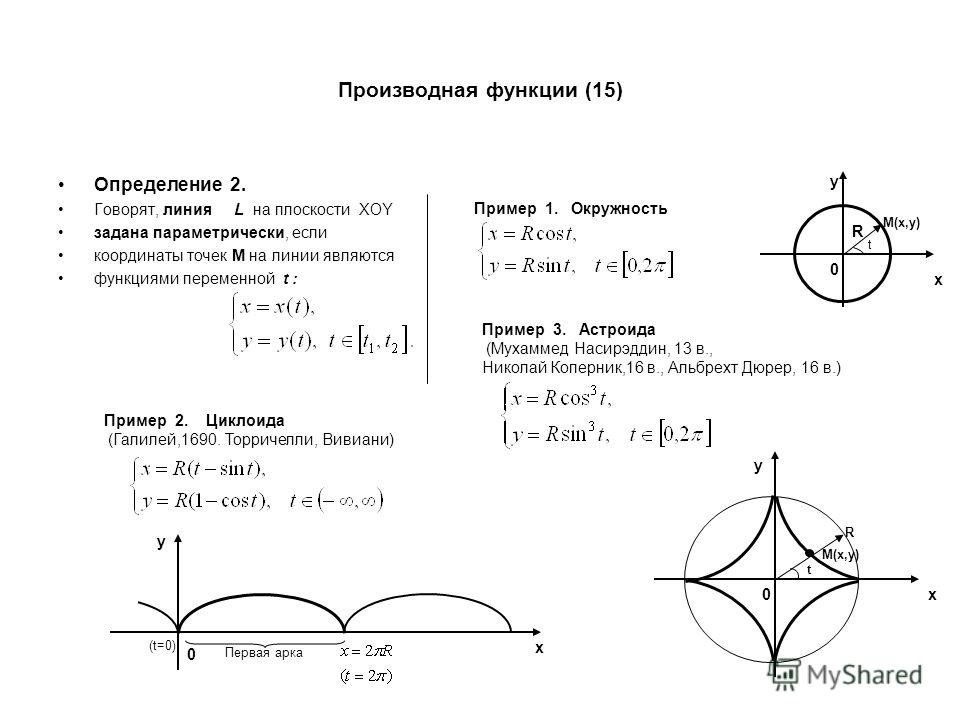 Обозначим одно из таких чисел у₀ и поставим его в соответствие числу x₀  (a, b). Тогда получим функцию y = f(x), определенную в интервале (a, b) и такую, что F (x, f(x)) = 0 для всех x  (a, b). В этом случае говорим, что функция y = f(x) задается неявно уравнением (18.30). Уравнение (18.30) задает, вообще говоря, не одну, а некоторое множество функций.

Функции, неявно задаваемые уравнениями вида (18.30), называются неявными функциями

в отличие от функций, задаваемых явно формулой y = f(x). Термин » неявная функция» отражает

не характер функциональной зависимости, а лишь способ ее задания.

Итак, функция y = f(x), x  (a, b) является неявной функцией, определяемой уравнением (18. 30), если

F (x, f(x))  0 x  (a, b),

т.е. функция y = f(x) есть решение уравнения F (x,y) = 0 относительно переменной y.

Пример 18.19. Рассмотрим уравнение х² + у² – 1 = 0, или х² + у² = 1, которое на плоскости Оху задает окружность радиуса r = 1 с центром в начале координат (см. рис. 18.16). Как легко проверить, функции , x [—1,1] и , x [—1,1] являются неявными функциями, заданными этим уравнением, графиками их служат верхняя и нижняя полуокружности (см. рис. 18.6).

Выберем x₀ =  [—1,1] и подставим в исходное уравнение. Тогда получим: + у² – – 1 = 0 или у² = , т. е. y = . Итак, при x₀ = мы получили два значения у. Если мы выберем у₀ = ; то, тем самым, мы выбрали неявную функцию , x [—1,1].

Правило нахождения производных функций, заданных неявно.

Для нахождения производной y функции y = f(x), заданной неявно уравнением F (x,y) = 0, необходимо продифференцировать это уравнение по переменной x как сложную функцию, рассматривая при этом y как функцию от x, и полученное уравнение разрешить относительно y.

Производная неявной функции выражается через аргумент х и функцию у, т.е. сама является функцией, заданной неявно.

Пример 18.20. Найти y (1) и y (1) в точке М₀(1,1), если y = f(x) является неявной функцией, определяемой уравнением х² + 2ху + у² – 4х + 2у —2= 0 (18. 31) Решение. Продифференцируем уравнение (18.31) по х, помня, что у есть функция от х:

2х + 2(у +ху) + 2уу — 4 + 2у = 0.

Находя из этого уравнения у , получим

. (18.32)

Чтобы вычислить y (1), нам необходимо знать значение у₀ неявной функции в точке x₀ = 1. Но из условия задачи следует, что у₀ = y (1) = 1, т. к. точка М₀(1,1) лежит на графике функции. Учитывая это, получим: y (1) = 0.

Для нахождения y, продифференцируем уравнение (18.32) еще раз по переменной x :

.

Исключив из последнего равенства y по формуле (18.32), получим выражение y через х и у : 1 + y = 1 – ,

тогда y = .

Отсюда, учитывая как и выше, что y (1) = 1, получим y (1) = – .

Замечание. Задав точку М₀(1,1), лежащую на кривой, определенной уравнением (18.31) (проверьте), мы тем самым, задали значение неявной функции y = f(x) в точке x₀ = 1: y (1) = 1. Дело в том, что уравнение (18.31) при x₀ = 1 имеет два решения: у = 1 и у = -5. Уравнение (18.31) можно разрешить относительно y, записав его в виде у² + 2(х + 1) у + х² – 4х – 2= 0, откуда получим: y = f₁(x) = – х – 1 + и y = f₂(x) = – х – 1 – . Легко видеть, что f₁(x) = 1, а f₂(x) = –5. Решить поставленную задачу можно теперь, дифференцируя функцию y = f₁(x), заданную уже в явном виде.

Это замечание показывает, что даже в случае, когда уравнение, задающее неявную функцию, можно разрешить относительно у, производную неявной функции проще находить по правилу, описанному выше.

Параметрическое уравнение | Определение и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — лучший ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Связанный контент

Численность, математика и статистика — набор академических навыков

Параметрические функции

ContentsToggle Главное меню 1 Определение 2 Построение графиков 2.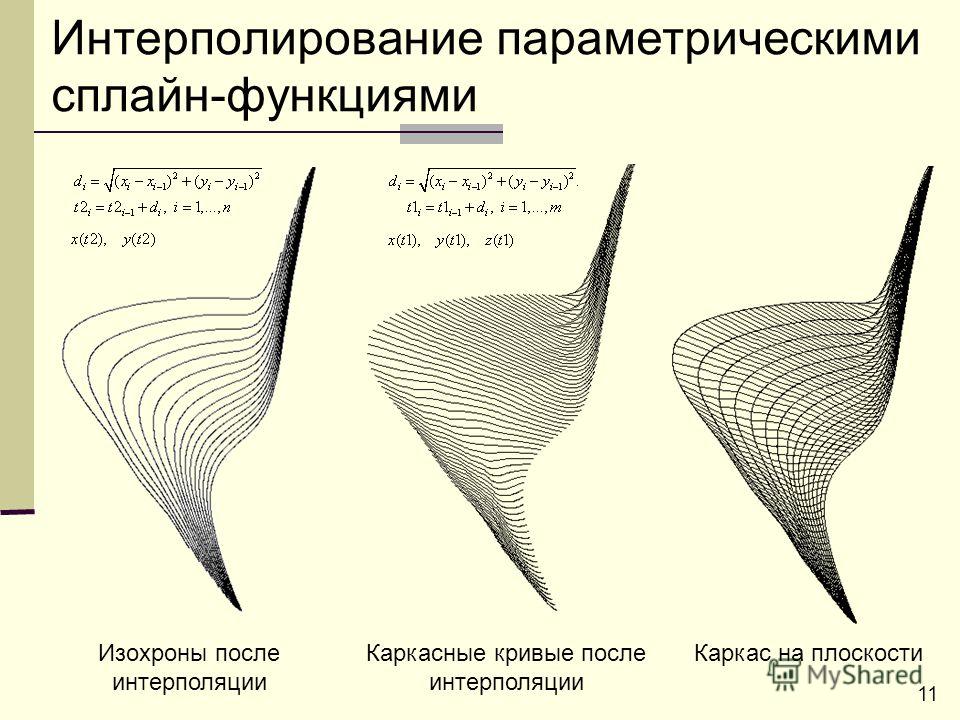 1 Определение 3 Декартово уравнение 3.1 Определение 3.2 Рабочие примеры 4 Поиск градиента 4.1 Определение 4.2 Рабочий пример 5 Рабочая тетрадь 6 См. также 7 Внешние ресурсы

Определение 92$.

Решение

Составьте таблицу и для каждого значения $t$ вычислите соответствующие значения $x$ и $y$.

т	-3	-2	-1	0	1	2	3
х	-3	-2	-1	0	1	2	3
г	9	4	1	0	1	4	9

Теперь у нас есть таблица координат $x$ и $y$, которую можно легко изобразить на графике.

Декартово уравнение

Определение 92$ и $y=2t$ в декартовой форме.

Решение

Переформулируйте первое уравнение, чтобы сделать $t$ субъектом

\[t = \sqrt{x}.\]

Подставьте это во второе уравнение, чтобы исключить параметр $t$

\[y = 2\sqrt{x}.\]

Таким образом, декартова форма этих параметрических уравнений равна

\[y = 2\sqrt{x}.\]

Рабочий пример

Выразите параметрические уравнения $x = 3 \sin\theta$ и $y=4\cos\theta$ в декартовой форме.

92}{9} = 1\]

Нахождение градиента

Определение

Чтобы найти градиент , мы используем цепное правило. Мы дифференцируем оба наших уравнения и используем правило: frac{\mathrm{d}t}{\mathrm{d}x}\] В качестве альтернативы параметрические уравнения можно сначала преобразовать в декартовы уравнения, а затем продифференцировать как обычно.

Рабочий пример

Найдите градиент кривой, заданной параметрическими уравнениями $x=t^2$ и $y=2t$.