Геометрия 7 класс первый признак равенства треугольников задачи: Задачи на признаки равенства треугольников: угол-сторона-угол и сторона-сторона-сторона

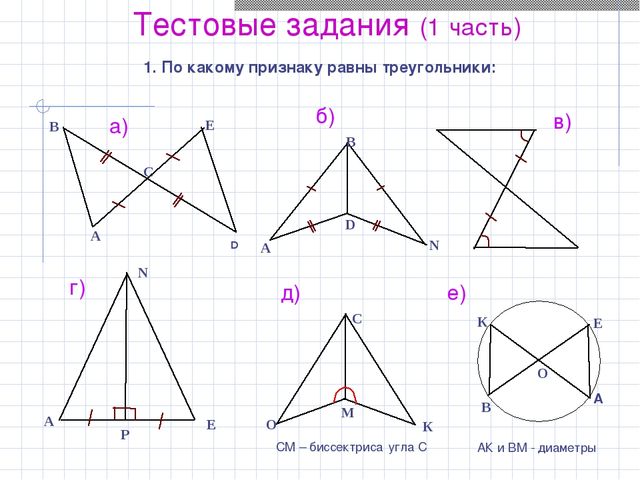
Задачи на признаки равенства треугольников: угол-сторона-угол и сторона-сторона-сторона

Второй признак равенства треугольников

Если сторона треугольника и два прилежащие к ней углы равны стороне другого треугольника и двум прилежащим углам, то эти два треугольника равны.

Отсюда вытекает следующее теоремма:

Если сторона треугольника и два к ней углы равны стороне другого треугольника и двум углам, то эти два треугольника равны.

Третий признак равенства треугольников

Если три стороны треугольника равны трём сторонам другого треугольника, то такие треугольники равны.

Задача 1
Дано:
ABC — равнобедренный треугольник.
АМ и BN биссектрисы угла.
Доказать: AM = BN.

Доказательство:
Треугольники AMB и BNA — равны (по второму признаку — угол-сторона-угол) потому что:
1. ∠CAB = ∠CBA
2. AB – в обеих треугольниках.
3. ∠MAB = ∠NBA = ¹/₂ ∠CAB.
Отрезки AM и BN являются соответствующими в этих равных треугольниках, и, следовательно, AM = BN.

---

Задача 2
Дано:
ABC — треугольник,
CM — медиана,
AA₁ ⊥ CM и BB₁ ⊥ CM.
Доказать: АА₁ = ВВ₁.

Доказательство:
1. ∠BB₁M = ∠AA₁M = 90&deg,
2. ∠AMA₁ = ∠BMB₁ как вертикальные,
3. AM = BM.
Следовательно △AA₁M = △BB₁M (по второму признаку).
Тогда AA₁ = BB₁ как соответствующие стороны в этих треугольниках.

---

Задача 3
Докажите, что перпендикуляры, проведённые из любой точки биссектрисы угла по отношению к его сторонам, вырезают на них равные отрезки.

Доказательство:
Давайте предположим, что ∠AOB точка M — неопределённая точка на биссектрисе OL.(fig.40)
Возьмём, что MP ⊥ OA и MQ ⊥ OB. Для того, чтобы доказать, что OP = OQ, достаточно доказать что △OPM = △OQM.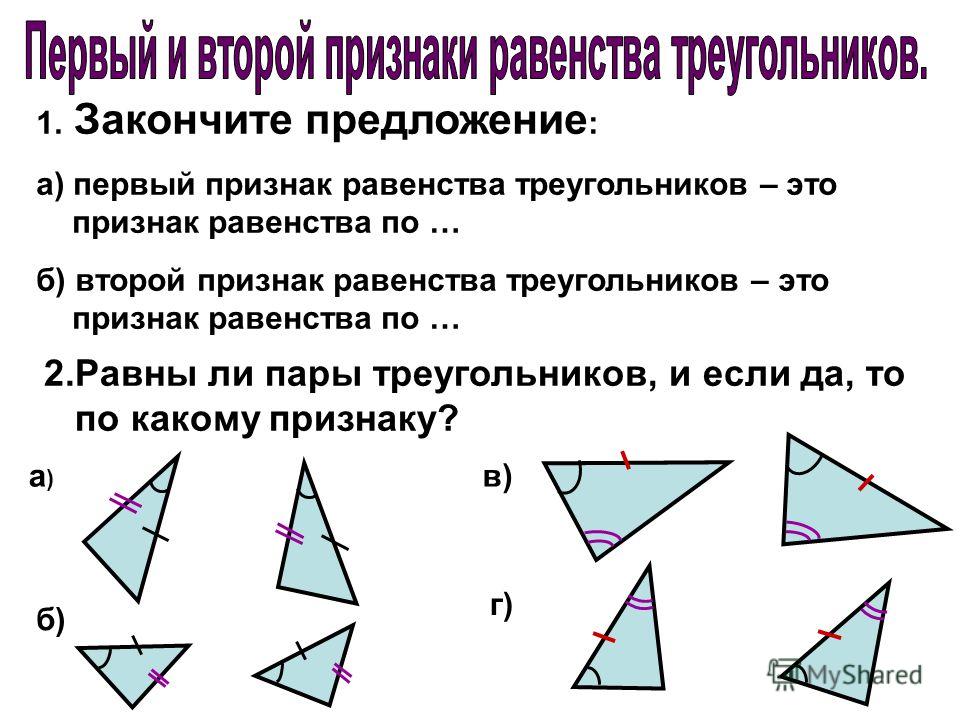

Но △OPM = △OQM(по второму признаку), потому что
1. OM — общая сторона,
2. ∠QOM = ∠POM (OL есть биссектриса),
3. ∠OQM = ∠OPM = 90°, откуда OP = OQ

Задача 4
Докажите, что если в треугольнике высота и биссектриса, проведенные из одной вершины, равны, то треугольник равнобедренный.

Доказательство:
Обозначим, что △ABC высота и биссектриса, проведённые из вершины C, совпадают (рис. 41).
Для того, чтобы доказать, что AC = BC, т.е. △ABC является равнобедренным, достаточно доказать, что △APC = △ BPC.
Но △APC = △BPC (по второму признаку) потому что
1. ∠ACP = ∠BCP (CP — биссектриса)
2. ∠ACP = ∠CPB = 90° (CP — высота)
3. CP — общая сторона
Следователвно AC = BC ⇒ ABC — равнобедренный

---

Задача 5

Дано:
AB = A₁B₁
BC = B₁C₁
AM = A₁M₁ — медианы
Докажите △ABC = △A

1B₁C₁

Доказательство:
Давайте посмотрим на треугольники △ABM и △A₁B₁M₁.
1. AB = A₁B₁
2. AM = A₁M₁
3. BM = $\frac{1}{2}$BC
B₁M₁ = $\frac{1}{2}$B₁C₁
Но BC = B₁C₁ следовательно
BM = B₁M₁

⇒ △ABM = △A₁B₁M₁(по третьему признаку).
Следовательно, ∠ABC = ∠A₁B₁C₁

Давайте посмотрим на треугольники △ABC и △A₁B₁C₁
1. AB = A₁B₁
2. BC = B₁C₁
3. ABC = A₁B₁C₁
Тогда, △ABC = △A₁B₁C₁ — равны по первому признаку.

Задачи на равенство треугольников по первому признаку

Первый признак равенства треугольников. Решение задач

Цели и задачи урока:

• повторение понятий треугольника и его элементов
• повторение понятия равных треугольников
• формирование у учащихся умения доказывать равенство треугольников
• умение выделять следствия, вытекающие из равенства треугольников.

Ход урока

Решение задач по готовым чертежам.

I. Проверка домашнего задания: № 90, № 94.

Перед уроком на доске выполнены чертежи и записано дано к каждой задаче:

№90.

Дано: треугол. АВС

АВ = 17 см, АС > AB в 2 раза, ВС < AC на 10 см.

Найти: P треугол. ABC = ?

№ 94.

Дано: АВ = АС, <1 = <2, АС= 15 см, DC= 5 см.  

а) Доказать: треугол. АВD = треугол. ACD

б) Найти: BD и АВ.

Далее с помощью фронтального опроса класса устно проверяем решение домашних задач.

№ 90. Решение:

1. Пусть АВ = 17 см (по условию), тогда AC = 2АВ = 17 * 2 = 34 см, а ВС = АС – 10 = 34 – 10 = 24 см
2. P АВС = АВ + ВС + АС = 17 + 34 + 24 = 75 см.

Ответ: Р треугольника. АВС = 75 см.

№ 94.

1) Рассмотрим треугольник АВС и треугольник АСD.

а) АВ = АС (по условию)

б) < 1 = < 2 (по условию)

в) AD – общая сторона

Из а, б, в следует => треугольник АВD = треугольнику АСD по двум сторонам и углу между ними (Первый признак равенства треугольников).

2) Треугольник АВD = треугольнику АСD, мы знаем, что в равных треугольниках против соответственно равных углов лежат равные стороны, т.е. т.к <1 = <2, то BD = DC = 5 см

3) АВ = АС = 15 см (по условию)

Ответ: АВ = 15 см, ВО = 5 см.

Попутно повторяем следующие понятия:

а) какая фигура называется треугольником;
б) элементы треугольника;
в) стороны и углы, противолежащие друг другу;
г) углы, прилежащие к сторонам треугольника;
д) что такое периметр треугольника

II. Опрос класса – доказательство I-ого признака равенства треугольников. Опрос называется – Каскад.

5 учеников из класса уже ответили учителю эту теорему и знают ее отлично. Знают все дополнительные вопросы (и ответы на них), которые надо задать по ходу доказательства этой теоремы. Причем это, как правило, слабые ученики класса, которые выучивают теорему, хорошо понимая ее, с помощью учителя. Они стремятся дотошно разобраться в доказательстве данной теоремы и всего теоретического материала, используемого в ней, так как знают, что на уроке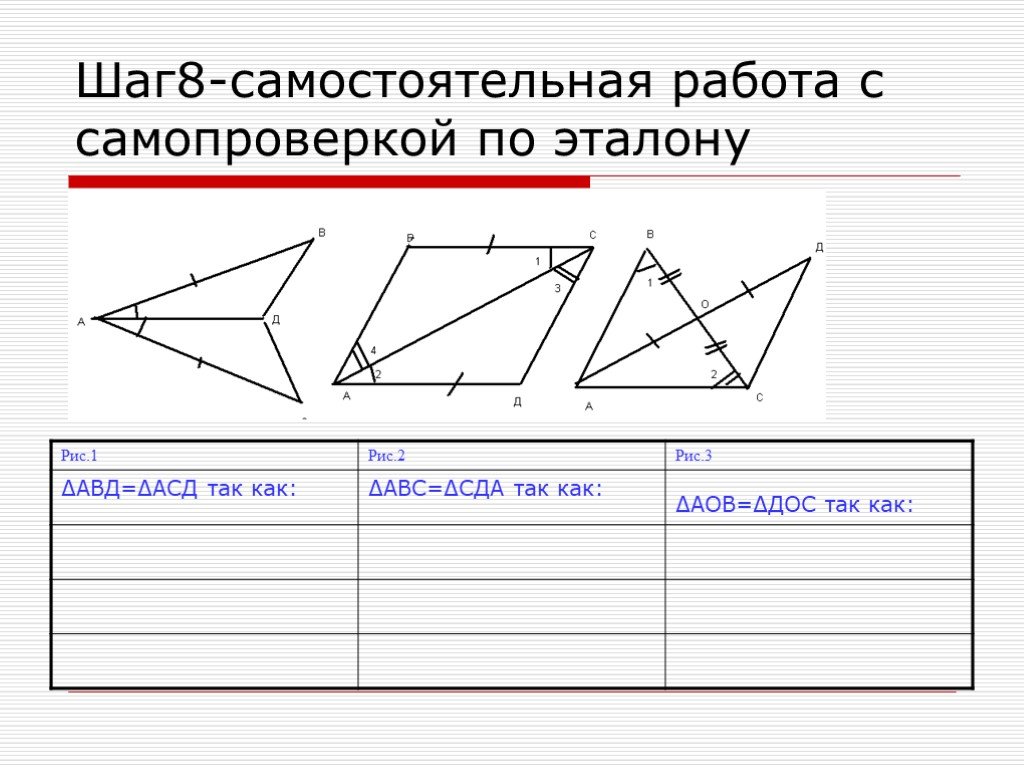

они будут опрашивать и оценивать сильных учеников класса. Это стимулирует их на хорошую подготовку к уроку, детям всегда хочется побывать в роли учителя, тем более, что дети послабее опрашивают тех, кто лучше разбирается в данном предмете. Все ученики класса, кроме этих пятерых, достают листки и делают на них чертежи к теореме, и пишут дано. На первый взгляд дети работают сами, но на самом деле вся работа хорошо спланировано учителями. Весь класс у него на контроле. Как только работа с листочками закончена, учащиеся готовые отвечать поднимают руки и им учитель предлагает занять место рядом с одним из пятерых, уже ответивших теорему. Дети начинают тихим шепотом отвечать друг другу. Через 3-4 минуты в классе уже 10 человек, которые спрашивают, и так по нарастающей. Когда все ответили, учитель называет всех учеников по списку, и отметку говорит тот, кто его опрашивал. Отметки, как правило, бывают хорошими, двоек нет совсем, так как дети знают, что спросят всех. (Если оценки чуть завышены, это не страшно, важно, что они с желанием готовятся, следовательно учат теорию, владеют ей начинают лучше решать задачи, а это то, чего мы хотим добиться на уроках геометрии.

III. В это время I ученик за доской готовит материал для доказательства этой теоремы. Как только все ответили друг другу теорему и получили оценки, он отвечает устно эту же теорему. Ребята должны владеть собой при ответе для полной аудитории, тренировать хороший математический язык, логическую последовательность ответа. А аудитория уметь слушать, улавливать ошибки, если они есть, задавать вопросы отвечавшему и учиться правильно, оценивать ответы одноклассников.

IV. Решение задач. Устно по готовым чертежам.

Доказать равенство треугольников.

1.			2.
Доказать: треугол. АОВ = треугол. COD			Доказать: треугол. АВD = треугол. CDB

У доски ученик.

У доски ученик + фронтальная помощь класса. Решим письменно задачу с полным оформлением решения в тетради.

Дано:

< ABE = < DCE, BE = CE

BK = LC, < BKE = 110°

1) Доказать: треугол.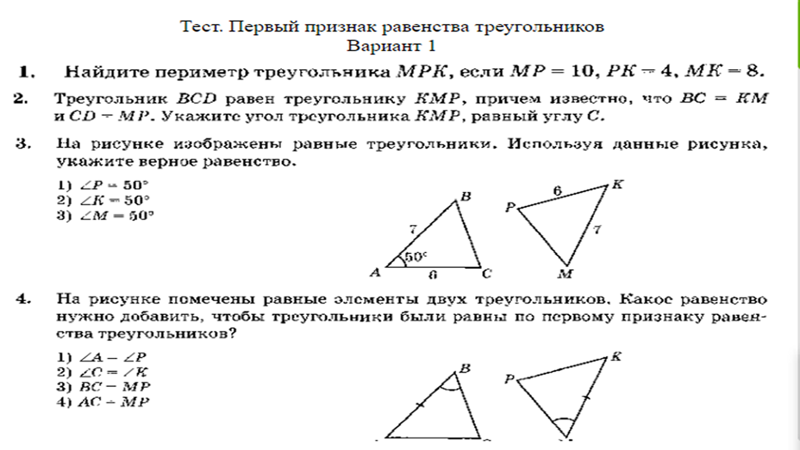 BEK = треугол. CEL

2) Найти: < ELC

Решение:

1) < ABE + < 1 = 180° (смежные углы)

< DCE + < 2 = 180° (смежные углы)

< 1 = 180° — < ABE

< 2 = 180° — < DCE

и по условию < ABE = < DCE, следовательно < 1 = < 2/

2) Рассмотрим треугол. BEK и треугол. CEL:

а) BE = СE (по условию)

б) BK = LC (по условию)

в) <1 = < 2

из а, б, в следует => треугол. BEK = CEL по двум сторонам м углу между ними (I признак равенства треугольников) ч.т.д.

3) Треугол. BEK = треугол. CEL , а в равных треугольниках против соответственно равных сторон лежат равные углы, т.е. т.к BE=CE, то < ELC = < BKE = 110°.

Ответ: < BKE = 110°

2.

Дано:

треугол. BEC = DFA

Доказать: 1) треугол. ABC = треугол. CDA

2) треугол. ABE = треугол CDE

Доказательство:

1) Т.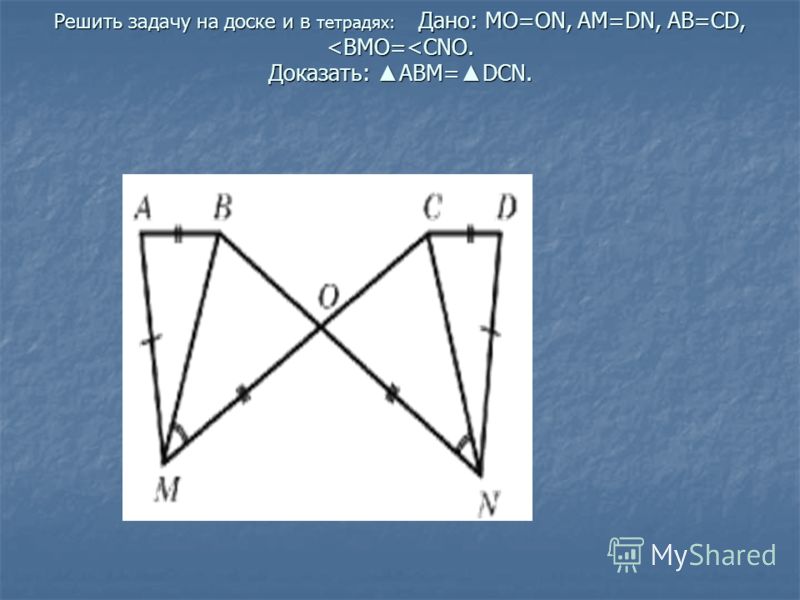 к. по условию треугол. BEC = треугол. DFA, то BC = DA, <BCE = < DAF.

2) Рассмотрим. треугол. ABC и треугол. CDA:

а) BC = DA

б) < BCA = <DAC

в) AC – общая сторона

Из а, б, в, следует => треугол. ABC = треугол. CDA по I признаку равенства треугольников (по двум сторонам и углу между ними).

3) Т.к треугол. BEC = треугол. DFA, то EC = FA.

Т.к треугол. АВС = треугол. CDA, то АС – общая сторона

Отсюда следует => AE = AC – EC

CF = AC – FA, т.е. AE = CF.

4) Т.к. треугол. BEC = треугол. DFA, то BE = Df и < BEC = < DFA, то они смежные соответственно с углами: < AEB и < CFD, т.е. < AEB = < СFD.

5) Рассмотрим треугол. ABE и треугол. СDF:

а) BE = DF

б) AE=СF

в) < AEB=< CFD

Из а,б,в следует => треугол. ABE = треугол. CDF по двум сторонам и углу между ними( I признак павенства треугольников) ч.т.д.

VI. Домашнее задание: параграф 14,15. № 95, 96, 92.

VII. Итог урока.

Как найти угол в прямоугольном треугольнике

Все ресурсы по базовой геометрии

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Справка по базовой геометрии » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти угол в прямоугольном треугольнике

Найти угол С.

Возможные ответы:

C=72

C=65

C=70

Ни один из этих

C=53

5 C=88

Пояснение:

Во-первых, знайте, что сумма всех углов треугольника равна 180 градусам.

У каждого треугольника 3 угла. Таким образом, у нас есть сумма трех углов, как показано на рисунке:

 

, где у нас есть углы A, B и C. В нашем прямоугольном треугольнике один угол равен 25 градусам, и мы назовем этот угол A. Другой известный угол 90 градусов, и мы назовем этот угол B. Таким образом, у нас есть

Упростите и решите для C.

Сообщить об ошибке

Какое из следующих

может быть двумя мерами угла прямоугольного треугольника?

Возможные ответы:

Правильный ответ:

Пояснение:

В прямоугольном треугольнике не может быть тупого угла; это исключает выбор между 100 и 10.

Острые углы прямоугольного треугольника должны составлять 90 градусов. По этому критерию можно исключить три варианта:

Оставшийся вариант правильный:

Сообщить об ошибке

Угол прямоугольного треугольника в 15 раз больше, чем у другого. Чему равен меньший угол?

Возможные ответы:

Правильный ответ:

Объяснение:

Сумма углов треугольника равна 180. В прямоугольном треугольнике один угол равен 90.  Таким образом, сумма двух других углов будет равна 90.

Пусть = первый угол и = второй угол

Таким образом, уравнение для решения становится или

Таким образом, первый угол равен, а второй угол равен .

Таким образом, меньший угол равен

Сообщить об ошибке

Угол  в показанном ниже треугольнике (не в масштабе) равен 35 градусам. Что такое угол?

Возможные ответы:

градусы

градусы

градусы

 градусы

Правильный ответ:

 градусы

Пояснение:

Сумма внутренних углов треугольника всегда равна 180 градусам. Нам дан угол  и, поскольку указано, что это прямоугольный треугольник, мы знаем, что угол   равен 90 градусам. Таким образом, мы знаем 2 из 3 и можем определить третий угол.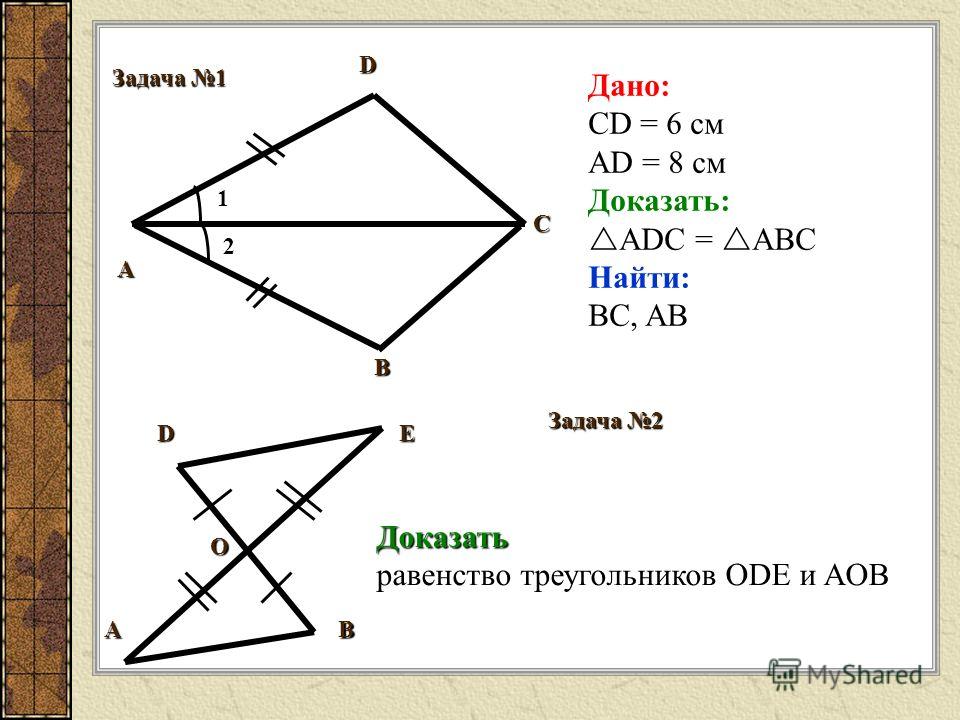

Угол равен 55 градусам.

Сообщить об ошибке

Что из следующего нельзя верно для прямоугольного треугольника?

Возможные ответы:

Прямоугольный треугольник может быть равносторонним.

Меры углов прямоугольного треугольника могут суммироваться.

Один катет может быть длиннее гипотенузы.

Прямоугольный треугольник может иметь тупой угол.

Ни одно из других утверждений не может быть верным для прямоугольного треугольника.

Правильный ответ:

Ни одно из других утверждений не может быть верным для прямоугольного треугольника.

Объяснение:

Все этих утверждений ложны.

Прямоугольный треугольник может быть равносторонним.

Неверно: Равносторонний треугольник должен иметь три угла, каждый из которых измеряется.

Один катет может быть длиннее гипотенузы.

Ложь: Каждый катет на короче, чем гипотенуза на .

Прямоугольный треугольник может иметь тупой угол.

Ложь:  Оба угла прямоугольного треугольника не являются прямыми  должно быть острым.

Меры углов прямоугольного треугольника могут суммироваться.

Ложь: Меры любой суммы треугольников .

Сообщить об ошибке

Чему равен угол в треугольнике?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для нахождения всех углов треугольника:

  

Чтобы найти меру угла, мы подставляем значения и . Поскольку угол прямой, мы знаем, что мера будет равна .

  

Сообщить об ошибке

Найдите градусную меру недостающего угла.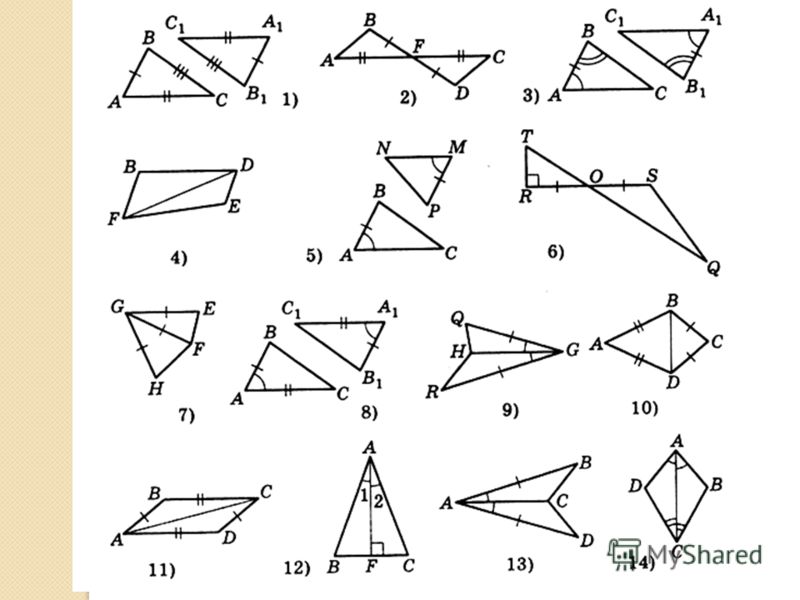

Возможные ответы:

Правильный ответ:

 

Пояснение:

Сумма всех углов треугольника равна 180º.

Чтобы найти значение остаточного угла, вычтите известные углы из 180º:

 

Следовательно, третий угол равен 43º.

 

Сообщить об ошибке

Прямоугольный треугольник  имеет два равных угла, какова их мера?

Возможные ответы:

Правильный ответ:

Пояснение:

Внутренние углы треугольника всегда составляют в сумме 180 градусов, и было дано, что треугольник прямоугольный, а это означает, что один из углов равен 90 градусов.

Это оставляет 90 градусов, чтобы равномерно разделить два оставшихся угла, как было показано в вопросе.

Следовательно, каждый из двух равных углов имеет размер 45 градусов.

Сообщить об ошибке

Какого угла не хватает в этом прямоугольном треугольнике?

Возможные ответы:

Правильный ответ:

Пояснение:

Сумма всех углов треугольника равна .

Это означает, что .

Используя тот факт, что 90 — это половина 180, мы можем вычислить, что недостающий угол x плюс 34 добавляется к оставшимся 90, и мы можем просто вычесть

.

Сообщить об ошибке

Решить:

Возможные ответы:

Правильный ответ:

Пояснение:

Сумма углов треугольника составляет 180 градусов.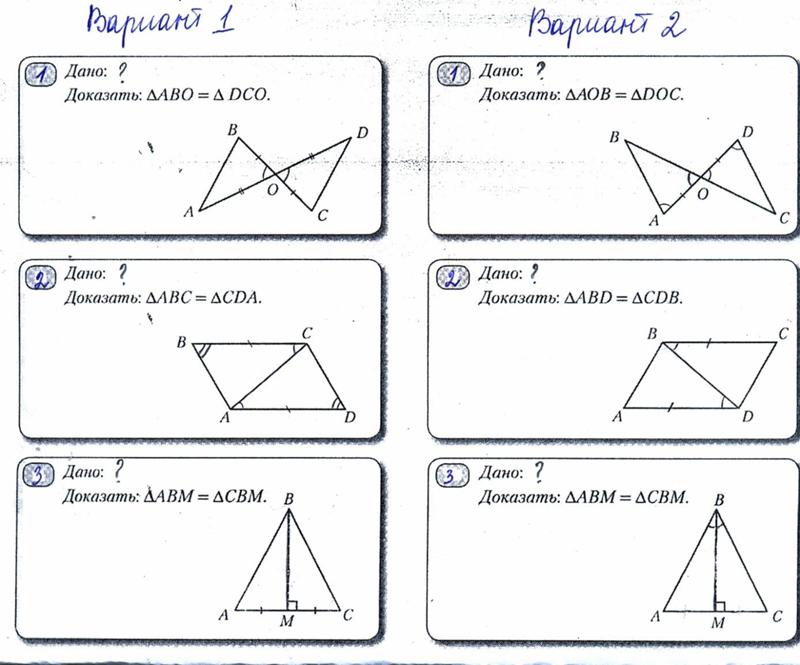 Мы уже знаем, что один из углов равен 9.0 градусов, поэтому мы можем вычесть 90 из 180: два других угла должны добавиться к 90 градусам.

Теперь мы можем вычесть, чтобы получить x:

Сообщить об ошибке

← Назад 1 2 3 Далее →

Уведомление об авторских правах

Все ресурсы по базовой геометрии

9 Диагностические тесты4 164 практических теста Вопрос дня Карточки Learn by Concept

Различные типы треугольников (видео и практика)

TranscriptFAQsFact SheetPractice

Привет и добро пожаловать в этот обзор различных типов треугольников! Прежде чем мы начнем, вот обзор основ.

Треугольник имеет три прямые стороны, которые соединяются. Длина сторон может быть разной, но длина наибольшей стороны не может быть равна или больше суммы двух других сторон. Кроме того, треугольник имеет три внутренних угла, и сумма этих трех углов всегда равна 180 градусам.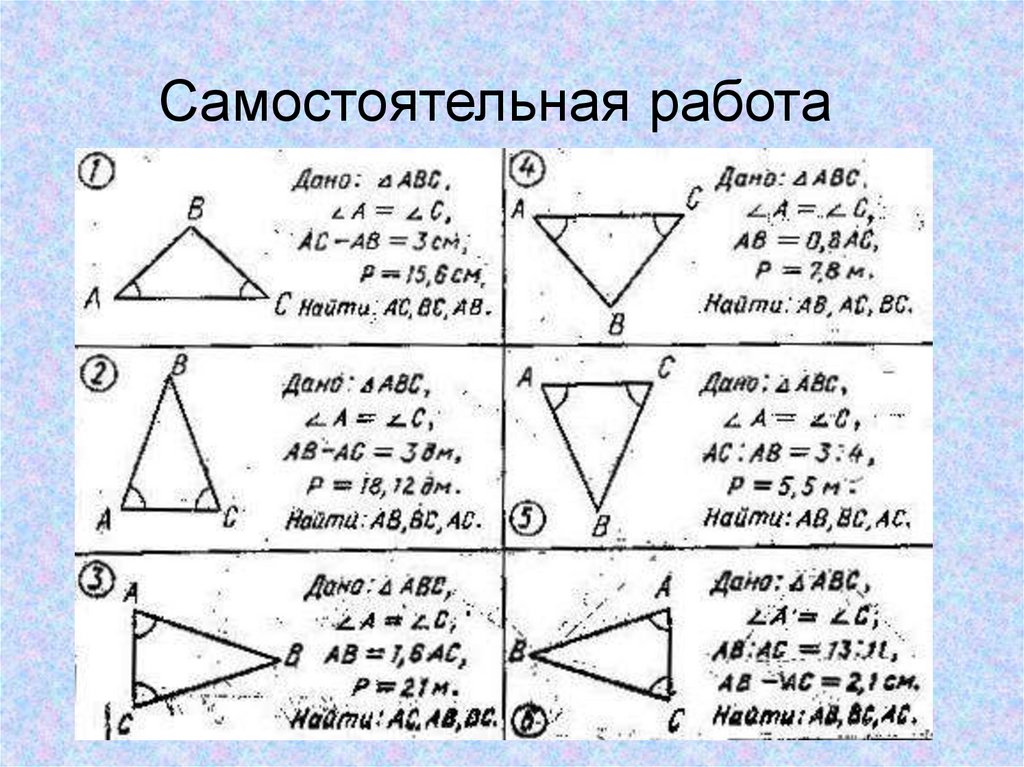 Это верно для всех треугольников, включая шесть типов, которые мы сегодня рассмотрим.

Различные типы треугольников

Мы собираемся разбить наши шесть типов треугольников на две группы по три.

Начнем с трех типов треугольников, которые классифицируются по величине их наибольшего угла. Это остроугольный, прямоугольный и тупоугольный треугольники.

Но как узнать, что есть что? Посмотрите на наибольший угол каждого треугольника и отметьте, больше ли он, меньше или равен 90 градусам.

Остроугольный треугольник

Мы видим, что наибольший угол в треугольнике слева равен 70 градусам. 70 меньше 90, так что это остроугольный треугольник. Только помните, что острые углы меньше 90 градусов. Это легко запомнить, так как «милые» вещи часто бывают маленькими, например, щенки и котята.

Прямоугольный треугольник

Мы видим, что в среднем треугольнике наибольший угол равен ровно 90 градусам. Возможно, вы помните, что угол в 90 градусов — прямой угол, поэтому этот треугольник — прямоугольный.

Тупоугольный треугольник

Наконец, в треугольнике справа наибольший угол равен 117 градусам. Поскольку это больше 90 градусов, это тупой угол, поэтому мы называем этот треугольник тупым треугольником.

Это все, что нужно для этих трех типов! Мы просто находим наибольший угол и название треугольника будет соответствовать названию этого угла.

Наш второй набор треугольников классифицируется по тому, сколько сторон имеют одинаковую длину. Вот три треугольника с включенными длинами сторон:

Равносторонний треугольник

В треугольнике слева мы видим, что все три стороны имеют одинаковую длину и составляют 9 сантиметров. Такой треугольник, у которого все стороны равны, называется равносторонним треугольником. Это имя несложно запомнить, так как начало равностороннего звучит как слово «равный», а слово «латеральный» означает «сторона».

Равнобедренный треугольник

В среднем треугольнике мы видим, что две стороны имеют одинаковую длину и составляют 8 см, а третья 9 см.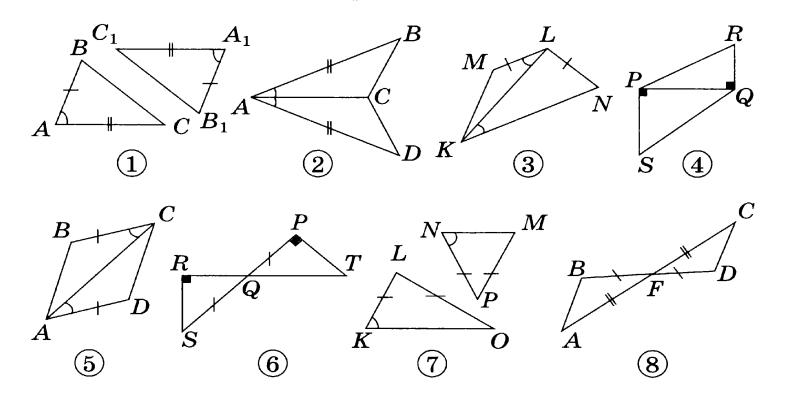 см. Когда две стороны треугольника равны, такой треугольник называется равнобедренным. Это сложно написать, но легко распознать!

Разносторонний треугольник

В нашем последнем треугольнике ни одна из сторон не имеет одинаковой длины, поэтому такой треугольник называется разносторонним.

Хотя эти три типа треугольников часто идентифицируют по длинам сторон, их также можно классифицировать по углам. Работает точно так же:

Когда все углы равны 60 градусам, это равносторонний треугольник . Технически это называется равноугольным треугольником, но это одно и то же, потому что все равносторонние треугольники также являются равноугольными треугольниками. Когда два угла равны, это равнобедренный треугольник. А когда ни один из углов не совпадает, это разносторонний треугольник.

Пока что мы рассмотрели шесть типов треугольников, что технически означает все типы, но это еще не все. Если мы хотим быть очень конкретными при именовании наших треугольников, мы можем комбинировать имена из каждой группы; один из первой группы и один из второй группы.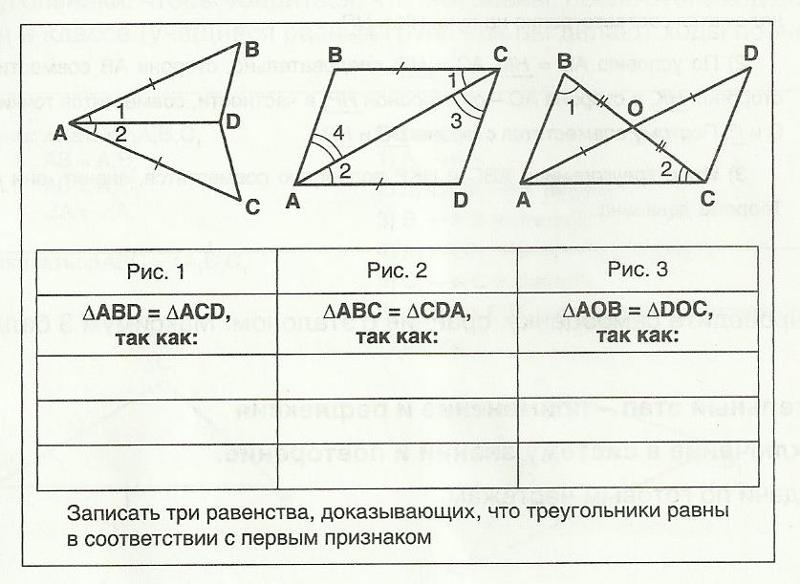

Например, приведенный выше треугольник представляет собой остроугольный треугольник . Его наибольший угол меньше 90 градусов, поэтому он острый, и ни один из его углов не является одинаковым, поэтому он неравносторонний.

Прежде чем мы уйдем, как насчет того, чтобы попробовать. Определите эти два треугольника, выбрав остроугольный, прямоугольный или тупоугольный, а затем выбрав равносторонний, равнобедренный или разносторонний.

Думаешь, понял? Треугольник слева — это тупоугольный треугольник , а справа — .0017 прямоугольный равнобедренный треугольник.

Надеюсь, отзыв был полезен! Спасибо за просмотр и удачной учебы!

Общие правила треугольников | Площадь и периметр треугольника

 

Часто задаваемые вопросы

Q

Какие существуют шесть типов треугольников?

A

Шесть типов треугольников: равнобедренный, равносторонний, разносторонний, тупоугольный, остроугольный и прямоугольный.

Равнобедренный треугольник — это треугольник с двумя конгруэнтными сторонами и одной уникальной стороной и углом.
Пример.

Равносторонний треугольник — это треугольник с тремя конгруэнтными сторонами и тремя конгруэнтными углами.
Пример.

Разносторонний треугольник — это треугольник без конгруэнтных сторон и конгруэнтных углов.
Пример.

Тупоугольный треугольник — это треугольник с тупым углом.
Пример.

Остроугольный треугольник — треугольник с тремя острыми углами.
Пример.

Прямоугольный треугольник — это треугольник с одним прямым углом.
Пример.

Q

Каковы свойства разностороннего треугольника?

A

Разносторонние треугольники — это треугольники с тремя уникальными длинами сторон и тремя уникальными размерами углов.

Q

Что такое разностороннее и правильное?

A

Разносторонний треугольник — это треугольник, у которого нет равных сторон и углов. Прямоугольный треугольник — это треугольник, у которого одна сторона (90°) угол. Треугольник может быть разносторонним и прямоугольным, если одна из его уникальных угловых величин равна 90°.
Пример.

Q

Сколько сторон равны в равнобедренном треугольнике?

A

У равнобедренного треугольника две равные стороны и два равных угла.

Q

Что такое правильный треугольник?

A

Настоящий треугольник — это фигура, имеющая три стороны и три угла. Сумма длин двух сторон должна быть больше, чем длина третьей стороны, а сумма трех углов должна составлять 180°.

Q

Какие углы равны в равнобедренном треугольнике?

A

Два угла равнобедренного треугольника равны при основании. В равнобедренном треугольнике две равные стороны пересекаются в одной точке. Угол, образованный слиянием этих двух линий, является уникальным углом. Углы, образованные основаниями этих линий и третьей единственной стороной, являются двумя равными углами, называемыми углами при основании.

Q

Каковы характеристики равностороннего треугольника?

A

Равносторонний треугольник — это треугольник, у которого три равные стороны и три равных угла.

Информационный бюллетень

Загрузить информационный бюллетень

Практические вопросы

Вопрос №1:

 
Что это за треугольник?

Острый

Равносторонний

Равнобедренный

Разносторонний

Показать ответ

Ответ:

Правильный ответ — разносторонний. Разносторонний треугольник — это треугольник, у которого нет равных сторон.

Скрыть ответ

Вопрос №2:

 
Что это за треугольник?

Тупой равнобедренный

Острый равнобедренный

Острый разносторонний

Тупой разносторонний

Показать Ответ

Ответ:

9000 Острый равнобедренный.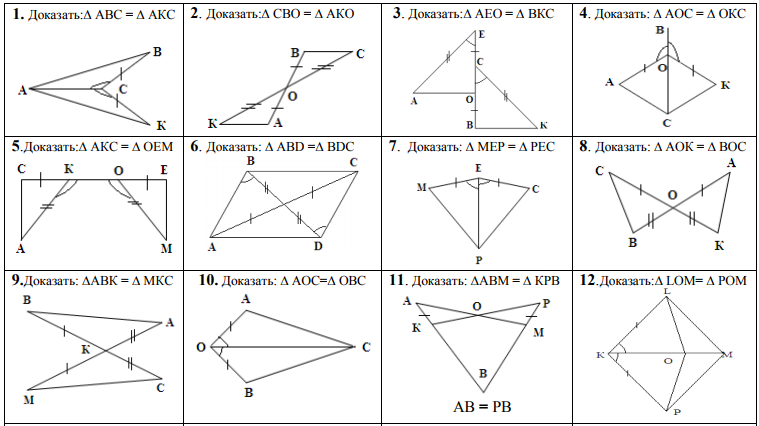 Равнобедренный треугольник имеет две конгруэнтные стороны (как показано двумя делениями) и одну уникальную сторону. Он острый, потому что единственный угол (тот, что сверху) меньше 90°.

Скрыть ответ

Вопрос №3:

 
Что это за треугольник?

Острый

Тупой

Равносторонний

Разносторонний

Показать ответ

Ответ:

Правильный ответ равносторонний. Равносторонний треугольник – это треугольник, у которого три равные стороны и три равных угла.

Скрыть ответ

Вопрос №4:

 
Что это за треугольник?

Острая равнобедренная

Острая лестничная

Тупая равнобедренная

Тупая лестничная

Показать ответ

Ответ:

Равнобедренный треугольник — это треугольник, у которого две равные стороны и два равных угла, а также одна единственная сторона и угол.