17 марта 2023 г. Геометрия — это раздел математики, посвященный размерам, формам и взаимному расположению фигур. Он был преобладающим в прежние времена и является практичным способом определения длин, объемов и площадей. Он разделен на две части: плоская геометрия и объемная геометрия. Существует множество геометрических формул, связанных с высотой, шириной, радиусом, площадями и объемами.
Мы попытались упомянуть некоторые геометрические формулы для классов с 8 по 12, которые можно использовать для решения задач. Если вы зашли в тупик при решении проблемы, это то место, куда вам следует заглянуть. Некоторые геометрические формулы довольно сложны, и вы вряд ли слышали о них. Кроме того, мы также предоставили основные математические формулы для классов 12, 11, 10, 9, 8, которые используются в нашей повседневной жизни для расчета пространства, длины и так далее.
Геометрические формулы для классов 8–12 Скачать PDF Главной заботой каждого изучающего предмет является изучение формул геометрии.
Учащиеся 12, 11, 10, 9, 8 классов могут сделать свою подготовку эффективной с помощью удобного списка формул. Используйте их при решении вопросов и легко приходите к выводу с помощью простого подхода. Загрузите формулы геометрии для классов 8–12 в формате PDF бесплатно и помогите в подготовке. Обратитесь к дополнительным модулям, чтобы воспользоваться быстрыми ссылками на PDF-формулы геометрии и легко решить вопросы и ответы в геометрии.
Геометрические формулы для класса 12 Геометрические формулы для класса 11 Геометрические формулы для класса 10 Геометрические формулы для класса 9 Геометрические формулы для класса 8 Вот список нескольких наиболее важных геометрических формул, которые вы используете для решения различных задач.
Формулы базовой геометрии Периметр квадрата = P = 4a Где а = длина сторон квадрата
Периметр прямоугольника = P = 2(l+b) Где, l = длина; b = Ширина
Площадь квадрата = A = a 2 Где a = длина сторон квадрата
Площадь прямоугольника = A = l×b Где, l = длина; b = ширина
Площадь треугольника = A = ½×b×h Где, b = основание треугольника; h = высота треугольника
Площадь трапеции = A = ½×(b 1 + b 2 )×h Где b1 и b2 — основания трапеции; h = высота трапеции
Площадь круга = A = π×r 2 Длина окружности = A = 2πr Где r = радиус окружности
Площадь поверхности куба = S = 6a 2 Где, a = длина сторон куба
Площадь криволинейной поверхности цилиндра = 2πrh Общая площадь поверхности цилиндра = 2πr(r + h) Объем цилиндра = V = πr 2 ч Где, r = радиус основания цилиндра; h = высота цилиндра
Площадь криволинейной поверхности конуса = πrl Общая площадь поверхности конуса = πr(r+l) = πr[r+√(h 2 +r 2 )] Объем конуса = V = ⅓×πr 2 ч Где r = радиус основания конуса, h = высота конуса
Площадь поверхности сферы = S = 4πr 2 Объем сферы = V = 4/3×πr 3 Где r = радиус сферы
Геометрические формулы Получите общие геометрические формулы для классов с 8 по 12 для различных форм и фигур.
Часто задаваемые вопросы по формулам геометрии 1. Где взять все формулы геометрии?
Формулу геометрии для классов 12, 11, 10, 9, 8 вы можете получить на нашей странице. Получите доступ к быстрым ссылкам, доступным здесь в формате PDF, и узнайте формулы по всем темам.
2. Можете ли вы привести некоторые важные формулы по геометрии?
Учащиеся 8-12 классов найдут здесь информацию, связанную с основными и важными формулами геометрии, которые помогут вам получить более высокие оценки на экзамене.
3. Как скачать формулы классовой геометрии в формате PDF?
Ознакомьтесь с прямыми ссылками, доступными на нашей странице, коснитесь их, чтобы просмотреть или загрузить формулы геометрии для соответствующего класса. Все они организованы в соответствии с классами, что может быть очень удобно для повышения вашей подготовки.
Заключение
Мы желаем, чтобы данные, которые мы получили в отношении формул геометрии, были вам полезны. Для получения дополнительной информации и если вы чувствуете, что какая-либо формула отсутствует, не стесняйтесь оставлять нам свои предложения в разделе комментариев. Оставайтесь на связи с нашим сайтом, чтобы получить информацию обо всех формулах.
Каждая формула геометрии GMAT, которую вам нужно знать • PrepScholar GMAT
Если вы похожи на меня, вы, вероятно, потратили много времени в старшей школе, запоминая разницу между синусом и косинусом и вздыхая над длинными многошаговыми доказательствами, только для того, чтобы забыть все эти с трудом заработанные знания в ту же секунду, когда занятия были распущены на каникулы.
Если вы забыли много школьных правил геометрии или вам просто нужно освежить знания перед сдачей GMAT, то вы нашли нужную статью. В этой статье Я дам вам исчерпывающий обзор геометрии GMAT.
Сначала расскажу о том, что и сколько геометрии на самом деле на GMAT. Далее я дам вам обзор наиболее важных формул и правил геометрии GMAT, которые вам необходимо знать. Затем я покажу вам четыре примера вопросов по геометрии и объясню, как их решать. Наконец, я расскажу о , как подготовиться к геометрии, с которой вы столкнетесь на GMAT, и дам вам советы по успешному экзамену.
Геометрия GMAT: чего ожидать Если вам кажется, что вы забыли многое из того, что изучали в школе, не волнуйтесь. GMAT охватывает только часть геометрии, которую вы, вероятно, изучали в старшей школе. В следующем разделе я расскажу о концепциях геометрии, которые вы найдете на GMAT.
Вы найдете концепции геометрии как в вопросах достаточности данных, так и в вопросах решения проблем. Вопросы по геометрии составляют чуть менее четверти всех вопросов в количественном разделе GMAT. Как и в случае со всеми количественными вопросами GMAT, вам нужно не просто знать, как применять принципы геометрии изолированно.
Не знаете, как и что изучать? Не знаете, как улучшить свой результат в кратчайшие сроки? Мы создали единственную онлайн-программу подготовки к GMAT, которая определяет ваши сильные и слабые стороны, настраивает учебный план, обучает вас с помощью уроков и тестов и адаптирует ваш учебный план по мере вашего улучшения.
Мы считаем, что PrepScholar GMAT — это лучшая программа подготовки к GMAT, доступная , особенно если вам трудно организовать свой учебный график и вы не хотите тратить кучу денег на универсальные программы других компаний. учебные планы.
Как я уже упоминал ранее, GMAT охватывает только часть геометрии, которую вы изучали в старшей школе. Как и в остальной части раздела GMAT Quant, вам нужно только знать, как применять концепции геометрии средней школы, что может быть облегчением для некоторых тестируемых.
К сожалению, в отличие от некоторых других стандартизированных тестов (таких как SAT), GMAT не предлагает никаких формул. Вам нужно будет запомнить все формулы и правила, которые вам понадобятся для теста.
В следующем разделе я расскажу вам о наиболее важных правилах и формулах, которые вам необходимо знать, чтобы отвечать на вопросы о решении геометрических задач и достаточности данных.
Самые важные формулы и правила GMAT по геометрии, которые нужно знать Хорошей новостью о геометрии GMAT является то, что вам не нужно освежать в памяти целую кучу тем, чтобы хорошо сдать экзамен. Плохая новость о геометрии GMAT заключается в том, что вам придется запомнить все правила и формулы, которые вам нужно знать для теста, потому что в день экзамена вам их не дадут. Вы также не можете приносить какие-либо вспомогательные средства, которые помогут вам на экзамене.
В этом разделе я расскажу об основных геометрических формулах и правилах GMAT, которые вам следует изучить и запомнить при подготовке к экзамену.
Линии и углы Линия — это одномерная абстракция, которая продолжается вечно. Через любые две точки проходит одна прямая (только одна!). Участок линии — это отрезок прямой линии, имеющий две конечные точки. Середина — это точка, которая делит отрезок на две равные части. Две прямые параллельны, если они лежат в одной плоскости и никогда не пересекаются. Две прямые перпендикулярны, если они пересекаются под углом 90°.
Угол образуется при пересечении двух прямых в одной точке. Эта точка называется вершиной угла. Углы измеряются в градусах (°). Острый угол – это угол, градусная мера которого меньше 90°. Градусная мера прямого угла равна ровно 90°. Градусная мера тупого угла больше 90°. Градусная мера прямого угла равна 180°.
Сумма углов на прямой равна 180°. Сумма мер углов вокруг точки (которые образуют окружность) составляет 360°. Два угла являются дополнительными, если их суммы составляют прямой угол. Два угла являются дополнительными, если их суммы составляют прямой угол.
Вертикальные углы – это противоположные углы, образованные двумя пересекающимися отрезками. Прямая или отрезок делит угол пополам, если он делит угол на два меньших равных угла. Вертикальные углы представляют собой пару противоположных углов, образованных пересекающимися прямыми углами. Два угла в паре вертикальных углов имеют одинаковую градусную меру.
Треугольники Треугольник — это замкнутая фигура с тремя углами и тремя прямыми сторонами. Сумма внутренних углов треугольника равна 180°. Каждый внутренний угол дополняет соседний внешний угол. Вместе они равны 180°. Формула для нахождения площади треугольника: $½bh$. $b$ = основание $h$ = высота
У равнобедренного треугольника две стороны одинаковой длины.
Равносторонний треугольник имеет три равные стороны и три угла по 60°.
Существуют два вида особых прямоугольных треугольников: Равнобедренные прямоугольные треугольники имеют соотношение сторон 1:1:$√2$. Треугольники 30°60°90° имеют соотношение сторон 1:$√3$:2. Два треугольника подобны, если их соответствующие углы имеют одинаковую градусную меру. Два треугольника равны, если соответствующие углы имеют одинаковую меру и соответствующие стороны имеют одинаковую длину. Площадь прямоугольника: $l$$w$ Площадь параллелограмма: $b$$h$
Площадь трапеции: $1/2(a + b)h$
Твердые тела Цилиндр – это твердое тело, горизонтальное поперечное сечение которого представляет собой круг. Объем цилиндра: $Bh$, где $B$ — площадь основания. Площадь основания цилиндра: ?r 2 (помните, что цилиндр имеет круглое поперечное сечение) Куб — прямоугольное тело, все грани которого — квадраты. Объем куба: $Bh$, где $B$ — площадь основания. Прямоугольное тело — это тело с шестью прямоугольными гранями. Объем прямоугольного тела: $lwh$
Координатная геометрия Наклон линии показывает, насколько круто эта линия идет вверх или вниз по координатной плоскости. $наклон$ = $подъем$/$бег$ $slope = изменение $y$ / изменение $x$ Подъем — это разница между значениями $y$-координат двух точек на прямой; пробег — это разница между значениями координат x двух точек на линии. Вы также можете найти наклон линии, используя уравнение пересечения наклона, которое выглядит следующим образом: $y = mx + b$, где наклон равен $m$, а $b$ — это значение $y$- перехват. Перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами. Чтобы определить расстояние между любыми двумя точками на координатной плоскости, можно воспользоваться теоремой Пифагора.
4 совета по вопросам GMAT по геометрии Даже самые подготовленные тестируемые могут испытывать сильное беспокойство в день экзамена. Следуйте этим советам, чтобы повысить свой балл и помочь вам справиться со сложными вопросами GMAT по геометрии.
#1: Используйте то, что знаете При ответе на все вопросы GMAT по геометрии начните с определения того, что вы знаете и что вам нужно выяснить. Используйте информацию, содержащуюся в вопросе и на любых диаграммах, чтобы лучше понять фигуру. Например, если вы знаете, что градусы двух разных углов треугольника равны 60 и 80 градусов соответственно, вы можете использовать эти знания для вычисления третьего угла. Чем больше у вас будет информации, тем больше вы сможете понять.
#2: Поиск связей в вопросах с несколькими фигурами Если на диаграмме присутствует более одной узнаваемой фигуры, между ними существует связь. Найдите, что одна из фигур говорит вам о другой. Возможно, диагональ квадрата равна радиусу круга. Или высота одного треугольника есть гипотенуза другого. Какой бы ни была связь, вероятно, это ключ к ответу на вопрос.
#3: Не думайте, что чертежи выполнены в масштабе Вы не можете предполагать, что диаграммы на GMAT соответствуют масштабу. Если вы предполагаете, что фигура является квадратом, а на самом деле это прямоугольник, вы можете допустить большие ошибки в своих вычислениях. Используйте только информацию, предоставленную вам на диаграмме или в самом вопросе.
#4: Создайте свою собственную диаграмму Если вы решаете вопрос, связанный с формой, но тест не дает вам диаграммы, сделайте свою собственную. Создание собственной диаграммы поможет вам лучше визуализировать вопрос. Вы также можете перерисовать диаграмму на своем листе бумаги, даже если тест предоставляет вам диаграмму для просмотра. Иногда повторное рисование диаграммы поможет вам лучше понять рисунок, чтобы вам было легче решить проблему.
Практические вопросы GMAT по геометрии Одной из наиболее важных частей подготовки к GMAT является практика решения реальных вопросов GMAT. Решая реальные вопросы по геометрии GMAT, вы сможете подготовиться к содержанию, которое вы действительно увидите на тесте. В этом разделе я познакомлю вас с четырьмя реальными примерными вопросами GMAT, в которых используются понятия геометрии: два вопроса на решение задач и два вопроса на достаточность данных.
Пример решения задач. Вопрос 1 Прямоугольный пол размером 8 на 10 метров должен быть покрыт квадратами ковра размером 2 на 2 метра каждый. Если квадраты ковра стоят 12 долларов за штуку, какова общая стоимость количества квадратов ковра, необходимого для покрытия пола?
200 долларов 240 долларов 480 долларов 960 $ $1920 Для начала, поскольку в этой задаче нет диаграммы, мы хотим нарисовать свою собственную на клочке бумаги. Нарисуйте собственную диаграмму, чтобы лучше визуализировать проблему. Итак, нарисуйте прямоугольник и обозначьте стороны «8 м» и «10 м», так как мы знаем это из задачи. 92 = 20 долларов – общее количество квадратов ковра, необходимое для покрытия пола.
Хотите определить свои сильные и слабые стороны GMAT?
Наша запатентованная диагностическая оценка GMAT создает для вас индивидуальный план обучения, который проведет вас от регистрации до дня тестирования! Он включен в каждую учетную запись, и доказано, что он значительно увеличивает ваш счет .
Получите индивидуальную оценку в рамках 5-дневной безрисковой пробной версии прямо сейчас:
Стоимость каждого квадрата ковра составляет 12, поэтому на последнем шаге мы умножим 20 (количество необходимых квадратов ковра) на 12. (стоимость квадрата ковра), чтобы получить в общей сложности 240 долларов.
Правильный ответ: B.
Пример решения задач 2 На рисунке выше показан путь вокруг треугольного участка земли. Мэри прошла расстояние в 8 миль от $P$ до $Q$, а затем прошла расстояние в 6 миль от $Q$ до $R$. Если Тед прошел прямо из $P$ в $R$, на сколько процентов расстояние, которое прошла Мэри, превысило расстояние, которое прошел Тед?
30% 40% 50% 60% 80% Как всегда, давайте начнем с выяснения того, что этот вопрос задает нам. Нас просят сравнить расстояние, которое прошла Мэри, с расстоянием, которое прошел Тед. Для этого нам нужно сначала выяснить, как далеко они на самом деле прошли.
Итак, мы знаем, что Мэри прошла 14 миль, а Тед прошел 10 миль. Таким образом, расстояние, которое прошла Мэри, превысило расстояние, которое прошел Тед, на 4 мили (14–10 долл. США = 4 долл. США). 4 составляет 40 % от 10, поэтому правильный ответ — B. Мэри преодолела расстояние, пройденное Тедом, на 40 %.
Пример вопроса 1 о достаточности данных На рисунке выше точка D находится на AC. Какова градусная мера $\angle ∠ {BAC}$?
Мера НМТ равна 60°. Градусная мера BAC меньше градусной меры $\angle ∠ {BCD}$. Утверждение (1) ALONE достаточно, но одного утверждения (2) недостаточно. Утверждения (2) ОДНОГО достаточно, но одного утверждения (1) недостаточно. ОБЕИХ утверждений ВМЕСТЕ достаточно, но НИ ОДНОГО утверждения НЕ достаточно. Достаточно КАЖДОГО оператора. Утверждений (1) и (2) ВМЕСТЕ НЕ достаточно. Этот вопрос требует от нас определить величину внутреннего угла треугольника. Что касается вопросов о достаточности данных, мы всегда хотим ПЕРВЫМ обращаться к каждому утверждению отдельно. Начнем с утверждения (1).
Утверждение (1) утверждает, что угол BDC равен 60 градусам. Поскольку мы знаем, что $\angle ∠ {BDC}$ лежит на прямой, мы знаем, что прилежащий к ней угол ($\angle ∠ {BDA}$) можно прибавить к $\angle ∠ {BDC}$, чтобы получить 180°. Итак, мы можем найти меру угла BDA, используя уравнение: $180 – 60$ = $\угол ∠ {BDA}$. Следовательно, мы знаем, что мера $\angle ∠ {BDA}$ равна 120°.
Далее, мы знаем, что все углы внутри треугольника в сумме составляют 180°. Поскольку теперь мы знаем меру угла BDA (120) и меру $\angle ∠ {ABD}$ (20), мы можем найти третий угол в этом треугольнике, используя уравнение 180 – (20 + 120) = $ \угол ∠{ВАС}$. Итак, утверждения (1) достаточно. Теперь мы можем исключить ответ B и ответ E.
Теперь давайте перейдем к утверждению (2).
Утверждение говорит нам, что градусная мера $\angle ∠ {BAC}$ меньше градусной меры $\angle ∠ {BCD}$. Однако у нас недостаточно информации, чтобы выяснить, какова на самом деле мера любого угла. Таким образом, утверждения (2) недостаточно.
Тогда правильный ответ А; одного утверждения (1) достаточно.
Пример вопроса о достаточности данных 2 Каково значение $z$ на рисунке выше?
$х = у = 1$ $w = 2$ Утверждение (1) ALONE достаточно, но одного утверждения (2) недостаточно. Утверждения (2) ОДНОГО достаточно, но одного утверждения (1) недостаточно. ОБЕИХ утверждений ВМЕСТЕ достаточно, но НИ ОДНОГО утверждения НЕ достаточно. Достаточно КАЖДОГО оператора. Утверждений (1) и (2) ВМЕСТЕ НЕ достаточно. Помните, что при решении вопросов достаточности данных вы хотите сначала взять каждое утверждение отдельно.
Утверждение (1) говорит, что $x = y = 1$. Это означает, что и $x$, и $y$ = 1. Можем ли мы использовать это, чтобы найти значение z?
Итак, мы знаем, что значение z равно 1 + значение основания прямоугольного треугольника. В задаче нет информации, которая могла бы сказать нам, каково значение основания прямоугольного треугольника. Итак, значение базы может варьироваться, поэтому значение $z$ может варьироваться.
Это означает, что утверждения (1) недостаточно.
Теперь давайте сначала рассмотрим оператор (2) сам по себе. Утверждение (2) говорит, что $w = 2$. Однако, хотя мы знаем, что $w = 2$, мы ничего не знаем об остальных сторонах. Это означает, что все остальные стороны могут меняться, поэтому z тоже может меняться.
Вам не нужно решать вопрос достаточности данных. Вам нужно только знать, что вы можете! Итак, поскольку мы знаем, что можем решить вопрос, используя оба утверждения, правильный ответ — C. Оба утверждения вместе достаточны.
Как подготовиться к GMAT по геометрии Подготовка к GMAT может показаться утомительной, потому что нужно просмотреть много материала. Хорошей новостью является то, что выполнение хорошо продуманного учебного плана поможет вам достичь ваших целей. Вот несколько советов по геометрии для GMAT.
#1: Используйте высококачественные практические материалы Лучший способ подготовиться к GMAT – использовать в своей подготовке настоящие вопросы по геометрии GMAT. . Вопросы по геометрии Real GMAT будут имитировать стиль и содержание GMAT. Например, вам придется использовать более одного навыка в вопросе или вы попрактикуетесь, используя свои навыки геометрии в вопросах достаточности данных, которые являются уникальными для GMAT. Использование таких ресурсов, как GMATPrep или Официальное руководство GMAT, даст вам доступ к реальным, устаревшим вопросам GMAT.
Как вы могли заметить из наших практических вопросов, вы редко встретите прямой вопрос на GMAT, который просто просит вас использовать свои навыки геометрии. Вам, вероятно, придется объединить свои знания геометрии со своими знаниями арифметики или числовых свойств или соотношений… или всего вышеперечисленного! Практика вопросов в стиле GMAT (настоящих, устаревших вопросов GMAT, если вы можете их получить) даст вам возможность попрактиковаться в использовании нескольких навыков в одном вопросе.
#2: Запомните важные формулы Как я уже упоминал ранее, вы не сможете использовать шпаргалку по формулам на GMAT. Вам придется запомнить все формулы, которые вам понадобятся в день экзамена. Использование карточек — отличный способ расширить свои знания, чтобы вы могли быстро вспомнить и использовать важные формулы в день экзамена.
 07KB
07KB 52KB
52KB 75KB
75KB 18KB
18KB
 21MB
21MB 98KB
98KB 12KB
12KB
 07KB
07KB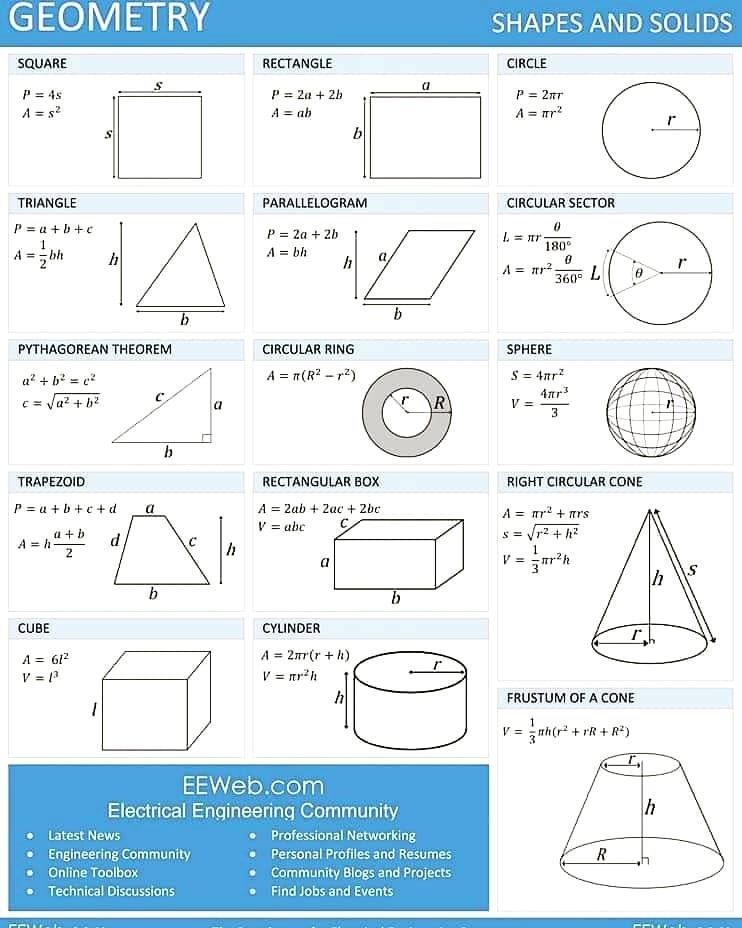 52KB
52KB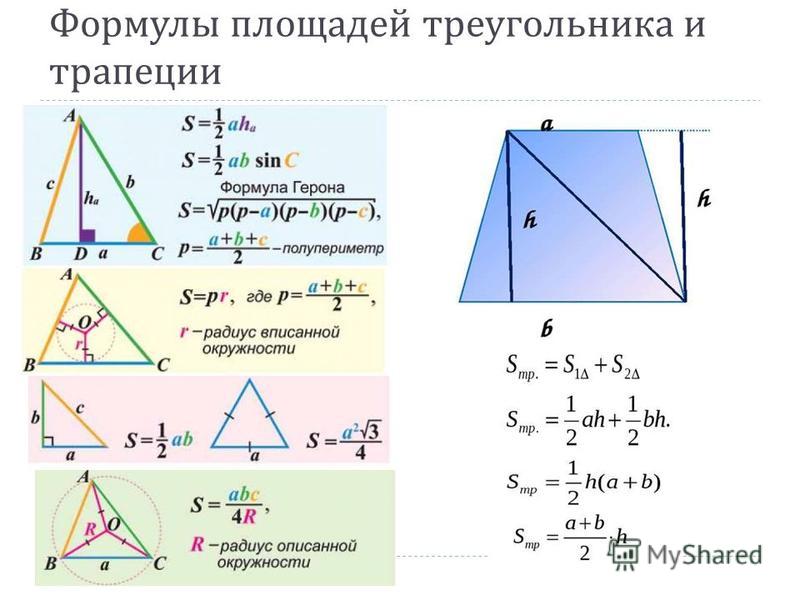 75KB
75KB 18KB
18KB
 21MB
21MB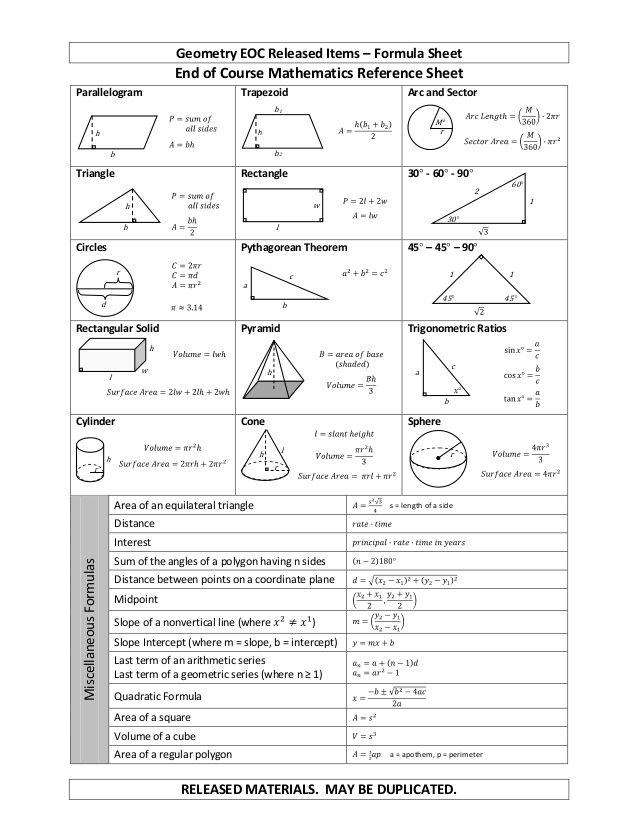 98KB
98KB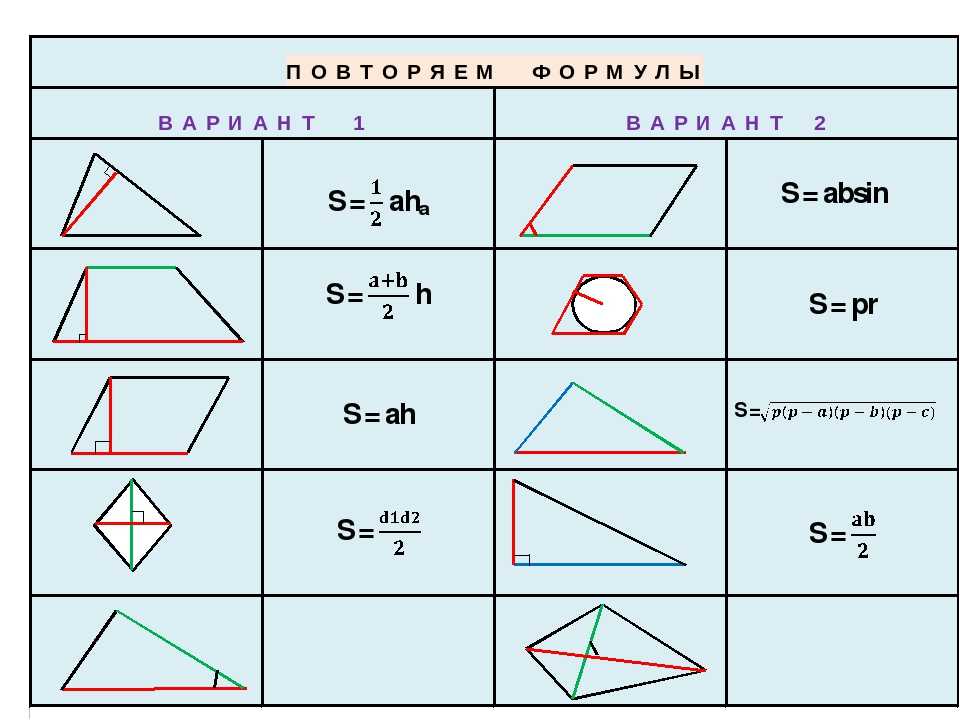 12KB
12KB