Геометрия объемные фигуры: Основные геометрические фигуры 🟢🟨🔺 и их названия

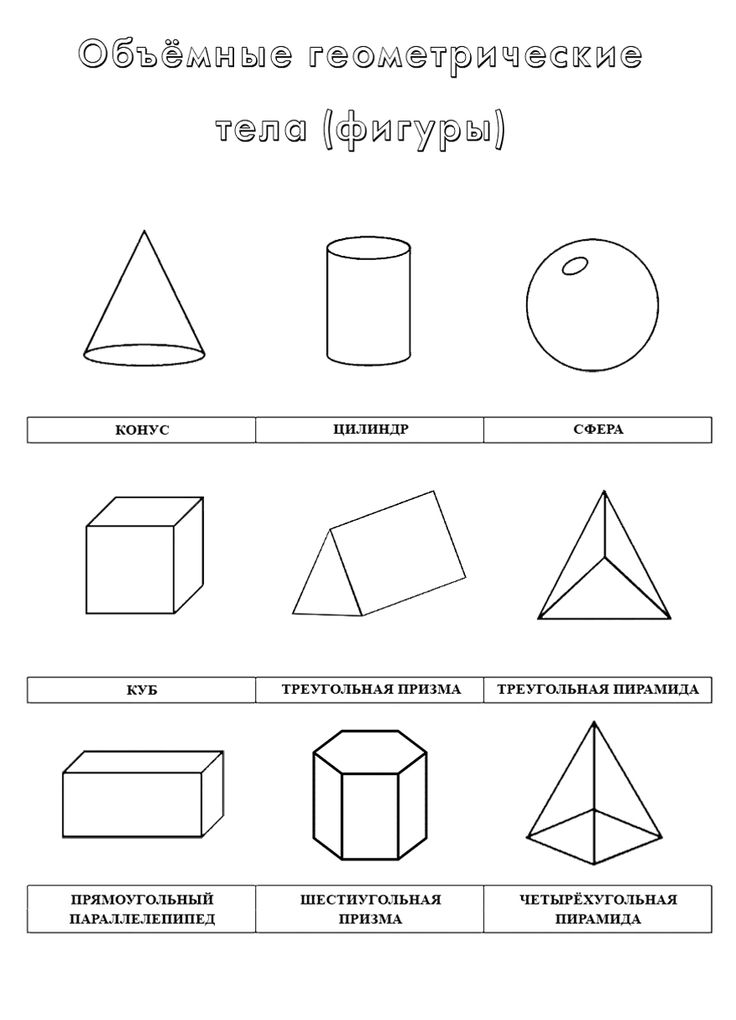
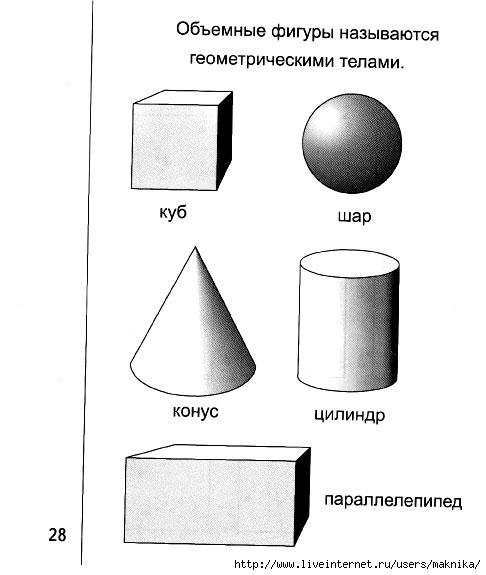
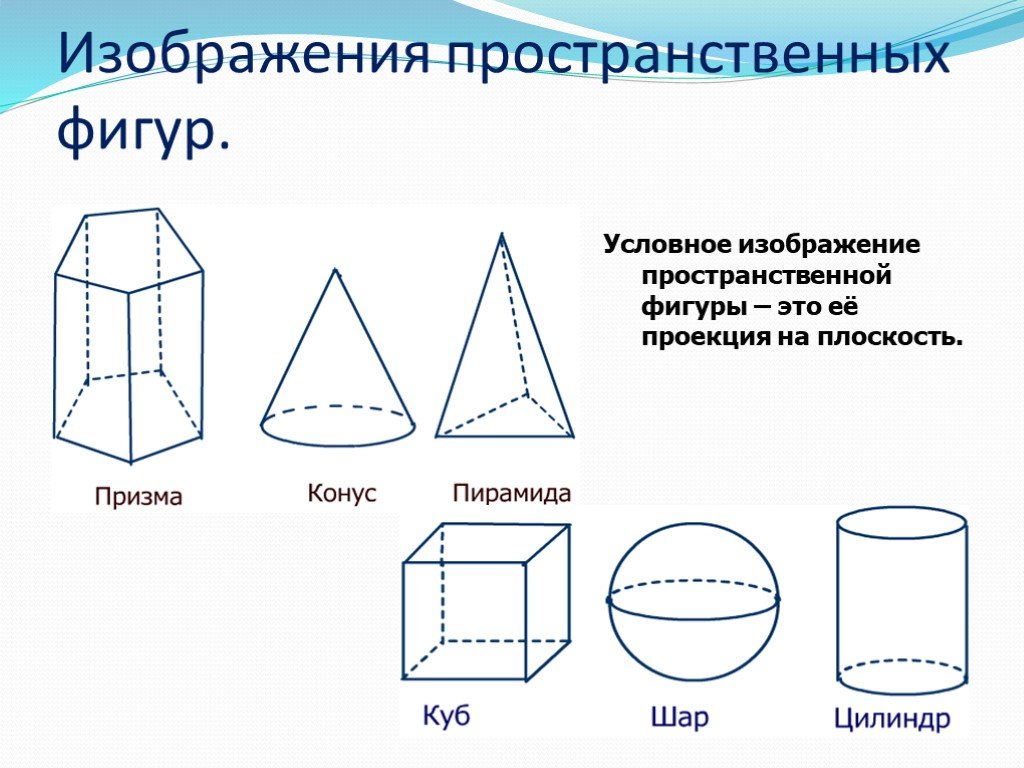
Тест по математике «Геометрия для детей.Объёмные фигуры».3 класс УМК «Школа России».

Стартовал зимний сезон олимпиад для учителей, учеников и дошкольников. Успейте принять участи по сниженной стоимости…

 

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

В тесте представлены задания на формирование у детей геометрических представлений об объёмных фигурах.

Тест поможет ученику в интересной интерактивной форме овладеть системой геометрических знаний и умений. Тест соответствует ФГОС НОО. Вариант 3.

Вопрос 1

Указать объёмную геометрическую фигуру:

Варианты ответов

• круг
• шар
• конус
• овал

Вопрос 2

Указать название фигуры:

Варианты ответов

• треугольник
• конус
• пирамида
• призма

Вопрос 3

Указать ряд геометрических фигур:

Варианты ответов

• Шар, куб, пирамида.
• Шар, куб, треугольник.
• Круг, треугольник,квадрат.
• Шар, куб, конус.

Вопрос 4

Указать, какую геометрическую фигуру имеет этот предмет:

Варианты ответов

• прямоугольник
• параллелепипед
• квадрат
• шар

Вопрос 5

Указать, какую объёмную фигуру имеет мяч:

Варианты ответов

• круг
• шар
• конус
• овоид

Вопрос 6

Указать фигуру:

Варианты ответов

• конус
• треугольник
• тетраэдр
• пирамида

Вопрос 7

Указать фигуру:

Варианты ответов

• трапеция
• призма
• квадрат
• куб

Вопрос 8

Указать, какой фигуры нет среди остальных:

Варианты ответов

• куб
• шар
• призма
• пирамида

Вопрос 9

Указать объёмную геометрическую фигуру:

Варианты ответов

• шар
• овал
• эллипсоид
• овоид

Вопрос 10

Указать название объёмной фигуры:

Варианты ответов

• призма
• многоугольник
• пятиугольник
• параллелепипед

Вопрос 11

Указать фигуру:

Варианты ответов

• треугольник
• конус
• призма
• шар

Вопрос 12

Указать, какую фигуру имеет ёлочная игрушка:

Варианты ответов

• конус
• шар
• круг
• куб

Вопрос 13

Указать название объёмных фигур:

Варианты ответов

• Треугольник, квадрат.
• Конус, куб.
• Пирамида , куб.
• Треугольник, куб.

Вопрос 14

Указать ,какую объёмную фигуру имеет огурец:

Варианты ответов

• эллипсоид
• овоид
• овал
• шар

Вопрос 15

Указать объёмную геометрическую фигуру:

Варианты ответов

• прямоугольник
• куб
• призма
• параллелепипед

Пройти тест

Сохранить у себя:

© 2020, Бойко Ирина Валентиновна  226

Геометрические фигуры плоские и объёмные

Цели урока:

• Познавательная: создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
• Коммуникативная: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного  отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
• Регулятивная: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых  операций, корректировать свою деятельность.
• Личностная: создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.

Планируемые результаты:

личностные:

• формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
  самостоятельность в приобретении новых знаний и практических умений;
• формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.

метапредметные:

• овладение навыками самостоятельного приобретения новых знаний;
• организация учебной деятельности, планирования;
• развитие теоретического мышления на основе формирования умений устанавливать факты.

предметные:

• усвоить  понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.

УУД общенаучные:

• поиск и выделение необходимой информации;
• применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.

УУД личностные:

• оценивать свои и чужие поступки;
• проявление доверия, внимательности, доброжелательности;
• умение  работать в паре;
• выражать  положительное отношение к процессу познания.

Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи,  Толковый  словарь.

Тип урока: изучение нового материала.

Методы:  словесные, исследовательские, наглядные, практические.

Формы работы:  фронтальная, групповая, парная, индивидуальная.

1. Организация начала урока.

Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!

2. Актуализация знаний.

Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!

Чтобы дойти до цели, надо прежде всего идти.

Перед вами высказывание, прочитайте. Что означает это высказывание?

(Чтобы чего-то добиться, нужно что-то делать)

— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.

— Начнем наш путь к достижению цели сегодняшнего урока.

3.  Подготовительная работа.

— Посмотрите на экран. Что вы видите? (Геометрические фигуры)

Назовите эти фигуры.

— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)

— У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.

— По какому признаку вы разделили эти фигуры?

• Плоские и объемные фигуры
• По основаниям объемных фигур

— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?

—  Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)

—  Чему мы должны научиться на уроке?

4. «Открытие» нового знания в практической  исследовательской работе.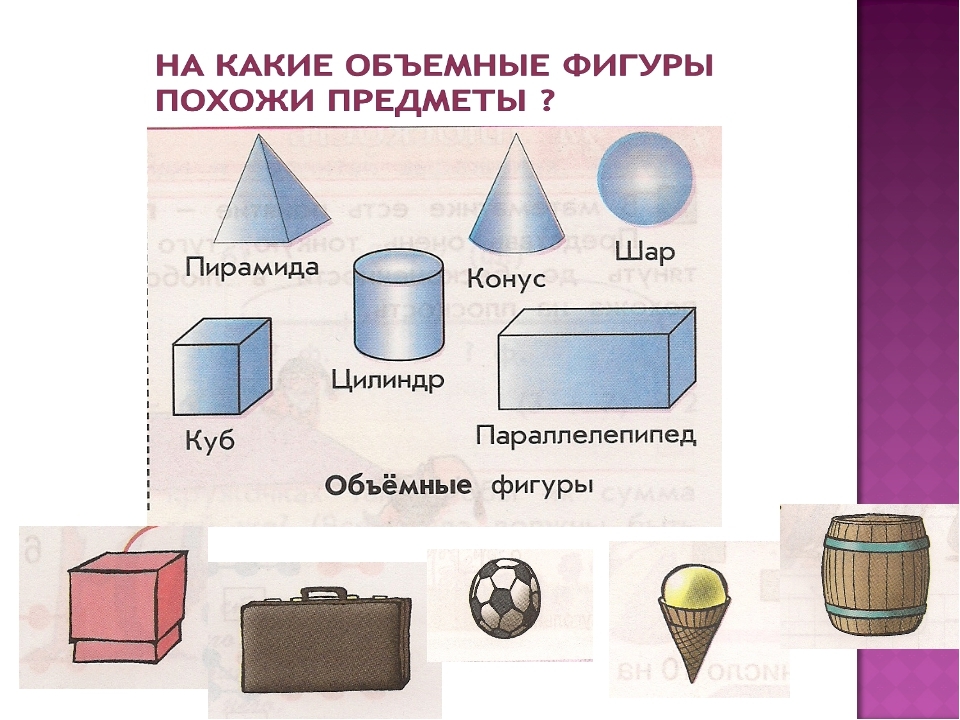

(Учитель показывает куб и квадрат.)

—  Чем они похожи?

—  Можно ли сказать, что это одно и тоже?

—  Чем же отличается куб от квадрата?

—  Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)

—  Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?

! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)

—  Можно ли куб полностью (весь) прижать к парте? Проверим.

—  Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?

! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)

ВЫВОДЫ:  Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)

ПЛОСКИЕ

• Можно целиком расположить на одной плоской поверхности.
  

ОБЪЁМНЫЕ

• занимают определённое пространство,
• возвышаются над плоской поверхностью.
  

Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.

4. Открытие новых знаний.

1. Назовите фигуры, изображенные на рисунке.

— Какую форму имеют основания этих фигур?

— Какие еще формы можно увидеть на поверхности куба и призмы?

2. Фигуры и линии на поверхности объемных фигур имеют свои названия.

 

 

— Предложите свои названия.

— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.

— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.

Работа с тетрадями: чтение нового материала

Соотнесение реальных объектов и объёмных тел.

— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.

+ Коробка – параллелепипед.

• Яблоко – шар.
• Пирамидка – пирамида.
• Банка – цилиндр.
• Горшок из-под цветка — конус.
• Колпачок – конус.
• Ваза – цилиндр.
• Мяч – шар.

5. Физминутка.

1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.

(Ученики «обхватывают» руками и гладят воображаемый шар.)

А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.

Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками  по боковой  поверхности.

Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!

6. Групповая работа:

(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед. Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1.  (Для изучения параллелепипеда)

Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .

Группа 2.  (Для изучения пирамиды)

Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .

Группа 3.  (Для изучения куба)

Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .

Далее каждая группа выступает, представляя свою объемную фигуру другим.

7. Решение кроссворда

8. Итог урока. Рефлексия деятельности.

Решение кроссворда в презентации

— Что нового вы для себя сегодня открыли?

+ Все геометрические фигуры можно разделить на объёмные и плоские.

+ А я узнал названия объёмных фигур

Трехмерные фигуры: определение, площадь и пример

Возможно, вы читаете это перед своим компьютером. Или, может быть, у вас есть стакан воды рядом с вами.

Если вы посмотрите на любой из этих объектов, которые вас окружают, станет ясно, что это объекты в 3D. Но каково математическое определение трехмерной фигуры?

В этой статье мы узнаем больше о трехмерных фигурах и их применении.

Что такое трехмерная фигура?

Трехмерная фигура представляет собой геометрическое тело с тремя пространственными измерениями: длина , ширина и глубина .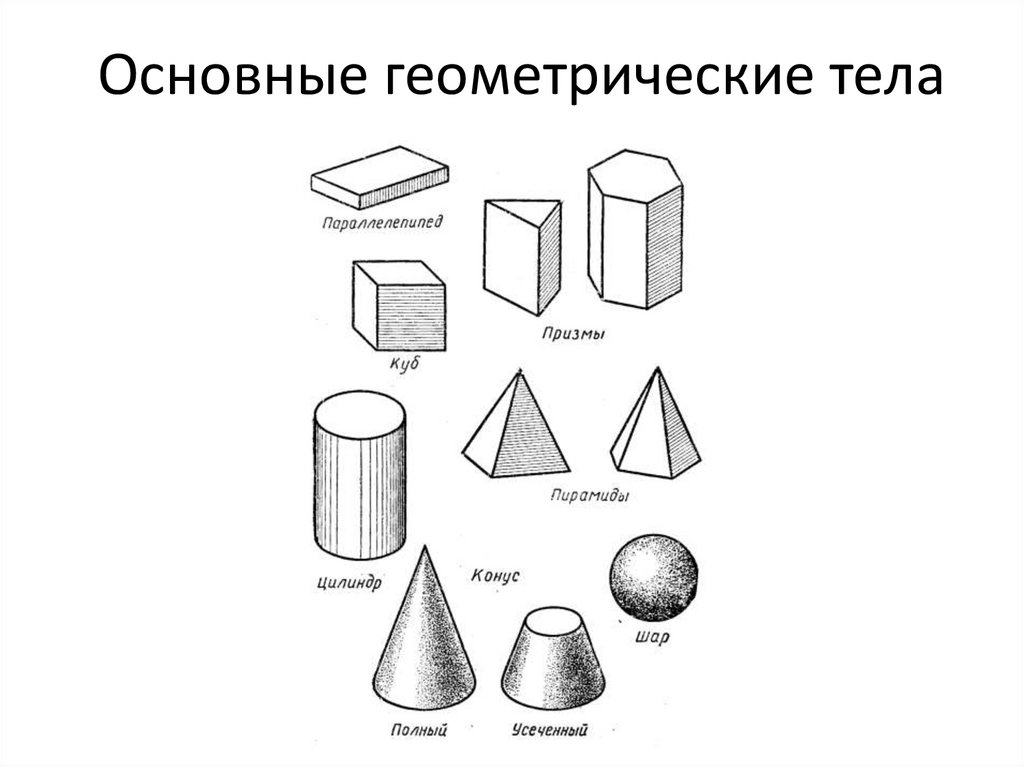 Иногда глубину называют высотой.

Например, представьте, что вы берете коробку из определенной службы доставки.

Если вы поместите коробку таким образом, что сможете наблюдать только одну из ее граней, вы будете наблюдать плоскую поверхность в 2D, а затем вы будете наблюдать только длину и ширину этой грани.

Но если вы немного повернете его, то увидите, что коробка тоже имеет некоторую глубину. Это то, что мы имеем в виду с трехмерными фигурами.

Как вы могли заметить, глядя на коробку, эти трехмерные фигуры имеют объем . В математике мы определяем объем как количество пространства внутри замкнутой поверхности.

Снова возьмите коробку, и если вы откроете ее сейчас, объем будет равен количеству места внутри коробки. Позже мы узнаем, как вычислить этот объем.

Эти геометрические фигуры обычно, за некоторыми исключениями, которые мы будем использовать, имеют граней , которые являются поверхностями с определенной площадью поверхности, ограничивающими фигуру. Эти лица соединяются в вершин , которые являются точками объединения.

Наконец, линии, ограничивающие эти поверхности и контур геометрической фигуры, называются ребрами . Мы бы сравнили их со сторонами двумерных фигур.

Примеры трехмерных фигур

Отвлекшись от этой статьи и осмотревшись вокруг, вы, вероятно, обнаружите множество трехмерных фигур с различной структурой. От кровати до стула, до стола или даже до книг, которые вы используете для учебы. Все они представляют собой трехмерные фигуры, поскольку они имеют 3 измерения, о которых мы упоминали ранее; длина, ширина и глубина, а также потому, что они имеют объем.

Мы различаем обычные и неправильные трехмерные фигуры. Мы сосредоточимся на обычных трехмерных фигурах, так как они более распространены в математике.

Конус

Конус — это трехмерная фигура, которую мы получили бы, если бы прямоугольный треугольник (с одним углом, равным 90º) повернулся с фиксированной одной из сторон, таким образом, мы получили бы форму в 3d . Эта фигура обычно имеет круглое основание и вершину , к которой сужается боковая поверхность конуса.

Основание не обязательно должно быть кругом, это может быть и другая двухмерная круглая фигура, например овал. Вы можете наблюдать эту форму в реальном мире, когда смотрите на дорожные конусы.

Пирамида

Эта фигура похожа на конус, но в этом случае основание не имеет круглой формы. Основание представляет собой двумерную фигуру с тремя или более сторонами, например треугольник, квадрат, прямоугольник и т. д.

Поскольку геометрическая форма основания может варьироваться, изменяется и количество ребер. Все его поверхности, сколько бы их ни было, сужаются к вершине.

Известные египетские пирамиды являются одним из примеров этих геометрических форм, в данном случае они имеют квадратное основание.

Куб

Эта геометрическая фигура состоит из шести равновеликих граней, три из которых сходятся в одной вершине, всего восемь вершин и двенадцать ребер.

Примером куба является игральная кость. Если вы заметите это, все грани обычной игральной кости имеют одинаковую поверхность, и каждая ее вершина работает как объединение трех разных граней.

Прямоугольная призма

Похожа на куб, так как также имеет восемь вершин, двенадцать ребер и шесть граней, но в этом случае не все грани равны. Каждая грань равна своей противоположности, поэтому у нас есть пары равных граней.

Примером прямоугольной призмы может быть ящик или даже коробка, хотя иногда они имеют форму куба.

Существуют и другие виды призм, в зависимости от формы основания и противоположной грани. Например, если эти грани имеют форму треугольника, это треугольная призма , которая будет иметь всего пять граней вместо шести, как у прямоугольной призмы. Но это основание (и противоположная грань) может иметь другую двумерную фигуру, которая дает разные типы призм: пятиугольные призмы , шестиугольные призмы и т. д.

Цилиндр

Форма этой фигуры может напомнить вам прямоугольной призмы, но в данном случае она имеет две поверхности, которые называются вершиной и низ (или основание) фигуры, состоящей из двухмерных круглых фигур.

У этой фигуры нет вершины. Поверхность, соединяющая эти две грани, по существу представляет собой прямоугольник, но изогнутый.

Такие геометрические фигуры можно найти в банках или стаканах.

Сфера

Футбол, баскетбол или, может быть, если мы не хотим ограничиваться только спортивным миром: пузырь. Все эти объекты имеют одну общую черту: они являются сферами.

Эти геометрические фигуры получаются, если мы делаем круг, который представляет собой двумерную фигуру, повернутую вокруг своего диаметра. Объем, описываемый этим оборотом, определяется как сфера.

Как и в случае с кругом в двух измерениях, все точки поверхности находятся на одинаковом расстоянии от точки в центре фигуры.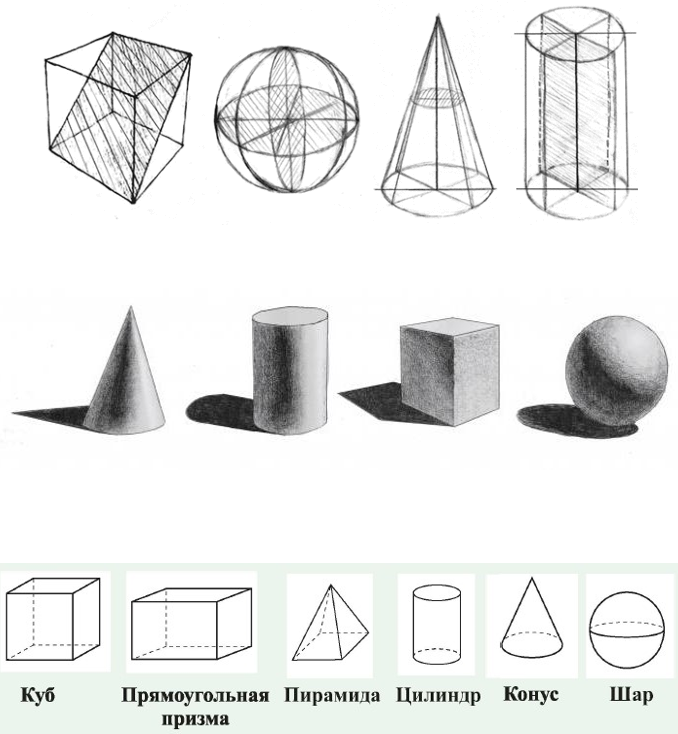 Это расстояние называется радиусом . Если мы проследим расстояние между двумя точками поверхности сферы, проходящей через ее центр, то это расстояние называется диаметр сферы, что соответствует удвоенному радиусу.

Формулы трехмерных фигур

При работе с трехмерными фигурами есть некоторые вещи, которые мы могли бы знать о них. В частности, нас интересуют две характеристики.

Первая — это площадь фигуры.

Площадь фигуры – это площадь поверхности, которую занимают грани фигуры. Единицами площади поверхности фигуры являются единицы площади, стандартными являются квадратные метры (м2).

Чтобы получить общую площадь поверхности фигуры, мы должны просуммировать площади каждой грани фигуры. Не следует путать площадь поверхности фигуры с ее объемом. Площадь состоит только из поверхности граней, независимо от того, что находится внутри них.

С другой стороны, у нас есть объем рисунка.

Объем фигуры – это количество пространства внутри поверхности, ограниченной гранями фигуры. Единицами объема являются единицы объема, стандартными являются кубические метры.

Если мы снова возьмем коробку, о которой мы говорили в этой статье, вы увидите, что поверхность картона, используемого для всех граней, соответствует площади поверхности коробки, но пространство внутри коробки соответствует к его объему.

Давайте посмотрим, как выглядят некоторые математические уравнения для трехмерных фигур, которые мы видели раньше.

Площадь и объем конуса

Площадь поверхности трехмерной фигуры равна сумме площадей ее граней.

Для конуса площадь поверхности его основания равна , где r — радиус окружности. Площадь боковой грани равна , будучи г расстояния между любой точкой ребра основания до вершины. Таким образом, площадь поверхности конуса обычно выражается как

.

Объем конуса определяется по следующей формуле:

,

, где h — расстояние от центра основания до вершины.

Площадь и объем пирамиды

В этом случае формулы площади и объема будут зависеть от количества ребер, которые имеет основание.

Например, если пирамида имеет квадратное основание, площадь поверхности пирамиды будет равна сумме площади квадрата и суммы площадей каждого треугольника, соединяющего вершины. В общем, мы можем выразить площадь поверхности пирамиды как

Будьте осторожны, так как основание не обязательно должно быть правильным, и площадь поверхности треугольников, соединяющихся с вершиной, тоже не обязательно должна быть правильной.

Объем пирамиды также зависит от ее основания. Для квадратной пирамиды объем вычисляется по формуле:

равно

Площадь и объем прямоугольной призмы и куба

В этом случае, поскольку прямоугольная призма и куб образованы шестью гранями, для получения общая площадь поверхности фигуры, нам просто нужно суммировать площади каждой грани.

Для куба все шесть граней будут иметь одинаковую площадь, но для прямоугольной призмы, поскольку каждая грань равна своей противоположности, есть три разных значения. Общее математическое выражение для площади поверхности прямоугольной призмы:

где A ₁ , A ₂ и A _{3 являются этими тремя различными областями. Площадь прямоугольника равна.}

Объем этих фигур равен произведению трех ребер; длина, ширина и глубина призмы, например,

В случае куба, поскольку все стороны имеют одинаковую длину, мы имеем

Площадь и объем цилиндра

Цилиндр состоит из двух окружностей, которые являются верхней и нижней частью фигуры, и изогнутого прямоугольника. Следовательно, если площадь круга равна , сумма всех площадей равна

, где h — высота от одной точки основания до точки наверху в том же положении.

Объем цилиндра описывается следующим уравнением:

Площадь и объем сферы

Известная нам сфера представляет собой другой тип геометрической фигуры, так как она не образована объединением разных граней. Вот почему нам нужно математическое выражение для вычисления площади его поверхности:

. А объем сферы определяется по следующей формуле:

.

Примеры задач на трехмерные фигуры

Теперь давайте рассмотрим некоторые примеры задач, с которыми вы можете столкнуться на трехмерных фигурах.

Найдите объем воды, необходимый для заполнения цилиндрического стеклянного стакана высотой 12 см и радиусом 7 см. Брать .

Решение

Используя

, затем

Кохе хочет сделать коническую кепку радиусом 14 см и высотой 20 см для 8 друзей в преддверии своего дня рождения. Какова общая площадь картонной бумаги, чтобы сделать все 8 для своих друзей?

Решение

Сначала найдем общую площадь поверхности одного конического колпачка.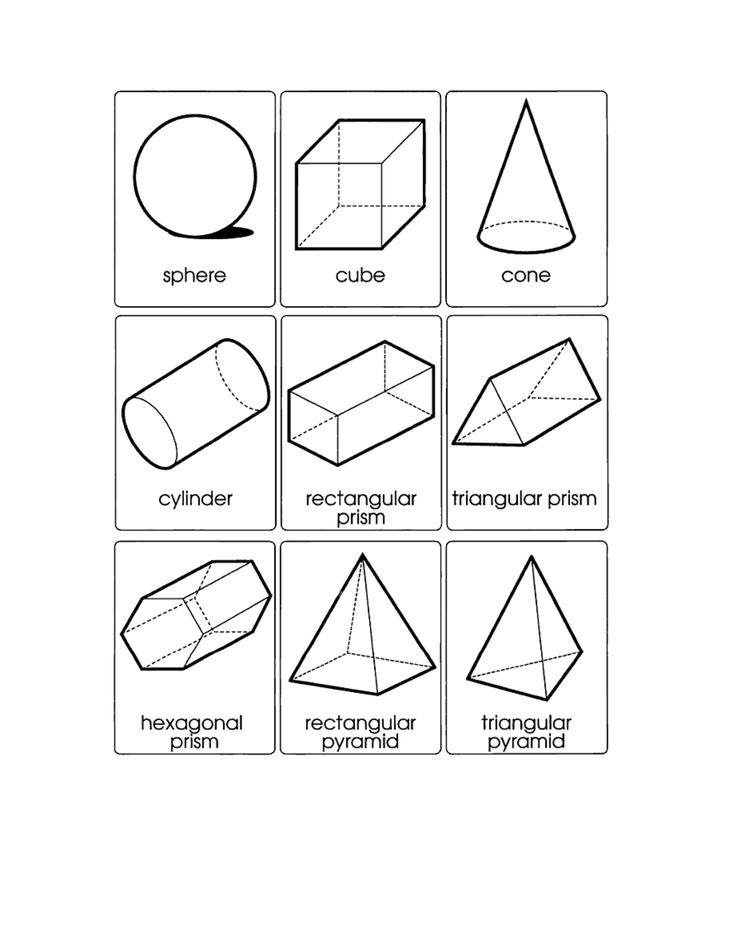 Использование

В этом случае g — высота конуса, равная 20 см, а r — 14 см. Следовательно,

Но это всего лишь площадь 1 конуса, вам нужно найти площадь 8 конусов. Таким образом,

Следовательно, Кохе понадобится картон с общей площадью поверхности 11 968 см ² , чтобы успешно изготовить 8 конических крышек для своих друзей перед вечеринкой по случаю его дня рождения.

Трехмерные фигуры. Ключевые выводы

• Трехмерные фигуры состоят из трехмерных фигур; длина, ширина и глубина. Иногда глубину называют высотой.
• Эти фигуры имеют образующие их поверхности, называемые гранями. Грани соединяются в вершинах. А линии, ограничивающие эти грани, называются ребрами.
• Существует множество различных примеров трехмерных фигур. Некоторые из наиболее часто используемых фигур — конус, пирамида, куб, призмы, цилиндр и сфера.
• Некоторые трехмерные фигуры, такие как конус, пирамида или сфера, получаются, если заставить двухмерную фигуру вращаться вокруг одной из ее осей или ребер.
• Площадь трехмерной фигуры – это поверхность, занимаемая ее гранями. Как правило, площадь трехмерной фигуры получается путем суммирования площадей всех ее граней. Объем трехмерных фигур — это пространство, которое находится внутри поверхности, ограниченной ее гранями. Чтобы получить его, мы используем различные формулы относительно фигуры, объем которой мы хотим рассчитать.

Части трехмерных фигур

В геометрии трехмерная фигура — это объемная фигура или объект или форма с тремя измерениями — длиной, шириной и высотой. В отличие от двумерных фигур трехмерные фигуры имеют толщину или глубину.

Атрибутами трехмерной фигуры являются грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.

Ниже приведены части трехмерной фигуры.

Грани :

Плоские поверхности трехмерных фигур называются гранями.

Ребро :

Отрезок, на котором сходятся две грани, называется ребром.

Вершина :

Вершина — это точка, в которой встречаются 3 ребра.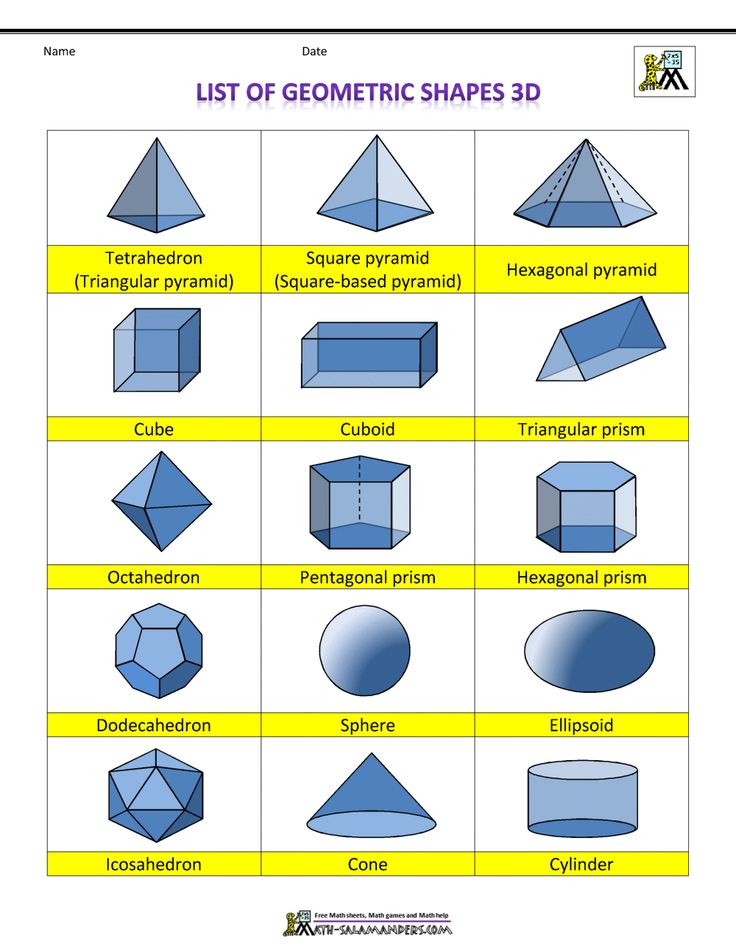

Пример 1 :

Назовите следующую трехмерную фигуру. Также найдите количество граней, ребер и вершин.

Решение :

Название формы = Треугольная пирамида

Грани :

Глядя на приведенный выше рисунок, мы узнаем, что существует четыре грани.

Имя каждой грани: Сторона 1 = ABD  Сторона 2 = ABC Сторона 3 = BCD Сторона 4 = ACD

Края :

Края — это прямые линии, используемые для рисования изображения.

Чтобы нарисовать вышеприведенную треугольную пирамиду, мы использовали 6 ребер. Это

AC, AB, BC, BD, CD и AD.

Вершины :

Вершины — это углы, где сходятся 3 ребра.

Здесь стороны AC, AB и AD пересекаются в точке A. Значит, «A» — одна из вершин данной треугольной пирамиды. Точно так же ребра B, C и D.

Итак, данная треугольная пирамида имеет 4 грани, 6 ребер и 4 вершины.

Пример 2 :

Назовите следующую трехмерную фигуру. Также найдите количество граней, ребер и вершин.

Решение :

Название фигуры = Куб

Грани :

Наблюдая за приведенным выше рисунком, мы узнаем, что существует шесть граней.

Имя каждой грани: Сторона 1 = ABCD Сторона 2 = ACEF Сторона 3 = CDEF Сторона 4 = BDHG Лицо 5 = ABEH (Задняя сторона) Лицо 6 = CDFG (Передняя сторона)

Края : Края — это прямые линии, используемые для рисования изображения. Здесь мы использовали 12 прямых линий, чтобы нарисовать куб. AB, AC, CD, BD, AE, CF, EF, FG, EH, GH, DG, BH

Вершины : Вершины — это углы, в которых сходятся 3 ребра. Вершины: A, B, C, D, E, F, G, H. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт