Основные правила математики. Геометрия. Теоремы, определения. 7 класс
Основные правила математики. Геометрия. Теоремы, определения. 7 класс | Сайт учителя математики Косыхиной Н.В.-
Репетитор по математике
Косыхина Наталья Владимировна - /whatsapp +7(908)682-97-49
Основные правила математики. Геометрия. Теоремы, определения. 7 класс
Геометрия — одна из самых древних наук, она возникла очень давно, еще до нашей эры .В переводе с греческого слово геометрия означает землемерие (гео- по-гречески земля, а метрео — мерить)
Школьный курс геометрии делится на планиметрию и стереометрию
В планиметрии рассматриваются свойства фигур на плоскости. Примерами таких фигур являются отрезки ,треугольники, прямоугольники.
В стереометрии изучаются свойства фигур в пространстве ,таких ,как параллелепипед ,шар, цилиндр.
Через любые две точки можно провести прямую и притом только одну
Взаимное расположение прямых:
- Если нет общих точек, то прямые параллельны
- Есть общая точка, то прямые пересекаются.
- Равные углы имеют равные градусные меры.
- Меньший угол имеет меньшую градусную меру.
- Развернутый угол равен 180 градусов.
- Неразвернутый угол — меньше 180 градусов
- Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов
- Угол называется прямым, если он равен 90 градусов.

- Острым углом называют, если он меньше 90 градусов.
- Тупым углом называют, если он больше 90 градусов.
- Cмежными углами называются два угла, у которого одна сторона общая ,а две другие являются продолжениями сторон друг друга.
- Сумма смежных углов равна 180 градусов.
- Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого
- Фигура, состоящая из трех точек, не лежащих на одной прямой и трех отрезков попарно соединяющих их, называется треугольником.
- Сумма длин трех сторон треугольника называется периметром.
- Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
- Отрезок биссектрисы угла треугольника ,соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
- Перпендикуляр ,проведенный из вершины треугольника к прямой ,содержащей противоположную сторону, называется высотой треугольника.
- Треугольник называется равнобедренным, если две его стороны равны.
- Треугольник, все стороны которого равны, называется равносторонним.
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
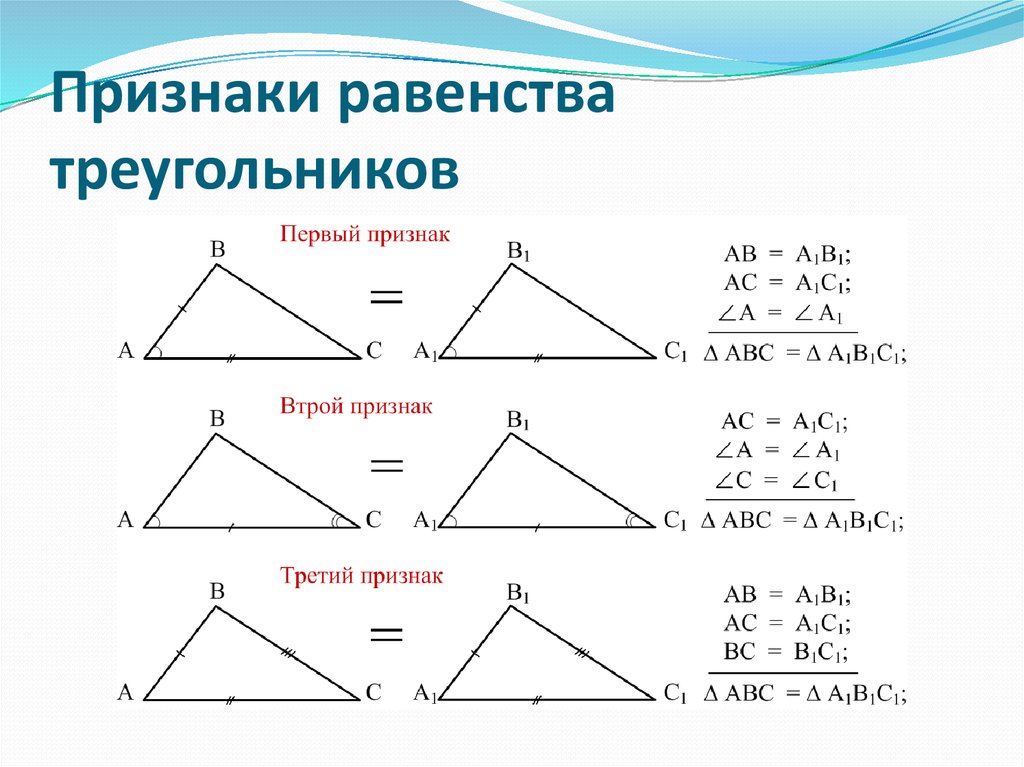
- Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольник, то такие треугольники равны
- Теорема 2. Если сторона и 2 прилежащих к ней угла одного треугольника равны стороне и 2 прилежащим к ней углам другого треугольник, то такие треугольники равны
- Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Отрезок, луч
Отрезком называют часть прямой, ограниченную двумя точками(концы отрезка)
Луч — это часть прямой ,имеющая начало, но не имеющая конца. Луч имеет направление.
Угол -это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла.
Угол называется развернутым, если обе его стороны лежат на одной прямой.
Любой угол разделяет плоскость на две части(полуплоскости).
Если угол неразвернутый, то одна из частей называется внутренней, а другая внешней областью этого угла.
Если угол развернутый, то любую из двух частей ,на которые он разделяет плоскость ,можно считать внутренней областью угла.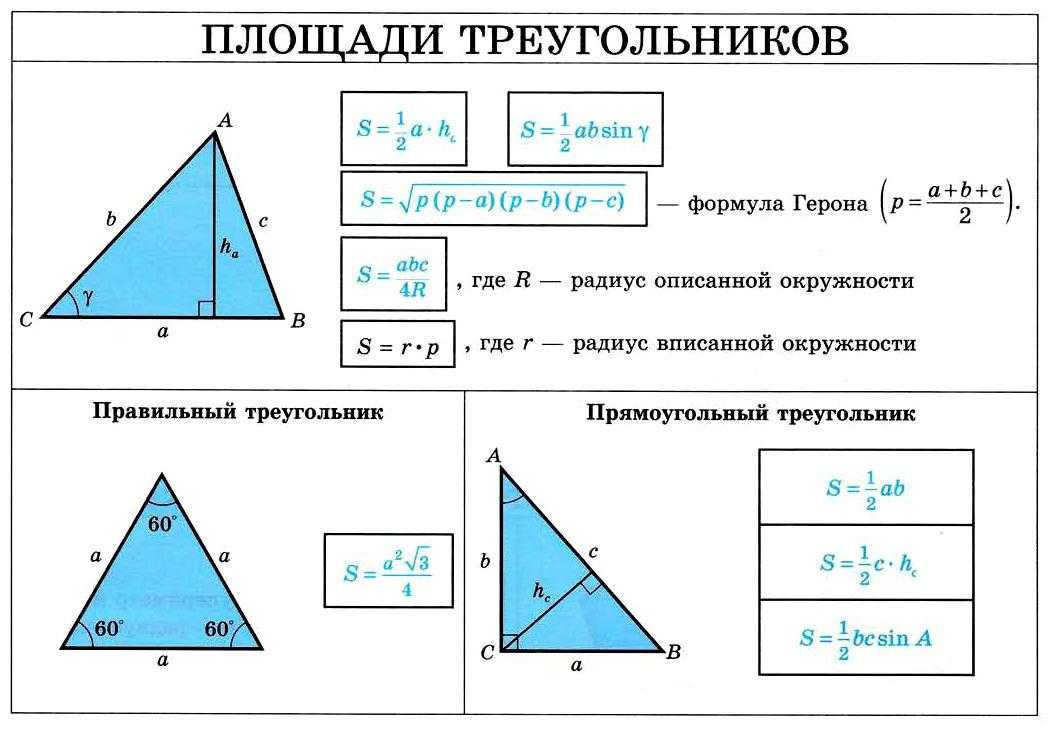
Фигуру, состоящую из угла и его внутренней области также называют углом.
Если луч исходит из вершины неразвернутого угла и проходит внутри угла, то он делит этот угол на два угла.
Равные фигуры, середина отрезка, биссектриса
Равными называют две фигуры, имеющие одинаковую форму и одинаковые размеры.
Две геометрические фигуры оказываются равными, если их можно совместить наложением.
Серединой отрезка называется точка отрезка, равно удаленная от концов отрезка ,т.е. это точка разбивает исходный отрезок на два равных.
Биссектрисой угла называют луч, исходящий из вершины угла и делящий его на два равных угла.
Единицы измерения отрезков, углов
Измерение отрезков основано на сравнении их с некоторыми отрезками. Выбрав единицу измерения , можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.

При измерении небольших расстояний, например расстояния между точками, изображенными на листе бумаги ,за единицу измерения принимают сантиметр и миллиметр. Расстояния между отдельными объектами в реальном мире измеряются в метрах, километрах и т.д.
Измерение углов аналогично измерению отрезков. Оно основано на сравнений их с углом, принятым за единицу измерения.
Обычно за единицу измерения углов применяют градус.
Градусной мерой угла называют положительное число, которое показывает, сколько раз градус и его части укладываются в данном угла.
Часть градуса называется минутой, часть минуты называется секундой.
Смежные и вертикальные углы
Перпендикулярные прямые
Две пресекающиеся прямые называются перпендикулярными, если они пересекаются под прямым углом.
Треугольник
Теоремой называют утверждение, справедливость которого устанавливается путем рассуждения.
Медиана, биссектриса, высота треугольника
Равнобедренный, равносторонний треугольники
Три признака равенства треугольников
Окружность
Для изображении окружности на чертеже пользуются циркулем.
- Окружностью называют геометрическая фигура ,состоящая из всех точек плоскости, расположенных на заданном расстоянии от заданной точки.
- Отрезок ,соединяющий две точки окружности ,называется хордой
- Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности.

- Формула длины окружности
- Формула площади круга
2018-2023
Словарь геометрических понятий 7-8 класс
Геометрия,7-9 Основные определения, теоремы, формулы
7 класс Глава I Начальные геометрические сведения
Первичные понятия: точка, прямая, плоскость, пространство, отрезок, луч, угол, равные фигуры, середина отрезка, биссектриса угла, измерение отрезков, измерение углов
Отрезок-часть прямой, ограниченная двумя точками.
Луч-часть прямой,ограниченная точкой с одной стороны и неограниченная с другой стороны.
Угол-часть плоскости, ограниченная двумя лучами, выходящими из одной точки.
Равные фигуры-фигуры, которые совпадают при наложении друг на друга.
Середина отрезка-точка на отрезке, делящая его пополам.
Биссектриса угла-луч,
выходящий из вершины угла и делящий его пополам.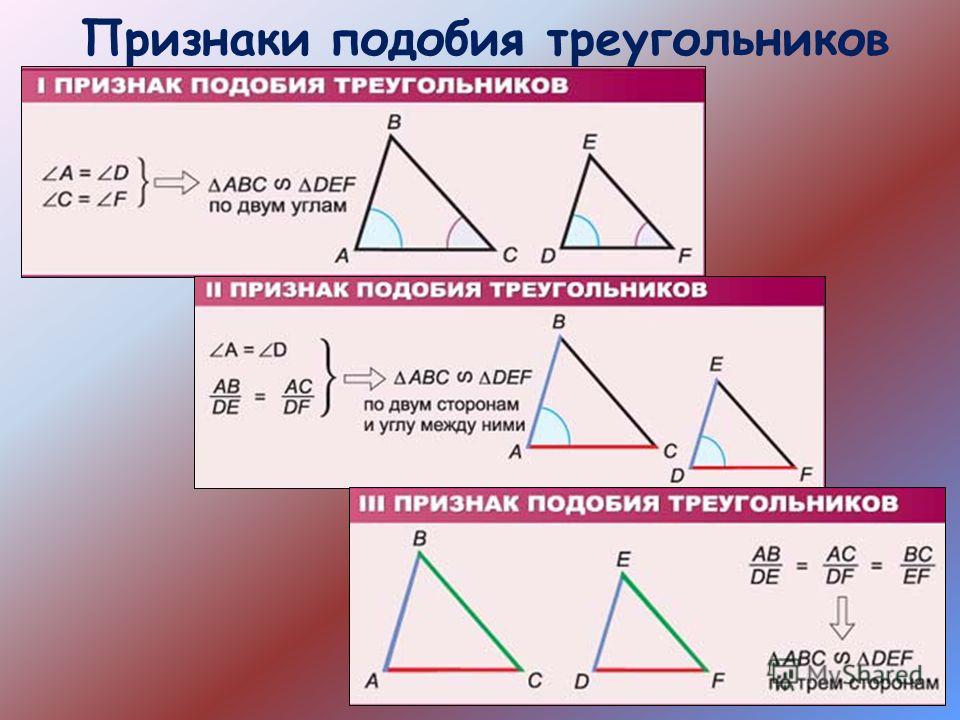
Единицы измерения длины отрезка: миллиметры, сантиметры, дециметры, метры, километры.
Единицы измерения углов: градус, минуты, секунды.
Длина отрезка-количество единиц измерения длины, вмещающихся между двумя концами отрезка.
Градусная мера угла-количество единиц измерения углов, вмещающихся между сторонами угла.
Прямой угол-угол,градусная мера которого равна 900.
Острый угол-угол,градусная мера которого меньше 900.
Тупой угол-угол,градусная мера которого больше 900,но меньше 1800.
Развёрнутый угол-угол,градусная мера которого равна 1800.
Смежные углы – это два угла, у которых одна сторона общая,а две других образуют прямую линию.
Свойство: сумма смежных углов равна 1800.
Вертикальные углы-два
угла, у которых стороны одного угла являются продолжением сторон другого.
Свойство: вертикальные углы равны.
Перпендикулярные прямые-прямые, которые при пересечении образуют прямой угол.
Параллельные прямые-прямые, лежащие в одной плоскости и не имеющие общих точек.
Глава II Треугольники
Треугольник-фигура, состоящая из трёх точек, соединённых между собой отрезками.Точки-вершины треугольника, отрезки-стороны треугольника.
Периметр – сумма длин всех сторон.
Теорема(первый признак равенства треугольников): если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Теорема: из точки,не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Медиана треугольника— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника—
отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой противоположной стороны.
Высота треугольника— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Равнобедренный треугольник-треугольник, у которого две стороны равные. Равные стороны – боковые, третья сторона – основание.
Равносторонний треугольник— треугольник, у которого все стороны равны.
Свойство:в равнобедренном треугольнике углы при основании равны.
Свойство:в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Теорема(второй признак равенства треугольников): если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема(третий признак равенства треугольников): если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Окружность-геометрическая
фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии
от данной точки-центра.
Радиус окружности-отрезок,соединяющий любую точку окружности с её центром.
Хорда-отрезок, соединяющий две любые точки окружности.
Диаметр-хорда, проходящая через центр.
Дуга – часть окружности, ограниченная двумя точками.
Основные задачи на построение циркулем и линейкой:
ü построение отрезка, равного данному
ü построение угла, равного данному
ü построение биссектрисы угла
ü построение середины отрезка
ü построение перпендикулярных прямых
Глава III Параллельные прямые
При пересечении двух прямых третьей прямо-секущей образуются следующие виды углов:
Ø накрест лежащие углы
Ø односторонние углы
Ø соответственные углы
Теорема(первый признак параллельности прямых):если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема(второй признак параллельности
прямых):если при пересечении двух прямых секущей
соответственные углы равны, то прямые параллельны.
Теорема(третий признак параллельности прямых):если при пересечении двух прямых секущей сумма внутренних односторонних углов равна углы равна 1800, то прямые параллельны.
Аксиома: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Теорема:если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Теорема:если две прямые параллельны третьей прямой, то они параллельны.
Теорема:если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Теорема:если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема:если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 1800.
Глава IV Соотношения между сторонами и углами треугольника
Теорема:
сумма внутренних углов треугольника равна 1800.
Внешний угол треугольника-угол, смежный с каким-либо внутренним углом треугольника.
Остроугольный треугольник-это треугольник, все внутренние углы которого острые.
Тупоугольный треугольник-это треугольник, у которого один из углов тупой.
Прямоугольный треугольник-это треугольник, у которого один из углов прямой.
Гипотенуза-это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Катеты-это стороны прямоугольного треугольника, образующие прямой угол.
Теорема:в треугольнике против большей стороны лежит больший угол.
Теорема:в треугольнике против большего угла лежит большая сторона.
Следствие:в прямоугольном треугольнике гипотенуза всегда больше катета.
Теорема(признак равнобедренного треугольника):если в треугольнике два угла равны, то он равнобедренный.
Теорема(неравенство треугольника):каждая
сторона треугольника меньше суммы двух других сторон.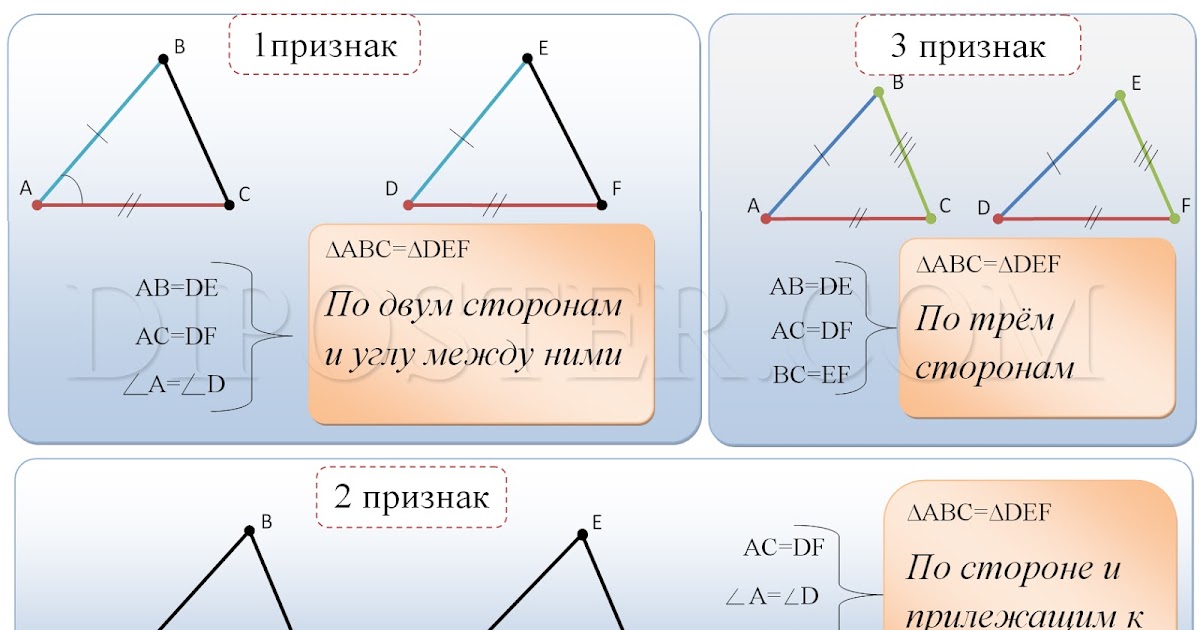
Свойство:сумма двух острых углов треугольника равна 900.
Свойство:катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
Свойство:если катет прямоугольного треугольника равен половине гипотенузы, то он лежит напротив угла в 300.
Теорема(признак равенства прямоугольных треугольников):если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):если катет и прилежащий к нему острый угол одного прямоугольного треугольника равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных
треугольников):если гипотенуза и острый угол одного
прямоугольного треугольника равны гипотенузе и острому углу другого
прямоугольного треугольника, то такие треугольники равны.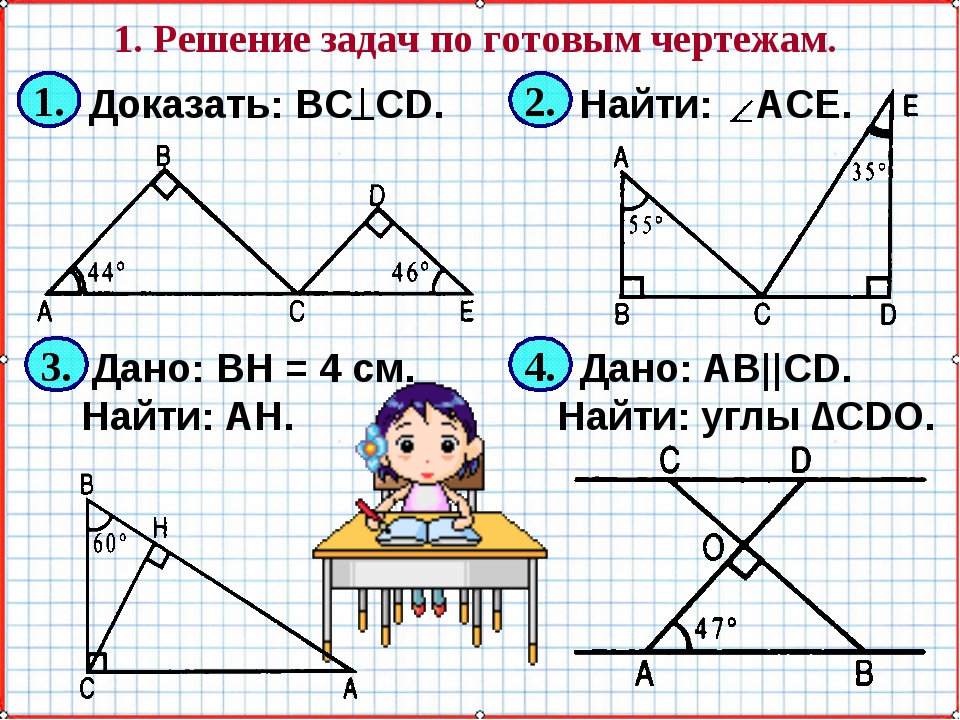
Теорема(признак равенства прямоугольных треугольников):если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на прямую.
Теорема:все точки каждой из двух параллельных прямых равноудалены от другой прямой.
8 класс. Глава V Четырёхугольники
Многоугольник-фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.
Диагональ-это отрезок, соединяющий две несоседних вершины многоугольника.
Выпуклый многоугольник— это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Теорема:Сумма
внутренних углов выпуклого n-угольника
равна (n-2)*1800.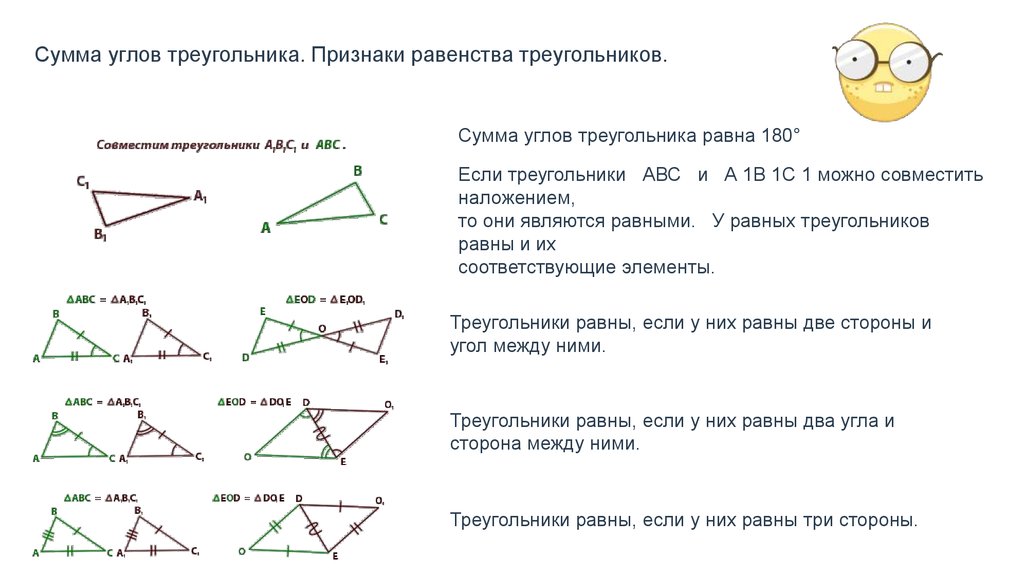
Параллелограмм— это четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство:диагонали параллелограмма точкой пересечения делятся пополам.
Теорема(признак параллелограмма):Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма):Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма):Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Трапеция-это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.
Равнобедренная трапеция-это
трапеция, у которой боковые стороны равны.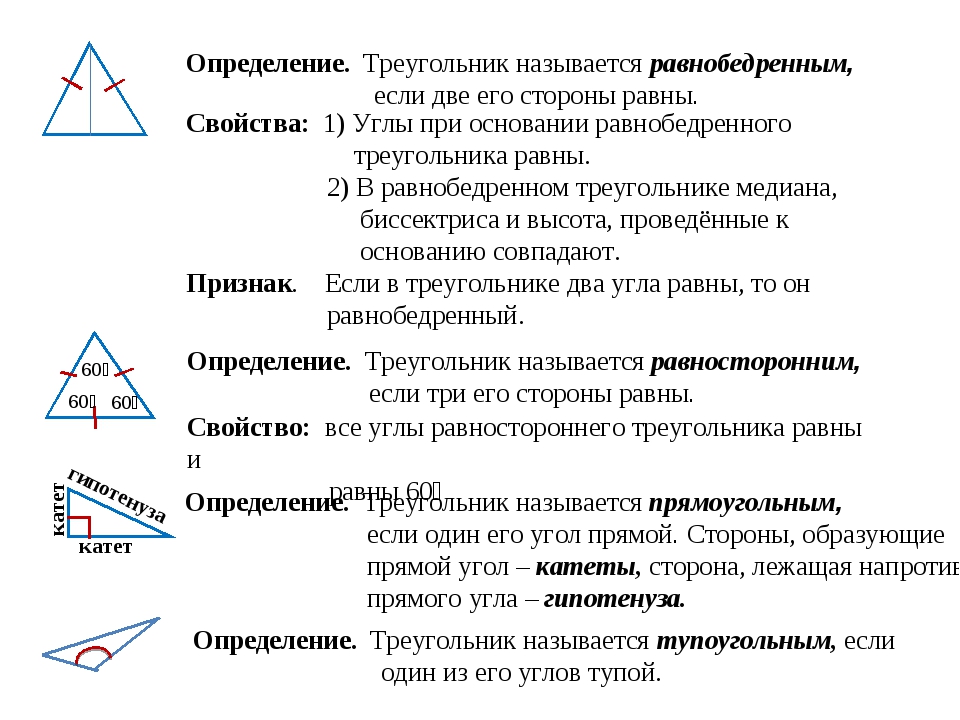
Прямоугольная трапеция-это трапеция, у которой один из углов прямой.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольник-это параллелограмм, у которого все углы прямые.
Свойство: диагонали прямоугольника равны.
Теорема(признак прямоугольника):если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Ромб-это параллелограмм, у которого все стороны равны.
Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат-это прямоугольник, у которого все стороны равны.
Глава VI Площадь
Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.
Единицы измерения площади: мм2,см2,
дм2, м2, ар=100м2, км2 , га=100км2.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна полусумме её оснований на высоту.
Теорема Пифагора:в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема(обр.):если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Глава VII Подобные треугольники
Отрезки m и n пропорциональны отрезкам
m1и
n1,если
отношения их длин равны m:m1=
n:
n1.
Подобные треугольники— это треугольники,у которых соответственные углы равны, а сходственные стороны пропорциональны.
Коэффициент подобия- это число, равное отношению сходственных сторон подобных треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Теорема(первый признак подобия треугольников):если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Теорема(второй признак подобия треугольников):если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Теорема(первый признак подобия
треугольников):если три стороны одного треугольника
пропорциональны трём сторонам другого треугольника, то такие треугольники
подобны.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.
Синус острого угла прямоугольного треугольника- это отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника- это отношение прилежащего катета к
гипотенузе.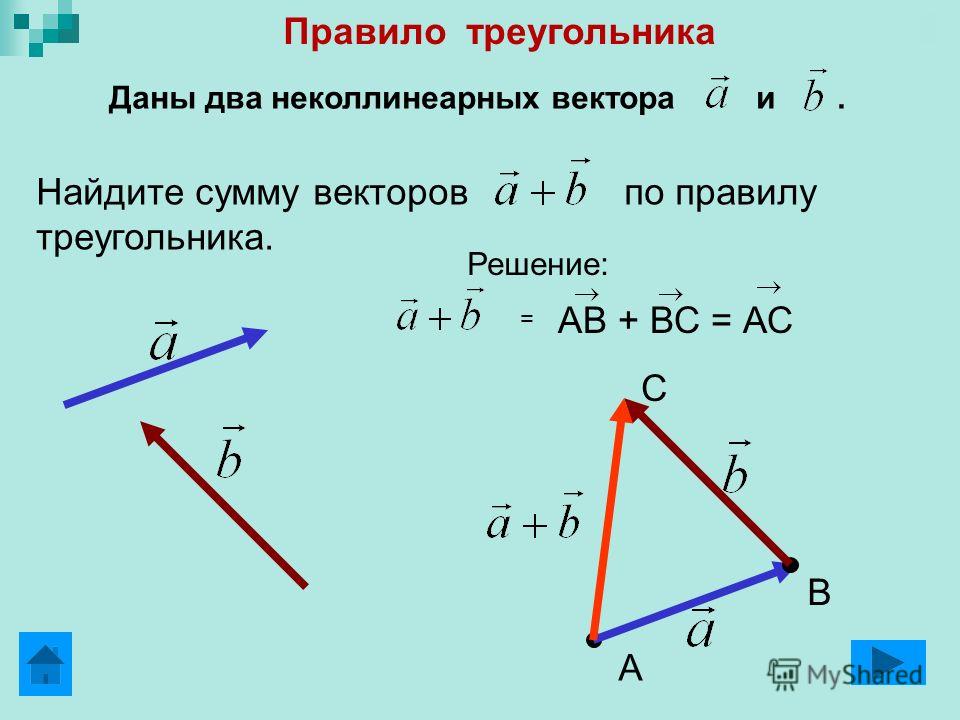
Тангенс острого угла прямоугольного треугольника- это отношение противолежащего катета к прилежащему .
Котангенс острого угла прямоугольного треугольника- это отношение прилежащего катета к противолежащему .
Глава VIII Окружность
Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.
Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Центральный угол – это угол с вершиной в центре окружности.
Дуга окружности измеряется центральным углом, который на неё опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Т.Вписанный угол равен половине дуги, на которую он опирается.
С. Вписанные углы, опирающиеся на одну и
ту же дугу, равны.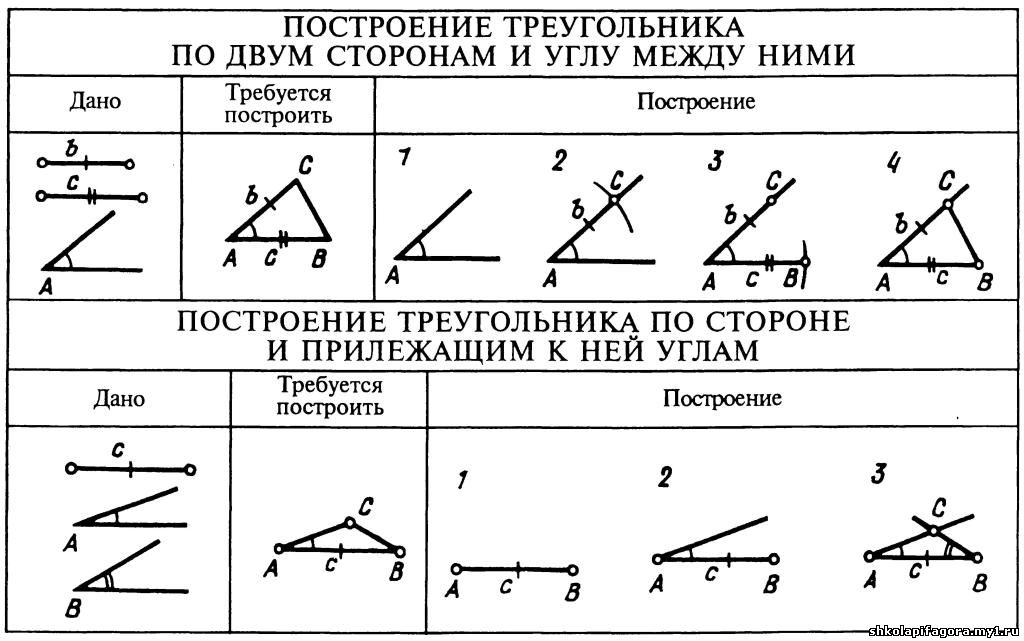
С. Вписанный угол, опирающийся на полуокружность, — прямой.
Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.
9 класс
Средняя линия трапеции— это отрезок, соединяющий середины её боковых сторон.
Теорема:средняя линия трапеции равна полусумме её оснований и параллельна им.
Свойства треугольника — формулы, теоремы, примеры
свойства треугольника помогают нам легко идентифицировать треугольник из заданного набора фигур. Треугольник — это многоугольник, который имеет три угла, три стороны и три вершины. Треугольники можно разделить на различные типы треугольников в зависимости от длины сторон и меры углов. Давайте узнаем больше о свойствах треугольников вместе с теоремами, основанными на них.
| 1. | Каковы свойства треугольников? |
2. | Треугольник и его свойства |
| 3. | Часто задаваемые вопросы о свойствах треугольников |
Каковы свойства треугольников?
Чтобы узнать о свойствах треугольников, нам нужно знать о различных типах треугольников. Хотя все треугольники имеют некоторые общие свойства, есть несколько свойств, которые основаны на их сторонах и углах.
Различные типы треугольников
Треугольники можно разделить на две широкие категории в зависимости от их углов и сторон. Обратите внимание на следующий рисунок, на котором показаны типы треугольников, которые различаются на основе их сторон и углов.
Треугольник и его свойства
Свойства треугольника помогают нам определить отношения между различными сторонами и углами треугольника. Некоторые из важных свойств треугольника перечислены ниже.
Свойство суммы углов
В соответствии со свойством суммы углов сумма трех внутренних углов треугольника всегда равна 180°.
В данном треугольнике ∠P + ∠Q + ∠R = 180°
Свойство неравенства треугольника
третья сторона.
Обратите внимание на приведенный выше рисунок, на котором показано △ABC, представляющее свойство неравенства треугольника. Если a = 4 единицы, b = 6 единиц, c = 3 единицы, проверим свойство неравенства треугольника следующим образом:
- а + б > в (4 + 6 > 3)
- с + а > б (3 + 4 > 6)
- с + b > а (3 + 6 > 4)
Свойство Пифагора
Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Математически это можно выразить как Гипотенуза² = Основание² + Высота². Обратите внимание на рисунок, приведенный ниже, чтобы увидеть высоту, основание и гипотенузу.
Сторона, противоположная большему углу, является самой длинной стороной
Чтобы понять это свойство, согласно которому сторона, противоположная большему углу, является самой длинной стороной, рассмотрите приведенный ниже треугольник. В этом треугольнике ∠B — наибольший угол. Таким образом, сторона AC является самой длинной стороной.
В этом треугольнике ∠B — наибольший угол. Таким образом, сторона AC является самой длинной стороной.
Свойство внешнего угла
Согласно теореме о внешнем угле внешний угол треугольника всегда равен сумме внутренних противоположных углов. В данном треугольнике Внешний угол (e) = ∠a + ∠b
Следует отметить, что в треугольнике можно продолжить 3 внешних угла, и все эти внешние углы в сумме составляют 360°.
Свойство конгруэнтности
Согласно свойству конгруэнтности два треугольника называются конгруэнтными, если все их соответствующие стороны и углы равны.
- ∠XYZ = ∠DEF
- ∠YXZ = ∠EDF
- ∠YZX = ∠EFD
- XY = DE
- ХЗ = ДФ
- YZ = ЭФ
Основные свойства треугольника , относящиеся к площади и периметру треугольника, приведены ниже.
- Площадь треугольника: Общая площадь внутри треугольника называется площадью треугольника.
 Площадь измеряется в квадратных единицах. Основная формула для вычисления площади треугольника: площадь (A) = (1/2) × основание × высота .
Площадь измеряется в квадратных единицах. Основная формула для вычисления площади треугольника: площадь (A) = (1/2) × основание × высота . - Периметр: Периметр треугольника = сумма всех трех его сторон.
- Формула Герона: Формула Герона используется для вычисления площади треугольника, если длины всех сторон известны, а высота треугольника неизвестна. Во-первых, нам нужно рассчитать полупериметр (ы). Для треугольника со сторонами a, b и c полупериметр (s) = (a + b + c)/2, площадь определяется выражением; A = \ (\ sqrt {s (s-a) (s-b) (s-c)} \)
Важные примечания
- Треугольник представляет собой многоугольник с тремя углами, тремя сторонами и тремя вершинами.
- Стороны и углы — очень важные аспекты треугольника. Мы можем классифицировать различные типы треугольников в математике, комбинируя стороны и углы.
- Основная формула для вычисления площади треугольника: Площадь (A) = (1/2) × Основание × Высота
- Периметр треугольника равен сумме всех трех сторон треугольника.

☛ Похожие статьи
- Свойства прямоугольника
- Свойства параллелограммов
- Подобные треугольники
- Критерий SSS в треугольниках
Примеры свойств треугольника
Пример 1: Два угла треугольника равны 75° и 60°. Какова будет мера его третьего угла?
Решение:
Два угла треугольника равны 75° и 60°
Сумма двух углов = 75° + 60° = 135°
Используя свойства треугольника, мы знаем, что сумма всех трех углов треугольника = 180°
Следовательно, мера третьего угла = 180° — 135° = 45°.
Пример 2: Тим хочет построить треугольник со сторонами 5 см, 4 см и 9 см. Сможет ли он это сделать?
Решение:
Длины сторон равны 5 см, 4 см, 9 см.
5 см + 4 см = 9 см
Здесь сумма двух меньших сторон равна третьей стороне. Но по теореме о неравенстве треугольника сумма любых двух сторон должна быть больше третьей стороны.

Следовательно, используя свойства треугольника, мы можем сказать, что Тим не сможет построить треугольник со сторонами 5 см, 4 см и 9 см.
Пример 3: Стороны треугольника равны 3 см, 4 см и 5 см. Вычислите периметр треугольника.
Решение:
Стороны треугольника: x = 3 см, y = 4 см и z = 5 см
Периметр треугольника определяется как P = x + y + z.
P = 3 + 4 + 5
P = 12 см
Следовательно, периметр данного треугольника равен 12 см.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по свойствам треугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о свойствах треугольника
Каковы 5 свойств треугольника?
Основные свойства треугольника перечислены ниже:
- Треугольник имеет три стороны, три вершины и три угла.

- Сумма трех внутренних углов треугольника всегда равна 180°.
- Сумма длин двух сторон треугольника всегда больше длины третьей стороны.
- Треугольник с вершинами P, Q и R обозначается как △PQR.
- Площадь треугольника равна половине произведения его основания на высоту.
Сколько типов треугольников существует в математике?
Существует шесть типов треугольников. Это разносторонние треугольники, равнобедренные треугольники, равносторонние треугольники, остроугольные треугольники, тупоугольные треугольники и прямоугольные треугольники.
Что такое прямоугольный треугольник?
Треугольник, у которого один из внутренних углов равен 90 градусов — прямоугольный треугольник.
Что общего у всех треугольников?
Треугольники бывают разных размеров и размеров, однако есть некоторые общие свойства, присущие всем треугольникам. Например, все треугольники имеют три стороны и три угла, сумма внутренних углов всегда равна 180°, а сумма длин двух сторон треугольника всегда больше длины третьей стороны.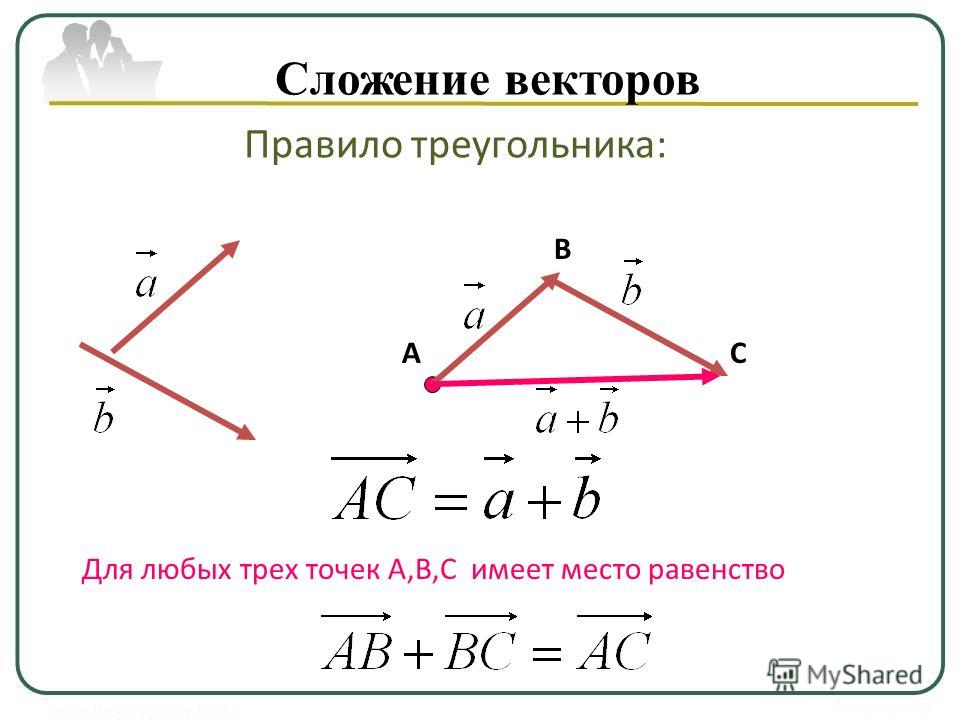
Какова площадь треугольника?
Площадь треугольника равна половине произведения его основания на высоту. Это пространство, ограниченное сторонами треугольника, выражается формулой Площадь треугольника = 1/2 × основание × высота. Площадь треугольника выражается в квадратных единицах.
Что такое теорема о неравенстве треугольников?
Теорема о неравенстве треугольника утверждает, что сумма длин любых двух сторон треугольника всегда больше длины третьей стороны.
Каковы свойства разностороннего треугольника?
Свойства разностороннего треугольника приведены ниже:
- У него три стороны разной длины.
- Имеет три угла разного размера.
- У него нет параллельных или равных сторон, следовательно, нет и линии симметрии.
- Внутренние углы треугольника могут быть острыми, тупыми или прямыми.
Каковы свойства прямоугольного треугольника?
Свойства прямоугольного треугольника задаются следующим образом:
- Наибольший угол всегда равен 90º, что означает, что у него не может быть тупого угла.

- Наибольшая сторона называется гипотенузой, которая всегда является стороной, противоположной прямому углу.
- Три стороны этого треугольника следуют теореме Пифагора.
Каковы свойства равнобедренного треугольника?
Свойства равнобедренного треугольника задаются следующим образом:
- Равнобедренный треугольник имеет две равные стороны, а угол между ними называется углом при вершине.
- Сторона, лежащая против угла при вершине, называется основанием, а углы при основании равны.
- Перпендикуляр, проведенный из угла при вершине, всегда делит пополам основание и угол при вершине.
Каковы свойства равностороннего треугольника?
Свойства равностороннего треугольника задаются следующим образом:
- Все стороны равностороннего треугольника имеют одинаковую длину.
- Все углы равностороннего треугольника равны 60°.
- Если из любой вершины провести перпендикуляр к противоположной стороне, он делит эту сторону пополам, а также угол при вершине.

- Ортоцентр и центр тяжести равностороннего треугольника попадают в одну и ту же точку.
Какое свойство суммы углов треугольника?
В соответствии со свойством суммы углов треугольника сумма внутренних углов треугольника всегда равна 180°. Например, если 3 внутренних угла треугольника заданы как ∠a, ∠b и ∠c, то это свойство можно выразить как ∠a + ∠b + ∠c = 180°.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по геометрии
Треугольники [300-страничный бесплатный курс GMAT][2023]
300-страничный бесплатный курс GMAT
Бесплатный курс GMAT > Основы GMAT по математике > 3. Геометрия > Треугольники
Основные правила
Есть несколько правил, которые верны для всех видов треугольников. Ниже приведены четыре наиболее важных правила. Примечание. Треугольники на рисунках представляют 90 136 любых 90 137 треугольников.
Правило 1 :
Сумма внутренних углов треугольника равна 180°.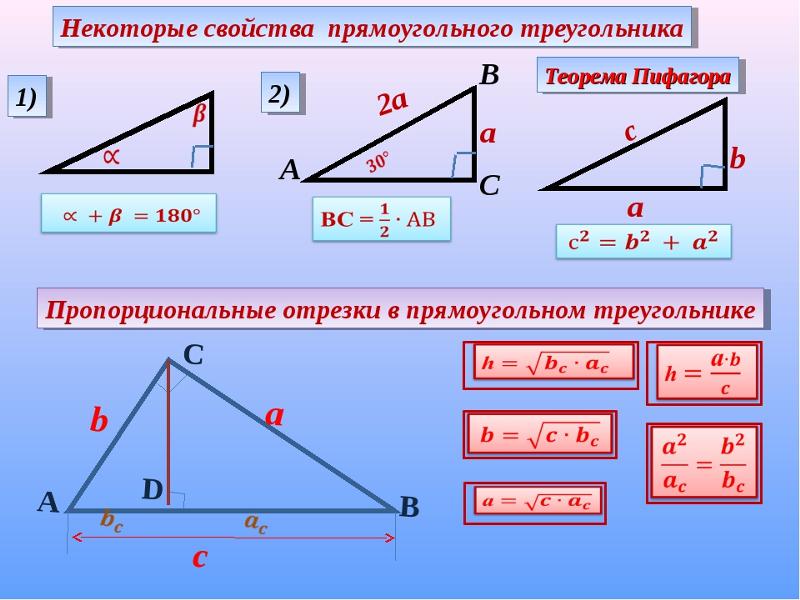
x ° + y ° + z ° = 180°
Правило 2 :
Длина наибольшей стороны треугольника должна быть меньше суммы длин двух других сторон треугольника, но больше разности длин.
( AB — до н.э. ) < AC <( AB + BC )
Правило 3 :
Сторонняя сторона. самый маленький угол.
∠B наибольший угол, поэтому AC это самая длинная сторона.
AB наименьшая сторона, поэтому ∠ C наименьший угол.
Правило 4 :
Если удлинить одну сторону треугольника, то внешний угол образованный будет равен сумме двух других внутренних углов треугольника.
x ° + z ° = n °
Найдите значение y .
Решение
Начните с треугольника справа. Используя внешние углы,
x ° + 120° = 150°, поэтому x ° = 30°.
Дуги в вершине треугольника означают, что углы равны. Поскольку x ° = 30°, его конгруэнтный угол также равен 30°.
Отсюда есть два способа найти значение y .
Одним из способов является использование внешних углов. y ° + 30° = 120°, поэтому y ° = 90°.
Другой метод заключается в том, чтобы сначала найти другой неизвестный угол. Поскольку неизвестный угол образует прямой угол с углом 120°, его мера равна 60°.
Сумма внутренних углов треугольника равна 180°.
Итак, 60° + 30° + y ° = 180°.
Опять же, y ° = 90°.
Периметр
периметр любой фигуры – это расстояние вокруг внешней стороны фигуры или сумма сторон фигуры. Многие вопросы GMAT о периметрах треугольников включают правило 2, указанное выше.
Треугольники A и B имеют одну сторону. Длины двух сторон треугольника A 4 дюйма и 6 дюймов.
Длины двух сторон треугольника B равны 3 дюймам и 8 дюймам. Каков диапазон возможных длин третьей общей стороны?
Решение
Рисование эскиза может облегчить визуализацию любого вопроса.
Длины двух сторон треугольника A равны 4 дюймам и 6 дюймам.
Таким образом, диапазон значений для третьей стороны треугольника A равен
(6 – 4) < x < (6 + 4), или 2 < x < 10.
Длины двух сторон треугольника B составляют 3 дюйма и 8 дюймов.
Таким образом, диапазон значений для третьей стороны треугольника B равен
(8 – 3) < x < (8 + 3) или 5 < x < 11.
Объедините два неравенства.
2 < x < 10 и 5 < x < 11
5 < x < 10
Таким образом, третья сторона должна быть длиннее 5 дюймов и короче 10 дюймов.
Площадь
Площадь любой фигуры – это площадь поверхности, которую занимает фигура.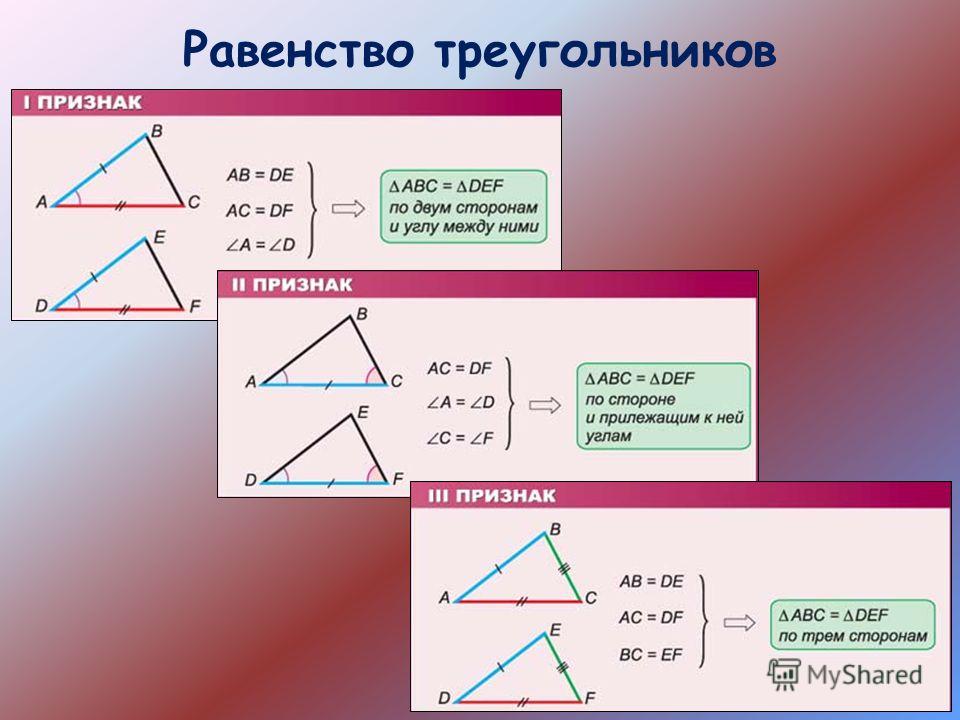 Каждый тип фигуры имеет свою формулу для нахождения его площади.
Каждый тип фигуры имеет свою формулу для нахождения его площади.
Чтобы найти площадь треугольника, вам нужны два измерения: основание и высота .
Формула площади треугольника: A = \dfrac{1}{2} (основание × высота) = \dfrac{1}{2} bh
Основание треугольника может быть любым из его сторон. Высота треугольника — это перпендикулярное расстояние от основания до противоположного угла. Вот несколько примеров треугольников с разными основаниями и высотами. Каждый треугольник имеет три основания и три соответствующие высоты. Обратите внимание, что высота может быть внутри треугольника, вне треугольника или одной из сторон треугольника.
Типы треугольников
Существует три основных типа треугольников.
[[https://www.youtube.com/watch?v=Cv_lt3jFseA]]
Равнобедренный треугольник имеет две равные стороны и два равных угла. В треугольнике ABC , ∠ B = ∠ C и AB = AC . Это применение правила 3 выше. Две стороны равны, значит равны и их противоположные углы.
Это применение правила 3 выше. Две стороны равны, значит равны и их противоположные углы.
Другая сторона, до н.э. может быть длиннее, короче или равным AB = AC .
Высота от стороны до н.э. делит пополам противоположный угол ∠ A . BD = DC и ∠ DAB = ∠ DAC . Получаются два конгруэнтных прямоугольных треугольника.
Треугольник RST равнобедренный, где ∠ R = 110°, RT = 12 и ST = 20. Высота из ST0137 к ∠ R равно 7. Найдите ∠ S , ∠ T , RS , периметр и площадь треугольника RST .
Решение
Лучший способ решить проблему — нарисовать эскиз.
Поскольку треугольник RST равнобедренный, у него два угла равны.
Поскольку ∠ R = 110°, он не может быть одним из равных углов.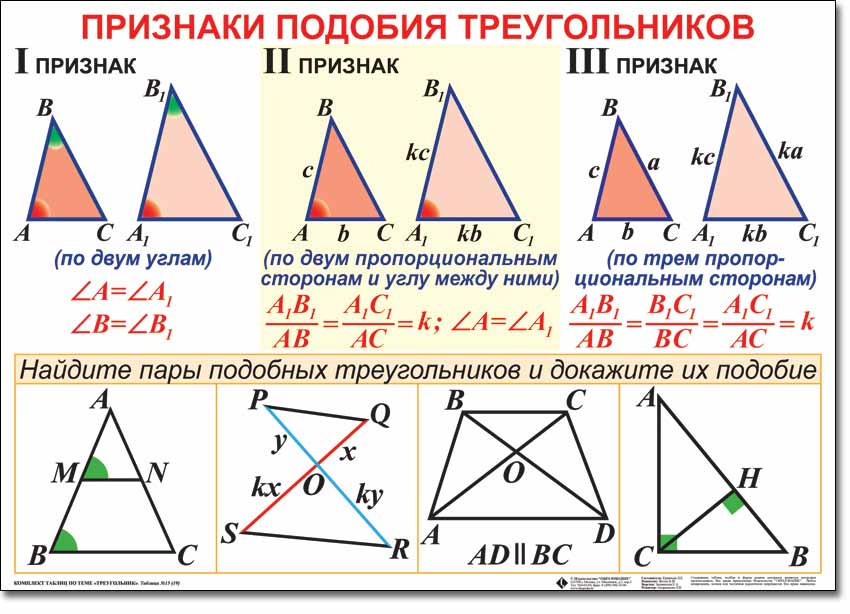
∠R + ∠ S + ∠ T = 180°
, поэтому ∠ S + ∠ T = 180° – 110° = 70°.
∠S = ∠ T так что они оба равны
\dfrac{70°}{2} = 35°.
Так как треугольник RST равнобедренный, то у него две стороны равны.
∠S = ∠ T , поэтому стороны, противоположные этим углам, равны.
RT = RS и RT = 12, поэтому RS = 12.
Периметр равен 12 + 12 + 20 = 44 единицы.
Так как высота от ST до ∠ R , ST является основанием, а ST = 20.
Площадь равна (\dfrac{1}{2})(20)(7) = 70 квадратных единиц.
Равносторонний треугольник имеет три равные стороны и три равных угла. Поскольку сумма углов треугольника составляет 180°, каждый угол равностороннего треугольника равен 60°.
Равносторонний треугольник является разновидностью равнобедренного треугольника, так как у него две равные стороны и два равных угла.
Высота равностороннего треугольника делит его пополам на два конгруэнтных прямоугольных треугольника. Углы прямоугольного треугольника равны 30° : 60° : 90°.
A прямоугольный треугольник — треугольник с углом 90°. Две перпендикулярные стороны называются катетами , а сторона, противоположная прямому углу, называется гипотенузой .
Чтобы найти площадь, катеты можно использовать как высоту и основание прямоугольного треугольника.
Гипотенуза всегда является наибольшей стороной прямоугольного треугольника. Это применение правила 3 выше: прямой угол — это самый большой угол, поэтому гипотенуза — это самая длинная сторона.
Прямоугольные треугольники
Для прямоугольных треугольников связь между катетами и гипотенузой определяется Теоремой Пифагора . Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов.
Видео предоставлено Подготовка к GMAT по Kaplan .
A 2 + B 2 = C 2 или
(нога) 2 или
(нога) 2 +282828,2+ 2 (нога) + 2 + 2 (нога) + 2 2 . С помощью теоремы Пифагора можно найти длину любой стороны прямоугольного треугольника.
Найдите длины неизвестных сторон.
Раствор
3 2 + 4 2 = A 2
9 + 16 = A 2
25 = A 2
5 = ANLY .
Solution
12 2 + b 2 = 13 2
144 + b 2 = 169
b 2 = 25
b = 5
Найдите длины неизвестных сторон.

Solution
4 2 + 8 2 = c 2
16 + 64 = c 2
80 = c 2
80 = 4 × 4 × 5
c =\sqrt{80} = 4\sqrt{5}
Особые прямоугольные треугольники, основанные на длинах сторон
Существует несколько особых прямоугольных треугольников, длины сторон которых образуют отношения целых числа. Эти треугольники часто появляются на GMAT, поэтому способность быстро распознавать их поможет вам быстрее и точнее решать задачи.
Общие пифагорейские тройки и некоторые их кратные
Видео предоставлено Подготовка к GMAT Kaplan .
3, 4, 5
6, 8, 10
9, 12, 15
30, 40, 50
3 x , 4 x , 5 x
 , 5 . , 13
, 5 . , 13 10, 24, 26
15, 36, 39
50, 120, 130
5 x , 12 x , 13 x
8, 15, 17
16,
9,
8, 15, 17
16, 30, 34
24, 45, 51
80, 150, 170
8 x , 15 x , 17 x
7, 24, 25
14, 48, 50
21, 72, 75
70, 240, 250
7 x , 24 x , 25 x
Важно помнить, что самая длинная сторона всегда является гипотенузой. Если два катета прямоугольного треугольника равны 3 и 5, то гипотенуза не равна 4.
Также обратите внимание, что числа, кратные этим треугольникам, также являются особыми прямоугольными треугольниками. Треугольник 3 : 4 : 5 также является треугольником 6 : 8 : 10 и 9.: 12 : 15.
5 : 12 : 13 равно 10 : 24 : 26.
Стороны равнобедренного треугольника равны 10, 10 и 16 футам.
Найдите площадь треугольника.
Решение
Используйте описание, чтобы нарисовать эскиз.
Чтобы найти площадь, начертите высоту треугольника.
Так как это равнобедренный треугольник, высота делит основание пополам и образует два конгруэнтных прямоугольных треугольника.
Стороны каждого прямоугольного треугольника равны h : 8 : 10. Это кратно прямоугольному треугольнику 3 : 4 : 5, поэтому h = 6.
A = \Big(\,\dfrac{\,1\,}{ 2}\,\Big) bh = \Big(\,\dfrac{\,1\,}{2}\,\Big)(16)(6) … Помните, что основание всего треугольника равно 16 ,
= (8)(6) = 48 … Площадь треугольника составляет 48 квадратных футов.
Площадь прямоугольного треугольника 60см 2 а высота 15см. Найдите периметр треугольника.
Решение
Подставьте значения в формулу площади.
A = \Big(\,\dfrac{\,1\,}{2}\,\Big) bh , поэтому 60 = \Big(\,\dfrac{\,1\,}{2 }\,\Big)( b )(15) … Найдите b .
120 = 15 b
b = \dfrac{120}{15} … Основание треугольника равно 8. прямоугольный треугольник.
Вместо того, чтобы вычислять гипотенузу, обратите внимание, что это катеты прямоугольного треугольника 8 : 15 : 17.
Периметр равен 8 + 15 + 17 = 40 см.
Особые прямоугольные треугольники, основанные на углах
На GMAT есть два особых прямоугольных треугольника, основанных на углах. Первый — это треугольник 45° : 45° : 90°.
Треугольник 45° : 45° : 90° является равнобедренным, поэтому у него две равные стороны и два угла по 45°.
Существует постоянная зависимость между длинами катетов и гипотенузой. Гипотенуза всегда в \sqrt{2} умножается на длину одного катета.
Следовательно, вам нужна только длина одной стороны, чтобы найти площадь.
Самая длинная сторона равнобедренного прямоугольного треугольника равна 10 единицам. Найдите площадь треугольника.
Решение
Равнобедренный прямоугольный треугольник
45° : 45° : 90° треугольник.
Самая длинная сторона — гипотенуза, равная 10.
Таким образом, каждый катет равен
\dfrac{10}{\sqrt{2}}= \dfrac{10}{\sqrt{2}} \times \dfrac {\ sqrt {2}} {\ sqrt {2}} = \ dfrac {10 \ sqrt {2}} {2} = 5 \ sqrt {2} 9{\ displaystyle {2}} = \ Big (\ dfrac {1} {2} \ Big) (25 × 2) = 25
Площадь треугольника составляет 25 квадратных единиц.
Прямоугольный треугольник 30° : 60° : 90° работает так же, как треугольник 45° : 45° : 90°, но с другими размерами.
Размеры треугольника 30° : 60° : 90°:
Опять же, вам нужна только длина одной стороны, чтобы иметь возможность найти площадь.
Один из способов запомнить это — применить Правило 3 сверху — наименьшая сторона находится напротив наименьшего угла и наоборот.
Так как x является наименьшей стороной, она всегда находится напротив угла 30°, а 2 x, , которая является наибольшей, всегда должна находиться напротив угла 90°.
Это означает, что 2 x является гипотенузой.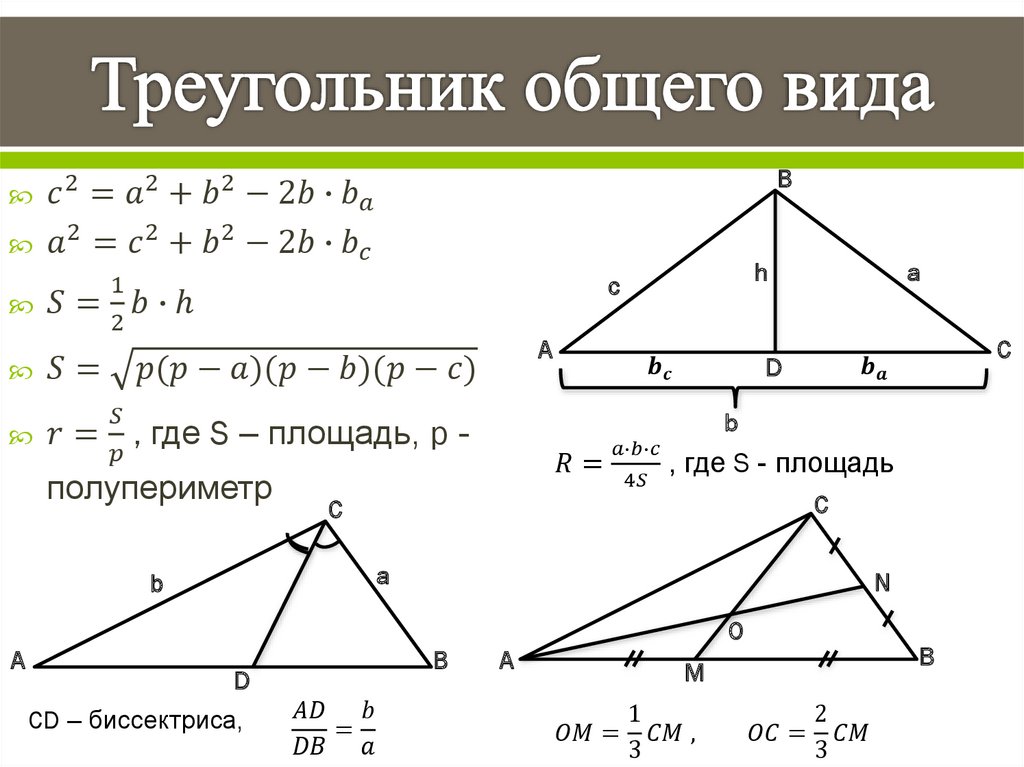 Поскольку x \sqrt{3} находится между x и 2 x ( x \sqrt{3} равно приблизительно 1,7), оно всегда противоположно углу 60 °.
Поскольку x \sqrt{3} находится между x и 2 x ( x \sqrt{3} равно приблизительно 1,7), оно всегда противоположно углу 60 °.
Равносторонний треугольник можно разделить пополам на два прямоугольных треугольника 30° : 60° : 90°.
Высота делит пополам основание и один угол треугольника, образуя два треугольника
, равные 30° : 60° : 90° прямоугольные треугольники.
Следовательно, вам нужна только длина одной стороны или высота, чтобы найти площадь равностороннего треугольника.
В равнобедренном треугольнике два угла равны 30°. Сторона между углами 30° имеет длину 4. Какова длина равных сторон?
Решение
Используйте описание, чтобы нарисовать эскиз.
Пусть y неизвестные длины. Углы в 30° подскажут вам, как искать прямоугольные треугольники. Затем вы можете использовать эти прямоугольные треугольники, чтобы найти стороны равнобедренного треугольника.
Нарисуйте высоту, чтобы разделить равнобедренный треугольник на два
треугольника 30° : 60° : 90°.
Длина наибольшей стороны исходного треугольника равна 4, поэтому длина более длинных катетов треугольников 30° : 60° : 90° равна 2.
Искомая сторона является гипотенузой, используя 2 в качестве длина более длинной ноги. Используйте соотношение
x : x \sqrt{3} : 2 x с x \sqrt{3} = 2, чтобы найти x , которое является основанием 30° : 60° : 90° треугольники.
Таким образом, основание треугольников 30° : 60° : 90° равно x = \dfrac{2\sqrt{3}}{3}
Гипотенуза треугольников 30°-60°-90° будет быть 2 x , что соответствует значению y .
y = 2 x = 2\Big(\dfrac{2\sqrt{3}}{3}\Big) = \dfrac{4\sqrt{3}}{3}
In равнобедренный треугольник, ∠ A = 60° и сторона AB = 12 единиц. Найдите периметр и площадь треугольника 9.
0136 АВС .
Решение
Этот трюк в этом вопросе заключается в том, чтобы понять, что равнобедренный треугольник с одним углом, равным 60°, является равносторонним треугольником.
Подумайте хорошенько: в равнобедренном треугольнике должны быть два равных угла. Таким образом, либо ∠ B , либо ∠ C равно ∠ A , то есть 60°. Вместе эти два угла составляют 120°, а поскольку сумма всех трех углов должна равняться 180°, третий угол должен равняться 60°.
С одной стороны треугольника ABC равно 12, все стороны равны 12.
3 × 12 = 36
Одна сторона треугольника ABC равна 12, что является гипотенузой прямой 30° : 60° : 90° треугольники, созданные высотой.
Итак, 12 = 2 x , x = 6, а высота
= 6\sqrt{3}.
Площадь A = \Big(\dfrac{1}{2}\Big)\textit{bh}
= \Big(\dfrac{1}{2}\Big)(12)(6\sqrt{ 3}) = 36\кв{3}.
Периметр 36 единиц. Площадь треугольника равна 36\sqrt{3} квадратных единиц. 9{\ displaystyle {2}} \ sqrt {3}} {4} = \ dfrac {144 \ sqrt {3}} {4} = 36 \ sqrt {3}
Площадь треугольника равна 36\sqrt{3} квадратных единиц. 9{\ displaystyle {2}} \ sqrt {3}} {4} = \ dfrac {144 \ sqrt {3}} {4} = 36 \ sqrt {3}
У треугольника углы равны 45° и 75°. °. Длина стороны, противоположной углу 45°, равна 6. Какова длина стороны, противоположной углу 75°?
Решение
Нарисуйте треугольник.
Третий угол равен 180° – (75° + 45°) = 60°.
Опять же, посмотрите, сможете ли вы решить задачу, создав прямоугольные треугольники.
Нарисуйте высоту треугольника и сформируйте два прямоугольных треугольника.
Теперь у вас есть треугольник 30° : 60° : 90° и треугольник 45° : 45° : 90°.
Обозначьте неизвестные длины x , y и z .
В треугольнике 30° : 60° : 90° гипотенуза равна 6, поэтому более короткий катет x = 3, а более длинный катет y = 3\sqrt{3} .
В треугольнике 45° : 45° : 90° x = z так что z = 3.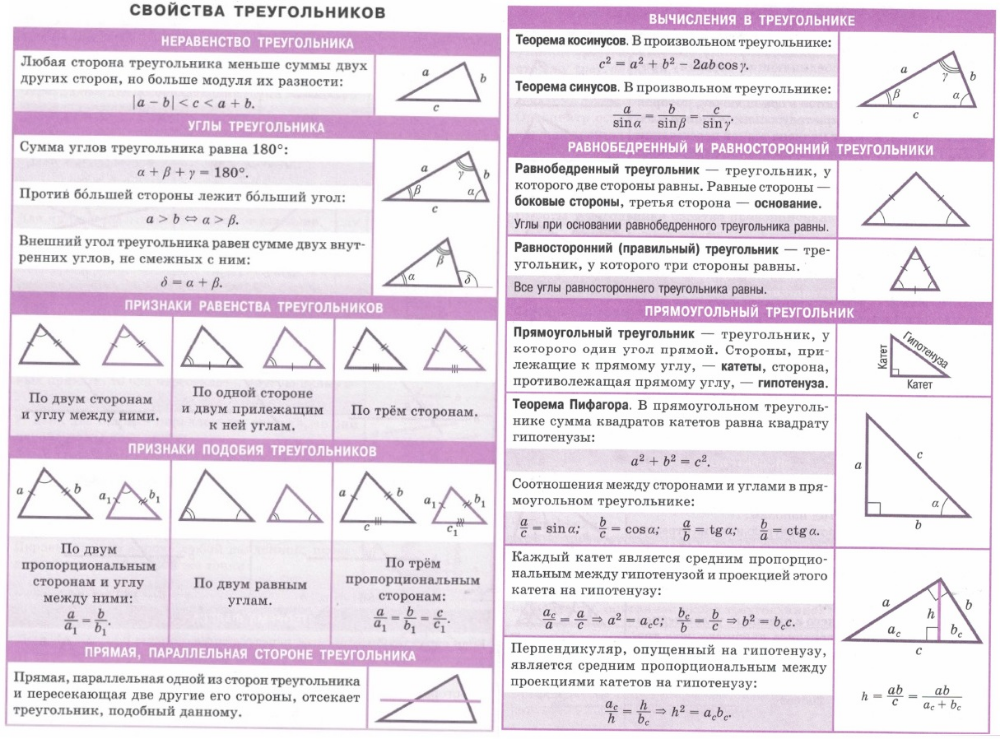
Длина стороны, противоположной углу 75°, равна
y + z = 3 + 3\sqrt{3} или 3 (1 + \sqrt{3} )
Подобные треугольники
Треугольники одинаковой формы называются подобными треугольниками 9 .
Есть два способа узнать, подобны ли два треугольника.
Если соответствующих углов равны, треугольники подобны.
Если отношение соответствующих сторон одинаково, треугольники подобны.
Отношение длин соответствующих сторон называется коэффициент масштабирования . Масштабный коэффициент для конгруэнтных треугольников равен 1.
Треугольник ABC подобен треугольнику DEF .
тий A = Ϫ D
T B = трясти E
T C = ♂ F
\dfrac{\textit{BC}}{\textit{EF}} = \dfrac{\textit{AC}}{\textit{DF}} Это отношение представляет собой коэффициент масштабирования.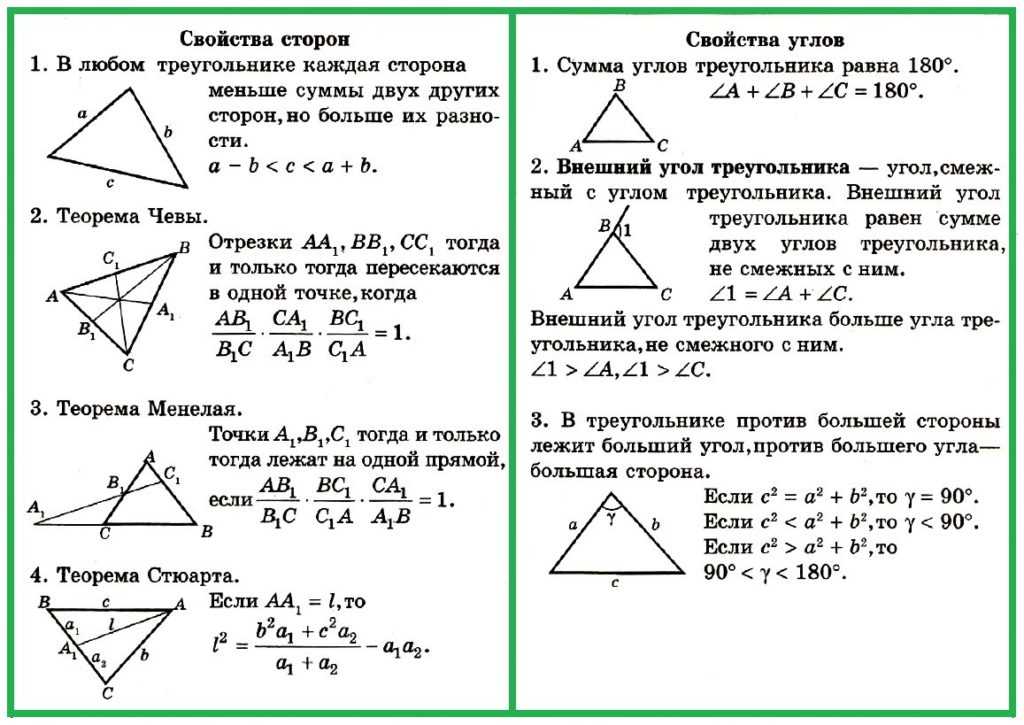
На GMAT есть три общих представления подобных треугольников.
Два треугольника с одинаковыми углами.
Вы можете видеть, что это подобные треугольники, потому что у них одинаковые углы или потому что стороны пропорциональны. Вам нужны только углы или стороны, чтобы знать, что треугольники подобны.
Масштабный коэффициент равен
\dfrac{small}{large} = \dfrac{4}{6} = \dfrac{2}{3}\, \textit{ or } \,\dfrac{small}{large } = \dfrac{6}{4} = 1,5
Один треугольник с линией, параллельной основанию треугольника.
Эта фигура состоит из двух треугольников.
У них общий угол y °.
Их основания параллельны, поэтому они оба имеют углы x ° и z°.
Вы также можете видеть, что это подобные треугольники, потому что стороны пропорциональны.
Масштабный коэффициент равен
\dfrac{small}{large} = \dfrac{4.5}{9} = \dfrac{1}{2}\, \textit{ or } \,\dfrac{small}{large } = \dfrac{9}{4.5} = 2
Два треугольника, соединенных вертикальными углами и имеющих параллельные основания.
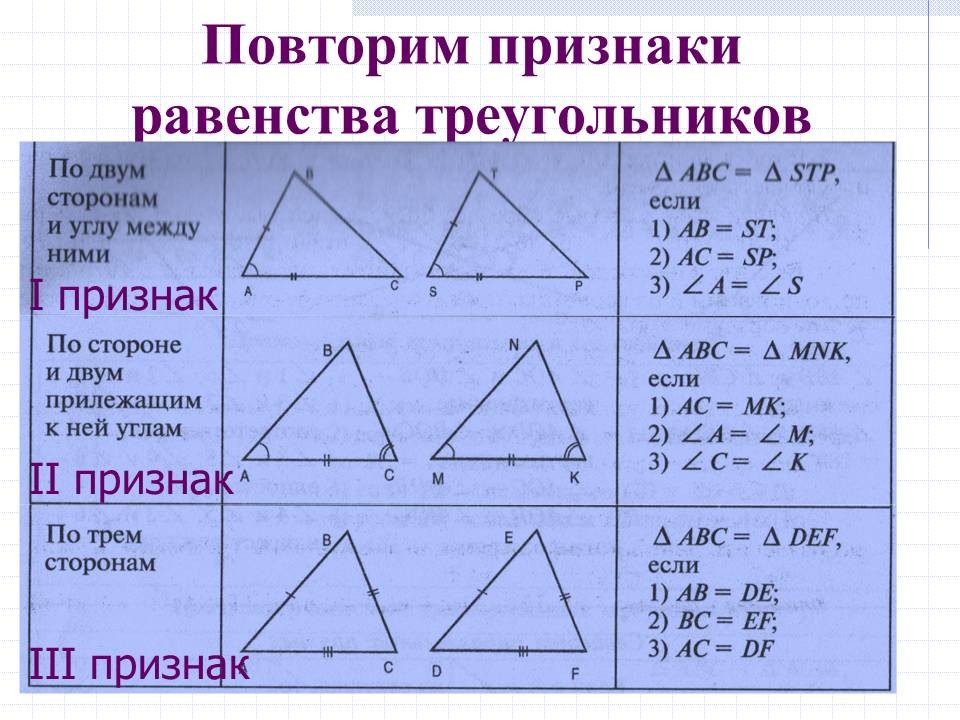
Эта фигура состоит из двух треугольников. У них вертикальные углы х °.
Их основания параллельны, поэтому они оба имеют углы y ° и z °.
Обратите внимание, что углы y ° и z ° находятся «на противоположных сторонах» друг от друга.
Найдите меру ∠ A и длину AD .
Решение
Сначала подтвердите, что треугольники подобны. Треугольники делят ∠ A . Основания треугольников, CD и BE , параллельны. Используя свойства углов, образованных параллельными линиями, ∠ AEB = ∠ ADC и ∠ ABE = ∠ ACD . Так как треугольники имеют 3 равных угла, треугольники подобны.
∠ AEB = 180° – 135° = 45° = ∠ ADC
Чтобы найти меру ∠ A , используйте сумму углов в треугольнике ADC .
∠ А = 180° – (45° + 30°) = 105°.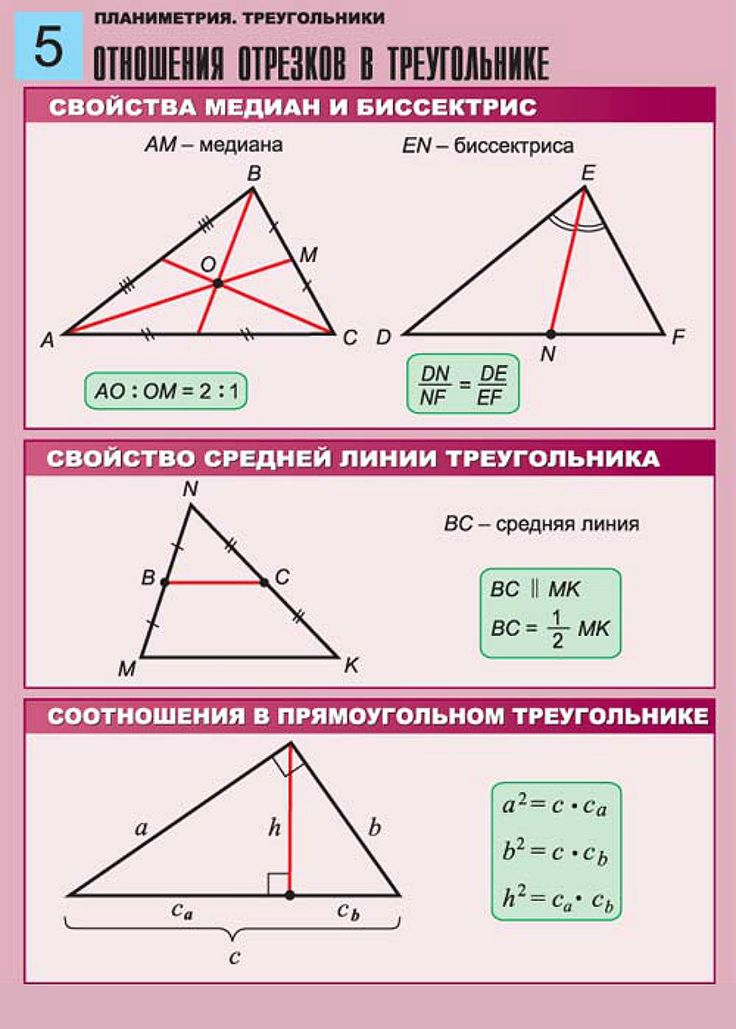
Используйте масштабный коэффициент, чтобы найти длины сторон.
\dfrac{маленький}{большой} = \dfrac{1,5}{3 + 1,5} = \dfrac{1}{\textit{AD}} = \dfrac{1}{1 + \textit{ED}}
\\[3ex] \dfrac{1.5}{4.5} = \dfrac{1}{1 + \textit{ED}} …перемножить
1,5(1 + ED ) = 4,5
1 + ED = 3 = AD
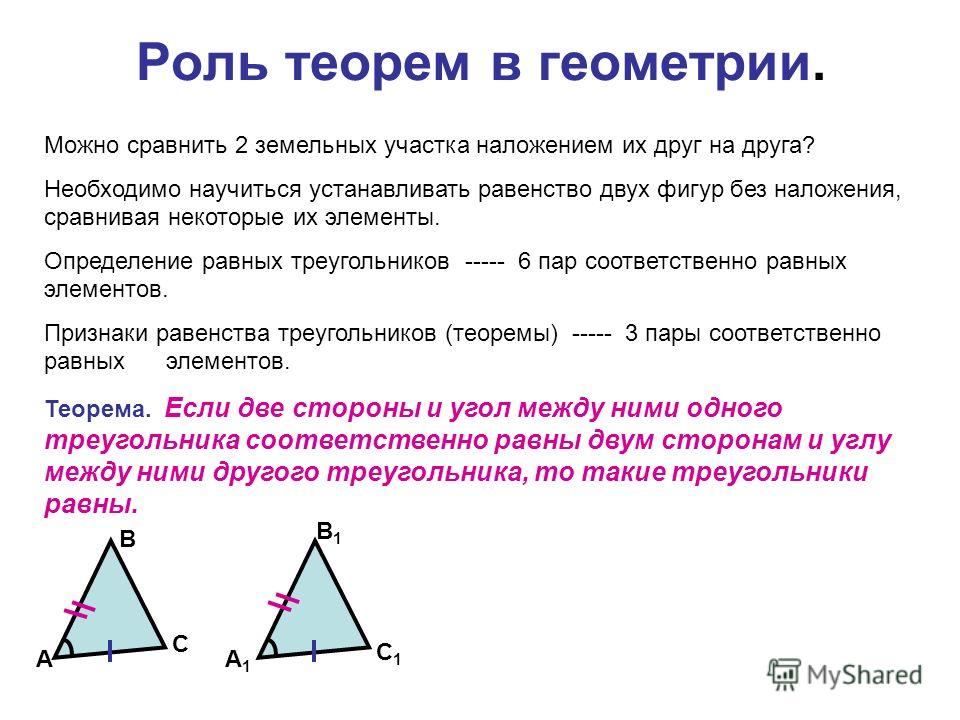
Треугольник R подобен треугольнику S . Найдите отношение площади треугольника R к площади треугольника С .
Решение
Чтобы найти площади, вам нужны основания и высоты обоих треугольников. Используйте единственную пару соответствующих сторон, которые имеют значения, чтобы найти коэффициент масштабирования.
\dfrac{сторона \,\textit{R}}{сторона \,\textit{S}} = \dfrac{34}{51} = \dfrac{2}{3}\\[3ex]
Использовать соответствующие стороны и масштабный коэффициент, чтобы найти значения x и w .
\dfrac{2}{3} = \dfrac{\textit{x}}{30}, поэтому x = 20.
\\[2ex]\dfrac{2}{3} = \dfrac{\textit{w}}{63}, поэтому w = 42.
Помните, что GMAT ищет рассуждения, а не долгие расчеты. Используйте то, что вы знаете о прямоугольных треугольниках.
Обратите внимание, что стороны наименьшего треугольника в R имеют длины сторон
12 : y : 20.
Это кратно прямоугольному треугольнику 3 : 4 : 5, поэтому высота y = 4(4 ) = 16.
Найти высоту z в треугольнике S с использованием масштабного коэффициента.
\dfrac{2}{3} = \dfrac{16}{\textit{z}}, поэтому z = 24.
Вычислите площади. Помните, что вопрос касается отношения, а не значения, поэтому оставьте ответы в факторизованной форме.
площадь R = \dfrac{1}{2}(42)(16) = (42)(8)
= 6 × 7 × 2 × 4
площадь S =\dfrac{1 {2}(63)(24) = (63)(12)
= 7 × 9 × 2 × 6
Отношение площадей равно
\dfrac{6 × 7 × 2 × 4}{7 × 9{\displaystyle{2}} = \dfrac{4}{9}.



 Площадь измеряется в квадратных единицах. Основная формула для вычисления площади треугольника: площадь (A) = (1/2) × основание × высота
Площадь измеряется в квадратных единицах. Основная формула для вычисления площади треугольника: площадь (A) = (1/2) × основание × высота



 Длины двух сторон треугольника B равны 3 дюймам и 8 дюймам. Каков диапазон возможных длин третьей общей стороны?
Длины двух сторон треугольника B равны 3 дюймам и 8 дюймам. Каков диапазон возможных длин третьей общей стороны? 
 Найдите площадь треугольника.
Найдите площадь треугольника.  0136 АВС .
0136 АВС .