Что изучает пространственная геометрия? — космический блог
Пространственная геометрия отвечает за изучение пространственных геометрических фигур, также называемых геометрическими телами, которые занимают пространство в пространстве благодаря своим трехмерным характеристикам (высоте, ширине и длине).
Пространственная геометрия изучает фигуры в пространстве, которые имеют три измерения, то есть высоту, ширину и длину. Пространственная геометрия изучает геометрические фигуры в пространстве. … Используя расположение точек, можно рисовать линии в пространстве, которые образуют плоскости и определяют геометрические формы и структуры.
Греческого происхождения («гео», земля и «метрия», что значит измерять), геометрия строится по методу, созданному математиком Евклидом Александрийским, аксиоматическому.
Мы также предлагаем, чтобы исследования по пространственной геометрии проводились с самых основных тем: примитивных понятий пространственной геометрии (точка, линия, плоскость и пространство) и основных определений более простых геометрических фигур.
Основные темы Геометрии для Энема — вычисление объемов и площадей, так как они чаще встречаются в тестах. Математика делится на три основные области: геометрия, алгебра и анализ или исчисление.
Пространство — это место, где происходит и имеет смысл вся пространственная геометрия, где могут быть построены все тела и геометрические фигуры. Это все пространство, которое нас окружает и которое бесконечно и безгранично простирается от точки, где мы находимся, во все стороны.
Позиционная геометрия изучает относительные положения между объектами и геометрическими фигурами. Многогранники – это геометрические тела, принадлежащие пространству. Геометрия положения — это область математики, изучающая относительные положения между геометрическими фигурами, присутствующими в пространстве.
Пространственные геометрические фигуры (куб, прямоугольный блок, пирамида, конус, цилиндр и сфера): распознавание, анализ, характеристика и планирование.
Пространственная геометрия — это область математики, изучающая фигуры в пространстве, то есть фигуры, имеющие более двух измерений. «Какой бы ни была плоскость, бесконечно много точек на этой плоскости и бесконечно много точек вне ее». «Если две различные плоскости имеют общую точку, то их пересечение представляет собой прямую линию».
«Какой бы ни была плоскость, бесконечно много точек на этой плоскости и бесконечно много точек вне ее». «Если две различные плоскости имеют общую точку, то их пересечение представляет собой прямую линию».
Линии — это плоские или пространственные геометрические фигуры, которые можно классифицировать как совпадающие, совпадающие и параллельные.
Плоская геометрия: также называемая евклидовой геометрией, изучает плоскость и пространство на основе постулатов Евклида; … В этой предметной области можно вычислить объем геометрического тела.
Геометрия — это область математики, изучающая геометрические фигуры по длине, площади и объему. Слово геометрия соответствует союзу терминов «гео» (земля) и «метрон» (мерить), то есть «измерение земли». Геометрия делится на три категории: Аналитическая геометрия.
Геометрия — это слово, происходящее от греческих терминов «гео» (земля) и «метрон» (измерять), общее значение которых — обозначать свойства, связанные с положением и формой объектов в пространстве. … Узнайте больше о геометрических фигурах.
… Узнайте больше о геометрических фигурах.
Аналитическая геометрия. Часть 2. Геометрия в пространстве
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Аналитическая геометрия
Часть 2Геометрия в пространстве
2. Аналитическая геометрия в пространстве.
Уравнения плоскости.
z
Плоскость Q определена единственным образом,
n
если задана одна точка M o Q и вектор n
Вектор n
Q
Q называют нормальным вектором.

Необходимое и достаточное условие того,
что точка М принадлежит плоскости Q.
Mo
0
Q.
y
M oM
n
M
n
Mo
х
1. Уравнение плоскости по точке и
нормальному вектору.
M o ( xo , yo , zo )
–
Заданы: точка
–
и нормальный вектор
–
Уравнение плоскости:
n A, B, C
A( x xo ) B( y yo ) C( z zo ) 0
Пусть точка
Тогда
M oM
n
M ( x, y, z) Q
M oM n 0
3. Аналитическая геометрия в пространстве.
2. Общее уравнение плоскости.
–
Уравнение вида
–
–
называется общим уравнением плоскости.
Коэффициенты A,B,C в уравнении определяют
координаты нормального вектора:
Ax By Cz D 0
n A, B, C
Теорема.
Всякое уравнение первой степени
с тремя переменными x,y,z вида
Ax By Cz D 0
(1)
задает плоскость в пространстве
и наоборот, всякая плоскость
в пространстве может быть задана
уравнением с тремя переменными x,y,z
вида (1).

n A, B, C
Q
Q
4. Аналитическая геометрия в пространстве.
3. Исследование общего уравнения плоскости.
–
1. Коэффициент D=0
–
2. Коэффициент A=0
–
3. Коэффициент B=0
–
z
точка O(0,0,0) Q
(рис. 1)
n ( A, B, C )
n (0, B, C) OX Q OX (рис. 2)
n ( A,0, C) OY Q OY (рис. 3)
4. Коэффициент C=0 n ( A, B,0) OZ Q OZ
(рис. 4)
Q
y
O
z
n (0, B, C )
n ( A,0, C )
z
Q
Рис. 1
x
Q
z
Q
y
O
n ( A, B,0)
y
x
O
Рис. 2
y
O
x
Рис. 3
x
Рис.4
5. Аналитическая геометрия в пространстве.
–5. Коэффициенты A=B=0
–
6. Коэффициенты A=C=0
–
7. Коэффициенты B=C=0
n (0,0, C) OZ Q OZ (рис. 5)
n (0, B,0) OY Q OY (рис. 6)
n ( A,0,0) OX Q OX (рис. 7)
z
z
n (0,0, C )
Q
z
n (0, B,0)
Q
Q
O
y
O
n (A,0,0)
y
O
x
x
x
Рис. 5
Рис.
 6
6Рис. 7
y
6. Аналитическая геометрия в пространстве.
z8. Коэффициенты A=B=D=0
z 0
–
9. Коэффициенты A=C=D=0
y 0
–
10. Коэффициенты B=C=D=0
x 0
Координатные
плоскости
x 0
y 0
0
y
z 0
x
7. Аналитическая геометрия в пространстве.
Уравнения прямой в пространстве.
1. Общее уравнение прямой.
– Аксиома: линия пересечения двух
плоскостей – прямая.
l:
11
Q2
A1 x B1 y C1 z D1 0 (Q1 )
A2 x B2 y C2 z D2 0 (Q2 )
(2)
Теорема.
Система уравнений (2) определяет
прямую в пространстве тогда и только
тогда, когда коэффициенты A1 , B1 , C1
не пропорциональны коэффициентам
2
A , B2 , C2
l
Система уравнений (2) называется общим уравнением прямой.
8. Аналитическая геометрия в пространстве.
2. Канонические уравнения прямой.
s m, n, p
M ( x, y, z )
l
Mo ( xo , yo , zo )
x xo y yo z zo
m
n
p
M ( x, y, z ) l.

MoM s MoM s
Пусть точка
Тогда
3. Параметрические уравнения прямой.
x xo
x xo m
m
y yo
y yo n
n
z zo
z z o p
p
x xo m
l : y yo n
z zo p
параметр
9. Аналитическая геометрия в пространстве.
Взаимное расположение плоскостей и прямых в пространстве.
1. Условие параллельности плоскостей.
n2 A2 , B2 , C2
Q2
Q1
Q1 : A1 x B1 y C1 z D1 0
Q2 : A2 x B2 y C2 z D2 0
Q1 Q2 n1 n2
A1 B1 C1
A2 B2 C2
n1 A1 , B1 , C1
2. Условие перпендикулярности плоскостей.
Q1
Q1 Q2 n1 n2
A1 A2 B1B2 C1C2 0
n2
n1
Q2
10. Аналитическая геометрия в пространстве.
3. Условие параллельности прямых.
s1 m1 , n1 , p1
l1
l2
l1 l2 s1 s2
s2 m2 , n2 , p2
l1
4. Условие перпендикулярности прямых.
l1 l2 s1 s2
m1 n1
p
1
m2 n2 p2
s1 m1 , n1 , p1
m1m2 n1n2 p1 p2 0
l2
s2 m2 , n2 , p2
11. Аналитическая геометрия в пространстве.

5. Условие параллельности прямой и плоскости.
n A, B, C
s m, n, p
l Q s n s n 0 Am Bn Cp 0
l
Q
6. Условие перпендикулярности прямой и плоскости.
s m, n, p
n A, B, C
l Q s n
Q
l
m n p
A B C
English Русский Правила
Геометрия в космической деятельности
Геометрия в космической деятельности Какова форма Вселенной? Интересный вопрос, безусловно, и тот, который несет в себе другие последствия — например, какой будет окончательная судьба Вселенной. В течение многих лет ученые предполагали, что существует три возможности искривления (или формы) Вселенной. Вселенная может быть плоской, как лист бумаги. Или он может иметь положительную кривизну, как сфера. Или он может иметь отрицательную кривизну, как средняя часть седла лошади. В определенной степени кривизна Вселенной зависит от того, сколько массы во Вселенной… и количество массы определит ее окончательную судьбу. Таким образом, это больше, чем просто мимолетная фантазия, что мы можем захотеть измерить кривизну Вселенной.
В этом уроке мы рассмотрим один из возможных способов измерения кривизны Вселенной, а именно измерение суммы углов треугольника во Вселенной. В зависимости от формы Вселенной сумма будет меньше, равна или больше 180 градусов. Конечно, мы не можем измерить ЛЮБОЙ треугольник… мы должны использовать очень большой треугольник, чтобы иметь возможность различить форму Вселенной. Каждый треугольник даст результат 180 градусов, если вы измерите лишь крошечную часть очень большого пространства… независимо от его кривизны.
| Плоская Вселенная | Положительная кривизна Вселенной | Вселенная с отрицательной кривизной |
Так как же измерить очень большой треугольник во Вселенной? Это также будет обсуждаться, поскольку это то, чем в ближайшие несколько лет займется миссия NASA Microwave Anisotrophy Probe (MAP).
Рабочий лист для учащихся
- Рабочий лист
Заметки учителя
Когда большинство студентов изучают геометрию, они изучают евклидову геометрию, которая по сути является геометрией плоского пространства. Евклидова геометрия основана на наборе постулатов или самоочевидных доказательств. Такие доказательства представлены «на очевидной истине, которая не может быть выведена из других постулатов». Вот постулаты Евклида:
- Вы можете провести прямую линию между любыми двумя точками.
- Вы можете бесконечно расширять любой сегмент.
- Вы можете нарисовать круг с любой заданной точкой в центре и любым заданным радиусом.

- Все прямые углы равны.
- Что, если прямая, падающая на две прямые, образует внутренние углы с одной и той же стороны меньше двух прямых, то две прямые, если их провести бесконечно, пересекутся с той стороны, на которой углы меньше двух прямых. .
Пятый постулат известен как Постулат Параллели. Этот постулат был переписан шотландским ученым и математиком Джоном Плейфером (1748-1819 гг.).) следующим образом (называемым аксиомой Плейфера): «Через данную точку, не принадлежащую данной прямой, проходит не более одной прямой, параллельной данной прямой».
Именно очевидное различие между первыми четырьмя постулатами и пятым привело математиков к мысли, что пятый на самом деле не постулат, а может быть выведен из первых четырех. Пытаясь сделать это, они открыли эллиптическую геометрию и гиперболическую геометрию. геометрия!
Если вы считаете пятый постулат ложным, есть 2 возможных отрицания:
- Через данную прямую не в данной точке проходит более одной прямой, параллельной данной прямой.

- Через данную точку, не лежащую на данной прямой, не проходит прямых, параллельных данной прямой.
Первое предположение было исследовано немецким математиком Карлом Фридрихом Гауссом (1777-1855), русским математиком Николаем Лобачевским (1792-1856) и венгерским математиком Яношем Бойяи (1802-1860). Они обнаружили, что это привело к новой геометрии, не противоречащей ни одному из других постулатов. Если бы они заменили Постулат Параллели этим новым предположением, они бы открыли неевклидову геометрию, называемую гиперболической геометрией.
Немецкий математик Георг Фридрих Бернхард Риман (1826-1866) исследовал второе предположение. Если Постулат Параллели заменить этим постулатом, то снова ни один из других постулатов не будет нарушен. Неевклидова геометрия, которую создает этот набор постулатов, называется эллиптической геометрией.
Все теоремы евклидовой геометрии, которые не опираются на постулат параллельности, применимы в неевклидовой геометрии без изменений. Одна теорема, возможно, самый известный пример, который опирается на постулат о параллельных, — это теорема о сумме треугольников, которая гласит: сумма трех углов в треугольнике равна 180°. Поскольку студенты, вероятно, уже знакомы с плоским пространством евклидовой геометрии и с тем, как сумма углов треугольника в этом пространстве составляет 180 °, мы сосредоточимся на том, чтобы увидеть, как выглядят треугольники и как они ведут себя в эллиптических и гиперболических пространствах.
Одна теорема, возможно, самый известный пример, который опирается на постулат о параллельных, — это теорема о сумме треугольников, которая гласит: сумма трех углов в треугольнике равна 180°. Поскольку студенты, вероятно, уже знакомы с плоским пространством евклидовой геометрии и с тем, как сумма углов треугольника в этом пространстве составляет 180 °, мы сосредоточимся на том, чтобы увидеть, как выглядят треугольники и как они ведут себя в эллиптических и гиперболических пространствах.
Эллиптическая геометрия
| | Вы можете использовать поверхность сферы в качестве модели для эллиптической геометрии. Но если вы это сделаете, вы должны немного изменить формулировку евклидовых постулатов. В эллиптической геометрии слово «линия» заменено на «большой круг». Большой круг определяется как любой круг на поверхности сферы, диаметр которого проходит через центр сферы. Для создания эллиптической геометрии Риман предположил, что через данную точку, не лежащую на прямой, не проходит прямых, параллельных данной прямой. Эта новая геометрия вносит несколько изменений. В евклидовой геометрии линии имеют бесконечную длину. В эллиптической геометрии большие окружности никогда не заканчиваются, но имеют конечную длину. Отрезок линии теперь определяется как дуга большого круга или расстояние по большому кругу между двумя точками. Когда прямая линия расширяется, ее концы в конце концов встречаются, образуя большой круг. Любые две «прямые линии» в конечном итоге встречаются, поскольку любые две большие окружности пересекаются в полюсных точках. Одним из результатов этого изменения постулата о параллельных является то, что теорема о сумме треугольников имеет другое окончание: Сумма трех углов треугольника в эллиптической геометрии всегда больше 180°. |
Гиперболическая геометрия
| | Чтобы найти модель гиперболической геометрии, нам нужна модель, в которой для каждой прямой и точки, не лежащей на этой прямой, имеется более одной параллельной прямой. Французский математик Анри Пуанкаре (1854-1912) придумал такую модель, названную диском Пуанкаре. Диск Пуанкаре состоит из всех точек внутри окружности. Линии в этой геометрии — это дуги внутри круга, но не просто дуги. Дуги должны иметь свои концы на окружности окружности и должны быть перпендикулярны окружности в обеих конечных точках. Как вы уже, наверное, догадались, эта геометрия также меняет окончание теоремы о сумме треугольников, так что оно звучит так: Сумма трех углов треугольника в этой геометрии всегда меньше 180°. |
Давайте исследовать неевклидову геометрию!
Материалы:
- Рабочий лист для учащихся
- Модели для евклидовой, эллиптической и гиперболической геометрий.
 Например, листы бумаги, большие пенопластовые сферы (продаются в магазинах для рукоделия) или глобусы, а также диски Пуанкаре или гиперболические листы (см. Приложение А) .
Например, листы бумаги, большие пенопластовые сферы (продаются в магазинах для рукоделия) или глобусы, а также диски Пуанкаре или гиперболические листы (см. Приложение А) . - Нить, нарезанная на несколько частей разной длины: несколько дюймов, фут, три фута и т. д. Свяжите каждую нить в петлю.
- Транспортиры
- Лента или кнопки для удержания тетивы на моделях
- Бумага и карандаш для записи измерений
Проезд:
- Попросите учащихся сформировать небольшие группы.
- Дайте каждой группе рабочий лист ученика и один отрезок веревки, разбросав их по комнате. Имейте разную длину строки для каждой группы.
- Предложите учащимся сначала нарисовать треугольник на плоском листе бумаги, используя веревку для формирования периметра. Используйте кнопки или ленту, чтобы закрепить вершины.
- Учащиеся должны измерить и сложить углы своего треугольника. Они должны увидеть, что их углы в сумме составляют 180 градусов.

- Затем попросите учеников нарисовать на бумаге новые треугольники, пока они не убедятся, что независимо от того, какую форму треугольника они образуют, общая сумма углов будет равна 180 градусам.
- Теперь попросите их построить треугольники на эллиптической модели, используя веревку в качестве периметра.
- Попросите их как можно туже натянуть нить на эллиптической модели. Помните, что эллиптическая модель, которую вы будете использовать, — это сфера.
- Учащиеся могут обнаружить, что стороны их треугольника не являются прямыми линиями. Это потому, что на поверхности сферы кратчайшее расстояние вдоль поверхности не является прямой линией. На самом деле это часть того, что называется Большим кругом. Помните, Большой круг — это круг на поверхности сферы, у которого центр сферы является центром. Напомните учащимся, что на земном шаре все линии долготы — это Большие круги, но единственная линия широты (которая также является Большим кругом) — это экватор.

- Предложите учащимся измерить углы своего треугольника и записать сумму углов. Повторите этот шаг несколько раз для разных треугольников. Учащиеся должны обнаружить, что сумма углов каждого треугольника в сумме составляет более 180 градусов.
- С вашей гиперболической моделью (будь то диск Пуанкаре или гиперлист), попробуйте ту же процедуру. Помните, что ваши линии — это особые дуги в этой геометрии. Чтобы измерить угол, образованный двумя линиями, измерьте угол, образованный касательными к дугам в точках пересечения. Учащиеся должны найти, что сумма углов каждого треугольника должна составлять менее 180 градусов.
- Предложите учащимся записать свои результаты на доске перед классом для каждой из поверхностей. Посмотрите, смогут ли они найти тенденции на основе длины строки и суммы углов. В евклидовой геометрии не имеет значения длина струны, сумма углов всегда должна составлять 180 градусов. В гиперболической геометрии чем короче струна (чем меньше периметр треугольника), тем ближе сумма углов к 180 градусам, но сумма всегда должна оставаться меньше 180 градусов.
 Для эллиптической геометрии чем короче периметр треугольника, тем ближе сумма углов должна быть к 180 градусам, но сумма всегда должна быть больше 180.
Для эллиптической геометрии чем короче периметр треугольника, тем ближе сумма углов должна быть к 180 градусам, но сумма всегда должна быть больше 180. - Студенты должны обсудить, как каждая из этих геометрий может изменить наше представление о Вселенной. Напомните им, что это может не только изменить нашу точку зрения, но и рассказать об окончательной судьбе нашей Вселенной. Что-то вроде геометрической гадалки!
Дополнительные ресурсы
Для более полного обсуждения евклидовой и неевклидовой геометрии и причин преподавания неевклидовой геометрии в вашем классе, пожалуйста, посетите http://math.rice.edu/~joel/NonEuclid/NonEuclid.html. содержит веб-программу, которую ваши студенты могут использовать для исследования диска Пуанкаре.
Национальные стандарты
Наука
Происхождение и эволюция Вселенной: В 9-12 классах все учащиеся должны понимать, что:
«В начале истории Вселенной материя, прежде всего в форме водорода и гелия, слипалась под действием гравитационного притяжения, образуя бесчисленные триллионы звезд.
 Миллиарды галактик, каждая из которых представляет собой гравитационно-связанное скопление миллиардов звезд, сейчас составляют большую часть видимой массы Вселенной; звезды производят энергию в результате ядерных реакций, в первую очередь синтеза водорода с образованием гелия. Эти и другие процессы в звездах привели к образованию всех остальных элементов».
Миллиарды галактик, каждая из которых представляет собой гравитационно-связанное скопление миллиардов звезд, сейчас составляют большую часть видимой массы Вселенной; звезды производят энергию в результате ядерных реакций, в первую очередь синтеза водорода с образованием гелия. Эти и другие процессы в звездах привели к образованию всех остальных элементов».Природа научного знания
Математика
- Анализ свойств и определение атрибутов двух- и трехмерных объекты;
- Установить правильность геометрических предположений с помощью дедукции, доказать теоремы и критические аргументы, сделанные другими;
- Используйте геометрические модели, чтобы получить представление и ответить на вопросы, другие области математики;
- Используйте геометрические идеи для решения задач и понимания других дисциплины и другие области интересов, такие как искусство и архитектура.
- Развить понимание аксиоматической системы путем исследования и сравнения евклидовой и неевклидовой геометрий
Этот сайт в настоящее время находится под
конструкция должна соответствовать стандарту 508.
Глава 11: Векторы и геометрия пространства
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 8604
- 11.1: Векторы на плоскости
- Некоторые величины, такие как или сила, определяются в терминах размера (также называемого величиной) и направления. Величина, имеющая величину и направление, называется вектором.
- 11.1E: Упражнения для векторов на плоскости
- 11.2: Векторы в пространстве
- Векторы — полезный инструмент для решения двумерных задач. Однако жизнь протекает в трех измерениях.
 Чтобы расширить использование векторов до более реалистичных приложений, необходимо создать основу для описания трехмерного пространства.
Чтобы расширить использование векторов до более реалистичных приложений, необходимо создать основу для описания трехмерного пространства. - 11.2E: Упражнения для векторов в пространстве
- 11.3: Скалярное произведение
- Скалярное произведение по существу говорит нам, какая часть вектора силы приложена в направлении движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, пересекаются ли два вектора под прямым углом.
- 11.3E: Упражнения для скалярного произведения
- 11.4: Перекрестное произведение
- заданные векторы. Вычисление крутящего момента является важным применением векторных произведений, и мы более подробно рассмотрим крутящий момент позже в этом разделе.
- 11.
 4E: Упражнения для перекрестного произведения
4E: Упражнения для перекрестного произведения
- 11.
- 11.5: Уравнения прямых и плоскостей в пространстве
- Чтобы написать уравнение прямой, мы должны знать две точки на прямой или мы должны знать направление прямой и хотя бы одну точку, через которую линия проходит. В двух измерениях мы используем понятие наклона для описания ориентации или направления линии. В трех измерениях мы описываем направление линии, используя вектор, параллельный линии. В этом разделе мы рассмотрим, как использовать уравнения для описания линий и плоскостей в пространстве.
- 11.5E: Упражнения для уравнений прямых и плоскостей в пространстве
- 11.6: Квадратичные поверхности
- Мы разработали векторные уравнения и векторные операции в трехмерном пространстве. описывать линии, плоскости и сферы. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями, для изучения множества других поверхностей, которые можно изобразить в трехмерной системе координат.




 Вам также необходимо определить «полюсные точки» как точки на противоположных концах любого диаметра сферы.
Вам также необходимо определить «полюсные точки» как точки на противоположных концах любого диаметра сферы.
 Например, листы бумаги, большие пенопластовые сферы (продаются в магазинах для рукоделия) или глобусы, а также диски Пуанкаре или гиперболические листы (см. Приложение А)
Например, листы бумаги, большие пенопластовые сферы (продаются в магазинах для рукоделия) или глобусы, а также диски Пуанкаре или гиперболические листы (см. Приложение А)
 Для эллиптической геометрии чем короче периметр треугольника, тем ближе сумма углов должна быть к 180 градусам, но сумма всегда должна быть больше 180.
Для эллиптической геометрии чем короче периметр треугольника, тем ближе сумма углов должна быть к 180 градусам, но сумма всегда должна быть больше 180. Миллиарды галактик, каждая из которых представляет собой гравитационно-связанное скопление миллиардов звезд, сейчас составляют большую часть видимой массы Вселенной; звезды производят энергию в результате ядерных реакций, в первую очередь синтеза водорода с образованием гелия. Эти и другие процессы в звездах привели к образованию всех остальных элементов».
Миллиарды галактик, каждая из которых представляет собой гравитационно-связанное скопление миллиардов звезд, сейчас составляют большую часть видимой массы Вселенной; звезды производят энергию в результате ядерных реакций, в первую очередь синтеза водорода с образованием гелия. Эти и другие процессы в звездах привели к образованию всех остальных элементов».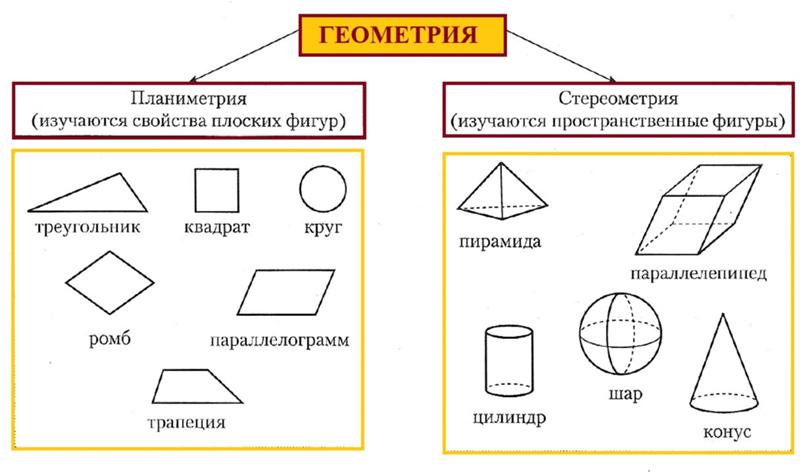 Чтобы расширить использование векторов до более реалистичных приложений, необходимо создать основу для описания трехмерного пространства.
Чтобы расширить использование векторов до более реалистичных приложений, необходимо создать основу для описания трехмерного пространства. 4E: Упражнения для перекрестного произведения
4E: Упражнения для перекрестного произведения