Формулы аналитической геометрии
Аналитическая геометрия на плоскости
- Прямая на плоскости
- Общее уравнение прямой
- Уравнение прямой, проходящей через точку (x0, y0) перпендикулярно нормальному вектору {A;B}
- Каноническое уравнение прямой, проходящей через точку (x0, y0) параллельно вектору {l;m}
- Параметрические уравнения прямой, проходящей через точку (x0, y0) параллельно вектору {l;m}
, t ∈ (-∞, ∞) - Уравнение прямой, проходящей через две заданные точки (x1, y1) и (x2, y2)
- Уравнение прямой с угловым коэффициентом k, где — угол наклона прямой к оси Оx
- Уравнение прямой в отрезках, где (a;0) и — координаты точек пересечения прямой с осями Оx и Оy
, a ≠ 0, b ≠ 0 - Нормальное уравнение прямой, где
- Нормальный вид общего уравнения прямой; знак нормирующего множителя противоположен знаку С
- Расстояние от точки (x0, y0) до прямой Ax+By+C=0
- Координаты точек пересечения двух прямых
A1x+B1y+C1=0 и A2x+B2y+C2=0 - Координаты точек пересечения прямых y=k1x+b1 и y=k2x+b2
- Условия параллельности прямых, заданных в общем виде A1x+B1y+C1=0, A2x+B2y+C2=0 и в виде y=k1x+b1, y=k2x+b2
- Условия перпендикулярности прямых, заданных в общем виде A1x+B1y+C1=0, A2x+B2y+C2=0 и в виде y=k1x+b1, y=k2x+b2
- Острый угол α между двумя прямыми, заданными в общем виде A1x+B1y+C1=0, A2x+B2y+C2=0 и в виде y=k1x+b1, y=k2x+b2
,
,
k1k2 ≠ -1, , если k1k2 = -1.
Аналитическая геометрия в пространстве
- Плоскость в пространстве
- Общее уравнение плоскости:
- Уравнение плоскости, проходящей через точку перпендикулярно вектору :
Пример 16. - Уравнение плоскости «в отрезках»:
.
Пример 17. - Нормальное уравнение плоскости (p – расстояние от начала координат до плоскости, {
xcosα + ycosβ + zcosγ — p = 0. - Нормальный вид общего уравнения плоскости (знак нормирующего множителя противоположен знаку D):
- Расстояние от точки до плоскости, заданной общим уравнением:
- Уравнение плоскости, проходящей через три точки (i=1, 2, 3):
- Угол между плоскостями :
- Условие параллельности плоскостей :
- Условие перпендикулярности плоскостей :
- Расстояние между двумя параллельными плоскостями
и :
- Прямая в пространстве
- Общие уравнения прямой
- Канонические уравнения прямой, проходящей через точку и имеющей направляющий вектор {l, m, n}
- Уравнения прямой в виде проекций на координатные плоскости
- Параметрические уравнения прямой
- Соотношения между координатами направляющего вектора прямой и коэффициентами общих уравнений прямой
- Канонические уравнения прямой, проходящей через точки с координатами
- Угол между прямыми с направляющими векторами {l1, m1, n1} и {l2, m2, n2}
- Условие параллельности двух прямых с направляющими векторами {l1, m1, n1} и {l2, m2, n2}
- Условие перпендикулярности двух прямых с направляющими векторами
{l1, m1, n1} и {l2, m2, n2}
- Прямая и плоскость в пространстве
- Уравнение пучка плоскостей, проходящих через прямую, заданную общими уравнениями
- Координаты точки пересечения прямой и плоскости
, где - Угол между прямой и плоскостью
- Условие перпендикулярности прямой и плоскости
- Условие параллельности прямой и плоскости
Формулы, уравнения, теоремы, примеры решения задач
Курс «Аналитическая геометрия»
Данный курс «Аналитическая геометрия» рассматриывает следующие темы: геометрические векторы, ориентация пространства, скалярное, векторное и смешанное произведение векторов, уравнения плоскости и прямой в пространстве в декартовой системе координат, различные системы координат на плоскости и в пространстве.
1. Геометрические векторы.
2. Ориентация пространства. Скалярное, векторное и смешанное произведение векторов.
3. Уравнения плоскости и прямой в пространстве в декартовой системе координат.
4. Различные системы координат на плоскости и в пространстве.
Наверх
1. Геометрические векторы.
§ 1. Определения свободного и закрепленного геометрических векторов.
Определение 1: Закрепленный вектор – отрезок с упорядоченными концами: AB,
A – начало вектора, В – конец вектора, АВ ≠ ВА.
Конец и начало вектора могут совпадать: АА – нулевой вектор.
Определение 2: Равенство закрепленных векторов:
Пусть AB и CD – закрепленные ненулевые векторы.
1) Соединим А с С и В с D (начальные и конечные точки векторов).
Если ABDC – параллелограмм, то AB = CD.
2) AB = CD, если закрепленный вектор EF : AB = EF и EF = CD.
3) Все нулевые векторы равны: АА = ВВ.
Определение 3: Свободный вектор (или просто вектор) – множество равных между собой (в смысле определения 2) закрепленных векторов.
Свободные векторы обозначаются прописными латинскими буквами – a.
Нулевой свободный вектор обозначается θ.
Определение 4: Закрепленный вектор AB является реализацией свободного вектора a, если a = { CD : CD = AB } ( То есть свободный вектор a – это множество закрепленных векторов CD, т.ч. CD = AB. )
Обозначение: AB a (допустимо а = АВ).
Предложение 1. с.в. а и т. О пространства ! з.в. ОА : ОА а.
( Т.е. для любого свободного вектора a и для любой точки О пространства существует единственный закреплённый вектор OA, который является реализацией а. )
Определение 5: Длина свободного вектора a – это длина его реализации:
|a| = |AB|, если AB a, |θ| = 0.
Определение 6: Угол между свободными векторами а и b – это наименьший угол между их реализациями ОА и ОВ ( ОАа, ОВb ).
Определение 7: Свободные векторы a и b равны (a = b), если они совпадают как множества.
Из определения свободного вектора очевидно, что для того, чтобы задать свободный вектор a, достаточно задать какую-либо его реализацию, т.е. закрепленный вектор AB a.
Определение 8: V3 – множество всех свободных векторов в пространстве R3.
§ 2. Операции над свободными векторами: сложение и умножение на число.
Определение 9: Сумма свободных векторов.
Пусть a, b V3. Возьмем произвольно точку О.
Тогда ! ОА a и ! AB b т.ч. OB a+b, т.е. a+b = { CD : CD = OB}
Корректность сложения: OB a+b, O’B’ a+b OB = O’B’.
Определение 10: Пусть a — свободный вектор, AB – его реализация, тогда BA является реализацией свободного вектора (-a).
(-a) – обратный вектор для a, т.е. (-a) = { BA : AB a }
Определение 11: Умножение вектора на число:
1) λ•θ = θ для λ R.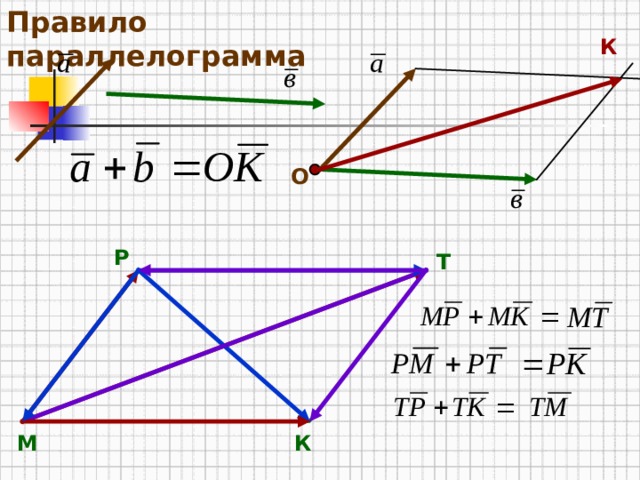
2) a ≠ θ, AB a, отрезок AB лежит на прямой l.
2.1) λ = 0 λ∙a = θ.
2.2) λ > 0 AC λ∙a, где AC т.ч. |AC| = λ•|AB|, C l и т. B и C находятся по одну сторону от т. А.
2.3) λ < 0 AD λ∙a, где AD т.ч. |AD| = |λ|∙|AB|, D l и т. B и D находятся по разные стороны от т. А.
Свойства операций над векторами: a, b, c V3 , λ, μ R
1) Коммутативность сложения
a + b = b + a.
2) Ассоциативность сложения
a + b + c = (a + b)+ c = a +( b + c).
3) a + θ = a.
4) a +(-a) = θ.
5) Ассоциативность умножения на число
λ(μ∙ a) = (λμ)∙ a
6) 1∙ a = a.
7) Дистрибутивность умножения на число относительно сложения векторов
λ∙( a + b) = λ∙ a +λ∙ b.
8) Дистрибутивность умножения на число относительно сложения чисел
(λ+μ)∙ a = λ∙ a +μ∙ a.
§ 3. Линейная зависимость векторов. Коллинеарность и компланарность векторов.
Определение 12: Векторы а1, а2, … , аn коллинеарны, если существует прямая l, содержащая реализацию каждого из них.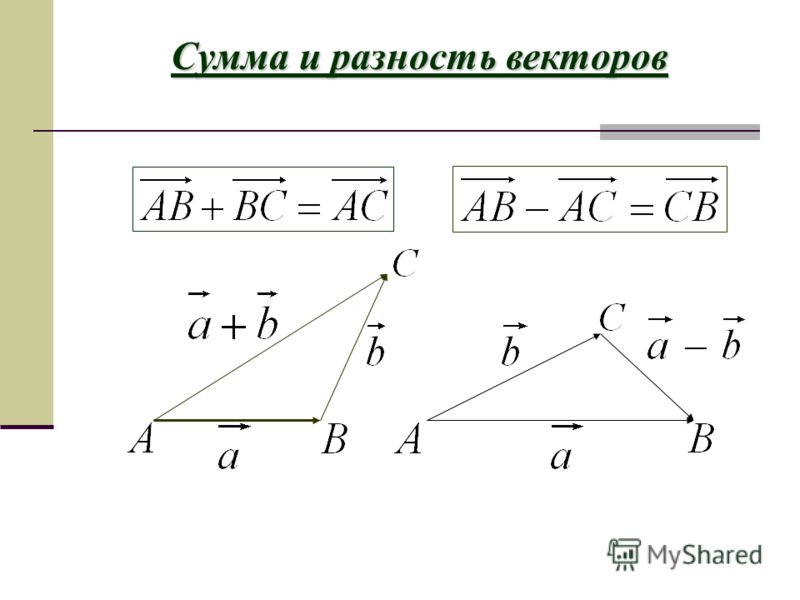
Обозначение: а || b
Предложение 2: a || b ó λ R, т.ч. a= λ∙b
Определение 13: Коллинеарные векторы а и b одинаково направлены, если ОАа, ОВb и т. А и В лежат по одну сторону от т. О.
Обозначение: а b
Определение 14: Коллинеарные векторы а и b разнонаправлены, если ОАа, ОВb и т. А и В лежат по разные стороны от т. О.
Обозначение: а b
Определение 15: Векторы а1, а2, … , аn компланарны, если существует плоскость в пространстве, содержащая реализацию каждого из них.
Пример : рассмотрим с.в. еа=а ( а≠ θ ).
еа коллинеарен а, одинаково направлен с а, |ea|=1.
Замечание: Любые два свободных вектора компланарны. Нулевой вектор имеет реализацию на любой плоскости в пространстве. Следовательно, три вектора: а, b, θ всегда компланарны.
Определение 16: Система векторов а1, а2, … , аn линейно зависима, если λ1, λ2, …, λ3 R, не все равные нулю, такие что λ1· а1+ λ2· а2+ λn· аn=0
Определение 17: Если λ1· а1+ λ2· а2+ λn· аn=0 только при λ1 = λ 2 = … = λ3 = 0, то система векторов а1, а2, … , аn линейно независима.
Предложение 3: Любая система из трёх и более ненулевых компланарных векторов линейно зависима.
Предложение 4: Любые три некомпланарных вектора линейно независимы.
§ 4. Проекции закреплённых и свободных векторов на плоскость и прямую.
Проецирование точек на плоскости и прямые хорошо изучается в школьном курсе геометрии, так что остаётся уговориться об обозначениях:
прΠ М; – ортогональная проекция т. М на плоскость Π,
прm М; ( || l ) – проекция т. М на прямую m параллельно прямой l
4.1 Ортогональная проекция на плоскость
Определение 18: Пусть А1= прΠ А, В1= прΠ B A1B1= прΠ AB.
( Т.е. з.в. A1B1 – это ортогональная проекция з.в. AB на плоскость Π )
Определение 19: Пусть АВ а и прΠ AB а1 а1= прΠ а.
( Т.е. с.в. а1 – это ортогональная проекция с.в. а на плоскость Π )
4.2 Общий случай проецирования на плоскость. ( Проецирование параллельно прямой l которая не || и не лежит на плоскости Π )
( Проецирование параллельно прямой l которая не || и не лежит на плоскости Π )
Начало и конец вектора проецируются на Π параллельно l , определения вводятся аналогично п. 4.1 .
4.3 Ортогональная проекция на прямую
Определение 20: Пусть А1= прm А, В1= прm B A1B1= прm AB.]
Определение 21: Пусть АВ а и прm AB а1 а1= прm а.
4.4 Общий случай проецирования на прямую. ( Проецирование параллельно прямой l которая не || и не совпадает с прямой m)
Начало и конец вектора проецируются на m параллельно l , определения вводятся аналогично п. 4.3 .
§ 5. Базисы в V3. Координаты векторов относительно базиса.
Определение 22: Базисом в пространстве свободных векторов V3 называется любая упорядоченная тройка некомпланарных векторов.
Пусть В : а1, а2, а3 – фиксированный базис в V3.
Определение 23: Координатами вектора b относительно базиса В называется упорядоченная тройка чисел {x, y, z}, т. ч. b=x·a1+ y·а2+z· а3.
ч. b=x·a1+ y·а2+z· а3.
Обозначение: b={x, y, z}B
Замечание: Под координатами закреплённого вектора понимают координаты соответствующего ему свободного вектора.
Теорема1: Соответствие между V3 и R3 при фиксированном базисе взаимно однозначно, т.е. b V3 ! {x, y, z} R3 и {x, y, z} R3 ! b V3, т.ч. b={x, y, z}B
Соответствие между вектором и его координатами в данном базисе обладает следующими свойствами:
Пусть b1={x1, y1, z1}B, b2={x2, y2, z2}B b1+ b2={x1+ x2, y1+ y2, z1+ z2}B
Пусть b={x, y, z}B, λ R λ·b={ λ·x, λ· y, λ·z}B
Пусть b1|| b2, b1= {x1, y1, z1}B, b2={x2, y2, z2}B
(Здесь: любое число).
Определение 24: Ортонормированный ( декартов ) базис – это i, j, k, т.ч.
1) | i |=| j |=| k |=1,
2) i j k i.
Замечание: i, j, k – это стандартное обозначение именно декартова базиса. Т.о., встречая его в тексте можно обойтись без дополнительных пояснений относительно системы координат.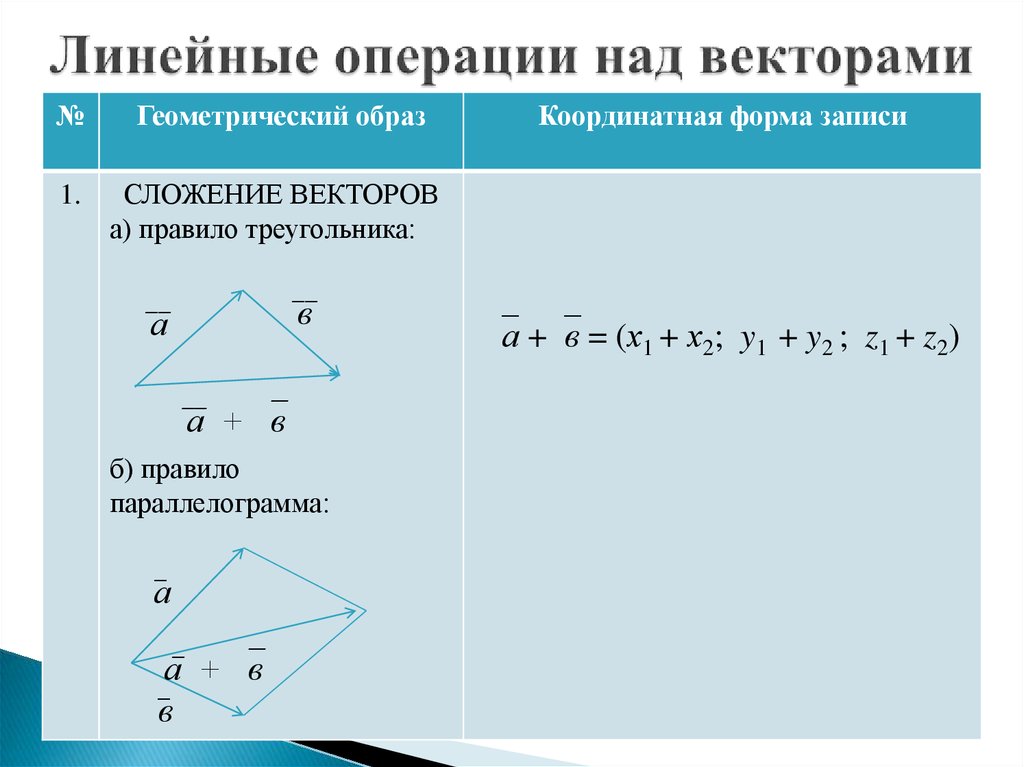
§ 6. Ортогональная система координат в пространстве. Длина вектора.
Определение 25: Ортогональная ( декартова ) система координат это
единица масштаба ( отрезок, длина которого будет считаться «единичной» ),
фиксированная т.О ( начало координат )
ортонормированный базис е1, е2, е3 (изменим стандартное обозначения для удобства)
пересекающиеся в т.О прямые l1, l2, l3, т.ч. li содержит реализацию еi, i=1,2,3.
Если на li зафиксировать «положительное» направление в соответствии с направлением еi, получим оси координат (стандартное обозначение осей: Ox, Oy и Oz).
Теорема2: Если известны координаты точек А=(x1,y1,z1) и B=(x2,y2,z2) , то координаты вектора АВ можно вычислить по формуле: АВ={ x2-x1 , y2-y1 , z2-z1 }.
Теорема3: Если в ортогональной системе координат b={x, y, z}, то | b |=.
Наверх
2.
 Ориентация пространства. Скалярное, векторное и смешанное произведение векторов.
Ориентация пространства. Скалярное, векторное и смешанное произведение векторов.§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
Для дальнейшего изучения свойств пространства необходимо ввести определение ориентации пространства. Строгая теория, касающаяся этого понятия не очень сложна, но достаточно суха. В связи с этим ограничимся лишь некоторыми “качественными” пояснениями.
Итак, все упорядоченные некомпланарные тройки векторов могут быть разбиты на два непересекающихся класса: правые тройки и левые тройки.
Определение 1: Упорядоченная тройка некомпланарных векторов а1, а2, а3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а1 к а2 и от а2 к а3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.
Есть и ещё один способ разделить эти два класса:
Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая.
Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая.
Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададимориентацию пространства.
Далее будем считать положительными правые тройки векторов. Все дальнейшие определения будем давать с учетом этого
§ 2. Скалярное произведение векторов.
Определение 2: Скалярное произведение ставит в соответствие паре векторов a и b число (a,b)=|a|·|b|·cosφa,b.
Свойства скалярного произведения:
1. коммутативность: (a,b)=(b,a)
2. (а,а)=|а|2
3. (a,b)=0 <=> a b
4. Дистрибутивность: (a1+а2,b)= (a1,b)+ (a2,b)
5. (а, λ·b)= λ·(a,b) λ R.
Утверждение 1: В декартовом базисе если а={x1,y1,z1}, b={x2,y2,z2}, то (a,b)=x1·x2+y1·y2+z1·z2.
§ 3. Векторное произведение векторов.
Определение 3: Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что
| [a,b] |=Sa,b, где Sa,b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то Sa,b=0.)
a [a,b] b.
a, b, [a,b] – правая тройка.
Свойства векторного произведения:
[a,b] = -[b,a]
[a,b] = θ ó a || b
[a1+a2,b] = [a1,b]+[a2,b]
λ·[a,b] = [λ·a,b] = [a,λ·b] λ R.
Утверждение 2: В декартовой системе координат (базис i, j, k), a={x1, y1, z1}, b={x2, y2, z2}
=> [a,b] =
=
§4. Смешанное произведение векторов.
Определение 4: Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c).
Утверждение 3: <a,b,c>=Va,b,c, если a,b,c – правая тройка, или <a,b,c>= -Va,b,c, если a,b,c – левая тройка. Здесь Va,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то Va,b,c=0.)
Здесь Va,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то Va,b,c=0.)
Утверждение 4: В декартовой системе координат, если a={x1, y1, z1}, b={x2, y2, z2},
с={x3, y3, z3}, => <a,b,c>=.
Наверх
3. Уравнения плоскости и прямой в пространстве в декартовой системе координат.
§ 1. Каноническое уравнение плоскости в пространстве
Пусть в декартовой системе координат дан вектор n={A,B,C} и точка М0=(x0,y0,z0).
Построим плоскость Π, проходящую через т. М0, перпендикулярную вектору n (этот вектор называютнормальным вектором или нормалью плоскости).
Утверждение 1: М Π ó М0М n.
М0М={x-x0, y-y0, z-z0} n ó A(x-x0)+B(y-y0)+C(z-z0)=0. (*)
(См. свойства скалярного произведения)
Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0.
Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости.
§ 2. Канонические и параметрические уравнения прямой в пространстве
Пусть в декартовой системе координат дан вектор a={p,q,r} и точка М0=(x0,y0,z0).
Построим прямую l, проходящую через т. М0, параллельную вектору a (этот вектор называютнаправляющим вектором прямой).
Утверждение 2: М l ó М0М || a.
М0М={x-x0, y-y0, z-z0} || a ó tR, т.ч. М0М=t·a =>
(**)
Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.
В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t0=0 он находится в точке М0, в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).
Теперь несколько преобразуем формулы (**).
Выразим из каждой строчки параметр t:
Замечание 2: Эта компактная запись на самом деле содержит три уравнения.
Замечание 3: Это формальная запись и выражение вида в данном случае допустимо.
Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.
§3. Расстояние от точки до плоскости в пространстве
Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М1=(x1,y1,z1).
Утверждение 3: расстояние от точки М1 до плоскости Π вычисляется по формуле:
§4. Координаты точки, делящей отрезок в заданном соотношении
Пусть в декартовой системе координат М1=(x1,y1,z1), М2=(x2,y2,z2) .
Утверждение 4: Координаты т. М, т.ч. М1М=λ∙ММ2, находятся по следующим формулам:
.
Наверх
4. Различные системы координат на плоскости и в пространстве.
§ 1. Декартова система координат на плоскости
Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы.
Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.
Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.
Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).
§ 2. Полярная система координат на плоскости
Для того, чтобы задать полярную систему координат на плоскости, надо зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный отрезок и положительное направление отсчета угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.
Положение точки на плоскости задаётся двумя числами. Первое – расстояние от точки до начала координат, а второе – угол между зафиксированным лучом и отрезком, соединяющим точку и начало координат.
Обычно направление отсчета угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ,φ). Очевидно, ρ0.
Существуют формулы перехода между заданными стандартным образом декартовой и полярной системами координат. Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то
Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то
x = ρ∙cosφ,
y = ρ∙sinφ.
В других случаях формулы зависят от постановки задачи, но получить их легко из геометрических соображений.
С помощью этих формул можно осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д..
В полярной системе координат очень просто выглядят уравнения прямых, проходящих через начало координат и окружностей с центром в этой точке. Кроме того, уравнения многих стандартных, часто используемых, кривых принято (с точки зрения простоты) записывать в полярных координатах.
§3. Декартова система координат в пространстве
Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.
Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.
§4. Цилиндрическая система координат в пространстве
Цилиндрическая система координат в пространстве – “родственница” полярной системы координат на плоскости. Чтобы получить цилиндрическую систему надо на плоскости ввести полярную систему координат и добавить вертикальную координатную ось. Т.о., координаты точки – три числа: первые два – полярные координаты проекции нашей точки на плоскость, третье – величина проекции точки на вертикальную ось.
Из геометрических соображений можно получить формулы перехода между цилиндрической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:
x = ρ·cosφ,
y = ρ·sinφ,
z = z.
§5. Сферическая система координат в пространстве
Сферическая система координат вводится следующим образом: фиксируем плоскость, на ней — точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение точки М задаётся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.
Положение точки М задаётся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.
Из геометрических соображений можно получить формулы перехода между сферической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:
x = ρ·sinθ·cosφ,
y = ρ·sinθ·sinφ,
z = ρ·cosθ.
Вектор. Определение и основные понятия
- Главная
- Справочник
- Геометрия
- Вектора
- Вектор. Определение и основные понятия
- Обозначение вектора
- Длина вектора
- Нулевой вектор
- Длина вектора на плоскости
- Длина вектора в трехмерном пространстве
- Длина вектора в n-мерном пространстве
- Коллинеарные вектора
- Сонаправленные вектора
- Противоположно направленные вектора
- Компланарные вектора
- Равные вектора
Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление.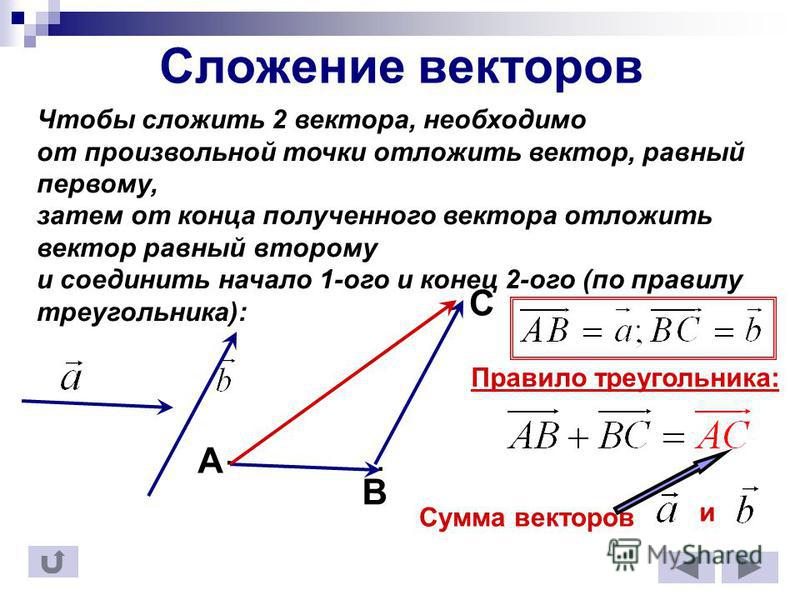 Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Обозначение вектора
Вектор началом которого есть точка , а концом — точка , обозначается . Также вектора обозначают одной маленькой буквой, например
Направление вектора (от начала к концу) на рисунках отмечается стрелкой.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа .
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора .
Нулевой вектор
Нулевой вектор обычно обозначается как .
Длина нулевого вектора равна нулю.
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Длина вектора на плоскости
Длина вектора в трехмерном пространстве
Длина вектора в n-мерном пространстве
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами
Сонаправленные вектора
Два коллинеарных вектора и называются сонаправленными векторами, если их направления совпадают:
Противоположно направленные вектора
Два коллинеарных вектора и называются противоположно направленными векторами, если их направления совпадают:
Компланарные вектора
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.
Равные вектора
Вектора и называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
, если и .
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Вектора Формулы Геометрия Алгебра Теория Обозначения 31453
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Координаты вектора
Координатами вектора называются проекции вектора на оси координат
Вектора Формулы Геометрия Алгебра Теория Обозначения
Сложение и вычитание векторов
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Декартовы координаты и векторы в пространстве
Декартовы координаты — система координат, состоящая из двух перпендикулярных осей.

Вектора Формулы Геометрия Алгебра Теория Обозначения
Умножение вектора на число
Произведением вектора u≠0 на число λ≠0 называется вектор w, модуль которого равен |λ||u|, направление которого совпадает с вектором u при λ>0 и противоположно ему при λ
Вектора Формулы Геометрия Алгебра Теория Обозначения
Скалярное произведение векторов
Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Векторное произведение векторов
Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Смешанное произведение векторов
Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w
Вектора Формулы Геометрия Алгебра Теория Обозначения
ЕГЭ: обязательные предметы для сдачи экзамена
ЕГЭ Экзамены
Что такое Ом
1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.

Электротехника Формулы Физика Теория Электричество
Конвертер возраста животных и человека
Калькуляторы времени и даты Калькулятор Расчёт Конвертер Преобразовать Время
Что такое масса, вес нетто и вес брутто: в чем разница? Что больше: вес, масса нетто или брутто?
Вес — это физическая величина, а именно сила, воздействующая на горизонтальную поверхность или вертикальную подвеску.
Масса и вес Масса Физика Теория Единицы измерения
Чему равен 1 литр в кг? Сколько весит литр воды в килограммах: цифры и факты
Вес одного литра воды примерно 998,5 грамм.
Масса и вес
Таблица мер измерения
Таблицы
Таблица квадратов
Таблицы по алгебре Математика Таблицы
Сколько в ампере ватт, как перевести амперы в ватты и киловатты
Мощность – это скорость расходования энергии, выраженная в отношении энергии ко времени: 1 Вт = 1 Дж/1 с.
 Один ватт равен отношению одного джоуля (единице измерения работы) к одной секунде.
Один ватт равен отношению одного джоуля (единице измерения работы) к одной секунде.Электротехника Формулы Физика Теория Электричество
определение, формула для нахождения, аналитический метод и графическое построение
В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block id=»32″]
…
Оглавление:
- Определения векторной математики
- Аналитический метод
- Вычисление разности графически
- Решение задач
[block id=»33″]
Максимально наглядно применение векторных величин объясняется в физике. Самыми простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, поскольку помимо численных значений они также обладают направлением действия. Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.
Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
- Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
- Длина (модуль) — это длина направленного отрезка.
- Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
- Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
- Вектора являются равными, когда они сонаправлены и одинаковы по модулю.

- Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
- Разностью векторов a и b называют сумму a и (— b), где (— b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.
Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a {a₁; a₂} и b {b₁; b₂} расчёты будут иметь следующий вид: c {c₁; c₂} = {a₁ — b₁; a₂ — b₂}.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a {a₁; a₂; a₃} и b {b₁; b₂; b₃} координаты разности будут также получены попарным вычитанием: c {c₁; c₂; c₃} = {a₁ — b₁; a₂ — b₂; a₃ — b₃}.
Вычисление разности графически
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
- По заданным координатам построить векторы, для которых нужно найти разность.
- Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).

- Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.
[block id=»4″]
Результат операции вычитания показан на рисунке ниже.
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:
- Построить исходные направленные отрезки.
- Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
- Построить сумму: соединить начало первого отрезка с концом второго.

Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:
AB {0 — 1; 4 — (— 3)} = {— 1; 7}
Аналогичный расчёт выполняется для CD:
CD {— 3 — 5; 2 — 8} = {— 8; — 6}
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид {c₁; c₂} = {a₁ — b₁; a₂ — b₂}. Для конкретного случая можно записать:
Для конкретного случая можно записать:
q = {— 1 — 8; 7 — ( — 6)} = { — 9; — 1}
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
[block id=»5″]
Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
[block id=»6″]
Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
- m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
- (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
- (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности.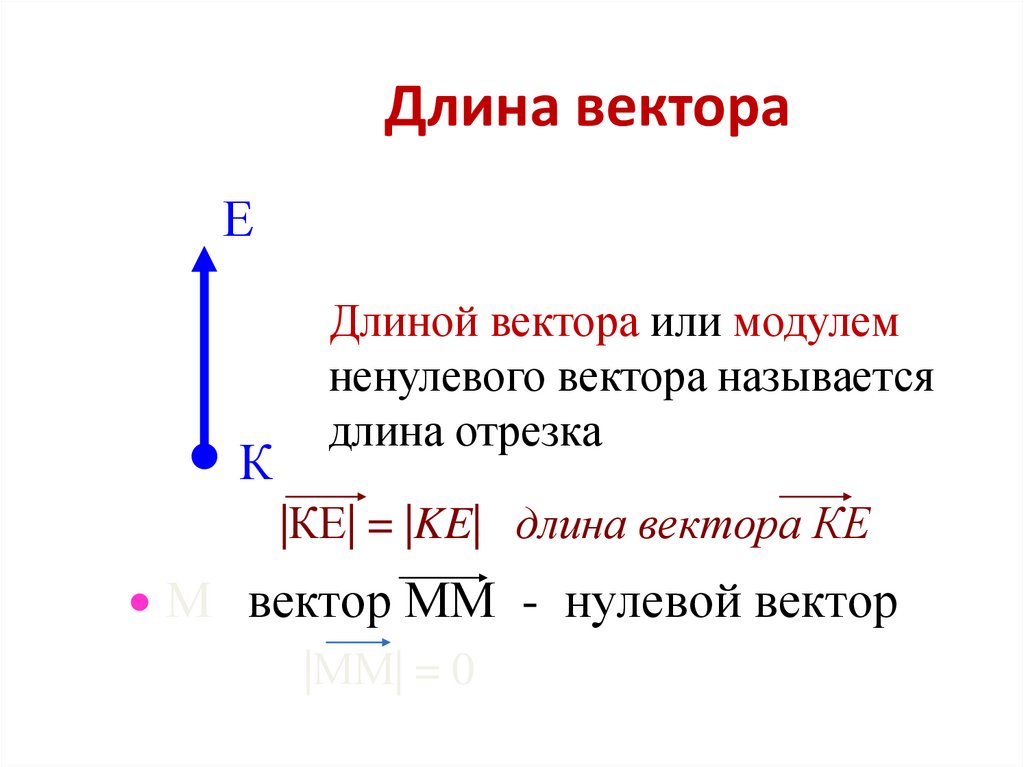 Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block id=»2″]
[block id=»10″]
Векторная геометрия – объяснение и примеры
Моделирование играет важную роль во всех разделах математики, включая векторную геометрию . Это:
«Изучение геометрических представлений векторов, а именно представления в виде направленных прямых
отрезков или стрелок».
В этом разделе мы обсудим следующие аспекты векторной геометрии:
- Что такое вектор в геометрии?
- Определение вектора в геометрии
Что такое вектор в геометрии?
Величины, имеющие как величину, так и направление, известны как векторы. Мы можем использовать график для визуального представления векторов. Например, вектор, соединяющий две точки A и B, называется:
Мы можем использовать график для визуального представления векторов. Например, вектор, соединяющий две точки A и B, называется:
AB
Вектор в стандартном положении будет иметь начало координат в качестве начальной точки.
В компонентной или столбцовой форме векторы записываются упорядоченной парой (x, y). Вектор, записанный в таком виде, начинается в начале координат и заканчивается в точке упорядоченной пары.
отрицательное заданного вектора находится путем изменения направления вектора на противоположное. В этом случае его величина (или длина) такая же, как у исходного вектора.
Например, вектор:
BA = – AB
является отрицательным вектором AB, и:
|| ВА || = ||- AB || = || АВ ||
Определение вектора в геометрии
Для двух точек P и Q стрелка от P до Q будет иметь длину и направление.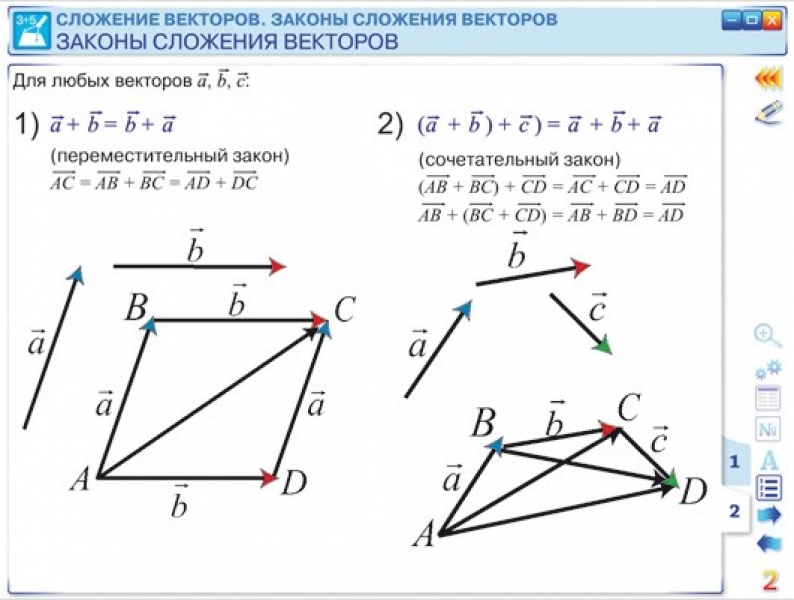
Предположим, что P и Q — две произвольные точки в пространстве R 3 . Отрезок линии от P до Q обозначается как PQ. В геометрии это известно как вектор от P до Q.
Этот вектор будет иметь величину и направление. Точка P называется хвостом (или начальной точкой) вектора PQ, , а точка Q называется кончиком (или головой или конечной точкой) вектора PQ . Его длина обозначается как || PQ ||.
Предположим, точка P имеет координаты (x 1 , y 1 ), а точка Q имеет координаты (x 2 , y 2 ) на плоскости R 3 2
. Затем длина вектора PQ определяется шагами, указанными ниже.
Шаг 1: Сначала вычтите первую составляющую точки P из первой составляющей точки Q. Затем найдите квадрат полученной разности.
Шаг 2: Аналогичным образом вычтите второй компонент точки P из второго компонента точки Q и возведите это число в квадрат.
Шаг 3: Затем сложите два квадрата вместе.
Шаг 4: Наконец, извлеките квадратный корень из числа, полученного на третьем шаге. Это скалярное число будет длиной вектора.
- Обратите внимание, что длина или величина вектора является скалярной величиной.
Теперь давайте попробуем на нескольких примерах попрактиковаться в работе с векторной геометрией.
Пример 1
Имея две точки, O в начале координат (0,0) и A с координатами (3,2), определите длину ||OA||.
Решение:
Сравнивая компоненты, получаем
(х 1 , у 1 ) = (0,0) и (х 2 , у ) 2 = 3, .
Используя вышеупомянутую формулу для нахождения длины двух векторов a, мы имеем: 92 )
Дополнительное упрощение дает нам:
‖ OA ‖ = √(9+4)
‖ OA ‖ = √13.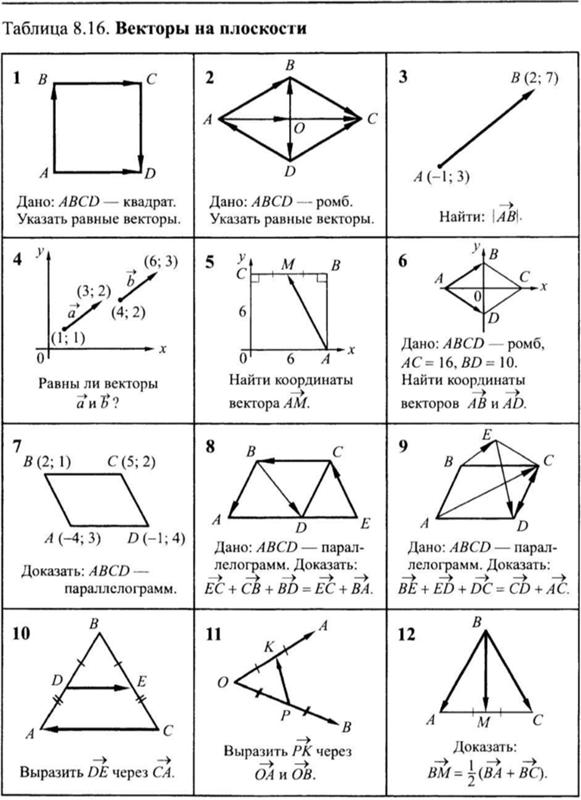
Таким образом, ||OA|| = √13 — длина вектора, соединяющего две точки.
Обратите внимание, что если начальная точка или хвост вектора находится в начале координат, т. е. если вектор записан в стандартной форме, то величина OA равна:
|| А || = √(x 2 + y 2 )
Где A = ОА = (х, у).
Пример 2
Имея две точки, A = (3, 2) и B = (2, 2), определите длину вектора AB.
Решение :
Сравнение компонентов, мы получаем
(x 1 , Y 1 ) = (3, 2) и (x 2 , Y 2 ) = (x 2 , Y 2 9003) = (x 2 , Y 2 9003) и (x 2 , Y 2 9003) и (x 2 , Y 2 9003) и (x 2 , Y 2 9003) и (x 2 , Y 2 9003). 2, 2).
Используя приведенную выше формулу для нахождения длины двух векторов a, мы имеем
‖ AB ‖ = √((x_2-x_1 )^2+(y_2 – y_1 )^2 ) 92 )
‖ AB ‖ = √1+ 0
‖ AB ‖ = 1
Таким образом, || АВ || = 1 — длина вектора, соединяющего две точки.
Пример 3
На рисунке ниже даны два вектора AB = 2 a и BC = 3 b, . Точка D — это середина BE, а E — середина BC.
Используя приведенную выше информацию, определите следующие векторы через a and b:
- (a) BC
- (b) BD
- (c) AD
Solution:
- ( а) Используя треугольный закон сложения векторов, имеем
ВС = ВА + АС
. Отметим связь между ВА и вектором известной длины, АВ 0 6 : 4 60002 = ( — AB ) + AC
Заменить известные значения AB и AC дает нам :
= -2 A + 3 B .
Таким образом, BC = -2 a + 3 b длина вектора.
- (b) Так как Е дано как середина ВС, а D — середина ВЕ, то D — одна четвертая часть расстояния до ВС:
BD = ¼ ВС
Подстановка значения BC из части (a) дает нам:
= ¼ (-2 a + 3 b )
= -1/2 a 4 0 б .
Таким образом, BD = -1/2 a + 3/4 b длина вектора.
- (c) Используя треугольный закон сложения векторов, мы имеем:
AD = AB + BD
Подставляя известные значения AB и AC дает нам:
= 2 a + (-1/2 a + 3/4 b )
Это можно упростить: -1/2 a ) + 3/4 b
= 3/2 a + 3/4 b .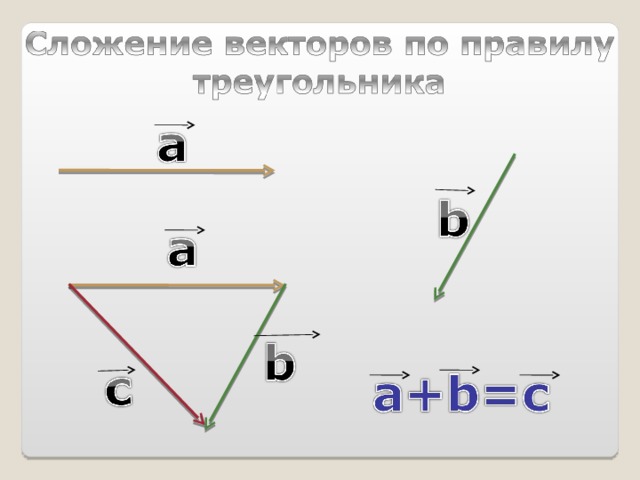
Таким образом, AD = 3/2 a + 3/4 b — это длина вектора.
Пример 4
Пусть A = (2, 0, -4) и B = (2, 1, -2) две точки в пространстве Р 3 . Если 2 a – || б || B = 3/2 ( A — 2 x ), где A = OA , B = OB и x = OX и X = (X 1 , x 2 , x 3 ), найдите значения x 1 , x 2 и x 3 .
Решение :
Получаем соотношение:
2 a – || б || b = 3/2 ( a – 2 x ),
Где a = (2, 0, -4), b = (2, 1, -2) и x = (х 1 , х 2 , х 3 ).
Сначала оценим норму (величину) || б || используя предыдущие определения и процедуру нахождения величины вектора, начальная точка которого находится в начале координат. Это дает нам:
|| б || = √(2 2 + 1 2 + (-2) 2 )
= √(4 + 1 + 4)
= √9
=3
Следовательно, || б || = 3. Теперь имеем:
|| б || b = 3 (2, 1, -2)
= (3∙2, 3∙1, 3∙(-2))
= (6, 3, -6)
Аналогично имеем:
2 a = 2 (2, 0, -4) = (4, 0, -8).
Следовательно, левая часть станет
2 a – || б || б = (4, 0, -8) – (6, 3, -6)
= (4-6, 0-3 , -8-(-6))
= (-2, -3) , -8+6)
= (-2, -3, -2).
Правая часть примет вид:
3/2 ( a – 2 x ) = 3/2 ((4, 0, -8)– 2(x 1 , x 2 , x 3 ))
= 3/2 ((4, 0, -8) – (2x 1 , 2x 2 , 2x 3 ))
= 3/2 (4-2x 1 , 2x 2 , -8-2x 3 ).
Подставив теперь эти значения в левую и правую части уравнения, мы получим:
2 a – || б || b = 3/2 ( a – 2 x )
(-2, -3, -2) = 3/2 (4-2x 1 , 2x 2 , -8-2x 3 )
2 (-2, -3, -2) = 3 (4-2x 1 , 2x 2 , -8-2x 3 )
(-4, -6, — 4) = (3(4-2x 1 ), 3(2x 2 ), 3(-8-2x 3 )).
Сравнение компонентов x, y и z дает нам:
-4 = 3(4-2x 1 )
-4 = 12 -6x 1
6x 1 = 12 -4
6x 1 = 8
x 1 = 8/6
Следовательно, x 1 = 4/6
. 3.
-6 = 3 (2x 2 )
-6 = 6x 2
x 2 = -6/6
Следовательно, x 2 = -1
-4 = 3 (x 2 = -1
-4 = 3 (x 2 = -1
-4 = 3 (X -8-2x 3 )
-4= -24 -6x 3
6x 3 = -24 + 4
6x 3 = -20
х 3 = -20/6
Следовательно, х 3 = -10/3.
Таким образом:
х 1 = 4/3, х 2 = -1 и х 3 = -10/3.
Практические вопросы- По двум точкам, V = (2, 5, 1) и C = (3, -2, 1), определите длину вектора VC .
- По двум точкам, G = (5, 5) и H = (4, -10), определить || ОГ || и || ОХ || 2 , где O = (0, 0) — начало координат.
- В треугольнике ABC CB = 4CX, XA = 5XY, а Z — середина треугольника AB. Пусть СХ = м и БЗ = n .
- (A) Определите длину XB и XA . С точки зрения M и N
- (B) и N
- (B) и N
- (B) 44444444443 CZ 43.
 и N
и N - . = (4 м + n )
- (в) Оценить ‖ CY ‖/‖ CZ ‖ и (площадь ACY)/(площадь ACZ)
- Пусть ABCDEF правильный шестиугольник, и пусть AB = n .
- (а) Объясните, почему вектор ED = n .
- (b) Если до н.э. = M и CD = P, Найти AC и AD
- (C) Найти FD .
- Дана прямая ABC, пусть БК = 3 АВ . Если OA = a и AB = b, то выразить OC через a и b .

Ответы
- || ВК || = 5√2
- || ОГ || = 5√2, || OH ||² = 116
- В данном треугольнике
- (a) XB = 3 м и XA =3 m + 2 n
- (b) CZ=CB+BZ=4m+n
- (c) Значения: , и (площадь ACY)/(площадь ACZ) = 2/5
4. Пусть ABCDEF — правильный шестиугольник и AB =
4n.
- (a) Напротив AB .
- (b) Если BC = м и CD = р . Затем AC = N + M и AD = N + M + P
- (C) FD = -( M + N ) ( т.
 е. отрицательный вектор AC ).
е. отрицательный вектор AC ).
- OC = a +4 b
3.5: Векторы с геометрической точки зрения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7115
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand1 Государственный университет долины
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе.
 Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы. - Что такое вектор?
- Как мы используем геометрическую форму векторов, чтобы найти сумму двух векторов?
- Как мы используем геометрическую форму векторов, чтобы найти скалярное число, кратное вектору?
- Как мы используем геометрическую форму векторов, чтобы найти разность двух векторов?
- Чему равен угол между двумя векторами?
- Почему сила является вектором и как мы используем векторы и треугольники для определения сил, действующих на объект?
Всем нам приходилось что-то ронять и смотреть, как оно падает на землю. Происходит, конечно, то, что сила тяжести заставляет объект падать на землю. На самом деле, мы каждый день испытываем силу гравитации, просто находясь на Земле. Вес каждого человека является мерой силы тяжести, поскольку фунты являются единицей силы.
 Поэтому, когда человек весит 150 фунтов, это означает, что гравитация оказывает прямое воздействие на этого человека силой в 150 фунтов. Обратите внимание, что мы описали это количеством и направлением (прямо вниз). Такая величина (с величиной и направлением) называется вектором.
Поэтому, когда человек весит 150 фунтов, это означает, что гравитация оказывает прямое воздействие на этого человека силой в 150 фунтов. Обратите внимание, что мы описали это количеством и направлением (прямо вниз). Такая величина (с величиной и направлением) называется вектором.Теперь предположим, что человек, который весит 150 фунтов, стоит на холме. В математике мы упрощаем ситуацию и говорим, что человек стоит на наклонной плоскости, как показано на рис. 3.20. (Сделав холм прямой линией, мы упростим математику.) На рисунке \(\PageIndex{1}\) объект находится на наклонной плоскости в точке \(P\). Наклонная плоскость составляет угол \(\тета\) с горизонтом. Вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз). На диаграмме также показаны два других вектора. Вектор \(\textbf{b}\) перпендикулярен
Рисунок \(\PageIndex{1}\): Наклонная плоскость
к плоскости представляет силу, с которой объект действует на плоскость. Вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости.
 Этот вектор представляет собой силу тяжести вдоль плоскости. В этом и следующем разделах мы узнаем больше об этих векторах и о том, как определить величины этих векторов. Мы также увидим, что с нашим определением сложения двух векторов \(\textbf{w} = \textbf{a} + \textbf{b}\).
Этот вектор представляет собой силу тяжести вдоль плоскости. В этом и следующем разделах мы узнаем больше об этих векторах и о том, как определить величины этих векторов. Мы также увидим, что с нашим определением сложения двух векторов \(\textbf{w} = \textbf{a} + \textbf{b}\).Определения
Существуют некоторые величины, для описания которых требуется только число. Мы называем это число величиной количества. Одним из таких примеров является температура, поскольку мы описываем ее только числом, таким как 68 градусов по Фаренгейту. Другими такими величинами являются длина, площадь и масса. Эти типы величин часто называют скалярными величинами . Однако есть и другие величины, требующие как величины, так и направления. Одним из таких примеров является сила, а другим — скорость. Мы бы описали скорость примерно 45 миль в час к северо-западу. Скорость и сила являются примерами количество векторов . Другими примерами векторов являются ускорение и перемещение.

Некоторые векторы тесно связаны со скалярами. В математике и естественных науках мы делаем различие между скоростью и скоростью . Скорость — это скаляр, и мы бы сказали, что наша скорость равна 65 милям в час. Однако, если бы мы использовали скорость, мы бы сказали что-то вроде 65 миль в час на восток. Это отличается от скорости \(65\) миль в час на север, хотя в обоих случаях скорость равна 65 милям в час.
Определения: Векторы и скаляры
- Вектор — это величина, которая имеет как величину, так и направление.
- Скаляр — это величина, которая имеет только величину.
Геометрическое представление векторов
Векторы могут быть представлены геометрически в виде стрелок (направленных отрезков). Наконечник стрелки указывает направление вектора, а длина стрелки описывает величину вектора.
Вектор с начальной точкой \(P\) (конец стрелки) и конечной точкой \(Q\) (конец стрелки) может быть представлен как
\[\overrightarrow{PQ}, \textbf{v} или \overrightarrow{v}.
 \]
\]Мы часто пишем \(v = \overrightarrow{PQ}\). В этом тексте мы будем использовать полужирный шрифт для обозначения вектора. При письме карандашом и бумагой мы всегда используем стрелку над буквой (например, \(\overrightarrow{v}\)) для обозначения вектора. величина (или норма или длина ) вектора \(\textbf{v}\) обозначается \(\textbf{|v|}\). Важно помнить, что \(|\textbf{v}|\) — это число, представляющее величину или длину вектора \(\textbf{v}\).
Согласно нашему определению, вектор обладает атрибутами длины (величины) и направления, но положение не упоминается. Таким образом, мы будем считать два вектора равными, если они имеют одинаковую величину и направление. Например, если два разных автомобиля движутся со скоростью \(45\) миль в час на северо-запад (но в разных местах), они имеют равные векторы скорости. Дадим более формальное определение.
Определение: Равные векторы
Два вектора равны тогда и только тогда, когда они имеют одинаковую величину и одно и то же направление.
 Когда векторы \(\textbf{v}\) и \(\textbf{w}\) равны, мы пишем \(\textbf{v} = \textbf{v}\).
Когда векторы \(\textbf{v}\) и \(\textbf{w}\) равны, мы пишем \(\textbf{v} = \textbf{v}\).Упражнение \(\PageIndex{1}\)
На следующих диаграммах вектор \(\textbf{v}\) показан рядом с четырьмя другими векторами. Какие (если есть) из этих четырех векторов равны вектору \(\textbf{v}\)?
- Ответ
Вектор \(\textbf{w}\) является единственным вектором, равным вектору \(\textbf{v}\). Вектор \(\textbf{u}\) имеет то же направление, что и \(\textbf{v}\), но другую величину. Вектор \(\textbf{a}\) имеет ту же величину, что и \(\textbf{v}\), но другое направление (обратите внимание, что направление a противоположно вектору \(\textbf{v}\)) . Вектор \(\textbf{b}\) имеет другое направление и другую величину, чем вектор \(\textbf{v}\).
Операции с векторами
Скалярное кратное вектору
Удвоение скалярной величины — это просто умножение ее величины на \(2\). Например, если в контейнере \(20\) унций воды, а количество воды удвоено, в нем будет \(40\) унций воды.
 Что мы подразумеваем под удвоением вектора? Основная идея состоит в том, чтобы сохранить то же направление и умножить величину на \(2\). Таким образом, если объект имеет скорость \(5\) футов в секунду на юго-восток, а второй объект имеет скорость в два раза больше, второй объект будет иметь скорость \(10\) футов в секунду в юго-восточном направлении. В этом случае говорят, что мы умножили вектор на скаляр \(2\). Теперь мы делаем определение, которое также учитывает, что скаляр может быть отрицательным.
Что мы подразумеваем под удвоением вектора? Основная идея состоит в том, чтобы сохранить то же направление и умножить величину на \(2\). Таким образом, если объект имеет скорость \(5\) футов в секунду на юго-восток, а второй объект имеет скорость в два раза больше, второй объект будет иметь скорость \(10\) футов в секунду в юго-восточном направлении. В этом случае говорят, что мы умножили вектор на скаляр \(2\). Теперь мы делаем определение, которое также учитывает, что скаляр может быть отрицательным.Определение
Для любого вектора \(\textbf{v}\) и любого скаляра \(c\) вектор \(c\textbf{v}\) (называемый скаляром, кратным вектору \(\textbf {v}\) — вектор, величина которого в \(|c|\) умножается на величину вектора \(\textbf{v}\).
- Если \(c > 0\), то направление \(c\textbf{v}\) совпадает с направлением \(\textbf{v}\).
- Если \(c < 0\), то направление \(c\textbf{v}\) противоположно направлению \(\textbf{v}\).
- Если \(c = 0\), то \(c\textbf{v} = 0 \textbf{v} = 0\).

Вектор \(\textbf{0}\) называется нулевым вектором , а нулевой вектор не имеет ни величины, ни направления. Иногда мы пишем \(\overrightarrow{0}\) для нулевого вектора.
В этом определении \(|c|\) является абсолютным значением скаляра \(c\). Следует соблюдать осторожность, чтобы не спутать это с обозначением \(\textbf{|v|}\), которое является величиной вектора \(\textbf{v}\). Это одна из причин, по которой важно иметь обозначения, которые четко указывают, когда мы работаем с вектором или скаляром.
Сложение векторов
Мы покажем, как складывать векторы с двумя векторами смещения. Как и в случае скорости и скорости, существует различие между смещением и расстоянием. Расстояние является скаляром. Таким образом, можно сказать, что мы проехали 2 мили. Перемещение , с другой стороны, представляет собой вектор, состоящий из расстояния и направления. Таким образом, векторы 2 мили на север и 2 мили на восток являются разными векторами смещения.

Теперь, если мы проедем 3 мили на север, а затем проедем 2 мили на восток, мы закончим в точке, которая определяет новый вектор смещения. См. схему справа. На этой диаграмме \(\textbf{u}\) — это «3 мили на север», а \(\textbf{v}\) — «2 мили на восток». Векторная сумма \(\textbf{u} + \textbf{v}\) идет от начальной точки \(\textbf{u}\) до конечной точки \(\textbf{v}\).
Определение: сумма двух векторов
Сумма двух векторов определяется следующим образом: мы располагаем векторы так, чтобы начальная точка \(\textbf{w}\) совпадала с конечной точкой \ (\textbf{v}\). Вектор \(\textbf{v} + \textbf{w}\) — это вектор, начальная точка которого совпадает с начальной точкой \(\textbf{v}\), а конечная точка совпадает с конечной точкой \( \textbf{ш}\).
Вектор \( \textbf{v} + \textbf{w}\) называется суммой или равнодействующей векторов \(\textbf{v}\) и \(\textbf{w}\).
В определении обратите внимание, что векторы \(\textbf{v}\), \(\textbf{w}\) и \(\textbf{v} + \textbf{w} \) размещаются так, чтобы в результате получился треугольник.
 Длины сторон этого треугольника равны величинам этих сторон \(|\textbf{v}|\), \(|\textbf{w}|\) и \(|\textbf{v} + \textbf {ж}|\). Если мы поместим два вектора \(\textbf{v}\) и \(\textbf{w}\) так, чтобы их начальные точки совпадали, мы можем использовать параллелограмм для сложения двух векторов. Это показано на рисунке \(\PageIndex{2}\).
Длины сторон этого треугольника равны величинам этих сторон \(|\textbf{v}|\), \(|\textbf{w}|\) и \(|\textbf{v} + \textbf {ж}|\). Если мы поместим два вектора \(\textbf{v}\) и \(\textbf{w}\) так, чтобы их начальные точки совпадали, мы можем использовать параллелограмм для сложения двух векторов. Это показано на рисунке \(\PageIndex{2}\).Рисунок \(\PageIndex{2}\): сумма двух векторов с использованием параллелограмма
Обратите внимание, что вектор \(\textbf{v}\) образует пару противоположных сторон параллелограмма, как и вектор \(\textbf{ш}\).
Упражнение \(\PageIndex{2}\)
На следующей диаграмме показаны два вектора, \(\textbf{v}\) и \(\textbf{w}\). Нарисуйте следующие векторы:
- \(\textbf{v} + \textbf{w}\)
- \(2\textbf{v}\)
- \(2\textbf{v} + \textbf{w}\)
- \(-2\textbf{ш}\)
- \(-2\textbf{ш + v}\)
- Ответить
Вычитание векторов
Прежде чем объяснять, как вычитать векторы, мы сначала объясним, что подразумевается под «отрицательным вектором».
 Это работает аналогично отрицательному вещественному числу. Например, мы знаем, что когда мы добавляем \(-3\) к \(3\), результатом будет \(0\). То есть \(3 + (-3) = 0\)
Это работает аналогично отрицательному вещественному числу. Например, мы знаем, что когда мы добавляем \(-3\) к \(3\), результатом будет \(0\). То есть \(3 + (-3) = 0\)Нам нужно нечто подобное для векторов. Для вектора \(\textbf{w}\) идея состоит в том, чтобы использовать скалярное число \((-1)\textbf{w}\). Вектор \((-1)\textbf{w}\) имеет ту же величину, что и \(\textbf{w}\), но имеет направление, противоположное вектору \(\textbf{w}\). Мы определяем \(-\textbf{w}\) как \((-1)\textbf{w}\). На рисунке показано, что когда мы добавляем \(-\textbf{w}\) к \(\textbf{w}\), конечная точка суммы совпадает с начальной точкой суммы, и поэтому результатом является ноль вектор. То есть \(\textbf{w} + (-\textbf{w}) = \textbf{0}\).
Рисунок \(\PageIndex{3}\): сумма вектора и его отрицательного значения
Теперь мы можем определить вычитание векторов. Идея почти такая же, как вычитание действительных чисел в том, что для любых двух действительных чисел \(a\) и \(b\), \(a — b = a + (-b)\).

Определение: разница между векторами
Для любых двух векторов \(\textbf{v}\) и \(\textbf{w}\) разница в между \(\textbf{v}\) и \(\textbf{w}\) обозначается \(\textbf{v} — \textbf{w}\) и определяется следующим образом:
\[ \textbf{v} — \textbf{w} = \textbf{v} + (-\textbf{w}).\]
Мы также говорим, что вычитаем вектор \(\textbf{w}\ ) из вектора \(\textbf{v}\).
Упражнение \(\PageIndex{3}\)
На следующей диаграмме показаны два вектора, \(\textbf{v}\) и \(\textbf{w}\). Нарисуйте следующие векторы:
- \(-\textbf{w}\)
- \(\textbf{v — w}\)
- \(-\textbf{v}\)
- \(\textbf{ш — v}\)
- Ответить
Угол между двумя векторами
Мы видели, что мы можем использовать треугольники, чтобы помочь нам сложить или вычесть два вектора. Длины сторон треугольника — это величины некоторых векторов.
 \circ — \theta\). Мы рассмотрим это в следующей проверке прогресса.
\circ — \theta\). Мы рассмотрим это в следующей проверке прогресса.Рисунок \(\PageIndex{3}\): Угол между двумя векторами
Упражнение \(\PageIndex{4}\)
Предположим, что векторы \(\textbf{a}\) и \(\ textbf{b}\) имеют величины 80 и 60 соответственно, а угол \(\theta\) между двумя векторами равен 53 градусам. На рис. 3.24 мы нарисовали параллелограмм, определяемый этими двумя векторами, и пометили вершины для справки.
Рисунок 3.24: Диаграмма для проверки выполнения 3.27Помните, что вектор определяется его величиной и направлением. Определим \(|\textbf{a + b}|\) и меру угла между \(\textbf{a}\) и \(\textbf{a + b}\)
Определим меру \(\угол АВС\).
В \(\треугольнике ABC\) длина стороны \(AB\) равна \(|\textbf{a}| = 80\), а длина стороны \(BC\) равна \(|\textbf {b}|=60\). Используйте этот треугольник и закон косинусов, чтобы определить длину третьей стороны, которая равна \(|\textbf{a + b}|\). 9\круг\).
Сила
Важной векторной величиной является сила.
 В физике сила, действующая на объект, определяется как любое взаимодействие, которое, если ему не противостоять, изменит движение объекта. Таким образом, сила заставит объект изменить свою скорость, то есть объект ускорится. Говоря более неформально, сила — это толчок или притяжение объекта.
В физике сила, действующая на объект, определяется как любое взаимодействие, которое, если ему не противостоять, изменит движение объекта. Таким образом, сила заставит объект изменить свою скорость, то есть объект ускорится. Говоря более неформально, сила — это толчок или притяжение объекта.Сила гравитации влияет на нашу жизнь. Величина силы тяжести, действующей на человека, равна его весу. Направление силы тяжести прямо вниз. Итак, если человек весом 150 фунтов стоит неподвижно на земле, то земля также оказывает на человека силу в 150 фунтов в направлении вверх. Чистая сила, действующая на неподвижного человека, равна нулю. Это пример того, что известно как 9\circ)}\]
\[|\textbf{a}| \приблизительно 53,21\]
Величина вектора a (и вектора b) приблизительно равна \(53,21\) фунта.Наклонные плоскости
В начале этого раздела мы обсудили силы, возникающие при размещении объекта на наклонной плоскости. Рисунок 3.25 — это схема, которую мы использовали, но теперь мы добавили метки для некоторых углов.
 Напомним, что вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз), вектор \(\textbf{b}\) перпендикулярен плоскости и представляет силу, с которой объект давит на плоскость, а вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости. Этот вектор представляет собой силу тяжести вдоль плоскости. Обратите внимание, что мы также добавили вторую копию вектора a, которая начинается с вершины вектора \(\textbf{b}\). 9\circ\), так как это два острых угла прямоугольного треугольника. Отсюда делаем вывод, что \(\beta = \theta\). Это дает нам окончательный вариант диаграммы сил на наклонной плоскости, показанной на рис. 3.26. Обратите внимание, что векторы \(\textbf{a}\),
Напомним, что вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз), вектор \(\textbf{b}\) перпендикулярен плоскости и представляет силу, с которой объект давит на плоскость, а вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости. Этот вектор представляет собой силу тяжести вдоль плоскости. Обратите внимание, что мы также добавили вторую копию вектора a, которая начинается с вершины вектора \(\textbf{b}\). 9\circ\), так как это два острых угла прямоугольного треугольника. Отсюда делаем вывод, что \(\beta = \theta\). Это дает нам окончательный вариант диаграммы сил на наклонной плоскости, показанной на рис. 3.26. Обратите внимание, что векторы \(\textbf{a}\),Рис. 3.26: Наклонная плоскость
\(\textbf{b}\) и \(\textbf{w}\) образуют прямоугольный треугольник, и поэтому мы можем использовать тригонометрию прямоугольного треугольника для задач, связанных с силами на наклонной плоскости.
Упражнение \(\PageIndex{6}\) 9\circ\) градусов по горизонтали.
 Используя диаграмму, подобную той, что изображена на рис. 3.26, определите величину силы, приложенной к плоскости со стороны объекта, и величину силы, действующей на плоскость, действующую на объект из-за гравитации.
Используя диаграмму, подобную той, что изображена на рис. 3.26, определите величину силы, приложенной к плоскости со стороны объекта, и величину силы, действующей на плоскость, действующую на объект из-за гравитации.Примечание : Величина силы, направленной вниз по плоскости, будет силой, направленной вверх по плоскости, которая необходима для удержания объекта в неподвижном состоянии.
- Ответить
Используя обозначения на рис. 3.26, получаем следующее: 9\circ)\]
\[|\textbf{b}| \приблизительно 244,54\]
\[|\textbf{a}| \около 51,98\]Объект прикладывает силу около \(244,54\) фунтов, перпендикулярную плоскости, а сила тяжести вниз по плоскости на объект составляет около \(51,98\) фунтов. Таким образом, чтобы удерживать объект неподвижным, к объекту должна быть приложена сила около \(51,98) фунта, направленная вверх по плоскости.
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
- Векторы и скаляры
- Вектор — это величина, которая имеет как величину, так и направление.

- Скаляр — это величина, которая имеет только величину.
- Два вектора равны тогда и только тогда, когда они имеют одинаковую величину и одно и то же направление.
- Вектор — это величина, которая имеет как величину, так и направление.
- Скаляр, кратный вектору
Для любого вектора \(\textbf{v}\) и любого скаляра \(c\) вектор \(c\textbf{v}\) (называемый скаляром, кратным вектору \(\textbf{v} \) — это вектор, величина которого в \(|c|\) умножается на величину вектора \(\textbf{v}\).0006
- Если \(c > 0\), то направление \(c\textbf{v}\) совпадает с направлением \(\textbf{v}\).
- Если \(c < 0\), то направление \(c\textbf{v}\) противоположно направлению \(\textbf{v}\).
- Если \(c = 0\), то \(c\textbf{v} = 0\textbf{v} = 0\).
Вектор \(\(\textbf{0}\)\) называется нулевым вектором, а нулевой вектор не имеет ни величины, ни направления. Иногда мы пишем \(\overrightarrow{0}\) для нулевого вектора.
- Сумма двух векторов
Сумма двух векторов определяется следующим образом: мы располагаем векторы так, чтобы начальная точка \(\textbf{w}\) совпадала с конечной точкой \(\textbf{v}\).
 Вектор \(\textbf{v} + \textbf{w}\) — это вектор, начальная точка которого совпадает с начальной точкой \(\textbf{v}\), а конечная точка совпадает с конечной точкой \( \textbf{ш}\).
Вектор \(\textbf{v} + \textbf{w}\) — это вектор, начальная точка которого совпадает с начальной точкой \(\textbf{v}\), а конечная точка совпадает с конечной точкой \( \textbf{ш}\).Вектор \( \textbf{v} + \textbf{w}\) называется суммой или равнодействующей векторов \(\textbf{v}\) и \(\textbf{w}\ ). 9\circ\)) когда они имеют одинаковую начальную точку.
Эта страница под названием 3.5: Векторы с геометрической точки зрения распространяется под лицензией CC BY-NC-SA 3.0, автором, ремиксом и/или куратором являются Тед Сандстром и Стивен Шликер (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- вектор смещения
- расстояние
- величина вектора
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12 - векторов
12.3 Скалярный продукт
Вот вопрос, ответ на который оказывается очень полезным: Даны два вектора, чему равен угол между ними?
Может быть не сразу понятно, что вопрос имеет смысл, но это не трудно превратить в вопрос, который делает. Так как векторы имеют нет позиции, мы, как обычно, вольны размещать векторы где угодно как. Если два вектора расположены «хвост к хвосту», теперь разумное толкование вопроса: мы ищем меру наименьший угол между двумя векторами в плоскости, в которой они лежат. Рисунок 12.3.1 иллюстрирует ситуацию. 92)\кр &=2a_1b_1+2a_2b_2+2a_3b_3\cr |{\bf A}||{\bf B}|\cos\theta&=a_1b_1+a_2b_2+a_3b_3\cr \cos\theta&=(a_1b_1+a_2b_2+a_3b_3)/(|{\bf A}||{\bf B}|)\cr }$$ Итак, немного простой арифметики с координатами $\bf A$ и $\bf B$ позволяет вычислить косинус угла между ними. Если необходимо, мы можем использовать арккосинус, чтобы получить $\theta$, но во многих задач $\cos\theta$ оказывается всем, что нам действительно нужно.

В числителе дроби, которая дает нам $\cos\theta$, получается много, поэтому мы даем ему имя и более компактную запись: мы называем это точечное произведение и запишите его как $${\bf A}\cdot{\bf B} = a_1b_1+a_2b_2+a_3b_3.$$ Это тот же самый символ, который мы используем для обычного умножения, но здесь никогда не должно быть никакой путаницы; вы можете сказать из контекста, были ли мы являются «перемножением» векторов или чисел. (Мы также можем использовать точку для скалярное умножение: $a\cdot{\bf V}=a{\bf V}$; опять же ясно что имеется в виду из контекста.)
Пример 12.3.1. Найдите угол между векторами ${\bf A}=\langle 1,2,1\rangle$ и ${\bf B}=\langle 3,1,-5\rangle$. Мы знаем это $\cos\theta={\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)= (1\cdot3 + 2\cdot1 + 1\cdot(-5))/(|{\bf A}||{\bf B}|)=0$, поэтому $\theta=\pi/2$, то есть векторы перпендикулярны. $\квадрат$
Пример 12.3.2. Найдите угол между векторами ${\bf A}=\langle 3,3,0\rangle$ и ${\bf B}=\langle 1,0,0\rangle$.
 2})=1$, поэтому угол
между ${\bf A}$ и собой равен нулю, что, конечно, правильно.
92})$, который не определен.
С другой стороны, обратите внимание, что, поскольку ${\bf A}\cdot{\bf 0}=0$, выглядит
сначала как будто $\cos\theta$ будет равно нулю, что, как мы видели, означает
что векторы перпендикулярны; только тогда, когда мы замечаем, что
знаменатель также равен нулю, если мы столкнемся с проблемами. Один из способов «исправить»
это означает принятие соглашения о том, что нулевой вектор ${\bf 0}$ равен
перпендикулярно всем векторам; то в общем случае можно сказать, что если
${\bf A}\cdot{\bf B}=0$, $\bf A$ и $\bf B$ перпендикулярны.
$\квадрат$
2})=1$, поэтому угол
между ${\bf A}$ и собой равен нулю, что, конечно, правильно.
92})$, который не определен.
С другой стороны, обратите внимание, что, поскольку ${\bf A}\cdot{\bf 0}=0$, выглядит
сначала как будто $\cos\theta$ будет равно нулю, что, как мы видели, означает
что векторы перпендикулярны; только тогда, когда мы замечаем, что
знаменатель также равен нулю, если мы столкнемся с проблемами. Один из способов «исправить»
это означает принятие соглашения о том, что нулевой вектор ${\bf 0}$ равен
перпендикулярно всем векторам; то в общем случае можно сказать, что если
${\bf A}\cdot{\bf B}=0$, $\bf A$ и $\bf B$ перпендикулярны.
$\квадрат$Обобщая примеры, отметим следующие полезные факты:
1. Если $\bf A$ параллелен или антипараллелен $\bf B$, то ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=\pm1$, и наоборот, если ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=1$, $\bf A$ и $\bf B$ параллельны, а если ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=-1$, $\bf A$ и $\bf B$ антипараллельны.
 (Векторы
параллельно
если они указывают в одном направлении,
антипараллельный
если они направлены в разные стороны.)
(Векторы
параллельно
если они указывают в одном направлении,
антипараллельный
если они направлены в разные стороны.)2. Если $\bf A$ перпендикулярно $\bf B$, то ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=0$, и наоборот, если ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=0$, тогда $\bf A$ и $\bf B$ перпендикулярны.
Имея два вектора, часто бывает полезно найти выступ одного вектора на другой, потому что это оказывается важным смысл во многих обстоятельствах. Точнее, учитывая ${\bf A}$ и ${\bf B}$ ищем вектор, параллельный $\bf B$, но с длиной определяется $\bf A$ естественным образом, как показано на рисунок 12.3.2. $\bf V$ выбран так, чтобы треугольник, образованный $\bf A$, $\bf V$ и ${\bf A}-{\bf V}$ является прямоугольным треугольником.
Рисунок 12.3.2. $\bf V$ — проекция $\bf A$ на $\bf B$.
Используя небольшую тригонометрию, мы видим, что $$ |{\bf V}|=|{\bf A}|\cos\theta= |{\bf A}|{{\bf A}\cdot{\bf B}\over|{\bf A}||{\bf B}|}= {{\bf A}\cdot{\bf B}\over|{\bf B}|}; $$ это иногда называют скалярная проекция $\bf A$ на $\bf B$ .
 2}{\bf B}.
$$
Убедитесь, что вы понимаете, почему ${\bf B}/|{\bf B}|$ является вектором
длина один (также называется
92}{\bf В}$$
антипараллелен $\bf B$, а его длина равна
$$\left|{{\bf A}\cdot{\bf B}\over|{\bf B}|}\right|.$$
Таким образом, скалярная проекция $\bf A$ на $\bf B$
может быть положительным или отрицательным. Если
он отрицательный, это означает, что вектор проекции антипараллелен
к $\bf B$ и что длина вектора проекции равна
абсолютное значение скалярной проекции. Конечно, вы также можете
вычислить длину вектора проекции, как обычно, применяя
формула расстояния до вектора.
2}{\bf B}.
$$
Убедитесь, что вы понимаете, почему ${\bf B}/|{\bf B}|$ является вектором
длина один (также называется
92}{\bf В}$$
антипараллелен $\bf B$, а его длина равна
$$\left|{{\bf A}\cdot{\bf B}\over|{\bf B}|}\right|.$$
Таким образом, скалярная проекция $\bf A$ на $\bf B$
может быть положительным или отрицательным. Если
он отрицательный, это означает, что вектор проекции антипараллелен
к $\bf B$ и что длина вектора проекции равна
абсолютное значение скалярной проекции. Конечно, вы также можете
вычислить длину вектора проекции, как обычно, применяя
формула расстояния до вектора.Рисунок 12.3.3. $\bf V$ — проекция $\bf A$ на $\bf B$.
Обратите внимание, что фраза «проекция на $\bf B$» немного вводит в заблуждение. если понимать буквально; все, что дает $\bf B$, — это направление; в длина $\bf B$ не влияет на конечный вектор. В рис. 12.3.4, например, $\bf B$ короче, чем вектор проекции, но это вполне приемлемо.
Рисунок 12.3.4. $\bf V$ — проекция $\bf A$ на $\bf B$.
 2$
2$2. ${\bf u}\cdot{\bf v} = {\bf v}\cdot{\bf u}$
3. ${\bf u}\cdot({\bf v}+{\bf w}) = {\bf u}\cdot{\bf v}+{\bf u}\cdot{\bf w}$
4. $(a{\bf u})\cdot{\bf v}=a({\bf u}\cdot{\bf v}) = {\ bf и} \ cdot (а {\ bf v}) $
$\qed$
Вы можете использовать Sage для вычисления скалярных произведений и связанных величин, таких как скалярная и векторная проекции.
Пример 12.3.1 Найдите $\langle 1,1,1\rangle\cdot\langle 2,-3,4\rangle$. (отвечать)
Пример 12.3.2 Найдите $\langle 1,2,0\rangle\cdot\langle 0,0,57\rangle$. (отвечать)
Пример 12.3.3 Найдите $\langle 3,2,1\rangle\cdot\langle 0,1,0\rangle$. (отвечать)
Пример 12.3.4 Найдите $\langle -1,-2,5\rangle\cdot\langle 1,0,-1 \rangle$. (отвечать)
Пример 12.3.5 Найдите $\langle 3,4,6\rangle\cdot\langle 2,3,4\rangle$. (отвечать)
Пример 12.3.6 Найдите косинус угла между $\langle 1,2,3\rangle$
и $\langle 1,1,1\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)
(отвечать)
Пример 12.3.7 Найдите косинус угла между $\langle -1, -2, -3\rangle$ и $\langle 5,0,2\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)
Пример 12.3.8 Найдите косинус угла между $\langle 47,100,0\rangle$ и $\langle 0,0,5\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)
Пример 12.3.9 Найдите косинус угла между $\langle 1,0,1\rangle$ и $\langle 0,1,1\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)
Пример 12.3.10 Найдите косинус угла между $\langle 2,0,0\rangle$ и $\langle -1,1,-1\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)
Пример 12.3.11 Найдите угол между диагональю куба и одной из сторон края, прилегающие к диагонали. (отвечать)
Пример 12.3.12 Найдите скалярную и векторную проекции $\langle 1,2,3\rangle$ на $\langle 1,2,0\rangle$. (отвечать)
Пример 12. 3.13 9\circ$ от горизонтали. Результирующая сила
тянуть вагон горизонтально вдоль
земля должна быть 10 фунтов. Какова величина необходимого
заставить ${\bf F}$?
(отвечать)
3.13 9\circ$ от горизонтали. Результирующая сила
тянуть вагон горизонтально вдоль
земля должна быть 10 фунтов. Какова величина необходимого
заставить ${\bf F}$?
(отвечать)
Пример 12.3.19 Используйте скалярное произведение, чтобы найти ненулевой вектор ${\bf w}$ перпендикулярно обоим ${\bf u}=\langle 1,2,-3\rangle$ и ${\bf v}=\langle 2,0,1\rangle$. (отвечать)
Пример 12.3.20 Пусть ${\bf x}=\langle 1,1,0 \rangle$ и ${\bf y}=\langle 2,4,2 \rangle$. Найдите единичный вектор, который перпендикулярен обоим $\bf x$ и $\bf y$. (отвечать) 92$. Чем этот результат лучше известный как?
Пример 12.3.25 Докажите, что диагонали ромба пересекаются под прямым углом.
Пример 12.3.26 Предположим, что ${\bf z}=|{\bf x}| {\bf у} + |{\bf у}| {\ бф х} $ где $\bf x$, $\bf y$ и $\bf z$ — ненулевые векторы. Доказывать что $\bf z$ делит пополам угол между $\bf x$ и $\bf y$.
Пример 12.3.27 Докажите теорему 12.3.5.
Угол между двумя векторами Формула
Векторная величина – это физическая величина, имеющая как величину, так и направление. Когда на частицу действуют два вектора, результирующее действие на частицу будет зависеть от угла между этими векторами. Поэтому важно знать угол между ними.
Когда на частицу действуют два вектора, результирующее действие на частицу будет зависеть от угла между этими векторами. Поэтому важно знать угол между ними.
Некоторые свойства вектора для вычисления угла
Вектор представлен стрелкой, параллельной направлению вектора.
- Вектор остается неизменным, если он передается параллельно самому себе.
- Два вектора, имеющие одинаковое направление, являются параллельными векторами.
- Два вектора, имеющие противоположные направления, являются антипараллельными векторами.
- Два вектора, имеющие одинаковую величину и направление, являются равными векторами.
- Два вектора, имеющие одинаковую величину и противоположное направление, называются отрицательными векторами.
Скалярное произведение
Также известно как скалярное произведение векторов. У него есть только величина, но нет направления.
Два вектора A и B
Тогда скалярное произведение A и B определяется как,
= |A| |Б| cosθ.
Особые случаи
- Когда угол между векторами равен 0 градусов.
То есть θ = 0°
⇒ |A| |Б| cosθ.
⇒ |А| |Б| cos0°
⇒ |A| |Б| [cos0° = 1]
- Когда угол между векторами равен 180 градусов.
⇒ |А| |Б| cosθ.
⇒ |А| |Б| cos180°
⇒ – |A| |Б| [cos180° = -1]
- Когда угол между векторами равен 90 градусов.
⇒ |А| |Б| cosθ.
⇒ |А| |Б| cos90°
⇒ |А| |Б| × 0 [cos90° = 0]
⇒ 0,
Формула для угла между двумя векторами
Косинус угла между двумя векторами равен сумме произведений отдельных составляющих двух векторов, разделенных произведением величины двух векторов.
Два вектора A и B
=| А | | Б | cosθ.
cosθ =
θ = cos -1
в картезианской форме,
A = A x I + A Y J + A Z K
B = B x I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I + I +.
B y j + B z k
cosθ =
Свойства скалярного произведения
- Скалярное произведение коммутативно.
- Дополнительный продукт является распределительным.
В физике при конвекции угол между двумя векторами лежит в пределах 0 ≤ θ ≤ 180. Когда хвосты или вершины обоих векторов совпадают, вычисляется угол между векторами.
Хвост совпадает
Голова совпадает
Проблемы с образцами
Вопрос 1: Найдите угол между векторами (если они образуют равностороннюю треуголь0004 ЭКВИЛАСТИЧЕСКИЙ ТРЕЙНЕЛЬНЫЙ совпадают друг с другом, следовательно, угол между векторами a и b равен углу между двумя сторонами равностороннего треугольника = 60°. Из рисунка выше видно, что начало или конец вектора b и c не совпадают друг с другом. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе. Вектор c смещен параллельно самому себе Теперь мы видим, что хвосты векторов b и c совпадают друг с другом, следовательно, такой же, как внешний угол при равностороннем треугольнике = 120°. Хвост векторов a и c совпадает Для векторов a и c хвосты обоих векторов совпадают, поэтому угол между векторами a и c равен углу угол между двумя сторонами равностороннего треугольника = 60°. Вопрос 2: Найдите углы между векторами, если они образуют равнобедренный прямоугольный треугольник. Решение: 
 Из приведенного выше рисунка видно, что начало или конец векторов a и b не совпадают друг с другом. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
Из приведенного выше рисунка видно, что начало или конец векторов a и b не совпадают друг с другом. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
вектор смещен параллельно самому себе
Теперь хвосты векторов a и b совпадают и образуют угол, равный внешнему углу прямоугольного равнобедренного треугольника = 135°.
- Векторы b и c
Прямоугольный равнобедренный треугольник
На приведенном выше рисунке вершина или решка векторов b и c не совпадают. Таким образом, при использовании свойства вектор остается неизменным, если он передается параллельно самому себе.
b вектор сдвинут параллельно самому себе
Теперь хвосты векторов b и c совпадают и образуют угол, равный внешнему углу прямоугольного равнобедренного треугольника = 135°.
- Векторы a и c
Прямоугольный равнобедренный треугольник
На приведенном выше рисунке вершины и решки векторов a и c не совпадают. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
Вектор с перемещается параллельно самому себе
Теперь хвосты векторов а и с совпадают и составляют угол, равный прямому углу равнобедренного треугольника = 90°.
Вопрос 3: Найдите угол между векторами A = i + j + k и вектором B = -2i – 2j – 2k.
Решение:
Из формулы,
A = A x I + A Y J + A Z K
B = B x I + B Y
B = B x I + B y j. + B z k
cosθ=
Здесь в заданном вопросе
A= i + j + k.
В= -2i -2j -2k.
Подстановка значений в формулу
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ = -6/6
⇒ cosθ = -1
⇒ θ = 180 °.
ВОПРОС 4: Угол нахождения между вектором A = 3i + 4J и B = 2i + J
Решение:
A = A x I + A Y J + A Z k
B = B x i + B y j + B z k
cosθ =
Здесь дано,
A = 3i + 4J + 0K
B = 2i + J + 0K
Заменить значения в формуле,
⇒ COSθ =
⇒ Cosθ =
⇒ cosθ =
⇒ Cosθ =
⇒ Cosθ =
⇒ Cosθ =
θ = cos -1 ()
⇒ θ = cos -1 ()
Вопрос 5: Найдите угол между вектором A = i + j и вектором B = j + k.
Решение:
Из формулы
A = A x i + A Y J + A Z K
B = B x I + B Y J + B Z K
COSθ =
Здесь, в данном вопросе,
⇒ A = I +. j
⇒ B = j + k
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =.
⇒ θ = cos -1 (1/2)
⇒ θ = 60°.
Векторный продукт: определение, формула и отношение
Что такое умножение \(4\) на \(5\), это \(20\), легко. Умножать числа довольно легко, и каждый может это сделать, но что, если вас попросили умножить два вектора, \(\vec{a}=2\hat{i} + 3\hat{j}\) и \(\vec {b}=\шляпа{i} — 3\шляпа{k}\), ну не все так просто. Векторы — это очень отдельная сущность, классические правила числового умножения здесь малопригодны. Чтобы получить произведение двух или более векторов, нам нужно понять концепцию Векторный продукт .
Определение векторного произведения
Обычное умножение двух чисел на этом этапе хорошо определено. Но умножить два вектора не так просто. Произведение двух векторов можно выполнить двумя разными способами; либо по скалярному произведению, либо по векторному произведению. Скалярное произведение двух векторов дает скалярную величину, как следует из названия. В то время как векторное произведение двух векторов дает вектор, поэтому оно и называется векторным произведением.
Векторное произведение двух векторов дает вектор, который находится в направлении, перпендикулярном плоскости, образованной двумя векторами. Величина результирующего вектора является произведением величин двух исходных векторов и синуса угла между их направлениями.
Предположим, есть два вектора, которые образуют панель xy между собой. Векторное произведение этих векторов будет перпендикулярно плоскости xy, то есть оси z.
Векторная производная продукта
Пусть есть два вектора, \(\vec{A}\) и \(\vec{B}\), и \(\theta\) — угол между ними.
Векторное произведение между ними обозначается \(\vec{A}\times\vec{B}\) (‘\(\times\)’ не следует путать со знаком умножения, здесь оно обозначает векторное произведение ) из-за символа креста векторное произведение также известно как перекрестное произведение . Теперь, когда векторы и угол между ними установлены, давайте еще раз посмотрим на определение, но в математической манере:
Векторное произведение двух ненулевых векторов \(\vec{A}\) и \(\vec{B}\) равно \(\vec{A}\times\vec{B}=AB\ space sin\theta\space\hat{n}\), где \(A\) и \(B\) — величины векторов, а \(\theta\) — острый угол между двумя векторами. И \(\шляпа{n}\) представляет собой единичный вектор в направлении, перпендикулярном плоскости, образованной двумя векторами.
Важно указать, что ни один из векторов не является нулевым вектором, т.е. нулевым вектором. В этом случае векторное произведение не имеет геометрического значения. В результате векторного произведения получается вектор, имеющий величину \(AB\space sin\theta\) и указывающий в направлении, которое перпендикулярно плоскости, образованной двумя векторами, то есть перпендикулярно обоим векторам одновременно.
Чтобы продемонстрировать, как это выглядит, рассмотрите диаграмму ниже:
Два вектора A и B образуют другой вектор как их векторное произведение, StudySmarter Originals
Предположим, что векторы ориентированы таким образом, что они лежат в плоскости xy, т.е. z-компонента векторов равна 0. Если мы возьмем векторное произведение, его можно представить как поворот винта в направлении \(\vec{A}\) к \(\vec{B}\), что равно направление против часовой стрелки. Направление, в котором будет двигаться винт, — вертикально вверх, т. Е. Положительная ось z. Вертикальная стрелка — это в точности вектор, образованный их векторным произведением. На приведенной выше диаграмме \(\vec{A}\) и \(\vec{B}\) имеют одну и ту же начальную точку, но это не обязательно. На самом деле это могут быть любые два вектора, здесь они показаны только для наглядного представления концепции.
Обозначим полученный вектор как \(\vec{C}\), тогда по определению:
$$\vec{C}=AB\space sin\theta\space\hat{n}$$
, а величина определяется путем простого взятия абсолютного значения с обеих сторон,
$$|\vec{C}|=AB\space sin\theta$$
Модуль единичного вектора становится \(1\ ), и все, что у нас осталось, это \(AB\space sin\theta\). Помните, что \(|\vec{C}|=C\), это просто вопрос удобства, какое обозначение предпочитается (то же самое касается \(\vec{A}\) и \(\vec{B} \) или любой другой вектор).
Помните, что \(|\vec{C}|=C\), это просто вопрос удобства, какое обозначение предпочитается (то же самое касается \(\vec{A}\) и \(\vec{B} \) или любой другой вектор).
Чтобы визуализировать направление, в котором будет указывать результирующий вектор, очень полезно правило правого винта. Просто поверните пальцы в направлении вектора вращения и наблюдайте за направлением большого пальца. Поверните пальцы от \(\vec{A}\) к \(\vec{B}\), и направление большого пальца задает направление результирующего вектора.
Компонентная форма векторного произведения
До сих пор вы знали, что геометрически означает векторное произведение. Теперь мы рассмотрим его алгебраическую форму более подробно. Чтобы обобщить векторное произведение:
Пусть A вектор такой, что \(\vec{A}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\), где \ (a_{1},a_{2} \space и \space a_{3}\) являются вещественными константами, такими, что они не являются одновременно \(0\) (иначе это был бы нулевой вектор) и \(\ vec{B}=b_{1}\шляпа{i}+b_{2}\шляпа{j}+b_{3}\шляпа{k}\) , где \(b_{1},b_{2} \ space и \space b_{3}\) являются вещественными константами и снова не являются одновременно \(0\). {o}=\vec{0}$$ 9{o}=0\), а величина всех единичных векторов равна \(1\). Точно так же \(\hat{j}\times\hat{j}=\vec{0}\) и \(\hat{k}\times\hat{k}=\vec{0}\), где \( \vec{0}\) представляет нулевой вектор. Вычисление других соотношений, например,
{o}=\vec{0}$$ 9{o}=0\), а величина всех единичных векторов равна \(1\). Точно так же \(\hat{j}\times\hat{j}=\vec{0}\) и \(\hat{k}\times\hat{k}=\vec{0}\), где \( \vec{0}\) представляет нулевой вектор. Вычисление других соотношений, например,
$$\шляпа{i}\times\шляпа{j}=sin\left(\frac{\pi}{2}\right)\шляпа{k}=\шляпа{ k}$$
Поскольку угол между единичным вектором вдоль оси x и единичным вектором вдоль оси y равен \(\frac{\pi}{2}\) радианам, что дает синусоидальное значение \ (1\). Точно так же мы можем вычислить другие сущности, а именно:
$$\шляпа{j}\times\шляпа{i}=-\шляпа{k}, \пробел \шляпа{i}\times\шляпа{k}=-\шляпа{j}, \пробел \шляпа {k}\times\hat{i}=\hat{j}, \space \hat{j}\times\hat{k}=\hat{i} \space and \space \hat{k}\times\ hat{j}=-\hat{i}$$
Теперь, используя приведенные выше объекты для единичных векторов, мы можем вычислить \(\vec{A} \times \vec{B}\) следующим образом:
$ $\vec{A}\times\vec{B}=(a_{1}\шляпа{i}+a_{2}\шляпа{j}+a_{3}\шляпа{k})\times(b_{ 1}\шляпа{i}+b_{2}\шляпа{j}+b_{3}\шляпа{k})$$
$$\vec{A}\times\vec{B}=(a_{ 2}b_{3}-b_{2}a_{3})\шляпа{i}-(a_{1}b_{3}-a_{3}b_{1})\шляпа{j}+(a_{ 1}b_{2}-a_{2}b_{1})\шляпа{k}$$
Взаимные произведения, которые привели к нулевому вектору, исключаются, и все, что у нас остается, это приведенное выше уравнение. Приведенное выше уравнение иногда может быть немного утомительным для запоминания и не очень удобным для записи. В результате приведенное выше уравнение часто представляется определителем \(3\) на \(3\), который равен:
Приведенное выше уравнение иногда может быть немного утомительным для запоминания и не очень удобным для записи. В результате приведенное выше уравнение часто представляется определителем \(3\) на \(3\), который равен:
$$\vec{A}\times\vec{B}=\begin{vmatrix} \шляпа{i} & \шляпа{j} & \шляпа{k} \\ a_{1} & a_{2} & a_{3} \\b_{1} & b_{2} & b_{3} \ end{vmatrix}$$
, что в конечном итоге соответствует уравнению, полученному ранее. Но определитель относительно легко запомнить. Для словесного выражения элементов определителя первая строка состоит из единичных векторов, вторая и третья строки — из скалярных компонент векторов. Давайте рассмотрим пример, чтобы получить представление о вычислении таких определителей, в конечном счете, векторного произведения.
Тройное произведение векторов
Произведение векторов не ограничивается двумя векторами, но также может быть расширено до трех различных векторов. Пусть есть три ненулевых вектора \(\vec{A}, \space \vec{B} \space и \space \vec{C}\) и мы хотим вычислить векторное тройное произведение между ними: \(\ vec{A} \times (\vec{B} \times \vec{C})\), где порядок векторного произведения очень важен, так как \(\vec{A} \times (\vec{B} \times \vec{C}) \neq (\vec{A} \times \vec{B}) \times \vec{C}\) т. е. векторное тройное произведение не является ассоциативным. По сути, существует два способа вычисления векторного тройного произведения: во-первых, вычисление векторного произведения \(\vec{A}\) и \(\vec{B}\), а затем выполнение его векторного произведения с \( \vec{С}\). Это включает в себя выполнение двух векторных продуктов, одного за другим.
е. векторное тройное произведение не является ассоциативным. По сути, существует два способа вычисления векторного тройного произведения: во-первых, вычисление векторного произведения \(\vec{A}\) и \(\vec{B}\), а затем выполнение его векторного произведения с \( \vec{С}\). Это включает в себя выполнение двух векторных продуктов, одного за другим.
Другой способ вычисления векторного произведения — скалярное произведение:
$$ (\vec{A} \times \vec{B}) \times \vec{C}=(\vec{A} \cdot \ vec{C}) \vec{B}-(\vec{B} \cdot \vec{C}) \vec{A} $$
Как видно, эта формула включает скалярное произведение \(\ vec{A}\) с \(\vec{C}\), а затем \(\vec{B}\) с \(\vec{C}\). На практике оба вышеуказанных способа одинаково удобны.
Для векторов: \(\vec{a}=\hat{i}+\hat{j}+\hat{k}\), \(\vec{b}=2 \hat{i}-\ hat{k}\) и \(\vec{c}=\hat{j}-\hat{k}\), найдите векторное тройное произведение: \((\vec{a} \times \vec{b} ) \times \vec{c}\)
Решение:
Мы будем использовать следующую формулу
$$ (\vec{a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec {c}) \vec{b}-(\vec{b} \cdot \vec{c}) \vec{a} $$
Шаг 1: Оценка \(\vec{a} \cdot \vec {c}\) :
$$ \begin{aligned} \vec{a} \cdot \vec{c} &=(\hat{i}+\hat{j}+\hat{k}) \cdot (\ шляпа {j}-\ шляпа {k}) \\ &=0+1-1 \\ \поэтому \vec{a} \cdot \vec{c} &=0 \end{aligned} $$
Шаг 2: Оценка \(\vec{b} \cdot \vec{c}\) :
$$ \begin{выровнено} \vec{b} \cdot \vec{c} &=(2 \шляпа{i}-\шляпа{k}) \cdot(\шляпа{j}-\шляпа{k}) \\ &=0+0+1 \\ &=1 \end{выровнено} $$
Шаг 3: Замена \(\vec{a} \cdot \vec{c}\) и \(\vec{b} \cdot \vec{c}\) в \((\vec {a} \times \vec{b}) \times \vec{c}=(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{b} \cdot \vec{ c}) \vec{a}\):
$$ \begin{aligned} (\vec{a} \times \vec{b}) \times \vec{c} &=0-(1) \vec {a} \\ &=-\шляпа{i}-\шляпа{j}-\шляпа{k} \end{aligned} $$
Следовательно, \((\vec{a} \times \vec{b}) \times \vec{c}=-\hat{i}-\hat{j}-\hat{k}\)
Связь между векторным произведением и скалярным произведением
Хотя векторное произведение и скалярное произведение сильно различаются по геометрическому применению и их значению, мы все же можем связать их определенным образом. {2}\theta$$ 9{2}\) для векторов \(\vec{p}=2 \hat{i}-\hat{k}\) и \(\vec{q}=\hat{j}+\hat{k} \).
{2}\theta$$ 9{2}\) для векторов \(\vec{p}=2 \hat{i}-\hat{k}\) и \(\vec{q}=\hat{j}+\hat{k} \).
Решение:
Шаг 1:
Сначала оценим \(\vec{p} \cdot \vec{q}\):
$$ \begin{aligned} \vec{p} \cdot \vec{q} &=(2 \шляпа{i}-\шляпа{k}) \cdot(\шляпа{j}+\шляпа{k}) \\ &=0+0-1 \\ \ поэтому \vec{p} \cdot \vec{q} &=1 \end{aligned} $$
Шаг 2:
Вычислить \(\vec{p} \times \vec{q}\) :
$$ \begin{aligned} \vec{p} \times \vec{q} &=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k } \\ 2 & 0 & -1 \\ 0 & 1 & 1 \end{массив}\right| \\ \поэтому \vec{p} \times \vec{q} &=\hat{i}(0+1)-\hat{j}(2+0)+\hat{k}(2-0) \\ \поэтому \vec{p} \times \vec{q} &=\hat{i}-2 \hat{j}+2 \hat{k} \end{aligned} $$ 9{2}\), мы уже вычислили его в шаге 3 :
$$ \text { RHS }=10 $$
Легко видеть, что
$$ \text{LHS}= \text {RHS} $$
Таким образом, личность подтверждена.
Векторное скалярное произведение
Векторное скалярное произведение, , также известное как Точечное произведение, — это еще один способ умножения двух векторов помимо векторного произведения. Альтернативное, но одинаково используемое название для . Точечный продукт — 9.0003 Скалярное произведение.
Альтернативное, но одинаково используемое название для . Точечный продукт — 9.0003 Скалярное произведение.
Скалярное произведение двух векторов дает скалярную величину, а не другой вектор. Основная причина существования скалярного произведения заключается в том, чтобы измерить величину вектора вдоль направления другого вектора.
Пусть \(\vec{a}\) и \(\vec{b}\) — два ненулевых вектора, образующих между собой острый угол \(\theta\). Формула для скалярного произведения дается следующим образом:
$$\vec{a} \cdot \vec{b}=ab \space cos\theta$$
9{2}}) \space cos(\pi/6)$$$$\vec{p} \cdot \vec{q}=(5)(10) \space \left( \frac{1}{ 2} \right)$$
$$\vec{p} \cdot \vec{q}=25$$
Следовательно, скалярное произведение двух векторов \(\vec{p}=4\hat{ i}+3\hat{j}\) и \(\vec{p}=6\hat{i}-8\hat{j}\) равно \(25\) единицам.
Примеры векторного произведения
Вычислить векторное произведение векторов \(\vec{C}=2\hat{i}+3\hat{j}-\hat{k}\) и \(\vec{D }=-\шляпа{i}+2\шляпа{k}\).
Решение:
Поместив единичные векторы и компоненты в детерминантную форму, как упоминалось ранее, мы получим
$$\vec{C}\times\vec{D}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & -1 \\- 1 & 0 & 2 \end{vmatrix}$$
Раскладывая определитель, получаем
$$\vec{C} \times \vec{D}=6\hat{i}-3\hat{j }+3\hat{k}$$
, который является результирующим вектором, полученным векторным произведением \(\vec{C}\) и \(\vec{D}\).
Для двух векторов \(\vec{p}=\hat{i}-2\hat{j}\) и \(\vec{q}=-2\hat{i}+\lambda\hat{j }\) такие, что их векторное произведение равно \(\vec{p} \times \vec{q}=2\hat{k}\). Вычислите значение \(\лямбда\).
Решение:
Используя полученную ранее формулу для вычисления векторного произведения двух векторов, мы имеем
$$\vec{p} \times \vec{q}=\lambda\hat{k}- 4\hat{k}=(\lambda-4)\hat{k}$$
Но также дано, что векторное произведение равно \(\vec{p} \times \vec{q}=2\hat {k}\), поэтому, сравнивая коэффициент единичного вектора, мы получаем
$$\lambda-4=2$$
, что дает \(\lambda=6\).
Продукт Vector — ключевые блюда на вынос
- Векторное произведение двух векторов — это вектор, указывающий в направлении, перпендикулярном плоскости, образованной двумя векторами.
- Для любых двух ненулевых векторов \(\vec{x}\) и \(\vec{y}\), образующих между собой острый угол \(\theta\), их векторное произведение равно \( |\vec{x} \times \vec{y}|=xy \space sin\theta \space \hat{n}\).
- Направление результирующего вектора можно определить с помощью правила правого винта, где пальцы указывают направление векторов, а большой палец указывает на результирующий вектор. 9{2}\).
Объяснение урока: Перпендикулярное расстояние между точками и прямыми линиями в пространстве
В этом объяснении мы узнаем, как рассчитать перпендикулярное расстояние между точкой и прямой линией или между двумя параллельными линиями в пространстве с помощью формулы.
Начнем с того, что напомним, что одна прямая однозначно задается в пространстве либо в том случае, если она проходит через известную неподвижную точку и имеет известное направление, как на диаграмме 1 ниже, либо если прямая проходит через две известные неподвижные точки, как на диаграмме 2.
В первом случае прямая, имеющая вектор направления ⃑𝑑, проходит через точку 𝐴(𝑥,𝑦,𝑧), имеющую вектор положения ⃑𝑎. Если 𝑃(𝑥,𝑦,𝑧) — любая точка на этой прямой, а ⃑𝑟 — позиционный вектор 𝑃, то ⃑𝑟=⃑𝑎+𝜆⃑𝑑 является векторным уравнением прямой. Здесь 𝜆 — скаляр, и каждое значение 𝜆 дает вектор положения одной уникальной точки на линии. Расширяя это, вспомним, что мы можем выразить уравнение линии в трех измерениях следующими способами.
Определение: формы уравнения прямой в трех измерениях
В общем, мы можем написать уравнение прямой, параллельной вектору направления в 𝑥-, 𝑦- и 𝑧-направлениях) и проходящей через точку 𝐴(𝑥,𝑦,𝑧) как ⃑𝑟 = 𝑥⃑𝑖+𝑦⃑𝑗+𝑧⃑𝑘+𝜆𝑎⃑𝑖+𝑏⃑𝑗+𝑐⃑𝑘, 𝑥 = 𝑥+𝜆𝑎, 𝑦 = 𝑦+𝜆𝑏, 𝑧 = 𝑧+𝜆𝑐, 𝑥−𝑥𝑎 = 𝑦 — 𝑦𝑏 — 𝑧𝑐. (векторная форма)(параметрическая форма)или(декартова форма)
Точка с координатами (𝑥,𝑦,𝑧) является одной из бесконечно многих точек на прямой и коэффициенты направления .
Во втором случае (диаграмма 2) для прямой, проходящей через две известные неподвижные точки 𝐴(𝑥,𝑦,𝑧) и 𝐵(𝑥,𝑦,𝑧) с ассоциированными векторами ⃑𝑎 и ⃑𝑏, вектор направления этой линии определяется выражением ⃑𝑑=⃑𝑏−⃑𝑎. То есть,
⃑𝑑=(𝑥−𝑥)⃑𝑖+(𝑦−𝑦)⃑𝑗+(𝑧−𝑧)⃑𝑘.
То есть,
⃑𝑑=(𝑥−𝑥)⃑𝑖+(𝑦−𝑦)⃑𝑗+(𝑧−𝑧)⃑𝑘.
Тогда отношения направлений равны (𝑥−𝑥)∶(𝑦−𝑦)∶(𝑦−𝑦)⃑ −𝑧), и используя либо 𝐴, либо 𝐵 в качестве фиксированной точки, мы можем снова записать линию в вектор , параметрический или Декартово формы.
В трех измерениях мы можем использовать свойство векторного произведения между векторами для вычисления перпендикулярного расстояния.
Теорема: перекрестное произведение векторов
Для любых трехмерных векторов ⃑𝑢 и ⃑𝑣, ‖‖⃑𝑢×⃑𝑣‖‖ площадь параллелограмма, натянутого на ⃑𝑢 и ⃑𝑣.
Мы хотим найти расстояние по перпендикуляру между точкой 𝑃(𝑥,𝑦,𝑧) и прямой ⃑𝑟=⃑𝑎+𝑡⃑𝑑.
Направление нашей линии задается ⃑𝑑, а вектор ⃑𝑎 дает нам точку на линии, которую мы будем называть 𝐴. Затем мы можем построить параллелограмм, как показано на следующем рисунке.
Площадь этого параллелограмма можно найти двумя способами. Во-первых, мы можем представить непараллельные стороны в виде векторов ⃑𝑑 и 𝐴𝑃, тогда площадь параллелограмма равна величине векторного произведения этих векторов:
площадь=‖‖𝐴𝑃×⃑𝑑‖‖.
Во-вторых, мы также можем найти эту площадь, вспомнив, что площадь параллелограмма равна произведению длины основания на его перпендикулярную высоту.
Учитывая, что мы добавляем перпендикулярное расстояние 𝐷 от точки 𝑃 к линии 𝐿 на нашу диаграмму, мы находим, что ‖‖⃑𝑑‖‖ может представлять собой основание параллелограмма, а 𝐷 может представлять соответствующую высоту основания ‖‖ ⃑𝑑‖‖; тогда у нас есть areabaseheight=×=𝐷×‖‖⃑𝑑‖‖.
Приравнивание этих двух выражений для площади параллелограмма дает нам ‖‖𝐴𝑃×⃑𝑑‖‖=𝐷×‖‖⃑𝑑‖‖.
Мы можем изменить это уравнение, чтобы сделать 𝐷 субъектом: 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖.
Приведем формулу для нахождения расстояния по перпендикуляру между точкой и прямой.
Теорема: Трехмерная формула для расстояния между точкой и прямой
Перпендикулярное расстояние 𝐷 между точкой 𝑃(𝑥,𝑦,𝑧) и прямой с вектором направления ⃑𝑑 определяется выражением 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖, где 𝐴 — любая точка на прямой.
Стоит отметить, что мы можем показать, что это кратчайшее расстояние между любой точкой и любой прямой. Если мы выберем произвольную точку 𝑄 на линии 𝐿, то мы всегда можем провести следующий перпендикуляр:
Если мы выберем произвольную точку 𝑄 на линии 𝐿, то мы всегда можем провести следующий перпендикуляр:
Тогда мы увидим, что 𝑃𝑄 является гипотенузой прямоугольного треугольника и, следовательно, длиннее, чем перпендикулярное расстояние.
Поскольку это кратчайшее расстояние между точкой и линией в трех измерениях, мы называем это расстоянием между точкой и линией в трех измерениях.
Давайте посмотрим на несколько примеров того, как мы можем применить эту формулу, чтобы найти перпендикулярное расстояние между точкой и линией в трех измерениях.
Пример 1. Нахождение длины перпендикуляра, проведенного из точки к прямой
Пусть 𝐿 — прямая, проходящая через точку (7,5,5) в направлении вектора (2,4,−9). Найдите расстояние между 𝐿 и точкой (2,6,6) с точностью до сотых.
Ответ
Мы хотим найти перпендикулярное расстояние между точкой и прямой линией. Мы можем сделать это, напомнив следующий результат.
Расстояние по перпендикуляру 𝐷 между точкой 𝑃(𝑥,𝑦,𝑧) и прямой с вектором направления ⃑𝑑 определяется выражением
𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖,
где 𝐴 — любая точка на прямой.
В нашем случае 𝑃(2,6,6), ⃑𝑑=(2,4,−9) и 𝐴(7,5,5). Чтобы найти перпендикулярное расстояние, нам сначала нужно определить 𝐴𝑃×⃑𝑑.
Начнем с поиска 𝐴𝑃: 𝐴𝑃=(2,6,6)−(7,5,5)=(−5,1,1).
Мы можем использовать это для вычисления перекрестного произведения: 𝐴𝑃×⃑𝑑=(−5,1,1)×(2,4,−9)=||||⃑𝑖⃑𝑗⃑𝑘−51124−9||||=||114−9||⃑𝑖−||−512 −9||⃑𝑗+||−5124||⃑𝑘=(−9−4)⃑𝑖−(45−2)⃑𝑗+(−20−2)⃑𝑘=−13⃑𝑖−43⃑𝑗−22⃑𝑘.
Затем мы можем вычислить величину этого вектора: ‖‖𝐴𝑃×⃑𝑑‖‖=‖‖−13⃑𝑖−43⃑𝑗−22⃑𝑘‖‖=(−13)+(−43)+(−22)=√
,Расстояние перпендикулярно данный 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖=√2502‖(2,4,−9)‖=√25022+4+(−9)=√2502√101.
Округление до сотых дает √2502√101≈4,98.lengthunits
Следовательно, перпендикулярное расстояние между точкой (2,6,6) и прямой, проходящей через точку (7,5,5) в направлении вектора (2,4,−9) с точностью до сотых составляет 4,98 единицы длины.
Пример 2. Нахождение длины перпендикуляра, проведенного из точки к прямой
Найдите длину перпендикуляра, проведенного из точки 𝐴(−8,1,10) к прямой ⃑𝑟=(−1, 2,−7)+𝑡(−9,−9,6) с округлением до сотых.
Ответ
Мы хотим найти перпендикулярное расстояние между точкой и прямой линией. Мы можем сделать это, напомнив следующий результат.
Расстояние по перпендикуляру 𝐷 между точкой 𝐴(𝑥,𝑦,𝑧) и линией с вектором направления ⃑𝑑 определяется выражением 𝐷=‖‖𝐵𝐴×⃑𝑑‖‖‖‖⃑𝑑‖‖, где 𝐵 — любая точка на прямой.
Напомним также, что прямая, заданная в векторной форме ⃑𝑟=⃑𝑏+𝑡⃑𝑑, проходит через точку с вектором положения ⃑𝑏 и имеет вектор направления ⃑𝑑.
В нашем случае 𝐴(−8,1,10), ⃑𝑑=(−9,−9,6) и 𝐵(−1,2,−7). Чтобы найти перпендикулярное расстояние, нам сначала нужно определить 𝐵𝐴×⃑𝑑.
Начнем с поиска 𝐵𝐴: 𝐵𝐴=(−8,1,10)−(−1,2,−7)=(−7,−1,17).
Мы можем использовать это для вычисления перекрестного произведения: ||||=||−117−96||⃑𝑖−||−717−96||⃑𝑗+||−7−1−9−9||⃑𝑘=(−6+153)⃑𝑖−(−42+153)⃑𝑗+(63−9)⃑𝑘=147⃑𝑖−111⃑𝑗+54⃑𝑘.
Затем мы можем вычислить величину этого вектора: ‖‖𝐵𝐴×⃑𝑑‖‖=‖‖147⃑𝑖−111⃑𝑗+54⃑𝑘‖‖=147+(−111)+54=√36846.
𝐷=‖‖𝐵𝐴×⃑𝑑‖‖‖‖⃑𝑑‖‖=√36846‖(−9,−9,6)‖=√36846(−9)+(−9)+(6)=√36846√ 198.
Округление до сотых дает √36846√198≈13,64.lengthunits
Следовательно, расстояние по перпендикуляру между точкой 𝐴(−8,1,10) и прямой линией ⃑𝑟=(−1,2,−7)+𝑡(−9,−9,6) с точностью до сотых составляет 13,64 единицы длины.
Давайте рассмотрим пример, где нам нужно найти перпендикулярное расстояние между точкой и линией, уравнение которой дано в декартовой форме.
Пример 3. Определение длины перпендикуляра, проведенного из данной точки к прямой
Определите с точностью до сотых длину перпендикуляра, проведенного из точки (−5,−7,−10) к прямой прямая 𝑥+82=𝑦−98=𝑧+7−8.
Ответ
Мы хотим найти длину перпендикуляра между точкой и линией, уравнение которой задано в декартовой форме. Для этого сначала напомним следующую формулу.
Расстояние по перпендикуляру 𝐷 между точкой 𝑃(𝑥,𝑦,𝑧) и прямой с вектором направления ⃑𝑑 можно найти по формуле 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖, где 𝐴 — любая точка на прямой.
Таким образом, мы можем рассчитать перпендикулярное расстояние, найдя точку на линии и вектор ее направления. Мы можем прочитать вектор направления из знаменателей уравнения прямой как ⃑𝑑=(2,8,−8). Мы можем решить каждую часть уравнения, равную нулю, чтобы найти точку на прямой, и это даст нам точку 𝐴(−8,9,−7).
Мы можем прочитать вектор направления из знаменателей уравнения прямой как ⃑𝑑=(2,8,−8). Мы можем решить каждую часть уравнения, равную нулю, чтобы найти точку на прямой, и это даст нам точку 𝐴(−8,9,−7).
Поскольку нам дано 𝑃(−5,−7,−10), мы можем найти 𝐴𝑃: 𝐴𝑃=(−5,−7,−10)−(−8,9,−7)=(3,−16,−3).
Тогда векторное произведение между вектором и ⃑𝑑 равно 𝐴𝑃×⃑𝑑=(3,−16,−3)×(2,8,−8)=||||⃑𝑖⃑𝑗⃑𝑘3−16−328−8||||=||−16−38−8|| ⃑𝑖−||3−32−8||⃑𝑗+||3−1628||⃑𝑘=(128+24)⃑𝑖−(−24+6)⃑𝑗+(24+32)⃑𝑘=152⃑𝑖+18⃑𝑗+56⃑𝑘.
Мы можем использовать это для вычисления перпендикулярного расстояния между точкой и линией: 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖=‖‖152⃑𝑖+18⃑𝑗+56⃑𝑘‖‖‖(2,8,−8)‖=√152+18+56 )=√26564√132.
Наконец, округляя до сотых, имеем √26564√132≈14.19.
Следовательно, мы смогли найти кратчайшее расстояние между точкой (−5,−7,−10) и прямой 𝑥+82=𝑦−98=𝑧+7−8, а с точностью до сотых — расстояние это 14.19.
В нашем следующем примере мы увидим, как применить эту формулу, учитывая две различные точки на линии вместо ее уравнения.
Пример 4. Нахождение перпендикулярного расстояния от заданной точки до прямой в двух заданных точках
Найдите с точностью до одного десятичного знака расстояние по перпендикуляру от точки (−3,−4,0) до прямой, проходящей через точки (1,3,1) и (4,3,2).
Ответ
Напомним, что расстояние по перпендикуляру 𝐷 между точкой 𝑃(𝑥,𝑦,𝑧) и прямой с направляющим вектором ⃑𝑑 можно найти по формуле 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖, где 𝐴 — любая точка на прямой.
Нам нужно найти его вектор направления. Если мы назовем 𝐴(1,3,1) и 𝐵(4,3,2), то мы можем найти вектор направления этой линии по координатам этих точек: ⃑𝑑=𝐴𝐵=(4,3,2)−(1,3,1)=(3,0,1).
Мы выбираем 𝐴(1,3,1), что дает нам 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖=‖‖𝐴𝑃×𝐴𝐵‖‖‖‖𝐴𝐵‖‖, куда 𝐴𝑃=(−3,−4,0)−(1,3,1)=(−4,−7,−1).
Оценка выходов перекрестных продуктов 𝐴𝑃×𝐴𝐵=(−4,−7,−1)×(3,0,1)=||||⃑𝑖⃑𝑗⃑𝑘−4−7−1301||||=||−7−101||⃑𝑖 −||−4−131||⃑𝑗+||−4−730||⃑𝑘=(−7+0)⃑𝑖−(−4+3)⃑𝑗+(0+21)⃑𝑘=−7⃑𝑖+⃑𝑗+21⃑𝑘 .
Следовательно,
𝐷=‖‖𝐴𝑃×𝐴𝐵‖‖‖‖𝐴𝐵‖‖=‖(−7,1,21)‖‖(3,0,1)‖=√491√10.
Следовательно, 𝐷=√491√10≈7.0.lengthunits
В нашем предыдущем примере мы нашли перпендикулярное расстояние между точкой и линией, определяемой двумя точками. Метод, используемый в этом примере, дает нам следующую формулу для перпендикулярного расстояния.
Расстояние между точкой и линией, определяемой двумя точками
Расстояние по перпендикуляру 𝐷 между 𝑃(𝑥,𝑦,𝑧) и линией, проходящей через различные точки 𝑄(𝑥,𝑦,𝑧) и 𝑅(𝑥,𝑦,𝑧) определяется выражением 𝐷=‖‖𝑄𝑃×𝑄𝑅‖‖‖‖𝑄𝑅‖‖.
Эта формула эквивалентна той, которую мы ранее получили для расстояния между точкой и линией, используя уравнение линии. Мы можем убедиться в этом, заметив, что вектор 𝑄𝑅 на самом деле является вектором направления этой линии. Таким образом, замена 𝑄𝑅 вектором направления ⃑𝑑 восстанавливает нашу предыдущую формулу.
В нашем последнем примере мы увидим, как мы можем расширить этот процесс, чтобы найти расстояние между двумя параллельными линиями.
Пример 5.
 Нахождение расстояния между двумя параллельными прямыми
Нахождение расстояния между двумя параллельными прямымиНайдите с точностью до сотых расстояние между параллельными прямыми 𝐿∶𝑥+79=𝑦+15=𝑧−7−6 и 𝐿∶𝑥+39= 𝑦+105=𝑧+10−6.
Ответ
Чтобы найти расстояние между 𝐿 и 𝐿, нам сначала нужно точно определить, что это означает. Давайте рассмотрим расстояние между произвольной точкой на каждой линии, скажем, 𝑃 и 𝑃, как показано на следующем рисунке.
Мы можем видеть, что это не кратчайшее расстояние между этими двумя прямыми, построив следующий прямоугольный треугольник.
Отрезок 𝑃𝑃 является гипотенузой прямоугольного треугольника, поэтому он длиннее, чем расстояние по перпендикуляру между двумя прямыми, 𝐷. Поскольку выбор 𝑃 и 𝑃 был произвольным, мы видим, что 𝐷 будет короче, чем расстояние между любой парой точек, лежащих на любой прямой.
Мы заметили, что поскольку линии параллельны, расстояние по перпендикуляру останется прежним. Следовательно, мы можем вычислить это перпендикулярное расстояние в любом месте на линиях. Если мы выберем произвольную точку 𝑃 на 𝐿, расстояние по перпендикуляру между точкой и прямой будет таким же, как кратчайшее расстояние между 𝐿 и 𝐿.
Если мы выберем произвольную точку 𝑃 на 𝐿, расстояние по перпендикуляру между точкой и прямой будет таким же, как кратчайшее расстояние между 𝐿 и 𝐿.
Вспомним следующую формулу для перпендикулярного расстояния между точкой и прямой. Расстояние по перпендикуляру 𝐷 между точкой 𝑃(𝑥,𝑦,𝑧) и прямой с вектором направления ⃑𝑑 можно найти по формуле 𝐷=‖‖𝐴𝑃×⃑𝑑‖‖‖‖⃑𝑑‖‖, где 𝐴 — любая точка на прямой.
Мы можем приравнять каждую часть уравнения 𝐿 к 0, чтобы найти, что 𝑃(−7,−1,7) лежит на прямой 𝐿. Мы также можем установить каждую часть уравнения 𝐿 равной нулю, чтобы найти, что 𝐴(−3,−10,−10) лежит на 𝐿. Вектор направления обеих прямых задается знаменателями их декартовых уравнений: ⃑𝑑=(9,5,−6).
Чтобы найти перпендикулярное расстояние, нам нужно найти 𝐴𝑃: 𝐴𝑃=(−7,−1,7)−(−3,−10,−10)=(−4,9,17).
Затем находим векторное произведение между 𝐴𝑃 и нашим направлением вектор: 𝐴𝑃×⃑𝑑=(−4,9,17)×(9,5,−6)=||||⃑𝑖⃑𝑗⃑𝑘−4
−6||||=||9175−6||⃑𝑖−||−4179 −6||⃑𝑗+||−4995||⃑𝑘=(−54−85)⃑𝑖−(24−153)⃑𝑗+(−20−81)⃑𝑘=−139⃑𝑖+129⃑𝑗−101⃑𝑘.






 и N
и N 
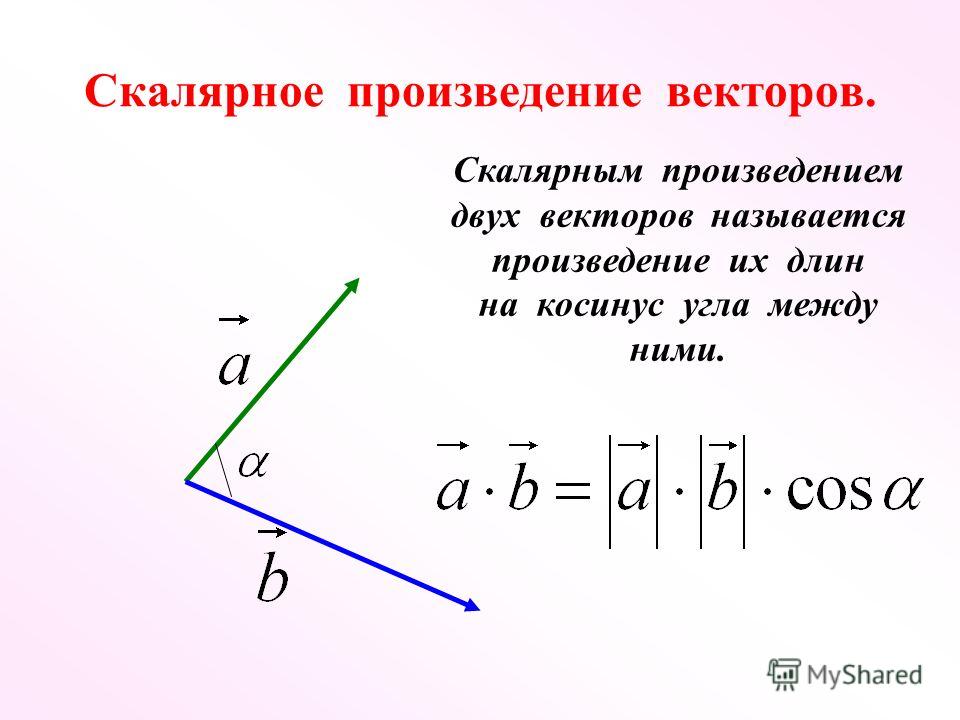 е. отрицательный вектор AC ).
е. отрицательный вектор AC ). Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.  Поэтому, когда человек весит 150 фунтов, это означает, что гравитация оказывает прямое воздействие на этого человека силой в 150 фунтов. Обратите внимание, что мы описали это количеством и направлением (прямо вниз). Такая величина (с величиной и направлением) называется вектором.
Поэтому, когда человек весит 150 фунтов, это означает, что гравитация оказывает прямое воздействие на этого человека силой в 150 фунтов. Обратите внимание, что мы описали это количеством и направлением (прямо вниз). Такая величина (с величиной и направлением) называется вектором. Этот вектор представляет собой силу тяжести вдоль плоскости. В этом и следующем разделах мы узнаем больше об этих векторах и о том, как определить величины этих векторов. Мы также увидим, что с нашим определением сложения двух векторов \(\textbf{w} = \textbf{a} + \textbf{b}\).
Этот вектор представляет собой силу тяжести вдоль плоскости. В этом и следующем разделах мы узнаем больше об этих векторах и о том, как определить величины этих векторов. Мы также увидим, что с нашим определением сложения двух векторов \(\textbf{w} = \textbf{a} + \textbf{b}\).
 \]
\] Когда векторы \(\textbf{v}\) и \(\textbf{w}\) равны, мы пишем \(\textbf{v} = \textbf{v}\).
Когда векторы \(\textbf{v}\) и \(\textbf{w}\) равны, мы пишем \(\textbf{v} = \textbf{v}\). Что мы подразумеваем под удвоением вектора? Основная идея состоит в том, чтобы сохранить то же направление и умножить величину на \(2\). Таким образом, если объект имеет скорость \(5\) футов в секунду на юго-восток, а второй объект имеет скорость в два раза больше, второй объект будет иметь скорость \(10\) футов в секунду в юго-восточном направлении. В этом случае говорят, что мы умножили вектор на скаляр \(2\). Теперь мы делаем определение, которое также учитывает, что скаляр может быть отрицательным.
Что мы подразумеваем под удвоением вектора? Основная идея состоит в том, чтобы сохранить то же направление и умножить величину на \(2\). Таким образом, если объект имеет скорость \(5\) футов в секунду на юго-восток, а второй объект имеет скорость в два раза больше, второй объект будет иметь скорость \(10\) футов в секунду в юго-восточном направлении. В этом случае говорят, что мы умножили вектор на скаляр \(2\). Теперь мы делаем определение, которое также учитывает, что скаляр может быть отрицательным.

 Длины сторон этого треугольника равны величинам этих сторон \(|\textbf{v}|\), \(|\textbf{w}|\) и \(|\textbf{v} + \textbf {ж}|\). Если мы поместим два вектора \(\textbf{v}\) и \(\textbf{w}\) так, чтобы их начальные точки совпадали, мы можем использовать параллелограмм для сложения двух векторов. Это показано на рисунке \(\PageIndex{2}\).
Длины сторон этого треугольника равны величинам этих сторон \(|\textbf{v}|\), \(|\textbf{w}|\) и \(|\textbf{v} + \textbf {ж}|\). Если мы поместим два вектора \(\textbf{v}\) и \(\textbf{w}\) так, чтобы их начальные точки совпадали, мы можем использовать параллелограмм для сложения двух векторов. Это показано на рисунке \(\PageIndex{2}\). Это работает аналогично отрицательному вещественному числу. Например, мы знаем, что когда мы добавляем \(-3\) к \(3\), результатом будет \(0\). То есть \(3 + (-3) = 0\)
Это работает аналогично отрицательному вещественному числу. Например, мы знаем, что когда мы добавляем \(-3\) к \(3\), результатом будет \(0\). То есть \(3 + (-3) = 0\)
 \circ — \theta\). Мы рассмотрим это в следующей проверке прогресса.
\circ — \theta\). Мы рассмотрим это в следующей проверке прогресса. В физике сила, действующая на объект, определяется как любое взаимодействие, которое, если ему не противостоять, изменит движение объекта. Таким образом, сила заставит объект изменить свою скорость, то есть объект ускорится. Говоря более неформально, сила — это толчок или притяжение объекта.
В физике сила, действующая на объект, определяется как любое взаимодействие, которое, если ему не противостоять, изменит движение объекта. Таким образом, сила заставит объект изменить свою скорость, то есть объект ускорится. Говоря более неформально, сила — это толчок или притяжение объекта.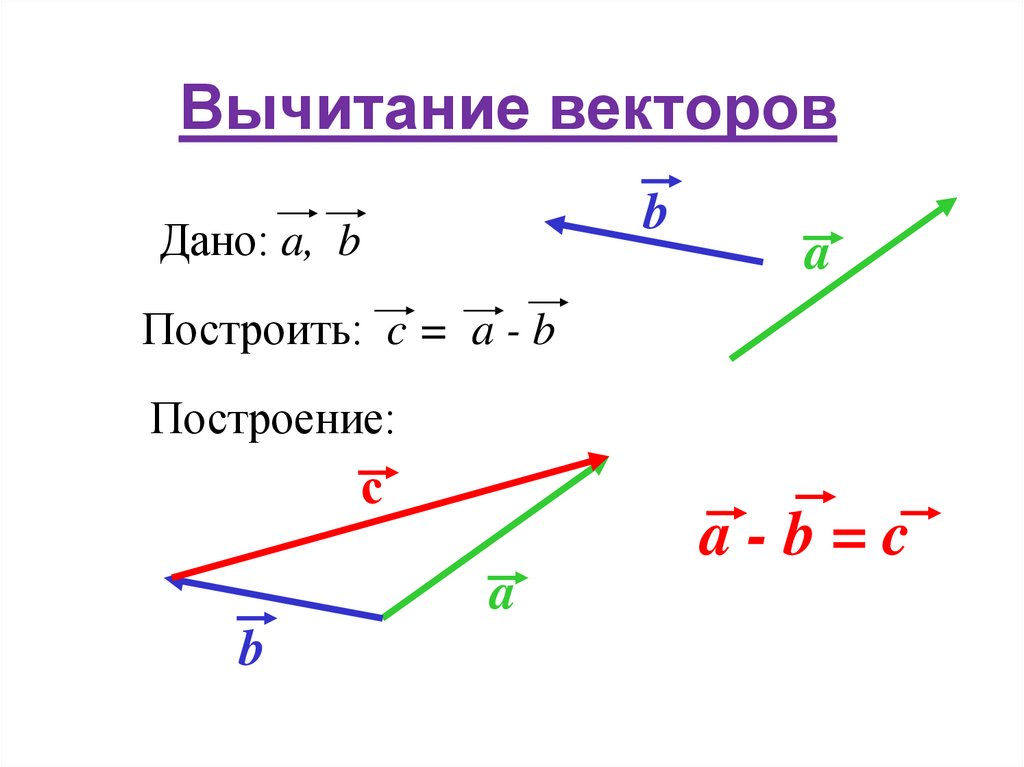 Напомним, что вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз), вектор \(\textbf{b}\) перпендикулярен плоскости и представляет силу, с которой объект давит на плоскость, а вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости. Этот вектор представляет собой силу тяжести вдоль плоскости. Обратите внимание, что мы также добавили вторую копию вектора a, которая начинается с вершины вектора \(\textbf{b}\). 9\circ\), так как это два острых угла прямоугольного треугольника. Отсюда делаем вывод, что \(\beta = \theta\). Это дает нам окончательный вариант диаграммы сил на наклонной плоскости, показанной на рис. 3.26. Обратите внимание, что векторы \(\textbf{a}\),
Напомним, что вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз), вектор \(\textbf{b}\) перпендикулярен плоскости и представляет силу, с которой объект давит на плоскость, а вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости. Этот вектор представляет собой силу тяжести вдоль плоскости. Обратите внимание, что мы также добавили вторую копию вектора a, которая начинается с вершины вектора \(\textbf{b}\). 9\circ\), так как это два острых угла прямоугольного треугольника. Отсюда делаем вывод, что \(\beta = \theta\). Это дает нам окончательный вариант диаграммы сил на наклонной плоскости, показанной на рис. 3.26. Обратите внимание, что векторы \(\textbf{a}\), Используя диаграмму, подобную той, что изображена на рис. 3.26, определите величину силы, приложенной к плоскости со стороны объекта, и величину силы, действующей на плоскость, действующую на объект из-за гравитации.
Используя диаграмму, подобную той, что изображена на рис. 3.26, определите величину силы, приложенной к плоскости со стороны объекта, и величину силы, действующей на плоскость, действующую на объект из-за гравитации.
 Вектор \(\textbf{v} + \textbf{w}\) — это вектор, начальная точка которого совпадает с начальной точкой \(\textbf{v}\), а конечная точка совпадает с конечной точкой \( \textbf{ш}\).
Вектор \(\textbf{v} + \textbf{w}\) — это вектор, начальная точка которого совпадает с начальной точкой \(\textbf{v}\), а конечная точка совпадает с конечной точкой \( \textbf{ш}\). gvsu.edu/books/12
gvsu.edu/books/12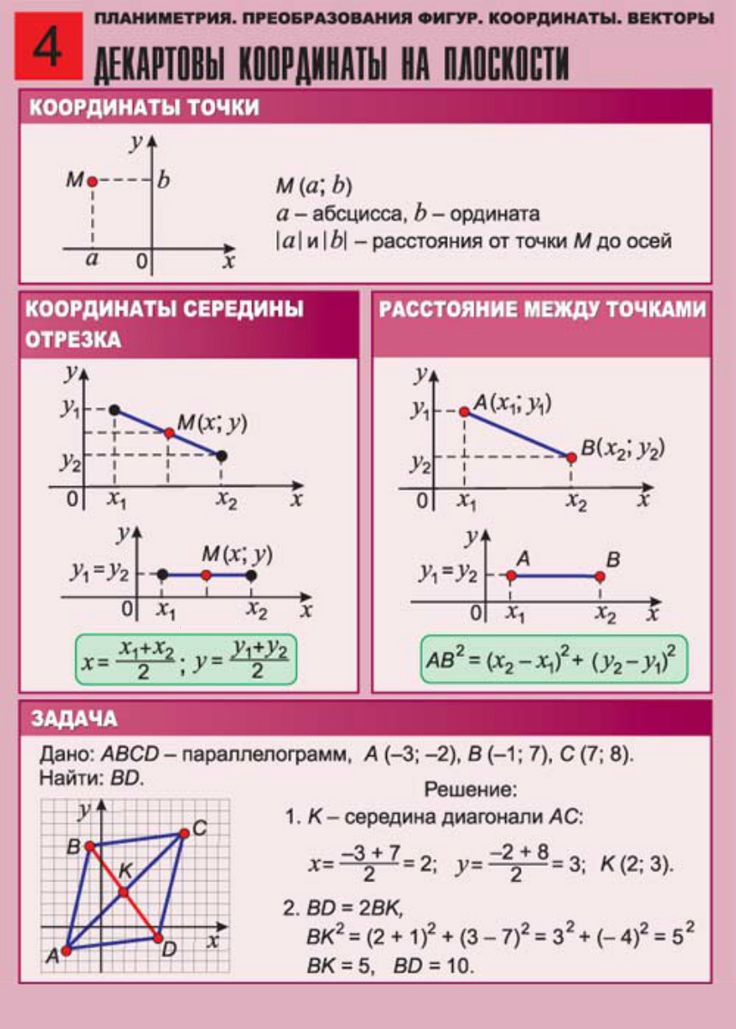
 2})=1$, поэтому угол
между ${\bf A}$ и собой равен нулю, что, конечно, правильно.
92})$, который не определен.
С другой стороны, обратите внимание, что, поскольку ${\bf A}\cdot{\bf 0}=0$, выглядит
сначала как будто $\cos\theta$ будет равно нулю, что, как мы видели, означает
что векторы перпендикулярны; только тогда, когда мы замечаем, что
знаменатель также равен нулю, если мы столкнемся с проблемами. Один из способов «исправить»
это означает принятие соглашения о том, что нулевой вектор ${\bf 0}$ равен
перпендикулярно всем векторам; то в общем случае можно сказать, что если
${\bf A}\cdot{\bf B}=0$, $\bf A$ и $\bf B$ перпендикулярны.
$\квадрат$
2})=1$, поэтому угол
между ${\bf A}$ и собой равен нулю, что, конечно, правильно.
92})$, который не определен.
С другой стороны, обратите внимание, что, поскольку ${\bf A}\cdot{\bf 0}=0$, выглядит
сначала как будто $\cos\theta$ будет равно нулю, что, как мы видели, означает
что векторы перпендикулярны; только тогда, когда мы замечаем, что
знаменатель также равен нулю, если мы столкнемся с проблемами. Один из способов «исправить»
это означает принятие соглашения о том, что нулевой вектор ${\bf 0}$ равен
перпендикулярно всем векторам; то в общем случае можно сказать, что если
${\bf A}\cdot{\bf B}=0$, $\bf A$ и $\bf B$ перпендикулярны.
$\квадрат$ (Векторы
параллельно
если они указывают в одном направлении,
антипараллельный
если они направлены в разные стороны.)
(Векторы
параллельно
если они указывают в одном направлении,
антипараллельный
если они направлены в разные стороны.) 2}{\bf B}.
$$
Убедитесь, что вы понимаете, почему ${\bf B}/|{\bf B}|$ является вектором
длина один (также называется
92}{\bf В}$$
антипараллелен $\bf B$, а его длина равна
$$\left|{{\bf A}\cdot{\bf B}\over|{\bf B}|}\right|.$$
Таким образом, скалярная проекция $\bf A$ на $\bf B$
может быть положительным или отрицательным. Если
он отрицательный, это означает, что вектор проекции антипараллелен
к $\bf B$ и что длина вектора проекции равна
абсолютное значение скалярной проекции. Конечно, вы также можете
вычислить длину вектора проекции, как обычно, применяя
формула расстояния до вектора.
2}{\bf B}.
$$
Убедитесь, что вы понимаете, почему ${\bf B}/|{\bf B}|$ является вектором
длина один (также называется
92}{\bf В}$$
антипараллелен $\bf B$, а его длина равна
$$\left|{{\bf A}\cdot{\bf B}\over|{\bf B}|}\right|.$$
Таким образом, скалярная проекция $\bf A$ на $\bf B$
может быть положительным или отрицательным. Если
он отрицательный, это означает, что вектор проекции антипараллелен
к $\bf B$ и что длина вектора проекции равна
абсолютное значение скалярной проекции. Конечно, вы также можете
вычислить длину вектора проекции, как обычно, применяя
формула расстояния до вектора. 2$
2$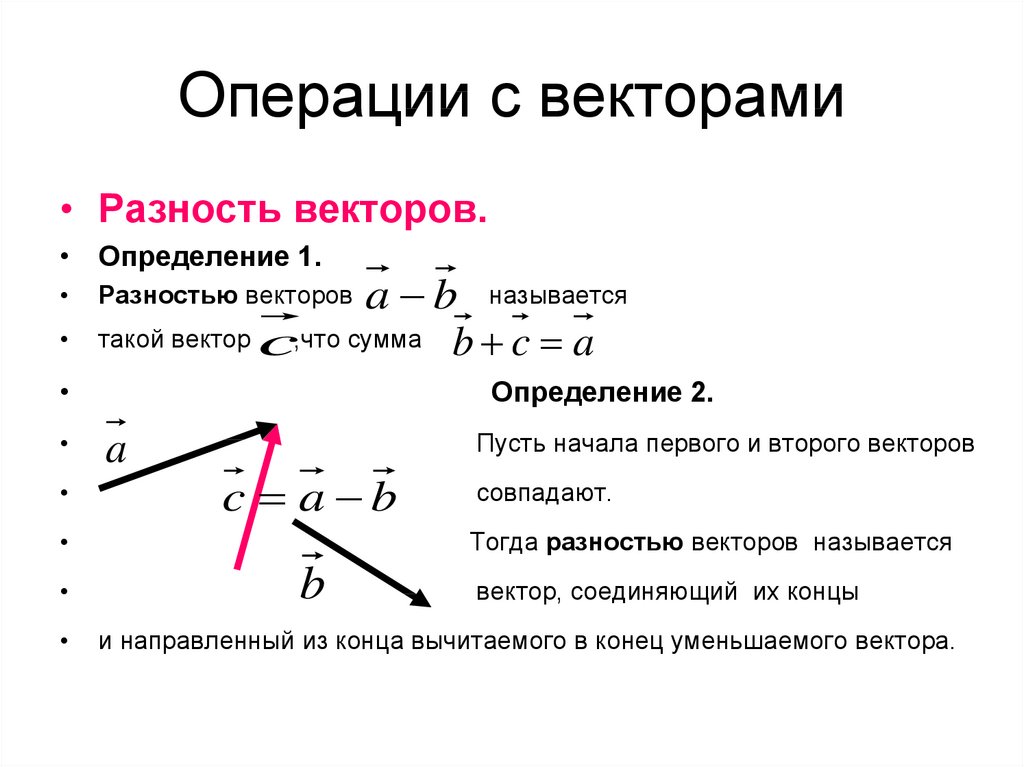 B y j + B z k
B y j + B z k