Площадь цилиндра: онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Введите 1 величину
Сторона A
Диагональ фигуры (D)
Диагональ грани (d)
Введите 1 величину
Радиус (r)
Диаметр (d)
Введите 3 величины
Сторона A
Сторона B
Сторона C
Диагональ фигуры (d)
Введите 2 величины (радиус и диаметр основания приняты за одну величину)
Высота (h)
Образующая конуса (s)
Радиус (r)
Диаметр (d)
Введите H и 1 величину
Высота (h)
Радиус (r)
Диаметр (d)
Введите 3 величины
Количество сторон (n)
Высота (h)
Сторона a
Количество сторон (n)
Введите 2 величины
Сторона основания (a)
Высота (h)
Длина бокового ребра (s)
Угол (α)
Между стороной и плоскостью основания
{$ main.
Результат расчёта
- Объём: {$ result.v|number:4 $}
- Площать: {$ result.s|number:4 $}
- Площать: {$ result.s $}
Цилиндр — это геометрическое тело, которое образовано вращением прямоугольника вокруг оси. Простыми словами, цилиндр — это призма, в основании которой лежат круги. Цилиндры широко распространены в реальной жизни, поэтому важно уметь находить площадь поверхности фигуры или хотя бы знать, как это можно сделать.
Геометрия цилиндра
Прежде всего, стоит разобраться с цилиндрической поверхностью. Цилиндрическая поверхность образуется движением прямой линии вдоль направляющей кривой. Если направляющая является окружностью, то образующая линия создает боковую поверхность цилиндра. Для завершения образа сверху и снизу поверхности следует добавить круги — наш цилиндр готов. Таким образом, полученная фигура представляет собой тело, состоящее из двух кругов, соединенных цилиндрической поверхностью.
Для завершения образа сверху и снизу поверхности следует добавить круги — наш цилиндр готов. Таким образом, полученная фигура представляет собой тело, состоящее из двух кругов, соединенных цилиндрической поверхностью.
Направляющая и образующая — это главные кривые, формирующие геометрию цилиндра. Если направляющая представляет собой эллипс, то образующая «курсирует» по эллипсу с минимальным шагом, создавая цилиндрическую поверхность и образуя эллиптический цилиндр. В качестве направляющей кривой помимо эллипса и окружности могут выступать парабола и гипербола, а цилиндр в этом случае будет параболическим или гиперболическим. Если образующая перпендикулярна направляющей или основанию фигуры, то такой тело называют прямым цилиндром, в ином случае — косым.
Цилиндр часто встречается в реальной жизни. К примеру, форму цилиндра имеют цистерны, консервные банки, трубы, бутылки, поршни двигателей внутреннего сгорания, колонны и даже архитектурные проекты, как штаб-квартиры известных концернов или масштабные бизнес-центры.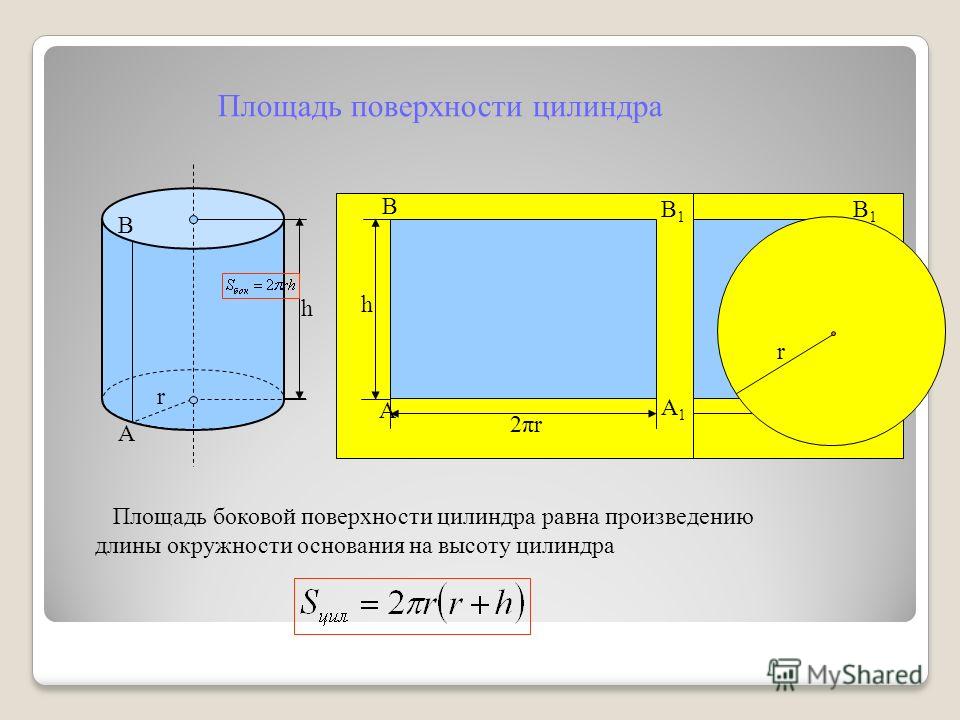 Кроме того, в производстве используется большое количество цилиндрических фигур и каждому технологу необходимо знать, как подсчитать площадь поверхности в нестандартных ситуациях.
Кроме того, в производстве используется большое количество цилиндрических фигур и каждому технологу необходимо знать, как подсчитать площадь поверхности в нестандартных ситуациях.
Площадь поверхности фигуры
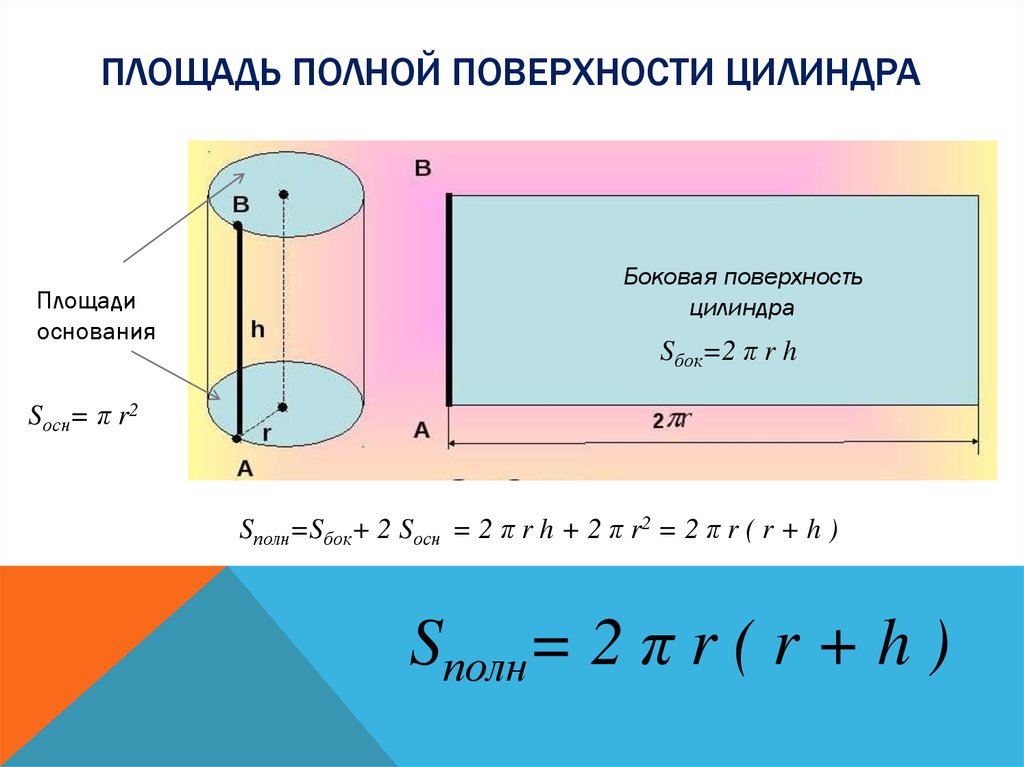
Площадь боковой поверхности кругового цилиндра определяется по простой формуле:
Sb = 2 pi × R × h,
где R — радиус окружности основания, h — высота цилиндра.
Полная поверхность геометрической фигуры добавит к этой формуле еще 2 площади основания. Если это круговой цилиндр, то площадь одного основания будет равна:
So = pi × R2.
Таким образом, полная площадь поверхности кругового цилиндра равна:
S = 2So + Sb = 2 pi × R2 + 2 pi × R × h= 2 pi × R × (R + h).
Если вам необходимо рассчитать площадь поверхности цилиндра, то вы должны знать всего 2 параметра фигуры: его высоту и радиус (диаметр) основания. Воспользуйтесь нашим онлайн-калькулятором для решения задач на определение площади поверхности. Рассмотрим примеры.
Примеры
Быт
Допустим, у вас на даче есть цистерна для сбора воды и вы решили, что пора привести ее в божеский вид и покрасить. Для сокращения расходов важно правильно выбрать количество краски, поэтому необходимо узнать полную площадь поверхности цистерны, которая, к счастью, представляет собой круговой цилиндр. Для этого вам необходимо замерить высоту цистерны h = 3 м и диаметр ее основанияd = 2 м. Введите эти данные в форму онлайн-калькулятора и получите результат в виде:
S = 2 × 9,42 + 18,84 = 37,69
Таким образом, площадь всей поверхности цистерны составляет 37,69 квадратных метров. Зная, что приблизительный расход масляной краски составляет 150 г на квадратный метр поверхности, вы можете посчитать, что вам понадобится 5,65 кг краски или 2 банки по 2,8 кг.
Производство
Допустим, вы работаете на производстве по изготовлению труб и отвечаете за процесс хромирования изделий. Вам необходимо узнать, сколько металла понадобится для нанесения хрома на поверхность трубы, соответственно, нужно знать площадь боковой поверхности изделия.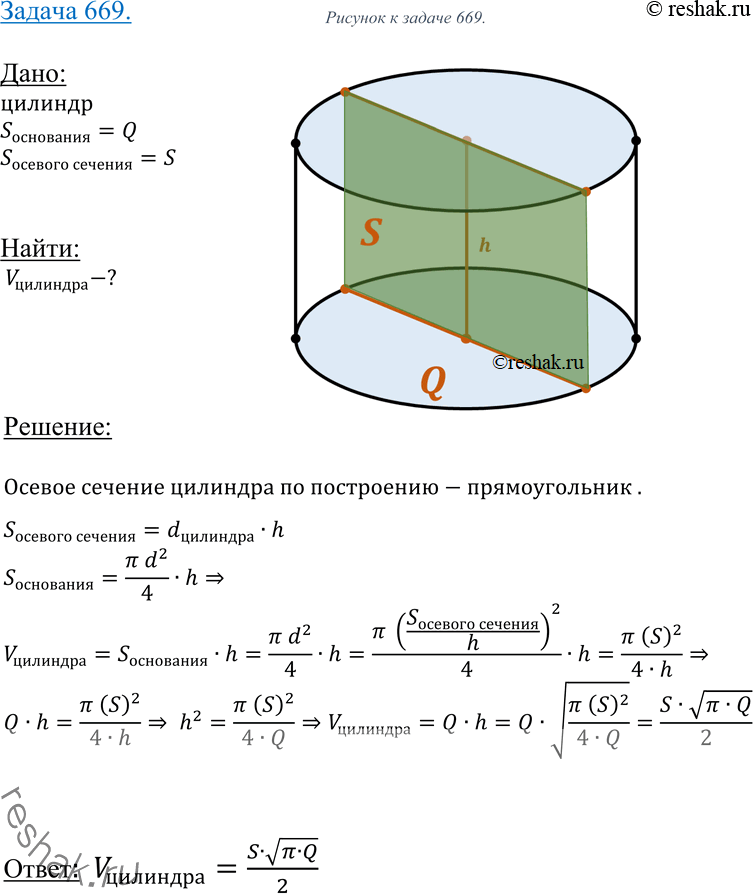 Пусть стандартная труба имеет длину 10 м, а ее радиус составляет 15 см = 0,15 м. Забейте эти данные в онлайн-форму калькулятора и вы получите результат:
Пусть стандартная труба имеет длину 10 м, а ее радиус составляет 15 см = 0,15 м. Забейте эти данные в онлайн-форму калькулятора и вы получите результат:
S = 2 × 0,17 + 4,71 = 5,06
Так как труба представляет собой цилиндр без оснований, то площадь обрабатываемой поверхности равна площади боковой поверхности геометрической фигуры и составляет 4,71 квадратных метра. Зная этот параметр, вы без проблем определите, сколько необходимо материала для хромирования стандартной трубы.
Заключение
Несмотря на то, что круговые цилиндры не так распространены в реальной жизни, как призматические фигуры, вам все равно может понадобиться удобный инструмент для расчета площади поверхности цилиндрических тел. Наш онлайн-калькулятор поможет вам вычислить необходимые параметры на работе, в быту или при решении школьных задач.
Посчитать площадь цилиндра калькулятор. Радиус цилиндра, онлайн расчет
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.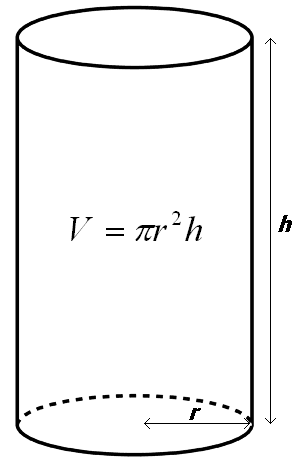
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
S бок. = 2πrh
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh.
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок. = 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb — площадь боковой поверхности, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
где S — площадь полной поверхности, h — высота
Цилиндр – это фигура, состоящая из цилиндрической поверхности и двух окружностей, расположенных параллельно. Расчет площади цилиндра – это задача геометрического раздела математики, которая решается достаточно просто. Существует несколько методов ее решения, которые в результате всегда сводятся к одной формуле.
Расчет площади цилиндра – это задача геометрического раздела математики, которая решается достаточно просто. Существует несколько методов ее решения, которые в результате всегда сводятся к одной формуле.
Как найти площадь цилиндра – правила вычисления
- Чтобы узнать площадь цилиндра, необходимо две площади основания сложить с площадью боковой поверхности: S= Sбок.+ 2Sосн. В более развернутом варианте данная формула выглядит так: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
- Площадь боковой поверхности данного геометрического тела можно высчитать, если известны его высота и радиус окружности, лежащей в основании. В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте. Формула боковой поверхности данного тела выглядит так: S= 2 π rh.
- Площадь основания считается по формуле нахождения площади круга: S osn= π r 2 . В некоторых задачах может не даваться радиус, но задаваться длина окружности.
 С данной формулы радиус выражается достаточно легко. С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.
С данной формулы радиус выражается достаточно легко. С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра. - При выполнении всех этих расчетов число π обычно не переводится в 3,14159… Его нужно просто дописывать рядом с числовым значением, которое было получено в результате проведения вычислений.
- Далее необходимо лишь умножить найденную площадь основания на 2 и прибавить к полученному числу вычисленную площадь боковой поверхности фигуры.
- Если в задаче указывается, что в цилиндре есть осевое сечение и это – прямоугольник, то решение будет немного другим. В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.

- Можно высчитать площадь данного геометрического тела через его объем. Для этого нужно из формулы V=π r 2 h вывести недостающую величину.
- В вычислении площади цилиндра нет ничего сложного. Нужно только знать формулы и уметь выводить из них величины, необходимые для проведения расчетов.
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.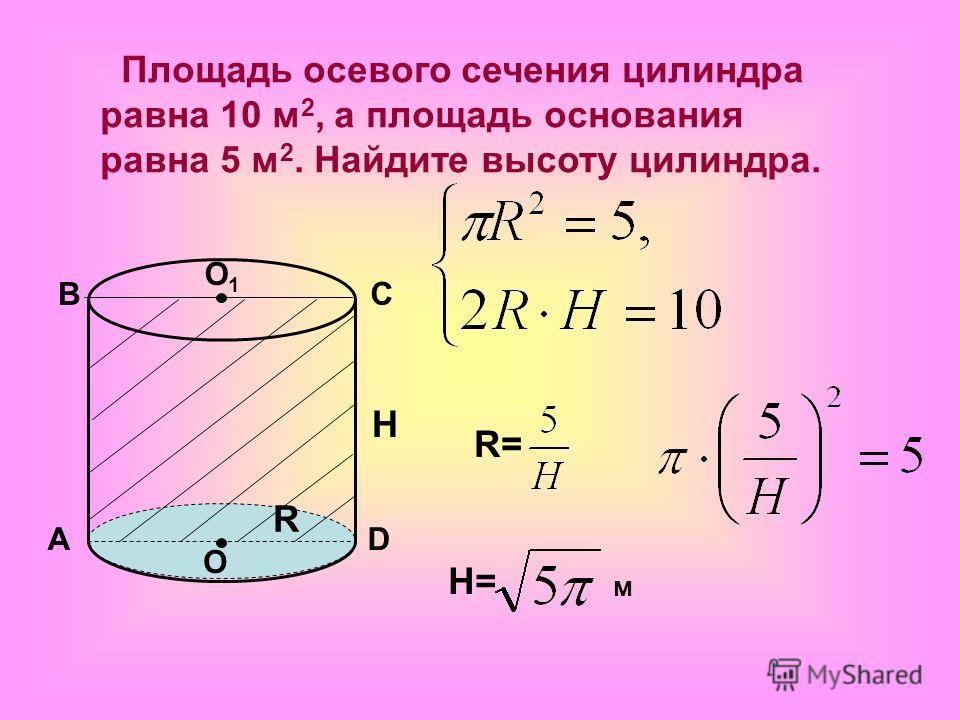
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Существует большое количество задач, связанных с цилиндром. В них нужно находить радиус и высоту тела или вид его сечения. Плюс ко всему, иногда требуется вычислить площадь цилиндра и его объем.
Какое тело является цилиндром?
В курсе школьной программы изучается круговой, то есть являющийся таковым в основании, цилиндр. Но выделяют еще и эллиптический вид данной фигуры. Из названия ясно, что его основанием будет эллипс или овал.
Оснований у цилиндра два. Они равны друг другу и соединены отрезками, которые совмещают соответствующие точки оснований. Они называются образующими цилиндра. Все образующие параллельны друг другу и равны. Именно они составляют боковую поверхность тела.
В общем случае цилиндр — это наклонное тело. Если образующие составляют прямой угол с основаниями, то говорят уже о прямой фигуре.
Интересно, что круговой цилиндр является телом вращения. Он получается от поворота прямоугольника вокруг одной из его сторон.
Он получается от поворота прямоугольника вокруг одной из его сторон.
Основные элементы цилиндра
Основные элементы цилиндра выглядят следующим образом.
- Высота. Она является кратчайшим расстоянием между основаниями цилиндра. Если он прямой, то высота совпадает с образующей.
- Радиус. Совпадает с тем, который можно провести в основании.
- Ось. Это прямая линия, которая содержит центры обоих оснований. Ось всегда параллельна всем образующим. В прямом цилиндре она перпендикулярна основаниям.
- Осевое сечение. Оно образуется при пересечении цилиндра плоскостью, содержащей ось.
- Касательная плоскость. Она проходит через одну из образующих и перпендикулярна осевому сечению, которое проведено через эту образующую.
Как связан цилиндр с вписанной в него или описанной около него призмой?
Иногда встречаются задачи, в которых нужно вычислить площадь цилиндра, а известны при этом некоторые элементы связанной с ним призмы. Как соотносятся эти фигуры?
Если призма вписана в цилиндр, то ее основания — равные многоугольники.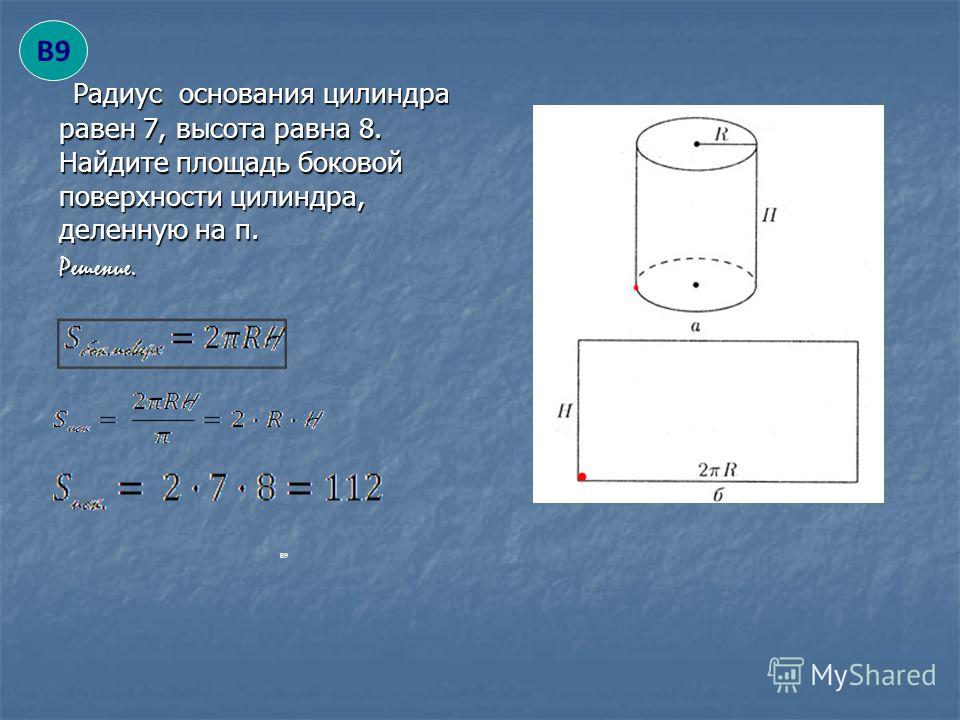 Причем они вписаны в соответствующие основания цилиндра. Боковые ребра призмы совпадают с образующими.
Причем они вписаны в соответствующие основания цилиндра. Боковые ребра призмы совпадают с образующими.
У описанной призмы в основаниях находятся правильные многоугольники. Они описаны около кругов цилиндра, являющихся его основаниями. Плоскости, которые содержат грани призмы, касаются цилиндра по образующим.
О площади боковой поверхности и основания для прямого кругового цилиндра
Если сделать развертку боковой поверхности, то получится прямоугольник. Его стороны будут совпадать с образующей и длиной окружности основания. Поэтому боковая площадь цилиндра будет равна произведению этих двух величин. Если записать формулу, то получится следующее:
S бок = l * н,
где н — образующая, l — длина окружности.
Причем последний параметр вычисляется по формуле:
l = 2 π * r,
здесь r — радиус окружности, π — число «пи», равное 3,14.
Поскольку основание — круг, то его площадь вычисляется с помощью такого выражения:
S осн = π * r 2 .
О площади всей поверхности прямого кругового цилиндра
Так как она образована двумя основаниями и боковой поверхностью, то нужно сложить эти три величины. То есть полная площадь цилиндра будет вычисляться по формуле:
S пол = 2 π * r * н + 2 π * r 2 .
Часто ее записывают в другом виде:
S пол = 2 π * r (н + r).
О площадях наклонного кругового цилиндра
Что касается оснований, то там все формулы те же, ведь они по-прежнему круги. А вот боковая поверхность уже не дает прямоугольника.
Для расчета площади боковой поверхности наклонного цилиндра потребуется перемножить значения образующей и периметра сечения, которое будет перпендикулярно выбранной образующей.
Формула выглядит так:
S бок = х * Р,
где х — длина образующей цилиндра, Р — периметр сечения.
Сечение, кстати, лучше выбирать такое, чтобы оно образовывало эллипс. Тогда будут упрощены расчеты его периметра.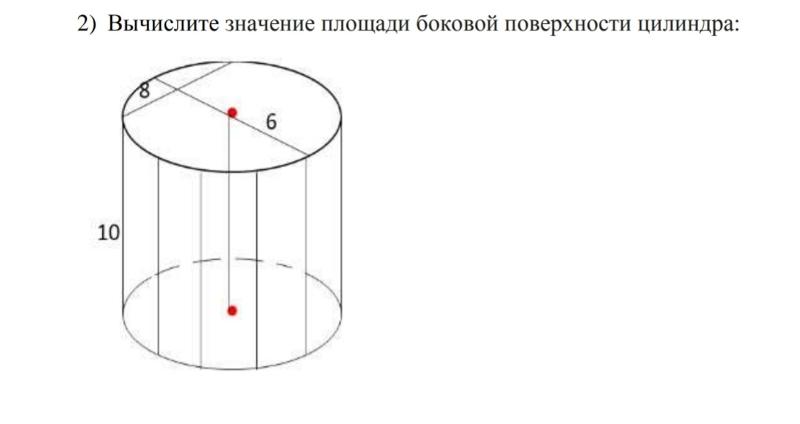 Длина эллипса вычисляется по формуле, которая дает приблизительный ответ. Но его часто бывает достаточно для задач школьного курса:
Длина эллипса вычисляется по формуле, которая дает приблизительный ответ. Но его часто бывает достаточно для задач школьного курса:
l = π * (а + в),
где «а» и «в» — полуоси эллипса, то есть расстояния от центра до ближайшей и самой дальней его точек.
Площадь всей поверхности нужно вычислять с помощью такого выражения:
S пол = 2 π * r 2 + х * Р.
Чему равны некоторые сечения прямого кругового цилиндра?
Когда сечение проходит через ось, то его площадь определяется как произведение образующей и диаметра основания. Это объясняется тем, что оно имеет вид прямоугольника, стороны которого совпадают с обозначенными элементами.
Чтобы найти площадь сечения цилиндра, являющегося параллельным осевому, потребуется тоже формула для прямоугольника. В этой ситуации одна его сторона будет по-прежнему совпадать с высотой, а другая равна хорде основания. Последняя же совпадает с линией сечения по основанию.
Когда сечение перпендикулярно оси, то оно имеет вид круга. Причем его площадь такая же, как у основания фигуры.
Причем его площадь такая же, как у основания фигуры.
Возможно еще пересечение под некоторым углом к оси. Тогда в сечении получается овал или его часть.
Примеры задач
Задание №1. Дан прямой цилиндр, площадь основания которого 12,56 см 2 . Необходимо вычислить полную площадь цилиндра, если его высота равна 3 см.
Решение. Необходимо воспользоваться формулой для полной площади кругового прямого цилиндра. Но в ней не хватает данных, а именно радиуса основания. Зато известна площадь круга. Из нее легко вычислить радиус.
Он оказывается равным квадратному корню из частного, которое получается от деления площади основания на пи. После деления 12,56 на 3,14 выходит 4. Квадратный корень из 4 — это 2. Поэтому радиус будет иметь именно такое значение.
Ответ: S пол = 50,24 см 2 .
Задание №2. Цилиндр с радиусом 5 см пресечен плоскостью, параллельной оси. Расстояние от сечения до оси равно 3 см. Высота цилиндра — 4 см. Требуется найти площадь сечения.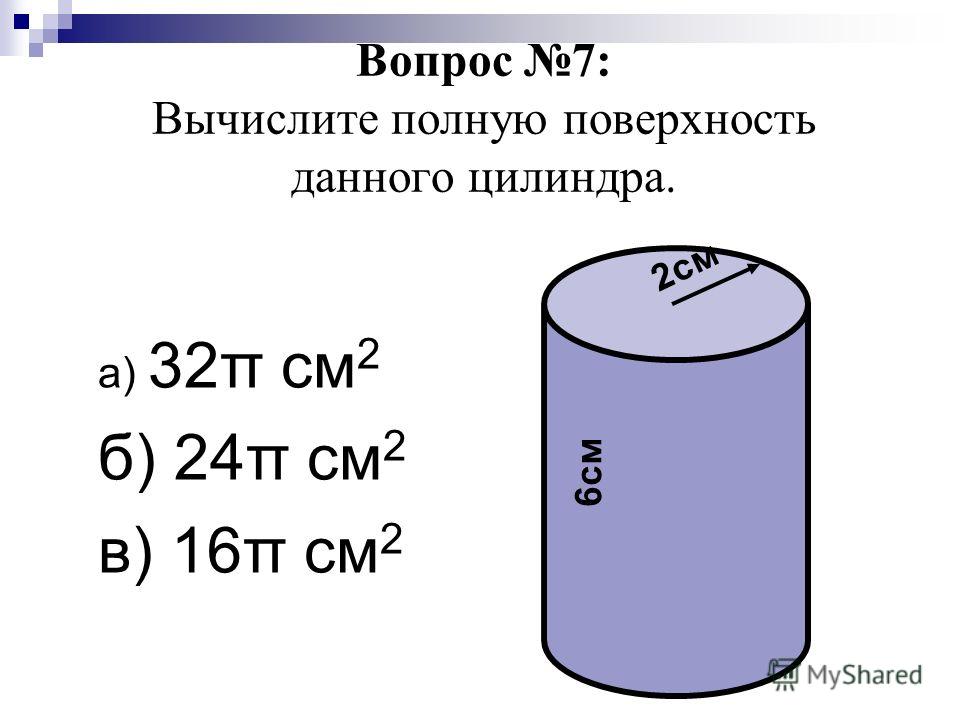
Решение. Форма сечения — прямоугольная. Одна его сторона совпадает с высотой цилиндра, а другая равна хорде. Если первая величина известна, то вторую нужно найти.
Для этого следует сделать дополнительное построение. В основании проводим два отрезка. Оба они будут начинаться в центре окружности. Первая будет заканчиваться в центре хорды и равняться известному расстоянию до оси. Вторая — на конце хорды.
Получится прямоугольный треугольник. В нем известны гипотенуза и один из катетов. Гипотенуза совпадает с радиусом. Второй катет равен половине хорды. Неизвестный катет, умноженный на 2, даст искомую длину хорды. Вычислим его значение.
Для того чтобы найти неизвестный катет, потребуется возвести в квадрат гипотенузу и известный катет, вычесть из первого второе и извлечь квадратный корень. Квадраты равны 25 и 9. Их разность — 16. После извлечения квадратного корня остается 4. Это искомый катет.
Хорда будет равна 4 * 2 = 8 (см). Теперь можно вычислить площадь сечения: 8 * 4 = 32 (см 2).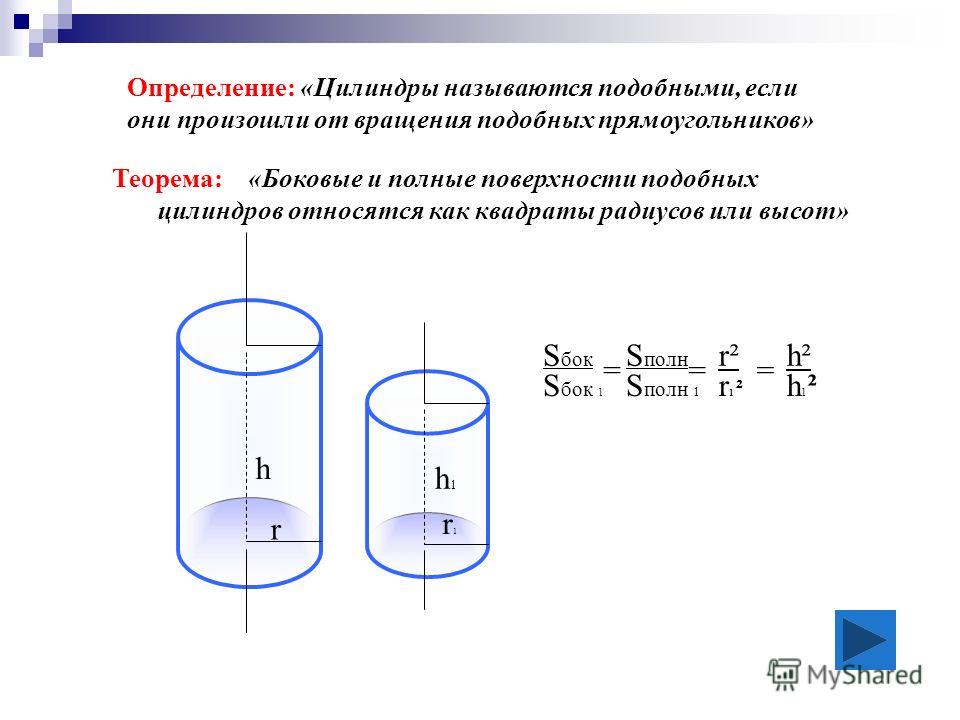
Ответ: S сеч равна 32 см 2 .
Задание №3. Необходимо вычислить площадь осевого сечения цилиндра. Известно, что в него вписан куб с ребром 10 см.
Решение. Осевое сечение цилиндра совпадает с прямоугольником, который проходит через четыре вершины куба и содержит диагонали его оснований. Сторона куба является образующей цилиндра, а диагональ основания совпадает с диаметром. Произведение этих двух величин даст площадь, которую нужно узнать в задаче.
Для поиска диаметра потребуется воспользоваться знанием того, что в основании куба — квадрат, а его диагональ образует равносторонний прямоугольный треугольник. Гипотенуза его является искомой диагональю фигуры.
Для ее расчета потребуется формула теоремы Пифагора. Нужно возвести в квадрат сторону куба, умножить ее на 2 и извлечь квадратный корень. Десять во второй степени — это сто. Умноженное на 2 — двести. Квадратный корень из 200 равен 10√2.
Сечение — это снова прямоугольник со сторонами 10 и 10√2. Его площадь легко сосчитать, перемножив эти значения.
Ответ. S сеч = 100√2 см 2 .
Площадь цилиндра калькулятор онлайн. Как найти площадь цилиндра
Рассмотрим цилиндр вращения радиуса R и высоты h (рис. 383). В основание этого цилиндра впишем правильный многоугольник (на рис. 383 — шестиугольник) и с его помощью построим правильную призму, вписанную в цилиндр. Таким же путем можно описывать вокруг цилиндра правильные призмы с произвольно большим числом боковых граней.
За площадь боковой поверхности цилиндра принимается по определению предел, к которому стремятся площади боковых поверхностей вписанных и описанных вокруг него правильных призм по мере неограниченного удвоения (или вообще увеличения) числа их боковых граней.
То, что такой предел существует, мы сейчас и докажем. Если возьмем вписанную правильную призму, построенную на правильном -угольнике, как на основании, то для ее боковой поверхности будем иметь выражение , где — периметр правильного -угольника, вписанного в круг основания цилиндра. При .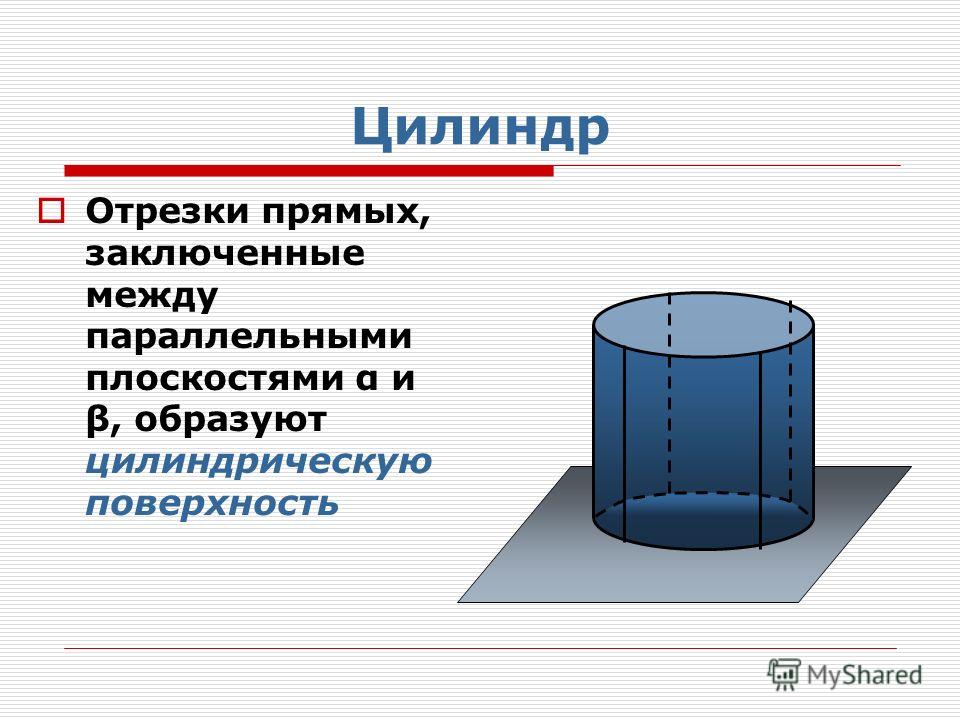 Точно такое же вычисление для описанной призмы дает тот же самый результат. Итак, площадь боковой поверхности цилиндра вращения выражается формулой
Точно такое же вычисление для описанной призмы дает тот же самый результат. Итак, площадь боковой поверхности цилиндра вращения выражается формулой
Боковая поверхность цилиндра равна произведению длины образующей на периметр (т. е. длину окружности) основания.
Задача 1. Отрезок, соединяющий диаметрально противоположные точки А и В верхнего и нижно оснований цилиндра (рис. 384), равен 10 см и наклонен к плоскости основания под углом в 60°. Найти площадь боковой поверхности цилиндра.
Решение. Проведем через отрезок Л Всечение плоскостью, перпендикулярной к основанию цилиндра. Из треугольника имеем
откуда находим для боковой поверхности цилиндра
Задача 2. Треугольник ABC, вершины А и В которого суть концы диаметра нижнего основания цилиндра, а вершина С-конец перпендикулярного к нему диаметра верхнего основания, равносторонний со стороной а,
Найти площади боковой и полной поверхностей цилиндра. Решение. Радиус основания цилиндра равен Высота треугольника ABC (рис.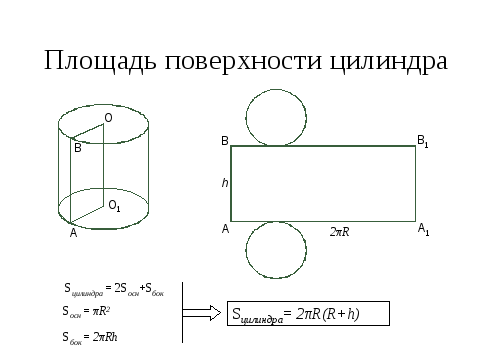 385) равна а образующая цилиндра вычисляется как
385) равна а образующая цилиндра вычисляется как
Отсюда боковая поверхность цилиндра получается равной
а полная поверхность (равная сумме площади боковой поверхности и площади двух оснований цилиндра) равна
Упражнения
1. Диагонали боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами, соответственно равными . Найти угол наклона к той же плоскости диагонали параллелепипеда.
2. В прямом параллелепипеде острый угол основания равен а, а одна из сторон основания равна а. Сечение, проведенное через эту сторону и противоположное ребро верхнего основания, имеет площадь Q, и плоскость его наклонена к плоскости основания под углом . Найти объем и полную поверхность параллелепипеда.
3. Основанием наклонной треугольной призмы служит равнобедренный прямоугольный треугольник, а проекция одного из боковых ребер на плоскость основания совпадает с медианой m одного из катетов треугольника. Найти угол наклона боковых ребер к плоскости основания, если объем призмы равен V.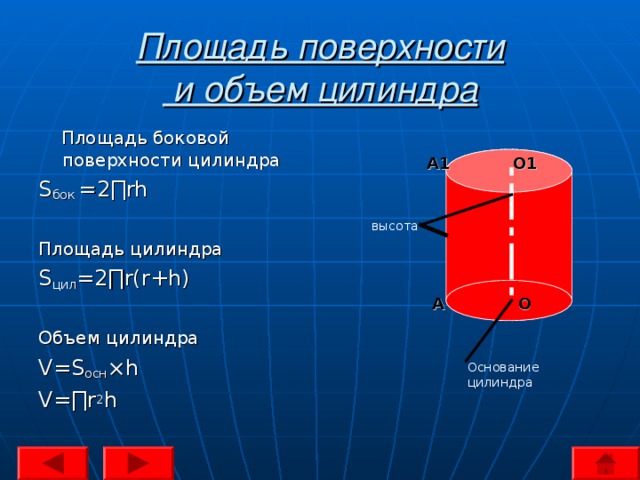
4. В правильной шестиугольной призме через сторону основания проведены два сечения: 1) содержащее противоположную сторону верхнего основания, 2) содержащее центр верхнего основания. При какой высоте призмы угол между плоскостями сечений имеет наибольшую величину и чему он равен в этом случае?
Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис.).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т. е. 2πrh .
Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).
За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S б.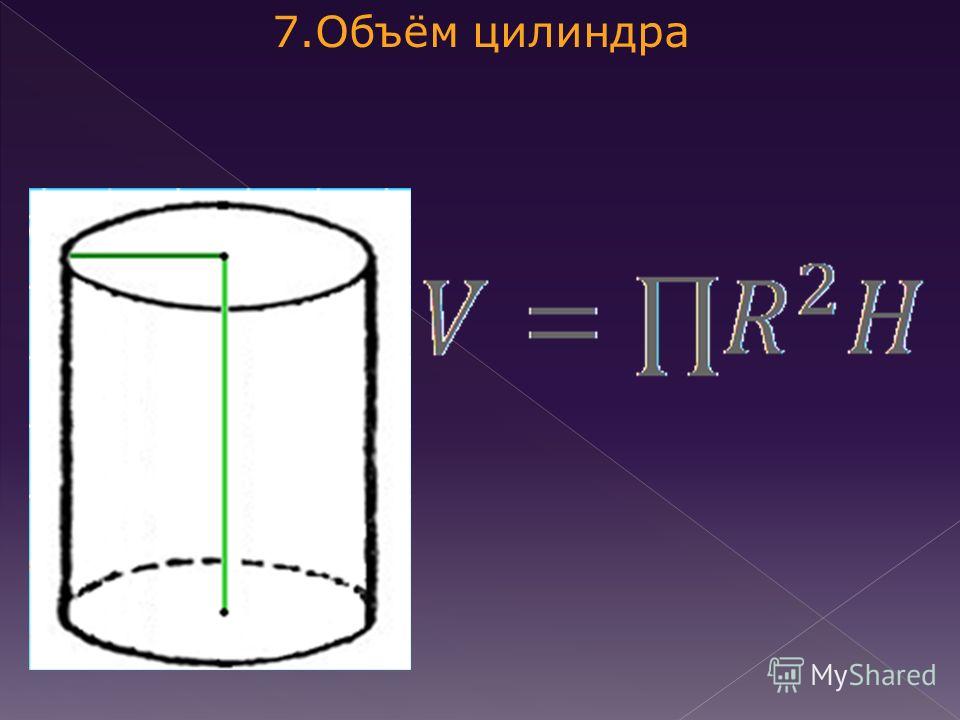 ц. = 2πRH, (1)
ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.
где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что
\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам
V n = Q n H и V’ n = Q’ n H.
Следовательно,
V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.

- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
- Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.
Существуют разновидности данной объемной фигуры:
- Под круговым подразумевают цилиндр, направляющая которого — это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
- Существует прямой цилиндр. Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
- Третий вид — скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием».
 Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
Данную фигуру определяет радиус основания, минимальная и максимальная высоты. - Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.
Условные обозначения
Традиционно основные «компоненты» цилиндра принято называть следующим образом:
- Радиус основания — R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая — L.
- Высота — H.
- Площадь основания — S осн (иначе говоря, необходимо найти указанный параметр круга).
- Высоты скошенного цилиндра — h 1 ,h 2 (минимальная и максимальная).
- Площадь боковой поверхности — S бок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры — V.
- Площадь полной поверхности — S.
«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных.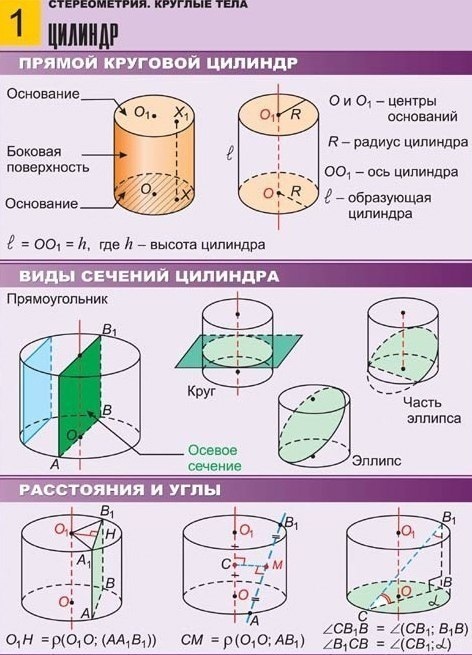 Поэтому необходимо быть хорошо подкованным в теории.
Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
- Боковая поверхность. Как известно, она получается благодаря движению образующей по заданной кривой.
- Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
- Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур. Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры.
- Под осевым сечением подразумевают расположение плоскости через центр тела.
- И наконец, завершающее определение. Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.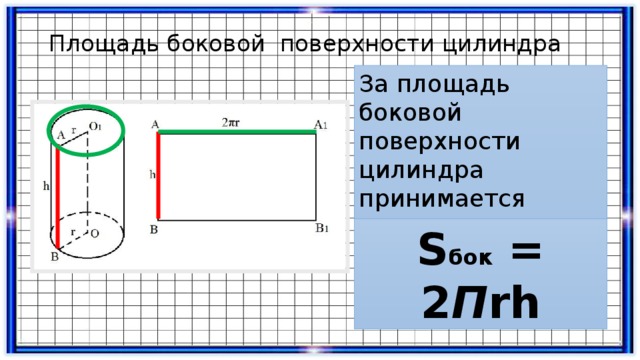
Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем — для прямого.
Примеры с разобранным решением
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается
Решение. Поскольку известны величины диагонали и угла, то в таком случае:
- CD = AC*cos 30°.
Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.
Аналогично, можно найти и значение AD:
- AD = AC*sin 30°
Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра.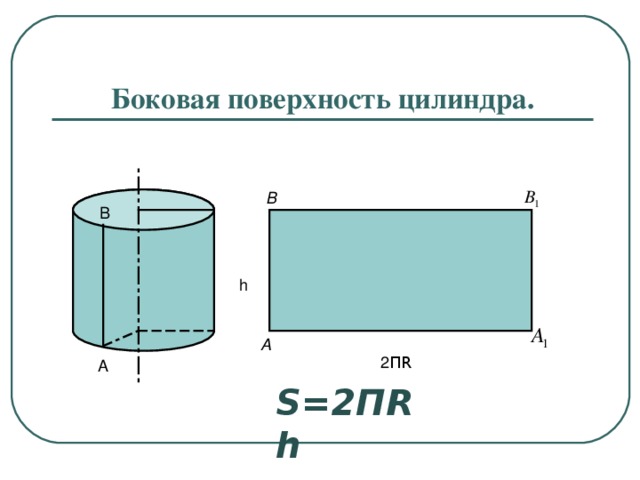 Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?
Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.
Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.
Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.
Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.
Ответ: S min будет достигнута при h = 1/32 см, R = 64 см.
Дана стереометрическая фигура — цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела.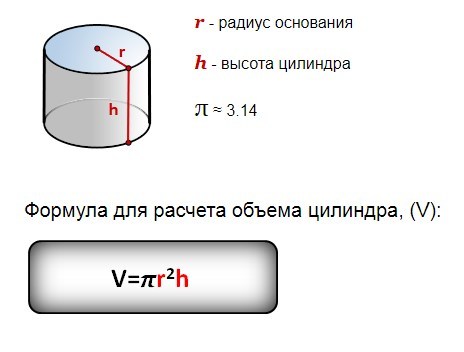 У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.
У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.
Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.
ВК² = ВМ² + МК²
МК² = ВК² — ВМ²
МК² = 17² — 15²
Отсюда можно сделать вывод, что МК = ВС = 8 см.
Следующий шаг — проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.
AD — диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.
BC — прямая, расположенная на плоскости имеющегося прямоугольника.
ABCD — трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.
Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.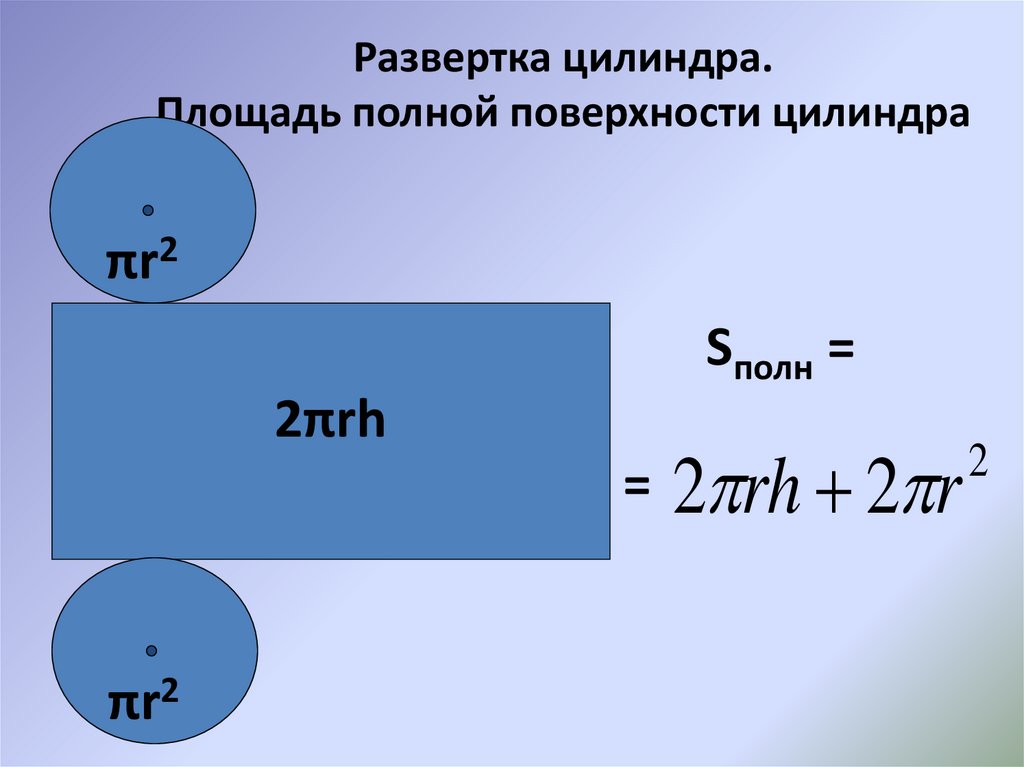
Для этого необходимо найти величины AD и ОС.
Ответ: сечение располагается 3 см от оси.
Задачи на закрепление материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания — Q, площадь осевого сечения — М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a . Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.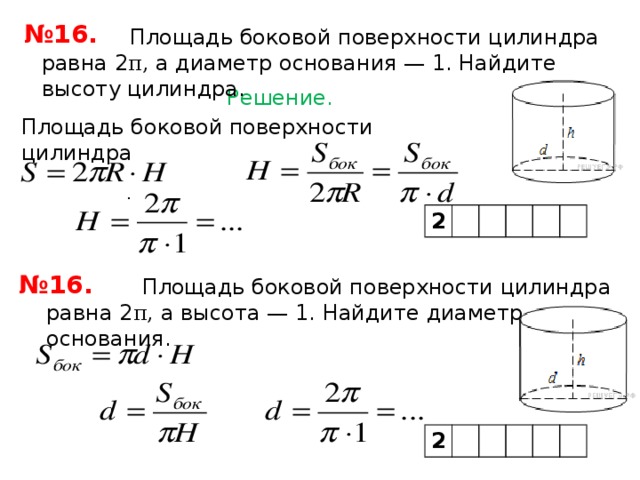
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N . Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.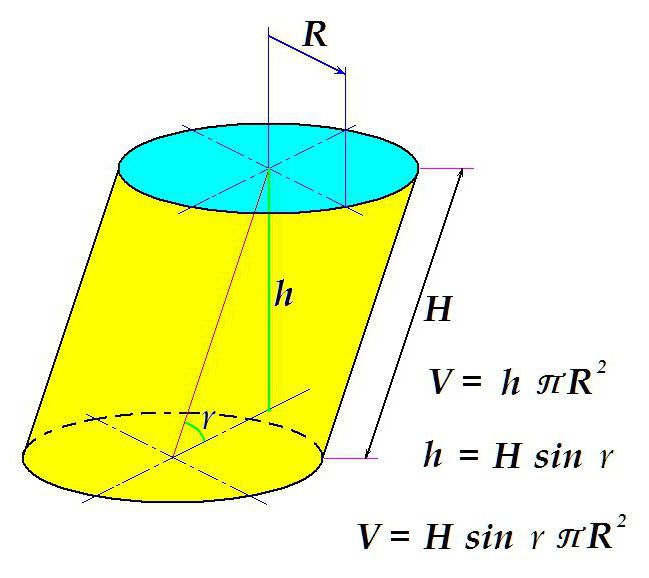
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Общая площадь полого цилиндра Калькулятор
✖Радиус 1 — это радиальная линия от фокуса до любой точки кривой для 1-го радиуса.ⓘ Радиус 1 [r1] | AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Радиус 2 — это радиальная линия от фокуса до любой точки кривой для 2-го радиуса. | AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо. | AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Площадь поверхности трехмерной формы — это сумма всех площадей поверхности каждой из сторон. |
акрАкко (служба США)НаходятсяарпанамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаМиля (римская)²Миля (Устав) ²MuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad |
⎘ копия |
👎
Формула
сбросить
👍
Общая площадь полого цилиндра Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.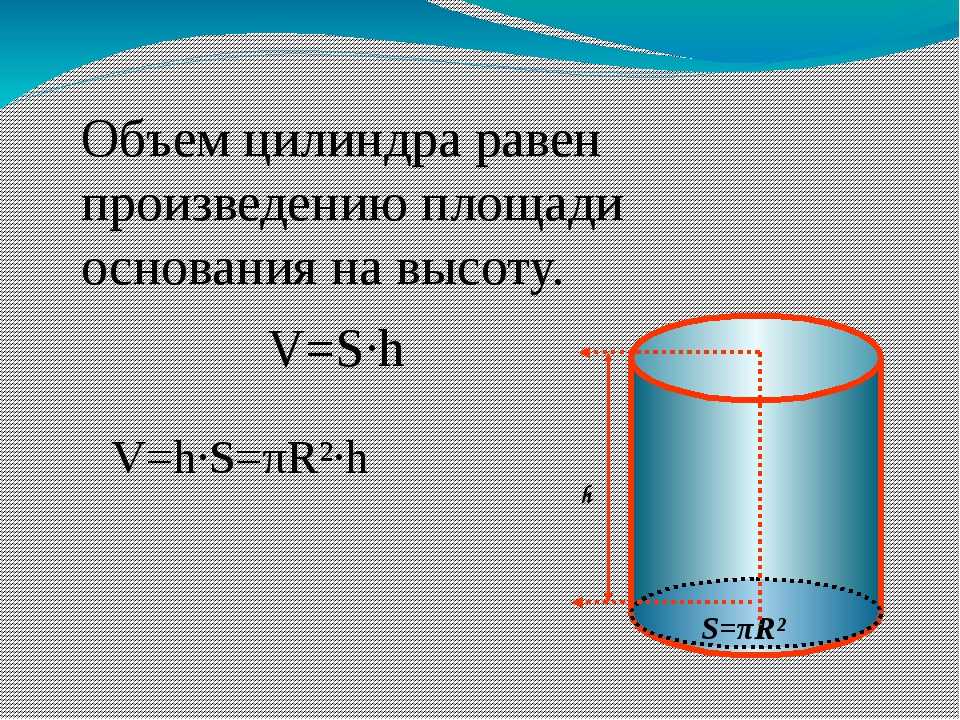 Преобразование входов в базовый блок
Преобразование входов в базовый блок
Радиус 1: 12 метр —> 12 метр Конверсия не требуется
Радиус 2: 13 метр —> 13 метр Конверсия не требуется
Высота: 12 метр —> 12 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
1727.87595947439 Квадратный метр —> Конверсия не требуется
< 2 Полый цилиндр Калькуляторы
Общая площадь полого цилиндра формула
Площадь поверхности = 2*pi*(Радиус 1+Радиус 2)*(Радиус 1-Радиус 2+Высота)
SA = 2*pi*(r1+r2)*(r1-r2+h)
В чем разница между полым цилиндром и цилиндром?
Правый круговой цилиндр — это прямой цилиндр, каждый конец которого перпендикулярен его центральной оси, он не обязательно должен быть полым. В середине полого цилиндра есть пустота, закрытая или открытая, сосуд, чашка или труба.
В середине полого цилиндра есть пустота, закрытая или открытая, сосуд, чашка или труба.
Share
Copied!
Чему равна площадь цилиндра. Как найти площадь цилиндра
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра — онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры.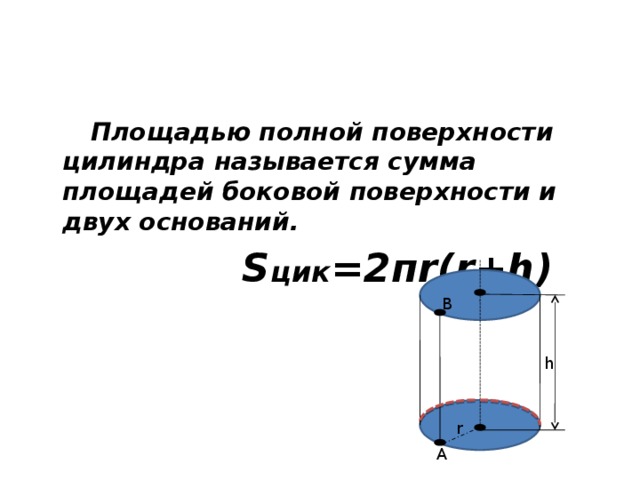 Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r , где r — радиус окружности. Другая сторона прямоугольника равна высоте h . Найти искомое не составит труда.
S бок = 2π * r * h ,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной S бок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S о = 2π * r 2 .
Конечная формула выглядит следующим образом:
S пол = 2π * r 2 + 2π * r * h.
Площадь цилиндра — формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
S пол = 2 π * r 2 + 2 π * r * h = 2 π * d 2 /4 + 2 π * h * d /2 = π * d 2 /2 + π * d * h ,
Вместо r в полную формулу нужно вставить значение r = d/2 .
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
S пол = 2 * 3.14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
Переводим в привычные м 2 и получаем 0,01868928, приблизительно 0.02 м 2 .
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
S пол = 3.14 * 0.2 2 /2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м 2 .
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
S бок = 2 * 3.14 * 1 * 1 = 6.28 м 2 .
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис.).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т.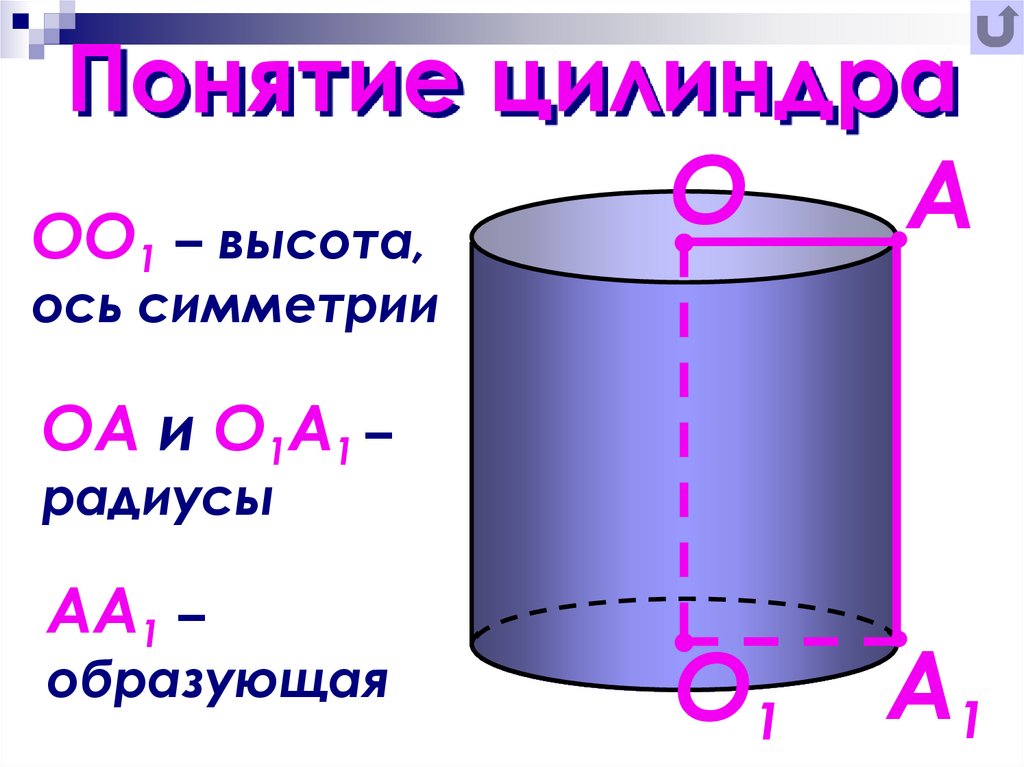 е. 2πrh .
е. 2πrh .
Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).
За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S б.ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.
где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что
\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам
V n = Q n H и V’ n = Q’ n H.
Следовательно,
V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.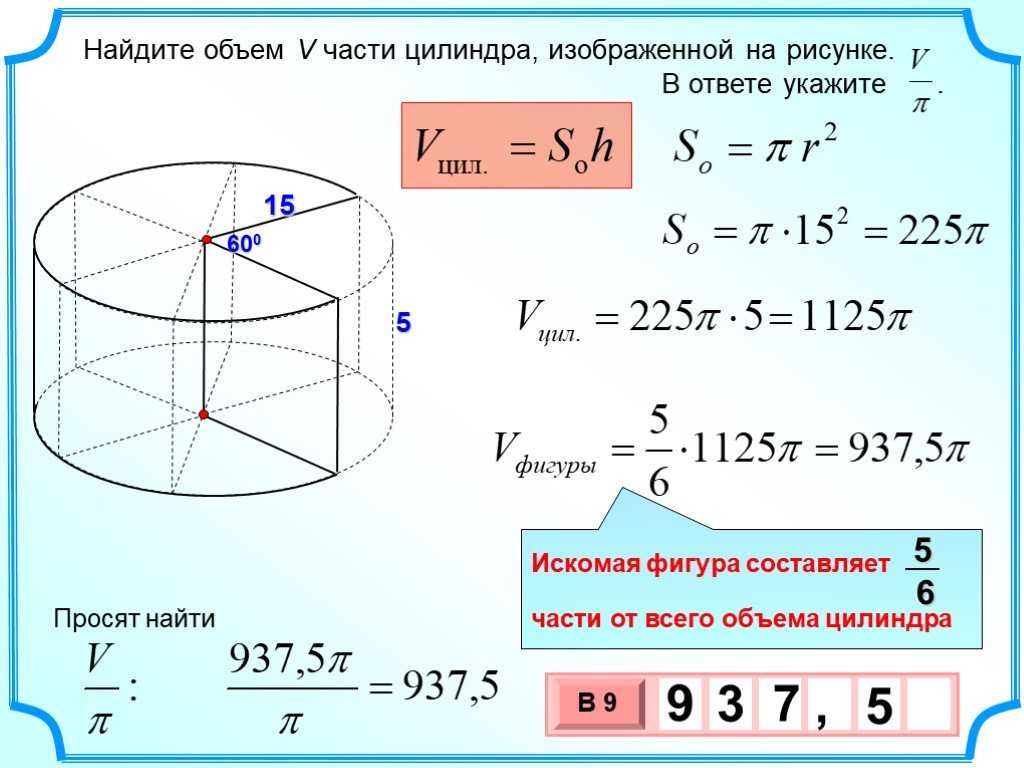
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
S бок. = 2πrh
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок. = 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая).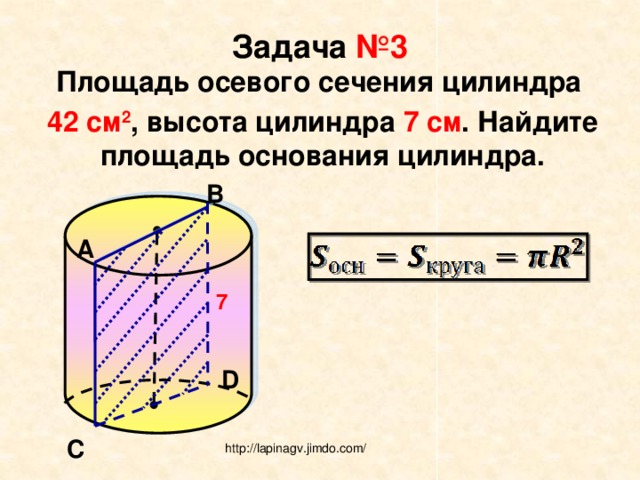 Данная прямая называется образующей цилиндрической поверхности.
Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb — площадь боковой поверхности, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S — площадь полной поверхности, h — высота
Расчет стенок цилиндра. Как найти площадь цилиндра
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.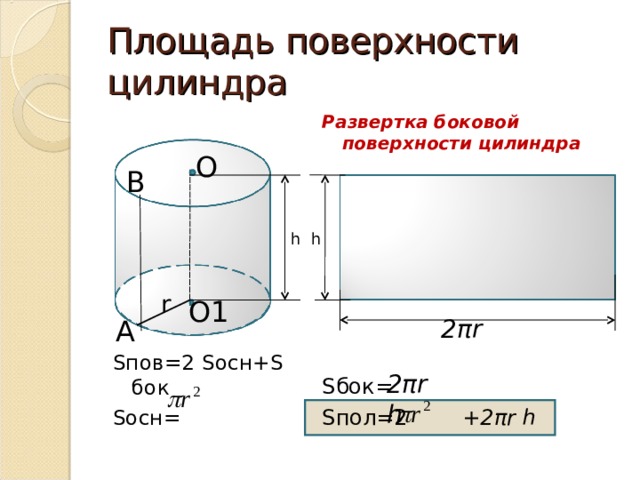 Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb — площадь боковой поверхности, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S — площадь полной поверхности, h — высота
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.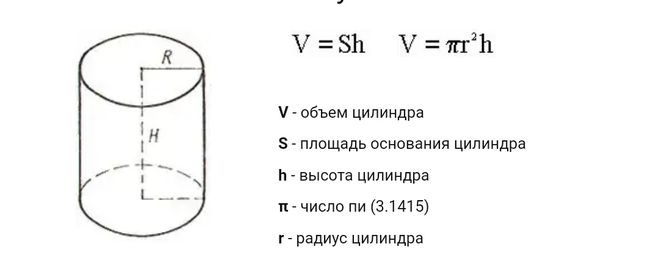
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра — онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности.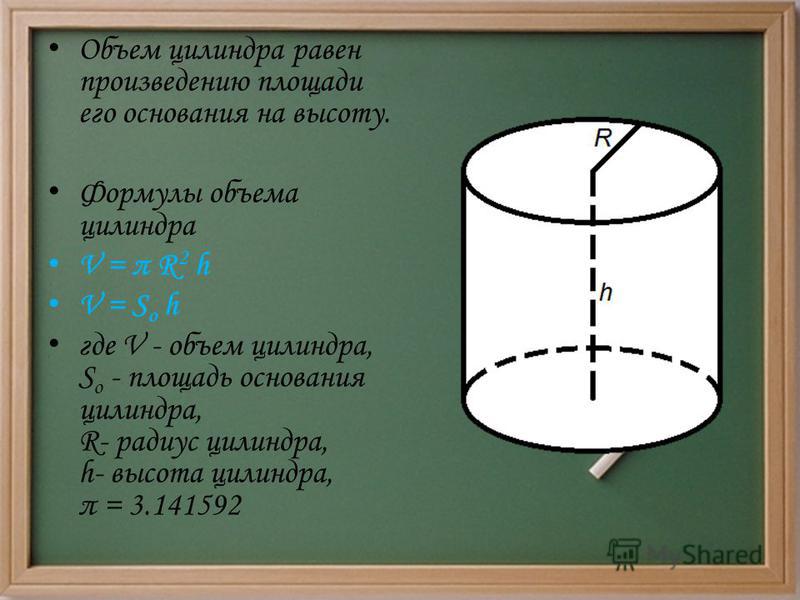 Формула ее известна с незапамятных времен —2π * r , где r — радиус окружности. Другая сторона прямоугольника равна высоте h . Найти искомое не составит труда.
Формула ее известна с незапамятных времен —2π * r , где r — радиус окружности. Другая сторона прямоугольника равна высоте h . Найти искомое не составит труда.
S бок = 2π * r * h ,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной S бок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S о = 2π * r 2 .
Конечная формула выглядит следующим образом:
S пол = 2π * r 2 + 2π * r * h.
Площадь цилиндра — формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
S пол = 2 π * r 2 + 2 π * r * h = 2 π * d 2 /4 + 2 π * h * d /2 = π * d 2 /2 + π * d * h ,
Вместо r в полную формулу нужно вставить значение r = d/2 .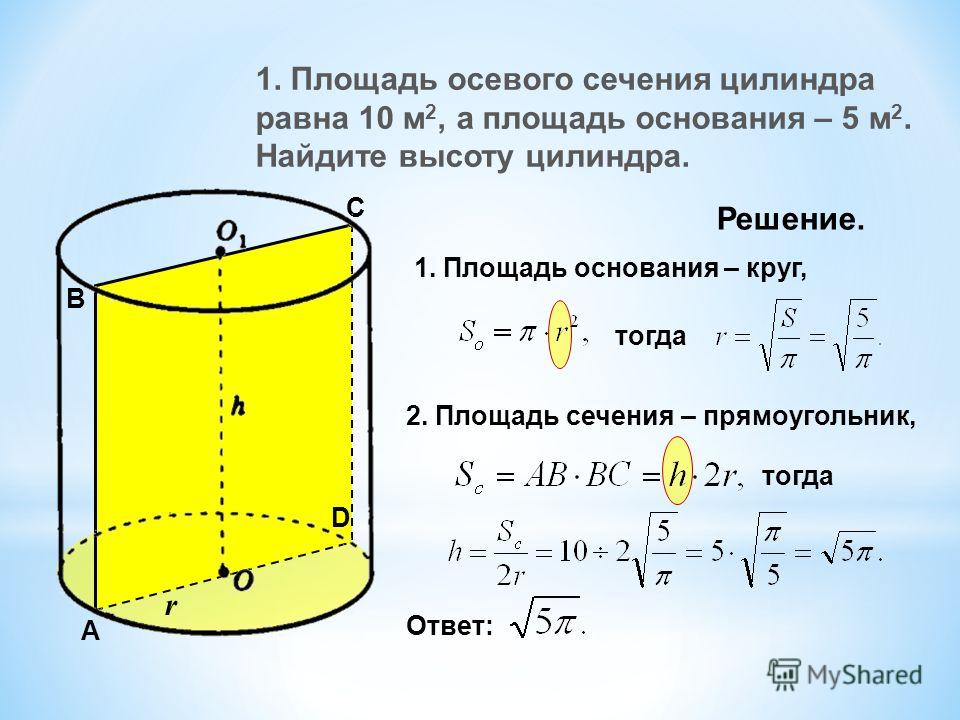
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
S пол = 2 * 3.14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
Переводим в привычные м 2 и получаем 0,01868928, приблизительно 0.02 м 2 .
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
S пол = 3.14 * 0.2 2 /2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м 2 .
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
S бок = 2 * 3.14 * 1 * 1 = 6.28 м 2 .
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh.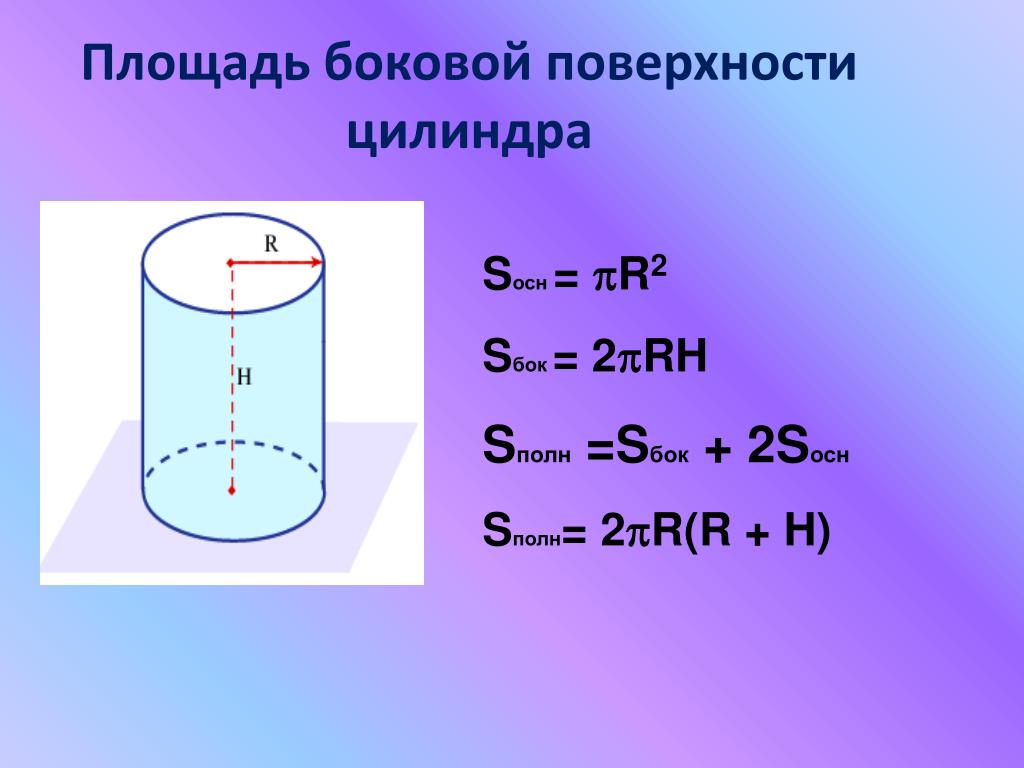 В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
S бок. = 2πrh
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок.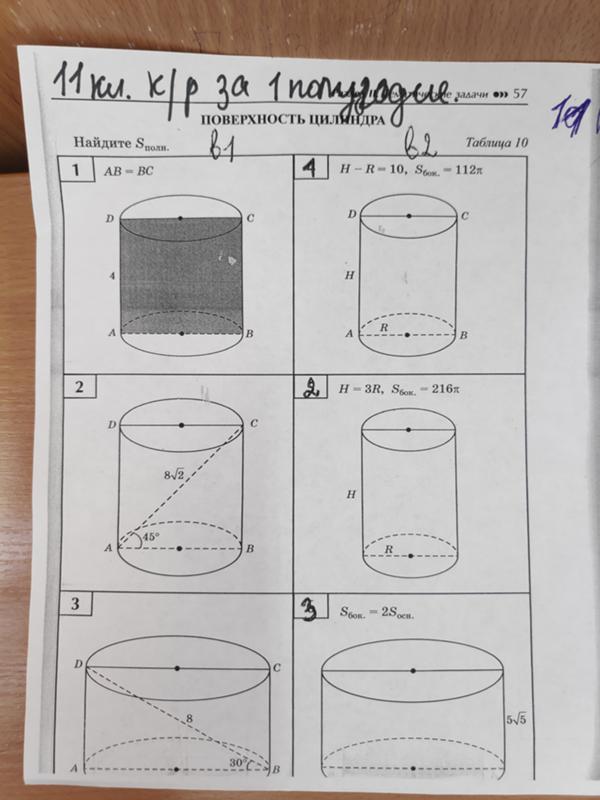 = 2πrh
= 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис.).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т. е. 2πrh .
Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).
За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.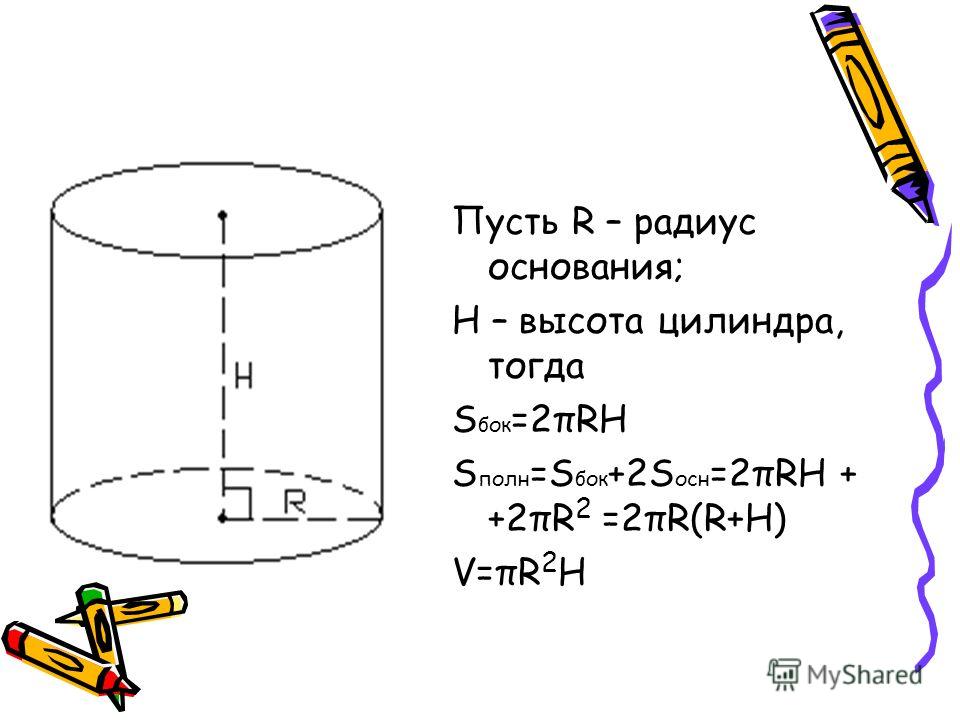 ) и вычисляется по формуле
) и вычисляется по формуле
S б.ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.
где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что
\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам
V n = Q n H и V’ n = Q’ n H.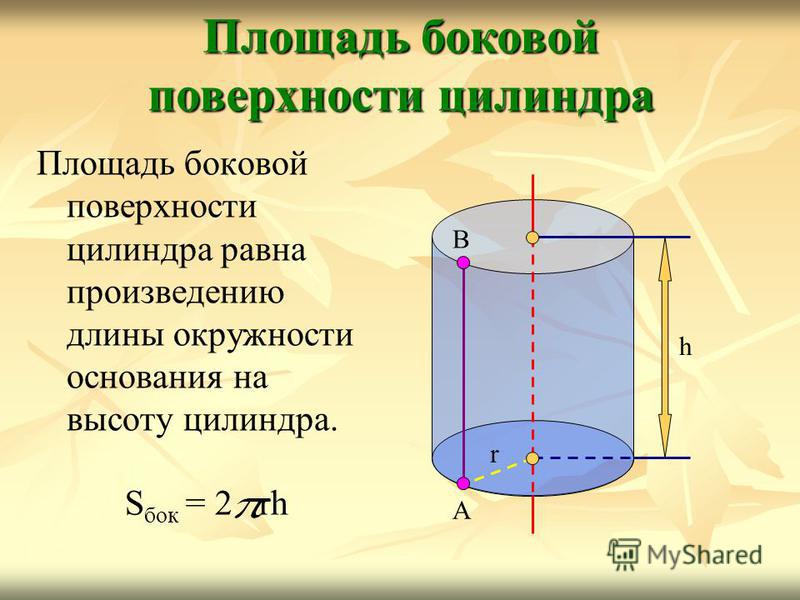
Следовательно,
V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру.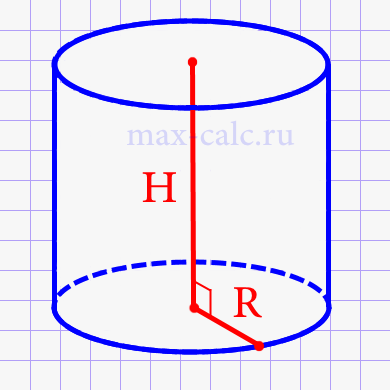 Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.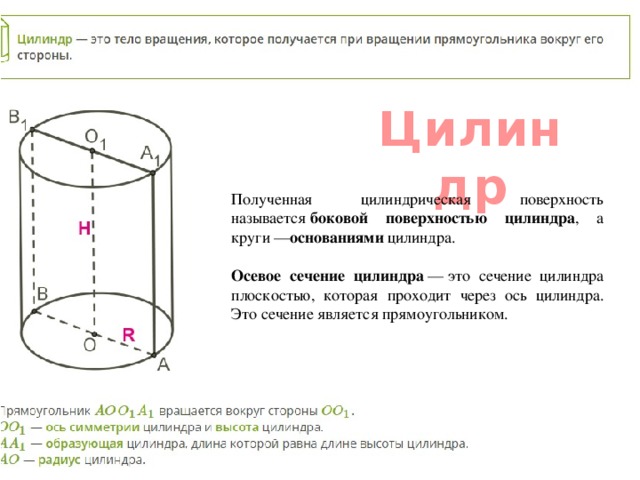
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Калькулятор объема и площади поверхности цилиндра
GENERATE WORK
сообщите об этом объявлении цилиндра. Калькулятор цилиндров — это онлайн-инструмент для геометрии, требующий длины радиуса основания и высоты цилиндра. Используя этот калькулятор, мы поймем методы, как найти площадь поверхности и объем цилиндра.
Необходимо выполнить следующие шаги:
- Введите длину радиуса основания и высоту цилиндра в поле. Эти значения должны быть положительными действительными числами или параметрами. Обратите внимание, что длина сегмента всегда положительна;
- Нажмите кнопку «СОЗДАТЬ РАБОТУ» , чтобы выполнить расчет;
- Калькулятор цилиндров вычисляет площадь поверхности и объем цилиндра.
Ввод: Два положительных действительных числа или параметра, такие как длина радиуса основания и высота цилиндра;
Вывод : Два положительных действительных числа или переменных как площадь поверхности и объем цилиндра и соответствующие единицы после этого.
Формула цилиндра:
Площадь поверхности цилиндра Формула:
Площадь поверхности, $S$, цилиндра определяется по следующей формуле
$$S = 2\pi r(h+r)$$
где $r$ — длина радиуса основания, $h$ — высота цилиндра и $\pi\ приблизительно3.14$.
Объем цилиндра Формула: 92\пи \раз ч$$ где $r$ — длина радиуса основания, $h$ — высота цилиндра и $\pi\ приблизительно3.14$.
Цилиндр представляет собой трехмерное твердое тело с конгруэнтными основаниями в паре параллельных плоскостей. Эти основания представляют собой конгруэнтные окружности. Осью цилиндра называется отрезок с концами в центрах оснований.
Высота или высота цилиндра, обозначаемая $h$, представляет собой перпендикулярное расстояние между его круглыми основаниями. Существует два типа цилиндров:
- Прямой цилиндр;
- Наклонный цилиндр.
Если осью цилиндра является высота, то цилиндр является прямым цилиндром, в противном случае цилиндр является наклонным цилиндром.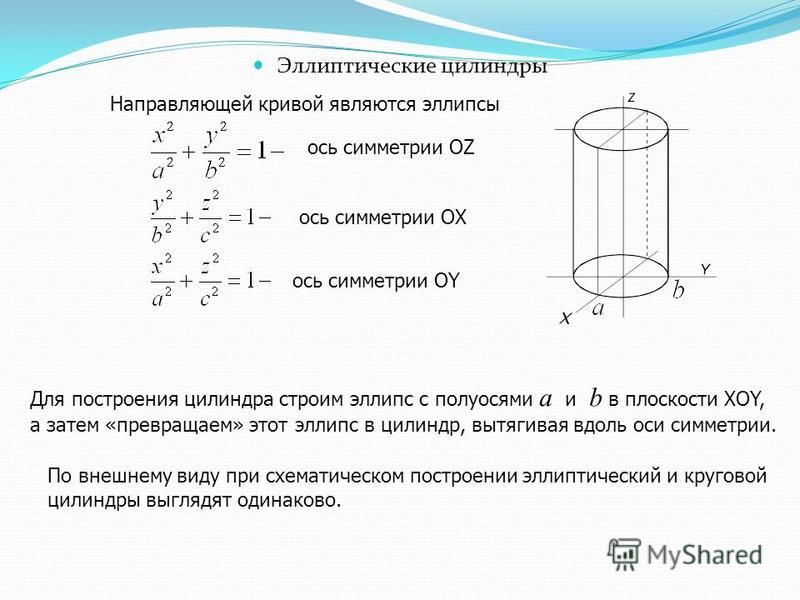
Если мы разрежем правильный цилиндр и положим его на плоскость, то получим шаблон или сетку для цилиндра. Сетка для цилиндра показана ниже.
Площадь поверхности цилиндра равна сумме площадей двух конгруэнтных кругов и прямоугольника. Площадь этого прямоугольника является боковой площадью цилиндра. Ясно, что длина прямоугольника равна длине окружности основания. Следовательно, площадь боковой поверхности цилиндра равна 93)$ и т.д.
Объем цилиндра и площадь поверхности с шагами показывает полный пошаговый расчет для нахождения площади поверхности и объема цилиндра с длиной его основания, радиусом $5\;in$ и высотой $10\;in$, используя формулы площади поверхности и объема. За
любые другие значения длины базового радиуса и высоты цилиндра, просто укажите два положительных действительных числа и нажмите кнопку «Создать работу».
кнопка. Учащиеся начальной школы могут использовать этот цилиндрический калькулятор для выполнения работы, проверки результатов площади поверхности и объема трехмерных тел или эффективного решения домашних задач.
Практические задачи на цилиндр
Практическая задача 1:
Найдите длину радиуса основания прямого цилиндра, если площадь поверхности равна $256$ кв.
метров, а высота составляет $18$ метров.
Практическое задание 2:
Бункер имеет цилиндрическую форму. Найдите боковую площадь силоса высотой 20$ метров с радиусом основания 5$ метров.
Высота второго бункера составляет 30 долларов США. Если оба бункера имеют одинаковую боковую площадь, найдите длину радиуса второго бункера.
Практическое задание 3:
Аквариум имеет цилиндрические резервуары. Если резервуар вмещает 100 000 литров и имеет глубину 5 долларов. Найдите радиус танка.
Калькулятор цилиндра, формула, пример расчета (работа с шагами), задачи из реальной жизни и практические задачи будут очень полезны учащимся начальной школы (образование K-12), чтобы понять концепцию объема и площади поверхности цилиндра. Это понятие может иметь значение в геометрии, чтобы найти объем и площадь поверхности цилиндра и трубы.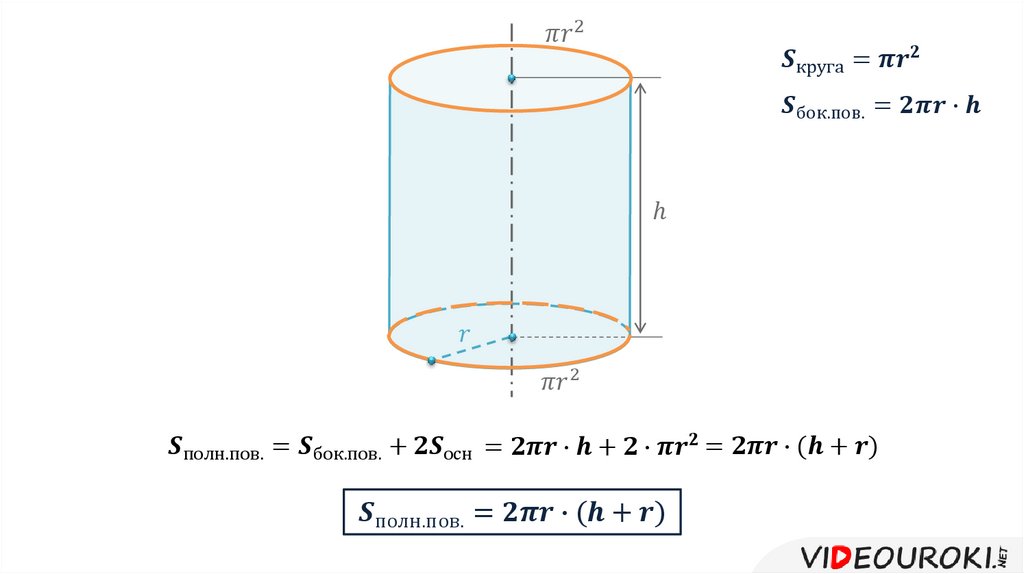 Реальные проблемы с объемом и площадью поверхности цилиндра очень распространены, поэтому эта концепция может иметь большое значение для решения проблем.
Реальные проблемы с объемом и площадью поверхности цилиндра очень распространены, поэтому эта концепция может иметь большое значение для решения проблем.
Калькулятор цилиндров 3D — Matheretter
LaTeX Ссылка
Графика цилиндра:
Результаты:
Вставьте два значения для цилиндра:
Используйте клавиши ↑ и ↓ для изменения значения Радиус
3 90: р Высота: час Диаметр: d = 2·r Периметр: р = 2·π·r Базовая площадь: A B = π·r 2 Боковая поверхность: А л = 2·π·r·h Площадь поверхности: А S = 2·π·r·(r+h) Объем: V = π·r 2 ·ч
Точность до 3 знаков после запятой
– +
Полноэкранный режим
Для большего удобства мы рекомендуем использовать Firefox или Chrome.
Все формулы для цилиндра с первого взгляда
Здесь вы видите необходимые формулы для расчета прямого кругового цилиндра:
Ссылка на графику: https://www. matheretter.de/img/wiki/cylinder-formulas.png
matheretter.de/img/wiki/cylinder-formulas.png
Пояснения:
Диаметр = 2·радиус → d = 2·r
Периметр = 2·Pi·радиус → p = 2·π·r
Площадь основания = Pi·радиус² → A B = π· r²
Боковая поверхность = периметр · высота → A L = 2·π·r·h
Площадь поверхности = 2·площадь основания + боковая поверхность → A S = 2·π·r² + 2·π· r·h = 2·π·r·(r+h)
Объем = площадь основания · высота → V = π·r²·h
Что такое цилиндр?
Определение:
Цилиндр (круговой цилиндр) состоит из двух параллельных противоположных круговых площадей и одной прямоугольной боковой поверхности, перпендикулярной круговым площадям (площади основания и верхней поверхности). Цилиндр – это геометрическая фигура. Круги имеют принципиальное значение для этой формы, поэтому нам понадобятся формулы для круга (площадь круга и периметр круга).
Для круглого цилиндра существуют следующие формулы: Периметр p равен 2·Pi·r (это формула для периметра круга), площадь основания A B равно Pi·r² (это формула площади круга), боковая поверхность равна периметру, умноженному на высоту, A L = p·h и, следовательно, A L = 2·Pi·r·h , площадь поверхности состоит из круглых площадей сверху и снизу (в 2 раза больше площади основания) и боковой поверхности, поэтому поверхность равна A S = 2·A B + A L и, таким образом, A S = 2·(π·r²) + (2·π·r·h), а 2·π·r часто выносится за скобки, и мы получаем: A S = 2·π·r·(r+h ). Объем цилиндра равен площади основания, умноженной на высоту, поэтому V = A B ·h = π·r²·h.
цилиндр с радиусом, площадью основания и диаметром площади основания. Характеристики цилиндра.
Объем цилиндра равен площади основания, умноженной на высоту, поэтому V = A B ·h = π·r²·h.
цилиндр с радиусом, площадью основания и диаметром площади основания. Характеристики цилиндра.
Пример из повседневной жизни (форма цилиндра):
Стакан для питья, трубка, строительный камень, цилиндр двигателя, ножка стула, ручка, форма таблетки и т. д.
Flächenberechnung beim Zylinder (График):
Часто задаваемые вопросы о цилиндрах:
- Рассчитать радиус цилиндра на заданной высоте и поверхности
- Рассчитать поверхность цилиндра? Упражнение
- Цилиндр с прикрепленным конусом. Вычислите высоту цилиндра.
- Вычислить объем цилиндра только по диаметру и высоте
- Заполните следующую таблицу для цилиндров.
- еще вопросы по баллонам…
| Значение 1 | Значение 2 | Радиус вычисляемый | Высота вычисляемая | Формула решения для радиуса Радиус всегда вычислим | Формула решения для высоты Радиус частично принят |
|---|---|---|---|---|---|
| Радиус | Высота | да | да | Радиус предоставлен | Предусмотренная высота |
| Радиус | Периметр | да | нет | Радиус предоставлен | Не вычисляемая высота — Детали |
| Радиус | Базовая зона | да | нет | Радиус предоставлен | Не вычисляемая высота — Детали |
| Радиус | Площадь поверхности | да | да | Радиус предоставлен | h = A S / 2·π·r – r См.  эквивалентное преобразование эквивалентное преобразование |
| Радиус | Боковая поверхность | да | да | Радиус предоставлен | ч = А Д / 2·π·r См. эквивалентное преобразование |
| Радиус | Том | да | да | Радиус предоставлен | h = В / r 2 ·h См. эквивалентное преобразование |
| Высота | Периметр | да | да | р = p / 2·π См. эквивалентное преобразование | Предусмотренная высота |
| Высота | Базовая зона | да | да | r = A B / π См. эквивалентное преобразование | Предусмотренная высота |
| Высота | Площадь поверхности | да | да | R 1,2 = — H / 2 ± √ ( H 2 / 4 + A S / 2 · π ) SEAVIVIV | Предусмотренная высота |
| Высота | Боковая поверхность | да | да | r = А Д / 2·π·ч См.  эквивалентное преобразование эквивалентное преобразование | Предусмотренная высота |
| Высота | Том | да | да | r = ± √( В / ч·π ) См. эквивалентное преобразование | Предусмотренная высота |
| Периметр | Базовая зона | да | нет | r = p / 2·π См. эквивалентное преобразование | Не вычисляемая высота — Детали |
| Периметр | Площадь поверхности | да | да | r = p / 2·π См. эквивалентное преобразование | h = A S / p – r См. эквивалентное преобразование |
| Периметр | Боковая поверхность | да | да | r = p / 2·π См. эквивалентное преобразование | h = A L / p См.  эквивалентное преобразование эквивалентное преобразование |
| Периметр | Том | да | да | р = p / 2·π См. эквивалентное преобразование | h = 2· В / u·r См. эквивалентное преобразование |
| Базовая зона | Площадь поверхности | да | да | r = A B / π См. эквивалентное преобразование | h = r · A S / 2·A B – r См. аналогичную трансформацию |
| Базовая зона | Боковая поверхность | да | да | r = A B / π См. эквивалентное преобразование | h = r · A L / 2·A B См. эквивалентное преобразование |
| Базовая зона | Том | да | да | r = A B / π См.  эквивалентное преобразование эквивалентное преобразование | h = A L / A B См. эквивалентное преобразование |
| Площадь поверхности | Боковая поверхность | да | да | Если у нас есть высота, мы можем вычислить радиус из формулы боковой поверхности: r = A L / 2·π·h См. эквивалентное преобразование | h = ± √( A L 2 / 2·π·A S – 2·π·M ) См. эквивалентное преобразование |
| 3 Площадь поверхности | Том | да | да | 0 = г 3 + A S / -2·π · r + V / π 3 Решения кубического уравнения См. эквивалентное преобразование | Если у нас есть высота, мы можем вычислить радиус по формуле боковой поверхности: h = A S / 2·π·r – r См.  эквивалентное преобразование эквивалентное преобразование |
| Боковая поверхность | Том | да | да | r = 2· В / А L См. эквивалентное преобразование | Если у нас есть высота, мы можем вычислить радиус по формуле боковой поверхности: h = A L / 2·π·r См. эквивалентное преобразование |
Калькулятор общей площади полого цилиндра
✖Радиус 1 — это радиальная линия от фокуса до любой точки кривой для 1-го радиуса.ⓘ Радиус 1 [r 1 ] | A.U. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖radius 2 является радиальной линией от фокусировки к любой точке кривой для 2 -го радиуса. | А.Е. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо. | |||
+10% -10% |
✖Площадь поверхности трехмерной формы представляет собой сумму всех площадей поверхности каждой из сторон. | AcreAcre (US Survey)AreArpentBarnCarreauCircular InchCircular MilCuerdaDecareDunamElectron Cross SectionHectareHomesteadMile (Roman)²Mile (Statute)²MuPingPlazaPyongRoodSabinSectionSquare AngstromSquare CentimeterSquare ChainSquare DecameterSquare DecimeterSquare FootSquare Foot (US Survey)Square HectometerSquare InchSquare KilometerSquare MeterSquare MicrometerSquare MilSquare MileSquare Mile (US Survey)Square MillimeterSquare NanometerSquare PerchSquare PoleSquare RodSquare Rod ( Исследование США) Square YardStremmaTownshipVaras Castellanas CuadVaras Conuqueras Cuad | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Общая площадь поверхности раствора полого цилиндра
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Радиус 1: 12 метров —> 12 метров, преобразование не требуется
Радиус 2: 13 метров —> 13 метров, преобразование не требуется Требуется
Высота: 12 метров —> 12 метров Преобразование не требуется
ШАГ 2: вычисление формулы
ШАГ 3: преобразование результата в единицу измерения
1727,87595947439 Квадратный метр —> преобразование не требуется
23 < 2 Калькулятор полых цилиндров
Общая площадь поверхности полого цилиндра Формула
Площадь поверхности = 2*pi*(радиус 1+радиус 2)*(радиус 1-радиус 2+высота)
SA = 2*pi*(r 1 +r 2 )*(r 1 -r 2 +h)
В чем разница между полым цилиндром и цилиндром?
Прямой круговой цилиндр представляет собой прямой цилиндр, каждый конец которого перпендикулярен его центральной оси, он не обязательно должен быть полым.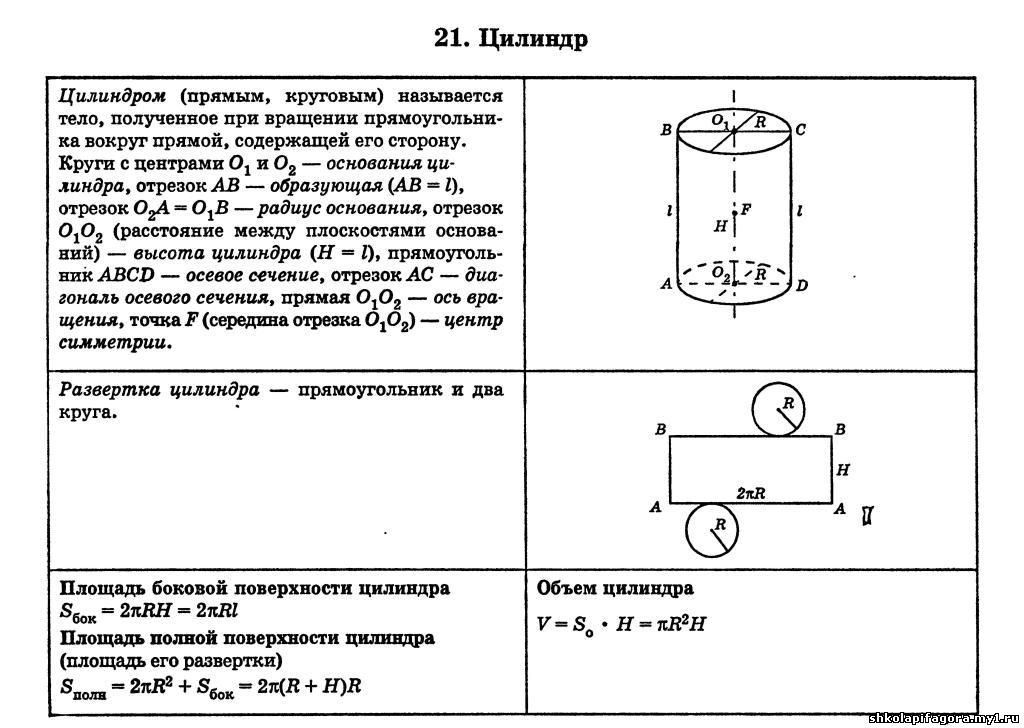 Полый цилиндр имеет в середине пустоту, закрытую или открытую, сосуд, чашу или трубку.
Полый цилиндр имеет в середине пустоту, закрытую или открытую, сосуд, чашу или трубку.
Как рассчитать общую площадь поверхности полого цилиндра?
Калькулятор общей площади поверхности полого цилиндра использует Площадь поверхности = 2*pi*(Радиус 1+Радиус 2)*(Радиус 1-Радиус 2+Высота) для расчета площади поверхности. Общая площадь поверхности полого цилиндра равна сумме двумерное пространство, занимаемое данным объектом. Площадь поверхности обозначается символом SA .
Как рассчитать общую площадь поверхности полого цилиндра с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для общей площади поверхности полого цилиндра, введите радиус 1 (r 1 ) , радиус 2 (r 2 ) и высота (h) и нажмите кнопку расчета. Вот как можно объяснить расчет общей площади полого цилиндра с заданными входными значениями -> 1727,876 = 2*pi*(12+13)*(12-13+12) .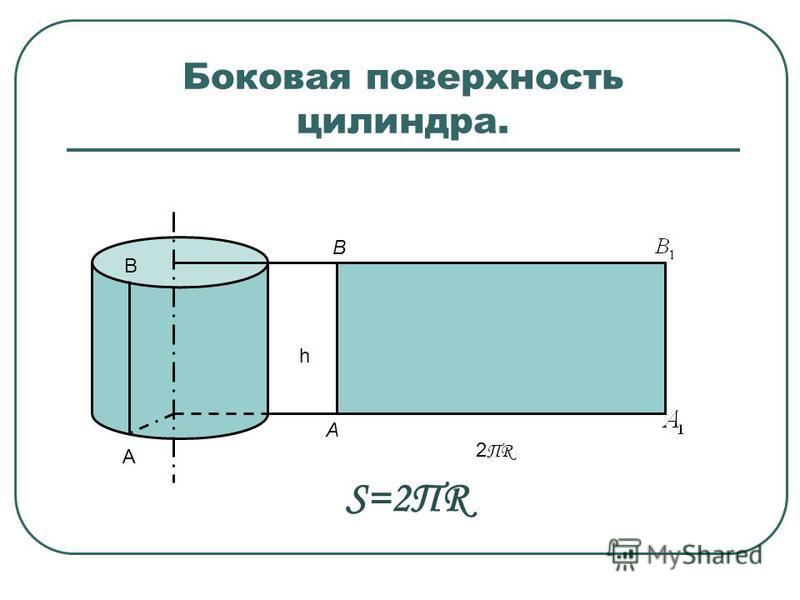
Часто задаваемые вопросы
Что такое общая площадь поверхности полого цилиндра?
Общая площадь поверхности полого цилиндра представляет собой объем двумерного пространства, занимаемого данным объектом, и представляется как SA = 2*pi*(r 1 +r 2 )*(r 1 -r 2 +h) или Площадь поверхности = 2*pi*(Радиус 1+Радиус 2)* (Радиус 1-Радиус 2+Высота) . Радиус 1 — это радиальная линия от фокуса до любой точки кривой для 1-го радиуса, Радиус 2 — это радиальная линия от фокуса до любой точки кривой для 2-го радиуса, а высота — это расстояние между самой низкой и самой высокой точками кривой. человек/форма/предмет, стоящий прямо.
Как рассчитать общую площадь поверхности полого цилиндра?
Общая площадь поверхности полого цилиндра — это количество двумерного пространства, занимаемого данным объектом, рассчитанное с использованием Площадь поверхности = 2*pi*(Радиус 1+Радиус 2)*(Радиус 1-Радиус 2+Высота) .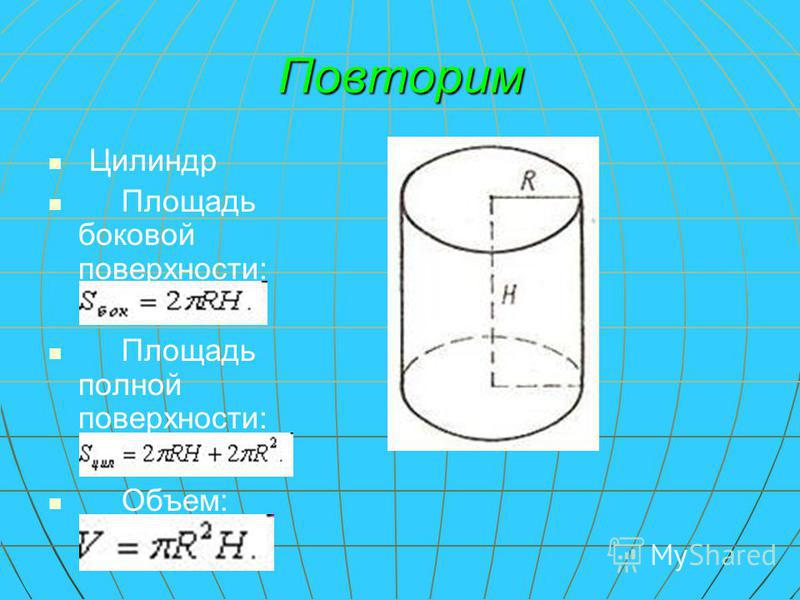 Чтобы рассчитать общую площадь поверхности полого цилиндра, вам потребуется радиус 1 (r 1 ) , радиус 2 (r 2 ) и высота (h) . С помощью нашего инструмента вам нужно ввести соответствующие значения для радиуса 1, радиуса 2 и высоты и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Чтобы рассчитать общую площадь поверхности полого цилиндра, вам потребуется радиус 1 (r 1 ) , радиус 2 (r 2 ) и высота (h) . С помощью нашего инструмента вам нужно ввести соответствующие значения для радиуса 1, радиуса 2 и высоты и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов вычисления площади поверхности?
В этой формуле площадь поверхности использует радиус 1, радиус 2 и высоту. Мы можем использовать 1 другой способ (способы) для вычисления того же самого, который выглядит следующим образом:
- Площадь поверхности = 2*pi*Высота*(Радиус 1+Радиус 2)
Доля
Скопировано!
| Геометрия | Формы | Контакты и конфиденциальность | Геометрические калькуляторы | Немецкий: Geometriechner, Formen |
| 1DЛиния, дуга окружности, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: Круглые формы: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron Archimedean Solids: Catalan Solids: Johnson Solids: Other Polyhedrons: Круглые формы: | Anzeige Расчеты на вертикальном половинном правильном круговом цилиндре или полуцилиндре. Формулы: пи: Радиус, высота и диагональ имеют одну и ту же единицу измерения (например, метр), площадь имеет эту единицу в квадрате (например, квадратный метр), объем имеет эту единицу в степени три (например, кубический метр). У аудио/видео есть этот блок -1 . Боковая поверхность представляет собой криволинейную часть площади поверхности. Поделиться: © Jumk.de Веб-проекты | Онлайн калькуляторы Anzeige |
Калькулятор площади поверхности цилиндра
от Ram
Калькулятор площади поверхности цилиндра: Поиск способов расчета общей площади поверхности цилиндра намного проще и быстрее. Тогда эта страница для вас. Используя наш калькулятор площади поверхности цилиндра, вы можете выполнять все расчеты в различных единицах измерения. Чтобы узнать больше о преобразованиях единиц измерения, ознакомьтесь с нашим калькулятором преобразования единиц измерения прямо сейчас на сайте areavolumecalculator.com
Перейдите к следующим разделам и узнайте, что такое площадь поверхности цилиндра и как легко найти площадь поверхности цилиндра.
Площадь поверхности цилиндра равна сумме площадей двух конгруэнтных кругов и прямоугольника. Площадь этого прямоугольника является боковой площадью цилиндра. Очевидно, что длина прямоугольника равна длине окружности основания. Следовательно, боковая площадь цилиндра равна L=2rπ×h, , где π ≈ 3,14.
Наконец, чтобы найти площадь поверхности цилиндра, сначала вычислите боковую площадь, а затем вычислите площади основных кругов путем суммирования. Формула площади поверхности прямого цилиндра: A = 2πrh + 2(πr 2 ) = 2πr(h+r).
Формула площади поверхности прямого цилиндра: A = 2πrh + 2(πr 2 ) = 2πr(h+r).
Площадь поверхности цилиндра Формула
Общая площадь поверхности замкнутого цилиндра Формула:
- A = L + T + B = 2πrh + 2(πr 2 ) = 2πr(h+r).
Площадь боковой поверхности цилиндра (только выгнутая наружу):
- Л = 2πrh
Площадь верхней и нижней поверхности цилиндра (2 круга):
- T = B = πr2
Как найти площадь поверхности цилиндра?
Чтобы вычислить площадь поверхности цилиндра, сначала вы должны разбить ее в своем воображении на три части. Три части могут быть представлены как
- Две окружности, составляющие концы цилиндра.
- Сторона цилиндра, которая в «развернутом» виде представляет собой прямоугольник.
Следовательно, площадь основания цилиндра равна удвоенной площади круга радиусом r, а площадь боковой поверхности цилиндра равна площади прямоугольника.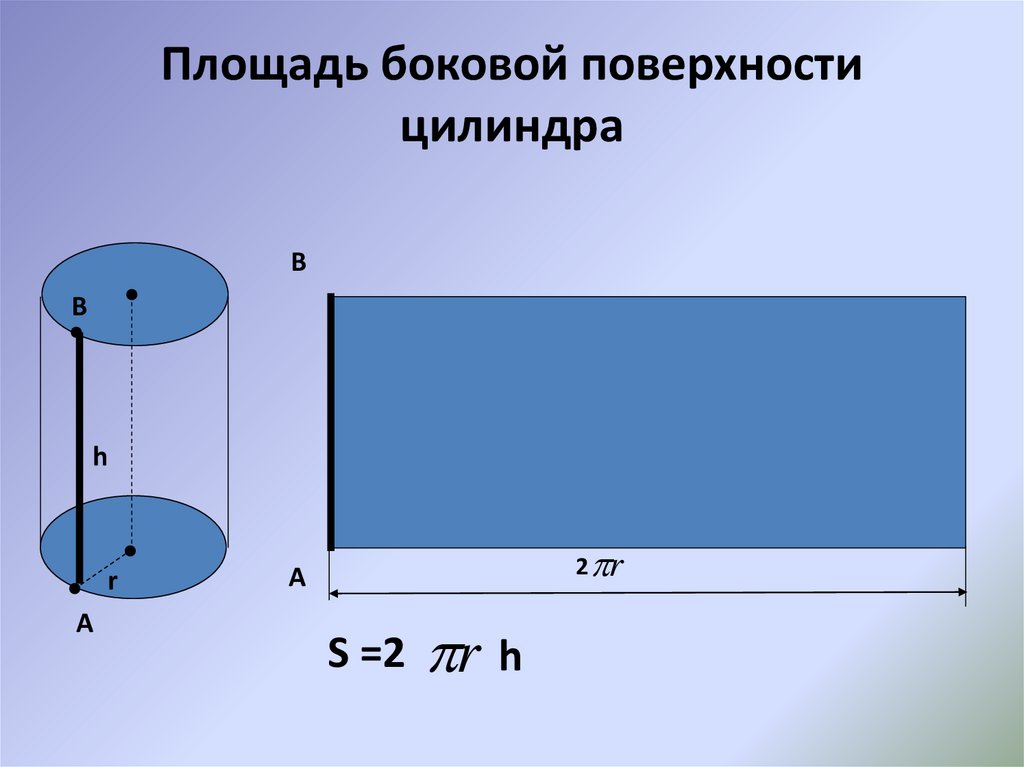 Первая сторона этого прямоугольника — высота цилиндра h, а вторая — длина окружности основания, т. е. 2 * π * r.
Первая сторона этого прямоугольника — высота цилиндра h, а вторая — длина окружности основания, т. е. 2 * π * r.
Таким образом, площадь боковой поверхности цилиндра равна 2 * π * r * h.
Теперь вам нужно вычислить площадь поверхности основания, поэтому вы должны вычислить площадь круга с радиусом r и умножить его на два, потому что каждый цилиндр имеет два основания.
Таким образом, площадь основания цилиндра равна 2 * π * r².
Наконец, формула общей площади поверхности цилиндра представляет собой сумму площади основания и площади боковой поверхности, т. е.
Общая площадь поверхности цилиндра = площадь основания + площадь боковой поверхности,
A = 2 * π * r² + (2 * π * r) * h,
A = 2 * π * r * (r + h)
Вот и все, теперь вы получили площадь поверхности цилиндра после подставляя значения радиуса основания и высоты.
Пример:
Найдите площадь поверхности цилиндра, если радиус равен 12 см, а высота 6 см?
Решение:
Учитывая, что радиус основания (r) = 12 см и
высота (h) = 6 см
Подставьте значения в формулу Площадь поверхности цилиндра = 2π * (радиус) 2 + 2π * (Радиус) * (Высота)
где Pi (π) приблизительно равно 3. 14.
14.
При дальнейшем упрощении получаем A= 2 (π) * (12 2 ) см 2 + 2 (π) * (12) см * (6,0) см
⇒ Возвести 12,0 см в степень 2.
2(π) * (144,0) см 2 + 2 (π) * (12,0) см * (6,0) см
⇒ Умножить 144,0 см 2 на 2
288,0 см 2 π + 2(π) * 12,0 см * 6,0 см 2 p 90,0023 ⇒ и 6,0 см
288,0 см π + 72,0 см 2 π * 2
⇒ Умножить 72,0 см 2 и 2
288,0 см 2 90,0 π + 144,0 см 2 . π
⇒ Добавить 288,0 π см 2 и 144,0 π см 2
Результат может быть представлен в нескольких формах как 432,0 π см 2
yl, высота которого и площадь поверхности C равны 1. & 6,0 см равно 432,0 π см 2
?
Студенты могут легко использовать наш Калькулятор площади поверхности цилиндра , потому что это очень удобный и бесплатный онлайн-инструмент.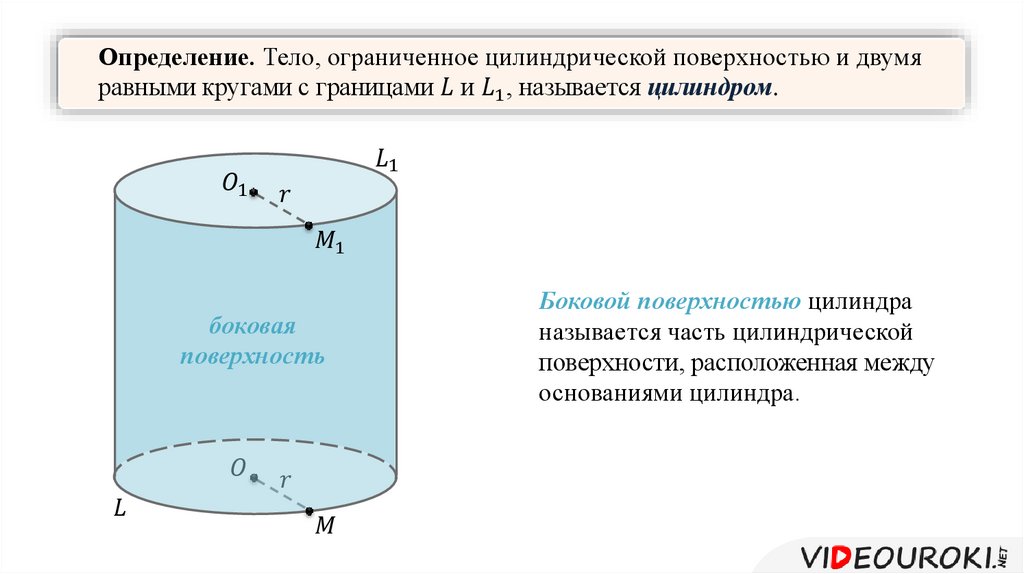 С помощью нашего удобного калькулятора вы можете сделать свои расчеты, например, как быстрее найти площадь поверхности цилиндра. Итак, следуйте приведенным ниже шагам и узнайте, как использовать этот бесплатный онлайн-калькулятор площади поверхности цилиндра:
С помощью нашего удобного калькулятора вы можете сделать свои расчеты, например, как быстрее найти площадь поверхности цилиндра. Итак, следуйте приведенным ниже шагам и узнайте, как использовать этот бесплатный онлайн-калькулятор площади поверхности цилиндра:
- Во-первых, введите свои параметры, такие как радиус основания и высоту, в качестве входных данных в появившихся полях.
- Теперь выберите данную метрику для каждого ввода в см, м, футах, ярдах, милях и т. д., щелкнув их в раскрывающемся списке.
- Затем нажмите кнопку «Область», расположенную ниже, чтобы перейти к полям ввода.
- Наконец-то вы получите площадь поверхности цилиндра в качестве выходных данных вместе с подробным решением.
Часто задаваемые вопросы о калькуляторе площади поверхности цилиндра
1. Что такое площадь поверхности цилиндра (закрытого) и формула?
Площадь поверхности замкнутого цилиндра можно вычислить, суммируя суммы площадей его основания и боковой поверхности:
- основание SA = 2πr2,
- боковой SA = 2πrh,
- Общая площадь поверхности цилиндра = 2πr(r + h), где «r» — радиус, а «h» — высота
2.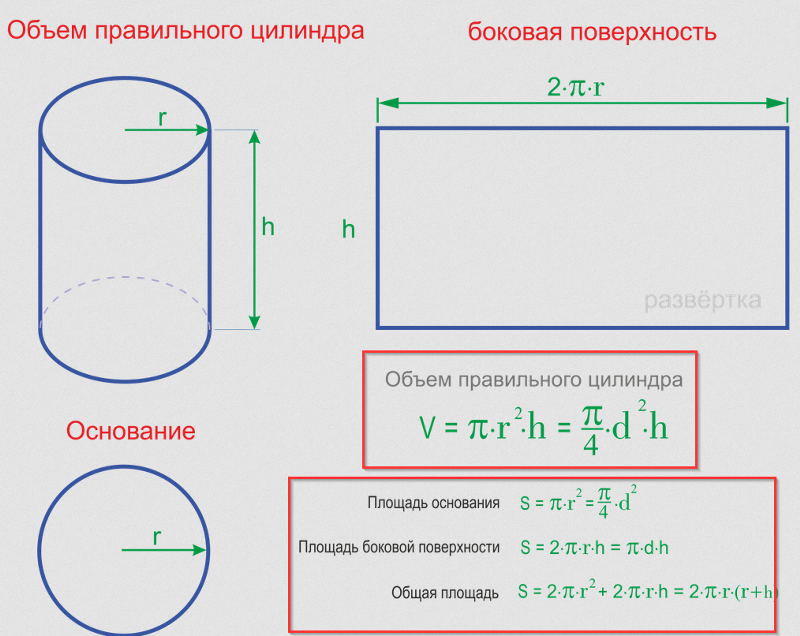 Как найти площадь поверхности закрытого цилиндра?
Как найти площадь поверхности закрытого цилиндра?
Вы можете найти площадь поверхности цилиндра с помощью нашего бесплатного удобного онлайн-калькулятора и получить результат за доли секунды.
3. Какова площадь поверхности цилиндра с радиусом основания r = 3 см и высотой h = 5 см?
После подстановки данных параметров в формулы площадь основания равна 56,55 см², а площадь боковой поверхности равна 94,25 см². Теперь подставьте два значения в формулу общей площади поверхности, и тогда выходная площадь поверхности цилиндра составит 150,8 см².
4. Что такое площадь поверхности калькулятора цилиндра?
Калькулятор площади поверхности цилиндра — это бесплатный онлайн-инструмент, который отображает площадь поверхности цилиндра в заданных метрических единицах.
Калькулятор цилиндров | Math Calculators
Online Cylinder Calculator, введите известные измерения для расчета свойств и объема цилиндра.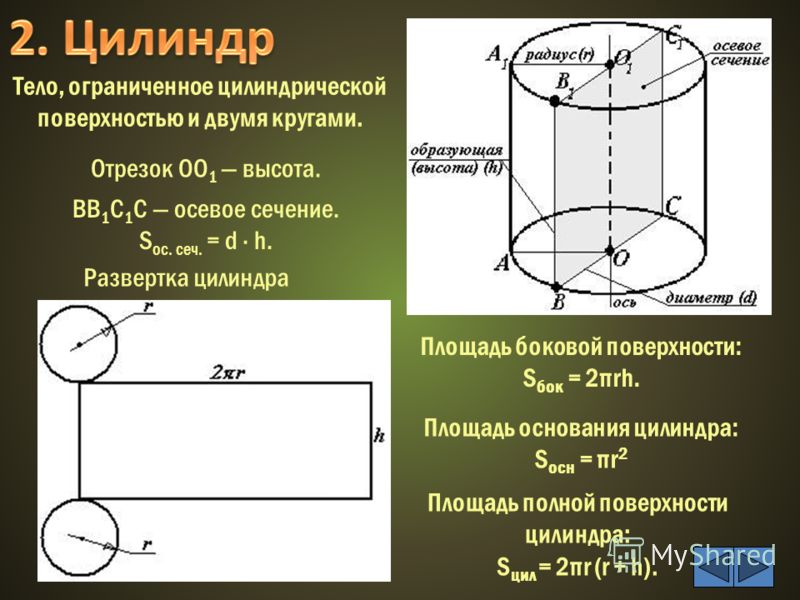 Каждое вычисление свойства цилиндра четко показано с соответствующим показанным уравнением и подробными разработками, поэтому вы можете проверить свою домашнюю / курсовую работу по математике на точность. Вы можете распечатать и / или отправить по электронной почте расчеты цилиндров, чтобы иметь справку для дальнейшего использования.
Каждое вычисление свойства цилиндра четко показано с соответствующим показанным уравнением и подробными разработками, поэтому вы можете проверить свою домашнюю / курсовую работу по математике на точность. Вы можете распечатать и / или отправить по электронной почте расчеты цилиндров, чтобы иметь справку для дальнейшего использования.
| 🖹 Обычный вид 🗖 Полный просмотр страницы |
| Calculator Precision (Decimal Places)012345678 12131415 |
| Diameter (d) |
| Radius (r) |
| Height [or Length] (h) |
| Площадь основания цилиндра | ||||
| Боковая поверхность цилиндра | ||||
| Площадь поверхности цилиндра составляет | ||||
| Объем цилиндра составляет | ||||
| Окружающая зона | ||||
| Основой зоны | ||||
|---|---|---|---|---|
Основой. πr 2 πr 2 A b = π × r 2 A b = × 2 A b = × A b = | ||||
| Lateral Surface of a cylinder calculation | ||||
| s l = 2πrh s l = 2 × π × r × h s l = 2 × × × s l = | ||||
| Surface area of a cylinder calculation | ||||
| A s = 2πrh + 2πr 2 A s = (2 × π × r × h) + (2 × π × r 2 ) А с = (2 × × × ) + (2 × × 2 ) A s = + (2 × × ) A s = + A s = | ||||
| Volume of Расчет цилиндра | ||||
| V = πr 2 H V = π × R 2 × H V = × 2 × V = 2 × 2 V = 62 2 × V = 62 2 × V = 62 2 × V = 62 2 × V = . 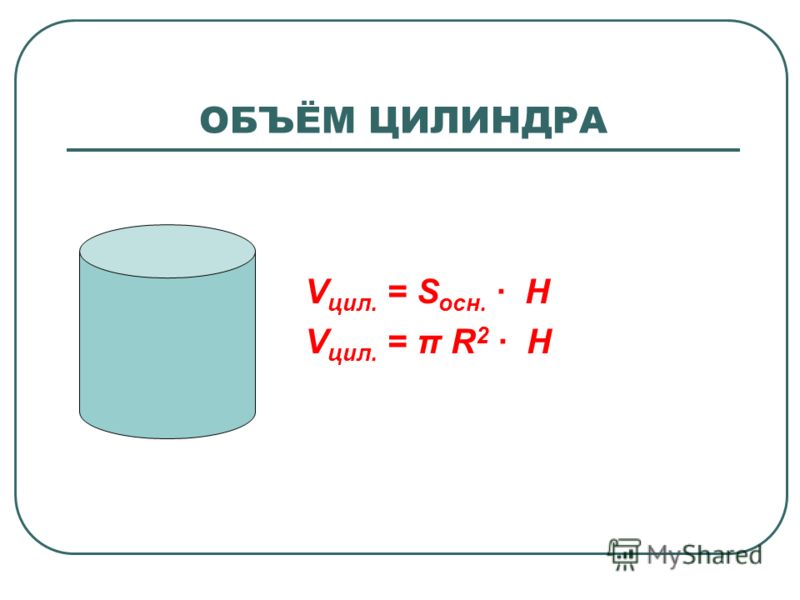 Окружность цилиндра расчет | C = 2πr | C = 2 × π × r C = 2 × × C = Cylinder Calculator. (r) | Высота [или длина] (L) | |
Калькулятор цилиндров был вам полезен? Пожалуйста, оставьте нам оценку, мы любим получать отзывы о наших бесплатных онлайн-калькуляторах.
★ ★ ★ ★ ★ [ 19 Голосов ]
самостоятельно? Вы пробовали делать математические расчеты вручную? Редко мы встречаем живого гения, который может сделать все математические расчеты самостоятельно и не нуждается в помощи. Воспроизведение и вычисление математических формул отлично подходит для математических гениев, но не все из нас способны вычислять математические фигуры и так быстро и точно вызывать формулы трехмерных фигур. Для таких людей, как вы и я, есть онлайн-калькуляторы, позволяющие делать самые длинные вычисления за секунды.
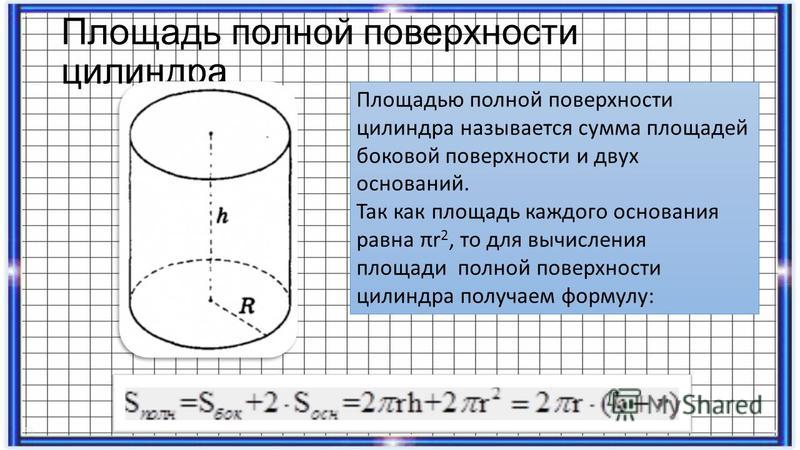 Таким образом, вы также можете выполнять цилиндрические расчеты с помощью этих инструментов расчета.
Таким образом, вы также можете выполнять цилиндрические расчеты с помощью этих инструментов расчета.Говоря только о цилиндрах, мы увидим, что из всех форм, с которыми мы сталкиваемся в нашей повседневной жизни, цилиндры являются самыми популярными. Будь то ручка или карандаш, которыми вы пишете, труба в вашей комнате, газовый баллон на вашей кухне, ваша бутылка с водой или электрический столб, все является цилиндром. Выполнение вычислений для нахождения их высоты, ширины, e и т. д. может оказаться непростой задачей в нашей повседневной жизни.
Зачем нужен калькулятор цилиндров?
Некоторым легко запомнить формулы, связанные с расчетом цилиндра, но применить их в любой ситуации невозможно. Это может быть возможно в классе, но подумайте о строительных или производственных единицах, сколько раз они должны выполнять эти вычисления. Им неудобно постоянно заниматься ручными вычислениями. Основная причина заключается в том, что основные операции в цилиндре связаны с числом π, а выполнение вычислений, включающих дробь, требует много времени.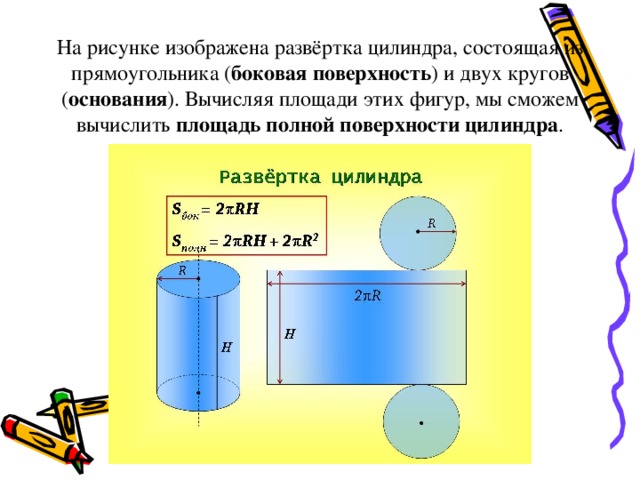
Использование цилиндрического калькулятора может сэкономить ваше время и тяжелый труд, которые можно использовать где-то еще. Давайте узнаем больше о цилиндре, его свойствах, некоторых расчетах, связанных с цилиндрами, и посмотрим, как цилиндры используются в нашей повседневной жизни.
Как определить цилиндр?
Цилиндр представляет собой трехмерную объемную фигуру, состоящую из боковой поверхности и двух конгруэнтных поверхностей (оснований). Хотя существует множество форм цилиндра (например, общий цилиндр или наклонный круговой цилиндр), всякий раз, когда мы говорим о цилиндрах, мы обычно имеем в виду правильные круговые цилиндры.
Основание цилиндра может быть круглым или прямоугольным.
Основные свойства цилиндра
Цилиндр — одна из самых распространенных форм, с которыми мы сталкиваемся в повседневной жизни. Вот некоторые из наиболее важных свойств цилиндра:
- Два основания цилиндра конгруэнтны и всегда параллельны друг другу.

- В случае, если основания цилиндра расположены точно друг над другом, а его ось образует прямой угол с основанием, то такой цилиндр называется «прямым цилиндром»
- Если основанием цилиндра являются окружности, то он называется правильным круговым цилиндром
- По той причине, что цилиндр имеет везде одинаковое поперечное сечение, он подобен призме
- Вместо круга, если основание цилиндра представляет собой эллипс, тогда цилиндр называется «эллиптическим цилиндром». в цилиндре полностью.
Формула для расчета объема цилиндра:
V= πr 2 h
Где
- V – объем цилиндра
- π – константа, значение которой равно 22/7 или 3,17
- r — радиус основания, h — высота цилиндра
Цилиндр имеет три площади поверхности, включая основание, боковую и общую поверхности e. Формулы для различных типов площадей поверхностей:
- Поверхность основания e — πr2 кв.ед. (для отдельного основания) 9
Где:
- π – постоянная
- r – радиус основания h
- высота цилиндра
Значение калькуляторов цилиндров в нашей повседневной жизни
Каждый день мы сталкиваемся с множеством цилиндров.


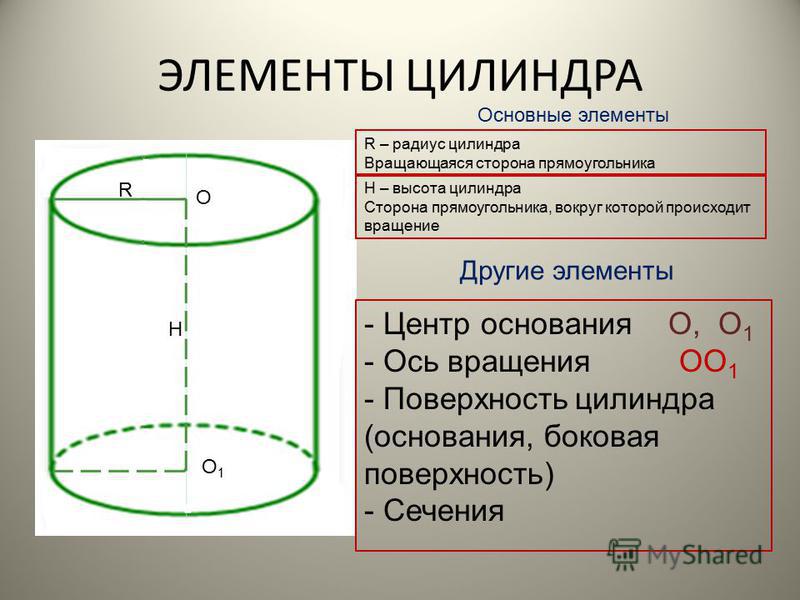 С данной формулы радиус выражается достаточно легко. С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.
С данной формулы радиус выражается достаточно легко. С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.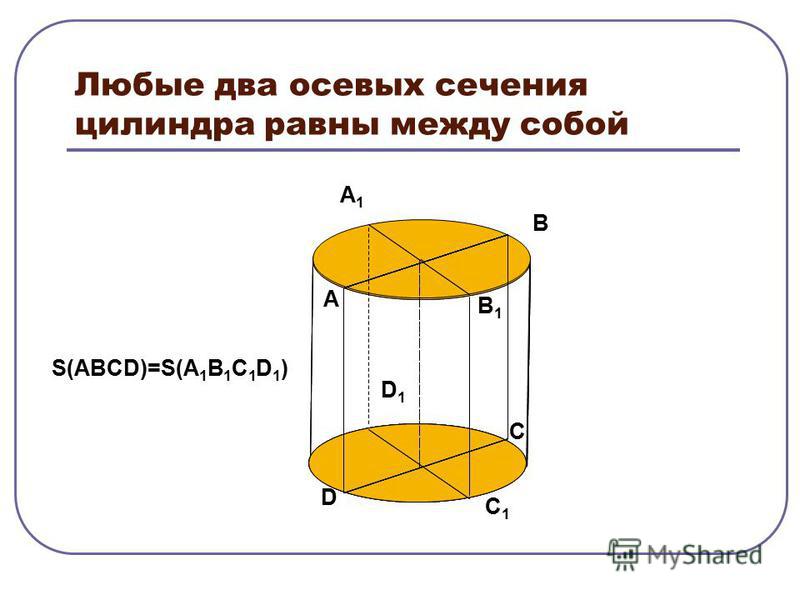

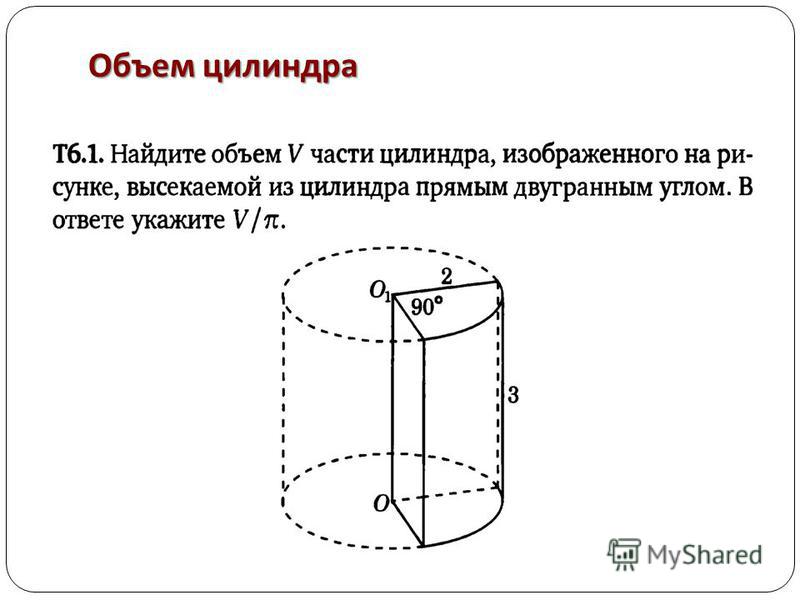 Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
Данную фигуру определяет радиус основания, минимальная и максимальная высоты.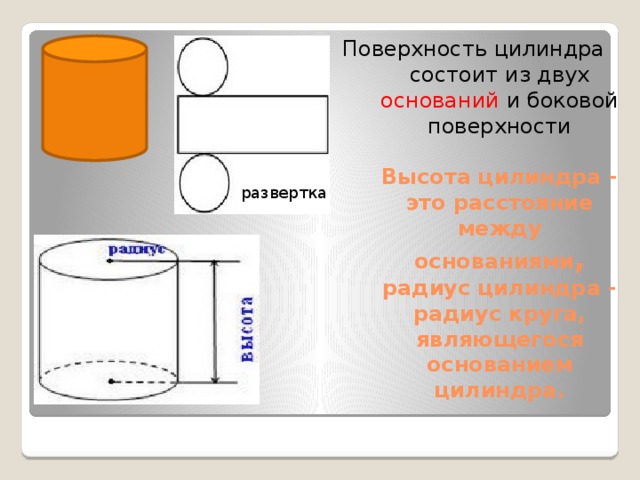 ⓘ Радиус 2 [r2]
ⓘ Радиус 2 [r2]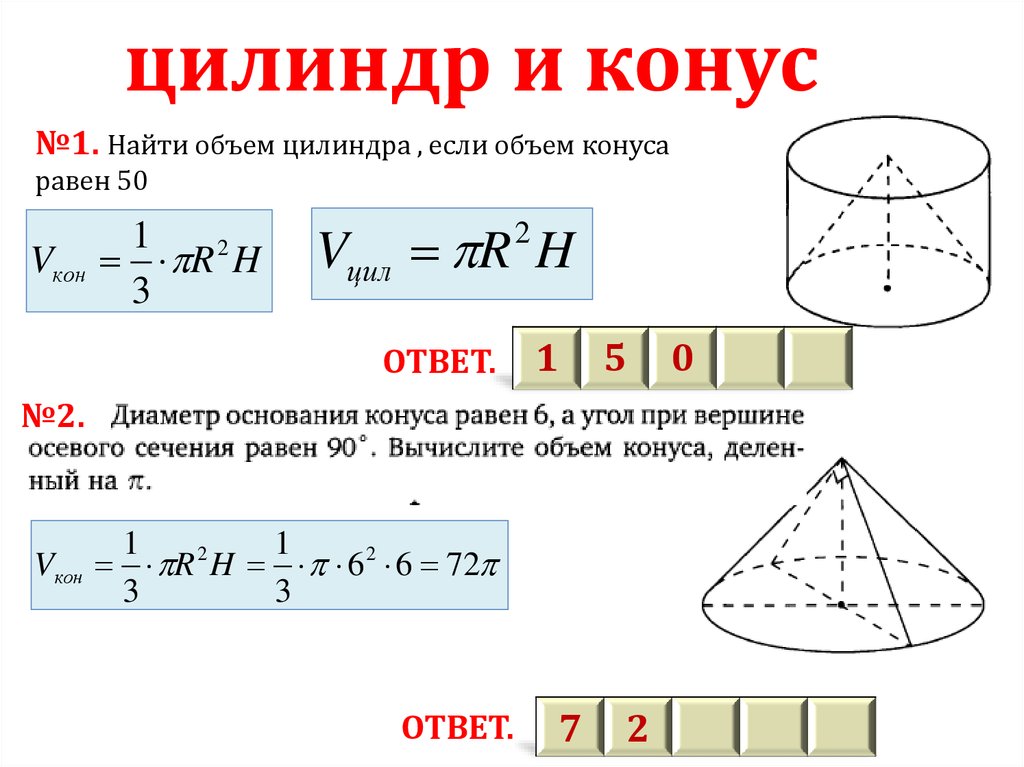 ⓘ Высота [h]
ⓘ Высота [h] ⓘ Общая площадь полого цилиндра [SA]
ⓘ Общая площадь полого цилиндра [SA]
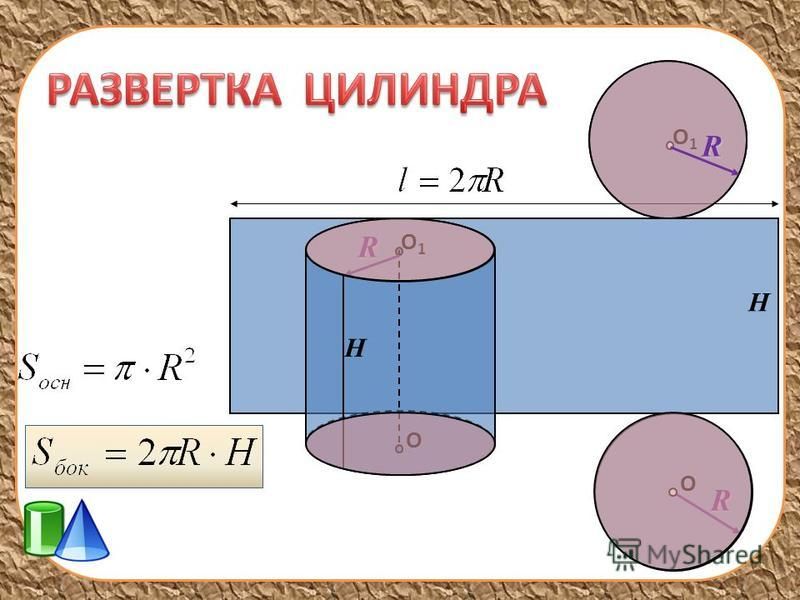
 ⓘ Высота [ч]
ⓘ Высота [ч]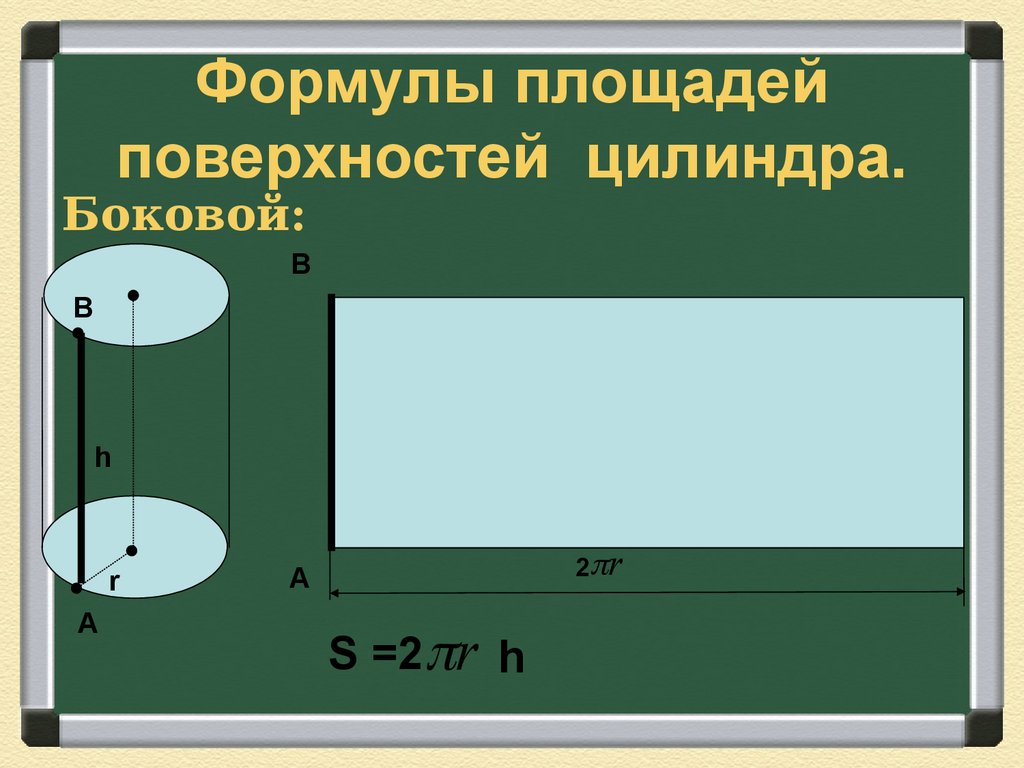 ⓘ Общая площадь поверхности полого цилиндра [SA]
ⓘ Общая площадь поверхности полого цилиндра [SA]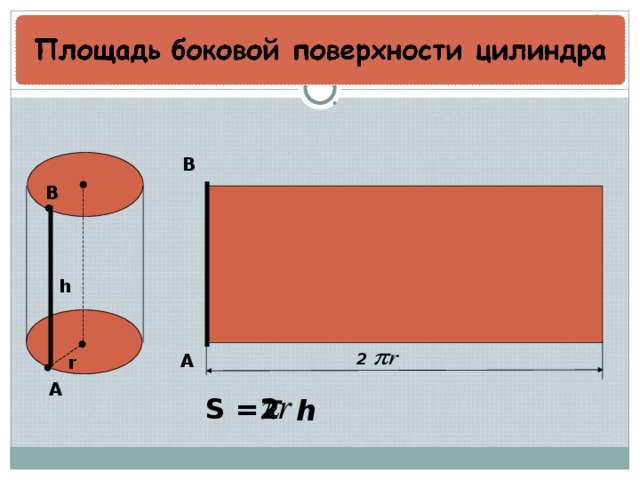 Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник 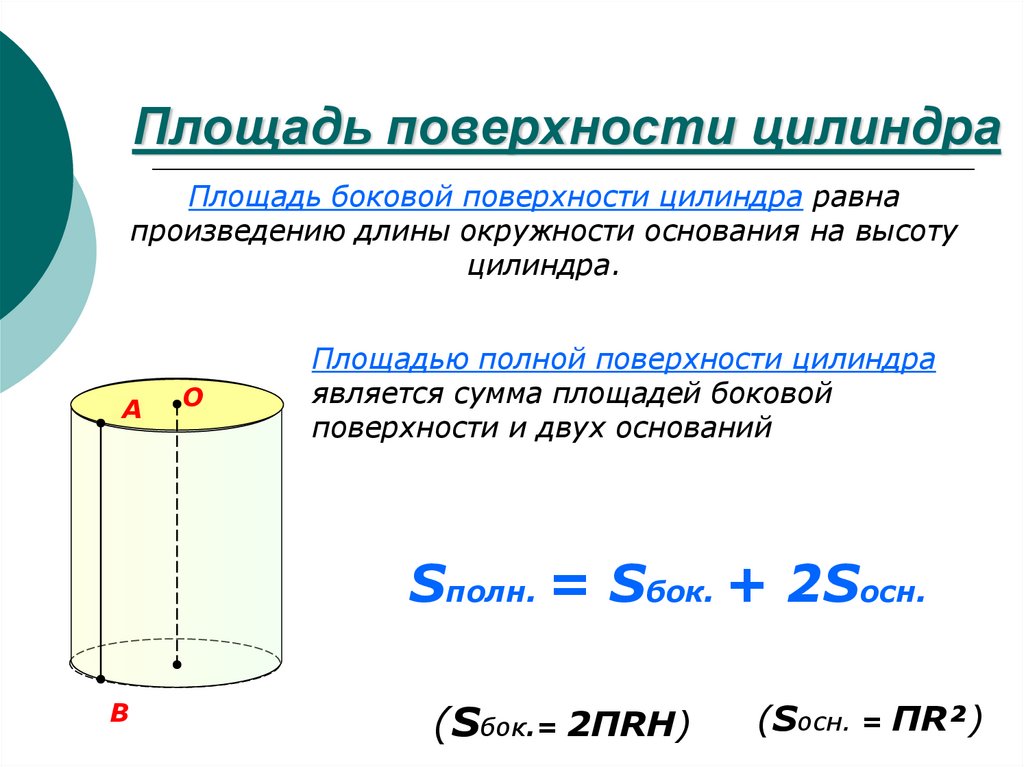 Это полуокружность, вытянутая перпендикулярно на высоту h. Полукруг – это основа. Введите радиус каландра и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать.
Это полуокружность, вытянутая перпендикулярно на высоту h. Полукруг – это основа. Введите радиус каландра и высоту и выберите количество знаков после запятой. Затем нажмите Рассчитать.