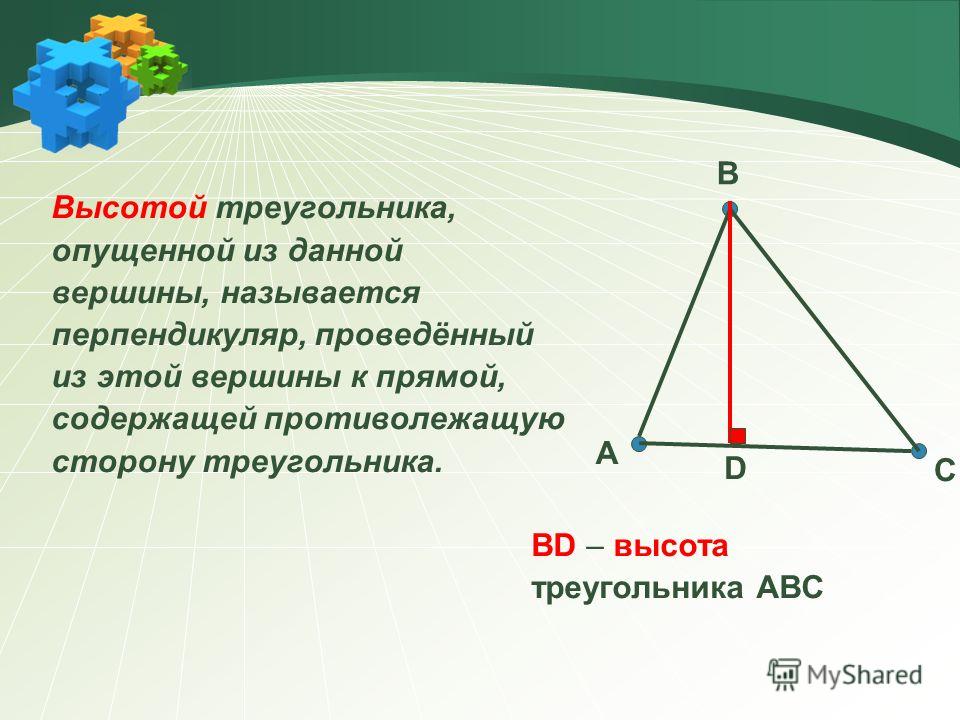
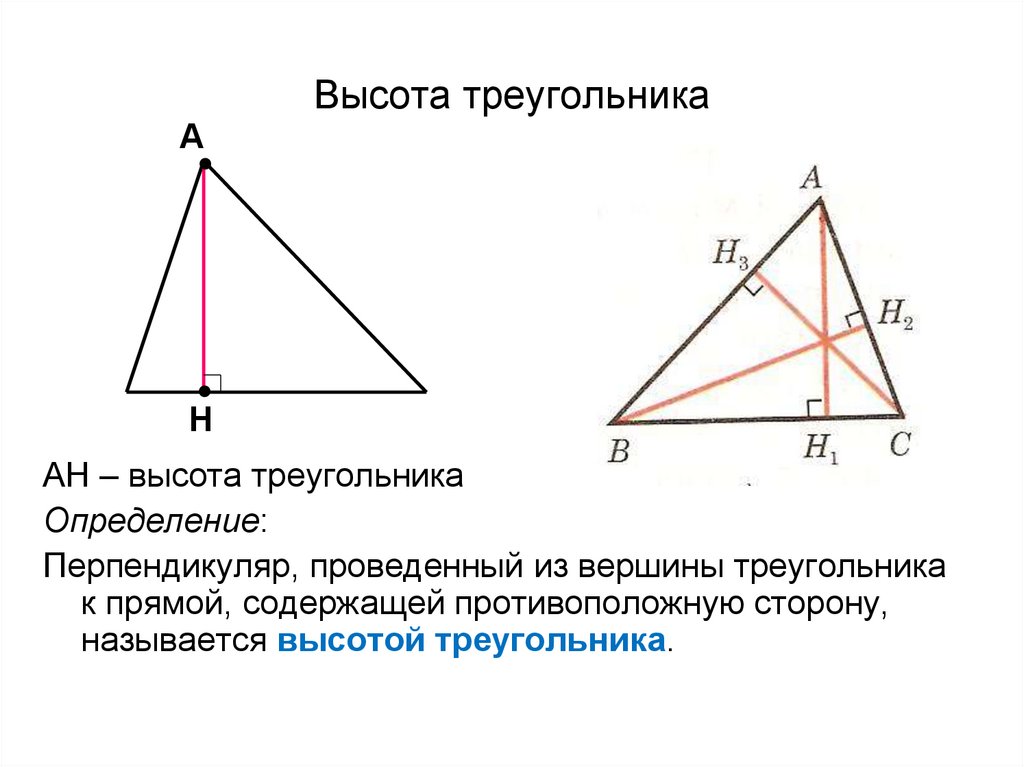
Высота треугольника
Урок содержит описание свойств и формулы нахождения высоты треугольника, а также примеры решения задач. Если Вы не нашли решение подходящей задачи — пишите про это на форуме. Наверняка, курс будет дополнен.
ВЫСОТА ТРЕУГОЛЬНИКАВысота треугольника – опущенный из вершины треугольника перпендикуляр, проведенный на противолежащую вершине сторону или на ее продолжение. Свойства высоты треугольника:
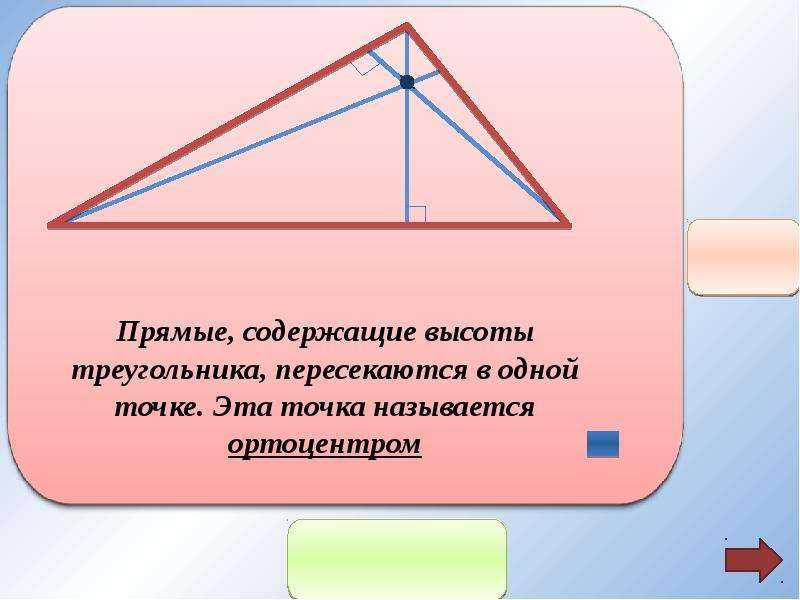
Ортоцентр треугольникаВсе три высоты треугольника (проведенные из трех вершин) пересекаются в одной точке, которая называется ортоцентром. Для того, чтобы найти точку пересечения высот, достаточно провести две высоты (две прямые пересекаются только в одной точке). Расположение ортоцентра (точка О) определяется видом треугольника. У остроугольного треугольника точка пересечения высот находится в плоскости треугольника. (Рис.1). У прямоугольного треугольника точка пересечения высот совпадает с вершиной прямого угла (Рис.2).
У тупоугольного треугольника точка пересечения высот находится за плоскостью треугольника (Рис. У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают. У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают. |
ВИСОТА ТРИКУТНИКА Висота трикутника — опущений з вершини трикутника перпендикуляр, проведений на протилежну вершині бік або на її продовження. Всі три висоти трикутника (проведені з трьох вершин) перетинаються в одній точці, яка називається ортоцентром. Для того, щоб знайти точку перетину висот, досить провести дві висоти (дві прямі перетинаються тільки в одній точці).
Розміщення ортоцентра (точка О) визначається видом трикутника. У гострокутного трикутника точка перетину висот знаходиться в площині трикутника. (Мал.1). У прямокутного трикутника точка перетину висот збігається з вершиною прямого кута (Мал.2). У тупоугольного трикутника точка перетину висот знаходиться за площиною трикутника (Мал.3). У рівнобедреного трикутника медіана, бісектриса і висота, проведені до основи трикутника, збігаються. У рівностороннього трикутника всі три «помітні» лінії (висота, бісектриса і медіана) збігаються і три «помітні» точки (точки ортоцентра, центру ваги і центру вписаного і описаного кіл) знаходяться в одній точці перетину «помітних» ліній, тобто теж збігаються. |
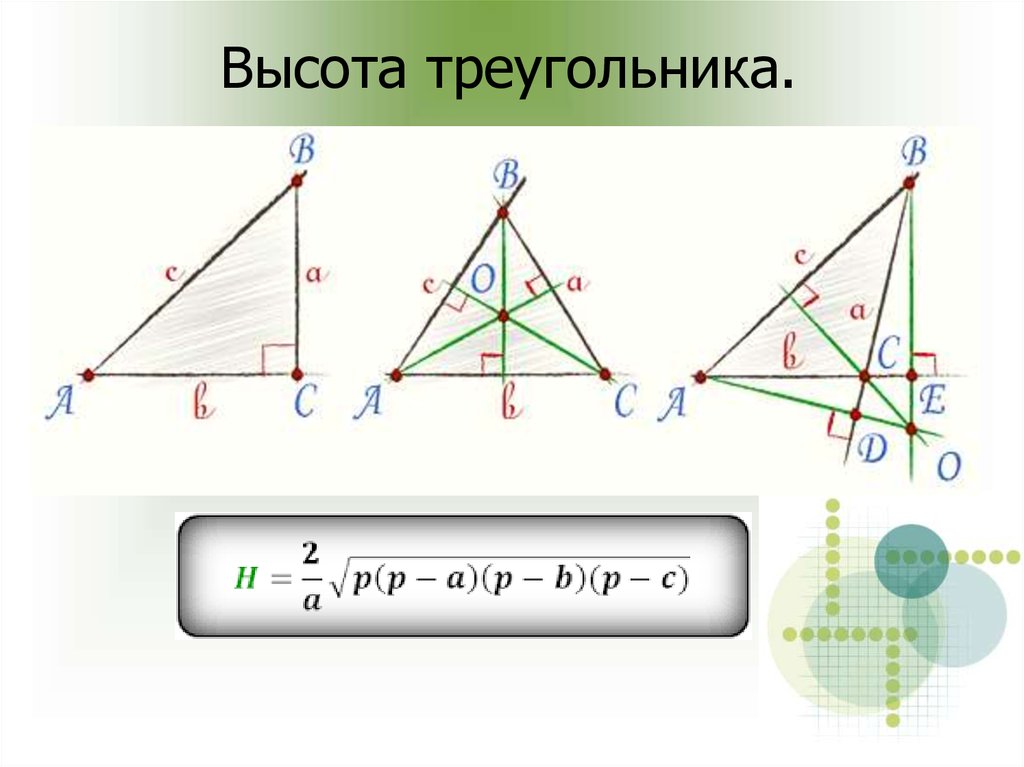
Формулы нахождения высоты треугольника
Рисунок приведен для облегчения восприятия формул нахождения высоты треугольника. Общее правило — длина стороны обозначена маленькой буквой, лежащей напротив соответствующего угла. То есть сторона a лежит напротив угла A.
Общее правило — длина стороны обозначена маленькой буквой, лежащей напротив соответствующего угла. То есть сторона a лежит напротив угла A.
Высота в формулах обозначается буквой h, нижний индекс которой соответствует стороне, на которую она опущена.
Другие обозначения:
a,b,c — длины сторон треугольника
hb — высота, проведенная к стороне b
hc — высота, проведенная к стороне c
R — радиус описанной окружности
r — радиус вписанной окружности
Пояснения к формулам.
Высота треугольника равна произведению длины стороны, прилежащей к углу, из которой опущена эта высота на синус угла между этой стороной и стороной, на которую такая высота опущена (Формула 1)
Высота треугольника равна частному от деления удвоенной величины площади треугольника на длину стороны, к которой опущена эта высота (Формула 2)
Высота треугольника равна частному от деления произведения сторон, прилежащих к углу, из которого опущена эта высота, на удвоенный радиус описанной вокруг него окружности (Формула 4).
Высоты сторон в треугольнике соотносятся между собой в той же самой пропорции, как соотносятся между собой обратные пропорции длин сторон этого же треугольника, а также в той же самой пропорции между собой относятся произведения пар сторон треугольника, которые имеют общий угол (Формула 5).
Сумма обратных значений высот треугольника равна обратному значению радиуса вписанной в такой треугольник окружности (Формула 6)
Площадь треугольника можно найти через длины высот этого треугольника (Формула 7)
Длину стороны треугольника, на которую опущена высота, можно найти через применение формул 7 и 2.
В прямоугольном треугольнике ABC (угол C = 900) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см
Решение.
Треугольники ABC, ACD и CBD подобны между собой . Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).
Прямоугольные треугольники — единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.
Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)
Треугольники ABC и CBD подобны. Значит:
AD/DC = DC/BD, то есть
DC2=AD*BD
DC2=9*16
DC=12 см
Задача на применение теоремы Пифагора.
Треугольник ABC является прямоугольным. При этом C-прямой угол. Из него проведена высота CD=6см. Разность отрезков BD-AD=5 см.
Найти: Стороны треугольника ABC.
Решение.
1.Составим систему уравнений согласно теореме Пифагора
CD2+BD2=BC2
CD2+AD2=AC2
поскольку CD=6
36+BD2=BC2
36+AD2=AC2
Поскольку BD-AD=5, то
BD = AD+5, тогда система уравнений принимает вид
36+(AD+5)2=BC2
36+AD2=AC2
Сложим первое и второе уравнение. Поскольку левая часть прибавляется к левой, а правая часть к правой — равенство не будет нарушено. Получим:
36+36+(AD+5)2+AD2=AC2+BC2
72+(AD+5)2+AD2=AC2+BC2
2. Теперь, взглянув на первоначальный чертеж треугольника, по той же самой теореме Пифагора, должно выполняться равенство:
AC2+BC2=AB2
Поскольку AB=BD+AD, уравнение примет вид:
AC2+BC2=(AD+BD)2
Поскольку BD-AD=5, то BD = AD+5, тогда
AC2+BC2=(AD+AD+5)2
3.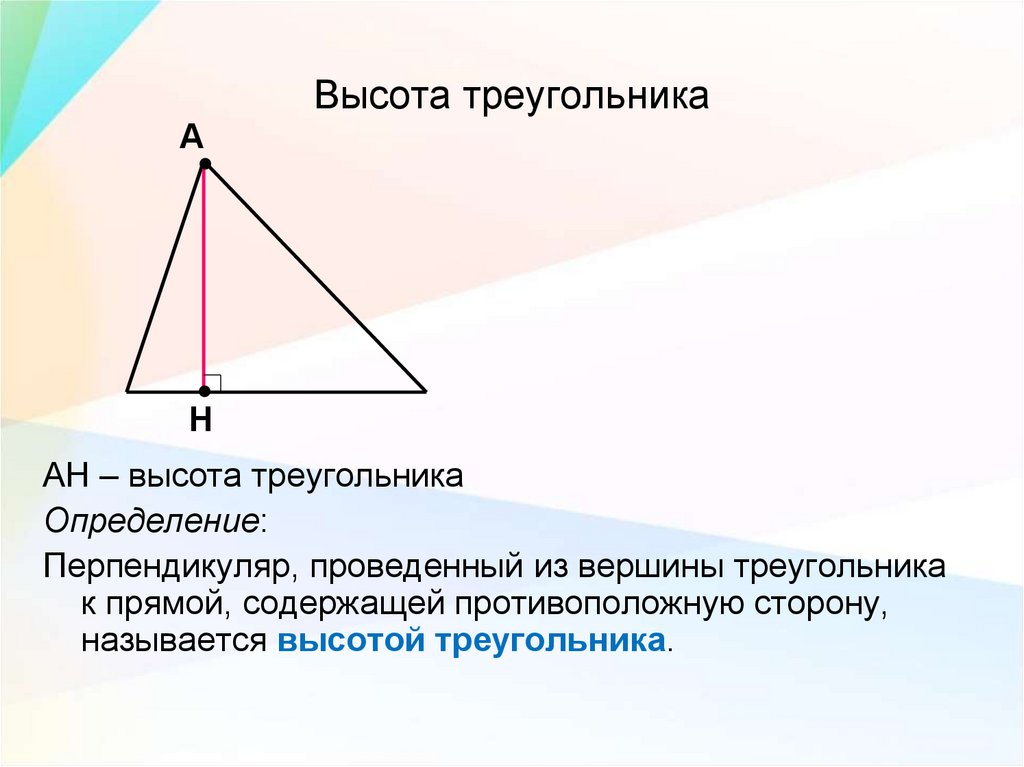 Теперь взглянем на результаты, полученные нами при решении в первой и второй части решения. А именно:
Теперь взглянем на результаты, полученные нами при решении в первой и второй части решения. А именно:
72+(AD+5) 2+AD2=AC2+BC2
AC2+BC2=(AD+AD+5)2
Они имеют общую часть AC2+BC2 . Таким образом, приравняем их друг к другу.
72+(AD+5)2+AD2=(AD+AD+5)2
72+AD2+10AD+25+AD2=4AD2+20AD+25
-2AD2-10AD+72=0
В полученном квадратном уравнении дискриминант равен D=676, соответственно, корни уравнения равны:
х1=-3,5
x2=4
Поскольку длина отрезка не может быть отрицательной, отбрасываем первый корень.
AD=4
Соответственно
BD = AD + 5 = 9
AB = BD + AD = 4 + 9 = 13
По теореме Пифагора находим остальные стороны треугольника:
AC = корень из (52)
BC = корень из (117).
0
Треугольник (Трикутник) | Описание курса | Сумма углов треугольника
Высота треугольника – определение, обозначение
4.6
Средняя оценка: 4.6
Всего получено оценок: 94.
Обновлено 11 Января, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 94.
Обновлено 11 Января, 2021
Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя отрезками составляют треугольник.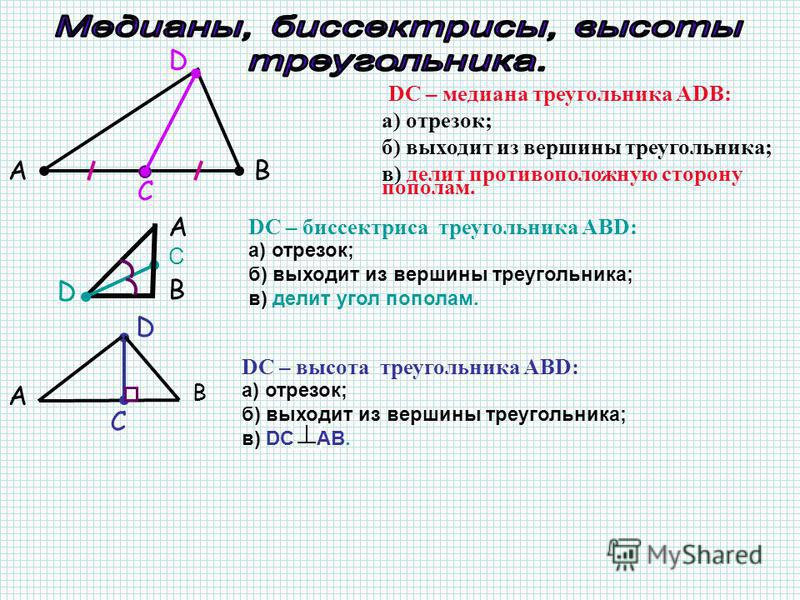
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, нестандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.
Рис. 1. Высота тупоугольного треугольника.Как правило, высоту треугольника обозначают буквой h. Также обозначается высота и в других фигурах.
Как найти высоту треугольника?
Существует три стандартных способа нахождения высоты треугольника:
Через теорему Пифагора
Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего. 2}=\sqrt{25-16}=3$$
2}=\sqrt{25-16}=3$$
Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.
Через площадь треугольника
Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.
Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.
Формула площади треугольника: $$S={1\over2}*bh$$, где b – это сторона треугольника ,а h – высота, проведенная к этой стороне. Выразим из формулы высоту:
$$h=2*{S\over b}$$
Если площадь равна 15, сторона 5, то высота $$h=2*{15\over5}=6$$
Через тригонометрическую функцию
Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.
Рис. 3. Рисунок к задаче.Угол ВСН=30 градусам , а сторона BC=8. У нас все тот же прямоугольный треугольник BCH. Воспользуемся определением косинуса угла прямоугольного треугольника. Косинус острого угла – это отношение прилежащего катета к гипотенузе, значит: BH/BC=cos BCH, а угол BCH равен 60 градусам, так как сумма острых углов прямоугольного треугольника равна 90 градусам.
У нас все тот же прямоугольный треугольник BCH. Воспользуемся определением косинуса угла прямоугольного треугольника. Косинус острого угла – это отношение прилежащего катета к гипотенузе, значит: BH/BC=cos BCH, а угол BCH равен 60 градусам, так как сумма острых углов прямоугольного треугольника равна 90 градусам.
Угол известен, как и сторона. Выразим высоту треугольника:
$$BH=BC*\cos (60\unicode{xb0})=8*{1\over2}=4$$
Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.
Что мы узнали?
Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Константин Никитич
9/10
Оценка статьи
4. 6
6
Средняя оценка: 4.6
Всего получено оценок: 94.
А какая ваша оценка?
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Высота треугольника. Свойство высоты прямоугольного треугольника |
| Расположение высот у треугольников различных типов |
| Ортоцентр треугольника |
| Расположение ортоцентров у треугольников различных типов |
| Ортоцентрический треугольник |
| Задача Фаньяно |
Высота треугольника. Свойство высоты прямоугольного треугольника
Определение 1. Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
Основанием высоты называют основание этого перпендикуляра (рис.1).
Рис.1
На рисунке 1 изображена высота BD, проведённая из вершины B треугольника ABC. Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
Утверждение. Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Рис.2
Доказательство. Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
В силу признака подобия прямоугольных треугольников треугольники BCD и ACD подобны. Следовательно,
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD, что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | Все высоты остроугольного треугольника лежат внутри треугольника. | |
| Прямоугольный треугольник | Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | |
| Тупоугольный треугольник | Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника Высота, проведённая из вершины тупого угла, лежит внутри треугольника | |
| Остроугольный треугольник | ||
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника | ||
| Остроугольный треугольник |
Все высоты остроугольного треугольника лежат внутри треугольника. |
| Прямоугольный треугольник |
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
| Тупоугольный треугольник |
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
Ортоцентр треугольника
Теорема 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Рис.3
Обозначим точки пересечения этих прямых символами A1, B1 и C1, как показано на рисунке 3.
В силу параллельности прямых AC и C1A1, а также BC и C1B1 четырёхугольники AC1BC и ABA1C – параллелограммыпараллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства
C1B = AC = BA1.
Следовательно, точка B является серединой стороны C1A1.
В силу параллельности прямых BC и C1B1, а также AB и B1A1 четырёхугольники AC1BC и ABCB1 – параллелограммы,параллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства
C1A = BC = A1B1.
Следовательно, точка A является серединой стороны C1B1.
В силу параллельности прямых AB и B1A1, а также AC и C1A1 четырёхугольники ABA1C и ABCB1 – параллелограммыпараллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства
A1C = AB = B1C.
Следовательно, точка C является серединой стороны B1A1.
Таким образом, высоты треугольника ABC являются серединными перпендикулярами треугольника A1B1C1 (рис. 4),
Рис.4
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.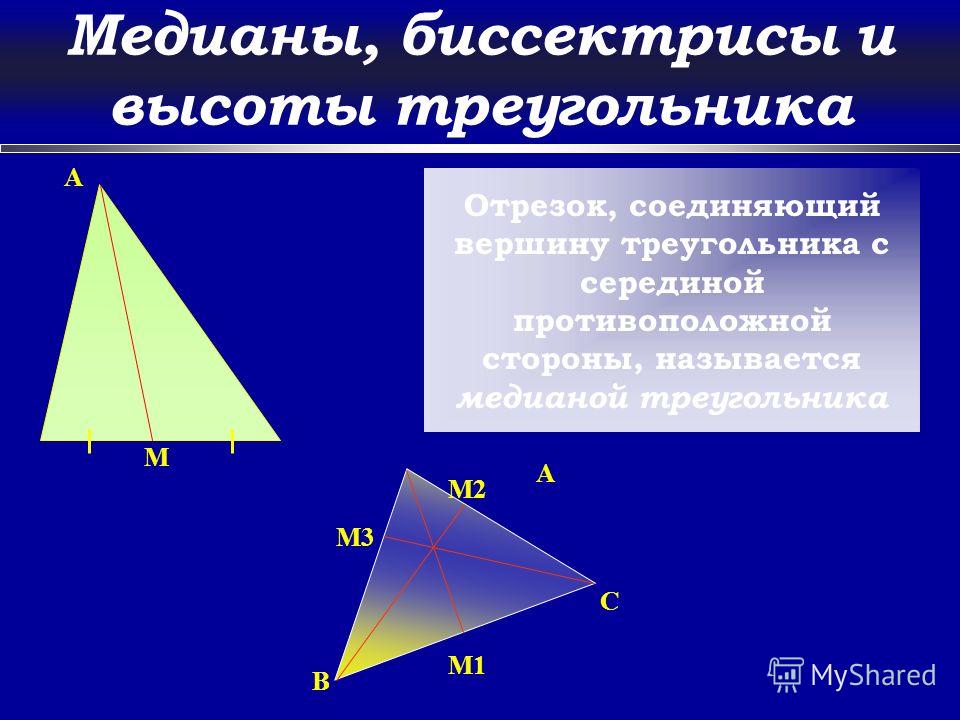
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | Ортоцентр остроугольного треугольника лежит внутри треугольника. | |
| Прямоугольный треугольник | Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла | |
| Тупоугольный треугольник | Ортоцентр тупоугольного треугольника лежит вне треугольника. |
| Остроугольный треугольник |
Ортоцентр остроугольного треугольника лежит внутри треугольника. |
| Прямоугольный треугольник |
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла |
| Тупоугольный треугольник |
Ортоцентр тупоугольного треугольника лежит вне треугольника. |
Ортоцентрический треугольник
Решим следующую задачу.
Задача. В остроугольном треугольнике ABC проведены высоты AD и BE (рис. 5). Доказать, что треугольник DCE подобен треугольнику ABC.
5). Доказать, что треугольник DCE подобен треугольнику ABC.
Рис.5
Решение. Рассмотрим треугольники ADC и BEC. Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
Из подобия треугольников ABC и EDC (рис.5) вытекает важное следствие.
Следствие 1.
Определение 3. Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
Рис.6
Из определения 3 и следствия 1 вытекает следствие 2.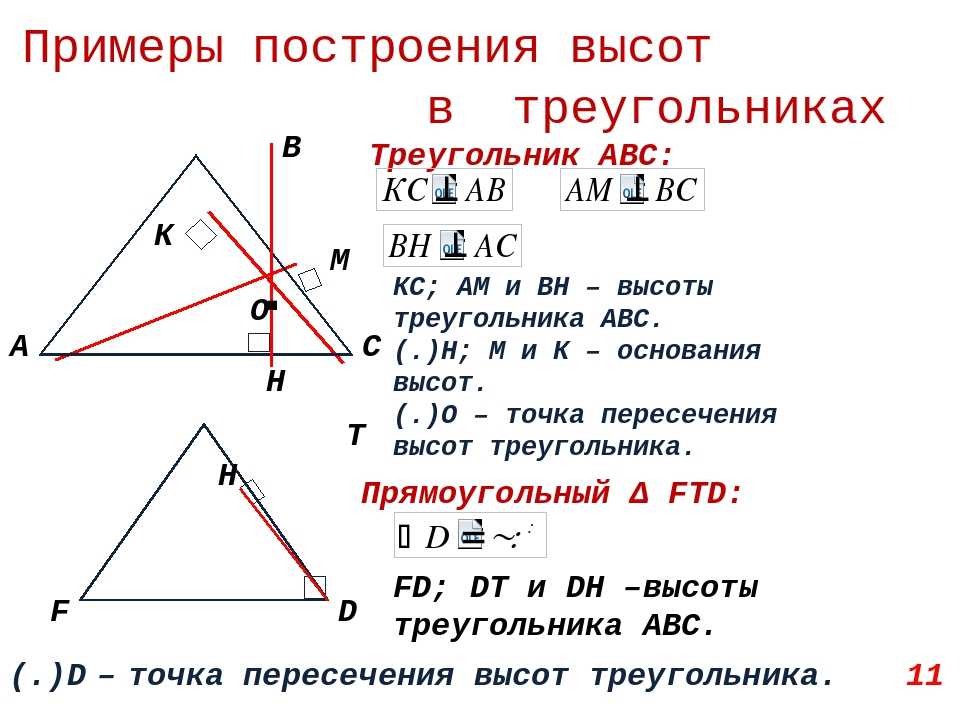
Следствие 2. Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
Рис.7
Тогда справедливы равенства
Из следствия 2 вытекает теорема 2.
Теорема 2. Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
Доказательство. Воспользовавшись следствием 2, получаем:
что и требовалось доказать.
Задача Фаньяно
Задача Фаньяно. Рассматриваются всевозможные треугольники DEF, вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC.
Решение. Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D1 точку, симметричную точке D относительно прямой AC, и обозначим символом D2 точку, симметричную точке D относительно прямой AB (рис.8).
Рис.8
Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D1D2. Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF, вершины F и E которого являются точками пересечения прямой D1D2 с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D1D2 (рис.9).
Рис.9
Заметим также, что выполнено равенство
AD = AD1 = AD2.
Кроме того, выполнено равенство
Поэтому
Отсюда вытекает, что длина отрезка D1D2 будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC. Другими словами, наименьшим периметром обладает такой треугольник DEF, у которого вершина D является основанием высоты треугольника ABC, проведённой из вершины A, а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.
Если обозначить длину высоты, проведённой из вершины A, длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:
Следовательно, наименьший периметр рассматриваемых треугольников DEF равен
Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.
Для этого воспользуемся следующей леммой.
Лемма. Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).
Рис.10
В этом случае отрезок D1D2 проходит через точки F и E.
Доказательство. Заметим, что в силу следствия 2 выполняются равенства:
Кроме того, в силу равенства треугольников DFK и KFD2, а также в силу равенства треугольников DEL и LED1 выполняются равенства:
Следовательно,
откуда вытекает, что углы AEF и D1EL , а также AFE и D2FK являются вертикальными углами. Это означает, что точки D1, F, E, D2 лежат на одной прямой. Лемма доказана.
Доказательство леммы и завершает решение задачи Фаньяно.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как найти высоту прямоугольного треугольника
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по базовой геометрии » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти высоту прямоугольного треугольника
Прямоугольный треугольник имеет гипотенузу 18 дюймов и основание 12 дюймов. Какова высота треугольника в дюймах?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы можем найти один катет прямоугольного треугольника, если у нас есть длина гипотенузы и другого катета. Возведите в квадрат гипотенузу и известный катет. Затем из квадрата длины гипотенузы вычесть квадрат длины катета. Наконец, найдите квадратный корень из результата.
Возведите в квадрат гипотенузу и известный катет. Затем из квадрата длины гипотенузы вычесть квадрат длины катета. Наконец, найдите квадратный корень из результата.
Сообщить об ошибке
Если c не является основанием треугольника, что из следующего является его высотой?
Возможные ответы:
Ни один из других ответов
или
Правильный ответ:
или
Объяснение:
Если не является базой, то либо или база. Если либо или является основанием, прямой угол находится внизу, поэтому или соответственно будет перпендикулярно. Высота треугольника — это расстояние от основания до высшей точки, а в прямоугольном треугольнике это будет найдено стороной, примыкающей к основанию под прямым углом. Итак, если основание равно , то и наоборот.
Сообщить об ошибке
Площадь прямоугольного треугольника равна 28. Если длина одной стороны равна 7, какова длина другой стороны?
Если длина одной стороны равна 7, какова длина другой стороны?
Возможные ответы:
Правильный ответ:
Пояснение:
Начнем с формулы площади треугольника.
Далее мы понимаем, что две стороны треугольника — это основание и высота; следовательно, подставляя то, что мы знаем, получаем
Тогда мы можем решить простым делением.
Мы нашли нашу высоту и, следовательно, вторую сторону нашего треугольника.
Сообщить об ошибке
Если площадь прямоугольного треугольника равна , а основание прямоугольного треугольника , какова высота прямоугольного треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Вспомните, как найти площадь прямоугольного треугольника:
Теперь мы собираемся манипулировать уравнением, чтобы найти высоту.
Теперь подставьте информацию из вопроса о значениях площади и основания треугольника, чтобы найти высоту.
Сообщить об ошибке
Если площадь прямоугольного треугольника равна , а основание треугольника равно , то какова высота треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольного треугольника:
Теперь мы собираемся манипулировать уравнением, чтобы найти высоту.
Теперь подставьте информацию из вопроса о значениях площади и основания треугольника, чтобы найти высоту.
Сообщить об ошибке
Если площадь прямоугольного треугольника равна , а основание треугольника , то какова высота треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольного треугольника:
Теперь мы собираемся манипулировать уравнением, чтобы найти высоту.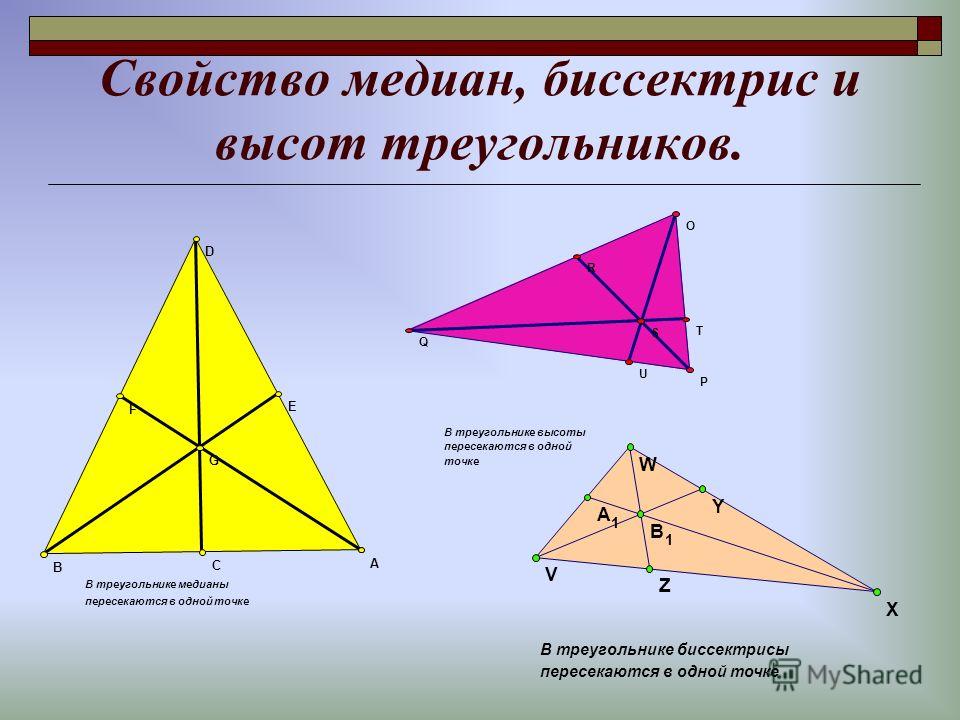
Теперь подставьте информацию из вопроса о значениях площади и основания треугольника, чтобы найти высоту.
Сообщить об ошибке
Если площадь прямоугольного треугольника равна , а основание треугольника равно , то какова высота треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольного треугольника:
Теперь мы собираемся манипулировать уравнением, чтобы найти высоту.
Теперь подставьте информацию из вопроса о значениях площади и основания треугольника, чтобы найти высоту.
Сообщить об ошибке
Если площадь прямоугольного треугольника равна и основание равно , какова высота треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольного треугольника:
Теперь мы собираемся манипулировать уравнением, чтобы найти высоту.
Теперь подставьте информацию из вопроса о значениях площади и основания треугольника, чтобы найти высоту.
Сообщить об ошибке
Если площадь прямоугольного треугольника равна и основание равно , какова высота треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольного треугольника:
Теперь мы собираемся манипулировать уравнением, чтобы найти высоту.
Теперь подставьте информацию из вопроса о значениях площади и основания треугольника, чтобы найти высоту.
Сообщить об ошибке
Если площадь прямоугольного треугольника равна и основание равно , какова высота треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольного треугольника:
Теперь мы собираемся манипулировать уравнением, чтобы найти высоту.
Теперь подставьте информацию из вопроса о значениях площади и основания треугольника, чтобы найти высоту.
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах 164 практических теста Вопрос дня Карточки Узнать по Концепту
Высота Треугольника (Высота). Калькулятор
Создано Ханной Памула, докторантом
Отзыв от Bogna Szyk
Последнее обновление: 27 сентября 2022 г.
Содержание:- Какова высота треугольника?
- Как найти высоту треугольника — формулы
- Как найти высоту равностороннего треугольника
- Как найти высоту равнобедренного треугольника
- Как найти высоту прямоугольного треугольника
- Как найти высота треугольника с помощью этого калькулятора высоты треугольника?
Если вы ищете простой инструмент для расчета высоты в любом треугольнике, вы находитесь в нужном месте — этот калькулятор высоты треугольника является инструментом для вас. Если вы ищете формулы высоты треугольника для особых треугольников, таких как прямоугольный, равносторонний или равнобедренный треугольник или любой разносторонний треугольник, этот калькулятор является безопасной ставкой — он может вычислить высоты треугольника, а также стороны треугольника, углы, периметр, площадь. Не ждите больше; Попробуй!
Если вы ищете формулы высоты треугольника для особых треугольников, таких как прямоугольный, равносторонний или равнобедренный треугольник или любой разносторонний треугольник, этот калькулятор является безопасной ставкой — он может вычислить высоты треугольника, а также стороны треугольника, углы, периметр, площадь. Не ждите больше; Попробуй!
Если вас все еще интересует формула высоты равностороннего треугольника или как найти высоту без площади, продолжайте прокручивать, и вы найдете ответ.
Какова высота треугольника?
Каждая сторона треугольника может быть основанием, и из каждой вершины можно провести линию, перпендикулярную линии, содержащей основание — это высота треугольника. Каждый треугольник имеет три высоты, которые также называются высот . Рисование высоты известно как падение высоты в этой вершине.
Как найти высоту треугольника — формулы
Существует много способов найти высоту треугольника. Самая популярная — с использованием площади треугольника, но существует много других формул:
- Заданная площадь треугольника
Известное уравнение площади треугольника можно преобразовать в формулу высоты прямоугольного треугольника:
-
площадь = b × h / 2, гдеb— основание,h— высота - , значит,
h = 2 × площадь / b
Но как найти высоту треугольника без площади? Самые популярные формулы:
- Даны стороны треугольника
Он использует уравнение, называемое формулой Герона, которое позволяет вычислить площадь по сторонам треугольника. Затем, когда вы знаете площадь, вы можете использовать основное уравнение, чтобы узнать, какова высота треугольника:
Затем, когда вы знаете площадь, вы можете использовать основное уравнение, чтобы узнать, какова высота треугольника:
- Формула Герона:
площадь = 0,25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) - , поэтому
h = 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) / b
Вы можете узнать больше об этом уравнении в нашем специальном калькуляторе формул Герона.
- Даны две стороны и угол между
Используйте тригонометрическую или другую формулу площади треугольника:
-
площадь = 0,5 × a × b × sin(γ)
(или площадь = 0,5 × a × c × sin(β) или площадь = 0,5 × b × c × sin(α) , если даны разные стороны)
-
h = 2 × 0,5 × a × b × sin(γ) / b = a × sin(γ)
Если ваша фигура представляет собой особый тип треугольника, прокрутите вниз, чтобы найти формулы высоты треугольника.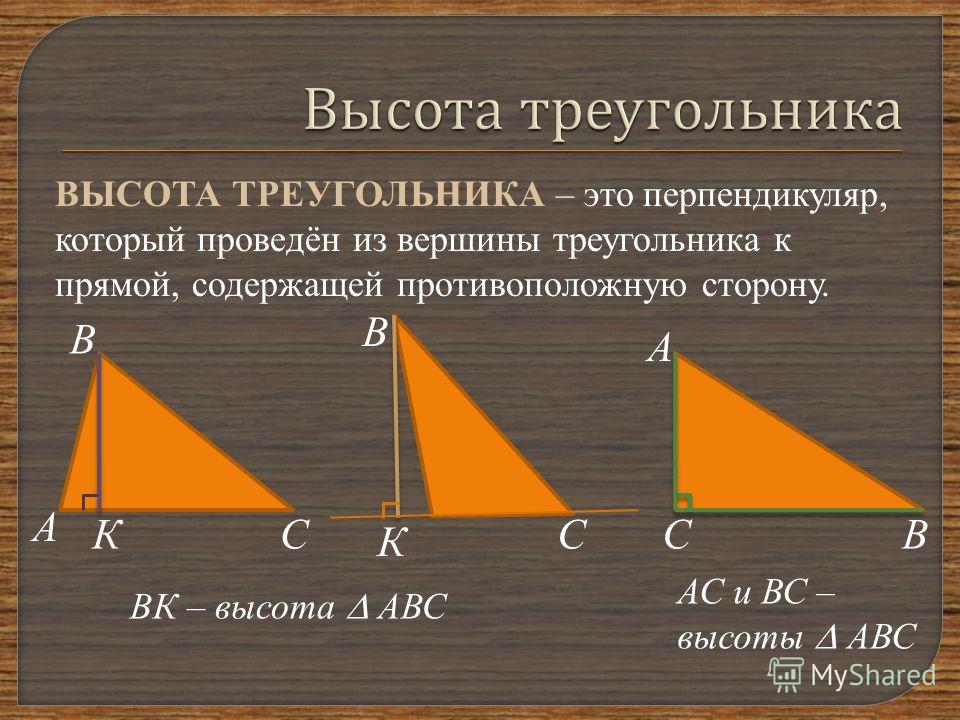 Упрощенные версии общих уравнений легче запомнить и вычислить.
Упрощенные версии общих уравнений легче запомнить и вычислить.
Как найти высоту равностороннего треугольника
Равносторонний треугольник — это треугольник, у которого все три стороны равны и все три угла равны 60°. Все три высоты имеют одинаковую длину, которая может быть рассчитана из:
-
h△ = a × √3/2, гдеa— сторона треугольника
В равностороннем треугольнике высоты, биссектрисы, биссектрисы и медианы совпадают.
Если вас интересуют формулы площади и периметра, посетите наш специальный калькулятор равностороннего треугольника.
Как найти высоту равнобедренного треугольника
Равнобедренный треугольник — это треугольник, две стороны которого имеют одинаковую длину. Есть две разные высоты равнобедренного треугольника; формула для вершины:
hᵇ = √(a² - (0,5 × b)²), гдеa— катет треугольника, аb— основание. Формула получена из теоремы Пифагора.
Высота от базовых вершин может быть рассчитана, например, из
- формула площади :
hᵃ = 2 × площадь / a = √(a² - (0,5 × b)²) × b / a - тригонометрия :
hᵃ = b × sin(β)
- формула площади :
Чтобы узнать формулы площади и периметра этого типа треугольника, посетите наш специальный калькулятор равнобедренного треугольника.
Как найти высоту прямоугольного треугольника
Прямоугольный треугольник — это треугольник, один из углов которого равен 90°. Две высоты найти несложно, так как катеты перпендикулярны: если более короткий катет — основание, то более длинный катет — высота (и наоборот). Третью высоту треугольника можно рассчитать по формуле:
-
hᶜ = площадь × 2 / c = a × b / c
Если вас интересуют уравнения площади и периметра этого треугольника, воспользуйтесь нашим калькулятором прямоугольного треугольника.
Как найти высоту треугольника с помощью этого калькулятора высоты треугольника?
Прочитав наше объяснение, мы почти уверены, что теперь вы понимаете, как найти высоту треугольника без заданной площади или какова высота треугольника. Но давайте рассмотрим простой пример, чтобы показать вам гибкость нашего инструмента:
Но давайте рассмотрим простой пример, чтобы показать вам гибкость нашего инструмента:
- Выберите тип треугольника . Предположим, мы хотим вычислить высоты разностороннего треугольника, поэтому мы не меняем параметр по умолчанию.
- Введите указанные значения . Это может быть три стороны или две стороны и угол. Остановимся на первом варианте: a = 6 дюймов, b = 14 дюймов, c = 17 дюймов.
- Калькулятор высоты треугольника показал все три высоты — они равны 13,17 дюйма, 5,644 дюйма и 4,648 дюйма. Более того, калькулятор показал нам все углы треугольника, площадь и периметр. Это потрясающе!
Ханна Памула, кандидат наук
Особый треугольник?
Heights (высоты)
Углы
другие
Периметр
Проверьте 18 аналогичных калькуляторов треугольника 🔺
30 60 90 ТРЕЗОНА 45 45 90 ТРИАНГРЕА ПРАВО ТРЕЙНАЛЯ… еще 15
ВЫСОВЫЙ Высот от треуанла. Пошаговое руководство с примерами и картинками
Высота $$ \треугольник $$ Рабочий лист
$$ \треугольник $$ Расчет высоты
Цель этой страницы : Попрактиковаться в применении обычной формулы площади треугольника для нахождения высоты, зная площадь треугольника и основание.
Пример 1
На диаграмме 1 площадь треугольника равна 17,7 квадратных единиц, а его основание равно 4.
Направления: Рассчитать высоту
Схема 1
Красные измерения относятся к этой проблеме.
Диаграмма 2
Помните, что у каждого треугольника может быть 3 пары основание/высота. Итак, чтобы решить этот тип вопроса, вы должны сначала определить базу.
Поэтому всякий раз, когда вы говорите о высоте, мы должны убедиться, что знаем, о каком из трех «оснований» (или сторон) треугольника мы говорим.Схема 3
Помните: высота перпендикулярна основанию , равному $$ \overline{CB}$$.
 А $$ \overline{CB} $$ имеет меру 4. Мы не можем использовать другие стороны для решения этой задачи. Итак, до конца этого урока ваша первая задача — определить, какая сторона является базовой, особенно когда вы доберетесь до более сложных сторон.
А $$ \overline{CB} $$ имеет меру 4. Мы не можем использовать другие стороны для решения этой задачи. Итак, до конца этого урока ваша первая задача — определить, какая сторона является базовой, особенно когда вы доберетесь до более сложных сторон.шагов :
Шаг 1Подставьте известные значения в формулу площади.
$ A = \ frac 1 2 \ cdot \ text { base } \ cdot \ red {\ text { height } } \\ 17,7 = \frac 1 2 \cdot 4 \cdot \red h $
Шаг 2Найдите высоту, решив $$\red h $$.
$ 17,7 = \frac 4 2 \cdot \red h \\ 17,7 = 2 \cdot \red h \\ \frac{17.7}{2} = \red h \\ \красный h = 8,85 $
Практика ПроблемыПроблема 1
Если площадь этого треугольника 658,8 квадратных фута, а его основание 24 дюйма, какова его высота?
Эта задача очень похожа на пример 1.
Шаг 1
Подставьте известные значения в формулу площади.
$ A = \frac 1 2 \cdot \text{основание} \cdot \text{высота} \\ 658,8 = \frac 1 2 \cdot 24 \cdot \red{ \text{h}} $
Шаг 2
Найдите высоту, решив $$h$$.
$ 658,8 = 12 \cdot \red h \\ \ гидроразрыва {658,8} {12} = ч \ч = 54,9 $
Задачи 2 и 3 .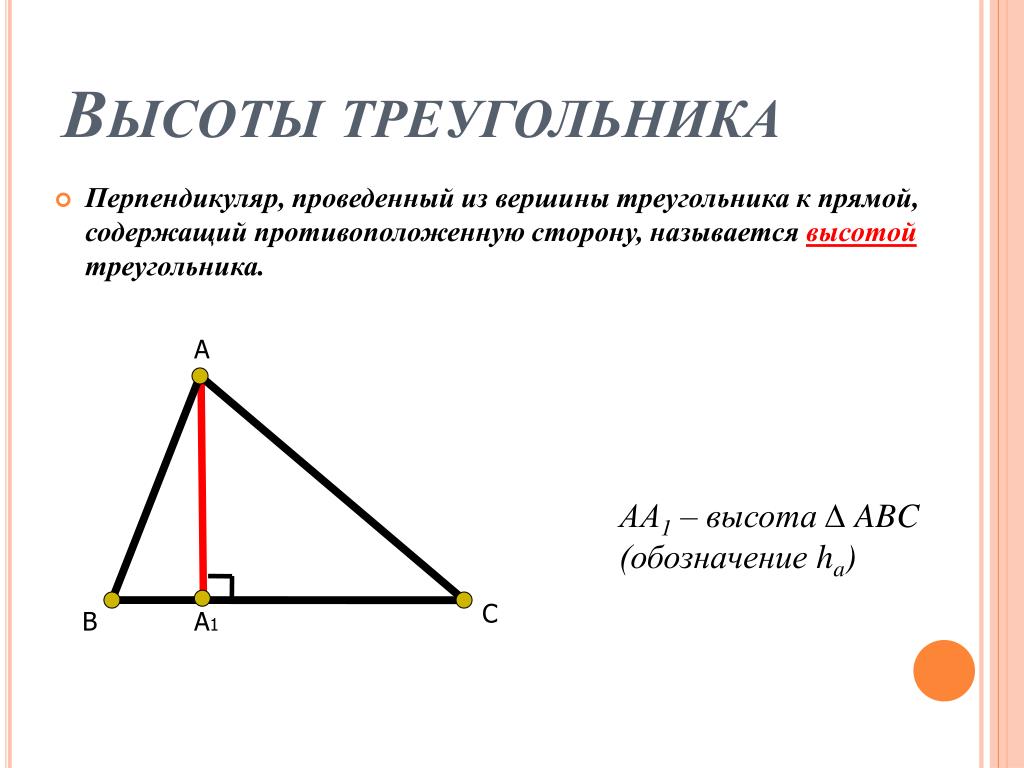 ..(попрактикуйтесь в применении формулы, нет необходимости выбирать основную сторону)
..(попрактикуйтесь в применении формулы, нет необходимости выбирать основную сторону)
Проблема 2
Если площадь этого треугольника равна 11,6 квадратных единиц, а его основание равно 2, какова его высота?
Шаг 1
Подставьте известные значения в формулу площади.
$ A = \frac 1 2 \cdot \text{основание} \cdot \red{ \text{высота} } \\ 11.6 = \frac 1 2 \cdot 2 \cdot \red{ \text{h } } $
Шаг 2
Найдите высоту.
$ 11,6 = 1 \cdot \red h \\ ч = 11,6 $
Проблема 3
Если площадь этого треугольника равна 17,7 квадратных единиц, а его основание равно 15, какова его высота?
Шаг 1
Подставьте известные значения в формулу.
$ A = \frac 1 2 \cdot \text{основание} \cdot \red{ \text{высота} } \\ 17.7 = \frac 1 2 \cdot \text{15} \cdot \red{ \text{ h } } \\ $
Шаг 2
Найдите высоту, решив $$h$$.
$ 17,7 = 7,5 \красный час \\ \ гидроразрыва {17,7} {7,5} = ч \\ ч = 2,4 $
Проблема 4
Если площадь треугольника слева равна 35,8 квадратных единиц, найдите его высоту.
Эта задача очень похожа на пример 1. В каждом треугольнике есть 3 пары основание/высота, но по рисунку видно, что основание — это сторона длины 12. Помните, что основание и высота перпендикулярны.
Шаг 1
Подставьте известные значения в формулу.
$ A = \frac 1 2 \cdot \text{основание} \cdot \red{ \text{высота} } \\ 35,8 = \frac 1 2 \cdot \text{12 } \cdot \red{ \text{h } } $
Шаг 2
Найдите высоту, решив $$h$$.
$ 35,8 = 6 ч \\ \фракция{35.8}{6} =ч \\ ч = 5,9$
Проблема 5
Если площадь треугольника слева равна 73,5 квадратных единиц, найдите высоту.
Эта задача очень похожа на пример 1. В каждом треугольнике есть 3 пары основание/высота, но по рисунку видно, что основание — это сторона длины 11. Помните, что основание и высота перпендикулярны.
Шаг 1
Подставьте известные значения в формулу.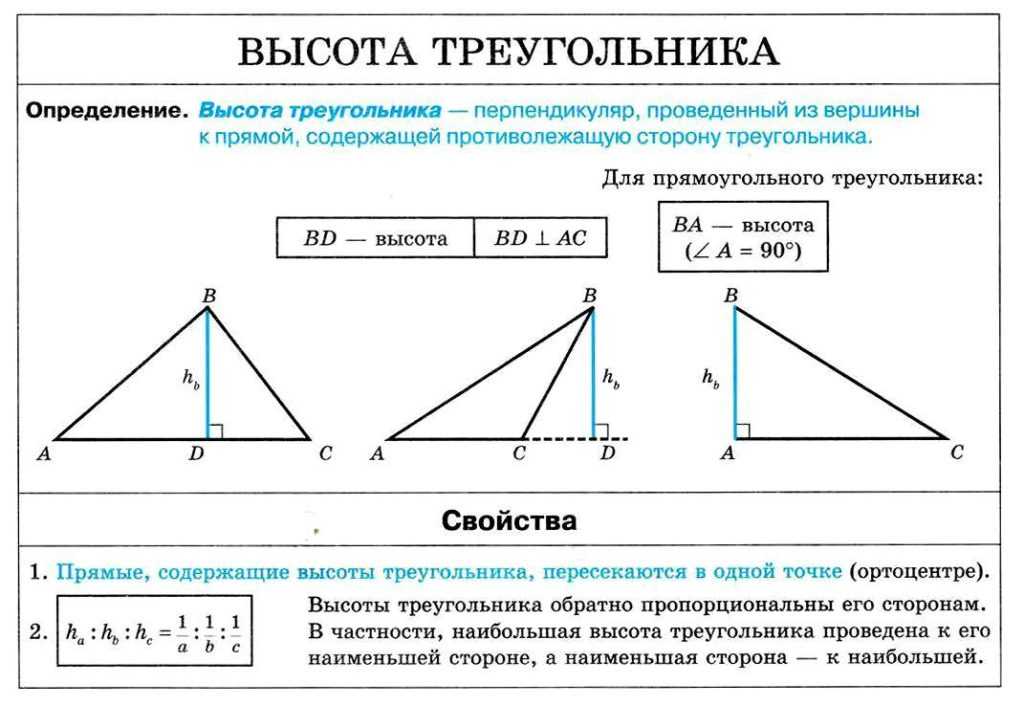
$ A = \frac 1 2 \cdot \text{основание} \cdot \red{ \text{высота} } \\ 73,5 = \frac 1 2 \cdot 11 \cdot \red{ \text{h} } $
Шаг 2
Найдите высоту.
$ 73,5 = 5,5 \красный час \\ \ гидроразрыва {73,5} {5,5} = ч \\ ч = 13,4 $
Проблема 6
Если площадь треугольника слева равна 141,9 квадратных единиц, найдите его высоту.
Эта задача очень похожа на пример 1. В каждом треугольнике есть 3 пары основание/высота, но по рисунку видно, что основание — это сторона, длина которой равна 21. Помните, что основание и высота перпендикулярны.
Шаг 1
Подставьте известные значения в формулу.
$ A = \frac 1 2 \cdot \text{основание} \cdot \red{ \text{высота} } \\ 141,9 = \frac 1 2 \cdot 21 \cdot \red{ \text{h} } $
Шаг 2
Решить.
$ 141,9 = 10,5 ч \\ \ гидроразрыва {141,9} {10,5} = ч \\ ч = 13,5 $
Некоторые задачи-вызовы
Хорошо, а теперь давайте попробуем решить более сложные задачи, связанные с нахождением высоты треугольника. Прежде чем задавать следующие вопросы, вы должны хорошо освоиться со свойствами равносторонних и равнобедренных треугольников.
Прежде чем задавать следующие вопросы, вы должны хорошо освоиться со свойствами равносторонних и равнобедренных треугольников.
Задача-вызов
Если периметр равностороннего треугольника равен 18, а его площадь равна 15,6 квадратных единиц, какова мера его высоты? Кроме того, имеет ли значение, какую сторону вы выберете в качестве своей базы?
Поскольку это равносторонний треугольник, и мы знаем, что его периметр равен 18, мы можем вычислить, что длина каждой стороны равна 6 (18/3 = 6). Неважно, какое основание мы выберем, поскольку все 3 высоты (или высоты) в равностороннем треугольнике конгруэнтны. С этого момента нужно просто следовать шагам, которые мы использовали на этой веб-странице:
Шаг 1
Эта задача очень похожа на пример 1.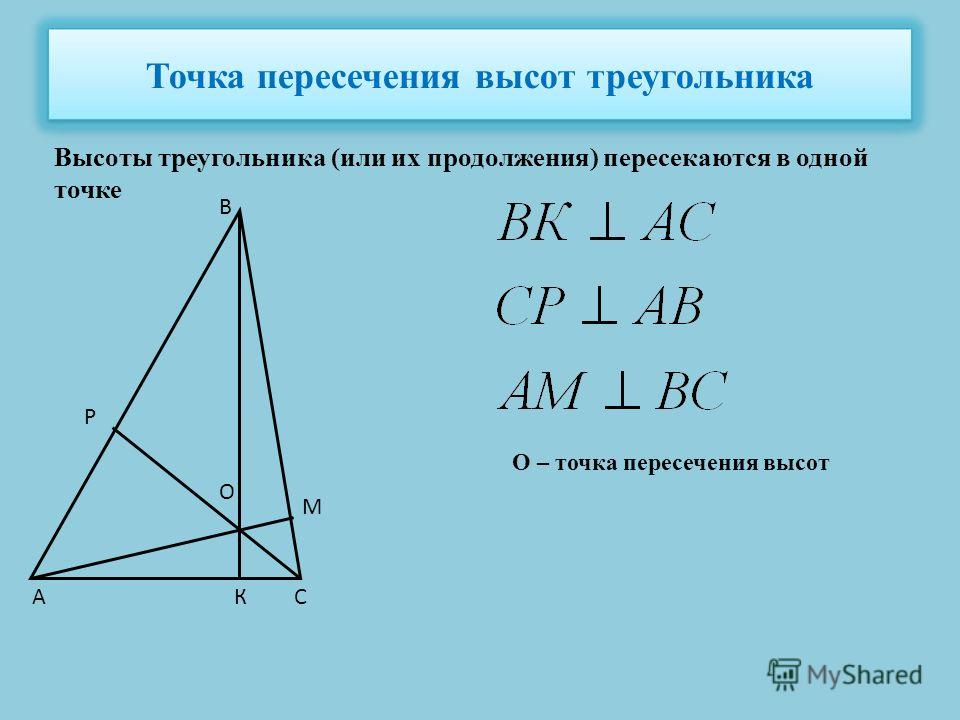


 3).
3).