Изобразить на комплексной плоскости онлайн: Комплексные числа онлайн

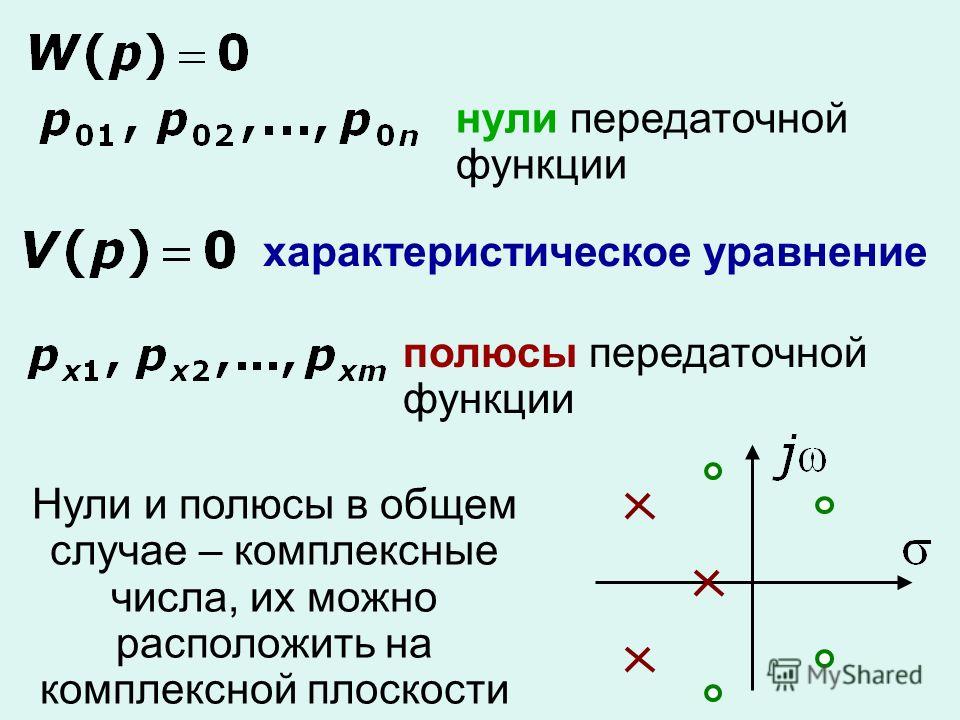
Комплексные числа — презентация онлайн

Похожие презентации:

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Действия над комплексными числами в алгебраической форме

Комплексные числа в алгебраической форме

1. Комплексные числа

Основные понятия
Геометрическое изображение
комплексных чисел
Тригонометрическая форма записи
комплексных чисел
Действия над комплексными числами
Показательная форма комплексного
числа

2. Основные понятия

Комплексным числом z называют выражение:
z a i b,
где а и b – действительные числа, i – мнимая единица,
определяемая равенством:
i 1
i 2 1
а называется действительной частью числа z,
b – мнимой частью. Их обозначают так:
a Re z;
b Im z.
Если а = 0, то число i b называется чисто мнимым.
Если b = 0, то получается действительное число а.
Два комплексных числа, отличающиеся только знаком мнимой
части, называются сопряженными:
z a i b,
z a i b,

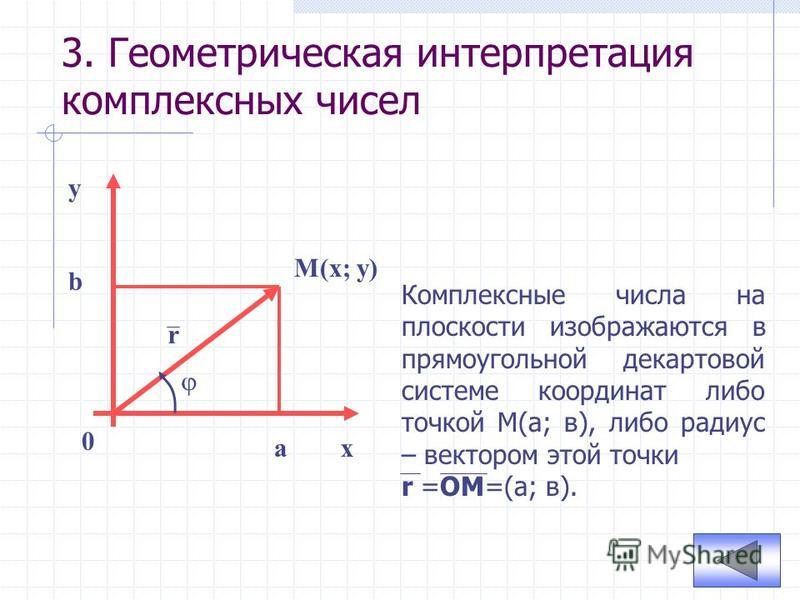
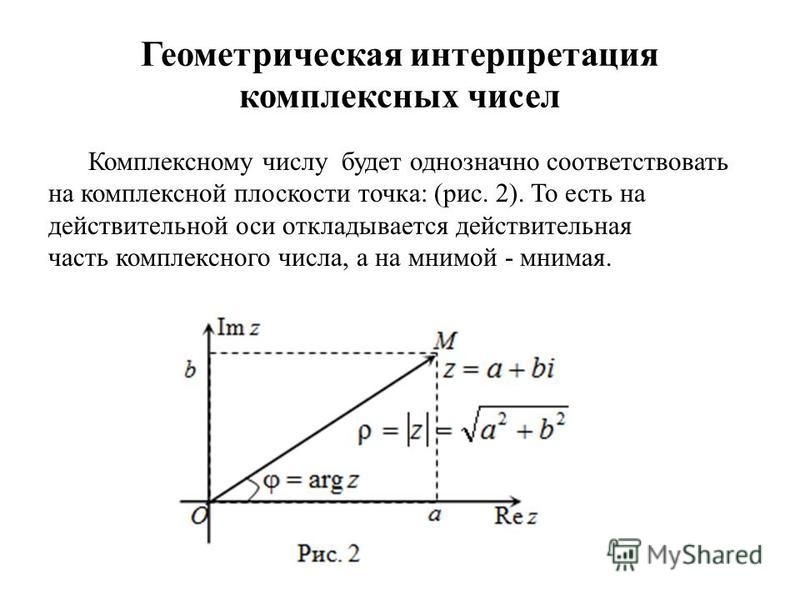
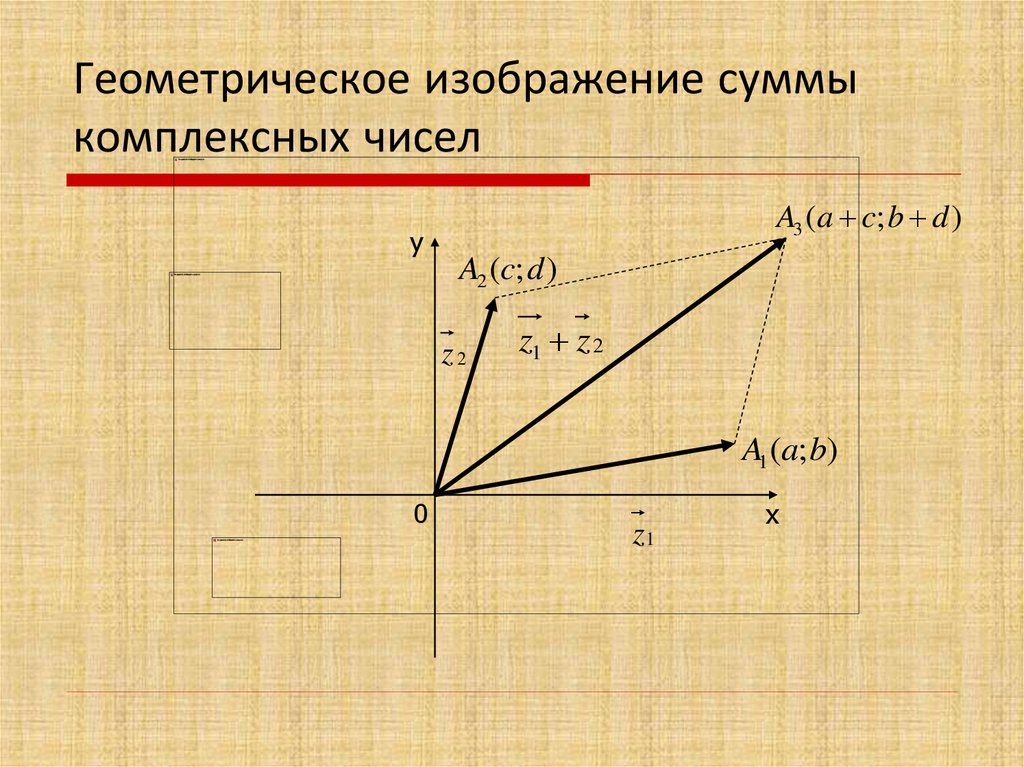
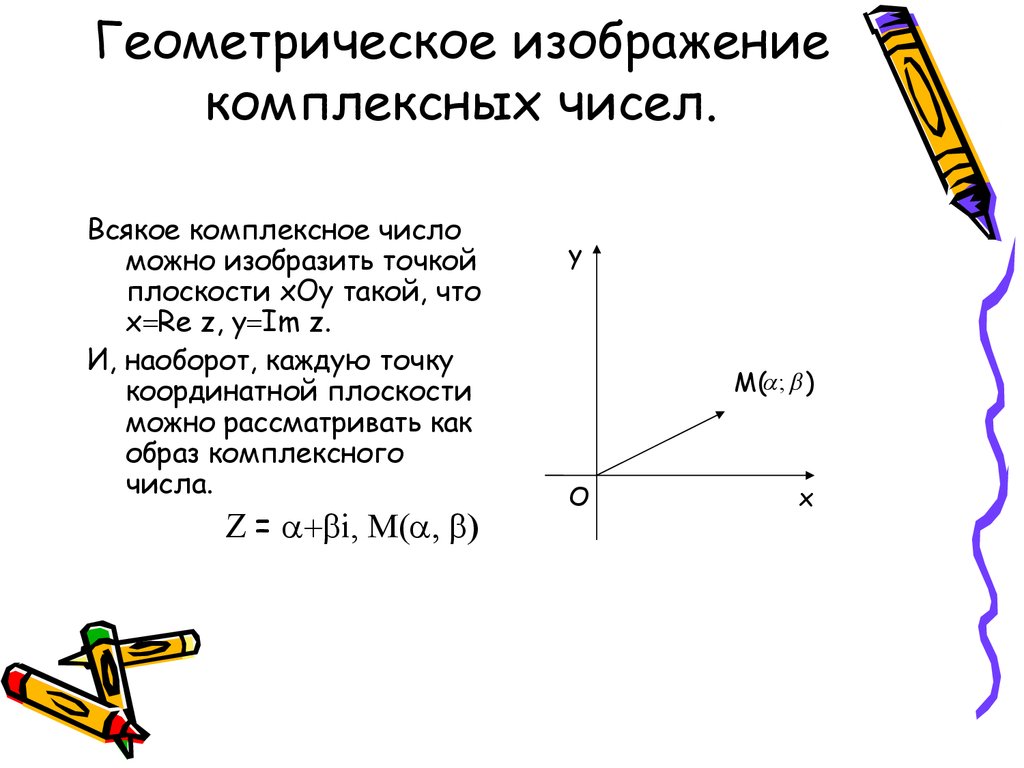
3. Геометрическое изображение комплексных чисел

Всякое комплексное число z a i b, можно изобразить на
плоскости XOY в виде точки A(a; b).
Плоскость, на которой изображаются комплексные числа,
называют плоскостью комплексной переменной.
y
z
Точкам, лежащим на оси OX,
A(a; b)
b
соответствуют действительные числа
(b = 0), поэтому ось OX называют
действительной осью.
a х
0
Точкам, лежащим на оси OY , соответствуют чисто мнимые числа
(a = 0), поэтому ось OY называют мнимой осью.
Иногда удобно считать геометрическим изображением
комплексного числа z вектор OA

4. Тригонометрическая форма записи комплексных чисел

Обозначим через r модуль вектора OA , через φ угол между
вектором OA и положительным направлением оси OX.
Тогда имеют место равенства:
y
z
a r cos ; b r sin
A(a; b)
b
r
0
Следовательно, комплексное число z
можно представить в виде:
φ
a х
a i b r cos i r sin
z r (cos i sin )
b
Модуль
комплексного
Аргумент
2комплексного
2
Тригонометрическая
arg z arctg
r zчисла
aчисла
b
форма записи
a
комплексного
числа числа z считается положительным, если
Аргумент
комплексного
он отсчитывается от положительного направления оси OX против
часовой стрелки. Очевидно, что φ определяется не однозначно, а
с точностью до слагаемого 2 k k Z.

5. Действия над комплексными числами

1
Равенство комплексных чисел.
Два комплексных числа z1 a1 i b1 и z2 a2 i b2
называются равными : z1 z2 , если a1 a2 , b1 b2
Комплексное число z
тогда, когда a 0,
2
a i b равно нулю , тогда и только
b 0
Сложение и вычитание комплексных чисел.
Суммой (разностью) комплексных чисел z1 a1 i b1 и
z2 a2 i b2 называется комплексное число, определяемое
равенством:
z1 z2 a1 i b1 a2 i b2 a1 a2 i b1 b2
z1 z2 a1 i b1 a2 i b2 a1 a2 i b1 b2

6. Действия над комплексными числами

Сложение и вычитание
комплексных чисел, изображенных
векторами производится по правилу
сложения или вычитания векторов:
y
z
z1
z1 — z2
0
3
z1 + z2
z2
х
Умножение комплексных чисел.
Умножением комплексных чисел z1 a1 i b1 и z2 a2
называется число, получаемое при умножении этих чисел по
правилам алгебры как двучлены, учитывая что
i 2 1;
i 3 i ;
i 4 i i 1;
i5 i
При любом целом k:
i 4k 1;
i 4k 1 i ;
i 4k 2 1;
i 4k 3 i
i b2

7.

Действия над комплексными числамиНа основании этого правила получим:
z1 z2 a1 i b1 a2 i b2
a1 a2 i b1 a2 i b2 a1 i 2 b1 b2
z1 z2 a1 a2 b1 b2 i b1 a2 b2 a1
Если комплексные числа заданы в тригонометрической форме:
z1 r1(cos 1 i sin 1) z2 r2 (cos 2 i sin 2 )
тогда произведение находится по формуле:
z1 z2 r1 r2 (cos( 1 2 ) i sin( 1 2 ))
Произведение сопряженных комплексных чисел:
2
2
2
2
a
(
i
b
)
a
b
z z ( a i b ) (a i b )
z z a b z
2
2
2

8. Действия над комплексными числами

4
Деление комплексных чисел.
Чтобы разделить z1 a1 i b1 на z2 a2 i b2
необходимо умножить делимое и делитель на число, сопряженное
делителю:
z1 a1 i b1
(a1 i b1 ) (a2 i b2 )
z2 a2 i b2 (a2 i b2 ) (a2 i b2 )
(a1a2 b1b2 ) i (a2b1 a1b2 ) a1a2 b1b2
a2 b1 a1b2
i
2
2
2
2
a2 b2
a2 b2
a22 b22
Если комплексные числа заданы в тригонометрической форме:
z1 r1(cos 1 i sin 1)
z2 r2 (cos 2 i sin 2 )
z1 r1
(cos( 1 2 ) i sin( 1 2 ))
z2 r2

9.

Действия над комплексными числамиНайти произведение и частное комплексных чисел:
z1 2 3i ,
z2 1 4i
= -1
z1 z2 2 3i 1 4i 2 3i 8i 12i 2
2 3i 8i 12 14 5i
z1 2 3i
(2 3i ) (1 4i ) 2 3i 8i 12i 2
2
2
z2 1 4 i
(1 4i ) (1 4i )
1 4
10 11
10 11i
2 3i 8i 12
i
17 17
17
17

10. Действия над комплексными числами

5
Возведение в степень комплексного числа.
При возведении комплексного числа z r (cos i sin )
в целую положительную степень модуль возводится в эту степень,
а аргумент умножается на показатель степени (формула Муавра)
z n r n (cos n i sin n )
6
Извлечение корня из комплексного числа.
Корень n – ой степени из комплексного числа
z r (cos i sin ) находится по формуле:
n
z r (cos
n
2k
n
i sin
2k
n
)
Арифметическое значение корня из
положительного числа r

11. Действия над комплексными числами

n
z r (cos
n
2k
n
i sin
2k
n
)
Придавая k значения 0, 1, 2, …,n –1, получим n различных
значений корня.
Для других значений k аргументы будут отличаться от
полученных на число, кратное 2π, и , следовательно будут
получаться значения корня, совпадающие с рассмотренными.
Итак, корень n – ой степени из комплексного числа имеет n
различных значений.
Корень n – ой степени из действительного числа также имеет n
значений, так как действительное число – частный случай
комплексного числа и может быть представлено в
тригонометрической форме:
A A (cos 0 i sin0) ( A 0)
A A (cos i sin ) ( A 0)

12. Действия над комплексными числами

Найти все значения кубического корня из единицы
1 cos 0 i sin0
3
(r 1; 0)
0 2k
0 2k
2k
2k
1 cos
i sin
cos
i sin
3
3
3
3
k 0
k 1
k 2
1 cos 0 i sin 0 1
3
3
2
2
1
3
1 cos
i sin
i
3
3
2
2
3
4
4
1
3
1 cos
i sin
i
3
3
2
2
y
z
В
A
х
С

13.

Показательная форма комплексного числаПусть z x i y . Если х и y – действительные переменные, то
z называется комплексной переменной.
Рассмотрим показательную функцию от комплексной
переменной z.
w ez
или
w e x i y
Комплексные значения функции w определяются по формуле:
e x i y e x (cos y i sin y )
z 2 i
Пример:
e
2 i
4
(1)
4
e2 2
e2 2
e (cos i sin )
i
4
4
2
2
2

14. Показательная форма комплексного числа

Если в формуле (1) положим x = 0, то получим:
ei y cos y i sin y
(2)
Эта формула называется формулой Эйлера, выражающая
показательную функцию с мнимым показателем через
тригонометрические функции.
Заменим в формуле (2) y на – y:
e i y cos( y ) i sin( y ) e i y cos y i sin y (3)
Складывая и вычитая равенства (2) и (3) получим :
e e
cos y
2
iy
iy
e iy e iy
sin y
2i

15. Показательная форма комплексного числа

Представим комплексное число z в тригонометрической форме::
z r (cos i sin )
По формуле Эйлера: cos i sin e i
Следовательно, всякое комплексное число можно представить в
показательной форме:
z r e i
Действия над комплексными числами в показательной форме:
Пусть имеем:
i 2
z
r
e
. Тогда:
z1 r1 e ; 2
2
i 1
z1 z2 r1 r2 e i 1 2 ;
z1 r1 i 1 2
e
;
z2 r2
zn r n ei n ;
n
z n r e
i
2 k
n
.

English     Русский Правила

Представление синусоидальных величин с помощью векторов и комплексных чисел (Лекция N 3)

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем

,

(1)

Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):

,

(2)

Диапазон частот, применяемых в технике: от сверхнизких частот (0. 01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i — мгновенное значение тока ;

u – мгновенное значение напряжения

;

е — мгновенное значение ЭДС ;

р— мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).

— амплитуда тока;

— амплитуда напряжения;

— амплитуда ЭДС.

Действующее значение переменного тока

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

,

(3)

Аналогично определяются действующие значения ЭДС и напряжения.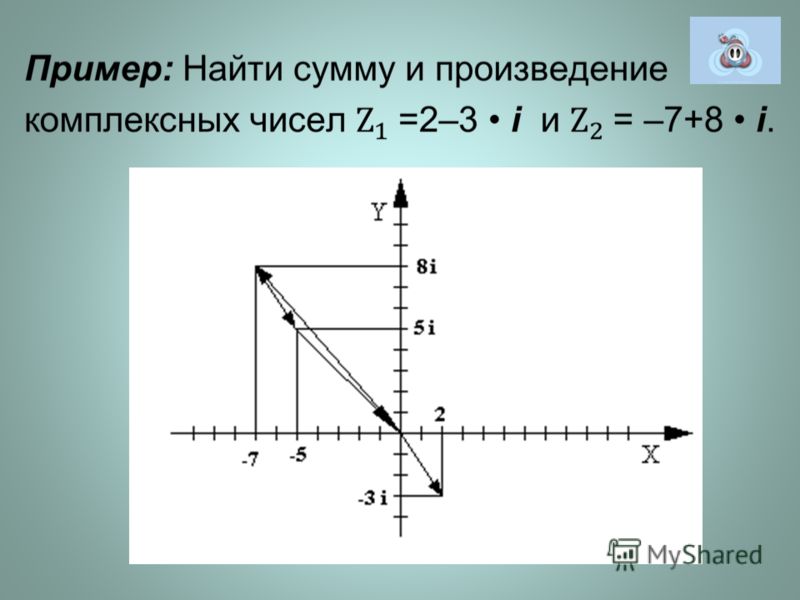

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е_{2соответствуют уравнения:}

.

Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t=0): и — начальной фазой ().

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют

углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂угол сдвига фаз:

.

Векторное изображение синусоидально
изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е_{2(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют}

векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток

равен сумме токов и двух ветвей:

.

Каждый из этих токов синусоидален и может быть представлен уравнением

и .

Результирующий ток также будет синусоидален:

.

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.

На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью

w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Представление синусоидальных ЭДС, напряжений
и токов комплексными числами

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной

тригонометрической или

алгебраической — формах.

Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число

.

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

.

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

,

(4)

 

Комплексное число удобно представить в виде произведения двух комплексных чисел:

,

(5)

 

Параметр , соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой: , а параметр — комплексом мгновенного значения.

Параметр является оператором поворота вектора на угол wt относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a.

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды и оператора поворота :

.

Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

,

(6)

Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

,

— то для записи ее в показательной форме, необходимо найти начальную фазу , т. е. угол, который образует вектор с положительной полуосью +1:

.

Тогда мгновенное значение напряжения:

,

где .

При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)

,

(7)

а при (третий квадрант)

(8)

или

(9)

Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:

.

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:

_где ;

.

 

Действующее значение синусоидальных ЭДС, напряжений и токов

В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

.

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:

.

(10)

Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения

.

 

Литература

1.                 Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2.                 Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1.     Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?

2.      Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?

3.     В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?

4.     Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.

5.     На рис. 5 , а . Определить .

Ответ: .

А)Изобразить на комплексной плоскости середину отрезка,соединяющего то… — Учеба и наука

Лучший ответ по мнению автора

Михаил Александров 23. 02.16 Лучший ответ по мнению автора Ответ понравился автору вопроса

Татьяна Александровна от 50 p. Читать ответы

Андрей Андреевич от 70 p. Читать ответы

Eleonora Gabrielyan от 0 p. Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Пользуйтесь нашим приложением

графических функций — Plot $|z — i| + |г + я| = 16$ на комплексной плоскости

Спросил 10 лет, 6 месяцев назад

Изменено 10 лет, 5 месяцев назад

Просмотрено 11 тысяч раз

$\begingroup$

Участок $|z — i| + |г + я| = 16$ на комплексной плоскости

Концептуально я вижу, что происходит.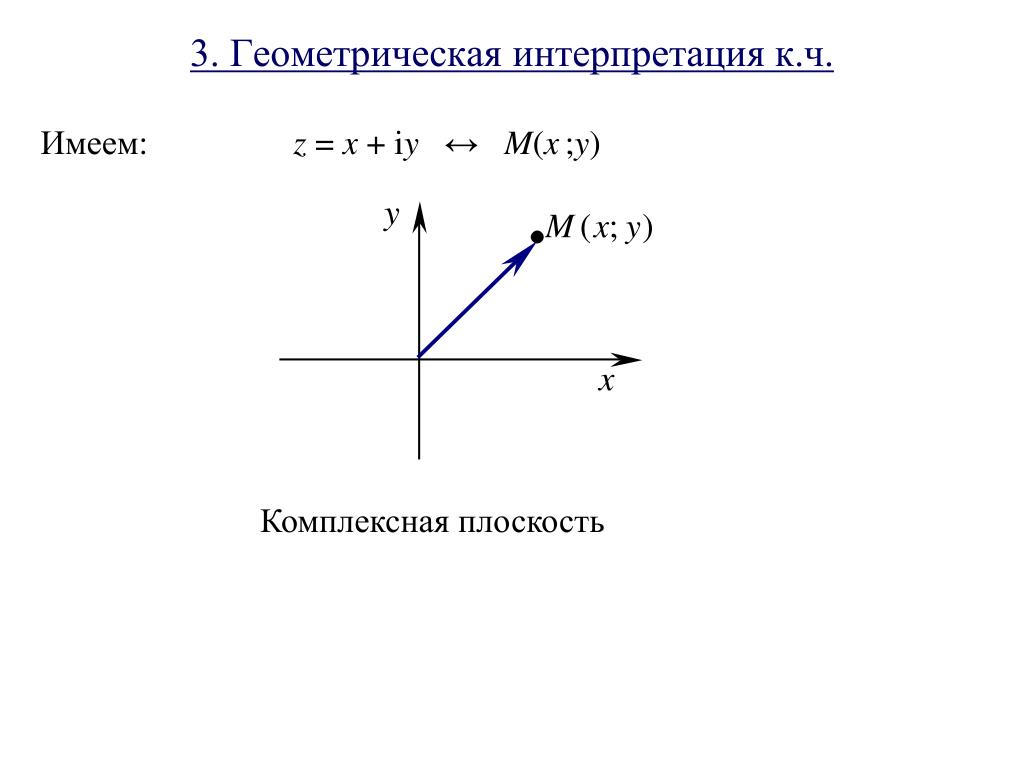 Я собираюсь нарисовать набор точек, объединяющих расстояния между $i$ и $-i = 16$, которые образуют эллипс. У меня возникли проблемы с получением уравнения эллипса алгебраически. 92} {64} = 1$$

$\endgroup$

$\begingroup$

Думаю, вы на правильном пути.

Wolframalpha также не имеет «более простой формы» алгебраического уравнения. (см. http://www.wolframalpha.com/input/?i=%28%7Cx%2Biy-i%7C%2B%7Cx%2Biy%2Bi%7C%29%5E2%3D256)

Возможно, этот вопрос предназначен для выполнения на компьютере. Обычно вопросы, сделанные от руки, просят вас «набросать» график.

$\endgroup$

$\begingroup$ 92} {64} = 1$$

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Экспресс- и графические комплексные номера

Результаты обучения

• Выразите квадратные корни из отрицательных чисел как кратные [latex]i[/latex] .
• Нанесение комплексных чисел на комплексную плоскость.

Мы знаем, как найти квадратный корень из любого положительного действительного числа. Аналогичным образом мы можем найти квадратный корень из отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренной черты отрицательное, корень называется мнимым числом . Мнимое число [latex]i[/latex] определяется как квадратный корень из минус 1. 9{2}=-1[/latex]

Мы можем записать квадратный корень из любого отрицательного числа как кратное [latex]i[/latex]. Возьмем квадратный корень из –25.

[латекс]\begin{align}\sqrt{-25}&=\sqrt{25\cdot \left(-1\right)}\\&=\sqrt{25}\cdot\sqrt{-1} \\ &=5i\end{align}[/latex]

Мы используем [latex]5i[/latex]   , а не [latex]-\text{5}i[/latex] , поскольку основной корень числа 25 является положительным корнем.

Комплексное число представляет собой сумму действительного числа и мнимого числа. Комплексное число выражается в стандартной форме, когда пишется [латекс]а+би[/латекс], где [латекс]а[/латекс] – действительная часть, а [латекс]би[/латекс] – мнимая часть. Например, [латекс]5+2i[/латекс] — это комплексное число. Так же и [латекс]3+4\sqrt{3}i[/латекс].

Мнимые числа отличаются от действительных чисел, поскольку возведение в квадрат мнимого числа дает отрицательное действительное число. Вспомните, когда возводится в квадрат положительное действительное число, результатом является положительное действительное число, а когда возводится в квадрат отрицательное действительное число, снова получается положительное действительное число. Комплексные числа представляют собой комбинацию действительных и мнимых чисел.

Общее примечание: мнимые и комплексные числа

Комплексное число — это число в форме [латекс]а+би[/латекс], где

• [латекс]а[/латекс] — действительная часть комплексного числа.
• [латекс]би[/латекс] — мнимая часть комплексного числа.

Если [латекс]b=0[/латекс], то [латекс]а+би[/латекс] — действительное число. Если [latex]a=0[/latex] и [latex]b[/latex] не равен 0, комплексное число называется мнимым числом . Мнимое число – это четный корень из отрицательного числа.

Как: Задать мнимое число, представить его в стандартной форме.

1. Напишите [латекс]\sqrt{-a}[/латекс] как [латекс]\sqrt{a}\cdot\sqrt{-1}[/латекс].
2. Выразите [латекс]\sqrt{-1}[/латекс] как i .
3. Напишите [латекс]\sqrt{a}\cdot i[/латекс] в простейшей форме.

Пример. Выражение мнимого числа в стандартной форме

Выразите [латекс]\sqrt{-9}[/латекс] в стандартной форме.

Показать решение

Попробуйте

Экспресс [латекс]\sqrt{-24}[/латекс] в стандартной форме.

Показать решение

Нанесение комплексных чисел на комплексную плоскость

Мы не можем наносить на числовую прямую комплексные числа, как настоящие числа. Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость , которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар [латекс](а, b)[/латекс], где [латекс]а[/латекс] представляет собой координату горизонтальной оси, а [латекс]b[/латекс ] представляет координату вертикальной оси.

Рассмотрим число [латекс]-2+3i[/латекс]. Действительная часть комплексного числа – [латекс]–2[/латекс], а мнимая часть – [латекс]3i[/латекс].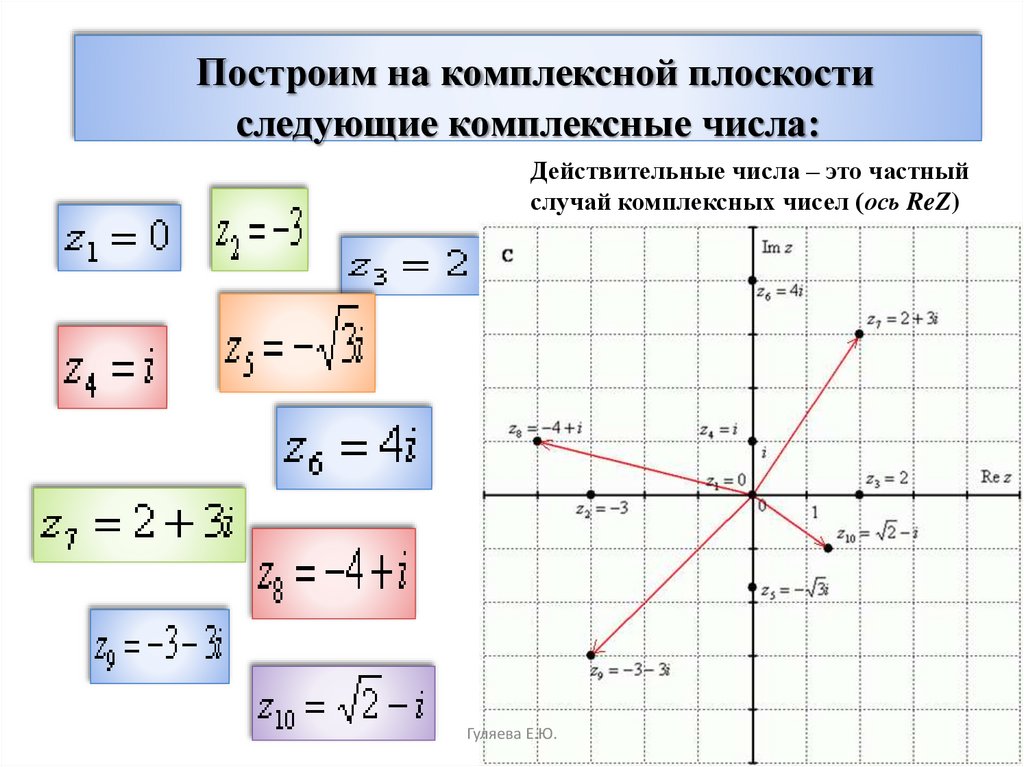 Мы строим упорядоченную пару [латекс]\влево(-2,3\вправо)[/латекс] для представления комплексного числа [латекс]-2+3i[/латекс] .

A Общее примечание: комплексная плоскость

В комплексной плоскости горизонтальная ось является реальной осью, а вертикальная ось — мнимой осью.

Как: Для заданного комплексного числа представить его компоненты на комплексной плоскости.

1. Определите действительную и мнимую части комплексного числа.
2. Перемещайтесь по горизонтальной оси, чтобы показать действительную часть числа.
3. Перемещение параллельно вертикальной оси для отображения мнимой части числа.
4. Нанесите точку.

Пример: построение комплексного числа на комплексной плоскости

Нанесение комплексного числа [латекс]3 — 4i[/латекс] на комплексную плоскость.

Показать решение

Попробуйте

Нанесите комплексное число [латекс]-4-i[/латекс] на комплексную плоскость.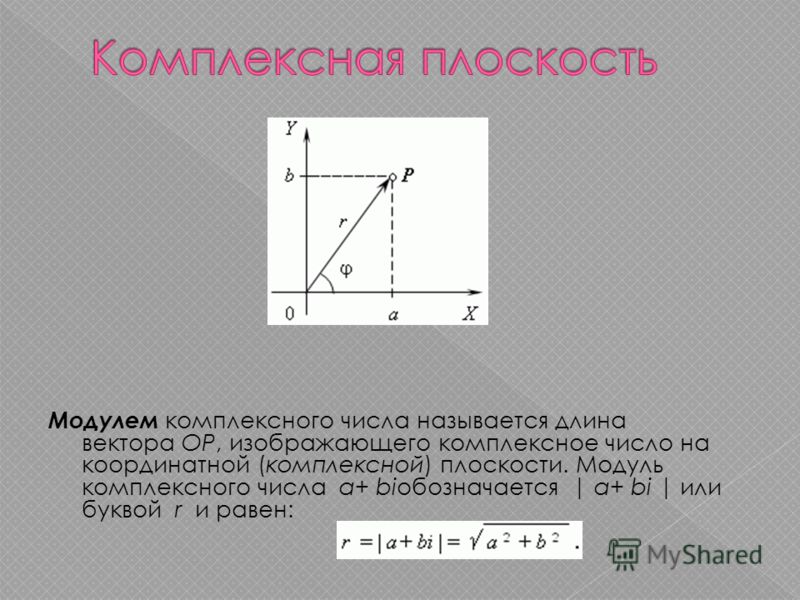

Показать решение

Поддержите!

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Комплексная плоскость

	Нет, не тот сложный самолет…
… этот сложный самолет :	A самолет на комплекс номера!

(также называемая «диаграммой Аргана»)

Действительные и мнимые составные части

Комплексное число представляет собой комбинацию действительного числа и мнимого числа:

Действительное число — это тип числа, который мы используем ежедневно.

Примеры: 12.38, ½, 0, −2000

Когда мы возводим в квадрат действительное число, мы получаем положительный (или нулевой) результат:

2 ² = 2 × 2 = 4
1 ² = 1 × 1 = 1
0 ² = 0 × 0 = 0

Что нужно возвести в квадрат, чтобы получить −1?

? ² = −1

Возведение в квадрат −1 не работает, потому что умножение отрицательных чисел дает положительное: (−1) × (−1) = +1, и никакие другие действительные числа также не работают.

Итак, кажется, что математика неполна…

… но мы можем заполнить пробел, представив число, которое при умножении само на себя дает -1
(назовем его i для мнимого):

i ² = −1

Мнимое число, при возведении в квадрат которого получается отрицательный результат

.

Примеры: 5 i , -3,6 i , i /2, 500 i

И вместе:

Комплексное число представляет собой комбинацию действительного числа и мнимого числа. 3,6 + 4 i , −0,02 + 1,2 i , 25 − 0,3 i , 0 + 2 i

Размещение комплексного числа на плоскости

Возможно, вы знакомы с числовой прямой:

Но куда мы поместим комплексное число, например 3+4 i ?

Пусть действительная числовая прямая движется слева направо, как обычно, а мнимая числовая прямая движется вверх и вниз :

Затем мы можем построить комплексное число, например 3 + 4i : 3 шт. по (действительной оси), и 4 единицы вверх (воображаемая ось).
А вот 4 — 2i : 4 шт. по (действительной оси), и на 2 единицы вниз (воображаемая ось).

 

А это комплексная плоскость :

• сложный потому что это комбинация реального и мнимого,
• плоскость потому что она похожа на геометрическую плоскость (двухмерную).

Весь новый мир

Теперь давайте перенесем идею плоскости (декартовы координаты, полярные координаты, векторы и т.д.) в комплексные числа.

Это откроет совершенно новый мир чисел, более полных и элегантных, как вы увидите.

Комплексное число как вектор

Комплексное число можно рассматривать как вектор.

Это вектор.
Имеет величину (длину) и направление.

А вот комплексный номер 3 + 4i как вектор :

Сложение

Вы также можете складывать комплексные числа как векторы:

Чтобы сложить комплексные числа 3 + 5i и 4 − 3i : добавить действительные числа и добавить мнимые числа отдельно, вот так: (3 + 5 i ) + (4 − 3 i ) = (3 + 4) + (5 − 3) i = 7+ 2 i

Полярная форма

Давайте снова воспользуемся 3 + 4i :
Вот это в полярной форме:

Таким образом, комплексное число 3 + 4i также может быть представлено как расстояние (5) и угол (0,927 радиан).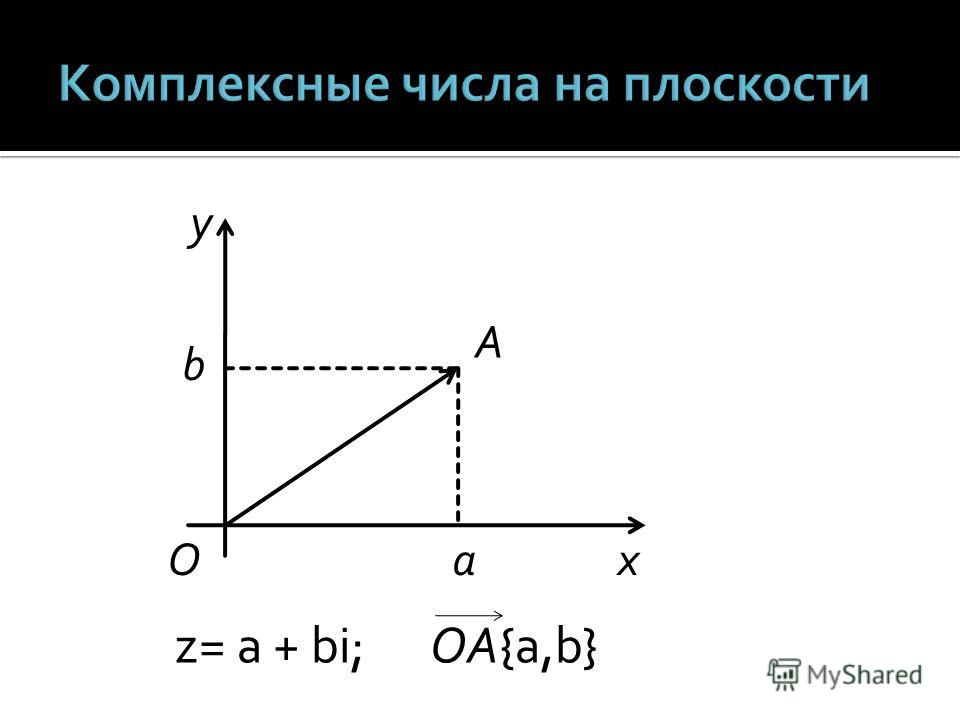

Давайте посмотрим, как преобразовать одну форму в другую, используя декартово преобразование в полярное:

Пример: число

3 + 4i

Из 3 + 4i :

• x 0329 2 + у ² ) = √(3 ² + 4 ² ) = √25 = 5
• θ = тангенс ^-1 (y/x) = тангенс ^-1 (4/3) = 0,927 (до 3 десятичных знаков)

И мы получаем расстояние (5) и угол (0,927 радиан)

Еще раз:

• x = r × cos( θ ) = 5 × cos( 0,927 ) = 5 × 0,6002… 3 (достаточно близко)
• у = г × грех( θ ) = 5 × sin( 0,927 ) = 5 × 0,7998… = 4 (достаточно близко)

И расстояние 5, и угол 0,927 снова становятся 3 и 4

На самом деле общепринятый способ записи комплексного числа в полярной форме: θ

= r(cos θ + i sin θ )

И «cos θ + i sin часто сокращают до0314 θ «, так:

x + IY = R CIS θ

CIS — это всего лишь шор.

No related posts.