Рис. 1. Графики гиперболического синуса и гиперболического косинуса.
Редакция математических наукДата публикации: 8 ноября 2022 г. в 10:55 (GMT+3)
Тригонометрические и гиперболические функции в Qlik Sense
1. Цель
Сегодня мы поговорим о тригонометрических и гиперболических функциях, чтобы применять тригонометрические операции к значениям данных, используемым в приложениях Qlik Sense. Кроме того, сначала мы познакомим вас со всеми важными тригонометрическими и гиперболическими функциями Qlik Sense, а затем разберем их более подробно, и вы узнаете, как использовать их с вашими данными в кодах скриптов.
Кроме того, выражения этих функций представляют угловые меры в радианах на x, который всегда является действительным числом.
Тригонометрические и гиперболические функции в Qlik Sense
2. Тригонометрические и гиперболические функции Qlik Sense
i. функция cos()
Возвращает значение косинуса x, которое является числом от -1 до 1.
Синтаксис функции cos ():
cos(x)
ii. функция acos()
Возвращает арккосинус x, где значение x должно удовлетворять условию -1≤x≥1, и дает результат от 0 до π.
Синтаксис функции acos() в Qlik Sense:
acos(x)
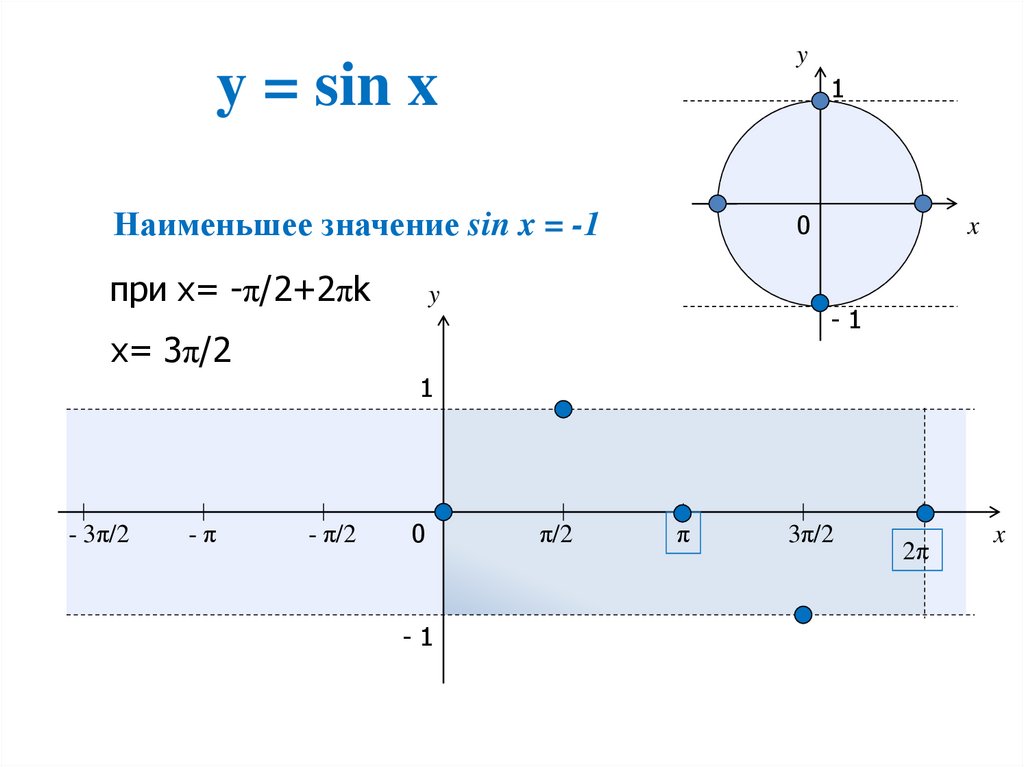
iii. функция sin()
Возвращает синус x, где результирующее значение будет в промежутке между -1 и 1.
Синтаксис sin():
sin(x)
iv. функция asin()
Возвращает арксинус x, при условии -1≤x≤1 для значения x. Результатом будет число от — π/2 до π/2.
Синтаксис функции asin():
asin(x)
v. функция tan()
Эта функция возвращает тангенс x, где результат – действительное число.
Синтаксис функции tan() в Qlik Sense:
tan(x)
vi. функция atan()
Эта функция возвращает арктангенс x, где результатом является число от — π/2 до π/2.
Синтаксис функции atan() в Qlik Sense:
atan(x)
vii. функция atan2()
Эта функция возвращает угол между началом координат и точкой, представленной координатами x и y. Это – двумерное обобщение функции обратной касательной, где результатом является число от -π до + π.
Синтаксис функции atan2():
atan2(y,x)
viii. функция cosh()
Функция возвращает гиперболический косинус x, где результатом является действительное положительное число.
Синтаксис функции cosh():
cosh(x)
ix.
функция sinh()Функция возвращает гиперболический синус x, где результатом является действительное число.
Синтаксис функции sinh():
sinh(x)
x. функция tanh()
Эта функция возвращает гиперболический тангенс x, где результатом является действительное число.
Синтаксис функции tanh() в Qlik Sense:
tanh(x)
xi. Образец кода
В приведенном ниже примере кода мы сначала загрузили таблицу с именем «SampleData», в которую загружено поле с именем «Value» (Значение). В следующей таблице с названием «Results» (Результаты) мы использовали все тригонометрические и гиперболические функции, которые мы только что изучили, чтобы скрипт генерировал таблицу с тригонометрическими и гиперболическими значениями для заданных значений.
Пример данных:
LOAD * Inline [Value 0 1]; Results: Load *, cos(Value), acos(Value), sin(Value), asin(Value), tan(Value), atan(Value), atan2(Value, Value), cosh(Value), sinh(Value), tanh(Value) RESIDENT SampleData; Drop Table SampleData;
cos (value) | acos (value) | sin (value) | asin (value) | tan (value) | (value) | atan2 (value,value) | cosh (value) | sinh (value) | tanh (value) |
1 | 1. | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0.540.. | 0 | 0.841.. | 1.570.. | 1.557.. | 0.785… | π/4 | 1.543.. | 1.175.. | 0.761.. |
570..Представленная ниже таблица результатов возвращает значение 0 и 1 для каждой функции.
Math Tutor — Функции — Теория
Math Tutor — Функции — Теория — Элементарные функции Эти функции удивительно похожи на тригонометрические функции, хотя
они не имеют ничего общего с треугольниками.
Сходство следует из
сходство определений. В конце этого раздела упомянем еще один
Причина, по которой тригонометрические и гиперболические функции могут быть близки.
Определение.
Гиперболический синус и гиперболический косинус определены кГиперболический тангенс и гиперболический котангенс определены к
Гиперболический синус. Домен:
D (ш) = &реал;.
График:
Функция непрерывна в своей области определения, неограничена и симметрична, а именно нечетно, так как у нас есть sinh(− x ) = −sinh( x ).
Существует одна нулевая точка, а именно x = 0, которая также является точкой перегиб. Локальных экстремумов нет, пределы на концах области
Производная:
[sinh( x )]′ = ch( x ).
Гиперболический косинус. Домен:
D (кош) = &реал;.
График:
Функция непрерывна в своей области определения, ограничена снизу и симметрична, а именно даже, так как мы имеем кош (− x ) = ш( x ).
Нулевой точки нет, а есть локальный минимум при x = 0, функция всегда вогнута вверх. Ограничения на конечных точках домена
Производная:
[cosh( x )]′ = sh( x ).
Гиперболический тангенс. Домен:
D (tanh) = &реал;.
График:
Функция непрерывна в своей области определения, ограничена и симметрична, а именно нечетным, так как мы имеем танх (− x ) = −tanh( x ).
Существует нулевая точка, а именно x = 0, которая также является точкой перегиб. Локальных экстремумов нет, пределы на концах области
Производная:
[тан( х )]’ = 1/ш 2 ( х ).
Гиперболический котангенс. Домен:
D (coth) = ℝ − {0} = (−∞,0) ∪ (0,∞).
График:
Функция непрерывна в своей области определения, неограничена и симметрична, а именно нечетным, так как мы имеем coth(- x ) = -coth( x ).
Нет нулевой точки и нет точки перегиба, нет локальных экстремумы. Ограничения на конечных точках домена
Производная:
[cotgh( x )]′ = −1/sinh 2 ( x ).
Обратите внимание, что мы часто пишем sinh n ( x ) вместо правильный [sinh( x )] n , аналогично для другого гиперболические функции.
Некоторые гиперболические тождества
Следующие тождества очень похожи на триггерные тождества, но они
сложно, так как время от времени знак бывает наоборот, что может
ввести в заблуждение неосторожного ученика.
Тождества для гиперболического тангенса и котангенса также аналогичны.
Обратные гиперболические функции
Тут дело обстоит гораздо лучше, чем с триггерными функциями. Отдельно от гиперболический косинус, все остальные гиперболические функции равны 1-1 и, следовательно, они иметь инверсии. Чтобы получить обратное значение ch( x ), мы ограничим его значением интервал [0,∞). обратные функции называются аргументом гиперболического синуса , обозначаются argsinh( x ), аргумент гиперболического косинуса
Основные свойства:
Теперь мы подошли к другому преимуществу гиперболических функций перед тригонометрическими.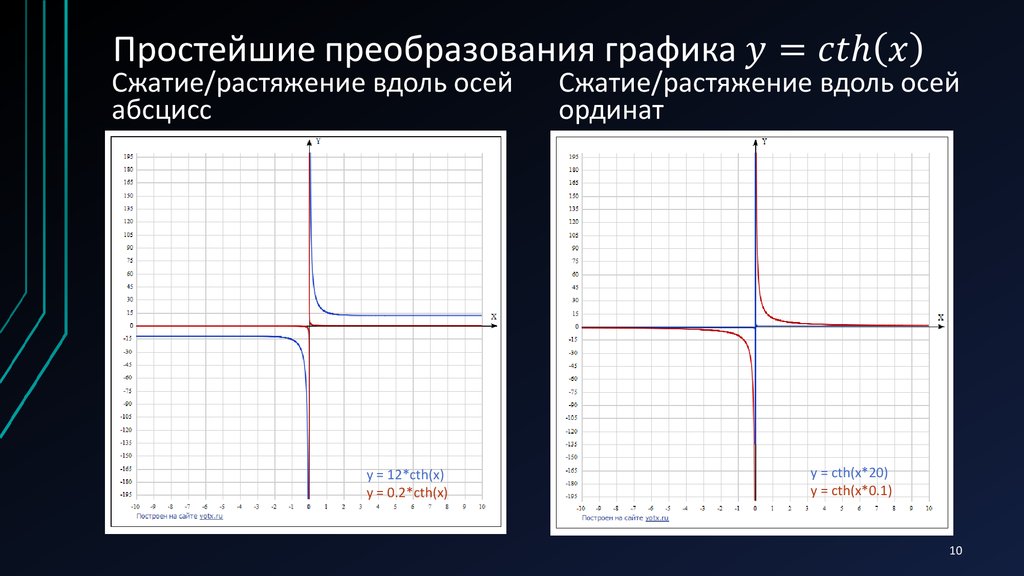
функции. На самом деле у нас есть «хорошие» формулы для обратных величин:
Примечание: Обратные функции также иногда называют «гиперболическими площадями».
функции». Есть два альтернативных обозначения, вместо
аргсин( х )
некоторые написали бы arcsinh( x ) или
sin −1 ( x ). Первый
нотация, вероятно, вдохновлена обратными триггерными функциями, вторая
к сожалению, весьма распространено, но это крайне обманчиво. Причина в том,
что многие студенты видят заведомо существующее сходство между
sin −1 ( x ) и
sinh 2 ( x ), так они думают
что sinh −1 ( x ) на самом деле
1/ш( x ). Мы говорили
о некотором оправдании этого вводящего в заблуждение обозначения, когда мы ввели
обратные функции в теории —
Реальные функции. Тем не менее, это очень жаль, тем более, что есть
вполне адекватная arg-нотация, которую мы ввели выше. Мы будем придерживаться этого
здесь, в Репетитор по математике.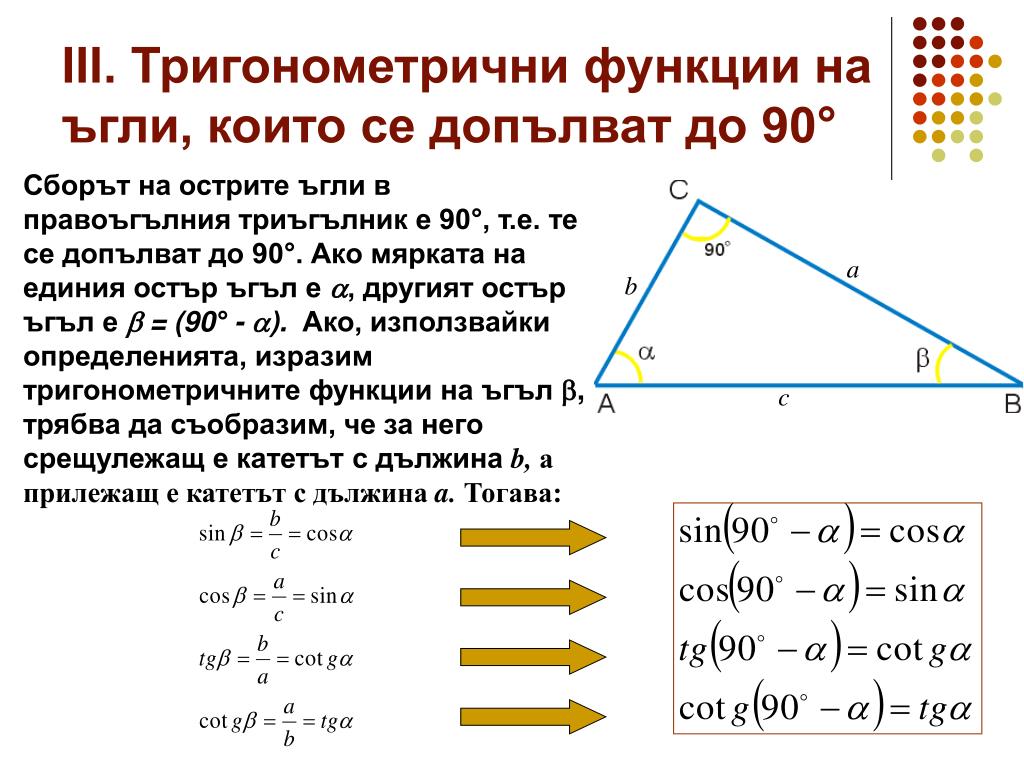
Примечание по параметрическим кривым
Одним интересным свойством триггерных функций является то, что они обеспечивают хороший описание круга. Действительно, окружность радиусом r с центром в происхождение (данное x 2 + y 2 = r 2 в декартовых координатах) задается параметрическими уравнениями x = r ⋅cos( t ), y = r ⋅sin( t ).
Что произойдет, если мы заменим эти функции их гиперболическими родственниками? уравнения x = r ⋅cosh( t ), y = r ⋅sinh( t ) точно описывают правую ветвь прямоугольная гипербола x 2 − y 2 = r 2 .
Абсолютная величина
Назад к теории — Элементарно
функции
Формулы сложения гиперболических функций синуса и косинуса с помощью линейной алгебры
Автор
Дэвид Рэдклифф
Последнее обновление
6 лет назад
Лицензия
Creative Commons CC BY 4.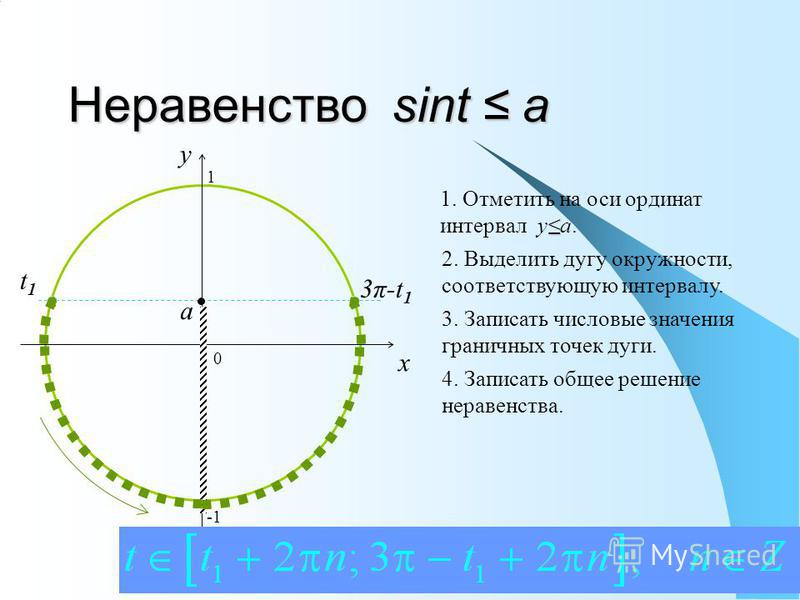
2 = 1$. Гипербола не связана — у нее две ветви. Правая ветвь ($x > 0$)
параметризуется $x = \cosh t$ и $y = \sinh t$ для $t \in \mathbb{R}$.
\emph{Гиперболический сектор} — это криволинейная треугольная область, ограниченная дугой гиперболы и двумя
отрезки прямой от начала до концов дуги. Если $t > 0$, то площадь гиперболы
сектор, ограниченный дугой из $(1, 0)$ в $(\cosh t, \sinh t)$, равен $t/2$.
Этот факт о гиперболических секторах дает $\emph{геометрическое}$ определение гиперболического синуса и
косинусные функции.
Гиперболические функции синуса и косинуса удовлетворяют правилам сложения, которые поразительно похожи на
аналогичные формулы для синуса и косинуса.
\начать{выравнивать*}
\cosh (s+t) &= \cosh s \cosh t + \sinh s \sinh t \\
\sinh (s+t) &= \sinh s \cosh t + \sinh s \sinh t
\конец{выравнивание*}
Мы докажем эти формулы в предположении, что $s$ и $t$ положительны, хотя на самом деле они
справедливо для всех действительных значений $s$ и $t$.
\section{Доказательство}
Пусть $s$ и $t$ — положительные действительные числа.
2=1$$
и сохраняет площади, поскольку $\det T = 1$.
Пусть $A$ — гиперболический сектор, ограниченный дугой из $(1, 0)$ в $(\cosh s, \sinh s)$, и
пусть $B$ — гиперболический сектор, ограниченный дугой из $(1, 0)$ в $(\cosh t, \sinh t)$.
Обратите внимание, что $A$ имеет площадь $s/2$, а $B$ имеет площадь $t/2$.
Образ $A’ := T(A)$ является гиперболическим сектором, так как $T$ сохраняет правую ветвь единичной гиперболы;
и имеет площадь $s/2$, поскольку $T$ сохраняет площади. $A’$ ограничен дугой из
$T(1,0) = (\cosh t, \sinh t)$
к
$$T(\ch s, \sinh s) = (\ch s \ch t + \sinh s \sinh t,\ \sinh s \ch t + \ch s \sinh t).$$
Теперь $A’ \cup B$ — это гиперболический сектор, ограниченный дугой из $(1, 0)$ в
$$(\cosh s \cosh t + \sinh s \sinh t,\ \sinh s \cosh t + \cosh s \sinh t).$$
Так как площадь $A’\cup B$ равна $(s+t)/2$, верхняя конечная точка может быть выражена как
$$(\сп (s+t),\ \sinh (s+t)).$$
Поэтому,
$$\cosh (s+t) = \ch s \ch t + \sinh s \sinh t$$
и
$$\sinh (s+t) = \sinh s \cosh t + \cosh s \sinh t.