Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа
Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа
ОглавлениеПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮГЛАВА 1.  РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ§ 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ § 8. ИНТЕГРАЛ ФУРЬЕ § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 6. ВЕКТОРНОЕ ПОЛЕ § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ § 8. ФОРМУЛА ОСТРОГРАДСКОГО § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ § 10.  ФОРМУЛА СТОКСА ФОРМУЛА СТОКСА§ 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА § 13. СИМВОЛИКА ГАМИЛЬТОНА § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ § 1. КОМПЛЕКСНЫЕ ЧИСЛА § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ § 3. СТЕПЕННЫЕ РЯДЫ § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ § 11. ИНТЕГРАЛ ТИПА КОШИ § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ § 14. РЯД ТЕЙЛОРА § 15. РЯД ЛОРАНА § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ § 18.  ПРИНЦИП АРГУМЕНТА ПРИНЦИП АРГУМЕНТА§ 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ Отображение, конформное в данной точке § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ Конформное отображение области на область Линейные преобразования Конформные отображения односвязных областей ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ § 1. ГАММА-ФУНКЦИЯ § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА § 4. СВЕРТКА ФУНКЦИЙ § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ § 7.  ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ§ 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ 2. Изображения функций, связанных с интегралом вероятностей 3. Изображения интегрального синуса и интегрального косинуса 4. Изображения интегралов Френеля § 10. ФОРМУЛЫ ОБРАЩЕНИЯ § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ |
cmath | Python
Модуль cmath предоставляет доступ к функциям, которые могут выполнять математические действия над комплексными числами. Помимо комплексных чисел, аргументами данных функций могут быть как целые так и вещественные (с плавающей точкой) числа, а так же любые объекты языка
__complex__() или __float__(), необходимые для преобразования комплексных чисел в вещественные и наоборот.
Некоторые функции комплексного переменного являются многозначными, поэтому для них необходимо определить ту область в которой их значение будет однозначным, а сама функция непрерывна. Такие области называются листами, а их края разрезами.
Наличие модуля cmath наряду с модулем math необходимо лишь потому что зачастую, комплексные числа вовсе не нужны. Например, кого-то сбивает с толку выражение:
>>> (-1)**0.5 (6.123233995736766e-17+1j)
Потому что некоторая часть программистов, вообще никак не связана с математикой и для них такое поведение не то что бы является странным — оно вообще является нежелательным. Поэтому они и пользуются библиотекой math, которая в этом случае просто выдаст ошибку:
>>> import math >>> >>> math.sqrt(-1) Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: math domain error
Модуль cmath в свою очередь, всегда возвращает комплексные числа, даже если для вывода достаточно целого или вещественного типа данных, просто множитель перед мнимой единицей будет равен нулю:
>>> cmath.{ib}\) – это \(\cos b + i\sin b\).>>> import cmath >>> >>> cmath.exp(0+0j) (1+0j) >>> >>> >>> x = 0 + (cmath.pi/2)*1j >>> cmath.exp(x) (6.123233995736766e-17+1j) >>> >>> cmath.e**x (6.123233995736766e-17+1j)
- cmath.log(x[, base])¶
- вычисляет логарифм комплексного числа с указанным основанием, если основание не указано, то возвращается значение натурального логарифма.
Для данной функции определен единственный, непрерывный сверху разрез главной ветви вдоль отрицательной действительной оси от \(0\) до \(-\infty\).
Как правило, на практике используется именно натуральный логарифм (обозначается \(\mathrm {Ln} \,z\) ), который так же как и логарифм для других оснований, определяется как функция обратная к показательной. Например, для комплексного числа \(x = a+ib\) натуральный логарифм определяется как некоторое значение \(\omega\), которое является решением уравнения \(e^{\omega}=x\).
>>> import cmath >>> >>> cmath.log(1 + 0j) 0j >>> >>> cmath.log(0 + 1j) 1.5707963267948966j >>> >>> >>> cmath.log(1 + 1j, 2) (0.5+1.1330900354567985j)
- cmath.log10(x)¶
- вычисляет десятичный логарифм комплексного числа.
Имеет тот же разрез главной ветви, что и log().
>>> import cmath >>> >>> x = 10**(2 + 0.5j) >>> x (40.73073101539468+91.32911666577952j) >>> >>> cmath.log10(x) (2+0.5j)
- cmath.sqrt(x)¶
- вычисляет квадратный корень комплексного числа.
Имеет тот же разрез главной ветви, что и log().
Для одного комплексного числа всегда существуют два значения его квадратного корня, например:
>>> (2 - 1j)**2, (-2 + 1j)**2 ((3-4j), (3-4j))
Но с учетом разреза главной ветви, будет возвращено только одно из них, имеющее положительную действительную часть:
>>> import cmath >>> >>> cmath.sqrt(3 - 4j) (2-1j)
Полярные координаты
Комплексное число в языке Python представляется в виде координаты точки на плоскости с прямоугольной системой координат и хранится в виде:
z == z.real + z.imag*1j
где z.real – это действительная часть (соответствует оси \(x\)), z.imag – мнимая часть (соответствует оси \(y\)), 1j – мнимая единица в языке Python.
Однако, помимо представления комплексных чисел в прямоугольной системе координат, существует еще один альтернативный способ — представление в полярной системе координат. В полярных координатах комплексное число определяется его модулем – длиной радиус-вектора \(\bar{r}\), соединяющим начало координат и точку \(z\), и, его аргументом – углом \( \varphi \) между радиус вектором и положительной частью оси \(x\), откладываемым против часовой стрелки, который еще называют фазовым углом или фазой.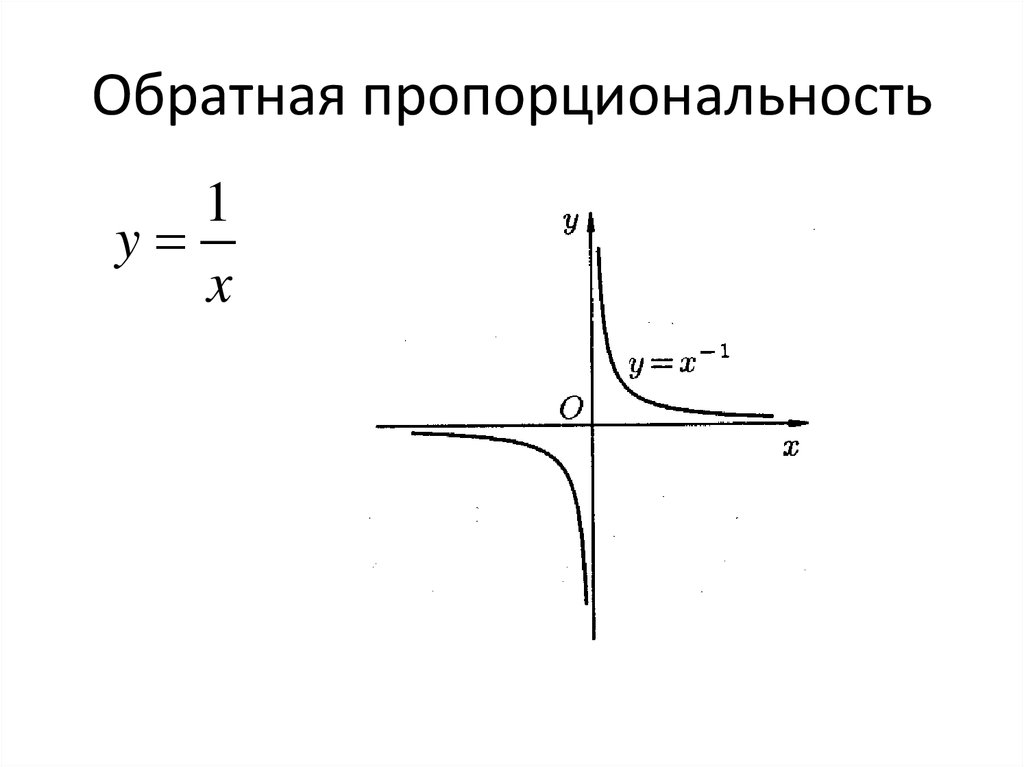
Представленные ниже функции позволяют переводить комплексные числа из одной системы координат в другую.
- cmath.phase(x)¶
- Возвращает фазу (так же известную как фазовый угол или аргумент) комплексного числа.
Данная функция эквивалентна команде math.atan2 (x.imag, x.real), т.е. это арктангенс, который возвращает значения из интервала \([-\pi;\pi]\) (в радианах) причем, возвращаемое значение фазы будет находиться в правильном квадранте, так как знаки x.imag и x.real известны.
Для данной функции определен единственный, непрерывный сверху разрез главной ветви вдоль отрицательной действительной оси от \(0\) до \(-\infty\). В системах с поддержкой нулей со знаком (в которых \(-0\) и \(0\) это разные числа) т.е. в большинстве систем, знак результата совпадает с x.imag, даже если x., например: imag = 0
imag = 0
>>> import cmath >>> >>> cmath.phase(complex(-5.0, 0.0)) 3.141592653589793 >>> >>> cmath.phase(complex(-5.0, -0.0)) -3.141592653589793
Возвращаемые значения являются радианной мерой угла, что бы конвертировать их в градусные значения можно воспользоваться функцией math.degrees(x):
>>> import cmath, math >>> >>> phi = cmath.phase(3 + 3j) >>> phi 0.7853981633974483 >>> >>> math.degrees(phi) 45.0
В модуле cmath нет функции для вычисления модуля комплексного числа, если вам необходимо вычислить его воспользуйтей функцией abs() модуля math.
- cmath.polar(x)¶
- Возвращает полярные координаты комплексного числа.
Возвращает кортеж вида (r, phi), где \(r\) – это модуль комплексного числа, a phi – это его фазовый угол \(\varphi\). Данная функция эквивалентна команде
Данная функция эквивалентна команде (math.abs(x), cmath.phase(x)).
>>> import cmath >>> >>> x = cmath.polar(3 - 3j) >>> x (4.242640687119285, -0.7853981633974483) >>> >>> r, phi = x >>> >>> cmath.rect(r, phi) (3-2.9999999999999996j)
- cmath.rect(r, phi)¶
- вычисляет действительную и мнимую части комплексного числа по его полярным координатам и возвращает полученное число.
Данная функция эквивалентна команде r*(math.cos(phi) + math.sin(phi)*1j).
>>> import cmath >>> >>> cmath.rect(7, 0.7) (5.35389531099142+4.509523810663837j) >>> >>> cmath.polar(cmath.rect(7, 0.7)) (7.000000000000001, 0.6999999999999998)
Тригонометрические функции
- cmath.
 sin(x)¶
sin(x)¶ - возвращает синус комплексного числа.
>>> import cmath >>> >>> cmath.sin(0) 0j >>> cmath.sin(1) (0.8414709848078965+0j) >>> >>> cmath.sin(1 + 1j) (1.2984575814159773+0.6349639147847361j) >>> >>> cmath.asin(cmath.sin(1 + 1j)) (1+1j)
- cmath.cos(x)¶
- возвращает косинус комплексного числа.
>>> import cmath >>> >>> cmath.cos(0) (1-0j) >>> >>> cmath.cos(1) (0.5403023058681398-0j) >>> >>> cmath.cos(1 + 1j) (0.8337300251311491-0.9888977057628651j) >>> >>> cmath.acos(cmath.cos(1 + 1j)) (0.9999999999999999+1j)
- cmath.tan(x)¶
- возвращает тангенс комплексного числа.
>>> import cmath >>> >>> cmath.tan(0) 0j >>> >>> cmath.tan(1) (1.5574077246549023+0j) >>> >>> cmath.tan(1 + 1j) (0.27175258531951174+1.0839233273386946j) >>> >>> cmath.atan(cmath.tan(1 + 1j)) (1+1j)
- cmath.asin(x)¶
- возвращает арксинус комплексного числа.
Для данной функции заданы два разреза главной ветви, оба вдоль действительной оси: первый \((-\infty , -1]\) непрерывный сверху, второй \([1 , +\infty)\) непрерывный снизу.
>>> import cmath >>> >>> x = cmath.sin(1 + 1j) >>> x (1.2984575814159773+0.6349639147847361j) >>> >>> cmath.asin(x) (1+1j)
- cmath.acos(x)¶
- возвращает арккосинус комплексного числа.
Для данной функциидва заданы два разреза главной ветви, оба вдоль действительной оси: первый \((-\infty , -1]\) непрерывный сверху, второй \([1 , +\infty)\) непрерывный снизу.
>>> import cmath >>> >>> x = cmath.cos(1 + 1j) >>> x (0.8337300251311491-0.9888977057628651j) >>> >>> cmath.acos(x) (0.9999999999999999+1j)
- cmath.atan(x)¶
- возвращает арктангенс комплексного числа.
Для данной функциидва заданы два разреза главной ветви, оба вдоль мнимой оси: первый \((-\infty i , -1i]\) непрерывный слева, второй \([1i , +\infty i)\) непрерывный справа.
>>> import cmath >>> >>> x = cmath.tan(1 + 1j) >>> x (0.27175258531951174+1.0839233273386946j) >>> >>> cmath.atan(x) (1+1j)
Гиперболические функции
- cmath.sinh(x)¶
- возвращает гиперболический синус комплексного числа.
>>> import cmath >>> >>> cmath.sinh(3) (10.017874927409903+0j) >>> >>> cmath.sinh(1 + 1j) (0.6349639147847361+1.2984575814159773j)
- cmath.cosh(x)¶
- возвращает гиперболический косинус комплексного числа.
>>> import cmath >>> >>> cmath.cosh(0) (1+0j) >>> >>> cmath.cosh(3) (10.067661995777765+0j) >>> >>> cmath.cosh(1 + 1j) (0.8337300251311491+0.9888977057628651j)
- cmath.tanh(x)¶
- возвращает гиперболический тангенс комплексного числа.
>>> import cmath >>> >>> cmath.tanh(0) 0j >>> >>> cmath.tanh(3) (0.9950547536867305+0j) >>> >>> cmath.tanh(1 + 1j) (1.0839233273386946+0.27175258531951174j)
- cmath.asinh(x)¶
- возвращает гиперболический арксинус комплексного числа.
Для данной функциидва заданы два разреза главной ветви, оба вдоль мнимой оси: первый \((-\infty i , -1i]\) непрерывный слева, второй \([1i , +\infty i)\) непрерывный справа.
>>> import cmath >>> >>> x = cmath.sinh(1 + 1j) >>> x (0.6349639147847361+1.2984575814159773j) >>> >>> cmath.asinh(x) (1+1j)
- cmath.acosh(x)¶
- возвращает гиперболический арккосинус комплексного числа.
Для данной функции задан один разрез главной ветви вдоль вещественной оси \((- \infty, 1]\) непрерывный сверху.
>>> import cmath >>> >>> x = cmath.cosh(1 + 1j) >>> x (0.8337300251311491+0.9888977057628651j) >>> >>> cmath.acosh(x) (1+0.9999999999999999j)
- cmath.atanh(x)¶
- возвращает гиперболический арктангенс комплексного числа.
Для данной функциидва заданы два разреза главной ветви, оба вдоль действительной оси: первый \((-\infty , -1]\) непрерывный сверху, второй \([1 , +\infty)\) непрерывный снизу.
>>> import cmath >>> >>> x = cmath.tanh(1 + 1j) >>> x (1.0839233273386946+0.27175258531951174j) >>> >>> cmath.atanh(x) (1+1j)
Классифицирующие функции
- cmath.isfinite(x)¶
- возвращает True если вещественная и (или) мнимая части не равны inf, -inf или nan.
>>> import cmath, math >>> >>> x = complex(math.inf, 3) >>> y = complex(3, -math.inf) >>> z = complex(3, math.nan) >>> >>> x, y, z ((inf+3j), (3-infj), (3+nanj)) >>> >>> cmath.isfinite(x) False >>> cmath.isfinite(y) False >>> cmath.isfinite(z) False >>> >>> >>> cmath.isfinite(1000 + 0.001j) True
Доступно в Python c версии 3.2.
- cmath.
 isinf(x)¶
isinf(x)¶ - возвращает True только если вещественная и (или) мнимая части равны inf, -inf.
>>> import cmath, math >>> >>> x = complex(math.inf, 3) >>> y = complex(3, -math.inf) >>> z = complex(3, math.nan) >>> >>> x, y, z ((inf+3j), (3-infj), (3+nanj)) >>> >>> cmath.isinf(x) True >>> cmath.isinf(y) True >>> cmath.isinf(z) False
- cmath.isnan(x)¶
- возвращает True только если вещественная и (или) мнимая части равны nan.
>>> import cmath, math >>> >>> x = complex(math.nan, math.nan) >>> y = complex(3, math.nan) >>> z = complex(300, 300) >>> >>> x, y, z ((nan+nanj), (3+nanj), (300+300j)) >>> >>> cmath.isnan(x) True >>> cmath.isnan(y) True >>> cmath.isnan(z) False
- cmath.isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)¶
- возвращает True если в пределах указанной точности, числа
aиbблизки настолько, что их можно считать равными.
Допустим у нас есть два числа и мы знаем, что по сути это одно и то же число, а все мизерные различия связаны с ошибками округления и двоичной арифметикой. Мы то понимаем что это как бы одно и то же число, а вот компьютер считает иначе:
>>> import cmath >>> >>> x = 1 + 1j >>> >>> y = cmath.acos(cmath.cos(x)) >>> y (0.9999999999999999+1j) >>> >>> >>> x == y False
Для таких ситуаций, в которых мы готовы считаться с некоторой погрешностью и подходит функция isclose():
>>> cmath.isclose(x, y) True
Считать числа близкими или нет, определяют два параметра rel_tol и abs_tol().
rel_tol (relative tolerances) – это относительный допуск, определяемый как максимально допустимая разница между числами a и b относительно большего из них по модулю. По умолчанию, rel_tol = 1e-09, это гарантирует, что числа a и b будут одинаковы, в пределах 9 десятичных цифр. Что бы числа считались равными, если они, допустим, отличаются меньше чем на 0.1%, то достаточно установить rel_tol = 0.001, но в любом случае данный параметр, должен быть больше нуля:
>>> y (0.9999999999999999+1j) >>> >>> z = 0.999 + 1j >>> >>> cmath.isclose(y, z) False >>> >>> cmath.isclose(y, z, rel_tol = 0.001) True
Параметр abs_tol (absolute tolerances) – это минимальный абсолютный допуск, который определяет как сравнивать значения близкие к нулю. Данный параметр должен быть не меньше нуля:
Данный параметр должен быть не меньше нуля:
>>> x = 2**(-1000) + 3**(-100)*1j >>> x (9.332636185032189e-302+1.9403252174826328e-48j) >>> >>> y = 0.000000000001 + 0.000000000001j >>> y (1e-12+1e-12j) >>> >>> cmath.isclose(x, y) False >>> cmath.isclose(x, y, abs_tol = 10.0e-13) False >>> cmath.isclose(x, y, abs_tol = 10.0e-12) True
Данная функция эквивалентна команде abs(a - b) <= max(rel_tol*max(abs(a), abs(b)), abs_tol). Значения inf, -inf считаются близкими только сами к себе, а NaN не является близким ни к одному значению, включая само NaN.
Математические константы
- cmath.pi¶
- математическая константа \( \pi\) в виде числа типа
float.
>>> import cmath >>> >>> cmath.pi 3.141592653589793
- cmath.e¶
- математическая константа \( e\) в виде числа типа
float.
>>> import cmath >>> >>> cmath.e 2.718281828459045
Гиперболические функции комплексных чисел
Показательная функция может быть определена для любого комплексного аргумент . Таким образом, мы можем расширить определения гиперболических функций до
также сложные аргументы.
Формула Эйлера для комплексных чисел:
| e ix | = | cos x + i sin x |
| Замена i | = | — я, у нас есть |
| e – ix | = | cos x – я sin x |
| кош(ix) | = | . .. по определению .. по определению |
| = | cos x ... из формул Эйлера выше | |
| синх(ix) | = | = я грех х |
| ∴ У нас есть | ||
| I. а) кош (ix) | = | соз х |
| б) синх (ix) | = | я грех х |
| в) танх(ix) | = | я загар х |
II. а) ch(x + iy) а) ch(x + iy) | = | кош х . уютно + я грешу х . грех у |
| б) sh(x + iy) | = | грех х . уютный + я кош х . грех у |
| III. а) кош х | = | cos(ix) |
| б) синх х | = | – я грешу (ix) |
| в) танх х | = | - я загар (ix) |
Выше приведены отношения между гиперболическими функциями и обычными
тригонометрические функции.
Гиперболические функции являются периодическими относительно мнимая компонента с периодом 2πi для
sinh, cosh, sech & cosech; и с периодом πi для tanh и coth.
Гиперболические функции в комплексной плоскости
z, представляющие комплексные числа, говорят, что функции sh z и ch z равны голоморфный или аналитический (см. рисунки ниже).
Maths — Функции комплексной переменной
На этой странице мы обсуждаем, как расширить скалярные функции (которые мы обсуждали на этой странице) на ситуацию, когда домен и/или кодовый домен являются комплексными числами, мы также обсуждаем такие функции, как нормализация, которые относятся к комплексным числам.
- Конъюгат
- Степени комплексных чисел
- Экспоненциальная функция
- журнал Функция
- Обратная функция
- Отражение в круге
- Норма (нормализация)
Мы можем классифицировать эти функции в соответствии со следующими свойствами:
- Конформные — сохраняет углы
- Антиконформный - переворачивает углы
- Неконформный - не сохраняет углы
| консервация углов | сохранение расстояний | Аналитик | |
|---|---|---|---|
| Конъюгат | Антиконформный | ||
| Степени комплексных чисел | |||
| Экспоненциальная функция | Поверхность Римана | ||
| Обратная функция | Конформный | да, кроме 0 и &in | |
| Отражение в круге | Антиконформный | ||
| Норма (нормализация) | |||
| Преобразование Мебиуса |
Вычисление сложных функций
Мы можем оценить значение многих сложных функций, используя бесконечные ряды так же, как мы можем вычислять скалярные функции. Мы просто используем тот же ряд, который мы использовали бы для скалярных функций, но подставляем комплексные значения вместо действительных значений. Итак, если ряд существует для действительных значений, мы можем оценить сложную функцию. Например:
Мы просто используем тот же ряд, который мы использовали бы для скалярных функций, но подставляем комплексные значения вместо действительных значений. Итак, если ряд существует для действительных значений, мы можем оценить сложную функцию. Например:
| пер(1+z) | z - z 2 /2! + г 3 /3! ... +(-1) r+1 z r /(r)! | -1 < z <= 1 |
| ехр(г) | 1 + г 1 /1! + г 2 /2! + г 3 /3! ... + z r /(r)! | все значения z |
В качестве альтернативы мы можем вывести действительную и мнимую части через действительные функции:
| функция комплексной переменной | действительные и мнимые термины |
|---|---|
| ехр(х+i у) | exp(x)*(cos(y)+i sin(y)) |
| пер(х+i у) | 0,5*ln(x²+y²) + i atan(x/y) |
| sin(x+iy) | cos(-y) sin(x) - i sh(-y) cos(x) |
| cos(x+iy) | cos(-y) cos(x) + i sh(-y) sin(x) |
| тан(х+i у) | (tan(x) -i tanh(-y)) / |
| sin(x+i y) | sin(x) cos(y) + i ch(x) sin(y) |
| кош(х+i у) | cos(x) cos(y) + i sh(x) sin(y) |
| танх(х+i у) | (танг (х) + я тангенс (у)) / (1 +i танх(х) тангенс(у)) |
Мы можем преобразовать круговую и гиперболическую функции следующим образом:
- sin(z) = -i sh(iz)
- cos(z) = -cosh(iz)
- тангенс (z) = -i тангенс (из)
См. также идентификаторы триггеров на этой странице.
также идентификаторы триггеров на этой странице.
Conjugate
Когда мы умножаем комплексное число на его сопряженное, мы получаем действительное число, другими словами, мнимая часть сокращается.
Обратная функция
Чтобы вычислить обратное значение (1/z), мы умножаем верх и низ на сопряженное, что делает знаменатель действительным числом.
| плоскость z | w самолет | |
|---|---|---|
--> ш=1/з |
как был создан этот сюжет.
Пусть компоненты входной и выходной плоскостей будут:
z = x + i y и w = u + i v
В этом случае w = 1/z
поэтому:
w = 1/(x + i y )
Как обычно, мы вычисляем обратное значение, умножая верх и низ на сопряженное:
w = (x - i y)/(x + i y)(x - i y)
w = (x - i y)/( x² + y²)
, поэтому компоненты u и v:
u = x /(x²+y²)
v = -y /(x²+y²)
У этой функции есть несколько очень интересных и полезных свойств:
- Прямые линии через исходную карту к самим себе.

- Прямые линии не проходят через исходную карту в окружности.
- Круги через исходную карту к прямым линиям.
- Круги не через исходную карту в круги.
- Двойное применение обратной функции восстанавливает оригинал.
- Обратная функция может быть разложена на сопряжение и отражение в окружности.
Таким образом, эту функцию можно использовать для сопоставления кругов и линий. Мы также можем расширить концепцию до трех измерений, что позволяет нам отображать поверхность сферы на плоскость (см. Стереографические проекции).
Преобразование Мёбиуса
Это можно обобщить до преобразования Мёбиуса (описанного здесь):
Где:
- z = ввод (комплексные значения)
- w = вывод (комплексные значения)
- a,b,c,d = параметры (комплексные значения)
Обратная функция — это особый случай, когда a=d=0 и b=c=1 мы получаем:
w=1/z
сместить линию в плоскости z:
w=1/(z+d)
Если теперь мы разрешим масштабирование c, мы увидим, что это изменит положение линии в плоскости z:
w =1/(cz+d)
Если теперь мы позволим a и b изменяться, все станет немного сложнее, но мы увидим, что можем перемещать круг вокруг плоскости w.
Экспоненциальная функция
Существует два метода расчета экспоненциальной функции:
- полярная форма и уравнение Эйлера, как описано на этой странице.
- бесконечных серий, как описано на этой странице.
| плоскость z | w самолет | |
|---|---|---|
--> ш=е г |
как был создан этот сюжет.
Пусть компоненты входной и выходной плоскостей будут:
z = x + i y и w = u + i v
В этом случае w = e z
поэтому: i y)
по правилам экспонент:
w = e x e i y
применяя уравнение Эйлера получаем:
w = e x (cos(y) + sin i(y) )
, поэтому компоненты u и v равны:
u = e x cos(y)
v = e x sin(y)
Логарифмическая функция
Натуральный логарифм, то есть логарифм по основанию e, является обратной экспоненциальной функцией. Итак, если
Итак, если
w = ln(z)
, то взятие показателя степени каждой стороны дает
e w = z
, поэтому мы имеем
x = e u cos(v) 9000 y = e u sin(v)
, что дает:
u = ln(√(x² + y²))
v = atan(x/y)
Степени комплексных чисел
Вот график для (x + i y)² более общее выражение для (x + i y) n дано на этой странице.
| плоскость z | w самолет | |
|---|---|---|
--> ш=г² |
как был создан этот сюжет.
Чистые действительные значения всегда возводятся в квадрат к положительному значению, а чисто мнимые значения всегда возводятся в квадрат к отрицательному значению. Однако действительная и мнимая части вместе покрывают всю плоскость.
Пусть компоненты входной и выходной плоскостей будут:
z = x + i y и w = u + i v
давайте возьмем пример функции квадрата w = z²
поэтому:
w = (x + i y)²
умножение дает:
w = x² - y² + i 2 x y
поэтому компоненты u и v равны:
u = x² - y²
v = 2 x y
Норма
Это расстояние (r) a + i b от начала координат.

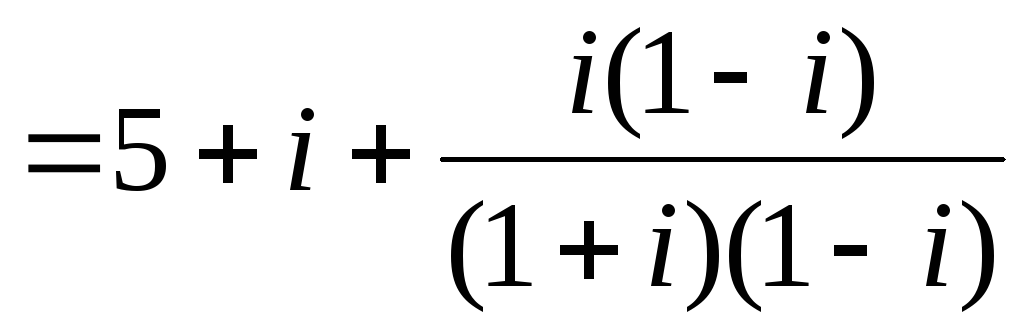
 sqrt(3 - 4j)
(2-1j)
sqrt(3 - 4j)
(2-1j) sin(x)¶
sin(x)¶ tan(1)
(1.5574077246549023+0j)
>>>
>>> cmath.tan(1 + 1j)
(0.27175258531951174+1.0839233273386946j)
>>>
>>> cmath.atan(cmath.tan(1 + 1j))
(1+1j)
tan(1)
(1.5574077246549023+0j)
>>>
>>> cmath.tan(1 + 1j)
(0.27175258531951174+1.0839233273386946j)
>>>
>>> cmath.atan(cmath.tan(1 + 1j))
(1+1j) sinh(3)
(10.017874927409903+0j)
>>>
>>> cmath.sinh(1 + 1j)
(0.6349639147847361+1.2984575814159773j)
sinh(3)
(10.017874927409903+0j)
>>>
>>> cmath.sinh(1 + 1j)
(0.6349639147847361+1.2984575814159773j)