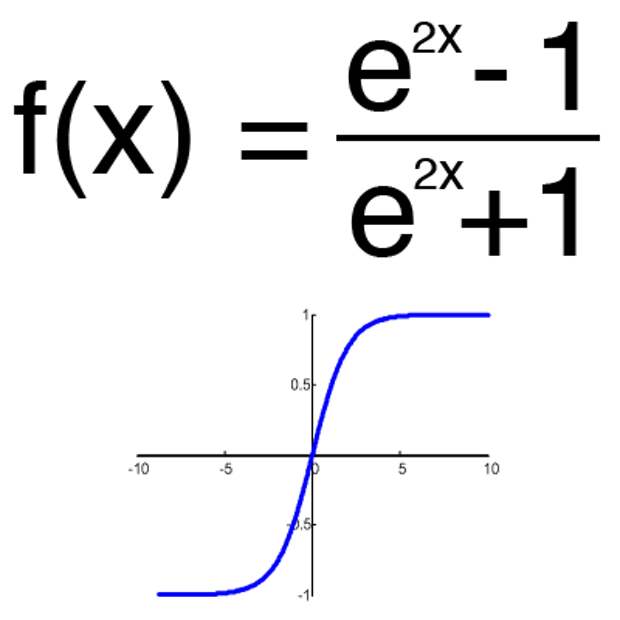Гиперболический синус 1: Открытая Математика. Функции и Графики. Гиперболические функции

alexxlab / / Разное

4.2.1. Определение гиперболических функций.

Опр. 4.2.1. Гиперболическими называются функции

— синус гиперболический; — косинус гиперболический;

— тангенс гиперболический;

— котангенс гиперболический.

Графики гиперболических функций:

4.2.2. Соотношения между гиперболическими функциями.

Исходя из определения гиперболических функций можно получить различные соотношения между этими функциями, схожие с соответствующими соотношениями между тригонометрическими функциями, или, в некоторых случаях, отличающиеся знаком перед некоторыми слагаемыми. Так, прямой подстановкой проверяется равенство (основное гиперболическое тождество, играющее в теории гиперболических функций ту же роль, какую в тригонометрии играет основное тригонометрическое тождество ).

Прямой проверкой или из основного гиперболического тождества можно получить аналог любой тригонометрической формулы, например

sh 2x

= 2 shx chx

и т. д. Получать эти соотношения можно также руководствуясь мнемоническим правилом (оно доказывается в комплексном анализе): вместо cos x пишется ch x, а вместо sin x пишется ish x, где i — мнимая единица ( i= i= -1).

4.2.3. Обратные гиперболические функции.

Обратные гиперболические функции определяются как функции, обратные соответствующим гиперболическим функциям. например:

если y = Ar sh x, то x = sh y, где : xR , yR.

Любую обратную гиперболическую функцию можно выразить через логарифм натуральный.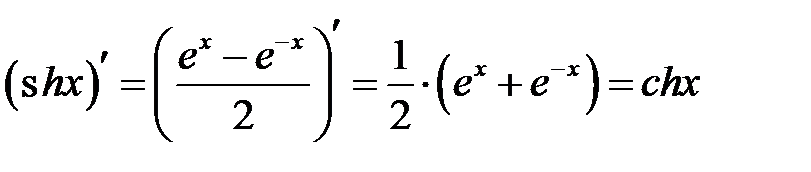

Так, решая уравнение относительно y с помощью подстановки z = e x, получим для z квадратное уравнение , при решении которого надо взять положительный корень , и окончательно . Для остальных функций так же можно получить

Справа и ниже на рисунках приведены графики прямых и обратных гиперболических функций.

4.3. Последовательность и её предел.

4.3.1. Определение последовательности и её предела.

Опр. 4.3.1. Последовательностью называется любой счётный набор действительных чисел а1, а2, а3,…, аn,….

Примеры:

1). 1, 1, 1,…,1,…; аn=1, nN;

3). ; nN;

2). ; аn=, nN;

4).

Обозначать последовательность мы будем либо перечислением её членов, как в приведённых примерах, либо более краткой записью , либо просто . Так как множество счётно, его члены могут быть пронумерованы, нижний индекс как раз и обозначает номер члена последовательности. В терминах функциональной зависимости последовательность можно определить как функцию натурального аргумента n, поэтому для последовательности имеют смысл введённые выше

опр.4.1.3 -4.1.11, описывающие её свойства.

Далее символом N будет обозначаться не множество натуральных чисел, а некоторый элемент этого множества, т.е. просто некоторое натуральное число.

Опр. 4.3.2.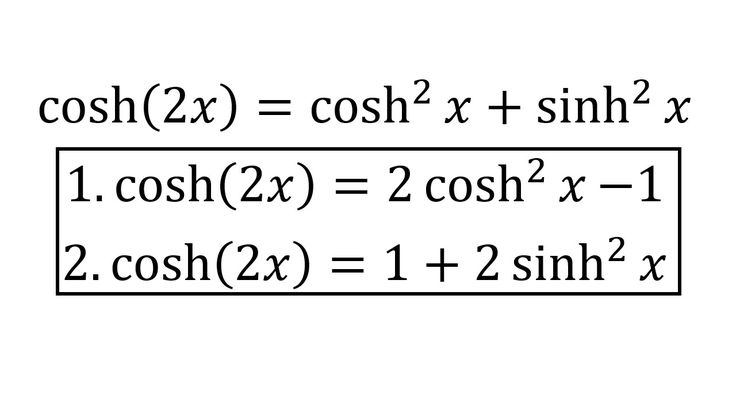 Число а называется пределом последовательности , если для любого положительного числа  существует такое натуральное число N (зависящее от ), что для членов последовательности с номерами n>N выполняется неравенство | an — a |<.

Обозначения: ; ; при .

Если при , то говорят также, что последовательность сходится к числу а.

Краткая форма записи определения: .

Неравенство |

an — a|< эквивалентно двустороннему неравенству -< an — a < или a-< an <a+. Таким образом, смысл неравенства | an — a |< заключается в том, что для >0 мы можем найти такое N, что все точки anс номерами индексов n>N лежат внутри интервала U(a) =

(a-,a+), т. е. вне этого интервала лежит не более чем конечное число точек последовательности. Докажем, например, что последовательность при сходится к двум. Возьмём >0. Требуется доказать, что существует такое

N=N(), что при n>N выполняется неравенство |an—a|<, т.е. . Таким образом, если в качестве N=N() мы возьмём N()= (где Е(х)-определённая выше функция — целая часть числа х), то при n>N выполняется неравенство , что и требовалось. Расположение нескольких первых членов последовательности на числовой оси приведено на рисунке снизу. Сходимость последовательности к числу 2 выражается в том, что члены последовательности сгущаются около точких=2.

SinH—Справка | ArcGIS for Desktop

Доступно с лицензией Spatial Analyst.

  • Краткая информация
  • Рисунок
  • Использование
  • Синтаксис
  • Пример кода
  • Параметры среды
  • Информация о лицензировании

Краткая информация

Вычисляет гиперболический синус значений ячеек растра.

Рисунок

OutRas = SinH(InRas)

Использование

  • В математике все тригонометрические функции имеют определенный диапазон корректных входных значений, называемый домен. Выходные значения каждой функции также имеют определенный диапазон. Для этого инструмента

    Обратите внимание, что здесь -∞ и ∞ представляют наименьшее отрицательное и наибольшее положительное значения, поддерживаемое определенным форматом растра, соответственно.

  • Входные и выходные значения для этого инструмента обрабатываются как безразмерные.

  • Выходные значения всегда с плавающей точкой, независимо от типа входных данных.

  • См. раздел Среда анализа и Spatial Analyst для получения дополнительной информации о среде геообработки данного инструмента.

Синтаксис

SinH (in_raster_or_constant)
ПараметрОбъяснениеТип данных

in_raster_or_constant

Входные данные для вычисления значений гиперболического синуса.

Чтобы использовать число в качестве входных данных для этого параметра, необходимо сперва указать экстент и размер ячейки в параметрах среды.

Raster Layer | Constant

Возвращено значение

ИмяОбъяснениеТип данных
out_raster

Выходной растр.

Значениями является гиперболический синус входных значений.

Raster

Пример кода

SinH. Пример 1 (окно Python)

В этом примере вычисляется гиперболический синус значений в входном растре GRID.

import arcpy
from arcpy import env
from arcpy.sa import *
env.workspace = "C:/sapyexamples/data"
outSinH = SinH("degs")
outSinH.save("C:/sapyexamples/output/outsinh")
SinH. Пример 2 (автономный скрипт)

В этом примере вычисляется гиперболический синус значений в входном растре GRID с сохранением результата в виде растра TIFF.

# Name: SinH_Ex_02. py
# Description: Calculates the hyperbolic sine of cells in a raster
# Requirements: Spatial Analyst Extension
# Import system modules
import arcpy
from arcpy import env
from arcpy.sa import *
# Set environment settings
env.workspace = "C:/sapyexamples/data"
# Set local variables
inRaster = "degs"
# Check out the ArcGIS Spatial Analyst extension license
arcpy.CheckOutExtension("Spatial")
# Execute SinH
outSinH = SinH(inRaster)
# Save the output 
outSinH.save("C:/sapyexamples/output/outsinh.tif")

Параметры среды

  • Автоподтверждение (Auto Commit)
  • Размер ячейки (Cell size)
  • Текущая рабочая область (Current Workspace)
  • Экстент (Extent)
  • Географические преобразования (Geographic Transformations)
  • Маска (Mask)
  • Выходное ключевое слово CONFIG (Output CONFIG Keyword)
  • Выходная система координат (Output Coordinate System)
  • Временная рабочая область (Scratch Workspace)
  • Растр привязки (Snap Raster)
  • Размер листа (Tile Size)

Связанные темы

Отзыв по этому разделу?

7.

7 Обратные гиперболические функции

Вычисление одной действительной переменной Автор Фенг Ким Винг
Глава 7: Экспоненциальные и логарифмические функции Раздел 7.7: Обратные гиперболические функции

 

7,7
Обратные гиперболические функции

 

 

Возврат К содержанию
Перейти к проблемам и решениям

 

1. Определения

 

 

График гиперболического синуса функция y = sh x показана на рис. 1.1. Ясно грех один к одному, как и
инверсия, обозначенная sinh 1 . Обратный гиперболический синус функция Sinh 1 определяется следующим образом:

График Y = SINH 1 X является зеркальным изображением

Y = SINH X в строке y = х . Это показано на рис. 1.1. У нас есть
дом (ш 1 ) = R и диапазон (sinh 1 ) = R .

 

Рис. 1.1

 

График y = sinh 1 x .

 

 

 

Рис. 1.2

 

График y = cosh 1 x .

 

 

График функции гиперболического тангенса y = tanh x изображен на рис. 1.3. Ясно, что танх один к одному, и поэтому имеет
обратный, обозначенный tanh 1

. Гиперболический арктангенс Функция tanh 1 определяется следующим образом:

 

Рис. 1.3

 

График y = tanh 1 x .

 

 

График функции гиперболического котангенса y = coth x изображен на рис. 1.4. Ясно, что coth взаимно однозначен, и таким образом имеет
инверсия, обозначенная coth 1 . Арктический гиперболический котангенс функция coth 1 определяется следующим образом:

Рис. 1.4

 

График y = coth 1 x .

 

 

 

Рис. 1.5

 

График y = сек 1 х .

 

 

График функции гиперболического косеканса y = csch x изображен на рис. 1.6. Ясно, что csch взаимно однозначен, и поэтому имеет
инверсия, обозначенная csch 1 . Арктический гиперболический косеканс функция csch 1 определяется следующим образом:

 

Рис. 1.6

 

График y = csch 1 x .

 

 

Докажите тождество:

 

 

. функция натурального логарифма. Поскольку гиперболические функции


определяются в терминах естественной экспоненциальной функции, это неудивительно что их обратные выражения могут быть выражены в терминах
функции натурального логарифма. Также см. Проблема & Решение 1 и Задача и Решение 2.

 

Решение

Пусть y = sinh 1 x . Тогда x = sinh y = ( е y e y )/2. Так e y e y 2 x = 0. Умножение обеих сторон на e y выходы e 2 y 1 2 хэ у = 0,
или e 2 y 2 xe y 1 = 0, что является квадратичным уравнение в e y . Его корни:

 

EOS

 

Перейти к проблемам и решениям Вернуться к началу Страница

 

2. Дифференциация

 

 

 

 

Докажем формулу [2. 1] следующим образом. Пусть у = синх 1 х . Тогда x = sinh и . Неявное дифференцирование этого уравнения с относительно x
получаем:

 

 

Остальные формулы дифференцирования доказываются в Подобный способ.

 

 

Дифференциальный синх 1 коричневый х .

 

Решение

EOS

 

Вернуться к началу страницы

1. В примере 1.1. 1 х . Тогда х = кош y = ( е y + e y )/2. Итак, е у + е у 2 x = 0. Умножение обеих сторон на E Y . 0 или e 2 y 2 xe y + 1 = 0, т.е. квадратное уравнение в e г . Его корни:

Возврат к вершине страницы

2. В примере 1.1 мы доказали 1 идентичность, и в проблеме и решение 1 вы попросили доказать другое тождество. Теперь снова
вас просят доказать следующее 2 тождества:

 

 

Решение

 

а. Пусть y = tanh 1 x . Итак, х = танх и и | х | < 1. Мы есть:

 

 

x e 2 y x = E 2 Y + 1,

E 2 y ( x 1) = х + 1,

 

 

Вернуться к началу страницы

 

 

0 0 8. Различайте следующие функции.


а. sinh 1 ( x / a ), a > 0.
b. COSH 1 ( x / A ), A > 0.

Решение

Вернуться к началу страницы

 

 

4. Различают следующие функции.
а. y = сек 1 ( х 2 ).
б. f ( t ) = csch 1 tan t .

 

Решение

 

 

Вернуться к началу страницы

 

5. Докажите, что:

Решение

LET Y = CSCH 1 X . Тогда х = csch и . Пусть z = sin 1 (1/ x ), так что 1/ x = sin z , или:

 

 

Вернуться к началу страницы Вернуться К содержанию 9{2} } } . $$

Обратные гиперболические функции комплексной переменной $ z $ определяются по тем же формулам, что и для вещественной переменной $x$, где $ \mathop{\rm ln} z $ понимается как многозначная логарифмическая функция.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *