Гиперболический синус и косинус формулы: Гиперболический синус sh(x), формулы и примеры

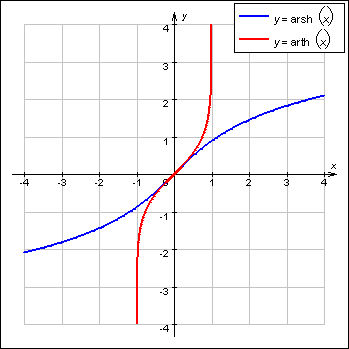
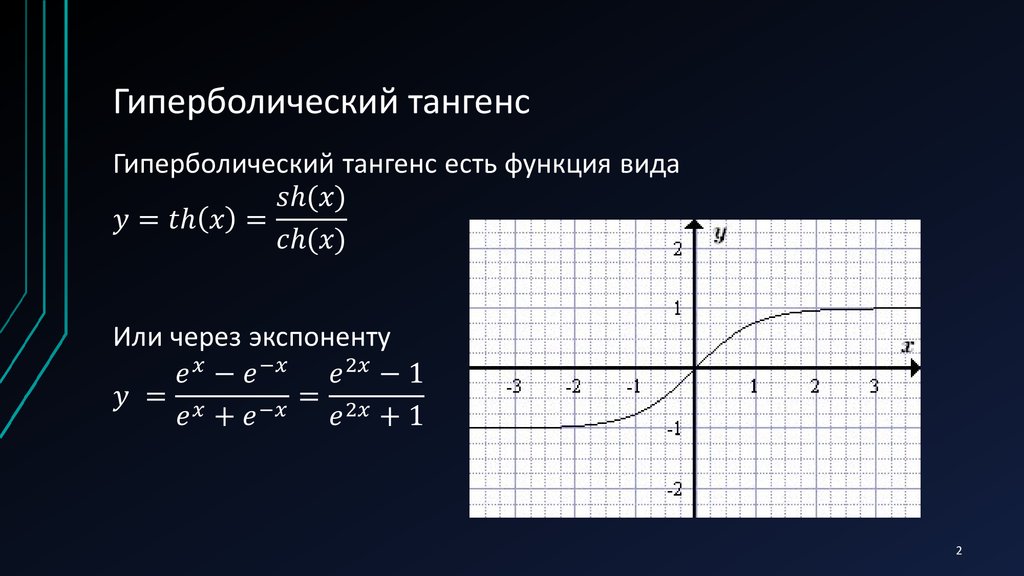
Как выводится производная косинуса

Производная косинуса находится по аналогии с производной синуса, основа доказательства ― определение предела функции. Можно воспользоваться другим способом, используя тригонометрические формулы приведения для косинуса и синуса углов. Выразить одну функцию через другую — косинус через синус, и продифференцировать синус со сложным аргументом.

Рассмотрим первый пример вывода формулы (Cos(х))’

Даем ничтожно малое приращение Δх аргументу х функции у = Cos(х). При новом значении аргумента х+Δх получаем новое значение функции Cos(х+Δх). Тогда приращение функции Δу будет равно Cos(х+Δx)-Cos(x).
Отношение же приращения функции к Δх будет таким: (Cos(х+Δx)-Cos(x))/Δх. Проведем тождественные преобразования в числителе получившейся дроби. Вспомним формулу разности косинусов углов, результатом будет произведение -2Sin(Δх/2) умножить на Sin(х+Δх/2). Находим предел частного lim этого произведения на Δх при Δх, стремящемся к нулю. Известно, что первый (его называют замечательным) предел lim(Sin(Δх/2)/(Δх/2)) равен 1, а предел -Sin(х+Δх/2) равен -Sin(x) при Δx, стремящемся к нулю.
Запишем результат: производная (Cos(х))’ равна — Sin(х).

Некоторым больше нравится второй способ вывода той же формулы

Из курса тригонометрии известно: Cos(х) равно Sin(0,5·∏-х), аналогично Sin(х) равно Cos(0,5·∏-x). Тогда дифференцируем сложную функцию — синус дополнительного угла (вместо косинуса икс).
Получим произведение Cos(0,5·∏-х)·(0,5·∏-х)’, потому что производная синуса х равна косинусу х. Обращаемся ко второй формуле Sin(х) = Cos(0,5·∏-x) замены косинуса на синус, учитываем, что (0,5·∏-х)’ = -1. Теперь получаем -Sin(x).
Итак, найдена производная косинуса, у’ = -Sin(х) для функции у = Cos(х).

Производная косинуса в квадрате

Часто используемый пример, где употребляется производная косинуса. Функция y = Cos²(x) сложная. Находим сначала дифференциал степенной функции с показателем 2, это будет 2·Cos(x), затем умножаем его на производную (Cos(x))’, которая равна -Sin(х). Получаем y’ = -2·Cos(х)·Sin(x). Когда применим формулу Sin(2·х), синуса двойного угла, получим окончательный упрощенный
ответ y’ = -Sin(2·х)

Гиперболические функции

Применяются при изучении многих технических дисциплин: в математике, например, облегчают вычисления интегралов, решение дифференциальных уравнений. Выражаются они через тригонометрические функции с мнимым аргументом, так, гиперболический косинус ch(х) = Cos(i·х), где i ― мнимая единица, гиперболический синус sh(x) = Sin(i·x). 

Производная гиперболического косинуса вычисляется достаточно просто.
Рассмотрим функцию у = (e^x+e^-x)/2, это и есть гиперболический косинус ch(х). Используем правило нахождения производной суммы двух выражений, правило выноса постоянного множителя (Const) за знак производной. Второе слагаемое 0,5·е^-х ― сложная функция (ее производная равна -0,5·е^-х), 0,5·е^х― первое слагаемое.            (ch(х)) ‘=((e^х+e^—x)/2)’ можно записать по другому: (0,5·e^х+0,5·е^—х)’ = 0,5·e^х-0,5·e^—х, потому что производная (e^—x)’ равна -1, умнноженная на  e^—x. Получилась разность, а это есть гиперболический синус sh(x).
Вывод: (ch(х))’ = sh(x).
Рассмитрим на примере, как вычислить производную функции у = ch(x³+1).
По правилу дифференцирования гиперболического косинуса со сложным аргументом у’ = sh(x³+1)·(x³+1)’, где (x³+1)’ = 3·x²+0.
Ответ: производная данной функции равна 3·х²·sh(х³+1).

Производные рассмотренных функций у = ch(х) и y = Cos(х) табличные

При решении примеров нет необходимости каждый раз дифференцировать их по предложенной схеме, достаточно использовать вывод.
Пример. Продифференцировать функцию у = Cos(x)+Cos²(-x)-Ch(5·х).
Легко вычислить (воспользуемся табличными данными), у’ = -Sin(x)+Sin(2·х)-5·Sh(5·х).

Математические и тригонометрические функции

Главная » Функции Excel »

28 Апрель 2011       Дмитрий       62939 просмотров

• ABS(ABS) — Находит модуль (абсолютную величину) числа.
• ACOS(ACOS) — Вычисляет арккосинус числа.
• ACOSH(ACOSH) — Вычисляет гиперболический арккосинус числа.
• ASIN(ASIN) — Вычисляет арксинус числа.
• ASINH(ASINH) — Вычисляет гиперболический арксинус числа.
• ATAN(ATAN) — Вычисляет арктангенс числа.
• ATAN2(ATAN2) — Вычисляет арктангенс для заданных координат x и y.
• ATANH(ATANH) — Вычисляет гиперболический арктангенс числа.
• ОКРВВЕРХ(CEILING) — Округляет число до ближайшего целого или до ближайшего кратного указанному значению.
• ЧИСЛКОМБ(COMBIN) — Находит количество комбинаций для заданного числа объектов.
• COS(COS) — Вычисляет косинус числа.
• COSH(COSH) — Вычисляет гиперболический косинус числа.
• ГРАДУСЫ(DEGREES) — Преобразует радианы в градусы.
• ЧЁТН(EVEN) — Округляет число до ближайшего четного целого.
• EXP(EXP) — Вычисляет число e, возведенное в указанную степень.
• ФАКТР(FACT) — Вычисляет факториал числа.
• ОКРВНИЗ(FLOOR) — Округляет число до ближайшего меньшего по модулю целого.
• НОД(GCD) — Находит наибольший общий делитель.
• ЦЕЛОЕ(INT) — Округляет число до ближайшего меньшего целого.
• НОК(LCM) — Находит наименьшее общее кратное.
• LN(LN) — Вычисляет натуральный логарифм числа.
• LOG(LOG) — Вычисляет логарифм числа по заданному основанию.
• LOG10(LOG10) — Вычисляет десятичный логарифм числа.
• МОПРЕД(MDETERM) — Вычисляет определитель матрицы, хранящейся в массиве.
• МОБР(MINVERSE) — Определяет обратную матрицу (матрица хранится в массиве).
• МУМНОЖ(MMULT) — Вычисляет произведение матриц, хранящихся в массивах.
• ОСТАТ(MOD) — Вычисляет остаток от деления.
• ОКРУГЛТ(MROUND) — Находит число, округленное с требуемой точностью.
• МУЛЬТИНОМ(MULTINOMIAL) — Вычисляет мультиномиальный коэффициент множества чисел.
• НЕЧЁТ(ODD) — Округляет число до ближайшего нечетного целого.
• ПИ(PI) — Вставляет число «пи».
• СТЕПЕНЬ(POWER) — Вычисляет результат возведения числа в степень.
• ПРОИЗВЕД(PRODUCT) — Вычисляет произведение аргументов.
• ЧАСТНОЕ(QUOTIENT) — Вычисляет целую часть частного при делении.
• РАДИАНЫ(RADIANS) — Преобразует градусы в радианы.
• СЛЧИС(RAND) — Выдает случайное число в интервале от 0 до 1.
• СЛУЧМЕЖДУ(RANDBETVEEN) — Выдает случайное число в заданном интервале.
• РИМСКОЕ(ROMAN) — Преобразует число в арабской записи к числу в римской как текст.
• ОКРУГЛ(ROUND) — Округляет число до указанного количества десятичных разрядов.
• ОКРУГЛВНИЗ(ROUNDDOWN) — Округляет число до ближайшего меньшего по модулю целого.
• ОКРУГЛВВЕРХ(ROUNDUP) — Округляет число до ближайшего по модулю большего целого.
• РЯД.СУММ(SERIESSUM) — Вычисляет сумму степенного ряда по заданной формуле.
• ЗНАК(SIGN) — Определяет знак числа.
• SIN(SIN) — Вычисляет синус заданного угла.
• SINH(SINH) — Вычисляет гиперболический синус числа.
• КОРЕНЬ(SQRT) — Вычисляет положительное значение квадратного корня.
• КОРЕНЬПИ(SQRTPI) — Вычисляет значение квадратного корня из числа «пи».
• ПРОМЕЖУТОЧНЫЕ.ИТОГИ(SUBTOTAL) — Вычисляет промежуточные итоги.
• СУММ(SUM) — Суммирует аргументы.
• СУММЕСЛИ(SUMIF) — Суммирует ячейки, удовлетворяющие заданному условию(читать подробнее).
• СУММЕСЛИМН(SUMIFS) — Суммирует ячейки, удовлетворяющие заданным критериям. Допускается указывать более одного условия(читать подробнее).
• СУММПРОИЗВ(SUMPRODUCT) — Вычисляет сумму произведений соответствующих элементов массивов(читать подробнее).
• СУММКВ(SUMSQ) — Вычисляет сумму квадратов аргументов.
• СУММРАЗНКВ(SUMX2MY2) — Вычисляет сумму разностей квадратов соответствующих значений в двух массивах.
• СУММСУММКВ(SUMX2PY2) — Вычисляет сумму сумм квадратов соответствующих элементов двух массивов.
• СУММКВРАЗН(SUMXMY2) — Вычисляет сумму квадратов разностей соответствующих значений в двух массивах.
• TAN(TAN) — Вычисляет тангенс числа.
• TANH(TANH) — Вычисляет гиперболический тангенс числа.
• ОТБР(TRUNC) — Отбрасывает дробную часть числа.

---

Статья помогла? Сделай твит, поделись ссылкой с друзьями!

© 2022 Excel для всех   Войти

геометрия — Геометрические значения гиперболических косинуса и синуса

Так же, как существуют тригонометрические формулы для соотношений между сторонами и углами плоского треугольника, существуют (не совсем) аналогичные формулы для соотношений между сторонами и углами сферического треугольник; аналогично для гиперболического треугольника. 2\, $$ в то время как соответствующая формула в сферической тригонометрии: $$ \cos c=\cos a\cos b\, $$ и здесь стороны измеряются как углы, стягивающие (окружности) дуги на поверхности.

Точно так же формула, связывающая три стороны гиперболического прямоугольного треугольника, имеет вид $$ \кош с=\кош а\кош б\, $$ но вы должны быть осторожны, измеряя свои длины в «натуральных» единицах, которые, признаюсь, я не знаю, как легко описать здесь.

Другой набор аналогичных формул: закон синусов для общих треугольников в плоской геометрии $$ \ frac a {\ sin A} = \ frac b {\ sin B} = \ frac c {\ sin C} \ , $$ и две аналогичные формулы: $$ \ frac {\ sin a} {\ sin A} = \ frac {\ sin b} {\ sin B} = \ frac {\ sin c} {\ sin C} \ quad, \ quad \frac{\sinh a}{\sin A}=\frac{\sinh b}{\sin B}=\frac{\sinh c}{\sin C}\,. $$ Вы можете искать сферо-тригонометрические формулы в любом количестве мест, а затем преобразовывать их в формулы гиперболических триггеров, заменяя обычные синус и косинус сторон соответствующими гиперболическими функциями.

РЕДАКТИРОВАТЬ : Меня попросили рассказать кое-что о «естественном» способе измерения расстояния в гиперболической плоскости. Я могу быть здесь только очень примитивным, пристрастным и неряшливым, может быть, кто-то другой согласится меня прикрыть. Конечно, правильнее было бы поговорить о роли кривизны в этой истории. Во всяком случае, посмотрите на сферический случай, где «естественным» способом измерения является использование сферы радиусом $1$, и в этом случае мера дуги в радианах совпадает с ее длиной. Нам нужно что-то подобное для гиперболической плоскости. Обратите внимание, что в этом случае площадь октанта (треугольника, в котором все углы равны $\pi/2$) составляет восьмую часть полной площади, то есть $\pi/2$. Теперь это стандартный результат, что площадь сферического треугольника пропорциональна «сферическому избытку», сумме всех трех углов минус $\pi$. Итак, на примере треугольника октанта вы видите, что здесь константа пропорциональности равна $1$.

Для гиперболической плоскости история аналогична, площадь треугольника пропорциональна «гиперболическому дефекту», а именно $\pi$ минус сумма углов. В частности, площадь треугольника, три вершины которого «уходят в бесконечность» с углами, равными нулю, должна быть равна $\pi$. Что ж, я собираюсь доказать, что в широко распространенной модели гиперболической плоскости, состоящей из верхней полуплоскости в $\mathbb C$, следующая метрика дает вам то, что вы хотите. Дело в том, что длина дуги определяется интегралом $\int_\gamma ds/y$. Можно проверить, что эта метрика инвариантна относительно действия группы голоморфных автоморфизмов плоскости, а именно $\text{PSL}(2,\mathbb R)$, реализуемой как группа всех дробно-линейных преобразований $z\ отображает на (az+b)/(cz+d)$, для которых коэффициенты действительны и $ad>

bc$. Конечно, любая константа, кратная этой метрике, также будет инвариантной, поэтому мне нужно убедить вас, что правильная константа — это всего лишь $1$. Для этого я возьму идеальный треугольник в UHP, две стороны которого являются вертикальными прямыми $x=\pm1$, а третья сторона которого является полуокружностью радиуса $1$ с центром в начале координат.

Обязательно нарисуйте картинку! Теперь я собираюсь найти площадь половины этого треугольника, части справа от оси $y$. 92}\, $$ а для этого вы отбрасываете всякую осторожность на ветер, отбрасываете свои заботы о неправильных интегралах и сразу же видите, что интеграл получается равным $\pi/2$, как и должно быть.

Я не обосновал ни одну из своих тригонометрических формул и не думаю, что смогу. Но это должно хотя бы частично убедить вас в том, что $ds/y$ — это то, что нужно интегрировать, чтобы получить «естественную» длину дуги в гиперболической плоскости.

тригонометрия — Можно ли гиперболические синус и косинус объединить в одну функцию сдвинутого аргумента?

Задавать вопрос

спросил

6 лет, 9 месяцев назад

Изменено 6 лет, 9 месяцев назад

Просмотрено 793 раза

$\begingroup$

Для тригонометрических функций у нас есть красивое тождество: 92x=1.

No related posts.