f x формула
Вы искали f x формула? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и все о производной, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «f x формула».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как f x формула,все о производной,все о производных,вычисления производных формулы,действия с производными,деление производных,значения производных,как найти производная функции,определение производная,первая производная,первая производная функции,правила взятия производной,правила взятия производных,правила вычисления производной,правила вычисления производных,правила нахождения производной,правила производная,правила производной,правила производной функции,правила производных,правила производных функций,правила функции производной,правило производной,правило производных,применение производных формулы,производная в точке,производная и функция,производная как обозначается,производная правила,производная разности формула,производная формула,производная функции,производная функции определение,производная функция,производная функция формулы,производная элементарных функций,производная это что,производное функции,производной,производной функции,производной функция,производную функции,производные и производные функции,производные формулы функции,производные функции,производные функций,производные это,производные это что,производных функции,теория производная,умножение производных,формула f x,формула производная,формула производной,формула производной функции,формулы вычисления производных,формулы нахождения производной,формулы производной функции,функции производной,функции производную,функции производных,функция и производная,функция производная,функция производной.
Решить задачу f x формула вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | -cos(x) | ||
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производные логарифмических функций | Brilliant Math & Science Wiki
Содержание
- Производная от lnx\ln {x}lnx
- Производное от logax\log_{a}xlogax
- Производная от lnf(x)\ln{f(x)}lnf(x)
ddxlnx=1x\frac{d}{dx} \ln {x} = \frac{1}{x}dxdlnx=x1
Теперь докажем это из первых принципов:
Из первых принципов ddxf (x) = limh → 0f (x + h) − f (x) h \ frac {d} {dx} f (x) = \ displaystyle \ lim_ {h \ rightarrow 0} {\ dfrac{f(x+h)-f(x)}{h}}dxdf(x)=h→0limhf(x+h)−f(x).
{\ гидроразрыва {х} {ч}}}} {х }} \\ & знак равно \lim_{h \rightarrow 0} {\dfrac{\ln{e}}{x}} \\ & = \dfrac{1}{x}.\ _\квадрат \end{align}dxdf(x)=h→0limhln(x+h)−lnx=h→0limxhxln(1+xh)=h→0limxln(1+ xh)hx=h→0limxlne=x1. □
Найдите производную lnx\ln {x}lnx при x=2x = 2x=2.
У нас есть
ддxlnx=1x. \dfrac{\text{d}}{\text{d}x} \ln {x} = \dfrac{1}{x}.dxdlnx=x1.
Отсюда
ддxlnx∣x=2=12. □ \dfrac{\text{d}}{\text{d}x} \ln x \Bigg |_{x=2}= \dfrac{1}{2}.\ _\squaredxdlnx∣∣∣∣ ∣x=2=21. □
Дифференцировать ln5x\ln 5xln5x
Решение 1: Используйте цепное правило.
Пусть f(x)=lnxf(x) = \ln xf(x)=lnx и g(x)=5xg(x) = 5xg(x)=5x. Затем нас просят найти (f∘g)′(f \circ g) ‘(f∘g)′.
Используя цепное правило, мы знаем, что (f∘g)′=(f′∘g)×g′.( f \circ g ) ‘ = ( f’ \circ g) \times g’ . (f∘g)′=(f′∘g)×g′.
Так как f′∘g=15xf’ \circ g = \frac{1}{5x}f′∘g=5×1 и g′(x)=5,g'(x) = 5,g′(x) =5, имеем (f∘g)′=15x×5=1x.
□( f \circ g ) ‘ = \frac{1}{5x} \times 5 = \frac{1}{x}.\ _\square(f∘g)′=5×1×5=x1. □
Решение 2: Используйте свойства логарифмов.
Мы знаем свойство логарифмов logab+logac=logabc\log_a b + \log_a c = \log_a bclogab+logac=logabc. Используя это свойство,
пер5x=lnx+ln5. \ln 5x = \ln x + \ln 5.ln5x=lnx+ln5.
Если мы продифференцируем обе стороны, мы увидим, что
ddxln5x=ddxlnx\dfrac{\text{d}}{\text{d}x} \ln 5x = \dfrac{\text{d}}{\text{d}x} \ln xdxd ln5x=dxdlnx
, поскольку дифференцирование константы ln5\ln 5ln5 равно 0,0,0.
Мы видели, что ddxlnx=1x\frac{\text{d}}{\text{d}x} \ln x = \frac{1}{x}dxdlnx=x1, и это ответ на этот вопрос. □_\квадрат□
Обобщение: Для любого положительного действительного числа ppp мы можем заключить, что ddxlnpx=1x\frac{\text{d}}{\text{d}x} \ln px = \frac{1}{x}dxdlnpx=x1 . Обратите внимание, что производная не зависит от ppp. Это можно доказать, написав ppp вместо 555 в приведенных выше решениях.
Если aaa — положительное действительное число и a≠1a \neq 1a=1, то
ddxlogax=1xlna.\dfrac{\text{d}}{\text{d}x}\log_{a} {x} = \dfrac{1}{x \ln {a}}.dxd logax=xlna1.
Мы будем использовать формулу изменения основания, чтобы изменить основание логарифма на e:e:e:
logax=lnxlnaddxlogax=ddxlnxlna.\log_{a}{x} = \dfrac{\ln{x}}{\ln{a}} \\ \dfrac{\ text{d}}{\text{d}x}\log_{a}x = \dfrac{\text{d}}{\text{d}x} \dfrac{\ln{x}}{\ln{ а}}. logax=lnalnxdxdlogax=dxdlnalnx.
Поскольку 1lna\frac{1}{\ln{a}}lna1 является константой,
ddxlnxlna=1lnaddxlnx=1xlna. □ \dfrac{\text{d}}{\text{d}x} \dfrac{\ln x}{\ln a} = \dfrac{1}{\ln a} \dfrac{\text{d}} {\text{d}x} \ln x = \dfrac{1}{x \ln{a}}.\ _\squaredxdlnalnx=lna1dxdlnx=xlna1. □
Оценить ddxlog10x\frac{{d}}{{d}x}\log_{10} {x}dxdlog10x при x=3x = 3 x=3.
Для любого другого типа логарифмической производной мы используем формулу изменения основания.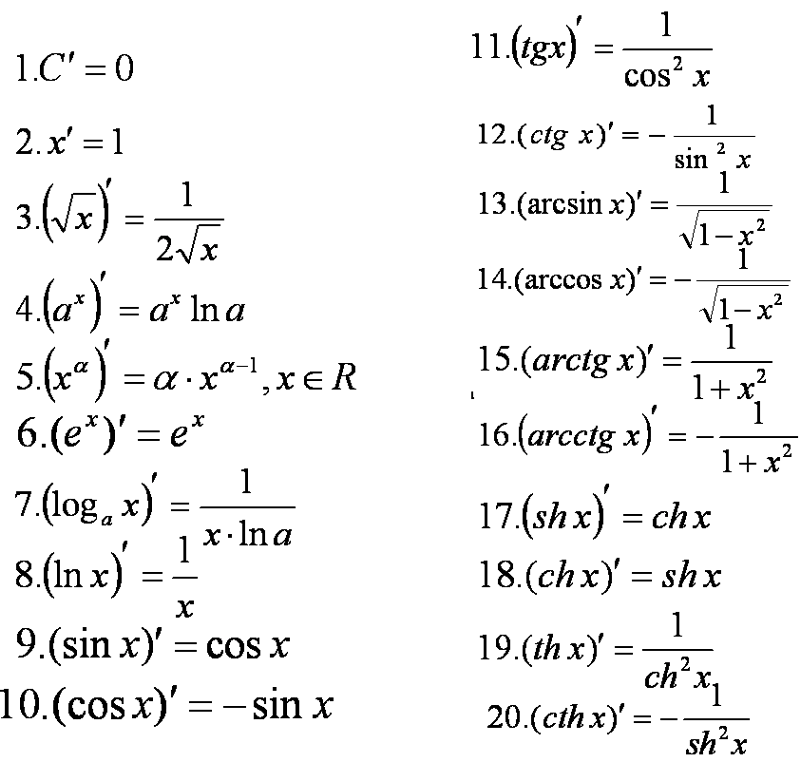


 □( f \circ g ) ‘ = \frac{1}{5x} \times 5 = \frac{1}{x}.\ _\square(f∘g)′=5×1×5=x1. □
□( f \circ g ) ‘ = \frac{1}{5x} \times 5 = \frac{1}{x}.\ _\square(f∘g)′=5×1×5=x1. □