Градиент функции калькулятор онлайн: Градиент функции онлайн

Производная по направлению, градиент функции: объяснение, примеры

• Понятие производной по направлению
• Примеры нахождения производной по направлению
• Градиент функции

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

1) функции одной переменной;

2) функции трёх переменных в нашем случае.

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x), соответствующее приращению аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения аргументов x, y, z отображаются на осях Оx, Оy, Оz. Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M), определённую в окрестности точки M с координатами x, y, z;

2) произвольный вектор

l с направляющими косинусами cosα, cosβ, cosγ.

Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l. На получившейся прямой отметим точку M1, координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:

Величину отрезка MM1 можно обозначить .

Функция u = f(M) при этом получит приращение

.

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M

) по направлению вектора l и обозначается , то есть

.

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

.

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Пример 1. Найти производную функции в точке M0(1; 2; 3) по направлению вектора .

Решение. Найдём частные производные функции в точке M0:

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Следовательно,

Теперь можем найти производную по направлению данной функции по её формуле:

Нет времени вникать в решение? Можно заказать работу!

А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Пример 2. Найти производную функции в точке M0(1; 2) по направлению вектора , где M1 — точка с координатами (3; 0).

Посмотреть правильное решение и ответ.

---

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции в точке

M0(1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M0:

Следовательно, можем найти производную по направлению данной функции по её формуле:

.

Градиент функции нескольких переменных в точке M0 характеризует направление максимального роста этой функции в точке M0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

.

То есть, должно получиться представление вектора по ортам координатных осей

, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

.

Пример 4. Найти градиент функции в точке M0(2; 4;).

Решение. Найдём частные производные функции в точке M0:

Следовательно, можем записать искомый градиент данной функции:

.

К началу страницы

Пройти тест по теме Функции нескольких переменных

Поделиться с друзьями

Производные

• Что такое производная
• Найти производную: алгоритм и примеры решений
• Производные произведения и частного функций
• Производная суммы дробей со степенями и корнями
• Производные простых тригонометрических функций
• Производная сложной функции
• Производная логарифмической функции
• Уравнение касательной и уравнение нормали к графику функции
• Дифференциал функции
• Дифференциал сложной функции, инвариантность формы дифференциала
• Правило Лопиталя

Функции нескольких переменных

• Функция двух и более переменных. Её область определения
• Поверхности второго порядка
• Частные производные
• Касательная плоскость и нормаль к поверхности
• Производная по направлению, градиент функции
• Экстремумы функции двух переменных
• Условные экстремумы и функция Лагранжа

ступенчатая, линейная, ReLu, Tahn, сигмоида

Что делает искусственный нейрон? Простыми словами, он считает взвешенную сумму на своих входах, добавляет смещение (bias) и решает, следует это значение исключать или использовать дальше (да, функция активации так и работает, но давайте пойдем по порядку).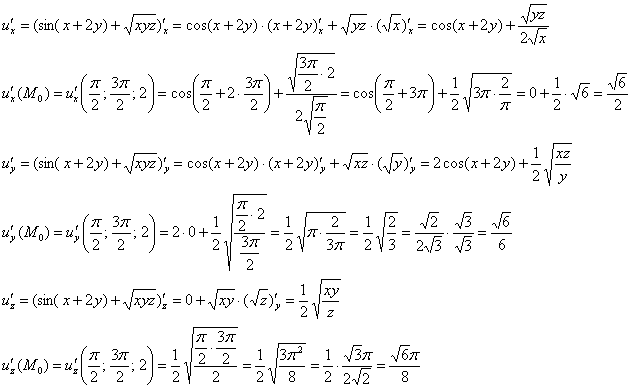  

Функция активации определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения.

---

Рассмотрим нейрон:

Теперь значение Y может быть любым в диапазоне от -бесконечности до +бесконечности. В действительности нейрон не знает границу, после которой следует активация. Ответим на вопрос, как мы решаем, должен ли нейрон быть активирован (мы рассматриваем паттерн активации, так как можем провести аналогию с биологией. Именно таким образом работает мозг, а мозг — хорошее свидетельство работы сложной и разумной системе).

Для этой цели решили добавлять активационную функцию. Она проверяет произведенное нейроном значение Y на предмет того, должны ли внешние связи рассматривать этот нейрон как активированный, или его можно игнорировать.

Ступенчатая функция активации

Первое, что приходит в голову, это вопрос о том, что считать границей активации для активационной функции. Если значение Y больше некоторого порогового значения, считаем нейрон активированным. В противном случае говорим, что нейрон неактивен. Такая схема должна сработать, но сначала давайте её формализуем.

• Функция А = активирована, если Y > граница, иначе нет.
• Другой способ:  A = 1, если Y > граница, иначе А = 0.

Функция, которую мы только что создали, называется ступенчатой. Такая функция представлена на рисунке ниже.

Функция принимает значение 1 (активирована), когда Y > 0 (граница), и значение 0 (не активирована) в противном случае.

Мы создали активационную функцию для нейрона. Это простой способ, однако в нём есть недостатки. Рассмотрим следующую ситуацию.

Представим, что мы создаем бинарный классификатор — модель, которая должна говорить “да” или “нет” (активирован или нет). Ступенчатая функция сделает это за вас — она в точности выводит 1 или 0.

Теперь представим случай, когда требуется большее количество нейронов для классификации многих классов: класс1, класс2, класс3 и так далее.

Что будет, если активированными окажутся больше чем 1 нейрон? Все нейроны из функции активации выведут 1. В таком случае появляются вопросы о том, какой класс должен в итоге получиться для заданного объекта.

Мы хотим, чтобы активировался только один нейрон, а функции активации других нейронов были равна нулю (только в этом случае можно быть уверенным, что сеть правильно определяет класс). Такую сеть труднее обучать и добиваться сходимости. Если активационная функция не бинарная, то возможны значения “активирован на 50%”, “активирован на 20%” и так далее. Если активированы несколько нейронов, можно найти нейрон с наибольшим значением активационной функции (лучше, конечно, чтобы это была softmax функция, а не max. Но пока не будем заниматься этими вопросами).

Но в таком случае, как и ранее, если более одного нейрона говорят “активирован на 100%”, проблема по прежнему остается. Так как существуют промежуточные значения на выходе нейрона, процесс обучения проходит более гладко и быстро, а вероятность появления нескольких полностью активированных нейронов во время тренировки снижается по сравнению со ступенчатой функцией активации (хотя это зависит от того, что вы обучаете и на каких данных).

Мы определились, что хотим получать промежуточные значения активационной функции (аналоговая функция), а не просто говорить “активирован” или нет (бинарная функция).

Первое, что приходит в голову — линейная функция.

Линейная функция активации

A = cx

Линейная функция представляет собой прямую линию и пропорциональна входу (то есть взвешенной сумме на этом нейроне).

Такой выбор активационной функции позволяет получать спектр значений, а не только бинарный ответ. Можно соединить несколько нейронов вместе и, если более одного нейрона активировано, решение принимается на основе применения операции max (или softmax). Но и здесь не без проблем.

Если вы знакомы с методом градиентного спуска для обучения, то можете заметить, что для этой функции производная равна постоянной.

Производная от A=cx по x равна с. Это означает, что градиент никак не связан с Х. Градиент является постоянным вектором, а спуск производится по постоянному градиенту. Если производится ошибочное предсказание, то изменения, сделанные обратным распространением ошибки, тоже постоянны и не зависят от изменения на входе delta(x).

Это не есть хорошо (не всегда, но в большинстве случаев). Но существует и другая проблема. Рассмотрим связанные слои. Каждый слой активируется линейной функцией. Значение с этой функции идет в следующий слой в качестве входа, второй слой считает взвешенную сумму на своих входах и, в свою очередь, включает нейроны в зависимости от другой линейной активационной функции.

Не имеет значения, сколько слоев мы имеем. Если все они по своей природе линейные, то финальная функция активации в последнем слое будет просто линейной функцией от входов на первом слое! Остановитесь на мгновение и обдумайте эту мысль.

Это означает, что два слоя (или N слоев) могут быть заменены одним слоем. Мы потеряли возможность делать наборы из слоев. Не важно, как мы стэкаем, вся нейронная сеть все равно будет подобна одному слою с линейной функцией активации (комбинация линейных функций линейным образом — другая линейная функция).

Сигмоида

Сигмоида выглядит гладкой и подобна ступенчатой функции. Рассмотрим её преимущества.

Во-первых, сигмоида — нелинейна по своей природе, а комбинация таких функций производит тоже нелинейную функцию. Теперь мы можем стэкать слои.

Еще одно достоинство такой функции — она не бинарна, что делает активацию аналоговой, в отличие от ступенчатой функции. Для сигмоиды также характерен гладкий градиент.

Если вы заметили, в диапазоне значений X от -2 до 2 значения Y меняется очень быстро. Это означает, что любое малое изменение значения X в этой области влечет существенное изменение значения Y. Такое поведение функции указывает на то, что Y имеет тенденцию прижиматься к одному из краев кривой.

Сигмоида действительно выглядит подходящей функцией для задач классификации. Она стремиться привести значения к одной из сторон кривой (например, к верхнему при х=2 и нижнему при х=-2). Такое поведение позволяет находить четкие границы при предсказании.

Другое преимущество сигмоиды над линейной функцией заключается в следующем. В первом случае имеем фиксированный диапазон значений функции — [0,1], тогда как линейная функция изменяется в пределах (-inf, inf). Такое свойство сигмоиды очень полезно, так как не приводит к ошибкам в случае больших значений активации.

Сегодня сигмоида является одной из самых частых активационных функций в нейросетях. Но и у неё есть недостатки, на которые стоит обратить внимание.

Вы уже могли заметить, что при приближении к концам сигмоиды значения Y имеют тенденцию слабо реагировать на изменения в X. Это означает, что градиент в таких областях принимает маленькие значения. А это, в свою очередь, приводит к проблемам с градиентом исчезновения. Рассмотрим подробно, что происходит при приближении активационной функции к почти горизонтальной части кривой на обеих сторонах.

В таком случае значение градиента мало или исчезает (не может сделать существенного изменения из-за чрезвычайно малого значения). Нейросеть отказывается обучаться дальше или делает это крайне медленно (в зависимости от способа использования или до тех пор, пока градиент/вычисление не начнет страдать от ограничений на значение с плавающей точкой). Существуют варианты работы над этими проблемами, а сигмоида всё ещё очень популярна для задач классификации.

Гиперболический тангенс

Еще одна часто используемая активационная функция — гиперболический тангенс.

Гиперболический тангенс очень похож на сигмоиду. И действительно, это скорректированная сигмоидная функция.

Поэтому такая функция имеет те же характеристики, что и у сигмоиды, рассмотренной ранее. Её природа нелинейна, она хорошо подходит для комбинации слоёв, а диапазон значений функции -(-1, 1). Поэтому нет смысла беспокоиться, что активационная функция перегрузится от больших значений. Однако стоит отметить, что градиент тангенциальной функции больше, чем у сигмоиды (производная круче). Решение о том, выбрать ли сигмоиду или тангенс, зависит от ваших требований к амплитуде градиента. Также как и сигмоиде, гиперболическому тангенсу свойственная проблема исчезновения градиента.

Тангенс также является очень популярной и используемой активационной функцией.

ReLu

Следующая в нашем списке — активационная функция ReLu,

A(x) = max(0,x)

Пользуясь определением, становится понятно, что ReLu возвращает значение х, если х положительно, и 0 в противном случае. Схема работы приведена ниже.

На первый взгляд кажется, что ReLu имеет все те же проблемы, что и линейная функция, так как ReLu линейна в первом квадранте. Но на самом деле, ReLu нелинейна по своей природе, а комбинация ReLu также нелинейна! (На самом деле, такая функция является хорошим аппроксиматором, так как любая функция может быть аппроксимирована комбинацией ReLu). Это означает, что мы можем стэкать слои. Область допустимых значений ReLu — [0,inf), то есть активация может “взорваться”.

Следующий пункт — разреженность активации. Представим большую нейронную сеть с множеством нейронов. Использование сигмоиды или гиперболического тангенса будет влечь за собой активацию всех нейронов аналоговым способом. Это означает, что почти все активации должны быть обработаны для описания выхода сети. Другими словами, активация плотная, а это затратно. В идеале мы хотим, чтобы некоторые нейроны не были активированы, это сделало бы активации разреженными и эффективными.

ReLu позволяет это сделать. Представим сеть со случайно инициализированными весами (или нормализированными), в которой примерно 50% активаций равны 0 из-за характеристик ReLu (возвращает 0 для отрицательных значений х). В такой сети включается меньшее количество нейронов (разреженная активация), а сама сеть становится легче. Отлично, кажется, что ReLu подходит нам по всем параметрам. Но ничто не безупречно, в том числе и ReLu.

Из-за того, что часть ReLu представляет из себя горизонтальную линию (для отрицательных значений X), градиент на этой части равен 0. Из-за равенства нулю градиента, веса не будут корректироваться во время спуска. Это означает, что пребывающие в таком состоянии нейроны не будут реагировать на изменения в ошибке/входных данных (просто потому, что градиент равен нулю, ничего не будет меняться). Такое явление называется проблемой умирающего ReLu (Dying ReLu problem). Из-за этой проблемы некоторые нейроны просто выключатся и не будут отвечать, делая значительную часть нейросети пассивной. Однако существуют вариации ReLu, которые помогают эту проблему избежать. Например, имеет смысл заменить горизонтальную часть функции на линейную. Если выражение для линейной функции задается выражением y = 0.01x для области x < 0, линия слегка отклоняется от горизонтального положения. Существует и другие способы избежать нулевого градиента. Основная идея здесь — сделать градиент неравным нулю и постепенно восстанавливать его во время тренировки.

ReLu менее требовательно к вычислительным ресурсам, чем гиперболический тангенс или сигмоида, так как производит более простые математические операции.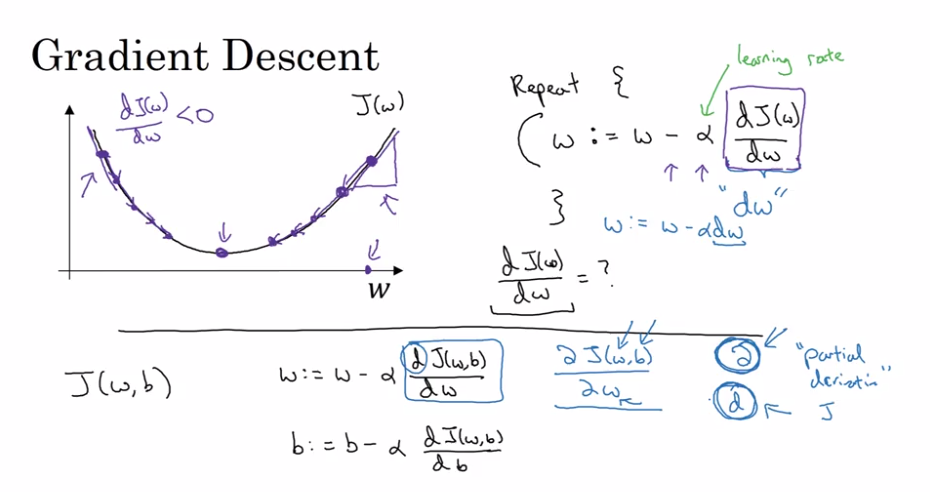 Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей.

Как выбрать функцию активации?

Настало время решить, какую из функций активации использовать. Следует ли для каждого случая использовать ReLu? Или сигмоиду? Или tanh? На эти вопросы нельзя дать однозначного ответа. Когда вы знаете некоторые характеристики функции, которую пытаетесь аппроксимировать, выбирайте активационную функцию, которая аппроксимирует искомую функцию лучше и ведет к более быстрому обучению.

Например, сигмоида хорошо показывает себя в задачах классификации (посмотрите еще раз на пункт про сигмоиду. Не присущи ли ей свойства идеального классификатора?), так как аппроксимацию классифицирующей функции комбинацией сигмоид можно провести легче, чем используя ReLu, например.

Используйте функцию, с которой процесс обучения и сходимость будут быстрее. Более того, вы можете использовать собственную кастомную функцию! Если вы не знаете природу исследуемой функции, в таком случае начните с ReLu и потом работайте в обратном направлении. В большинстве случаев ReLu работает как хороший аппроксиматор.

Циферблаты Apple Watch и их функции

На Apple Watch доступно множество циферблатов, многие из которых Вы можете настраивать. Подробнее см. в разделе Настройка циферблата.

Проверяйте обновления ПО; набор циферблатов, доступный в следующих обновлениях, может отличаться от того, что отображается на Ваших Apple Watch. Некоторые циферблаты доступны не во всех регионах и не на всех моделях. Чтобы посмотреть новейший набор циферблатов, убедитесь, что программное обеспечение обновлено.

Активность (аналог.)

На этом циферблате отображается Ваша активность, наложенная на традиционный аналоговый циферблат. Вы можете отобразить кольца Активности в обычном вложенном формате или в виде отдельных шкал.

• Настраиваемые функции: Стиль («Кольца», «Субшкалы») • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Активность (цифр.

)

Этот циферблат с крупными равномерными шрифтами показывает время в цифровом формате, а также Вашу активность.

• Настраиваемые функции: Время в секундах • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Творчество

Этот оригинально оформленный циферблат меняется при каждом касании дисплея. Алгоритмы в основе циферблата обеспечивают миллионы возможных комбинаций.

Астрономия

Этот циферблат показывает постоянно обновляющуюся 3D-модель Земли, Луны или Солнечной системы.

• Настраиваемые функции: Вид (Земля, Луна, Солнечная система, Случайный выбор) • Стиль (Полный, Случайный выбор) • Шрифт

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота, Уровень) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Секундомер • Сообщения • Таймер • Тренировка • Шум • Элементы управления (Аккумулятор)

Совет. Если добавить расширение «Луна» в угол циферблата, который его включает, Вы сможете видеть время следующего восхода или захода луны. Например, 23:44, 12 ч 4 мин означает, что в Вашей геопозиции луна зайдет за горизонт в 23:44 и это произойдет через 12 часов 4 минуты.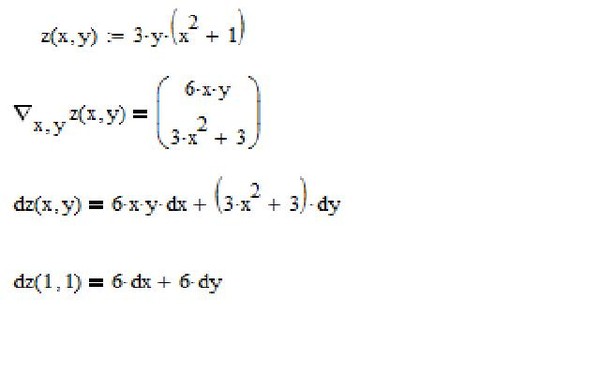

Дыхание

Этот циферблат напоминает, что нужно расслабиться и сосредоточиться на дыхании. Просто коснитесь экрана, чтобы начать упражнение.

• Настраиваемые функции: Стиль (Классика, Покой, Фокус)

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Калифорния

Этот циферблат отображает сочетание римских и арабских цифр.

• Настраиваемые функции: Деления («Полный экран», «Круг») • Цвет • Цифры («Пилюли», «Римские», «Калифорния», «Арабские», «Индо-арабские», «Деванагари»)

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Фаза Луны, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Монограмма • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Хронограф

Этот циферблат показывает время с невероятной точностью, как классический аналоговый секундомер. Прямо с этого циферблата можно запустить секундомер.

• Настраиваемые функции: Цвет • Шкала времени

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Хронограф Pro

Коснитесь ободка основного 12-часового циферблата — и он преобразуется в хронограф. Фиксируйте время на шкалах на 60, 30, 6 или 3 секунды. Или выберите шкалу тахиметра, чтобы измерять скорость по времени в пути на заданное расстояние.

• Настраиваемые функции: Цвет • Шкала времени

• Доступные расширения: Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Цвет

На этом циферблате показано время и выбранные Вами функции в яркой цветовой гамме на Ваш вкус.

• Настраиваемые функции: Цвет • Стиль (Круг или Деления. Есть полноэкранный вариант) • Монограмма

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Контур (только на Apple Watch Series 7 и Apple Watch Series 8)

Этот циферблат постепенно меняется, выделяя текущий час. Шрифт для этого циферблата разработан таким образом, чтобы цифры умещались на гранях дисплея и плавно перетекали от часа к часу.

• Настраиваемые функции: Стиль (стандартный, округлый) • Цвет • Цвет делений

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Монограмма • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Дайвер

Этот циферблат можно использовать для отслеживания истекшего времени.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Монограмма • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Чтобы начать отсчет, коснитесь основного 12‑часового циферблата для совмещения маркера на внешнем ободке с минутной стрелкой, поверните колесико Digital Crown для настройки длительности, затем коснитесь «Старт». Чтобы вернуться к циферблату в стандартном состоянии, коснитесь красной кнопки истекшего времени.

Искатель

На циферблате «Искатель» (доступен только на моделях Apple Watch с поддержкой сотовой связи) есть зеленые точки, показывающие мощность сигнала сотовой сети.

• Настраиваемые функции: Стиль • Цвет стрелок

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Монограмма • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Вода и пламя

Анимация включается каждый раз, когда Вы поднимаете запястье или касаетесь дисплея.

• Настраиваемые функции: Цвет («Огонь», «Вода», «Вода и пламя») • Стиль (Есть полноэкранный вариант)

• Доступные расширения (только для стиля «Круг»): Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

GMT

Внутренний 12-часовой циферблат показывает местное время, а внешний 24-часовой циферблат — время в другом часовом поясе.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Чтобы установить второй часовой пояс, коснитесь циферблата, затем поворотом колесика Digital Crown выберите часовой пояс. Коснитесь , чтобы подтвердить выбор и вернуться к циферблату. Красная стрелка показывает час во втором часовом поясе.

Градиент

Этот циферблат отображает градиенты, которые движутся с течением времени.

• Настраиваемые функции: Деления («Полный экран», «Круг») • Стиль • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Луна, Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Инфограф

Этот циферблат отображает до восьми полноцветных расширений и шкал.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Цифровое время) • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Монограмма • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Калейдоскоп

Выберите снимок, чтобы создать циферблат с меняющимся узором из разноцветных фигур. Прокрутите колесико Digital Crown, чтобы изменить узор.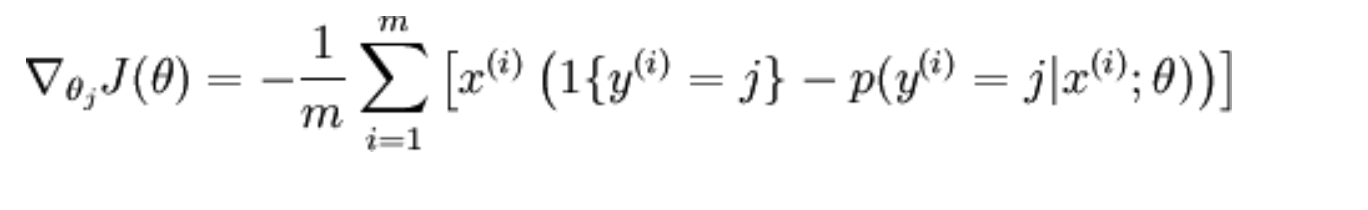

• Настраиваемые функции: Изображение • Стиль (есть полноэкранный вариант)

• Доступные расширения (Стили «Грани», «Радиус» и «Розетта») Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Время (Цифровое время) • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Жидкий металл

Анимация включается каждый раз, когда Вы поднимаете запястье или касаетесь дисплея.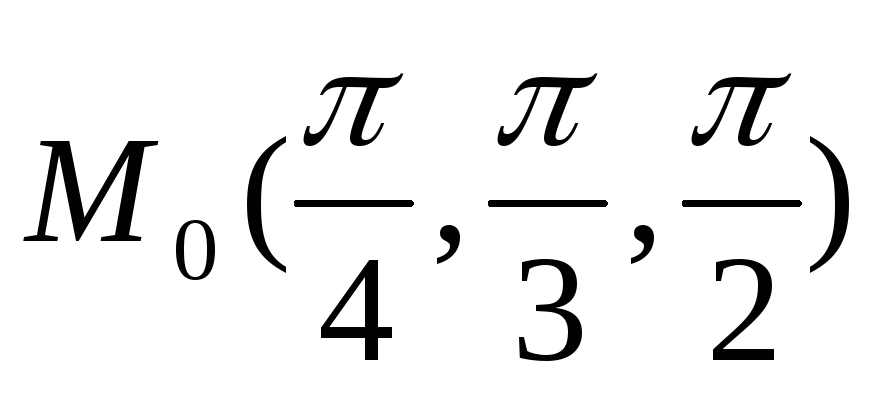

• Настраиваемые функции: Цвет • Стиль (есть полноэкранный вариант)

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Луна

На этом циферблате наглядно представлено соотношение даты и времени с фазами Луны.

• Настраиваемые функции: Время (Аналоговое, Цифровое) • Календарь (Китайский, Еврейский, Исламский) • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Memoji

Этот циферблат содержит персонажи Memoji, которые создали Вы, а также все доступные персонажи Memoji.

• Настраиваемые функции: Персонаж

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота, Уровень) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Путевые точки на компасе • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Меридиан

Этот полноэкранный циферблат имеет классическое оформление с четырьмя шкалами.

• Настраиваемые функции: Деления («Черный», «Белый») • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Монограмма • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Мегаполис

Это классически оформленный циферблат с акцентом на шрифте. Цифры с настраиваемым дизайном динамически меняют свой стиль и форму с каждым поворотом колесика Digital Crown. Если опустить запястье, цифры, развернувшись, превращаются в черточки.

• Настраиваемые функции: Деления • Стиль • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Микки Маус и Минни Маус

Веселые персонажи Микки Маус и Минни Маус показывают Вам время: их руки поворачиваются, чтобы показывать часы и минуты, а ноги отсчитывают каждую секунду.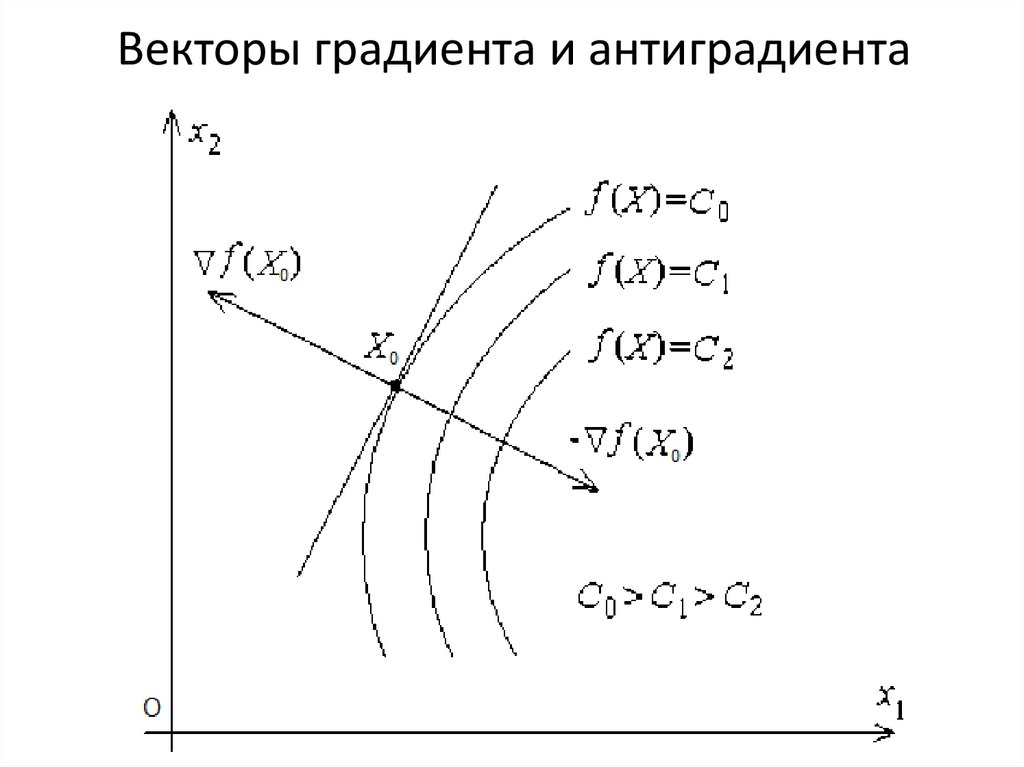

• Настраиваемые функции: Персонаж • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Чтобы персонажи Микки Маус или Минни Маус сообщали время голосом на Apple Watch, откройте приложение «Настройки»  на Apple Watch, коснитесь «Часы» и включите параметр «Время вслух». Поднимите запястье и затем положите два пальца на циферблат, чтобы услышать время.

Модульный

Этот циферблат предлагает шесть слотов расширений с предельно ясным типографическим интерфейсом.

• Настраиваемые функции: Фон • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Модули (компактный)

Этот циферблат позволяет выбрать до трех расширений, а также цифровой или аналоговый стиль.

• Настраиваемые функции: Деления («Аналоговый», «Цифровой») • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Модули (двойной) (только на Apple Watch Series 7 и Apple Watch Series 8)

На этом циферблате отображаются время в цифровом формате и до трех расширений. Два из них — прямоугольные элементы, крупный размер которых позволяет показывать важную для Вас информацию более подробно.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Движение

На этом циферблате отображаются красивые анимированные темы.

• Настраиваемые функции: Анимированный объект (Бабочки, Цветы, Медуза)

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Nike (аналоговый)

Этот циферблат в аналоговом стиле, разработанный совместно с компанией Nike, показывает время крупными цифрами.

• Настраиваемые функции: Стиль • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Приложение Nike Run Club • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Nike (на пружинах)

Этот циферблат движется вместе с Вами. Цифры реагируют на каждый шаг, прыжок или движение запястья. Вы также можете коснуться дисплея или повернуть колесико Digital Crown, чтобы привести объекты в движение.

Nike (компактный)

Созданный на основе циферблата «Модули (компактный)», этот циферблат обладает настраиваемой шкалой с тремя вариантами дизайна на выбор. К каждому из них можно добавить до трех расширений.

• Настраиваемые функции: Стиль • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Приложение Nike Run Club • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Nike (цифровой)

Разработанный совместно с Nike, этот циферблат выполнен в стиле цифровых часов. Центральное место на нем занимают отображение времени и постоянное расширение для запуска приложения Nike Run Club.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Приложение Nike Run Club • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Nike (гибридный)

На этом циферблате сочетаются элементы аналогового и цифрового стилей, а также вдохновленное стилистикой Windrunner оформление. Для циферблата доступны персональная настройка и возможность добавить до пяти расширений.

• Настраиваемые функции: Время • Деления • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Луна, Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Время (Секунды (аналоговое), Время (аналоговое), Секунды (цифровое), Цифровое время) • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Приложение Nike Run Club • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Цифры

Этот циферблат показывает время аналоговыми стрелками на фоне крупного маркера часа. Вы можете выбирать любые из 7 различных шрифтов и многочисленных цветов, чтобы создать идеальное сочетание.

• Настраиваемые функции: Символы • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Кислород в крови • Компас (Компас, Высота, Уровень) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Путевые точки на компасе • Секундомер • Советы • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Двухцифровой

Циферблат с крупными цифрами, для показа которых используется шрифт Apple, созданный специально для Apple Watch.

• Настраиваемые функции: Символы («Арабские», «Индо-арабские», «Деванагари») • Стиль («С заливкой», «Гибрид», «Контурный») • Цвета

Одноцифровой

Циферблат с крупными цифрами, для показа которых используется шрифт Apple, созданный специально для Apple Watch.

• Настраиваемые функции: Символы («Арабские», «Индо-арабские», «Деванагари», «Римские») • Стиль («С заливкой», «Контурный») • Цвет

Фото

Этот циферблат отображает новое фото каждый раз, когда Вы поднимаете запястье или касаетесь дисплея. Выберите альбом, воспоминание или до 24 произвольных фотографий.

• Настраиваемые функции: Контент («Синхрон. альбом», «Фото», «Динамическая») • Положение времени • Фильтры

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Создание циферблата «Фото» на Apple Watch. Когда отображается текущий циферблат, коснитесь и удерживайте дисплей, смахните вправо до конца, коснитесь кнопки «Новый» (+), затем коснитесь «Фото». Или при просмотре фотографий в приложении «Фото» на Apple Watch коснитесь , прокрутите к нижней части экрана, затем коснитесь «Создать циферблат».

Создание циферблата «Фото» на iPhone. Откройте приложение «Фото» на iPhone, коснитесь снимка, коснитесь кнопки , смахните вверх, затем коснитесь «Создать циферблат». Выберите, какой циферблат создать — «Портреты», «Фото» или «Калейдоскоп».

Добавление фильтра. На Apple Watch коснитесь и удерживайте циферблат «Фото», коснитесь «Изменить», затем поворотом колесика Digital Crown выберите фильтр. Чтобы выбрать из более широкого списка цветов, прокрутите до конца списка, коснитесь элемента «Коснитесь, чтобы добавить еще цвета», выберите цвет, затем коснитесь «Готово».

На iPhone откройте приложение Apple Watch, перейдите в раздел «Циферблаты» > «Фото», затем выберите фильтр. Коснитесь , чтобы выбрать из более широкого списка цветов.

Если Вы не видите фотографий, убедитесь, что они есть в синхронизируемом альбоме. Подробнее см. в разделе Выбор фотоальбома и управление коллекцией на Apple Watch.

Время играть

Этот циферблат — динамическое произведение искусства, доступное только на Apple Watch. Фон меняется при повороте колесика Digital Crown, а персонажи реагируют на касания циферблата.

Портреты

Циферблат «Портреты» использует фотографии из медиатеки на iPhone. К фотографиям людей, собак, котов и ландшафтов применяются эффекты наложения. Можно выбрать один из трех стилей и добавить до 24 фотографий. Новое фото появляется каждый раз, когда Вы поднимаете запястье или касаетесь дисплея.

• Настраиваемые функции: Стиль (Фон, Два цвета) • Цвет • Шрифт

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Совет. Прокрутите колесико Digital Crown, чтобы увеличить фотографию.

Простой

Лаконичный и элегантный циферблат. Рядом с его делениями можно добавлять дополнительные элементы, а в углы — функции.

• Настраиваемые функции: Стиль (I, II, III) • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Siri

Этот циферблат показывает актуальную и полезную информацию. Это могут быть ближайшие встречи, пробки по дороге домой или время заката солнца. Можно коснуться экрана и посмотреть подробную информацию. Можно также прокрутить колесико Digital Crown, чтобы пролистать события дня.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Siri • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Солнечный (деления)

Этот циферблат имеет круговую 24-часовую шкалу, которая показывает положение солнца, а также аналоговую или цифровую шкалу, которая двигается напротив солнца.

Совет. Коснитесь циферблата, чтобы увидеть длину светового дня.

• Настраиваемые функции: Деления («Аналоговый», «Цифровой»)

• Доступные расширения: Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Солнце (графический)

На основе Вашей геопозиции и времени суток циферблат «Солнце (графический)» показывает положение солнца на небе, а также день, дату и время в данный момент.

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Пульт Камеры • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Полосы

На этом циферблате Вы можете выбирать количество полос и их цвета, а также менять их угол.

• Настраиваемые функции: Количество полос • Стиль • Цвета полос

• Доступные расширения (расширения доступны только для стиля «Круг»): Активность • Акции • Астрономия (Луна) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Таймлапс

На этом циферблате отображается замедленное видео природы или города, которое Вы выберете.

• Настраиваемые функции: Место (Лейк-Мак, Нью-Йорк, Гонконг, Лондон, Париж, Шанхай)

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

История игрушек

Любимые персонажи Истории игрушек оживут на Вашем запястье.

• Настраиваемые функции: Персонаж (Ящик с игрушками, Базз, Вуди, Джесси)

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Типографика

Этот циферблат предлагает три настраиваемых шрифта.

Единство

Дизайн этого циферблата вдохновлен цветами панафриканского флага. Фигуры меняются по мере Вашего движения, создавая уникальный, присущий только Вам стиль циферблата.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза луны) • Аудиокниги • Будильники • Быстрые команды • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Компас (Компас, Компас/Высота, Высота) • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Напоминания • Новости • Погода • Подкасты • Пульс • Секундомер • Сообщения • Таймер • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор)

Огни единства

Дизайн этого циферблата вдохновлен афрофутуризмом — философией, исследующей опыт африканской диаспоры через призму науки, технологий и самовыражения.

• Настраиваемые функции: Стиль (Прямоугольник, Круг) • Цвет • Шкалы

• Доступные расширения (расширения доступны только для стиля «Круг»): Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Служебный

Это удобный и информативный циферблат; добавьте на дисплей до трех расширений, которые нужно отображать всегда.

• Настраиваемые функции: Гарнитура шрифта • Стиль • Цвет

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Пар

Анимация включается каждый раз, когда Вы поднимаете запястье или касаетесь дисплея.

• Настраиваемые функции: Цвет • Стиль (есть полноэкранный вариант)

• Доступные расширения (только для стиля «Круг»): Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Исполняется • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Компас/Высота, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Вокруг света

На этом циферблате можно отслеживать время в 24 часовых поясах одновременно.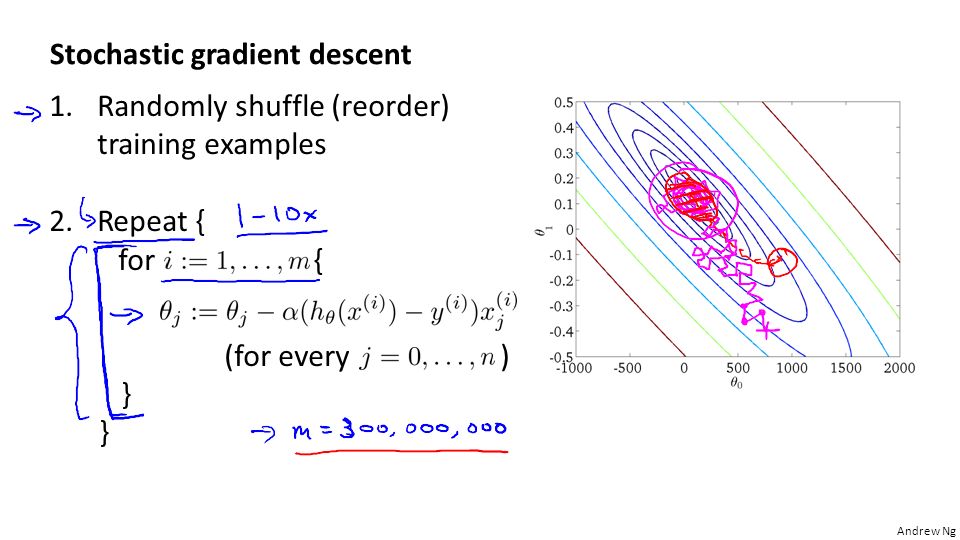 На внешней шкале показаны локации в разных часовых поясах, а на внутренней шкале — текущее время для каждой локации. Коснитесь глобуса, чтобы отобразить в центре текущий часовой пояс, который также обозначен стрелкой, указывающей на 6 часов.

Значки солнца и луны показывают время рассвета и заката там, где Вы находитесь, а светлая и темная зоны глобуса показывают движение ночи и дня по планете.

• Настраиваемые функции: Аналоговое или цифровое время

• Доступные расширения: Активность • Акции • Астрономия (Фаза Луны) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Лекарства • Мировые часы (Рассвет/Закат) • Музыка • Найти вещи • Найти людей • Найти устройства • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

X-Large

Для тех случаев, когда Вам нужен самый большой дисплей. Когда Вы добавляете расширение, оно заполняет весь экран.

• Настраиваемые функции: Цвет

• Доступные расширения: Активность • Акции • Астрономия (Земля, Луна, Солнце, Солнечная система) • Аудиокниги • Будильники • Быстрые команды • Диктофон • Дневник цикла • Дом • Календарь (Сегодняшняя дата, Ваше расписание) • Калькулятор • Карты (Карты, Общественный транспорт рядом) • Кислород в крови • Компас (Компас, Высота, Уровень) • Контакты • Мировые часы (Рассвет/Закат) • Музыка • Найти (Найти людей) • Напоминания • Новости • Осознанность • Погода • Подкасты • Почта • Пульс • Пульт • Пульт Камеры • Путевые точки на компасе • Рация • Секундомер • Советы • Сон • Сообщения • Таймер • Телефон • Тренировка • Шум (Уровни звука) • Элементы управления (Аккумулятор, Сотовые данные) • ЭКГ

Калькулятор стоимости анализов в медицинском центре «СМ-Клиника»

Общеклинические исследования крови

Группа крови

Группа крови и резус — принадлежность (Blood group, ABO и Rh-factor, Rh)

Общий анализ крови + СОЭ без лейкоцитарной формулы

Резус-фактор

Биохимические исследования крови

Железо

Калий

Кальций

Кальций, натрий, калий

Магний

Натрий

Определение 25-гидроксивитамина Д-25(ОН)Д

Аланин-аминотрансфераза — АЛТ

Альбумин

Аспартат-аминотрансфераза — АСТ

Билирубин непрямой

Билирубин общий

Билирубин прямой

Гамма-глутамилтрансфераза — ГГТ

Гликозилированный гемоглобин

Глюкоза

Креатинин

Липопротеины высокой плотности-ЛПВП

Липопротеины низкой плотности-ЛПНП

Мочевая кислота

Мочевина

Общий белок

С-реактивный белок(ультрачувствительный)-СРБу

С-реактивный белок-СРБ

Биохимический анализ крови (скрининг 9 показателей)

Биохимический анализ крови (расширенный 16 показателей)

Триглицериды

Ферритин

Холестерин общий

Щелочная фосфатаза

Гормональные исследования

Тестостерон

Антитела к тиреопероксидазе (Thyroid peroxidase autoantibodies) АТ-ТПО

Xорионический гонадотропин человека — в — ХГЧ кол.

Тиреотропный гормон (Thyroid Stimulating Hormone) — ТТГ

Трийодтиронин свободный — Т3 свободный

Лютеинизирующий гормон — ЛГ

Прогестерон

Пролактин

Фолликулостимулирующий гормон — ФСГ

Эстрадиол -E2

Коагулологические исследования (Гемостаз)

Международное нормализованное отношение — МНО

Протромбин (Prothrombin)

Протромбиновое время

Тромбиновое время (Thrombin Time)

Фибриноген (Fibrinogen)

D-димер(D-dimer)

Активированное частичное тромбопластиновое время (Activated Partial Thromboplastin Time) — АЧТВ

Комплексная оценка системы гемостаза: протромбиновое время, МНО, фибриноген, АЧТВ, тромбиновое время

Вирусные инфекции

Гепатит В, антиген поверхностный (HbsAg), кровь колич.

Гепатит С, суммарные антител (Anti — HCV), кровь кач.

Антитела к ВИЧ (HIV) 1 и 2 типов + антиген

Сифилис, RPR (антикардиолипиновый тест, нетрепонемный), кровь, кач.

Сифилис, антитела класса IgG, IgM cуммарные

Исследования мочи

Посев на микрофлору с использованием автоматических методов без чувствительности (моча)

Посев на микрофлору с использованием автоматических методов и чувствительность к бактериофагам (моча)

Посев на микрофлору с использованием автоматических методов и чувствительность к основному спектру антибиотиков (моча)

Посев на микрофлору с использованием автоматических методов и чувствительность к основному спектру антибиотиков и бактериофагов (моча)

Анализ мочи по Нечипоренко

Посев на микрофлору с использованием автоматических методов и чувствительность к расширенному спектру антибиотиков (моча)

Посев на микрофлору с использованием автоматических методов и чувствительность к расширенному спектру антибиотиков и бактериофагов (моча)

Общий анализ мочи

Исследования кала

Анализ на яйца гельминтов

Исследование соскоба на энтеробиоз

Общий анализ кала — копрограмма

Проверить, является ли векторное поле F соленоидальным и потенциальным

Задачи по исследованию векторного поля, что включают нахождение циркуляции, потока рассмотрены на предыдущих уроках. Здесь мы покажем, как быстро проверить, а если и нужно то и доказать, что поле является потенциальным и соленоидальным. Условия за которых это выполняется детально расписанны в объяснениях к вычислениям.
Детальный анализ каждого из примеров позволяет самостоятельно освоить данную тему каждому студенту.

ЗАДАНИЕ 10.4 Проверить, является ли векторное поле F=(5x+4yz) *i+(5y+4xz)*j+(5z+4xy)*k
потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Для того, чтобы заданое поле было потенциальным, необходимо и достаточно, чтобы ротор векторного поля был равен нулю rot(F)=0.
За условием выписываем функции, которые необходимы для дальнейших расчетов
P=P(x;y;z)=5x+4yz, Q=Q(x;y;z)=5y+4zx, R=R(x;y;z)=5z+4xy.
Отсюда ротор векторного поля через частичные производные находим по формуле
Из вычислений видим что векторное поле является потенциальным.
Найдем потенциал u=u(x;y;z) заданного векторного поля .
Согласно теории, векторное поле равно градиенту потенциала:
Выпишем компоненты градиента из начального условия F= (5x+4yz) *i+ (5y+4xz) *j+ (5z+4xy) *k
 потенциальным и соленоидным. Если полетпотенциальное, то найти его потенциал.
Решение: Для того, чтобы задано поле было потенциальным, необходимо и достаточно, чтобы ротор векторного поля был равен нулю rot (F) =0.
За условием выписываем функции, которые необходимы для дальнейших расчетов
P=P (x;y;z) =5x+4yz, Q=Q (x;y;z) =5y+4zx, R=R (x;y;z) =5z+4xy.
Отсюда ротор векторного поля через частичные производные находим за формулой
Из вычислений видим, что векторное поле является потенциальным.
Найдем потенциал u=u (x;y;z) заданного векторного поля .
Согласно теории векторное поле равно градиенту потенциала :
Выпишем компоненты градиенту из начального условия F=(5x+4yz)*i+(5y+4xz)*j+(5z+4xy)*k

Дальше интегрированием возобновляем потенциал, сначала интегрируем производную по x, потом найденный потенциал дифференцируем по y и приравниваем ко 2 частичной производной, и так далее
Здесь не ставили знак интегрирования, поскольку имеем дело с простыми табличными интегралами, а такая запись экономит время, храня при этом суть операций.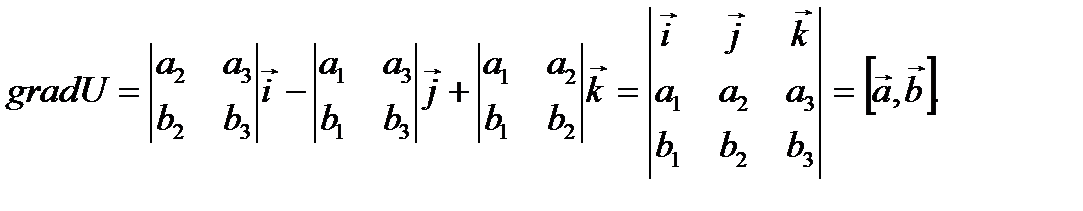
Окончательно записываем потенциал u векторного поля :
u(x;y;z)=2,5(x²+y²+z²)+4xyz+C, где C — произвольная константа.
Чтобы векторное поле было соленоидным, необходимо и достаточно, чтобы его дивергенция была равна нулю
Проверяем это условие:
Она не выполняется, следовательно рассмотреное векторное поле не является соленоидным.

 

ЗАДАНИЕ 10.5 Проверить будет ли векторное поле F=(x+2yz) *i+(y+2xz)*j+(z+2xy)*k
потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Необходимым и достаточным условием, что векторное поле — потенциальное является равенство нулю ротора
Из начального условия записываем P=P(x;y;z)=x+2yz, Q=Q(x;y;z)=y+2xz, R=R(x;y;z)=z+2xy.
По формуле находим ротор векторного поля
Делаем вывод о том, что полет является потенциальным.
Найдем потенциал u(x, y, z).
Градиент равен:
Выписываем частичные производные

а дальше интегрированием возобновляем функцию

Потенциал векторного поля принимает значение
u (x;y;z)=0,5(x²+y²+z²) +2xyz+C,
где C — произвольная константа.
Условие что векторное поле соленоидальное равносильная равенству нулю его дивергенции

Выполняем необходимые расчеты

Из записи видим, что условие не выполняется, следовательно  векторное поле не является соленоидным.

 

ЗАДАНИЕ 10.6 Проверить, является ли векторное поле F=(4x-7yz)*i+(4y-7xz)*j+(4z-7xy)*k
потенциальным и соленоидным.
Если полет потенциальное, то найти его потенциал.
Решение: Полет F является потенциальным, если его ротор равен нулю
За условием выписываем составляющие P=P(x;y;z)=4x-7yz, Q=Q(x;y;z)=4y+7xz, R=R(x;y;z)=4z-7xy
и подставляем в формулу ротора
Получили в результате нуль, можем сделать вывод, что векторное поле является потенциальным.
Потенциал u=u(x;y;z) векторного поля находим через формулу градиента :
Частичные производные, согласно начальному условию, имеют следующие значение

Повторно интегрируя их определяем функцию u(x;y;z)
Внимательно пересмотрите и разберите, в чем суть вышеприведенных формул.
Интегрированием за переменной ‘х’ мы получаем потенциал + функцию от двух других координат phi(y,z).
Найдя частичную производную потенциала за переменной ‘y’ и, приравняв к частичной производной из векторного поля, доопределяем функцию phi(y,z), остается одна неизвестная psi(z).
Для ее определения находим частичную производную потенциала по ‘z’ приравниванием к третьей компоненте векторного поля, получаем ее частичную производную.
Далее через интеграл ее доопределяем. Напоследок остается подставить все найденные функции в начальную запись.
Таким образом, потенциал поля равен 
u(x;y;z)=2(x²+y²+z²)-7xyz+C, где C — произвольная константа.
Проверка  поля F на соленоидальность равносильня нахождению дивергенции и проверке  равна ли она нулю.
Сами вычисления не сложны, стоит лишь знать или иметь под рукой формулу дивергенции

Видим, что поле не является соленоидным.

 

ЗАДАНИЕ 10.7 Проверить, или будет векторное поле F=(12x+yz)*i+(12y+xz)*j+(12z+xy)*k
потенциальным и соленоидным.
Если поле  потенциальное, то найти его потенциал.
Решение: Проверяем равен ли ротор векторного поля  нулю
Имеем функции P=P(x;y;z)=12x+yz, Q=Q(x;y;z)=12y+xz, R=R(x;y;z)=12z+xy
которые подставляем в формулу
Условие равенства нулю ротора выполняется, следовательно векторное поле является потенциальным.
Отыщем потенциал u(x;y;z).
Для этого применяем форму записи векторного поля через градиент потенциала:
Таким образом получим частичные производные

Методика нахождения потенциала векторного поля детально расписана в предыдущих задачах.
Следует отметить, что за первое приближение можно брать любую из трех частичных производных.
Выбирать порядок Вам, конечный интеграл от этого не изменится.
Формула потенциала векторного поля примет вид:
u(x;y;z)=6(x²+y²+z²)+xyz+C, где C — произвольная сталая.
Проверим, является ли векторное поле   соленоидным.
Для этого должно выполняться условие div(F)=0:
Из расчетов видим, что дивергенция не равна нуля, следовательно делаем вывод что поле не является соленоидным.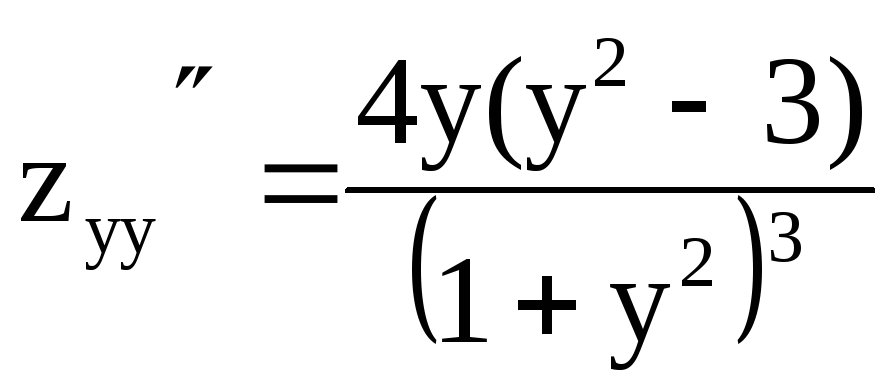

 

ЗАДАНИЕ 10.10 Проверить, является ли векторное поле F=(6x+7yz)*i+(6y+7xz)*j+(6z+7xy)*k
потенциальным и соленоидным.
Если поле  потенциальное, то найти его потенциал.
Решение: Из предыдущих примеров Вы уже возможно запомнили что сначала нужно найти ротор векторного поля.
Выписываем функции
P=P(x;y;z)=6x+7yz, Q=Q(x;y;z)=6y+7xz, R=R(x;y;z)=6z+7xy
и по формуле находим ротор
Он равен нулю, а это значит, что исследуемое векторное поле является потенциальным.

Для возобновления потенциала u(x;y;z) воспользуемся схемой, которая детально повторяется из примера в пример.
Выписываем уравнение градиента потенциала:
из него имеем частичные производные

какие используем при интегрировании и доопределении u(x;y;z)
После всех расчетов потенциал векторного поля будет равен:
u(x;y;z)=3(x²+y²+z²)+7xyz+C, где C — произвольная константа.
Осталось проверить, является ли поле F соленоидным.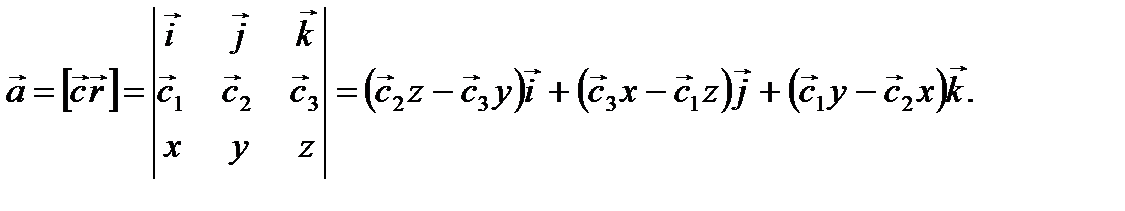
Для этого имеем условие :

Вычисления показали, что условие равенства нулю дивергенции не выполняется.
Следовательно, векторное поле не является соленоидным.

 

ЗАДАНИЕ 10.12 Проверить, будет ли векторное поле F=(3x+yz)*i+(3y+xz)*j+(3z+xy)*k
потенциальным и соленоидным.
Если поле  потенциальное, то найти его потенциал.
Решение: Вы уже должны были бы знать, чтобы  векторное поле было потенциальным, необходимо и достаточно, чтобы ротор rot(F) был равен нулю.
Выписываем функции P=P(x;y;z)=3x+yz, Q=Q(x;y;z)=3y+xz, R=R(x;y;z)=3z+xy.
и за нижеприведенной формулой находим ротор
Он равен нулю, поєтому  векторное поле F является потенциальным.
Найдем потенциал u(x;y;z).
Формула градиента потенциала имеет вид:
Из нее выписываем частные производные

а дальше через неопределенные интегралы находим потенциал
Как уже отмечалось выше, в приведенных формулах для уменьшения громоздкости опущены знаки интегрирования.
В вычислениях это допустимо, однако, если преподаватели от Вас требуют детального расписания всех промежуточных объяснений, не забывайте, что здесь мы имеем в виду неопределенные интегралы.
Окончательно записываем явный вид потенциала поля
u (x;y;z)=1,5(x²+y²+z²)+xyz+C, здесь C — любая константа.
И последняя проверка на условия, что векторное поле  является соленоидным (div (F) =0)
Видим что поле F не является соленоидным (дивергенция отличается от нуля).

 

ЗАДАНИЕ 10.21 Доказать, что векторное поле F=yz*i+xz*j+xy*k
является потенциальным и соленоидным.
Решение: Условие соответствия векторного поля F потенциальному имеет вид

Выписываем функции P=P(x;y;z)=yz, Q=Q(x;y;z)=xz, R=R(x;y;z)=xy
и ичитываем в уравнении ротора

Имеем равенство нулю ротора, таким образом проверили и доказали, что векторное поле F является потенциальным.
Чтобы найти потенциал u(x;y;z) векторного поля используем градиент:
Из входных данных задания выписываем частичные производные u(x;y;z)

Дальше интегрированиям постепенно возобновляем u(x;y;z)

Формула потенциала векторного поля приобретет вид:
u (x;y;z)=xyz+C, где C — любая сталая.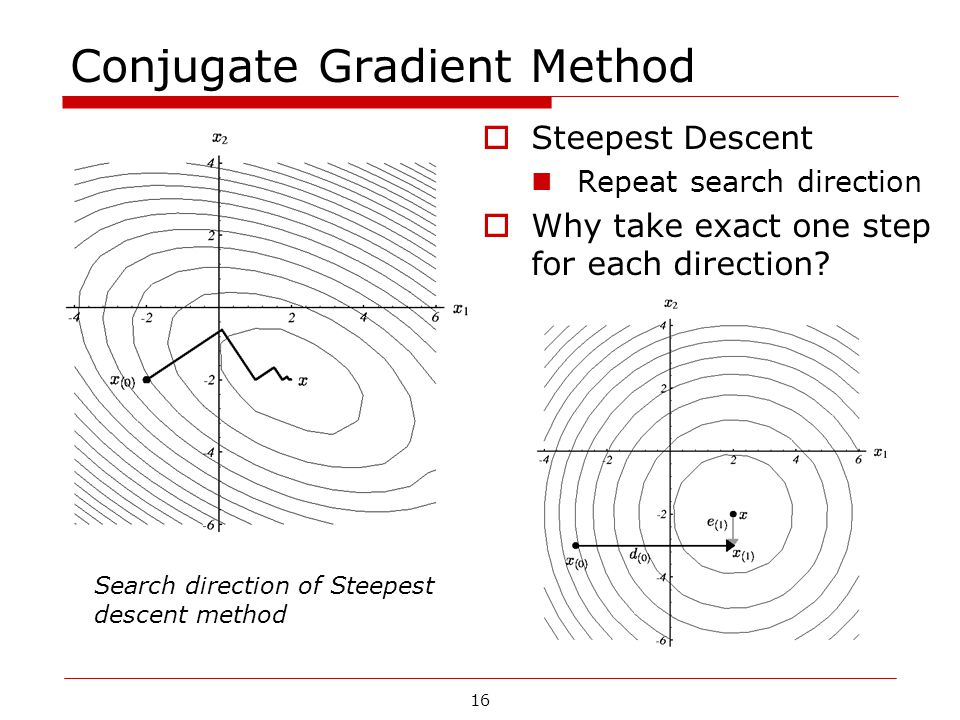
Осталось доказать, что векторное поле является соленоидным.
Для этого находим дивергенцию
и убеждаемся, что она равна нулю.
Это значит, что векторное поле является соленоидным, что и следовало досказать.

 

ЗАДАНИЕ 10.23 Проверить, является ли векторное поле F=(x²+yz)*i+(y²+xz)*j+(z²+4xy)*k
потенциальным и соленоидным.
Если поле  потенциальное, то найти его потенциал.
Решение: Проверка условия равенства нулю ротора векторного поля однозначно позволяет выяснить, является ли векторное поле потенциальным, или нет.
Из начального условия выписываем
P=P(x;y;z)=x²+yz, Q=Q(x;y;z)=y²+xz, R=R(x;y;z)=z²+xy
и применяем формулу ротора

Условие выполняется, поэтому делаем вывод что векторное поле является потенциальным.
Как найти потенциал  (x;y;z) детально описано в методике и объяснениях к расчетам.
Но снова и снова проходимся по пунктам, поскольку, как показывает практика студенты живут по правилу «выучил — сдал — забыл».

Нам нужно записать градиент поля через частные производные:
Дальше их выписываем

Потом поочередно интегрируя их и дифференцируя найденные потенциалы, находим явный вид uВ результате получим следующее уравнение потенциала
u(x;y;z)=1/3*(x³+y³+z³)+xyz+C
Проверка поля на выполнение условия div(F)=0 позволяет установить, является ли векторное поле соленоидным.
Выполняем вычисления:
Делаем вывод, что задано векторное поле F не является соленоидным.

Из рассмотренных примеров Вы могли заметить, что не каждое потенциальное поле является соленоидным.
Формул для проверки условий не так много и они детально расписаны. Считаем, что приведенный материал в полной мере позволяет Вам выполнить самостоятельно расчеты аналогичных примеров.

Оператор Лапласа в Вольфрам Альфа

Оператор Лапласа в Вольфрам Альфа

Это пост посвящен использованию оператора Лапласа в системе Вольфрам Альфа. В конце поста я дам ответ на вопрос одного из читателей блога, связанный с этой темой.

Оператор Лапласа — математическое действие применительно к скалярному или векторному полю (скалярной или векторной функции), которое чаще всего используется в электростатике, электродинамике, физике сплошных сред, при изучении равновесия мембран, пленок или же поверхностей раздела фаз с поверхностным натяжением, а также в стационарных задачах диффузии и теплопроводности.

Три формы запроса оператора Лапласа

Для математика, оператор Лапласа — это дифференциальный оператор, который определяется, как сумма вторых частных производных по координатам, и действие которого эквивалентно последовательному отысканию дивергенции и градиента функции.

Поэтому первая форма запроса, которая используется в системе Вольфрам Альфа, чтобы найти результат действия оператора Лапласа на некоторую скалярную функцию, выглядит так (порядок операторов важен):

div grad r^cos(phi)/(r^2+r*sin(phi))

Эта форма запроса оператора Лапласа применительно к векторной функции выглядит аналогично.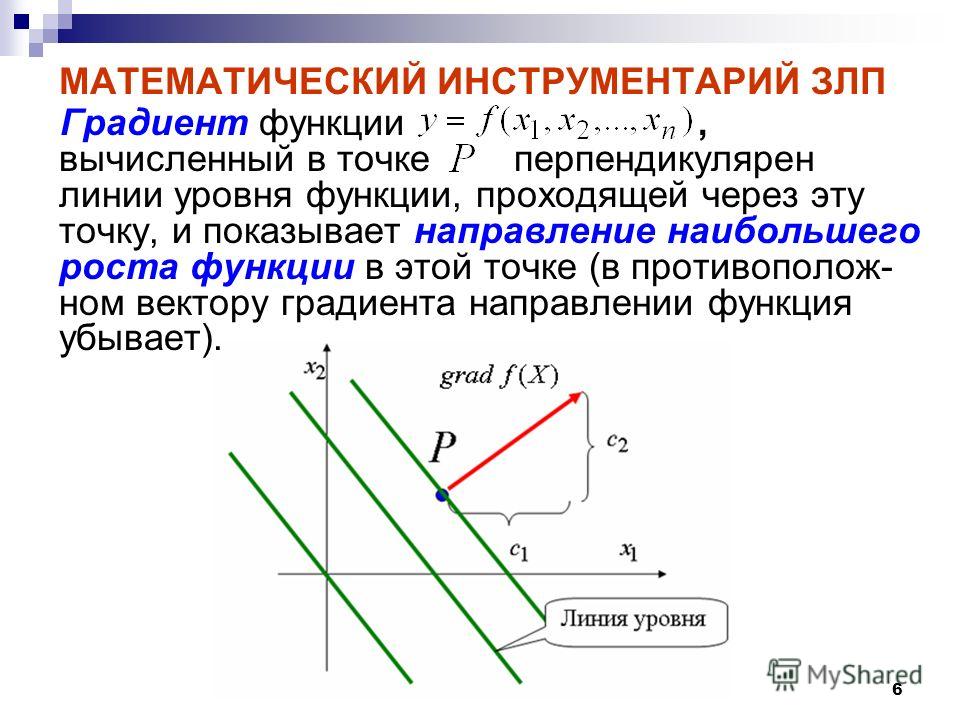 (3z)}

Кроме способов применения дифференциального оператора Лапласа, указанных выше, в системе Вольфрам Альфа имеется специальный калькулятор оператора Лапласа, который выводится по запросу:

laplace operator

Как видим, этот калькулятор не очень удобен, поскольку он приспособлен к работе только со скалярными функциями.

Оператор Лапласа, если функция задана в общем виде

Система Вольфрам Альфа позволяет применить дифференциальный оператор Лапласа даже к функциям, заданным в общем виде. Вот несколько примеров:

nabla nabla f(x)*p(y)

nabla nabla p(y)*(1-cos(2*Pi*x/a)) или div grad p(y)*(1-cos(2*Pi*x/a))

Двойной оператор Лапласа

В некоторых задачах возникает необходимость применить оператор Лапласа дважды подряд. Соответствующие запросы в системе Вольфрам Альфа имеют следующий вид (два примера):

laplace laplace p(y)*f(x)

laplace laplace p(y)*(1-cos(2*Pi*x/a))

Последний пример — это ответ на вопрос одного из любознательных читателей блога, полученный мною через форму обратной связи. Именно он стал главной причиной этого поста.

Следующее Предыдущее Главная страница

Калькулятор градиента — определите градиент функции с помощью точек

Онлайн-калькулятор градиента поможет вам найти градиент прямой линии через две и три точки. Этот калькулятор поля градиента дифференцирует данную функцию для определения градиента с пошаговыми вычислениями. Итак, читайте дальше, чтобы узнать, как рассчитать векторы градиента, используя формулы и примеры.

Что такое градиент?

В векторном исчислении градиент может относиться к производной функции. Этот термин чаще всего используется в сложных ситуациях, когда у вас есть несколько входов и только один выход. Вектор градиента хранит всю информацию о частных производных каждой переменной.

Неофициальное определение градиента (также называемого уклоном) выглядит следующим образом: Это математический метод измерения скорости подъема или спуска линии. Когда наклон увеличивается влево, линия имеет положительный градиент. Когда линия наклонена слева направо, ее градиент отрицательный. Вертикальная линия должна иметь неопределенный уклон. Символ m используется для обозначения градиента. В алгебре дифференцирование можно использовать для нахождения градиента линии или функции.

Однако онлайн-калькулятор уклона помогает найти уклон (м) или уклон между двумя точками и в декартовой координатной плоскости.

Обозначение градиента:

Градиент функции f в точке x обычно выражается как ∇f(x). Его также можно назвать:

• ∇f(x)
• Град ф
• ∂ф/∂а
• ∂_if и f_i

Обозначения градиента также обычно используются для обозначения градиентов. Уравнение градиента определяется как уникальное векторное поле, и скалярное произведение его вектора v в каждой точке x является производной f по направлению v.

$$(∇f(а)) . v = D_vf(x)$$

Декартовы координаты:

В трехмерной декартовой системе координат с евклидовой метрикой градиент, если он существует, определяется выражением:

$$∇f = ∂f /∂x a + ∂f/∂y b + ∂f/∂z c$$

Где a, b, c — стандартные единичные векторы в направлениях координат x, y и z соответственно.

Формула градиента с примером:

• Найдите любые две точки на линии, которые вы хотите исследовать, и найдите их декартовы координаты. Предположим, мы хотим определить наклон прямой, проходящей через точки (8, 4) и (13, 19).).
• Возьмите координаты первой точки и введите их в калькулятор поля градиента как \(a_1 и b_2\). Сделайте то же самое для второй точки, на этот раз \(a_2 и b_2\).
• Калькулятор градиента автоматически использует формулу градиента и вычисляет ее как (19-4)/(13-(8))=3.

Однако онлайн-калькулятор производной по направлению находит градиент и производную по направлению функции в заданной точке вектора.

Как рассчитать градиент?

Для расчета градиента находим две точки, заданные в декартовых координатах \((a_1, b_1) и (a_2, b_2)\). На реальном примере мы хотим понять взаимосвязь между ними, то есть, насколько высок излишек между ними. Это определяется по формуле градиента:

градиент = подъем/разбег

С подъемом \(= а_2-а_1, а разбег = b_2-b_1\). Подъем — это подъем/спуск второй точки относительно первой точки, а бег — расстояние между ними (по горизонтали). 93) | (x, y) = (1, 3) = (2, 27)$$

Как работает калькулятор радиации G ?

Калькулятор поля градиента вычисляет градиент линии, следуя этим инструкциям:

Ввод:

• Во-первых, выберите координаты для градиента.
• Теперь введите функцию с двумя или тремя переменными.
• Затем подставьте значения в разных полях координат.
• Чтобы увидеть ответ и расчеты, нажмите кнопку расчета.

Вывод:

• Калькулятор градиента обеспечивает стандартный ввод со знаком набла и ответом.
• Этот калькулятор вектора градиента отображает пошаговые расчеты для различения различных терминов.

Часто задаваемые вопросы:

Что такое градиент векторного поля?

Градиент функции представляет собой векторное поле. Он получается применением векторного оператора V к скалярной функции f(x, y). Это векторное поле называется градиентным (или консервативным) векторным полем.

Существует ли векторный градиент?

Градиент вектора — это тензор, который говорит нам, как векторное поле изменяется в любом направлении. Мы можем выразить градиент вектора как его компонентную матрицу по отношению к векторному полю.

Что такое градиент скалярной функции?

Градиент является скалярной функцией. Величина градиента равна максимальной скорости изменения скалярного поля, а его направление соответствует направлению максимального изменения скалярной функции.

Является ли градиент вектором строки или столбца?

Градиент по-прежнему является вектором. Он указывает направление и величину самой быстрой скорости изменения.

Что такое символ градиента потенциала?

Это выражение является важной особенностью каждого консервативного векторного поля F, т. е. F имеет соответствующий потенциал ϕ. Это означает, что кривизна векторного поля, представленная ∇×, исчезает.

Вывод:

Используйте этот онлайн-калькулятор градиента для вычисления градиентов (наклона) заданной функции в различных точках. Нет необходимости находить градиент с помощью руки и графика, так как это увеличивает неопределенность. Просто воспользуйтесь нашим бесплатным калькулятором, который выполняет точные расчеты градиента.

Ссылка:

Из источника Википедии: Мотивация, Обозначение, Декартовы координаты, Цилиндрические и сферические координаты, Общие координаты, Градиент и производная или дифференциал.

Из источника Академии Хана: Скалярные многомерные функции, два измерения, три измерения, Интерпретация градиента, градиент перпендикулярен контурным линиям.

Из источника Revision Math: Градиенты и графики, Нахождение градиента прямолинейного графика, Нахождение градиента кривой, Параллельные линии, Перпендикулярные линии (ВЫСОКИЙ УРОВЕНЬ).

Из источника лучшего пояснения: Векторное исчисление: понимание градиента, свойства градиента, направление наибольшего увеличения, градиент перпендикулярно линиям.

 

Калькулятор градиента линии, проходящей через две точки

Создано Maciej Kowalski, кандидатом докторских наук

Отредактировано Bogna Szyk и Jack Bowater

Последнее обновление: 05 декабря 2021 г.

Что такое градиент2: 900?

Определение градиента

Как рассчитать градиент?

Формула градиента: пример применения

Распространенные заблуждения и ошибки

Добро пожаловать в калькулятор градиента , где у вас будет возможность узнать, как рассчитать градиент линии, проходящей через две точки. « Что такое градиент? » спросите вы. Ну, вы когда-нибудь смотрели на гору и говорили себе: « Ого, эта гора довольно крутая, но не такая крутая, как близлежащая! »? И если такого рода вопрос заставил вас задаться вопросом, как сравнить их крутизну, вы попали в нужное место !

Если вы хотите найти градиент нелинейной функции, рекомендуем воспользоваться калькулятором средней скорости изменения.

Что такое градиент?

Прежде чем мы рассмотрим определение градиента, давайте вернемся к нашей горной сцене и абсолютно важному вопросу о крутизне.

Допустим, вы спускаетесь со склона на лыжах, когда вас настигает Большой вопрос . Вы останавливаетесь и думаете об этом, прежде чем идти дальше. Как мы упоминали выше, все, что вам нужно, это две точки, чтобы найти градиент , так почему бы не быть немного эгоцентричным и выбрать себя как… ну, центр , то есть точка (x₁,y₁) = (0,0) на плоскости.

Теперь нам осталось найти вторую точку , (x₂,y₂) , вверх или вниз по склону. Вы оглядываетесь вокруг, чтобы найти какое-нибудь особенно густое дерево или хорошенькую юную лыжницу. Или старый вонючий, если уж на то пошло, я не сужу.

Скажите дереву или лыжнику стоять на месте, пока вы используете свою удобную линейку (которую вы всегда носите с собой, конечно) и посчитаете насколько они выше/ниже от вас (это будет y₂ ) и как далеко они от вас (это будет x₂ ). Не забудьте считать расстояние между вами двумя по горизонтали, а не параллельно склону . И вот оно! Отношение y₂ / x₂ — это ваш градиент или крутизна горы в этой точке.

За то, что задержитесь, пока проводите быстрый эксперимент, купите этому лыжнику горячего шоколада или обнимите дерево. Они заслуживают столько же.

Определение градиента

Неофициальное определение градиента (также известного как наклон) выглядит следующим образом: это математический способ измерения скорости подъема или падения линии . Думайте об этом как о числе, которое вы присваиваете холму, дороге, тропинке и т. д., которое говорит вам, сколько усилий вы должны приложить, чтобы проехать его. Если вы идете в гору , вам придется прилагать усилия, чтобы достичь пика, поэтому необходимая энергия (т. е. градиент) велика. Если вы идете под гору , вам даже не нужно крутить педали, чтобы набрать скорость, так что усилие, по сути, отрицательное. И , если вы находитесь на ровной поверхности , это не помогает и не усложняет, поэтому оно нейтрально или имеет нулевой градиент.

А какой если перед вами вертикальный склон ? Ну, не всегда ясно, хотите ли вы упасть (что не требует усилий) или взобраться по нему. Следовательно, в этом случае градиент не определен .

Как рассчитать уклон?

Для расчета градиента найдем две точки . Обозначим эти точки декартовыми координатами (x₁,y₁) и (x₂,y₂) соответственно. Это также обозначение, используемое в калькуляторе. Обратите внимание, что мы использовали те же символы в реальном примере. Мы хотим увидеть, как они соотносятся друг с другом, то есть каково между ними соотношение подъема и пробега. Описывается формулой градиента :

градиент = подъем / бег

с рост = у₂ - у₁ и пробег = х₂ - х₁ .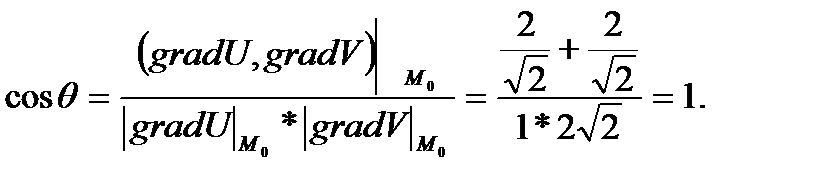 Подъем — насколько выше/ниже вторая точка от первой, а пробег — насколько далеко (по горизонтали) они друг от друга.

Формула градиента: пример применения

Теперь, когда мы знаем определение градиента, пришло время увидеть калькулятор градиента в действии и пройти его вместе, шаг за шагом:

1. Найти две произвольные точки на линию, которую вы хотите изучить, и найти их декартовы координаты. Допустим, мы хотим вычислить градиент линии, проходящей через точки (-2,1) и (3,11) .
2. Возьмите координаты первой точки и введите их в калькулятор как x₁ и y₁ .
3. Проделайте то же самое со второй точкой, на этот раз как x₂ и y₂ .
4. Калькулятор автоматически использует формулу градиента и считает ее равной (11 - 1) / (3 - (-2)) = 2 .
5. Наслаждайтесь знанием того, какой крутой склон у вашей линии, и расскажите об этом всем своим друзьям!

Распространенные заблуждения и ошибки

Вы можете спросить себя: » Подожди, кажется, я видел это где-то еще. Не происходит ли чего-то подобного при подсчете наклона или подъема над пробегом? » Ты абсолютно прав. Все эти три понятия: градиент, уклон и подъем над пробегом описывают одно и то же , и не волнуйтесь, между ними нет никакой разницы.

Вы также можете задаться вопросом, насколько крутой крутой ; то есть, что говорит нам цифра 2 в приведенном выше примере. Это много или нет? Будет ли симпатичная лыжница впечатлена этим числом? Ну, все дело в точке зрения , и одни могут сказать одно, а другие противоположное. В качестве точки отсчета вы должны помнить, что линия, параллельная горизонту, здесь считается нейтральной, так как градиент равен нулю. Когда она поднимается (или опускается), она все больше становится похожей на линию, перпендикулярную горизонту, где наклон уходит в бесконечность, когда она поднимается (или минус бесконечность, когда она падает).

Мацей Ковальский, кандидат наук

Координаты первой точки

координаты второй точки

Результат

Градиент

Проверьте 38 аналогичные калькуляторы геометрии координат 📈

Средняя скорость изменений. используется для вычисления производной по направлению функции с точки зрения двух переменных x и y в заданной точке.

Производная функции — это скорость изменения функции. D прямолинейная производная обычно определяется как скорость изменения функции в любом заданном направлении .

Производные по направлению имеют широкий спектр применения в реальной жизни, поскольку входные данные постоянно меняются. Калькулятор также вычисляет вектор градиента заданной функции. Градиент определяет наклон функции.

Что такое калькулятор производной по направлению?

Калькулятор производной по направлению — это онлайн-калькулятор, который находит производную по направлению функции двух переменных f(x, y) в точке (x, y) вдоль единичного вектора U, а также выводит градиент grad f( x,y) входной функции.

Направление определяется единичным вектором:

\[   \overrightarrow{U} = (U_{1})\hat{e_{x}} + (U_{2})\hat{e_{y} }   \]

U1 указывает направление по оси x , а U2 указывает направление по оси y .

Калькулятор вычисляет производную по направлению функции в заданной точке . Координата x указывает точку на оси x, а координата y указывает точку на оси y, для которой необходимо вычислить производную по направлению.

Он также вычисляет градиент функции. Градиент функции — это скорость изменения или наклон функции.

Для функции с двумя переменными нам нужно определить скорость изменения функции f по осям x и y. Это дает понятие частной производной.

Частная производная по оси x представляет собой скорость изменения функции f(x, y) в направлении x, а частная производная по оси y представляет собой скорость изменения функции f(x , у) в направлении у. 9{(0,1)} \]

Частная производная отличается от производной по направлению .

Частная производная дает мгновенную скорость изменения функции только вдоль трех перпендикулярных осей, которые являются осью x, осью y и осью z в ​​заданной точке.

С другой стороны, производная по направлению дает мгновенную скорость изменения в любом направлении в определенной точке.

Как пользоваться калькулятором производной по направлению?

92.y    \]

по умолчанию.

Шаг 2

Введите часть единичного вектора, показывающую направление вдоль оси x. Это U1 в окне ввода калькулятора. Калькулятор показывает U1 как $(\dfrac{3}{5})$ по умолчанию.

Шаг 3

Введите значение U2, которое является частью единичного вектора, показывающего направление вдоль оси Y. Калькулятор отображает U2 как $(\dfrac{4}{5})$ по умолчанию.

Шаг 4

Калькулятору также требуется точка (x,y), для которой должны быть определены производная по направлению и уклон.

Введите x-координату в окно ввода калькулятора, которое показывает положение точки по оси x. Координата x по умолчанию равна 1.

Шаг 5

Введите координату y, , которая является положением точки вдоль оси y, для которой пользователю требуется производная по направлению. Координата Y по умолчанию равна 2.

Шаг 6

Пользователь должен нажать Отправить  после ввода всех необходимых входных данных для результатов.

Перед пользователем открывается окно вывода , которое показывает следующие окна. Если введенные пользователем данные неверны или неполны, калькулятор выдает сообщение «Недействительный ввод, попробуйте еще раз».

Интерпретация ввода

Калькулятор интерпретирует ввод и отображает его в этом окне. Во-первых, он показывает функцию f(x,y), для которой требуется производная по направлению.

Затем показывает направление (U1, U2) и точку (x -координата , y -координата ), которую ввел пользователь.

Результат

В этом окне показана результирующая производная по направлению после помещения точки (координата x, координата y) в функцию производной по направлению.

Он показывает уравнение производной по направлению в открытой форме, которое показывает значения частных производных относительно x и y.

Градиент

В этом окне отображается градиент f (x,y) входной функции f. Он также отображает x — первую декартову координату и y — вторую декартову координату.

Кроме того,

\[   \frac{\partial f(x,y)}{\partial x}   \]

в уравнении градиента представляет собой частную производную f(x,y) по x и

\[   \frac{\partial f(x,y)}{\partial y}   \]

представляет собой частную производную f(x,y) по y.

Решенные примеры

Следующие примеры решаются с помощью калькулятора производной по направлению.

Пример 1

Вычислить производную по направлению заданной функции: 92   \]

В точке (1 , 2)

Где,

\[    U_{1} = \frac{1}{2}   \]

и

\[    U_{2} = \frac {\sqrt{3}}{2}   \]

Кроме того, оцените вектор градиента данной функции.

Решение

Калькулятор отображает f(x,y), что является заданной функцией.

Также показывает направление и точку (1,2), в которой требуется производная по направлению. Это показано в окне интерпретации ввода выходных данных калькулятора. 9где {1}{4}   \]

Кроме того, найдите вектор градиента функции.

Решение

Калькулятор отображает заданную функцию, направление ( $\dfrac{1}{2}$, $\dfrac{1}{4}$ ) и точку (3,2), для которой производная по направлению требуется для. Окно интерпретации ввода показывает этот результат.

Калькулятор вычисляет производную по направлению и показывает результат следующим образом: 92  \]

В точке (1 , 3) ​​

Где,

\[    U_{1} = \frac{1}{3}   \]

и

\[    U_{2} = \frac {1}{2}   \]

Кроме того, найдите вектор градиента функции.

Решение

Калькулятор отображает функцию ввода, направление (U1, U2) и точку (3,2).

Окно интерпретации ввода калькулятора показывает эти характеристики.

Результат для производной по направлению: 9{(1,0)}(1,3) = 2 )   \]

Затем калькулятор вычисляет вектор градиента входной функции f.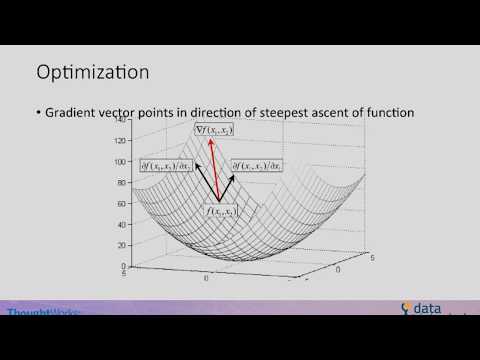

Но сначала для градиента вычисляются частные производные функции f относительно x и y.

Для частной производной f(x,y) по x:

\[    \frac{\partial f(x,y)}{\partial x} = 2x  \]

Для частной производной f(x,y) относительно y:

\[    \frac{\partial f(x,y)}{\partial y} = – 2y   \]

Градиент функции:

\[    grad f ( x, y ) =  \Big\{ \frac{\partial f(x,y)}{\partial x} = 2x \Big\} .e_{ x} + \Big\{ \frac{\partial f(x,y)}{\partial y} = – 2y \Big\} .e_{y}   \]

Где $e_{x}$ и $e_y $ — единичные векторы с величиной 1, указывающие в направлении оси x и оси y соответственно.

                                      Список математических калькуляторов

Калькулятор производной по направлению с шагами и решением

Калькулятор производной по направлению

Производную по направлению и градиент функции в определенной точке вектора можно рассчитать с помощью онлайн-калькулятора производной с несколькими переменными. Этот бесплатный векторный калькулятор градиента также покажет вам, как шаг за шагом вычислять определенные точки. Давайте рассмотрим формулы и примеры, чтобы узнать, как найти производные по направлению.

Направление многомерного дифференциального уравнения заданного вектора v в конкретной позиции x интуитивно выводится в математике. Это мгновенная скорость изменения неявной функции, движущейся по x со скоростью v. Все остальные координаты, с другой стороны, остаются постоянными.

Но не путайте производную по направлению и неявную производную, так как они оба выполняются над неявной функцией. Правила неявного дифференцирования отличны от производной по направлению. Вы можете точно рассчитать неявное дифференцирование, используя калькулятор dy/dx с шагами.

Связанный: Найдите многомерные производные с помощью калькулятора вектора направления на этом веб-сайте.

Обозначения, используемые Калькулятором производных по направлениям

Пусть f — кривая с касательным вектором v в заданном месте. Любое из следующего может быть использовано в калькуляторе производной по направлению, чтобы найти функцию f для p:

$$ ∇_p \; f(x) $$ $$ f_p'(x) $$ $$ D_p \; f(x) $$ $$ D \; е (х) \; (р) $$ $$ ∇ \; f(x) $$

Калькулятор вектора направления использует эти обозначения для вычисления производной функции.

$$ ∇_v f(x) \;=\; лим \; f(x+hv) \;-\; \frac{f(x)}{h} $$

Связанный: Также найдите калькулятор уравнения нормальной линии для решения уравнения прямой.

Как работает калькулятор производной по направлению?

Выполните следующие действия, чтобы получить точки градиента и производную по направлению заданной функции с помощью этого онлайн-калькулятора вектора градиента:

Введите:

Вот несколько простых шагов для правильного ввода значений в калькулятор вектора направления.

• Чтобы вычислить производную по направлению, введите функцию, для которой требуется производная.
• Теперь выберите f(x, y) или f(x, y, z).
• Введите значение для U1 и U2.
• Введите значение для координат x и y.
• Нажмите кнопку расчета, чтобы получить результат калькулятора многомерной производной.

Выход:

Калькулятор производной по направлению вычисляет производную функции в направлении двух векторов, поэтому он также известен как калькулятор векторной производной. Градиент вычисляется путем взятия производной для каждой функции переменной, введенной в калькулятор вектора направления.

Решенный пример производной по направлению:

Найдите производную по направлению от x2y + xy2 относительно x и y, где U1= 2 и U2 = -3.

Решение:

$$ \frac{36}{13} \; \приблизительно\; 9.9846 $$

Вывод:

Так как калькулятор частных производных с шагами используется для оценки наклона только в одном заданном направлении переменной, производные и градиенты рассчитываются в трех измерениях с использованием онлайн-калькулятора производных с шагами, который называется калькулятором производной по направлению.

Для нахождения производной по направлению и векторов требуется миллиметровая бумага, но это также повышает риск ошибок. Но калькулятор векторной производной облегчает нам задачу, теперь мы получаем производные по направлениям, используем этот бесплатный онлайн-калькулятор вектора градиента, который обеспечивает пошаговое решение со 100-процентной точностью.

Если вы пытаетесь найти линейную аппроксимацию заданной функции, попробуйте калькулятор дифференциальной аппроксимации. Онлайн-инструмент мгновенно найдет линейное приближение шаг за шагом вместе с графиком и возможными промежуточными шагами.

Часто задаваемые вопросы:

Какое значение имеет происхождение направления?

Ответ: Направление многомерной дифференциальной функции заданного вектора v в конкретной позиции x интуитивно выводится в математике. Это мгновенная скорость изменения функции, движущейся в точке x со скоростью v. Вывод Гато является частным случаем направленного выведения.

Различать производную по направлению и вторую производную?

Ответ: Скорость изменения функции в определенном направлении называется производной по направлению. Производную по направлению можно рассчитать, используя градиент в формуле. Но вторая производная есть производная от производной. Он измеряет мгновенную скорость изменения первой производной функции. Для такого расчета используйте онлайн-калькулятор производных высших порядков с шагами для точного расчета.

Что такое градиент направления?

Ответ: Направление градиента — это направление, в котором быстро возрастает функция p, где величина градиента — скорость роста, и если градиент функции в точке «p» не равен нулю.

Найти производную по направлению от x2y + xy2+ z2 относительно x и y, где U1= 2, U2 = -3 и U3= -1 координата 2, -4, 3.

Ответ:

$$ 15 \sqrt{\frac{2}{7}} \примерно 8,01874 $$

Могут ли производные по направлению быть отрицательными?

Ответ: Производная по направлению может быть положительной, отрицательной или нулевой, так как это изменение направления.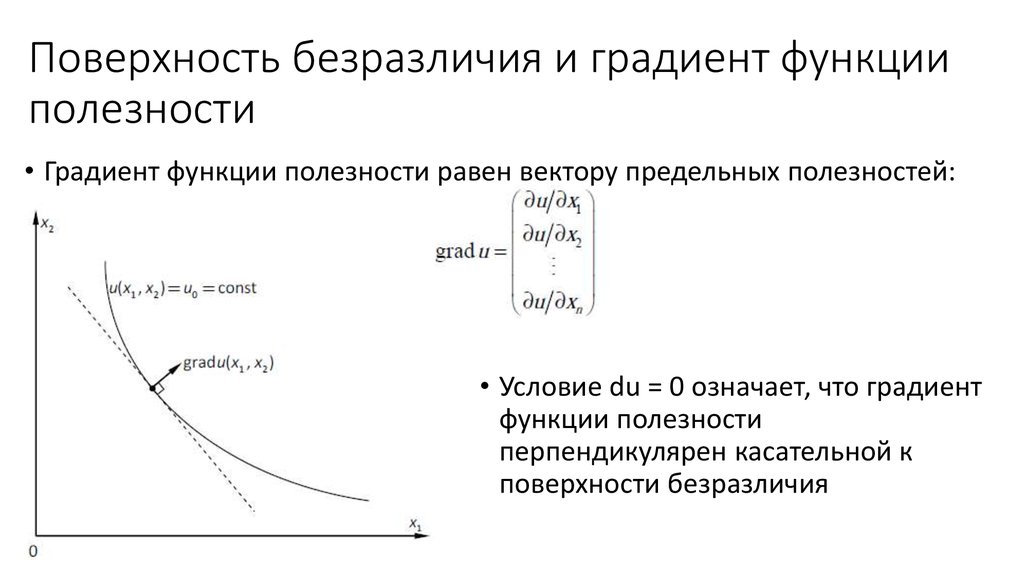 Функция падает в этом направлении или растет в противоположном направлении, если производная по направлению отрицательна.

Алан Уокер

Последнее обновление 26 августа, 2022

Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.

Вычисление градиентного спуска вручную | Чи-Фэн Ван

Часть 4 книги «Шаг за шагом: математика нейронных сетей»

Заглавное изображение: Источник

Вот наша проблема. У нас есть нейронная сеть только с одним слоем (для простоты) и функцией потерь. Этот один слой представляет собой простой полностью связанный слой только с одним нейроном, многочисленными весами 90 223 w₁, w₂, w₃ 90 224 …, смещением 90 223 b 90 224 и активацией ReLU. Наша функция потерь — это обычно используемая среднеквадратическая ошибка (MSE). Зная нашу сеть и нашу функцию потерь, как мы можем настроить веса и смещения, чтобы минимизировать потери?

В части 1 мы узнали, что нам нужно найти наклон нашей функции потерь (или затрат), чтобы минимизировать ее. Мы обнаружили, что наша функция стоимости:

Изображение 1: Функция стоимости

Во второй части мы научились находить частную производную. Это важно, потому что в этой функции есть более одного параметра (переменной), которые мы можем настроить. Нам нужно найти производную функции стоимости как по весам, так и по смещениям, и частные производные вступают в игру.

В части 3 мы научились находить производные векторных уравнений. И веса, и смещения в нашей функции стоимости являются векторами, поэтому очень важно научиться вычислять производную функций, включающих векторы.

Теперь у нас наконец есть все инструменты, необходимые для нахождения производной (наклона) нашей функции стоимости!

К этой проблеме нужно подходить поэтапно. Давайте сначала найдем градиент одного нейрона относительно весов и смещений.

Функция нашего нейрона (вместе с активацией):

Изображение 2: Наша нейронная функция

Где она принимает x в качестве входных данных, умножает их на вес w и добавляет смещение b .

Эта функция представляет собой комбинацию других функций. Если мы допустим f( x )= w∙x +b, и g(x)=max(0,x) , то наша функция равна нейрон( x

0

)=g(f( x )) . Мы можем использовать правило цепочки векторов, чтобы найти производную этой композиции функций!

Производная нашего нейрона выглядит просто:

Изображение 3: Производная функции нашего нейрона по правилу векторной цепочки

Где z=f( x )= w∙x +b .

Эта производная состоит из двух частей: часть z относительно w и часть нейрона (z) относительно z .

Какова частная производная z относительно

w ?

Есть две части z : w∙x и +b . Давайте сначала посмотрим на w∙x .

w∙x , или скалярное произведение, на самом деле просто сумма поэлементного умножения каждого элемента в векторе. Другими словами:

Изображение 4: Расширенная версия w∙x или скалярное произведение

. Это снова композиция функций, поэтому мы можем записать v = w ⊗ x и u= сумма( против ). Мы пытаемся найти производную от u относительно w . Мы узнали об обеих этих функциях — поэлементном умножении и суммировании — ранее, в части 3. Их производные таковы:

Изображение 5: Производная u по v и производная v по w; где u=sum( w ⊗ x )

(Вернитесь и просмотрите их, если не помните, как они получены)

Следовательно, по правилу векторной цепочки:

Изображение 6: Производная от u по w

Вот и все! Теперь давайте найдем производную от z= u+b , где u= w∙x , относительно весов w и смещения b. Помните, что производная функции по переменной, не входящей в эту функцию, равна нулю, поэтому:

Изображение 7: Производная от z по весам и смещениям, где z=sum( w ⊗ x ) +b

Вот оно! Эти два являются производными от u как по весам, так и по смещениям.

Чему равна частная производная нейрона(z) по z?

Нейрон(z)=max(0,z)=max(0, sum( w ⊗ x )+b).

Функция max(0,z) просто обрабатывает все отрицательные значения как 0. Таким образом, график будет выглядеть примерно так:

Изображение 8: Max(0,z) // Источник

Взглянув на этот график, мы сразу видим, что производная является кусочной функцией: она равна 0 для всех значений z, меньших или равных 0, и 1 для всех значений z больше 0, или:

Изображение 9: Производная от max(0,z)

Теперь, когда у нас есть обе части, мы можем перемножить их вместе, чтобы получить производную нашего нейрона:

Изображение 10: Производная по весам нашего нейрона: max( 0, sum( w ⊗ x )+b)

И подставить z= w∙x +b обратно в:

Изображение 11: Подставить 90 3

w0009

Вуаля! У нас есть производная для нейрона по его весам! Точно так же мы можем использовать те же шаги для смещения:

Изображение 12: Производная нашего нейрона по отношению к смещению

Вот и все! Теперь у нас есть градиент нейрона в нашей нейронной сети!

Наша функция потерь, определенная в Части 1, имеет вид:

Изображение 13: Функция потерь

Мы можем сразу определить это как набор функций, для которых требуется цепное правило. Мы определим наши промежуточные переменные как:

Изображение 14: Промежуточные переменные для функции потерь

*Обратите внимание, u и v здесь отличаются от u и v , использованные в предыдущем разделе.

Давайте сначала вычислим градиент относительно весов w .

Градиент относительно весов

u — это просто наша нейронная функция, которую мы решили ранее. Следовательно:

Изображение 15: Производная от u= max(0, sum( w ⊗ x )+b) относительно весов

v(y,u) просто

2 2 y-u4 . Следовательно, мы можем найти его производную (по w ) используя распределительное свойство и подставляя в производную u :

Изображение 16: Производная v=y-u по весам

Наконец, нам нужно найти производную всей функции стоимости по отношению к ш . Используя цепное правило, мы знаем, что:

Изображение 17: Производная функции стоимости

Давайте найдем первую часть этого уравнения, часть C(v) по отношению к v первая:

Изображение 18: Производная функция стоимости относительно v

Из приведенного выше (Изображение 16 ) мы знаем производную v по отношению к w . Чтобы найти часть C(v), мы перемножаем две производные вместе:

Рисунок 19: Производная функции стоимости по отношению к w

Теперь замените y-u на v и max(0, w∙x + b) вместо u :

Изображение 20: Производная функции стоимости по отношению к w

Функция 0223 max находится во второй строке нашей кусочной функции, где w∙x + b больше 0, функция max всегда будет просто выводить значение w∙x + b . :

Изображение 21: Производная функции стоимости по отношению к w

Наконец, мы можем переместить суммирование внутрь нашей кусочной функции и немного привести ее в порядок:

Изображение 22: Производная функции стоимости по отношению к w

Это Это! У нас есть производная по весам! Однако что это значит?

w∙x + b-y можно интерпретировать как член ошибки — разницу между предсказанным выходом нейронной сети и фактическим выходом. Если мы назовем этот член ошибки ei, наша окончательная производная будет:

Изображение 23: Производная функции стоимости по отношению к w , представленная членом ошибки

Здесь, чем больше ошибка, тем выше производная. Другими словами, производная представляет собой наклон или то, насколько мы должны сместить наши веса, чтобы минимизировать нашу ошибку. Если наша нейронная сеть только начала обучение и имеет очень низкую точность, ошибка будет высокой, а значит, и производная тоже будет большой. Поэтому нам придется сделать большой шаг, чтобы минимизировать нашу ошибку.

Вы могли заметить, что этот градиент указывает в сторону увеличения стоимости, то есть мы не можем добавить градиент к нашим текущим весам — это только увеличит ошибку и отодвинет нас на шаг от локального минимума. Поэтому мы должны вычесть наши текущие веса с производной, чтобы приблизиться на один шаг к минимизации нашей функции потерь:

Изображение 24: Функция градиентного спуска

Здесь η представляет скорость обучения, которую мы, как программисты, можем установить. Чем больше скорость обучения, тем больше шаг. Однако установка слишком большой скорости обучения может привести к слишком большому шагу и отклонению от локального минимума. Дополнительные сведения см. в этой статье о градиентном спуске и в этой статье о настройке скорости обучения.

Градиент относительно смещения

И снова у нас есть наши промежуточные переменные:

Изображение 25: Промежуточные переменные для функции потерь

У нас также есть значение производной u относительно смещения, которое мы рассчитали ранее:

Изображение 26: Производная u по смещению.

Точно так же мы можем найти производную v по отношению к b , используя распределительное свойство и подставив в производную u :

Изображение 27: Производная v по отношению к смещению

Опять же, мы можем использовать правило цепочки векторов, чтобы найти производную C :

Изображение 28: Производная функции стоимости по отношению к смещению

производная C относительно v идентична той, которую мы рассчитали для весов:

Изображение 29: Производная функции стоимости относительно v b , и подставив в y-u вместо v и max(0, w∙x + b) вместо u , мы получим: к смещению

Еще раз, поскольку во второй строке явно указано, что w∙x + b >0, функция max всегда будет просто значением w∙x + b.

Изображение 31: Производная функции стоимости относительно смещения

Как и прежде, мы можем заменить член ошибки, e = w∙x + b-y :

image 32: Производная функции стоимости относительно смещения, представленная членом ошибки

Так же, как производная с относительно весов величина этого градиента также пропорциональна ошибке: чем больше ошибка, тем больший шаг к локальному минимуму мы должны сделать. Это также указывает на направление более высокой стоимости, а это означает, что мы должны вычесть градиент из нашего текущего значения, чтобы приблизиться на один шаг к локальному минимуму:

Изображение 33: Функция градиентного спуска для смещения

Поздравляем с окончанием этой статьи! Скорее всего, это было нелегкое чтение, но вы упорствовали до конца и преуспели в выполнении градиентного спуска вручную!

Как я уже говорил в первой части этой серии, без понимания лежащих в основе математики и вычислений каждой строки кода мы не можем по-настоящему понять, что на самом деле означает «создание нейронной сети», или оценить сложные тонкости, которые поддерживают каждую функцию, которая мы пишем.

Я надеюсь, что эти уравнения и мои объяснения имеют смысл и помогли вам лучше понять эти расчеты. Если у вас есть какие-либо вопросы или предложения, не стесняйтесь оставлять комментарии ниже!

Если вы еще этого не сделали, прочтите части 1, 2 и 3 здесь:

• Часть 1. Введение
• Часть 2. Частные производные
• Часть 3. Векторное исчисление

Загрузите исходную статью здесь.

Если вам понравилась эта статья, не забудьте поставить хлопки! Оставьте комментарий ниже, если у вас есть какие-либо вопросы или предложения 🙂

Нахождение потенциальной функции для консервативных векторных полей

Процесс нахождения потенциальной функции консервативного векторного поля представляет собой многоэтапную процедуру, которая включает как интегрирование, так и дифференцирование, при этом особое внимание уделяется переменным, которые вы интегрируете или дифференцируете. уважение к. По этой причине, учитывая векторное поле $\dlvf$, мы рекомендуем сначала определить, что что $\dlvf$ действительно консервативен до начала этой процедуры. 2x +g(y)\right)\\ &= \sin x + 2yx + \diff{g}{y}(y). \конец{выравнивание*} Сравнивая это с условием \eqref{cond2}, нам повезло. Мы можем легко заставить эту $f(x,y)$ удовлетворять условию \eqref{cond2}, пока в качестве \начать{выравнивать*} \diff{g}{y}(y)=-2y. \конец{выравнивание*} Если бы векторное поле $\dlvf$ зависело от пути, мы бы имели обнаружил невозможность одновременного выполнения условия \eqref{cond1} и условия \eqref{cond2}. Мы бы столкнулись с проблемой в этом точку, так как мы обнаружили бы, что $\diff{g}{y}$ должна быть функцией $x$, а также $y$. Поскольку $\diff{g}{y}$ является функцией только $y$, наш расчет подтверждает, что $\dlvf$ является консервативным. 92, \sin x + 2xy -2y) = \dlvf(x,y). \конец{выравнивание*}

Имея это в виду, вычисляем интеграл \начать{выравнивать*} \dlint \конец{выравнивание*} прост, независимо от того, какой путь $\dlc$. Мы можем применить градиентная теорема сделать вывод, что интеграл просто $f(\vc{q})-f(\vc{p})$, где $\vc{p}$ — начальная точка, а $\vc{q}$ — конечная точка $\dlc$.